Avoidable deaths and random variation in patients' survival

Abstract

Background:

Random error in the numbers of avoidable deaths among cancer patients has not been considered in earlier studies.

Methods:

Methods to obtain valid confidence intervals (CIs) for numbers of avoidable deaths were developed. The excess mortality rates were estimated for patients diagnosed with colon cancer in five cancer control regions in Finland during 2000–2007 using a relative survival regression model. Numbers of avoidable deaths due to colon cancer and other causes, respectively, were estimated in different scenarios.

Results:

Altogether, 4139 and 1335 out of 10 772 patients under 90 years at diagnosis were estimated to have died due to colon cancer and other causes, respectively, during the first 5 years after diagnosis. If all the patients had shared the relative survival of the largest cancer control region to which the country capital belongs, the estimated number of avoidable deaths would have been 146 (95% CI 3–290).

Conclusion:

Random error in numbers of avoidable deaths, often substantial, can be quantified by realistic error margins, based on appropriate statistical methods.

The numbers of avoidable deaths within a given time since diagnosis have been estimated to describe what could have been achieved in the presence of competing mortality, if the same high level of cancer survival had been shared by different countries (Abdel-Rahman et al, 2009; Møller et al, 2010; Lambert et al, 2011; Holmberg et al, 2012), or by all regions, social classes (Dickman et al, 1997) or educational groups (Pokhrel et al, 2010) within one country. These estimates are subject to random error that was not considered in these papers. Confidence intervals (CIs) for the numbers of avoidable deaths are important, because, apart from real differences, a substantial fraction of the total variation in regional survival figures may be caused by chance, especially if the groups compared are small.

The aim of this study was to derive a method computing valid CIs for the numbers and proportions of avoidable deaths. We assessed, how many deaths in patients diagnosed with colon cancer in the five cancer control regions in Finland in 2000–2007 would have been avoided in the first 5 years after diagnosis, if all the regions had shared either the same relative survival as that in the most populated region where Helsinki, the capital of Finland is located, or the same expected survival as that in the region with the lowest background mortality.

Materials and methods

Patients diagnosed with colon cancer at the age range of 0–89 years in Finland during 2000–2007 and reported to the Finnish Cancer Registry were followed up for death from any cause until the end of 2007. In Finland, cancer care is organised by five cancer control regions (regional populations 0.7–1.8 million), each of which is led by a university central hospital providing advanced tertiary care for the patients of its region (Seppä et al, 2010).

Regional differences in the patients’ survival were described by the 5-year relative survival ratios obtained by dividing the observed survival proportions of the patients by the expected ones in a comparable reference population. This is accomplished by dividing the observed hazard of death of the patients into the expected hazard and the excess hazard which correspond to the expected and the relative survival, respectively. These measures were standardised for age and sex (Pokhrel and Hakulinen, 2008; Hakulinen et al, 2011) and their estimation is explained in detail in Supplementary Appendix. The methods of relative survival are preferred by population-based cancer registries in estimating the cause-specific net survival of the patients as they do not rely on cause of death information (Ries et al, 2007; Coleman et al, 2008; Sant et al, 2009).

The predicted numbers of deaths due to colon cancer and other causes, respectively, during the first 5 years after diagnosis were estimated for each region using the theory of competing risks of death (Chiang, 1968) the excess hazard from colon cancer being modelled by a relative survival regression model (Dickman et al, 2004). The numbers and proportions of avoidable deaths were estimated in three scenarios. In scenario A, the regional excess hazards (also the relative survival ratios) stratified by sex, age group at diagnosis and follow-up time interval were assumed to equal those in the most populated cancer control region, to which Helsinki belongs (region 1). In scenario B, the regional expected hazards (also the expected survival proportions) stratified by sex, age year and calendar year were assumed to equal those in region 2, where the background mortality was the lowest. In scenario AB, the assumptions of scenarios A and B were simultaneously enforced.

The estimation of the numbers of deaths and the numbers and proportions of avoidable deaths is described in Supplementary Appendix. The variances for these estimators were approximated by the delta method (Casella and Berger, 2001) based on the first-order partial derivatives of the estimators with respect to the parameters of the excess and expected hazard on a logarithmic scale. The estimated covariances of the estimators of the regression coefficients of the excess hazard were provided by the iterative weighted least squares algorithm used to fit the generalised linear model of relative survival, and the variance of the estimate of the logarithm of the expected hazard of death was estimated by the inverse of number of deaths in national population. The estimation of the variances is explained in detail in Supplementary Appendix. The CIs were obtained by applying the asymptotic normal distribution to the estimators of the numbers of deaths and the numbers and proportions of avoidable deaths.

Results

Altogether 10 772 patients were diagnosed with colon cancer at ages 0–89 years during 2000–2007 (Supplementary Table 1). Region-specific age- and sex-standardised 5-year relative survival ratios ranged from 58 to 61% (Supplementary Table 2). According to the conventional hypothetical interpretation of the relative survival ratio, 39–42% of the patients would have died from colon cancer during the first 5 years after diagnosis, if this cancer had been the only possible cause of death.

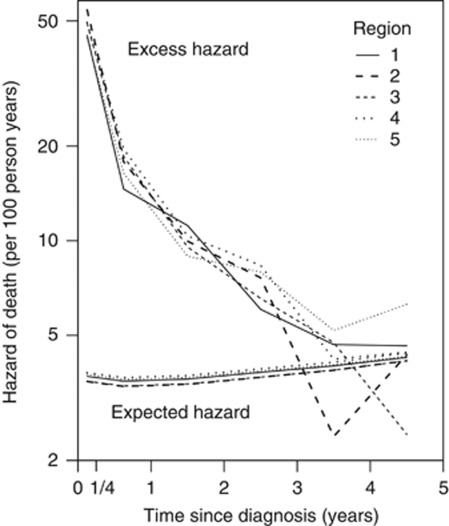
The excess hazard from cancer was dominating over the expected hazard in the first 3 years after diagnosis (Figure 1) being 12 times larger than the expected hazard in the first 3 months, such that 92% of all deaths occurring then were estimated to be due to colon cancer itself (see formula 1 in Supplementary Appendix). In the 4th and 5th year of follow-up, only about half of all deaths were due to the cancer. The regional excess hazards varied much more than the expected ones, only small differences in the latter (<2 deaths per 1000 person years) being observed.

Figure 1.

 Age- and sex-standardised hazard of death (number of deaths per 100 person years) due to colon cancer (excess hazard) and due to other causes (expected hazard) by time since diagnosis for colon cancer patients diagnosed in Finland in 2000–2007 under 90 years of age in the five cancer control regions. The vertical axis is on a logarithmic scale.

Altogether 5474 patients were estimated to have died in the first 5-year period after diagnosis, out of which 4139 due to colon cancer (Table 1), that is, 38% of the patients were estimated to have died from that cause in the presence of other causes of death in contrast to 39–42% that were estimated to have died in the absense of other causes of death. In patients aged 0–64 years at diagnosis, 93% of all deaths were due to colon cancer, whereas this proportion was 70% among those 65–89 years old.

Table 1. Predicted numbers of deaths from colon cancer, from other causes and from any cause, respectively, in colon cancer patients diagnosed in Finland in 2000–2007 during the first 5 years after diagnosis, by age at diagnosis and cancer control region (point estimates (Est.) and 95% confidence intervals (CI) are shown).

		Cancer		Other causes		Any cause
Age at diagnosis (years)	Region	Est.	95% CI	Est.	95% CI	Est.	95% CI
0–64	1	397	(368, 426)	33	(31, 35)	430	(402, 458)
	2	168	(153, 183)	12	(11, 13)	180	(166, 194)
	3	290	(268, 312)	21	(19, 22)	310	(289, 332)
	4	227	(208, 245)	17	(16, 18)	243	(225, 261)
	5	132	(119, 145)	10	(10, 11)	142	(129, 155)
	Total	1213	(1144, 1283)	93	(90, 96)	1306	(1238, 1374)
65–89	1	837	(786, 887)	382	(369, 396)	1219	(1178, 1260)
	2	509	(471, 546)	203	(193, 213)	712	(681, 742)
	3	758	(711, 805)	316	(304, 328)	1074	(1036, 1112)
	4	513	(477, 550)	206	(197, 216)	720	(690, 749)
	5	309	(281, 337)	135	(127, 142)	443	(421, 466)
	Total	2926	(2806, 3045)	1242	(1214, 1271)	4168	(4067, 4268)
All: 0–89	1	1234	(1165, 1302)	415	(402, 429)	1649	(1590, 1708)
	2	677	(629, 725)	215	(205, 225)	892	(851, 932)
	3	1048	(987, 1109)	336	(324, 349)	1384	(1333, 1436)
	4	740	(690, 790)	223	(213, 233)	963	(921, 1005)
	5	441	(402, 480)	145	(137, 152)	586	(552, 619)
	Total	4139	(4001, 4277)	1335	(1306, 1364)	5474	(5353, 5595)

If all the cancer control regions had shared the same relative survival as that in region 1 to which Helsinki belongs (scenario A), the predicted number of avoidable deaths from colon cancer would have been 176 (95% CI 3–349) (Table 2). An additional 30 deaths were estimated to occur due to other causes and the vast majority of those, 28 deaths, were estimated to occur in patients 65–89 years at diagnosis. Hence, the total number of avoidable deaths was 146 (CI 3–290), that is 3% (CI 0–5%) of all deaths.

Table 2. Predicted numbers (Diff) and proportions (Prop, %) of avoidable deaths from colon cancer, from other causes and from any cause, respectively, in colon cancer patients diagnosed in Finland in 2000–2007 during the first 5 years after diagnosis, stratified by age at diagnosis, in three different hypothetical scenarios (point estimates (Est.) and 95% confidence intervals (CI) are shown).

		Cancer		Other causes		Any cause
Diff/Prop	Age at diagnosis	Est.	95% CI	Est.	95% CI	Est.	95% CI
Scenario A: same relative survival as that in region 1
Diff	0–64	50	(1, 100)	−2	(−3, 0)	49	(1, 97)
	65–89	126	(2, 249)	−28	(−56, −1)	97	(2, 193)
	All: 0–89	176	(3, 349)	−30	(−59, −1)	146	(3, 290)
Prop	0–64	4	(0, 8)	−2	(−3, 0)	4	(0, 7)
	65–89	4	(0, 9)	−2	(−4, 0)	2	(0, 5)
	All: 0–89	4	(0, 8)	−2	(−4, 0)	3	(0, 5)
Scenario B: same expected survival as that in region 2
Diff	0–64	−1	(−1, 0)	3	(−2, 8)	3	(−2, 7)
	65–89	−5	(−8, −1)	26	(−3, 56)	22	(−5, 48)
	All: 0–89	−5	(−9, −2)	30	(−1, 60)	25	(−3, 52)
Prop	0–64	0	(0, 0)	4	(−2, 9)	0	(0, 1)
	65–89	0	(0, 0)	2	(0, 5)	1	(0, 1)
	All: 0–89	0	(0, 0)	2	(0, 5)	0	(0, 1)
Scenario AB: same relative and expected survival as those in regions 1 and 2, respectively
Diff	0–64	50	(0, 99)	2	(−4, 7)	52	(3, 100)
	65–89	121	(−2, 245)	−1	(−42, 40)	120	(20, 220)
	All: 0–89	171	(−2, 344)	1	(−42, 43)	172	(25, 319)
Prop	0–64	4	(0, 8)	2	(−4, 8)	4	(0, 8)
	65–89	4	(0, 8)	0	(−3, 3)	3	(0, 5)
	All: 0–89	4	(0, 8)	0	(−3, 3)	3	(0, 6)

If all the regions had shared the same expected survival as that in region 2 (scenario B), the total number of avoidable deaths would have been clearly smaller than in scenario A: 3 (CI 2–7) and 22 (CI 5–48) deaths were estimated to be avoidable among patients aged 0–64 and 65–89 years at diagnosis, respectively. If the relative and the expected survival had been equal to those in region 1 and 2, respectively (scenario AB), the estimated numbers of avoidable deaths from colon cancer would have been a bit smaller but from any cause larger than those in scenario A.

Discussion

In this paper, we presented a method for quantifying random error in the numbers and proportions of avoidable deaths. The method was illustrated using the follow-up data of the patients diagnosed with colon cancer in Finland during 2000–2007 under 90 years of age. Among these patients, 146 (95% CI 3–290) deaths, that is 3% (CI 0–5%) out of the total number 5474 were estimated to be avoidable during the first 5 years after diagnosis, if all the cancer control regions were assumed to share the same relative survival as that in the largest region where the capital of the country is located. However, given the wide error margin, it is not so evident whether any deaths could have been avoided at all.

In colon cancer, the number of avoidable deaths in the first 5 years after diagnosis was a reasonable estimate to summarise the regional differences in relative survival, because patients experienced most of the excess hazard within the first 5 years. In addition, colon cancer patients had high excess hazard, but, on the other hand, the cancer was not too fatal. Otherwise, the number of avoidable deaths would have been close to zero and uninteresting as such.

In scenario A, region 1 where the capital is located was a reasonable baseline for the relative survival, because the estimated excess hazard in region 1 was on average lower than that in the other regions, and it would be desirable that patients in the more remote areas of Finland could achieve the same level of the relative survival as patients in Helsinki or its surroundings. In the expected hazard, small but systematic differences existed across the regions. Hence, in scenario B, the region with the lowest background mortality was chosen as baseline for the expected survival to illustrate the effects of the regional differences in the background mortality on the numbers of deaths. Scenario AB was developed to estimate the ‘maximum’ number of avoidable deaths that would have been achieved, if the favourable assumptions of scenarios A and B had been enforced simultaneously.

Relative survival analysis allows estimation of the avoidable deaths without relying on classification of the causes of deaths. Hence, our method is universally applicable, even when cause of death information do not exist, are of poor quality, or data protection rules do not allow linking the patients with their causes of deaths. However, the division into deaths from the target disease and from other causes is not valid, if the excess hazard of death is allowed to be negative. When relative survival is estimated for a small patient population stratified by region, sex and age, the estimated excess hazards are likely to be negative in some follow-up intervals. This would indicate that the patients survived better over that interval than expected, according to the mortality of a comparable cancer-free population. If the excess hazard is forced to be zero for the intervals where the estimate is negative, it may bias the cumulative estimate of the crude probability (Cronin and Feuer, 2000). Statistical modelling was helpful in controlling such random variation in the excess hazard, because a separate parameter may not be needed for each combination of covariates. Alternatively, flexible parametric models could be used to smooth the excess hazard in the estimation of the crude probability (Lambert et al, 2010).

When the estimation of avoidable deaths is based on relative survival methods, background mortality should be estimated for each region, because the regional differences in the background mortality affect the estimates of the excess hazard, and furthermore the estimates of the numbers of deaths from target cancer and from other causes, respectively. If a patient’s survival time was censored in the end of the follow-up, before the first 5 years of follow-up within which the numbers of avoidable deaths were estimated, the expected hazard was required for some further calendar years. We utilised the annual mortalities of the reference population as the estimates of the expected hazard until the end of 2009. For calendar years 2010–2012, the estimate of the expected hazard in 2009 was used.

The numbers and proportions of avoidable deaths are useful in assessing the public health impact of survival differences. These estimates are also prone to random error, which can be substantial, especially when survival experience between small populations is compared. The random error can be appropriately quantified by CIs using the methods proposed in this paper.