Enhanced self-association of mucins possessing the T and Tn carbohydrate cancer antigens at the single-molecule level

Abstract

Mucins are linear O-glycosylated glycoproteins involved in inflammation, cell adhesion and tumorigenesis. Cancer associated mucins often possess increased expression of the T (Galβ1,3GalNAcαThr/Ser) and Tn (GalNAcαThr/Ser) cancer antigens, which are diagnotic markers for several cancers including colon cancer. We have used AFM based single-molecule forced unbinding under near physiological conditions to investigate the self-interactions between porcine submaxillary mucin (PSM) as well as between PSM analogs possessing various carbohydrates including the T- and Tn-antigen. Distributions of unbinding forces and corresponding force loading rates were determined for force loading rates from 0.18 nN/s to 39 nN/s, and processed to yield most probable unbinding forces f* and lifetimes of the interactions. Parameter f* varied in the range 27 to 50 pN at force loading rates of about 2 nN/s among the various mucins. All mucin samples investigated showed self-interaction, but the tendency was greatest for PSM displaying only the Tn-antigen (Tn-PSM) or a mixture of Tn-, T-antigen and the trisaccharide Fucα1,2Galβ1,3GalNAc (Tri-PSM). Weaker self-interactions were observed for native PSM (Fd-PSM), which consists of a nearly equal mixture of the longer core 1 blood group A tetrasaccharide (GalNAcα1,3(Fucα1,2)Galβ1,3GalNAcαSer/Thr) and Tn-antigen. The data are consistent with the truncated Tn and T glycans enhancing self-interaction of the mucins. These carbohydrate cancer antigens may thus play an active role in the disease by constitutively activating mucin and mucin-type receptors by self-association on cells.

Introduction

Complex oligosaccharides are involved in the control of many normal and pathological processes through their interaction with other biomacromolecules. However, understanding of how glycans influence these complex processes at the molecular level is in its infancy¹ and the role of direct carbohydrate self-interactions in these events has seldom been addressed experimentally, and may have been under-rated.² Challenges faced in revealing the mechanisms for glycoconjugate interactions are their inherent structural variation, complicating the preparation of homogeneous samples, and low strength and multivalency of their self-interactions. Due to these challenges, the emerging field of glycomics requires the application of new methodologies. Recently, the quartz crystal microbalance (QCM) was used for the analysis of the self-binding activity of the glycan of marine sponge origin that is responsible for species-specific cell adhesion.³ Another approach for the experimental study of carbohydrate self-interaction involves the use of 2D and 3D functionalized surfaces that mimic glycolipid presentation in natural systems.⁴ The study of self-assembly of glyconanoparticles is another approach⁵ and kinetic studies of carbohydrate self-interactions have been investigated by surface Plasmon resonance (SPR).⁶ These experimental approaches confirm the propensity of certain carbohydrates for self-interactions, as well as the specificity of these interactions.

In the human body, one important location of complex oligosaccharides is on the epithelial surfaces, which throughout the body are covered by mucous secretions. More than 80% of the organic components of the mucous layer are elongated high molecular weight glycoproteins known as mucins.⁷ Mucins mediate various biological functions such as modulating immune response, inflammation, adhesion and tumorigenesis.^{1, 8, 9} In particular, the levels of expression of mucin peptide antigens and type of carbohydrate chains of mucins are diagnostic markers for a variety of cancers.^{8, 10} Colon cancer associated mucins differ in their core carbohydrate structures compared to normal mucins, in many cases by presenting truncated carbohydrate chains compared to normal mucins. They display increased expression of the GalNAc-α–Thr/Ser (Tn-antigen), Galβ1,3GalNAc (T- or TF-antigen) and NeuAc- α2,6GalNAc (sialyl Tn-antigen).⁸ The oligosaccharide decorations on mucins have also been shown to be important for biological properties such as their interactions with animal lectins including selectins, siglecs and galectins.⁹

O-linked glycosylation is the most abundant form of glycosylation found in higher eukaryotes. It is termed “mucin-like” and is characterised by the presence of an α-N-acetylgalactosamine (GalNAc) residue attached to the hydroxyl groups of Ser/Thr peptide core residues.¹¹ The further substitution of the GalNAc by additional sugars results in O-glycan structural diversity, including a distribution of structures that can vary from individual to individual. Mucin-type O-linked glycans typically occur clustered together in “mucin domains” which are commonly made up of tandemly repeated amino acid sequences. The net sequence lengths of the mucin domains range from a few peptide residues (as in IgA1) to thousands of residues (mucins). The glycan decoration of mucins typically comprises more than 50% of their molecular weight. Structural studies of mucins using atomic force microscopy (AFM),^12–14 light scattering,^{15, 16} small angle X-ray scattering,¹⁷ and nuclear magnetic resonance (NMR) spectroscopy¹⁸ have demonstrated that clustered O-linked glycosylation results in extended protein structures up to hundreds of nanometers in length.¹⁹

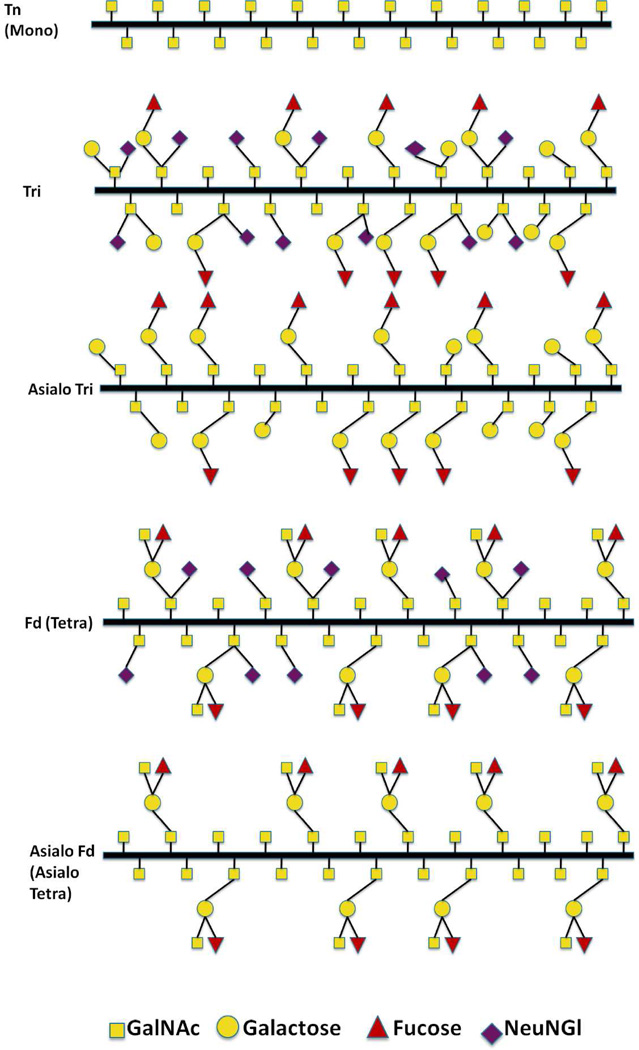
Porcine submaxillary mucin (PSM) is a well characterized mucin with respect to biochemical and physical properties. Its peptide sequence has been completely determined,²⁰ revealing that its central O-glycosylated mucin domain contains 99 to 135 repeats of an 81 residue tandem repeat. Likewise, PSM’s O-glycan structures have been fully determined by chemical²¹ and NMR techniques,²² and PSM is the only mucin to have its O-glycan structures characterised as a function of position along its tandem repeat.²³ Figure 1 shows the possible O-glycan structures of the PSM tandem repeat. The glycan structures vary in length, ranging from α-GalNAc residue linked to the peptide backbone through the amino acids Ser/Thr (Tn-antigen) to the oligosaccharide structures characteristic for blood group A. The negatively charged, carboxylic acid containing N-glycolylneuraminic acid (NeuNGl) residue is present in some but not all of the glycan sidechain structures (Figure 1). The presence of the tri- and tetrasaccharide structures varies among individual pigs, with some individuals nearly completely lacking one or the other structures.²²

Figure 1.

Schematic illustration of the O-glycans of wild type PSM (Fd-PSM) and the analogs Asialo Fd -PSM, Tri-PSM, Asialo Tri-PSM and Tn-PSM. The latter four analogs were obtained by partial deglycosylation of the fully decorated PSM, using chemical and enzymatic deglycosylation procedures. The percentage of the different O-glycan structures of Fd-PSM and the different mucin analogs are listed in Table 1.

In the present paper we extend the strategies previously used for quantitating mucinlectin interactions at the single-molecular pair level²⁴ to determination of mucin self-interactions. Based on experimental data of the probability and strength of the self-interactions observed for five different mucin samples with well-defined carbohydrate decoration pattern, we provide information related to the structure–function relationship of these molecules at the molecular level.

Materials and Methods

Preparation of mucin samples

Mucins with different carbohydrate decoration patterns were prepared based on pig submaxillary mucin (PSM). Appropriate PSM was obtained from frozen porcine submaxillary glands and the O-glycosylated tandem repeated domains of PSM were prepared from individual glands as previously described.²⁵ The oligosaccharide composition of the mucin samples investigated, determined using¹³C NMR spectroscopy, are summarized in Table 1.²² The Tn-PSM tandem repeat domains containing only α-GalNac residues were obtained from the isolated O-glycosylated domains of native PSM using mild trifluoromethane sulfonic acid.²⁶ Asialo Tri and Asialo Fd-PSM samples were prepared from the Tri- or Fd-PSM tandem repeat domains by enzymatic removal of the sialic acid groups using neuraminidase.²⁷ All preparations were purified by gel filtration on Sephacryl S200 and the highest MW (excluded volume) fractions collected for this study. The mucin samples were lyophilized and stored at −18 °C.

Table 1.

Fraction of different carbohydrate structures and NeuNGl in the PSM samples.

Sample	Size of carbohydrate side chains
	Mono	Di	Tri	Tetra	NeuNGla
Tn	100	0	0	0	0
Tri	28	26	46	0	54
Asialo Tri	24	28	48	0	0
Fd	58	0	2	40	45
Asialo Fd	58	0	2	40	0

^aThe relative amount of charged groups is the total fraction of charged groups obtained by adding the fractions of the mono, di, tri and tetra saccharide side chains carrying charges.

Immobilization of mucins on AFM tips and mica surfaces

Freeze dried mucins samples were dissolved in Mq-water (deionized water, resistivity 18 MΩ cm, obtained using a MilliQ unit, Millipore) at the desired concentration and used for the immobilization to solid surfaces, as fresh solutions. All reagents used during the sample preparation were of analytical grade. The PSM tandem repeat domains were covalently linked to freshly cleaved mica (mineral muscovite) surfaces as well as to AFM tips (Veeco OTR4-10 Silicon Nitride, the cantilevers with nominal spring constant k = 0.02 N/m were used), following the steps in the previously reported procedure.²⁴ In brief, surfaces were cleaned by 1:1 v/v solutions of MeOH/HCl, rinsed and aminosilanized (1% (v/v) freshly prepared solution of trimethoxysilylpropyldiethylenetriamine in 1 mM acetic acid) at room temperature, and rinsed in Mq-water. The mucins were covalently anchored to the AFM tips and mica surfaces using the following approach: 1-(3-dimethylaminopropyl)-3-ethylcarbodiimide hydrochloride (EDAC) was added to catalyze the formation of peptide bonds between the amino groups on the silane and carboxyl groups on the mucins. Appropriate PSM grafting densities on the mica and AFM tip supporting single-molecule pair interactions were obtained by using low concentrations of the PSM during the immobilization. PSM functionalized mica slides were prepared by incubating the slides in a solution containing 100 µg/mL mucin in 5 mM boric acid pH 5.8 and 1.0 mg/ml EDAC overnight. When preparing PSM functionalized AFM tips, the concentration of mucin was reduced to 50 µg/mL, and the incubation time was reduced to 1 hour.

In some experimental series Fd-PSM, Tn-PSM and Tri-PSM were immobilized through their N-terminal peptide backbone amino groups (note that the PSM tandem repeat domain does not contain lysine residues²⁸) by the following procedure: Mica slides or AFM cantilevers were cleaned as described above. The tips and mica surfaces were silanized with a freshly prepared solution of 1% (v/v) N-(trimethoxysilylpropyl) ethylenediamine triacetic acid in 1 mM acetic acid over night. Fd-PSM, Tn-PSM and Tri-PSM molecules were immobilized to the surfaces by conjugating their N-terminal primary amine groups to this silane.

Dynamic Force Spectroscopy Measurements

The force-distance curves were obtained at room temperature using the AFM ForceRobot 300 (JPK instruments, Berlin) equipped with a JPK precision mapping stage and a liquid cell filled with aqueous 100 mM Hepes buffer, pH 7.2 containing 1mM CaCl₂ and 1mM MnCl₂. The deflection sensitivity and spring constant of the functionalized AFM tips were determined prior to each series of measurements. The deflection sensitivity was determined based on force versus distance curves obtained towards a hard surface (non-functionalized glass surfaces were used). The spring constants of the cantilevers were determined based on the thermally excited fluctuations of the cantilever when positioned far from the surface.²⁹ The mucin functionalized AFM tips were then brought in contact with the mucin functionalized mica slides and were immediately retracted (some experimental series of Tn-PSM) or retracted after 0.5s pause at the surface. In the present study the z-piezo retraction speed was varied from v_ret= 1.0 µm/s to 4.0 µm/s.

Analyses of forced unbinding data

Unbinding between molecular pairs under external force is viewed as a scenario where the external force aids the thermal activation in the unbinding process and decreases the activation barrier(s) separating the bound from the free states. Consequently, the rate of dissociation rate under a constant loading force f, k_off(f), increases as

$$k_{\mathit{\text{off }}}(f)=k_{\mathit{\text{off }}}(0)\text{ exp}({\mathit{\text{fx}}}_{\mathrm{b}}/k_{B}T)$$ (1)

where k_off(0) is the dissociation rate extrapolated to zero loading force, x_β is the thermally averaged distance from the bound complex to the transition state projected along the direction of the applied force and k_BT is the thermal energy.^{30, 31} When the applied force along the unbinding pathway exceeds the force f_β governed by the distance x_β, i.e., f_β = k_BT/x_β, the most probable rupture force f* is predicted:^30–32

$$f^{*}=f_{\beta }\text{ ln}(r_f/r_f^0)$$ (2)

Parameter r_f is the actual force loading rate, and ${r_f}^0$ a thermal scale for loading rate, ${r_f}^0=f_{\beta }/t_0$ where t₀ is the inverse of the transition rate.

In the present work the experiments performed using a constant pulling speed were processed based on the assumption that the irreversible ruptures associated with crossing the free energy barrier is quasi-adiabatic. Following the approach described by Dudko and co-workers³³ this yields information about the force-dependent lifetime of the system, τ (f). The practical implementation requires that the force dependence of dissociation rate (k_off(f)) is calculated from the probability density distribution of rupture forces. The theory is based on the application of Kramer’s theory to different free-energy profiles and results in an analytic expression for the force-dependent lifetime that contains the free energy of activation in the absence of forces [ΔG^#] as an additional parameter:³³

$$\tau (f)={\tau }_0{(1-\frac{\nu {\mathit{\text{fx}}}_{\beta }}{\mathrm{\Delta }{G}^{\#}})}^{1-1\nu }\text{exp }[-\frac{\mathrm{\Delta }{G}^{\#}}{k_{B}T}(1-{(1-\nu {\mathit{\text{fx}}}_{\beta }/\mathrm{\Delta }{G}^{\#})}^{1/\nu }\left)\right]$$ (3)

In this expression, τ₀ is the lifetime of the interaction. The scaling factor ν reflect the geometry of the underlying free energy potential, which is ν = 0.5 for a harmonic well with a cusp-like barrier. ν = 2/3 represent a potential containing linear and cubic terms. For ν = 1, it becomes equal to the Bell and Evans model, which constitutes a special case within the formalism.

In the Bell-Evans model, the probability density P(f) for observing a bond rupture between a molecular pair at the force f subjected to constant force loading rate r_f is:³¹

$$\mathrm{P}(\mathrm{f})={\mathrm{k}}_{\text{off}(\mathrm{f})}\text{ exp}\left(\frac{{\mathrm{x}}_{\mathrm{\beta }}\mathrm{f}}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}\right)\text{ exp}\left[\frac{{\mathrm{k}}_{\text{off}(\mathrm{f})}{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}{{\mathrm{x}}_{\mathrm{\beta }}{\mathrm{r}}_{\mathrm{f}}}\right(1-\text{exp}\left(\frac{{\mathrm{x}}_{\mathrm{\beta }}\mathrm{f}}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}\right)\left)\right]$$ (4)

In the present study, force jumps observed in the force – distance curves were interpreted as evidences of interactions between mucins immobilized to the AFM tip and to the sample surface. Since the mucin segments connect the interacting segments to the respective surfaces, the loading rate does not only depend on the tip retraction velocity, but also on e.g. the length of the polymer segments linking the two surfaces³¹ The loading rate acting on an inter molecular bond was determined for each force jump from the slope Δf/Δt prior to each observed dissociation event. The following rules were applied for the selection of force jumps: accepted jumps should only contain one peak and prior to deflection the cantilever should be in its resting position (i.e. not deflected).

For each mucin sample investigated, the data obtained were displayed in dynamic force spectra. The total distribution of force jumps were grouped into intervals with equal width of the ln(r_f) along the axis of increasing loading rates. Based on the allocated data in each interval, histograms over number of force jumps against unbinding force were made. The theoretical probability density function P(f) (Eq. 4) was fitted to the experimentally determined distributions of unbinding forces, using the average force loading rate in the interval as a constant and the parameters k_off and x_β as fitting parameters. This procedure yields estimates of f*.

Results

To reveal the importance of the precise carbohydrate decoration patterns on the self-interaction properties of the PSM samples: Tn-PSM, Tri-PSM, Asialo Fd-PSM, Asialo Tri-PSM as well as Fd-PSM were studied. Structural information of the samples is presented in Figure 1 and in Table 1.

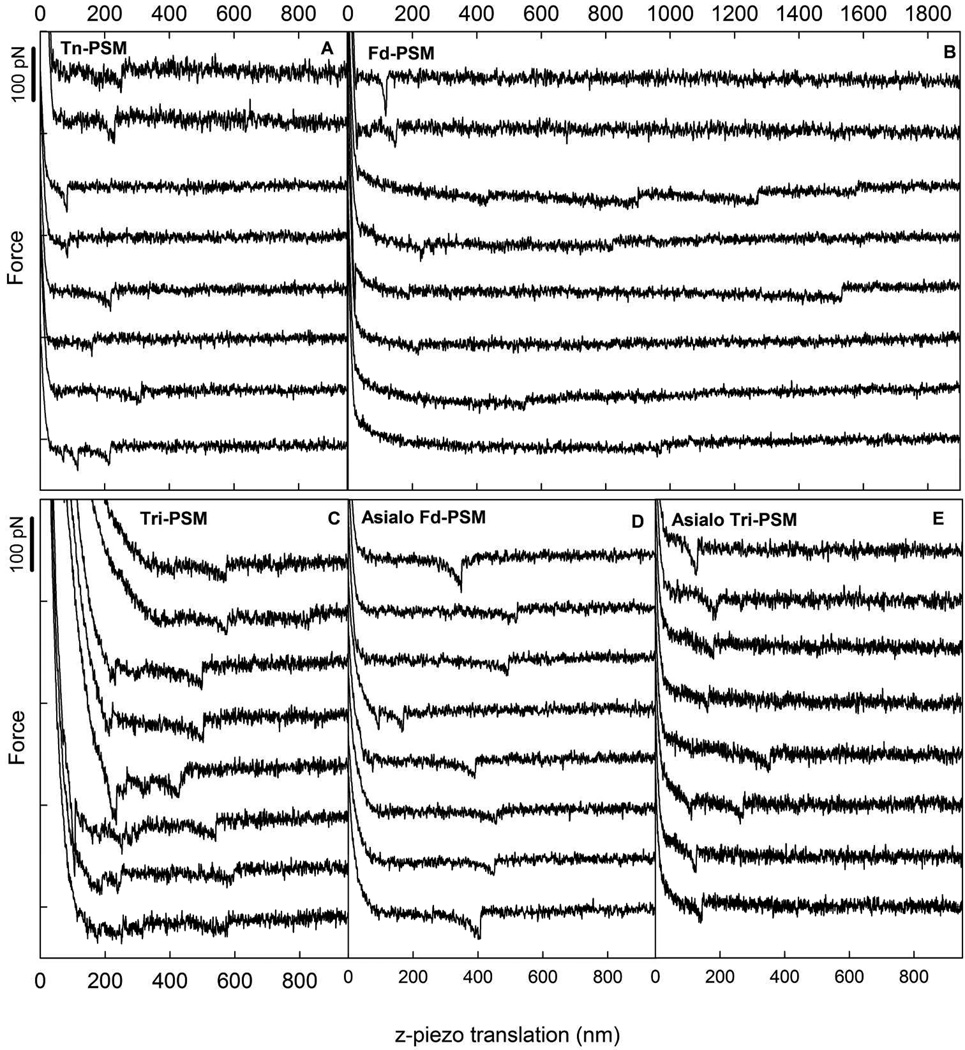
Figure 2 presents force distance curves, selected among curves with force jumps close to the f* determined for each sample, for Tn-PSM, Fd-PSM, Tri-PSM, Asialo Fd-PSM and Asialo Tri-PSM mucin samples. The rupture events were observed at tip-surface separations up to about 1500 nm. This is compatible with the expected chain length for the Tn-PSM which, based on information about the mass per unit length of Tn-PSM and the molecular length of the sample used, is expected to be ~5 µm. For each of the samples, the probability for observation of an interaction event was determined based on the obtained force curves containing force jumps (Table 2). These probabilities indicate that Tri- and Tn- PSM show a high probability for self-interaction, whereas the other mucins show significantly lower probability.

Figure 2.

Examples of force-z-piezo retraction curves for mucin functionalized AFM tips against Tn-PSM functionalized mica obtained at room temperature in aqueous 100 mM Hepes buffer pH 7.2 containing 1 mM CaCl₂ and 1 mM MnCl₂ using a retractive piezo velocity equal to 2 µm/s. The curves include signatures of forced disruption of self-interaction events between (A) Tn-PSM (B) Fd-PSM (C) Tri-PSM (D) Asialo Fd-PSM (E) Asialo Tri-PSM molecules. For (A) and (B), the two upper curves were obtained for samples where the mucin molecules were immobilized through amino groups, whereas the lower 6 curves were obtained for samples were the mucin molecules were immobilized through carboxylic acid groups.

Table 2.

Fraction of force curves containing force jumps for different mucin samples and for control measurements.

	Samples
Experimental series	Tn		Tri		Asialo Tri		Fd		Asialo Fd
	Pinta	Total	Pinta	Total	Pinta	Total	Pinta	Total	Pinta	Total
MucinCOOH- linkedb	23.1%d	1179 d	61.7%	1123	7.3%	3231	6.3%	1661	4.5%	4795
MucinNH2- linkedc	28.7%	581	55.1%	1855			7.5%	600
Control 1 e	3.4%	384	8%	767	2.4%	577	-	-	2.9%	526
Control 2 f	0.3	1045	0	1200	-	-	-	-	-	-

^aP_int: Fraction of curves containing forced rupture of self-interaction events (% of total curves).

^bMucin_COOH-linked: Immobilization of mucins through carboxylic acid groups on the mucins.

^cMucin_{NH2- linked}: Immobilization of mucins through amino groups on the mucins.

^dThe results reported for the Tn-PSM immobilized through carboxylic acid groups are based on supplementary measurements performed using a pause of 0.5s to make the results comparable with the other mucins.

^eControl 1: silanized AFM tips interacting with mucin coated mica surfaces.

^fControl 2: AFM tips functionalized with mucin interacting with silanized mica surfaces.

Additional test studies were performed in order to verify that the unbinding events observed arises from dissociation between mucins connected to the mica surface and AFM tip. As a control, aminosilanized tips were allowed to interact with aminosilanized mica surfaces. The force-distance curves obtained when retracting the AFM tips from these surfaces, did not contain any force jumps. Furthermore, separate test studies demonstrated a reduction in anchoring events when immobilising mucins to the mica surface or the AFM tip, and allowing this surface to approach an uncoated AFM tip or a bare unfunctionalized mica surface, respectively. The reduction of anchoring events in force curves obtained under these conditions demonstrates the low probability for adsorption of mucins to aminosilanized AFM tips or mica surfaces. When Tri-PSM and Tn-PSM were covalently linked only to the tip and measured against aminosilanized surfaces, no anchoring events were observed. These observations therefore underpin the interpretation that the experimentally observed unbinding events (Figure 2) arise from dissociation of mucin self-interactions.

In order to investigate the possible influence of the immobilization strategy on the results obtained, Fd-PSM, Tri-PSM and Tn-PSM were in a separate experimental series study immobilized via the amino groups at the end of the molecules. The observations obtained for this experimental series did not deviate significantly from the results obtained when anchoring the molecules via the carboxylic acid group (Figures 2A and B).

Dynamic Force Spectroscopy Measurements

In the following, the experimental data as well as the results of the data analysis used for the study of Tn-PSM are described. The same experimental approach was also used to investigate the other mucin samples. For these samples, examples of the raw data as well as the results of the analysis are presented (Figures 2 and 5, Tables 3 and 4).

Figure 5.

Lifetime τ (f) as a function of the rupture force f for (A) Tn-PSM (B) Tri-PSM and (C) Asialo Tri- PSM, obtained as described by Dudko et al.³³ By fitting Eq. 3 to the experimental data, τ(f) and x_β are determined. For the dotted line the parameter ν = 1 which gives the Bell-Evans formalism (Eq.4). For the continuous line ν = 0.5 which corresponds to a harmonic well potential with cusp like barriers.

Table 3.

Estimated parameters for the energy landscape of the mucin self-interactions

Sample		rf (nN/s)	f* (pN)	koff (s−1)	xβ (nm)	xβ mean (nm)	xβa mean (nm)	R2b
Tn		0.64	34	1.2 ± 0.27	0.52 ± 0.03			0.79
		1.8	42	4.0 ± 0.67	0.37 ± 0.02			0.85
		3.6	40	4.7 ± 0.79	0.45 ± 0.02	0.37	0.34	0.94
		7.1	49	16.1 ± 2.0	0.28 ± 0.01			0.89
	c	14	78	10.6 ± 2.6	0.23 ± 0.02			0.74
		39	256	57 ± 13	0.02 ± 0.004	0.02		0.79
Tri		0.18	40	0.64 ± 0.8	0.30 ± 0.16			0.56
		0.63	42	0.13 ± 0.1	0.65 ± 0.008			0.95
		1.4	38	2.7 ± 1.0	0.43 ± 0.05	0.40		0.96
		2.8	39	2.2 ± 0.8	0.55 ± 0.04			0.88
		5.8	44	5.8 ± 1.0	0.45 ± 0.02			0.96
		11	48	11 ± 2.0	0.39 ± 0.017			0.96
Asialo Tri		1.7	50	3.0 ± 1.5	0.30 ± 0.05			0.92
		4.7	54	0.57 ± 0.2	0.54 ± 0.03	0.34		0.96
		9.0	53	10 ± 1.5	0.32 ± 0.01			0.98
		19	64	48 ± 16.1	0.19 ± 0.02			0.81
Asialo Fd		0.75	27	2.5 ± 1.1	0.56 ± 0.07			0.94
		2.0	27	0.88 ± 0.4	0.93 ± 0.07			0.98
		4.0	34	19 ± 2.9	0.36 ± 0.022	0.55		0.98
		8.0	39	27 ± 8.5	0.32 ± 0.007			0.95
		17	56	1.2 ± 1.7	0.56 ± 0.11			0.84

^ax_β from f* vs r_f.

^bR² = coefficient of determination

^cinner energy barrier has become the rate limiting.

Table 4.

Estimated parameters of mucin self-interactions based on force dependence of the lifetime

Sample	ν	τ (s)		1/ τ (1/s)		xβ (nm)		R2
		τ1 (s)	τ2 (s)	1/ τ1	1/ τ2	xβ1	xβ2
Tn	1	1.46	0.006	0.69	166	0.30	0.04	0.94
	1/2	2.40	0.023	0.42	43	0.40	0.09	0.95
Tri	1	3.69	0.006	0.27	166	0.42	0.05	0.90
	1/2	4.32	0.016	0.23	63	0.43	0.10	0.90
	2/3	4.29	0.013	0.23	77	0.45	0.09	0.90
Asialo Tri	1	0.682	0.001	1.47	1000	0.33	0.03	0.91
	1/2	0.698	0.001	1.43	1000	0.334	0.04	0.91
Fd	1	4.7	0.078			0.63	0.19	0.607
Asialo Fd	1	2.54	0.032			0.21	0.02	0.963
	1/2	3.10	0.083			0.26	0.08	0.748

Tn-PSM Self-Interactions

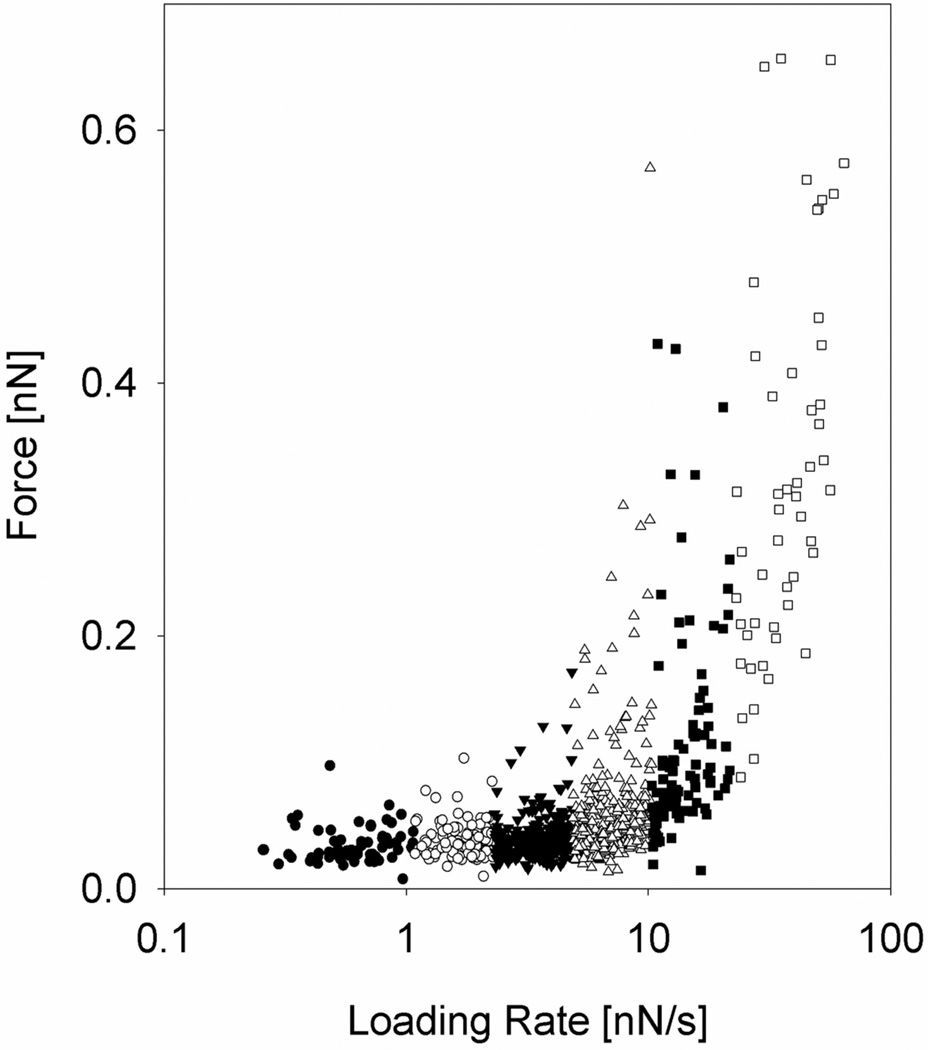
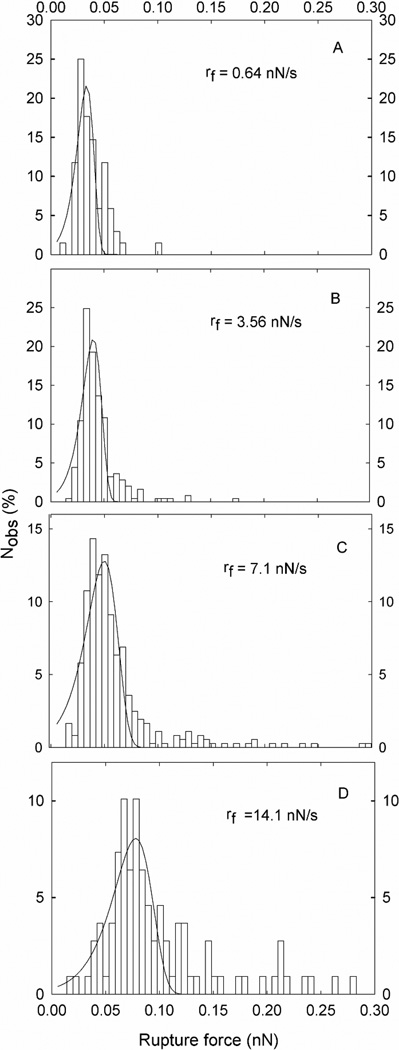
In total 955 molecular dissociation events were identified and used to determine the rupture forces and associated loading rates. The observed forces were grouped into 6 subgroups based on the determined loading rate (Figure 3). The mean loading rates calculated for each of the intervals increased from 0.64 nN/s to 39 nN/s (Table 3). The magnitude of the most probable rupture force f^*, as determined from the fit of P(f) to the observed distributions of unbinding forces (Figure 4), was found to increase with increasing loading rate (Table 3). However, a clear shift in the slope of the dependence of unbinding force on ln(r_f) is observed when r_f increases beyond ~10 nN/s. For loading rates below 10 nN/s, the observed unbinding forces were in the interval 30 to 50 pN, while at higher loading rates the unbinding force increased rapidly, and reached 256 pN at a loading rate equal to 39 nN/s. (Figure 4 and Table 3).

Figure 3.

Distribution of Tn-PSM self-interaction rupture forces at increasing force loading rates. The data are collected from 3922 force curves obtained using tip retraction speed in the interval 1–4 µm/s and no pause at the sample surface. The loading rate acting at a molecular bond was determined for each force jump from the slope Δf/Δt prior to each bond dissociation event. The observations were divided into 6 subgroups, each characterised by a certain range of loading rates. Each subgroup was analysed separately, and f* (large symbols), determined as explained in Figure 4.

Figure 4.

Tn-PSM self-interactions. Histograms based on the observed unbinding forces within each subgroup of observations grouped based on defined intervals of loading rate. For each histogram, the average loading rate valid for the observations is indicated. Fitting Eq. 4 to the experimental data allows determination of the parameters x_β, k_off, and f*. The fitted curves are overlaid on the distributions presented.

The estimated x_β parameter (Table 3) decreased gradually from 0.52 nm to 0.28 nm for loading rates from 0.64 to about 7.1 nN/s. For higher loading rates a significantly lower value of x_β was obtained (x_β=0.02±0.004nm at r_f = 39 nN/s).

An alternative approach to determine x_β is based on determination of the slope of the linear regimes observed in the dynamic force spectra (Figure 3), which is defined as k_BT/x_β. Applying this approach for r_f < 10 nN/s yields x_β = 0.34 nm for the Tn-PSM self-interaction. This estimate of x_β is consistent with the approach based on analysis of the distributions of the unbinding events within the intervals of force loading rates (x_β = 0.37 nm (Table 3)).

The lifetimes of the Tn-PSM self-interactions reveal that k_off increases with increasing loading rate (Table 3). This behavior is expected in dynamic force spectroscopy since an applied force f decreases the activation energy for dissociation from ΔE^‡ to ΔE^‡(f) with the relation ΔE^‡ − ΔE^‡(f) = −x_βf, leading to an exponential increase of the off-rate with increasing force (Eq. 1). The value obtained for k_off at low applied force (in the interval with r_f = 0.64 nN/s), reflects an average duration of the Tn-PSM self-interaction in the range 0.6 seconds. The value obtained for k_off(f) in the subinterval r_f = 14 nN/s corresponds to an average lifetime of the Tn-PSM-lectin interaction equal to 0.063 seconds, whereas the distribution of observations obtained at the highest loading rates (the subinterval with r_f= 39 nN/s) indicate a lifetime equal to 0.018 seconds.

Figure 4 presents experimentally obtained rupture-force histograms obtained for Tn- PSM, converted into τ (f) distributions as described by Dudko et al.³³ By fitting Equation 4 to the experimental data (Figure 5, dotted line) we found that τ₁ (i.e. the lifetime estimated based on the observations obtained at low loading rate) was equal to 2.4 s, whereas τ₂ i.e. the lifetime estimated based on the observations obtained at high loading rate (second linear segment in Figure 5) was equal to 0.006 s. The distance x_β was, when determined based on the low loading rates, 0.30 nm, and decreased to 0.04 nm when determined based on the higher loading rates. Equation 4 was fitted to the experimental data obtained for the different mucins samples investigated in the present paper. The paramters τ (f) and x_β (nm) obtained for the values of ν = 1/2, 2/3 and 1, are presented in Table 4.

Tri-, Asialo Fd, Asialo Tri-, and Fd-PSM Self-Interactions

The distances x_β from the bound complex to the activation barrier governing the strength of the PSM self-interactions (Table 3 and 4) are, in the case of low external forces, in the range x_β = 0.34 (Asialo Tri-PSM) nm to x_β = 0.55 nm (Asialo Fd-PSM). For Tn-PSM, a transition from one linear regime to a second linear regime is observed at force loading rates > 15 nN/s (Figure 3). Data obtained at an average loading rate equal to 39 nN/s reflect the existence of a second energy barrier, located at x_β =0.02 nm. This inner barrier, which is revealed only at high loading rates, is the rate limiting barrier for bond disrupture under high external force load.^{30, 31} Values obtained for k_off (Table 3 and 4) indicate a longer average lifetime of the Tri- PSM self-interactions compared to Tn-PSM. For Asialo Fd-, Asialo Tri-, and Fd-PSM, parameter estimation is challenging due to the low number of observations of unbinding events, but the obtained parameter values indicate that these self-interactions have the shortest lifetime among the mucin samples investigated.

Discussion

A key prerequisite for successful investigation of molecular recognition forces by AFM is that the interacting molecules are firmly anchored to solid surfaces while not introducing steric constraints for the interaction.³⁴ In this study, mucins with different well defined glycan decoration patterns were immobilized on mica surfaces as well as on AFM tips by covalently conjugating carboxylic acids groups or amino group on the mucins with amino groups or carboxylic acid groups on the reactive surfaces, respectively. Control of the density of interacting molecules is in these processes obtained through tuning of the molecular concentrations and reaction times. In the present study the same PSM concentration and reaction times were used when preparing the PSM functionalized AFM cantilevers and tips.

Another requirement for successful investigation of molecular recognition forces by AFM is the absence of non-specific interactions. The observed absence of force jumps when retracting aminosilanized tips from aminosilanized mica surfaces, as well as when immobilising mucins onto only one of the two interacting surfaces, strengthens the conclusion that the force jumps observed when retracting mucin terminated AFM tips from surfaces functionalized surfaces are indeed due to the self-interactions of the mucins.

The Strength of Carbohydrate Self-Interactions

The number of published quantitative studies of carbohydrate self-interactions is limited. Tromas and coworkers studied the self-interaction of the trisaccharide Lewis^x (Le^X) determinant (Galβ1,4[Fucα1,3]GlcNAcα) using AFM.³⁵ The AFM force distance curves revealed multiple interactions, resulting in histogram distributions with multiple peaks. Autocorrelation analysis of the histograms with the pronounced periodicity of 20 ± 4 pN was used as a basis to suggest the interaction strength between two Le^x molecules to 20 ± 4 pN. This is in the same range as observed for hydrophobically modified hydroxyethyl cellulose self-interactions as well as hydroxymethylcellulose – amylose interactions investigated at low force loading rate.³⁶ For cell adhesion proteoglycans an average adhesive force of 40 ± 15 pN was measured.³⁷ The values observed in the present study for the strength of the mucin self-interaction (Table 3) are thus within the range observed for other carbohydrate selfinteractions. This supports the interpretations that the force induced rupture events observed in the present study are caused by the rupture of carbohydrate self – interactions and not interactions between the protein backbones of the mucins. The fact that the interaction strengths measured in the present study are also lower than those reported for specific protein - protein interactions using the same technique³⁸ strengthens this interpretation. However, resolving the contributions of protein-protein and carbohydrate–carbohydrate interactions will require further studies.

Lifetime of Mucin Self-Interaction

The dissociation rate constant k_off, determined for the different mucin self-interactions (Table 3) indicate that at low applied force loading rate, the lifetimes of the interactions are close to 1 second. At higher force loading rates it decreases a factor 10 or more (Table 3). The lifetime of the interactions determined using the procedure proposed by Dudko and coworkers³³ are presented in Table 4. They are, at low applied forces, in the range 0.5 – 4.5 seconds, and decreases to below 0.02 seconds for the high external force regime. The consistency between the data obtained for the mucin samples when using different analytical approaches to extract the relevant parameters, adds credibility to the data obtained. Furthermore, in recent studies of cartilage aggrecan, Harder and coworkers determined k_off to 0.178 ± 0.08 s⁻¹, corresponding to a mean lifetime of τ = 7.9 ± 4.9 s for the glycosaminoglycan self-interactions.³⁹ This is in the same range as the present data. However, for mucin-antibody interactions, larger lifetimes have been determined.⁴⁰ Harder and coworkers suggested that the short glycosaminoglycan bond allows the biological tissue to quickly respond to external load changes and thereby guarantee the integrity as well as the dynamic adaptiveness of the architecture of the extracellular matrix. It was further argued that the experiments revealed novel and fascinating aspects relating macroscopic tissue architecture and physiology to molecular properties. This notion also applies to our observations of the mucin self-interactions.

Energy Landscape of Mucin Self-Interactions

The correspondence between the x_β and τ data (Table 4), obtained for different values of ν, indicate that the precise nature of the free-energy surface of the underlying free-energy profile is not easy to determine. Furthermore, the experimental data presented in Figure 5 required the use of a two component model in order to account for τ (f) over the extended range of f to obtain a good fit of the data. The results presented in Table 4 for the different mucin samples are thus consistent with energy landscapes with two separate energy barriers. In Table 3 the existence of a second inner barrier, becoming rate limiting for r_f > 15 nN/s is revealed only for Tn-PSM. For Tri-PSM and Asialo Fd-PSM this transition appears not to have been captured when using the analysis approach underlying the numbers presented in Table 3. However, the data presented in Table 4 reveal the existence of a second barrier, hidden at low applied forces, also in the case of the other mucin samples investigated using this approach. For Tn-, Tri-, and Asialo Tri-PSM the outer energy barrier is located in the interval x_β = 0.30 – 0.45 nm, whereas the inner energy barrier is located in the interval x_β = 0.03 – 0.10 nm.

Carbohydrate self-interactions have to our knowledge not previously been investigated using this approach and The values of x_β obtained in the present study are however, at low external force, within the range reported for other biomolecular interactions. For GAG-self-interactions of cartilage aggrecan, x_β ≈ 0.31 ± 0.08 nm has been obtained.³⁹ For individual mucin1-antibody bonds, x_β ≈ 0.28 ± 0.02 nm.⁴⁰ Other examples include x_β ≈ 0.12 nm, x_β ≈ 0.3 nm and x_β ≈ 3 nm for the high, intermediate and low strength regime reported for the avidin-biotin interaction^41,42 as well as x_β ≈ 0.26 nm determined for the mannuronan AlgE4 polysaccharide – protein interaction.⁴³ The distance characterised by x_β ≤ 0.10 nm (Table 3 and 4), is shorter than reported previously for protein – ligand interactions.

Influence of Mucin Carbohydrate Decoration Pattern on Self-Interaction

All of the mucins showed self-interaction, but the probability for self-interaction (P_int in Table 2) was significantly higher in the case of Tn- and Tri-PSM. These differences could be due to either the different intrinsic interactions of the mucins, or to different conformation or density of the interacting molecules on the functionalized surfaces due to different reactivity during the immobilization reaction. The coupling via carboxyl groups on the mucin could potentially produce very tightly bound species since there are two glutamic acid units in the backbone tandem repeat in addition to the sialic acid residue carboxyl group. Due to a different content of sialic acid units in the different mucin samples, the observed low probability for interactions for some of the samples could be due to it being more tightly coupled to the surface than the others, and thus sterically constrained. However, the observed self-interaction probabilities of samples immobilized through N-terminal coupling to the surface revealed a consistency between the experimental series obtained using the different immobilization strategies (Table 2). These observations thus indicate that the influence of the immobilization strategies tested in this study on the observed self-interaction probabilities can not explain the observed differences in self-interaction probabilities.

Unlike proteins and nucleic acids, glycoprotein biosynthesis is not under direct genetic control, potentially resulting in heterogeneous products. The mucins investigated in the present study were obtained from pig glands, and hence contain a mixture of PSM molecules possessing glycan heterogeneity that exist in single and different animals. This should be kept in mind when evaluating the observed differences in self-interactions of the mucins. Data in Table 1 indicate that the Tn-, Asialo Fd-PSM and Fd-PSM samples are more homogenous in terms of glycan chains (mostly mono- and tetrasaccharide) than the Tri-, Asialo Tri- and Asialo Fd-PSM samples (mixture of mono-, di- and trisaccharide). In addition, Fd- and Tri- PSM possess different amounts of NeuNGl attached to the peptide bound GalNAc residues (Table 1). Therefore, conclusions concerning the influence of carbohydrate decoration patterns on self-interactions of the mucins appear more evident for Tn- and Asialo Fd-PSM. The observation that Fd-PSM and Asialo Fd-PSM show similar self-interaction probabilities (Table 2) indicates that the NeuNGl in Fd-PSM has little affect on this activity of the mucin. On the other hand, Tn-PSM consistently shows much greater probability of self-interaction than Asialo Fd-PSM and Fd-PSM (Table 2).

Biological Implications

The aggregation of mucins by intermolecular disulfide bonds between their cysteine rich terminal protein domains play important roles in their biological properties.⁹ However, the role of carbohydrate-carbohydrate interactions in mucins has not been investigated to our knowledge. Data in Table 2 indicates that PSM analogs lacking terminal protein domains but possessing the T- and Tn-antigens show evidence of self-association via carbohydrate-carbohydrate interactions. Importantly, Tn-PSM undergoes substantially greater self-association than Fd-PSM and asialo Fd (Table 2), which suggests that a higher density of GalNAcαSer/Thr epitopes leads to enhanced self-association. Indeed, the low self-association of Fd-PSM and asialo Fd-PSM may be due to the lower density of GalNAcαSer/Thr epitopes. The relatively high self-association of Tri-PSM (similar to Tn-PSM when corrected for background binding) may be due to the presence of the T- and Tn-antigens and NeuGl T and NeuGl Tn in the mucin. The latter two epitopes resemble the sialyl T- and sialyl Tn-antigens, respectively, which are also cancer antigens in man.⁴⁴ Removal of the NeuGl moieties in asialo Tri-PSM reduces self-association, which may be due to removal of NeuGl T- and Tn- antigens. However, more work is needed to answer this question.

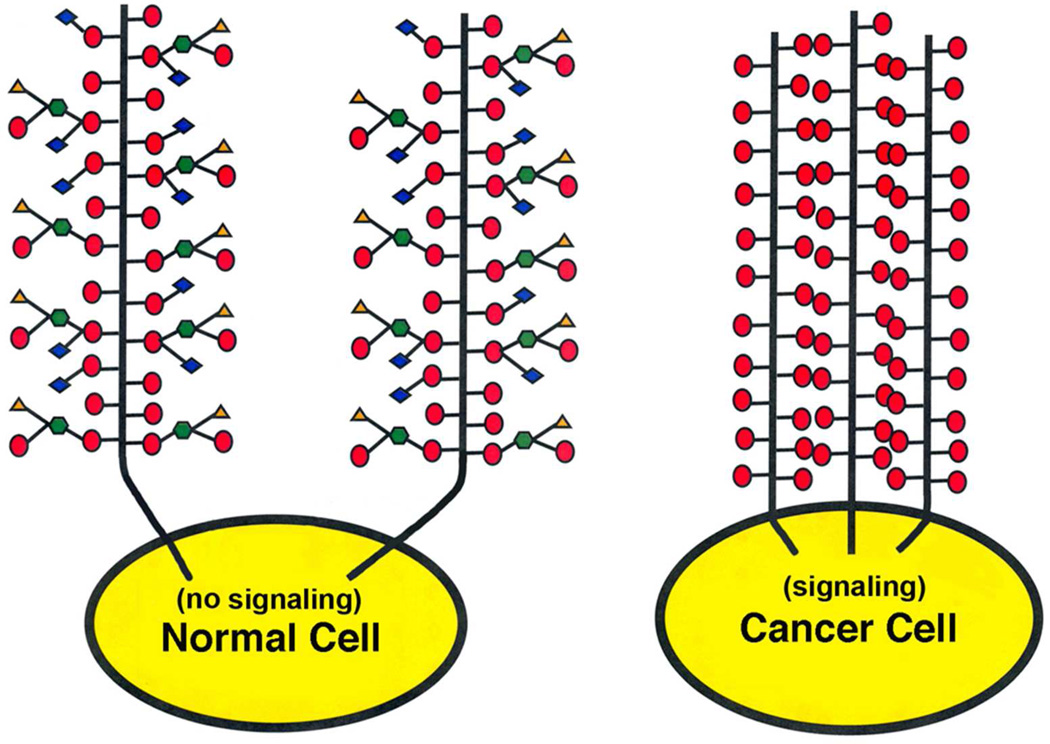
The present results have important implications for the enhanced expression of the Tn (and T) epitope in mucins such as MUC1 in adenocarcinomas.⁴⁵ MUC1 is a polymorphic transmembrane mucin found on epithelial cells that possess 20 to 120 polypeptide tandem repeat domains⁴⁶. Evidence indicates that the C-terminal cytoplasmic domain of MUC1 is involved in signal transduction mechanisms including T-cell activation and inhibition, and adhesion signaling responses (cf).^{47, 48} The naturally occurring longer chain carbohydrate epitopes on MUC-1 can be recognized by lectins such as the siglecs, E-selectin and galectins. Since many transmembrane glycoproteins undergo lectin mediated cross-linking leading to cytoplasmic signaling^{49, 50}, the possibility exist that the aggregation state of MUC1 and other members of the MUC family may be involved in signaling. It follows that aberrant expression of MUC1 possessing the Tn-antigen (or T-antigen) may enhance self-association via carbohydrate-carbohydrate interactions (Figure 6) and result in constituently active signaling by the receptor^{47, 48}, which is a hallmark of cancer.

Figure 6.

Hypothetic model of a normal cell possessing a transmembrane mucin receptor with both long and short chain O-linked glycans with no self-association, and a cancer cell possessing the same mucin with an aberrant high density of short chain Tn-antigen with self-association. The cytosolic domain of the aggregated cancer mucin constituently signals, while the normal cell mucin does not in the absence of a cross-linking ligand such as a lectin.

Importantly, studies by other groups have provided evidence for carbohydrate-carbohydrate interactions for truncated sugars including the Lewis^x cancer antigen (Galβ1,4(Fucα1,3)GlcNAcβ1,3Gal-) when presented in clustered arrays (cf).^{35, 51} Our data raises the possibility that expression of specific carbohydrate cancer antigens in high density may lead to self-association and alteration of the activity of mucins or mucin-like receptors. Interestingly, many carbohydrate cancer antigens including T, Tn and Le^x appear to be stage specific embryonic antigens⁵², and the present results may relate to their possible roles in embryonic development.

Conclusion

The results obtained in the present study add to the body of experimental evidence published over the last years suggesting a role of carbohydrate – carbohydrate interactions in intermolecular recognition processes. By quantifying the strength and lifetimes of self-associations between single molecular pairs of mucin molecules with different carbohydrate decoration patterns, we have taken a step towards unraveling the properties governing these molecular self-associations. Our observations reveal that the probabilities for self-interactions, as well as their strengths and lifetimes, depend on the precise decoration pattern. The probability for self interaction was highest for Tri- and Tn-PSM. The strength of the interactions varied in the range 27 to 50 pN at force loading rates close to 2 nN/s. The data indicate that the presence of a sialic acid group, as found in Fd-PSM and Tri-PSM, cannot alone account for the differences in interaction probability. The experimental data provided in the present paper illustrate the ability of complex carbohydrates found on glycoconjugates to modulate interaction strengths through variation in lifetime of low affinity binding sites created by oligosaccharide groups of varying structure and relative location. The data thus illustrate that sensitive force probes open for direct observations of the rupture of carbohydrate-mediated intermolecular bonds, and therefore have the potential to lead to important advances in our understanding of the relationship between structure and function in carbohydrate interactions. Furthermore, the data point towards a possible role of the T and Tn carbohydrate cancer antigens in modulating the self-association and signaling properties of membrane bound mucins in normal and transformed cells.

Abbreviations

PSM

porcine submaxillary mucin

Tn-PSM, Tri-PSM, Asialo Fd-PSM, Asialo Tri-PSM and Fd-PSM

are porcine submaxillary mucin with oligosaccharide distributions described in Table 1

AFM

atomic force microscopy

DFS

dynamic force spectroscopy

GalNAc

N-acetyl-D-galactosamine

Gal

D-galactose

Fuc

L-fucose

NeuNGl

N-glycolylneuraminic acid

Tn-antigen

GalNAcαThr/Ser

T-antigen

Galβ1,3GalNAcαThr/Ser