Abstract
Particle focusing in microfluidic devices is a necessary step in medical applications, such as detection, sorting, counting, and flow cytometry. This study proposes a microdevice that combines insulator-based and metal-electrode dielectrophoresis for the three-dimensional focusing of biological cells. Four insulating structures, which form an X pattern, are employed to confine the electric field in a conducting solution, thereby creating localized field minima in the microchannel. These electrodes, 56-μm-wide at the top and bottom surfaces, are connected to one electric pole of the power source. The electrodes connected to the opposite pole, which are at the sides of the microchannel, have one of three patterns: planar, dual-planar, or three-dimensional. Therefore, low-electric-field regions at the center of the microchannel are generated to restrain the viable HeLa cells with negative dielectrophoretic response. The array of insulating structures aforementioned is used to enhance the performance of confinement. According to numerical simulations, three-dimensional electrodes exhibit the best focusing performance, followed by dual-planar and planar electrodes. Experimental results reveal that increasing the strength of the applied electric field or decreasing the inlet flow rate significantly enhances focusing performance. The smallest width of focusing is 17 μm for an applied voltage and an inlet flow rate of 35 V and 0.5 μl/min, respectively. The effect of the inlet flow rate on focusing is insignificant for an applied voltage of 35 V. The proposed design retains the advantages of insulator-based dielectrophoresis with a relatively low required voltage. Additionally, complicated flow controls are unnecessary for the three-dimensional focusing of cells.
INTRODUCTION
Microfluidic devices, which have low-volume sample consumption and fast processing time, are widely used to manipulate both biological and synthetic particles. Particle focusing in microfluidic devices is a necessary step in medical applications, such as detection, sorting, counting, and flow cytometry.1 Numerous methods of particle focusing have been reviewed in the literature.2 For application in microflow cytometers and continuous-flow sorters, three-dimensional focusing avoids some of the problems that occur in two-dimensional focusing, such as the probability of coincident events due to the translocation of two or more particles past the detection region at the same time, and the variance of detected signals from particles passing through the sensor at different heights.3 Furthermore, three-dimensional focusing allows the particles to pass through the center of the microchannel with a steady velocity, which enables high-precision analysis of the particles.4
The methods of focusing particles in microfluidic devices can be simply classified as sheath flow focusing and sheathless focusing.2 Sheath flow focusing employs sheath fluids to pinch and focus the suspended particles. Hydrodynamic focusing by sheath flow5, 6 is widely employed for particle focusing; however, additional buffer inlets and precise flow control are required. Strip-based and chevron-based designs of grooved microchannels have been proposed6 for three-dimensional sheath flow focusing. A contraction-expansion array microchannel was proposed for three-dimensional hydrodynamic focusing with a single sheath flow.7 Sample and sheath flows are exposed to Dean flow in the contraction region; the sample flow is thus wrapped by the sheath flow, allowing focusing in three dimensions to be achieved. Sheathless focusing achieves particle focusing using either an externally applied or an internally induced force field in a pressure-driven or electrokinetic suspension flow. The transverse pressure gradient is generated by a V-shaped obstacle array to hydrophoretically confine the particles in the center of the microchannel.8 Standing surface acoustic wave (SSAW) and axisymmetric flow focusing9, 10, 11 have been also developed to achieve three-dimensional particle focusing.
Dielectrophoresis (DEP) is achieved under a non-uniform electric field generated by various electrode patterns. The direction of the DEP force is dominated by the dielectric properties of the cells and medium, which are functions of frequency. This has been widely used for the manipulation of DNA,12 bacterial,13 and cells14, 15 in diverse microdevices. Microelectrode patterns used for DEP and their applications have been previously reviewed.16, 17 Gagnon et al.18 have used the crosslinking agent glutaraldehyde (GLT) as a means to increase the DEP mobility differences between viable and nonviable yeasts to improve dielectrophoretic separation. The cross-over frequency of DEP was also measured to study the effect in their work. Geometrical constrictions in insulating structures have been proposed to produce non-uniform electric fields by squeezing the electric field in a conductive medium, a process termed insulator-based dielectrophoresis (iDEP).19 Group of Xuan 20, 21 has developed curvature-induced dielectrophoresis to separate and focus particles in serpentine or spiral microchannels under DC-biased AC electric fields. The position of particles in a microchannel can be accurately manipulated using dielectrophoresis generated by an electric field between liquid electrodes.22 Flores-Rodriguez and Markx23 proposed a design in which non-uniform electric fields are generated between microelectrodes on the top and the bottom of the microchannel, focusing particles along channels. Cheng et al.24, 25 proposed an integrated DEP microfluidic device using planar electrodes that form 3D DEP gates for the continuous filtering, sorting and detecting of bioparticles. The dielectrophoretic confinement of particles generated by microelectrodes on the top and the bottom of the channel has been employed to achieve particle focusing, detection, and counting.26, 27 Valero et al.28 proposed a cell sorting device based on multiple frequency dielectrophoresis (MFDEP), where forces arising from electric fields with different frequency components acted on cells flowing in the microfluidic device. Thus, cells with different dielectric responses were continuously focused to different equilibrium positions in the microchannel. Fiedler et al.29 manipulated latex beads and living cells in a device consisting miniaturized electrode arrays, which generated negative dielectrophoretic force to guide, trap, and deflect particles in the flowing liquid via the electrode arrangements of a planar funnel, an aligner, a field cage, and a switch. In a field-flow-fractionation (DEP-FFF) device proposed by Wang et al.,30 different cells were levitated by the balance between negative dielectrophoretic and sedimentation forces to different equilibrium heights and separated at differing velocities. Yu et al.31 fabricated an elliptic-like channel by the isotropic etching of glass and patterned microelectrodes on the circumference of the channel to generate negative DEP (nDEP) and achieve three-dimensional focusing of HL60 cells. Most existing approaches employ nDEP to achieve three-dimensional particle focusing. Chu et al.4 proposed a three-dimensional particle focusing channel that utilizes positive dielectrophoresis (pDEP) guided by a dielectric structure between two planar electrodes without any additional fluidic ports and top electrodes. An iDEP microdevice that can achieve the two-dimensional focusing of HeLa cells was designed and demonstrated in our previous work.32 The main purpose of the present study is to design and fabricate a microdevice that combines insulator-based and metal-electrode DEP for the three-dimensional focusing of biological cells. The nDEP force is employed to confine particles. Planar, dual-planar, and three-dimensional electrodes are used to achieve the three-dimensional focusing of particles. The effects of parameters, such as the strength of the applied electric field and the inlet flow rate, are also investigated.
THEORY AND DESIGN
The DEP force (FDEP) acting on a spherical particle of radius R suspended in a fluid with permittivity is given as
| (1) |
where is the real part of the Clausius-Mossotti factor and Erms is the root-mean-square of the external electric field, in an alternating current (AC) field. The Clausius-Mossotti factor (fCM) is a parameter of the effective polarizability of a particle. It varies with the complex dielectric properties of the particle and the surrounding medium, which are functions of the frequency of the applied field (f). The Clausius-Mossotti factor for a spherical particle is represented as
| (2) |
where and are the complex permittivities of the particle and the medium, respectively. The complex permittivity is related to the conductivity σ and angular frequency ω = 2πf as
| (3) |
where j equals . Therefore, the DEP force depends on the dielectric properties of particles and the medium solution, the particle size, and the frequency of the applied electric field. It can be either a positive DEP, which pulls particles toward the location of the high-electric-field region, or a negative DEP, which repels particles away from the high-electric-field region. Cells perform large induced-dipole moments which are significantly dependent on the frequency of the electric field applied.33 Previous studies34, 35 indicated that the dielectrophretic properties of cells could be classified based on their response in three frequency bands. The dielectrophoresis of cells is governed by the Clausius-Mossotti factor which is primarily determined by the cell surface charge at frequency below 200 Hz. The effective conductivity of the cell is the dominant contributing factor, while the frequency lies between 200 Hz to around 1.5 kHz. When the frequency is above 1.5 kHz, the dielectric permittivity of the cell becomes the controlling parameter of the dielectrophoretic response. The dielectric property of mammalian cells can be formulated by the protoplast model, in which the protoplast is a spherical particle consisting of a cytoplasm and a lossless membrane.36 According to this model and assuming that the conductance of the membrane is negligible, the effective permittivity could be derived; thus, the Clausius-Mossotti factor for viable cells can be rewritten as
| (4) |
where and are the time constants, while and are the electrical conductivity and permittivity of the cytoplasm, respectively. The parameter of and R represent the effective capacitance of the membrane and the radius of the cell, respectively. Moreover, the constants of and can be defined as and , respectively, where and are the electrical conductivity and permittivity of the suspension medium.
Based on the protoplast model, viable HeLa cells exhibit a negative dielectrophoretic response in a sucrose medium (ɛr = 78; σ = 1.76 × 10−3 S/m) at a low frequency of 1 kHz. The relative dielectric permittivity and conductivity of cytoplasm vary from 35 to 60 and 0.435 to 1.25 S/m, respectively.37 The average values of dielectric permittivity and conductivity of cytoplasm ( F/m; S/m,) were adopted herein to evaluate the Clausius-Mossotti factor. The diameter of a HeLa cell is around 10 μm ( 5 μm). The membrane capacitance of a HeLa cell () is 1.9 μF/cm2.38 Therefore, the relative dielectric permittivity and conductivity of viable HeLa cells are calculated as 1.073 × 104 and 1.1 × 10−10 S/m, respectively.39
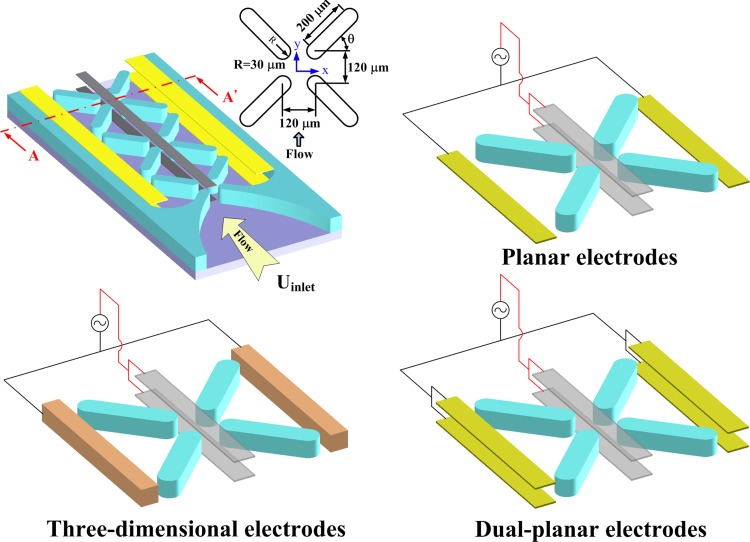
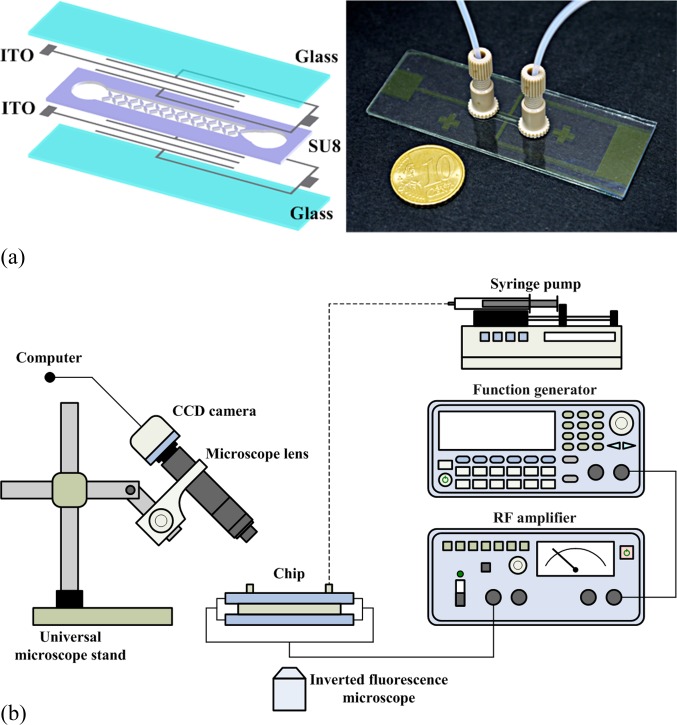
A schematic diagram of the proposed microfluidic chip is shown in Fig. 1. The microfluidic channel is 600 μm wide and 100 μm high. Four insulating structures, which form an X pattern, as shown in the microchannel, are employed to confine the electric field in a conducting solution, thereby creating localized field minima in the microchannel. The geometry and pattern of the insulators were investigated and optimized in our previous investigation.40 The insulator is 60 μm wide and 200 μm long. The length of the insulators along the direction of flow and that along the direction of the electric field are both 120 μm, while the inclined angle of the insulators is 45°. The designs of the inclined angle of the insulators equal to 30°, 45°, and 60° have been studied in our previous work.40 The design of 45° performed the highest value of the square of the electric field at the constriction, and it also exhibited the relatively high velocity at the center of the insulating structure. It implied that this design is the optimal one for the dielectrophoretic focusing of particles. The inlet flow field and the electric field are applied vertically. These electrodes, 56 μm wide at the top and the bottom surfaces, are connected to one electric pole. The electrodes connected to the opposite pole, which are at the sides of the microchannel, have one of three patterns: planar, dual-planar, or three-dimensional.
Figure 1.
Schematic illustration of three electrode designs for generating non-uniform electric fields.
NUMERICAL SIMULATIONS
Simulations of the electric and flow fields, as well as the particle trajectories, were performed using the commercial software package cfd-ace+ (ESI Group Inc., France). The finite element method and three-dimensional structured grids were employed to solve the governing equations. The governing equations for the flow field in this study are the continuity and momentum conservation (Navier-Stokes) equations. Discrete particles were tracked in the microchannel by solving the Lagrangian equations, taking into consideration both the dielectrophoretic force and the drag force in the simulation. Particle-particle interactions were ignored, and the electric field was assumed to be unaffected by the presence of particles.
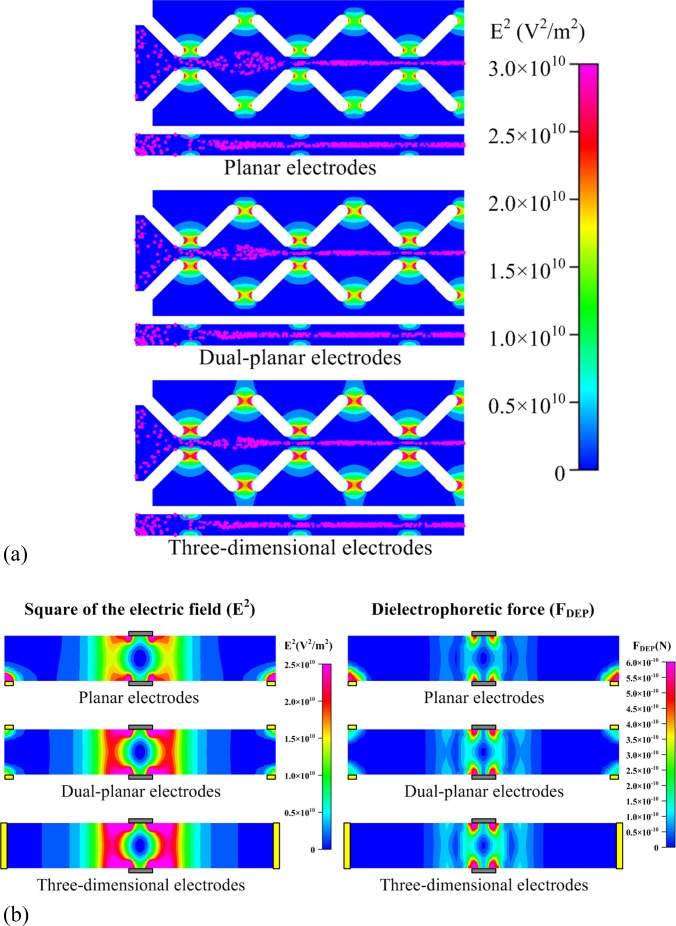
The simulation results of the square of the electric field (E2) and transient tracks of cells from the top view (at the middle plane in the microchannel, Z = 50 μm) and a side view (Y = 0) for the three electrode patterns are depicted in Fig. 2a. The applied voltage and the inlet flow rate were 25 V and 2 μl/min, respectively. Viable cells exhibit negative dielectrophoretic responses in a sucrose medium (ɛr = 78; σ = 1.76 × 10−3 S/m) at low frequency, and their electrical conductivities and permittivities can be calculated based on the protoplast model aforementioned.39 The relative dielectric permittivity and conductivity of the viable cells are 1.073 × 104 and 1.1 × 10−10 S/m, respectively. The electric field was constricted to the gap region between the insulating structures; thus, a stronger and highly non-uniform electric field was created near the edges of the insulating structures. The side view of the electric field reveals that high-electric-field regions formed at both the top and the bottom of the channel corresponding to the constricting areas, thereby providing dielectrophoretic confinement in the Z-direction. The cell sample was introduced into the microchannel and pre-confined hydrodynamically by the funnel-shaped insulating structures close to the inlet. The cells were distributed randomly at the inlet and confined by the negative dielectrophoretic forces when they passed through the constricting regions. The cells were repelled from the high-electric-field region and moved to the center of the microchannel, allowing the focusing of cells. The results of numerical simulations of the square of the electric field and the magnitude of the negative dielectrophoretic force (FDEP) acting on HeLa cells at the AA’ cross-section denoted in Fig. 1 are shown in Fig. 2b. The simulated square of the electric field reveals that low-electric-field regions at the center of the microchannel are generated by the insulating structures integrated with the proposed electrode designs to restrain the negative-dielectrophoretic-response cells. A suspended cell can move along with the fluid and pass through the constricting region. The DEP force (FDEP) acting on the negative-dielectrophoretic-response particles directs them toward the local minima of the electric field; the particles experience a repulsive force when they move near the constricting region. The direction of FDEP acting on HeLa cells with a negative dielectrophoretic response is toward the center of the channel. Hence, the cells deviated from the streamline and moved toward the confined region at the center of the microchannel. Stronger electric field for the dual-planar and three-dimensional electrodes than that for the design of planar electrodes was generated in both the vertical and horizontal directions.
Figure 2.
(a) Simulation results of the square of the electric field (E2) and transient tracks of cells from the top view (at the middle plane in the microchannel, Z = 50 μm) and a side view (Y = 0) for three electrode designs. (b) Simulation results of the square of the electric field (E2) and negative dielectric force (FDEP) at the AA’ cross-section denoted in Fig. 1 for three electrode designs. The inlet flowrate was 2 μl/min and the applied voltage was 25 V acting on HeLa cells in a sucrose medium (ɛr = 78; σ = 1.76 × 10−3 S/m).
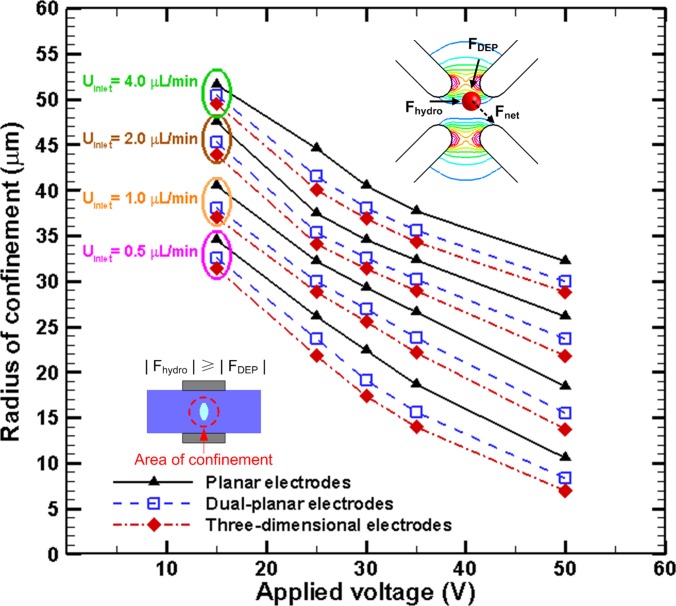
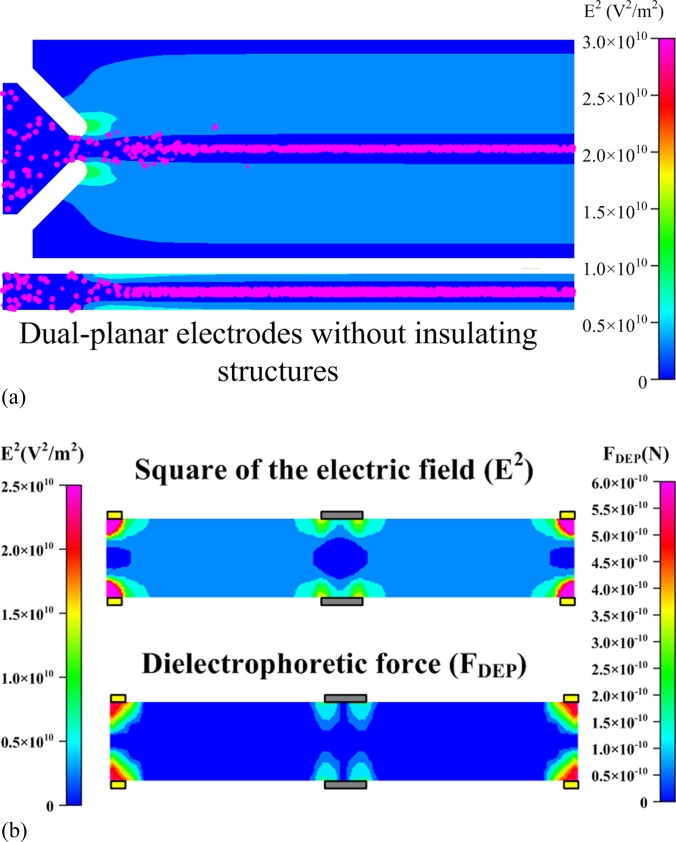
When cells are passing through a microfluidic channel, they not only experience the DEP force but also a hydrodynamic force along the direction of flow (X-direction). The hydrodynamic force (Fhydro) can be estimated using Stokes’s Law, which is = 6πμRU(x), where R and U are the radius and the velocity of the cell, respectively. The magnitude of the dielectrophoretic force acting on the cells in the YZ plane of the microchannel () has to be greater than, or comparable to, the hydrodynamic force the cells experience () for the cells to deviate from the streamline and move toward the confined region at the center of the microchannel. This indicates that the equilibrium between the hydrodynamic force and the DEP force can be employed to define the confined region and evaluate the performance of focusing. The areas of dielectrophoretic confinement under various inlet flow rates (Qinlet) and applied voltages for the three electrode patterns are illustrated in Fig. 3. The confined area was obtained by evaluating the area inside the contour where using NIH imagej software, and the radius of confinement was calculated using the expression . Inside the confined region, the magnitude of FDEP acting on the cells is smaller than that of (); therefore, the cells do not deviate from the streamline and tend to stay in this region. According to the simulation results, decreasing the inlet flow rate enhances focusing performance, which implies that the radius of the confined area is smaller. This also indicates that increasing the applied electric field significantly enhances focusing performance. According to numerical simulations, three-dimensional electrodes exhibit the best focusing performance, followed by dual-planar and planar electrodes. However, the fabrication of dual-planar electrodes is easier than that of three-dimensional electrodes. Based on this consideration, dual-planar electrodes were adopted for experiments on the three-dimensional focusing of cells. Moreover, the simulation results of the square of the electric field (E2) and transient tracks as well as the magnitude of the negative dielectrophoretic force (FDEP) acting on HeLa cells for the design of dual-planar electrodes without insulating structures under the applied voltage of 25 V and the inlet flow rate of 2 μl/min are revealed in Fig. 4 to investigate the effects of the insulators on the performance of focusing. For the design of dual-planar electrodes without insulating structures, the cells are focused at the center of the microchannel due to the Poiseuille velocity profile of flow and the dielectrophoretic confinement generated by the dual planar electrodes, as shown in Fig. 4a. However, the width of the cells distributed for the design without insulators is larger than that for the design with insulators; implying that the performance of focusing is improved by the insulating structures. The numerical results in Fig. 4b indicate that the insulating structures significantly enhance the dielectrophoretic confinement at the center of the microchannel. The area of dielectrophoretic confinement for the design of dual-planar electrodes with insulators is much smaller than that for the design without insulators. Therefore, the enhancement of focusing resulted from insulating structures is apparently proved herein.
Figure 3.
Simulation results of the area of dielectrophoretic confinement under various inlet flow rates (Qinlet) and applied voltages for three electrode patterns. The radius of the confined area for HeLa cells (with a cellular radius R) was obtained by computing the area of confinement illustrated in the inset, where FDEP at the cross section is smaller than the hydrodynamic force, Fhydro (estimated using Stokes’s Law, Fhydro = 6πμRU(x)).
Figure 4.
Simulation results of (a) the square of the electric field (E2) and transient tracks of cells; (b) the square of the electric field (E2) and negative dielectric force (FDEP) at the AA’ cross-section denoted in Fig. 1 for the design of dual-planar electrodes without insulating structures. The inlet flowrate and the applied voltage were 2 μl/min and 25 V, respectively.
EXPERIMENTAL RESULTS AND DISCUSSION
A lower conductive material of photoresist was adopted as a structure in the microchip for cell focusing, instead of a metallic pattern, to squeeze the electric field in a conducting solution and generate the regions of high field gradient. A schematic illustration of the fabricated microchip is shown in Fig. 5a. Nine sets of X-patterned insulating structures were designed for fabrication. The electrodes were patterned by etching two indium tin oxide (ITO) glass substrates using an HCl solution. The SU8-50 (MicroChem Corp. Newton, MA, U.S.A.) photoresist was spun onto one of the ITO glass substrates with microelectrodes to pattern the insulating microstructures (around 100 μm in height) for constricting the electric field. Inlet and outlet ports were drilled in the ITO glass substrate without insulating microstructures, which was then bonded to the ITO glass substrate with insulating microstructures by a UV-curable adhesive (ACU-TITE UV095, Chem-Mat Technologies Co. Ltd., USA). The HeLa cells used in this study were serially passaged as monolayer cultures in Dulbecco’s modified Eagle’s medium (DMEM, Gibco, Grand Island, NY, USA), 3.7 g of NaHCO3 per liter of medium added, and supplemented with 10% fetal bovine serum (FBS, Gibco, Grand Island, NY, USA) and 1% penicillin/streptomycin (Gibco, Grand Island, NY, USA). The cell culture dish (Falcon, Franklin Lakes, NJ, USA) was incubated in a humidified atmosphere containing 5% carbon dioxide at 37 °C; the medium was replaced every 1 to 2 days. Cells grown to sub-confluence were washed with phosphate-buffered saline (PBS, Biochrome, pH 7.4) and harvested by a 3.5-min treatment with Trypsin and 0.5% ethylenediaminetetraacetic acid (EDTA, Sigma, USA). Cells were stained using a standard live/dead fluorescence assay with calcein AM and propium iodide (Molecular Probes, Eugene, OR, USA) to identify the viability of cells. Samples with a concentration of 106 cells/ml were injected into the microfluidic channel using a syringe pump (Model KDS 101, KD Scientific Inc., Holliston, MA, USA). A function/arbitrary waveform generator (Agilent 33220A, Agilent Technology, Palo Alto, CA, USA), which was employed as the AC signal source, was connected to an RF amplifier (HSA-4011, NF Corporation, Japan) to apply the electric fields required for dielectrophoretic focusing in the microchannel. The top-view fluorescence images of cells in the microchannel were observed and recorded using an inverted fluorescence microscope (model CKX41, Olympus, Tokyo, Japan) mounted a CCD camera (DP71, Olympus, Tokyo, Japan) and a computer with Olympus DP controller image software. The dielectrophoretic focusing of HeLa cells in the direction of the height of the microchannel (Z-direction) was observed and recorded using a CCD camera (Moticam 2000; Motic China Group Co. Ltd.) with an Optem Zoom 125 microscopic lens (Qioptiq Imaging Solutions, USA) mounted on a universal microscope stand which was tilted 45°. A schematic illustration of the device is shown in Fig. 5b.
Figure 5.
Illustration of the (a) microchip for three-dimensional particle focusing and (b) experimental setup. An inverted fluorescence microscope mounted a CCD camera was employed to observe the track of fluorescent particles. A microscope lens was mounted on a microscope stand which is tilted 45° for observing the performance of three-dimensional focusing.
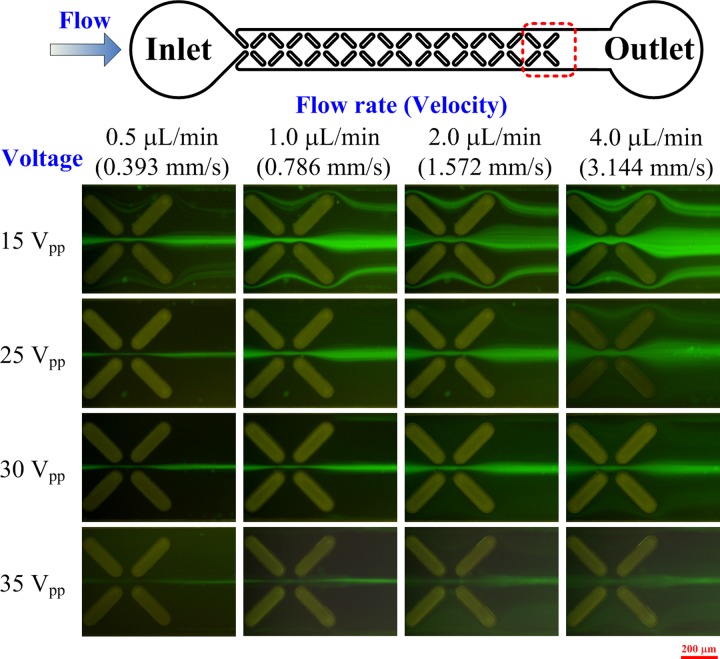
The experimental results of focusing HeLa cells at various inlet flow rates (0.5, 1, 2, and 4 μl/min) and applied voltages (15, 25, 30, and 35 V peak-to-peak; 1 kHz) are shown in Fig. 6. The fluorescent tracks of HeLa cells were observed at the last set of X-patterned insulating structures in the microchannel to demonstrate the performance of focusing. Experimental results reveal that increasing the strength of the applied electric field or decreasing the inlet flow rate significantly enhances focusing performance. When the applied voltage was 15 V, the cells were not focused even when the inlet flow rate was decreased to 0.5 μl/min. When the applied voltage was increased to 25 V and the inlet flow rate was 0.5 μl/min, the cells were focused at the center of the microchannel. Furthermore, when the applied voltage was increased to 35 V, the effect of the inlet flow rate on focusing became insignificant. A quantitative comparison of focusing experiment results is shown in Fig. 7.
Figure 6.
Experimental results of focusing HeLa cells at various inlet flow rates and electric field strengths at a frequency of 1 kHz. The images of the last set of X-patterned insulating structures demonstrate the performance of three-dimensional focusing.
Figure 7.
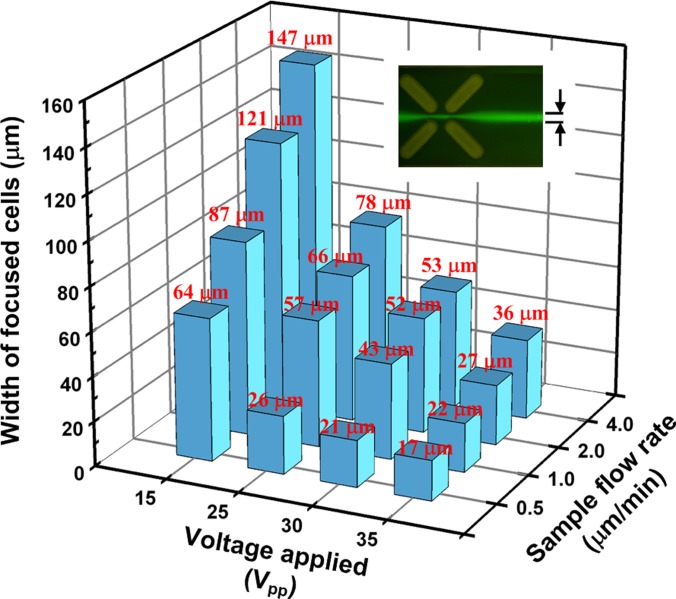
Measured widths of cells distributed at the outlet under various electric field strengths and inlet velocities. The widths of focused cells at the last set of X-patterned insulating structures were estimated using NIH imagej software.
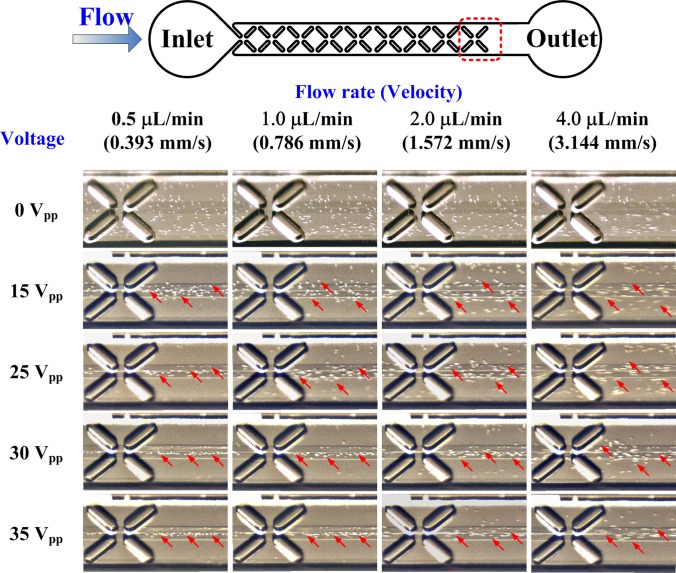
The widths of the cells distributed at the outlet were measured using the NIH imagej software to evaluate the focusing efficiency under various conditions. The measurement results reveal that the smallest width of focused cells was 17 μm when the applied voltage and the inlet flow rate were 35 V and 0.5 μl/min, respectively. HeLa cells, which have a diameter of approximately 10 to 15 μm, were focused into single file in the proposed microchip. When the inlet flow rate was below 2.0 μl/min at an applied voltage of 35 V, the widths of focused cells were below 30 μm. Fig. 8 shows the inclined view of the microchannel for various inlet flow rates and applied voltages to demonstrate the performance of three-dimensional focusing at the outlet. The cells are indicated by arrows. When the applied voltage was turned off, the cells became randomly distributed. The cells were focused for all inlet flow rates for an applied voltage of 35 V or above. Experimental results also reveal that the focusing performance in the Z-direction improved with increased applied electric field strength and decreased inlet flow rate. It is worthy to address that the electroosmotic induced fluid flow did not be observed in experiments since the external pressure-driven flow is much stronger than the electroosmotic flow.
Figure 8.
Experimental results of three-dimensional focusing at the last set of X-patterned insulating structures of the channel. The applied voltages had a frequency of 1 kHz. The arrows indicate HeLa cells.
The proposed device uses nDEP to achieve the three-dimensional focusing of cells at the center of the microchannel. For application in microflow cytometers and continuous-flow sorters, this device avoids some problems that occur in two-dimensional focusing. Furthermore, the problem of cells sticking to the channel walls is also avoided without using a surface coating, since particles are focused in both the horizontal and the vertical directions. iDEP utilizes insulating structures across the depth of the channel to distort the electric field, generating regions with a high electric field gradient. Thus, the non-uniform electric field is across the entire depth of the channel. However, a high voltage is required for iDEP manipulation. Metallic electrodes were fabricated in the microchannel to reduce the required voltage while retaining the advantages of iDEP. The proposed device is especially suitable for application in continuous-flow sorters and microfluidic detectors. Moreover, undesired biological objects can be filtered simultaneously using pDEP when they pass through the X-patterned insulating structures. The separation of viable/dead HeLa cells using the X-patterned structures was preliminarily demonstrated in our previous investigation.40
CONCLUSION
Insulator-based and metal-electrode dielectrophoresis were employed to confine cells with negative dielectrophoretic responses. Three electrode patterns, namely planar, dual-planar, and three-dimensional, were numerically designed to achieve the three-dimensional focusing of cells. According to numerical simulations, three-dimensional electrodes exhibit the best focusing performance, followed by dual-planar and planar electrodes. However, the fabrication of dual-planar electrodes is easier than that of three-dimensional electrodes. Based on this consideration, dual-planar electrodes were adopted for experiments on the three-dimensional focusing of cells. Experimental results reveal that increasing the strength of the applied electric field or decreasing the inlet flow rate significantly enhances focusing performance. When the applied voltage was 35 V, the effect of the inlet flow rate on focusing was insignificant. Furthermore, the smallest width of focused cells (17 μm) was achieved using an applied voltage and an inlet flow rate of 35 V and 0.5 μl/min, respectively. Complicated flow controls are unnecessary for the three-dimensional focusing of cells. The proposed microdevice is easy to operate and integrate into biological and synthetic particle focusing applications.
References
- Mostert B., Sleijfer S., Foekens J. A., and Gratama J. W., Cancer Treat. Rev. 35, 463 (2009). 10.1016/j.ctrv.2009.03.004 [DOI] [PubMed] [Google Scholar]
- Xuan X., Zhu J., and Church C., Microfluid. Nanofluid. 9, 1 (2010). 10.1007/s10404-010-0602-7 [DOI] [Google Scholar]
- Godin J., Chen C.-H., Cho S. H., Qiao W., Tsai F., and Lo Y.-H., J. Biophotonics 1, 355 (2008). 10.1002/jbio.200810018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu H., Doh I., and Cho Y., Lab Chip 9, 686 (2009). 10.1039/b812213j [DOI] [PubMed] [Google Scholar]
- Watkins N., Venkatesan B. M., Toner M., Rodriguez W., and Bashir R., Lab Chip 9, 3177 (2009). 10.1039/b912214a [DOI] [PMC free article] [PubMed] [Google Scholar]
- P. B.Howell, Jr, Golden J. P., Hilliard L. R., Erickson J. S., Mott D. R., and Ligler F. S., Lab Chip 8, 1097 (2008). 10.1039/b719381e [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee M. G., Choi S., and Park J. K., Lab Chip 9, 3155 (2009). 10.1039/b910712f [DOI] [PubMed] [Google Scholar]
- Choi S., Song S., Choi C., and Park J. K., Small 4, 634 (2008). 10.1002/smll.v4:5 [DOI] [PubMed] [Google Scholar]
- Shi J., Mao X., Ahmed D., Colletti A., and Huang T. J., Lab Chip 8, 221 (2008). 10.1039/b716321e [DOI] [PubMed] [Google Scholar]
- Kim Y. W. and Yoo J. Y., Lab Chip 9, 1043 (2009). 10.1039/b815286a [DOI] [PubMed] [Google Scholar]
- Kim Y. W. and Yoo J. Y., Biosens. Bioelectron. 24, 3677 (2009). 10.1016/j.bios.2009.05.037 [DOI] [PubMed] [Google Scholar]
- Du J.-R., Juang Y.-J., Wu J.-T., and Wei H.-H., Biomicrofluidics 2, 044103 (2008). 10.1063/1.3037326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koklu M., Park S., Pillai S. D., and Beskok A., Biomicrofluidics 4, 034107 (2010). 10.1063/1.3479998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang F., Yang X., Jiang H., Bulkhaults P., Wood P., Hrushesky W., and Wang G., Biomicrofluidics 4, 013204 (2010). 10.1063/1.3279786 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sancho M., Martínez G., Muñoz S., Sebastián J. L., and Pethig R., Biomicrofluidics 4, 022802 (2010). 10.1063/1.3454129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pethig R., Biomicrofluidics 4, 022701 (2010). 10.1063/1.3457488 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pethig R., Biomicrofluidics 4, 022811 (2010). 10.1063/1.3456626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gagnon Z., Mazur J., and Chang H.-C., Biomicrofluidics 3, 044108 (2009). 10.1063/1.3257857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lapizco-Encinas B. H., Simmons B. A., Cummings E. B., Fintschenko Y., Electrophoresis 25, 1695 (2004). 10.1002/elps.v25:10/11 [DOI] [PubMed] [Google Scholar]
- Church C., Zhu J., Wang G., Tzeng T. -R. J., and Xuan X., Biomicrofluidics 3, 044109 (2009). 10.1063/1.3267098 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J. and Xuan X., Biomicrofluidics 5, 024111 (2011). 10.1063/1.3599883.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demierre N., Braschler T., Linderholm P., Seger U., van Lintel H., and Renaud P., Lab Chip 7, 355 (2007). 10.1039/b612866a [DOI] [PubMed] [Google Scholar]
- Flores-Rodriguez N. and Markx G. H., J. Micromech. Microeng. 16, 349 (2006). 10.1088/0960-1317/16/2/020 [DOI] [Google Scholar]
- Cheng I.-F., Chang H.-C., Hou D., and Chang H.-C., Biomicrofluidics 1, 021503 (2007). 10.1063/1.2723669 [DOI] [Google Scholar]
- Cheng I.-F., Lin C.-C., Lin D.-Y., and Chang H.-C., Biomicrofluidics 4, 034104 (2010). 10.1063/1.3474638 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes D., Morgan H., and Green N. G., Biosens. Bioelectron. 21, 1621 (2006). 10.1016/j.bios.2005.10.017 [DOI] [PubMed] [Google Scholar]
- Morgan H., Morgan H., Holmes D., and Green N. G., IEE Proc.: Nanobiotechnol. 150, 76 (2003). 10.1049/ip-nbt:20031090 [DOI] [PubMed] [Google Scholar]
- Valero A., Braschler T., Demierre N., and Renaud P., Biomicrofluidics 4, 022807 (2010). 10.1063/1.3430542 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiedler S., Shirley S. G., Schnelle T., and Fuhr G., Anal. Chem. 70, 1909 (1998). 10.1021/ac971063b [DOI] [PubMed] [Google Scholar]
- Wang X.-B., Yang J., Huang Y., Vykoukal J., Becker F. F., and Gascoyne P. R. C., Anal. Chem. 72, 832 (2000). 10.1021/ac990922o [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu C., Vykoukal J., Vykoukal D. M., Schwartz J. A., Shi L., and Gascoyne P. R. C., J. Microelectromech. Syst. 14, 480 (2005). 10.1109/JMEMS.2005.844839 [DOI] [Google Scholar]
- Jen C. P., Huang C. T., and Weng C. H., Microelectron. Eng. 87, 773 (2010). 10.1016/j.mee.2009.11.118 [DOI] [Google Scholar]
- Pethig R. and Kell D. B., Phys. Med. Biol. 32, 933 (1987). 10.1088/0031-9155/32/8/001 [DOI] [PubMed] [Google Scholar]
- Burt J. P. H., Al-Ameen T. A. K., and Pethig R., J. Phys. E: Sci. Instrum. 22, 952 (1989). 10.1088/0022-3735/22/11/011 [DOI] [Google Scholar]
- Burt J. P. H., Pethig R., Gascoyne P. R. C., and Fecker F. F., Biochim. Biophys. Acta 1034, 93 (1990). [DOI] [PubMed] [Google Scholar]
- Jones T. B., Electromechanics of particles (Cambridge University Press, New York, 1995). [Google Scholar]
- Pethig R., in Encyclopedia of Surface and Colloidal Science (Taylor & Francis, London, 2006), pp. 1719–1736. [Google Scholar]
- Asami K., Takahashit Y., and Takashima S., Biophys. J. 58, 143 (1990). 10.1016/S0006-3495(90)82360-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jen C. P. and Chen T. W., Biomed. Microdevices 11, 597 (2009). 10.1007/s10544-008-9269-1 [DOI] [PubMed] [Google Scholar]
- Jen C. P., Huang C. T., and Shih H. Y., Microsyst. Technol. 16, 1097 (2010). 10.1007/s00542-009-0947-6 [DOI] [Google Scholar]