Manipulating particle trajectories with phase-control in surface acoustic wave microfluidics

Abstract

We present a 91 MHz surface acoustic wave resonator with integrated microfluidics that includes a flow focus, an expansion region, and a binning region in order to manipulate particle trajectories. We demonstrate the ability to change the position of the acoustic nodes by varying the electronic phase of one of the transducers relative to the other in a pseudo-static manner. The measurements were performed at room temperature with 3 μm diameter latex beads dispersed in a water-based solution. We demonstrate the dependence of nodal position on pseudo-static phase and show simultaneous control of 9 bead streams with spatial control of −0.058 μm/deg ± 0.001 μm/deg. As a consequence of changing the position of bead streams perpendicular to their flow direction, we also show that the integrated acoustic-microfluidic device can be used to change the trajectory of a bead stream towards a selected bin with an angular control of 0.008 deg/deg ± 0.000(2) deg/deg.

INTRODUCTION

Over the past decade, there has been significant progress made in the field of acoustic-microfluidic devices.^{1, 2, 3, 4} Acoustic-microfluidic devices have been used to demonstrate a host of novel applications: individually addressable pumps,^{5, 6} jetting,⁷ atomization,^{1, 8} turbulent mixing,^{9, 10, 11, 12} particle separation,^{13, 14, 15, 16, 17, 18, 19, 20} and focusing particles into discrete foci.^{21, 22, 23, 24, 25} In many instances, a surface acoustic wave (SAW) is generated by an interdigitated transducer (IDT) that couples the electromagnetic wave to an acoustic wave by a piezoelectric substrate. Two IDTs that oppose each other form a SAW resonator where an acoustic wave can be transmitted from one IDT to the other. As a function of frequency, the magnitude of the transmission is a maximum at the resonance frequency. SAW resonators are particularly attractive, because this configuration can be used in some cases to generate a standing acoustic shear wave along the surface of the piezoelectric substrate,²⁶ creating pressure nodes. Particles dispersed in a buffer solution respond to the pressure wave by localizing in a manner that can be precisely controlled by an easily tunable external means (phase, frequency, or amplitude). Importantly, experiments have shown that SAWs at low powers (comparable to those investigated here) do not damage some types of cells;²⁷ hence it is feasible to extend this technology for applications in biomedical devices (such as fluorescence-activated cell sorting).

In these experiments, the force (F_r) acting on an individual particle was determined by assuming a homogeneous distribution of non-interacting spheres dispersed in a fluid interacting with a standing acoustic plane wave.^{28, 29, 30, 31} The acoustic force is given by

$$F_r\approx -F_o\sin (2\mathit{kx}+\Delta \varphi ),$$ (1)

where the constants F_o and k are the wavelength and the maximum acoustic force, respectively. F_o is dependent on a number of particle and fluid properties for more details see Refs. ^{23, 24, 25}. The independent variable x is the position of the particle in the lateral direction in the microfluidic channel. Note that we have included the phase difference (Δϕ) between the SAW transducers in Eq. 1. Included in the supplementary material,³² we derived approximate expressions for the equation of motion of particle in the presence of an acoustic force, the time to coalesce, and a means to approximate the maximum acoustic force.

From Eq. 1, we see that the acoustic phase difference is a particularly elegant means to tune the position of the acoustic nodes and maxima and hence the location of the particles. This is due to the fact that it is trivial to precisely change the phase (e.g., with voltage-controlled phase shifters), which is also conducive to automation. Therefore, the inherent spatial limitations are mostly dictated by the precision of the phase shift. Arguably, the most significant potential impact of phase-control is on the reemerging field of acoustic tweezers,^{21, 22, 23} where phase-based manipulation could provide a means to control a particle in the x-y plane. Such a manipulation approach could achieve precision comparable to the precision of dielectrophoretic techniques like optical tweezers.³³ In contrast with optical tweezers, this approach would have comparatively simpler bench-top setup, making integration with other portable microfluidic sensing and manipulation techniques easier. One imminent application is that phase-control could provide access to multiple bins for ultrafast sorting, rather than using a single IDT and changing the state of the IDT from “on” to “off” to control the particle collection location or bin.^{19, 20}

To date, no reports have demonstrated pseudo-static (or time independent) phase-based control in acoustic-microfluidic devices; however, experiments on a large-scale device (more than 3 orders of magnitude larger cross-sectional area) have been performed.³⁴ This large-scale experiment found a nonlinear dependence of node position on phase,³⁴ which they attribute to a mismatch between their transducers. Nonlinear phase control could limit the precision of the manipulation technique and could be irreproducible device-to-device. Related experiments explored the dependence on detuning the frequency of one SAW transducer relative to the other,³⁵ creating a beat pattern. This produces a traveling stream that can be moved right or left by varying the frequency difference between the sources rather than the phase. Phase-control is a precise means to manipulate particles that does not require a second frequency source, which could limit applications for portable diagnostic equipment. This work is the first demonstration of predictable and precise manipulation of microscopic particles by a pseudo-static phase shift using simple electronics that are easily integrated with microfluidics.

In what follows, we quantitatively demonstrate the pseudo-static phase-based control of the position of a set of collimated non-interacting particles (or beads streams) in a microfluidic channel and use this control to predictably change the trajectories of those streams in an expansion region. We first explain the experimental setup and the various components used to perform the proof-of-concept experiment. We give a qualitative overview of the effect of turning the SAW on and off and changing the phase. We subsequently extract quantitative information about each bead stream from the measurements, such as the average height and width of each stream. We quantitatively determine the phase control of the position of each bead stream and demonstrate that by changing the position of each stream in a direction perpendicular to its flow, we can change the trajectory of a stream in an expansion region and affect its direction to a corresponding bin. Finally, we provide expressions to predict the phase control position in a straight channel (for a given wavelength) and trajectory (for a given wavelength and geometry).

MATERIALS AND METHODS

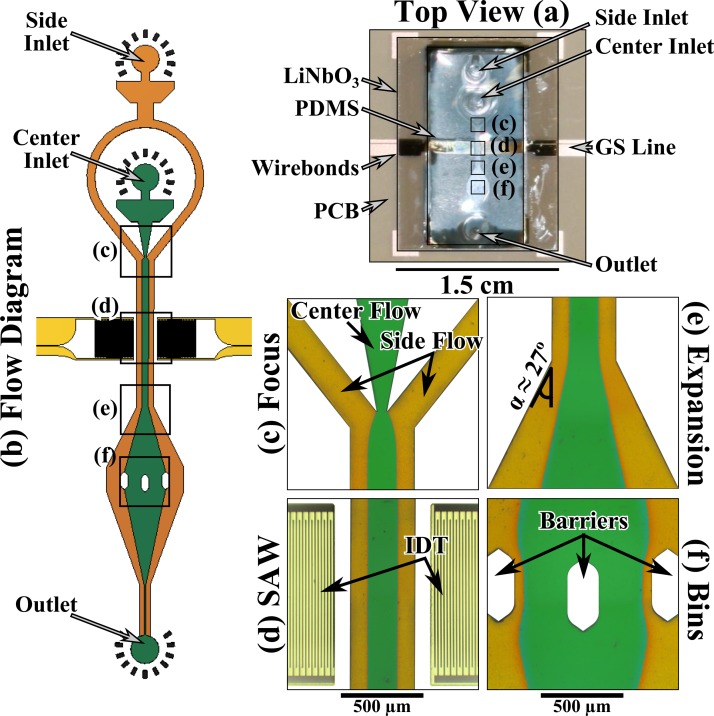
The acoustic microfluidic device consists of three components: a polydimethylsiloxane (PDMS) microfluidic circuit, a piezoelectric double-side polished single crystal LiNbO₃ substrate with microelectronics, and a custom-fabricated printed-circuit board (PCB) with a window. In Fig. 1a, we show a top view of the completed device. The integrated acoustic-microfluidic device was mounted on a PCB carrier such that the device could be imaged through the window.³² The PDMS microfluidic circuit was bonded to a 100 nm thick SiO₂ layer sputtered on the 128° Y-X cut double-side polished single crystal LiNbO₃ chip. The gold ground-signal (GS) transmission lines on the LiNbO₃ chip were connected to the copper GS transmission lines on the PCB by gold wirebonds. Finally, SubMiniature version A (SMA) edge connectors were soldered onto the PCB to allow for connector-based measurement. The entire assembly was finally mounted onto a brass holder to add structural support and allow for easy handling. Figure 1b shows a schematic of the fluid flows. Figures 1c–1f show corresponding micrographs of the microfluidic circuit filled with green and yellow buffers. A thorough description of the fabrication and an additional picture of the complete device can be found in the supplementary material.³²

Figure 1.

(a) The integrated acoustic microfluidic device (about the size of a US 10¢ piece) mounted on a PCB. The PDMS microfluidic circuit was bonded to a double-side polished single crystal LiNbO₃ chip. (b) The flow diagram of the microfluidics. (c) The flow focus that was used to focus the green buffer into the center of the channel and away from the side walls with yellow buffer. (d) The SAW region consists of two IDTs made from 750 nm of gold that were fed by ground-signal lines with a 91 MHz signal. The SAW was encased in an air void fabricated in the PDMS that also contains the microfluidics. (e) The 27° expansion region that was used to change the trajectory of the bead streams. (f) The binning region that consists of 3 barriers placed on an arc, creating four equally spaced bins. The panels (c)-(f) are digitally manipulated micrographs.

In Fig. 1c, there were two inlets that created a flow focus, where the side flows kept the particles suspended in the center flow away from the side walls of the microfluidic channel. After the flow focus, the IDTs enabled us to apply a standing SAW on the fluid (see Fig. 1d). The fluid then entered a 27° expansion region (Fig. 1e) that had the effect of changing the angular trajectory of a particle (or bead) positioned in the microfluidic channel by the SAW. The fluid was then divided into four bins (Fig. 1f) by three barriers in the PDMS.

EXPERIMENTAL SETUP AND IMAGE PROCESSING

Once the device was fabricated, we connected the SMA connectors to an arbitrary waveform generator (AWG) and a pair of radio frequency +30 dBm amplifiers. The AWG had two outputs whose phase and amplitude could be controlled independently. At the operating frequency of 91 MHz, the insertion loss of the SAW resonator was approximately −16 dB.³² By working at a higher frequency, we were able to significantly decrease the footprint of the microelectronics compared to the literature.^{23, 24, 25} We amplified the signal by +30 dBm to a total incident power of around 25 mW (or 14 dBm) for each SAW without the presence of the fluid. This power was comparable to bulk acoustic wave techniques.^{16, 17, 18} After we connected the electronics, we attached the microfluidics to a syringe pump by polyethylene tubing. The tubing was seated and sealed into the PDMS circuit and then routed to the syringe pump and a conical tube for the waste. When both the electronics and microfluidics were connected, the entire device was mounted upside down such that we could image the microfluidics through the LiNbO₃ chip. A linear polarizer was placed over the window to eliminate reflections.

We mixed a buffer solution of equal parts of water to concentrated buffer in two 500 ml batches. We then mixed in 10 mg of red dye for the side flow and 10 mg blue dye for the center flow, which appear as yellow and green due to the linear polarizer. Finally, 500 μl of 3 μm diameter latex beads at a concentration of 1% by weight was added to the blue colored buffer. The experiment was performed with the position of the microscope fixed and the flow rate of the syringe pump was set to 30 μl/min. After the flow was stabilized, we acquired a background image with the IDTs off, and another image with the phase set to a fixed value. We stepped the relative phase shift between the IDTs (Δϕ) by 36° from 360° to −360°, for a total of 21 discrete phase shifts. The beads in the SAW region were moving at a rate of approximately 30 mm/s in the flow direction. The beads took approximately 3 ms to coalesce into streams and the maximum acoustic force on the beads due to the SAW was 95 pN.³² The total time spent by a given bead in the SAW region was 30 ms, but the force decreased significantly once the beads coalesced into streams. Furthermore, we did not see any evidence of acoustic forces radiating beyond the extent of the SAW region, which is likely due to acoustic damping by the PDMS.

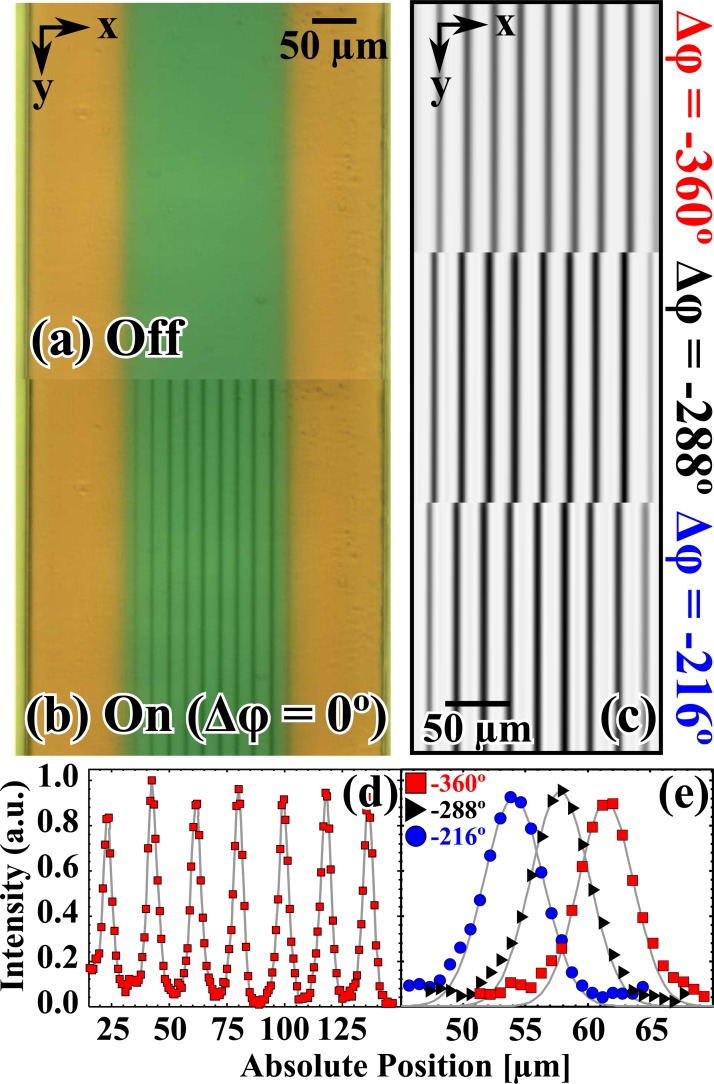
Given the experimental limitations (speed of the image acquisition), we were unable to resolve the individual beads while the flow was turned on; however, when the flow was turned off we could see individual beads in the streams. The exposure time was set to 200 ms, which in effect produced a time-averaged image. As a consequence, the individual beads appeared as darkly shaded vertically running lines (or bead streams), which indicated their average lateral position (see Fig. 2b). Once the IDTs were turned “on” (Fig. 2b) the beads coalesced into coherent streams that formed at the nodes of the pressure wave, and when IDTs were turned “off” the bead streams disappeared due to the fluid flow (Fig. 2a). There are a total of 9 streams, which is due to the fact that the width of the center flow is roughly 9 times half the acoustic wavelength. This enabled us to simultaneously explore multiple trajectories for a given Δϕ, bead collimation near the side flows, and it was more suited to our instrumentation. In Fig. 2c, we show change in the position of the bead streams as Δϕ was stepped through Δϕ = −360° (top panel), Δϕ = −288° (middle panel), and Δϕ = −216° (bottom panel). The bead streams move to the left in Fig. 2c, which qualitatively shows the effect of varying the pseudo-static acoustic phase shift.

Figure 2.

Micrographs of the SAW region with the 91 MHz signal in the off (a) and on (b) states, Δφ = 0° in (b). The center flow (green) was the buffer with 3 μm latex beads, and the side flows were yellow. (c) Close-ups of the beads streams (vertically running dark stripes) with different relative phase shifts: Δφ = −360° (top panel), Δφ =− 288° (middle panel), and Δφ =− 216° (bottom panel). (d) The peak height of the bead streams after the SAW region for Δφ =− 360° (red squares). (e) The third peak in (d) and that peak shown at different phases: Δφ =− 288° (black triangles), and Δφ =− 216° (blue circles). The gray lines are the Gaussian fits to data.

We cropped the images to same absolute position and ensured that the y-axis orientation ran vertically with the microfluidic channel. We then averaged the intensity along the vertical pixels and subtracted the background (a successive image with the transducers in the “off” state). In Fig. 2d, we show the normalized intensity averaged over the vertically running pixels for Δϕ = −360° (red squares). Then, each peak of each image was isolated and fit individually to a Gaussian distribution, $f(x)=A·\mathit{exp}(-\frac{{(x-\mathit{xo})}^2}{2{\sigma }^2})$ and the centroid (x_o), amplitude (A), and square root of the variance (σ) were obtained. In Fig. 2d, we show the effect of changing the relative phase on a single peak: Δϕ = −360° (red squares), Δϕ = −288° (black triangles), and Δϕ = −216° (blue circles). The gray lines in Fig. 2e are the Gaussian fits to the bead streams. In the supplementary material,³² we show a table of A and σ of the Gaussian peaks that fell in the specified x-position in the microfluidic channel. Interestingly, the peaks appeared to be sharp in width and uniform in height over the channel width regardless of the position in the channel. The stream widths were approximately 1.5 bead widths.

ANALYSIS AND RESULTS

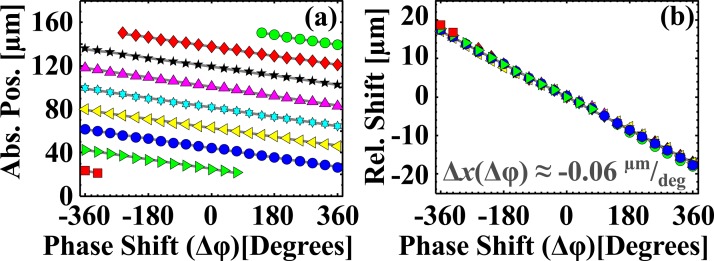
Once we obtained the centroids of each bead stream at a given Δϕ, we performed a linear fit as a function of phase (i.e., centroid versus phase), which yielded both the phase control of the bead stream position and the stream spacing. The results and uncertainties are shown in Table TABLE I.. Figure 3 shows the centroids of each bead stream as a function of Δϕ (Fig. 3a) shown as different colored symbols.

TABLE I.

Peak vs. phase. We report the fit equations for the corresponding solid gray lines shown in Fig. 3a.

Symbol	Δx/Δϕ (μm/deg)	xo(μm)
	− 0.064	5.450
	− 0.059 ± 0.002	30.421 ± 0.306
	− 0.059 ± 0.001	54.013 ± 0.138
	− 0.056 ± 0.001	76.975 ± 0.248
	− 0.058 ± 0.001	99.986 ± 0.220
	− 0.059 ± 0.001	123.240 ± 0.145
	− 0.056 ± 0.001	145.981 ± 0.223
	− 0.057 ± 0.001	168.711 ± 0.142
	− 0.062 ± 0.002	193.111 ± 0.594

Figure 3.

(a) The centroid of the Gaussian fit shown for each bead stream as a function of phase. The different symbols and colors indicate a distinct bead stream. (b) We subtracted the intercepts from linear fits in (b) from the data to show that the collapse wline, Δx(Δφ) ≈ −0.06 μm/deg.

After we obtained the linear fits, we fit the intercepts of the streams versus stream number to obtain the acoustic wavelength from the slope, $\frac{\lambda }{2}$= 23.120 μm ± 0.174 μm. We subtracted the intercept from each data set to confirm that the data collapsed to a single line (Fig. 3b). We obtained the phase control of the bead streams, $\frac{\Delta x}{\Delta \phi }$=− 0.058 μm/deg ± 0.001 μm/deg. Inserting the wavelength into Eq. 1, we calculated a slope of $\frac{\Delta x}{\Delta \phi }$= $\frac{\lambda }{4\pi }$= −0.064 μm/deg, which was consistent with the measured value. When the phase was varied through Δϕ = −360° to Δϕ = 360°, streams near the edges of the center flow (e.g., red squares or green circles) disappeared or appeared from the boundary between the center flow and side flows. As a result, some bead streams have more or fewer data points when compared to others. This could point to a novel means to shuttle particles in and out of a center flow, and it is a natural extension of the existing work in the literature.²⁴

Active control of node position in an acoustic-microfluidic device will enable many new techniques. As alluded to in the introduction, one possible application of phase-based control is the ability to change trajectory of a stream of particles, which was accomplished by the 27° expansion region in Fig. 1e. By moving a stream of particles in a direction perpendicular to the direction of their flow in the SAW region (Fig. 1d), the trajectory of the particles is changed and preserved by laminar flow in the expansion region (Fig. 1e).

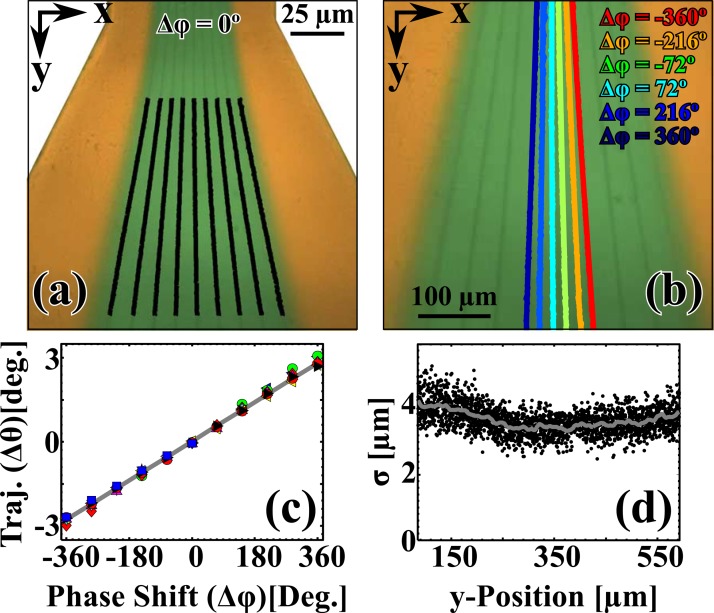
In Fig. 4a, we show the expansion region at Δϕ = 0° with the centroids of each bead stream shown as the solid black lines. Figure 4b shows composite image of the deflection of the center-most bead stream in Fig. 4a as a function of Δϕ superimposed over Fig. 4a. Here, we show a discrete selection of Δϕ with Δϕ = {−360° (red), −216° (orange), −72° (green), 72° (cyan), 216° (light blue), and 360° (navy)}. The collapsed change in trajectory as a function of Δϕ is shown in Fig. 4c. Note that all ten bead streams collapse to the same curve, as this indicates uniform behavior even for the streams near the interface with the sideflow. This suggests that devices designed with a single stream that swept a wider range of trajectories would also follow a linear dependence. The slope of the composite data set was 0.008 deg/deg ± 0.000(2) deg/deg. The trajectory can be written in terms of the x-position in the channel relative to the width of the channel and angle that parameterizes the expansion region, θ = $\frac{2\alpha x}{w}$. Inserting the values for this experiment, we found a slope of $\frac{\Delta \phi }{\Delta \theta }$= $\left(\frac{\alpha \lambda }{2\pi w}\right)$ = 0.009 deg/deg, which was consistent with the measured value.

Figure 4.

(a) The expansion region of the device at Δφ = 0°. The solid black lines are the centroids of the Gaussian fits for each stream taken for each x-axis row of pixels. (b) A close-up of the expansion region at Δφ = 0°. The centroids of the Gaussian fits shown for the center-most bead stream as a function of phase (Δφ = {−360° (red), −216° (orange), −72° (green), 72° (cyan), 216° (light blue), and 360° (navy)}). (c) The change in trajectory (Δθ) as a function of Δφ. The different colored points are the collapsed data for the different streams. The solid gray line is the fit (Δθ(Δφ) ≈ −0.01 deg/deg). (d) The square root of the variance (σ) of the Gaussian fit shown as a function of the y-Position. The origin was taken at the beginning of the black lines in (a). The gray solid line was added to guide the eye.

Furthermore, it is interesting that the relative widths of the streams (shown in Fig. 4d) remained essentially constant over the entire stream path and did not vary from stream to stream. This indicates that the beads remained collimated even significantly far away from the SAW region (Fig. 1d) and in an expansion region (Fig. 1e), where one might expect to see some broadening. In this case (e.g., temperature, particle size, and viscosity of the solution, etc.), the broadening of the collimated streams is dominated by the deviation in the beads initial position in the SAW region, rather than by diffusion. For example, a small perturbation in the SAW region of 0.5 μm would result in a broadening of about 1 μm approximately 2 mm into the expansion region, while diffusion would contribute around 10 nm to the total broadening over the same distance. Fig. 1d could indicate that the streams were highly collimated, or it is also possible that we were unable to resolve this effect with our instrumentation. The average σ in this region was 3.665 μm ± 0.191 μm, which is comparable to σ in the SAW region (Fig. 1d). We further demonstrated the applicability of phase-based control of particle binning in a movie that is shown in the supplementary material.³² The supplementary movie shows a close up of the binning region (Fig. 1f).³² We show a user continuously sweeping Δϕ from −360° to 360° in steps of 36°. From the movie, one can see that the two center-most bead streams could be directed from one bin to the other by shifting the phase.

CONCLUSIONS

We fabricated a compact integrated acoustic-microfluidic device that used interdigitated transducers on a piezoelectric substrate to create a standing surface acoustic wave that could be predictably controlled by a pseudo-static acoustic phase shift. We showed simultaneous position control of nine distinct streams of 3 μm diameter latex beads suspended in a water-based buffer. We found that the position of the beads streams perpendicular to the direction of flow could be tuned by approximately −0.058 μm/deg. In the region between the transducers, we measured the spacing between the streams (23.120 μm ± 0.174 μm). We then characterized the effect of varying the position of the streams perpendicular to the direction of the flow in an expansion region. We found that the trajectory of the bead streams in an expansion region was linearly related to the acoustic phase difference ($\frac{\Delta \phi }{\Delta \theta }$ ≈ 0.008 deg/deg). We empirically demonstrated lateral displacements as small as 2 μm and as large as 46 μm and changes in trajectory as small as 0.3° and as large as 5.8°. We provided simple expressions that can be used to predict the position and trajectory dependence on phase shift for future devices. By combining the shift of the stream with the change in trajectory, one can access a large number of bins with a single device or control multiple streams. Moreover, we provided a proof-of-concept demonstration of particle binning by a pseudo-static acoustic phase shift in surface acoustic wave microfluidics.

There are dozens of possible applications of the techniques and predictive expressions presented in this manuscript. One possible application is the use of phase to actively sort a diverse population of particles based on a physical property (e.g., fluorescence) into multiple bins for fast-particle sorting. Ongoing research will also explore the potential of phase as a means to shuttle particles in and out of a center flow into a sheath flow. We will also study the effect of a dynamic change in phase on the position of a single particle as a function of size and flow velocity. In summary, the impact of pseudo-static phase-based control of acoustic sorting could have far-reaching applications that have the potential to extend well beyond the concepts presented here.