Abstract
In the high-temperature cuprate superconductors, the pervasiveness of anomalous electronic transport properties suggests that violation of conventional Fermi liquid behavior is closely tied to superconductivity. In other classes of unconventional superconductors, atypical transport is well correlated with proximity to a quantum critical point, but the relative importance of quantum criticality in the cuprates remains uncertain. Here, we identify quantum critical scaling in the electron-doped cuprate material La2-xCexCuO4 with a line of quantum critical points that surrounds the superconducting phase as a function of magnetic field and charge doping. This zero-temperature phase boundary, which delineates a metallic Fermi liquid regime from an extended non-Fermi liquid ground state, closely follows the upper critical field of the overdoped superconducting phase and gives rise to an expanse of distinct non-Fermi liquid behavior at finite temperatures. Together with signatures of two distinct flavors of quantum fluctuations, these facts suggest that quantum criticality plays a significant role in shaping the anomalous properties of the cuprate phase diagram.
A longstanding issue in the quest to understand high-temperature superconductivity in the cuprates is in regard to the nature of the underlying ground state. Exotic transport properties (1, 2) are widely considered to arise due to the nontrivial consequences of quantum criticality (3–6), resulting in a strongly correlated electronic ground state that underpins the infamous phase diagram of the cuprates (7). The recent observations of quantum oscillations in underdoped YBa2Cu3O6+x (8) have provided a significant advance to our knowledge of the progression of this ground state through the cuprate phase diagram. The presence of small Fermi surface (FS) pockets distinct from the large FS structure observed in overdoped cuprates (9) requires the existence of an FS reconstruction, which logically occurs at a quantum phase transition between ground states that modify the symmetry of the Brillouin zone. With the origin of superconductivity still under hot debate, how the phase diagram is “shaped” by the evolution of these ground states remains a crucial question.
AN FS transformation has also been directly observed in the electron-doped cuprates as a function of doping, for instance as observed in Nd2-xCexCuO4 (10, 11). This evolution is consistent with several indications of a quantum critical point associated with the suppression of antiferromagnetic order near optimal doping for superconductivity and the appearance of a Fermi liquid (FL) ground state on the overdoped side. With relatively low upper critical field values, the electron-doped cuprates allow for a unique opportunity to study the underlying ground state of the phase diagram in much detail (12). La2-xCexCuO4 (LCCO) is particularly unique in that its superconducting (SC) “dome” is centered at relatively lower Ce concentrations (13), making it possible to study the complete suppression of superconductivity by both doping and magnetic field. One of the most extraordinary characteristics of the cuprates is the hallmark temperature-linear resistivity, which was shown in LCCO to persist over three decades in temperature and to have a strong correlation with the pairing strength itself (14). Here, we study in detail the effects of applied magnetic field on LCCO, using the selective response of spin fluctuations and superconductivity to magnetic field and charge doping to segregate a complicated mixture of behaviors into two distinct signatures of criticality.
Results and Discussion
The nonsuperconducting FL ground state of overdoped LCCO can be readily accessed by either of two ways: doping in electrons beyond a critical value xc, or increasing magnetic field above a critical value Bc that is greater than the superconducting upper critical field Bc2. Both tuning parameters suppress superconductivity and induce a FL ground state that appears to emerge continuously beyond a series of quantum critical points that evolve with both magnetic field and doping, as shown in Fig. 1. These form a continuous line along the ground state (T = 0) plane, constructing a dramatic landscape as a function of both doping and field, summarized in Fig. 2. A direct signature of this criticality—i.e., critical divergence as a function of an experimental tuning parameter (15)—is found as a function of magnetic field B: Upon approach to the critical field Bc from above, a divergence in the quasiparticle–quasiparticle scattering cross-section occurs as the temperature range of Fermi liquid behavior, denoted by TFL, is driven to zero at Bc. At each doping the quadratic temperature coefficient A2, determined from fits of the form Δρ = ρ - ρ0 = A2T2 in the FL state (Fig. 3), strongly increases with decreasing field magnitude and diverges as a function of field ΔB = B - Bc(x). Furthermore, the reduced field scale ΔB/Bc(x) diverges with a universal critical exponent, α = 0.38 ± 0.01, that is the same for all dopings considered (Fig. 4A) indicating that Bc(x) acts as a line of quantum critical points (SI Text).
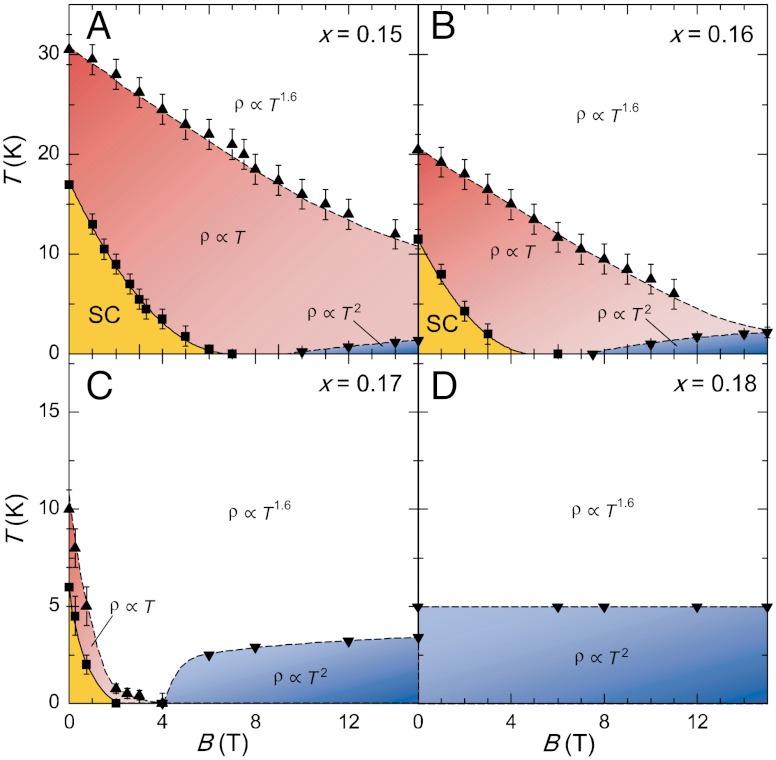
Fig. 1.
Doping evolution of magnetic field-temperature phase diagrams of La2-xCexCuO4. (A–D), The magnetic field dependence of the evolution of superconducting (yellow), Fermi liquid (blue), and non-Fermi liquid (red, white) ground states of the electron-doped cuprate system La2-xCexCuO4 is shown for several electron doping levels (x). These constant-doping magnetic field (B) temperature (T) phase diagrams illustrate the interplay of two distinct transport scattering rates, represented by both Δρ ∝ T (red regions) and Δρ ∝ T1.6 (white regions) power laws, that envelope the superconducting state and characterize the non-Fermi liquid behavior emanating from the quantum critical points marking the onset of the Fermi liquid state. The cross-overs between Δρ ∝ T and Δρ ∝ T1.6 scattering behavior dramatically shift with doping along with the onset field of the Fermi liquid state (Δρ ∝ T2), indicating a strong dependence on both doping and magnetic field that persists with doping toward a dominant, field-independent state at x = 0.18 (D).
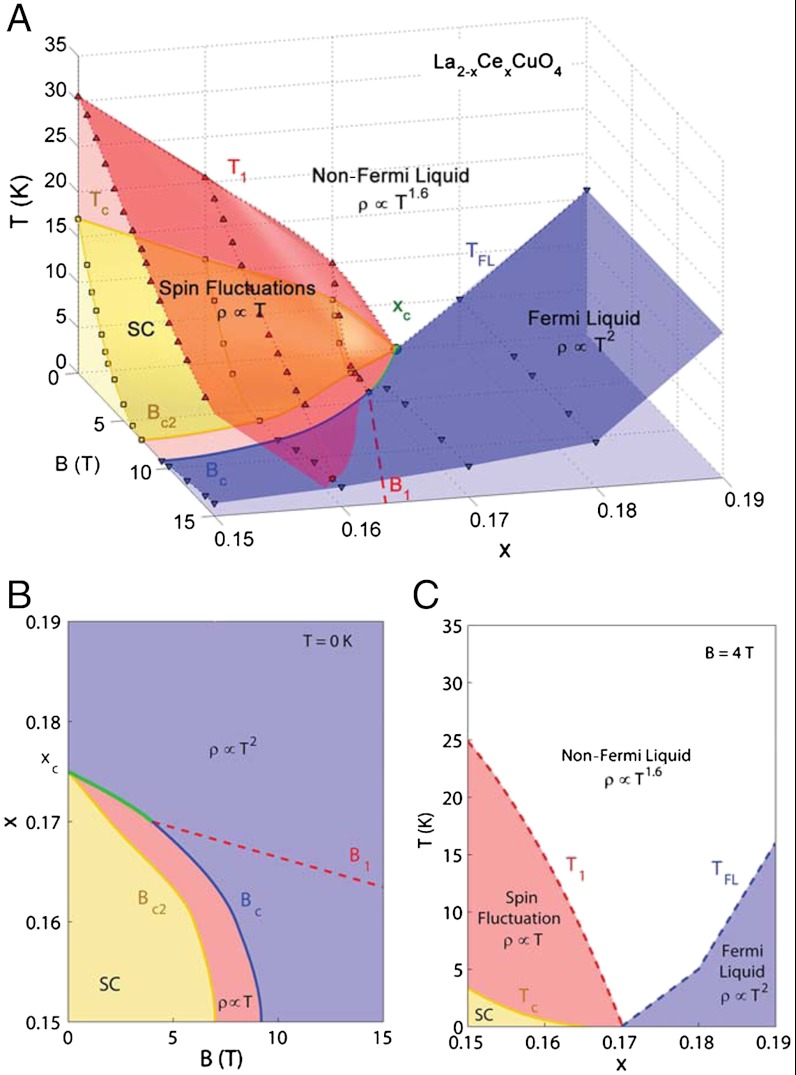
Fig. 2.
Shaping of the overdoped cuprate phase diagram. (A) The interplay between superconducting, quantum fluctuation, and Fermi liquid phases in La2-xCexCuO4 near the quantum critical endpoint xc evolves as a function of electron doping (x), magnetic field (B), and temperature (T). Distinct phase boundaries between SC (yellow) and FL (blue) ground states are determined by a competition of two distinct yet related types of quantum fluctuations that give rise to separable non-Fermi liquid behavior, characterized by Δρ ∝ T (red) and Δρ ∝ T1.6 (white) resistivity temperature dependences. This behavior is found throughout the phase diagram at temperatures above the line of quantum critical points Bc (x) that extends to the zero-field critical doping xc where the SC critical temperature Tc and cross-over temperatures T1 and TFL meet. Unconventional approximate T1.6 scattering persists in applied magnetic fields above both the FL and SF regions, but is dominated by a linear-T scattering mechanism in the regime below T1, where SF scattering is dominant. The origin of the SF regime is a quantum critical point at x = 0.14 (21). (B) The ground state evolution of these phases in the T = 0 doping-field plane exhibits a distinct separation between FL and SF ground states, with an extended non-Fermi liquid phase (red) characterized by linear-T scattering in the T = 0 limit. Closer to xc, T1.6 behavior dominates and extends to the T = 0 limit in a confined region (green line). Although the extrapolated limit of the SF phase B1 (red dashed line) extends to high field, the SC upper critical field Bc2 and the FL phase boundary Bc restrict the range of the actual SF ground state. Critical scaling behavior is associated with Bc, establishing it as a line of quantum critical points that terminates at xc. (C) A constant-field cut of the phase diagram at 4 T highlights the region where the SF ground state separates the SC phase from the FL phase and T1.6 resistivity extends to zero temperature.
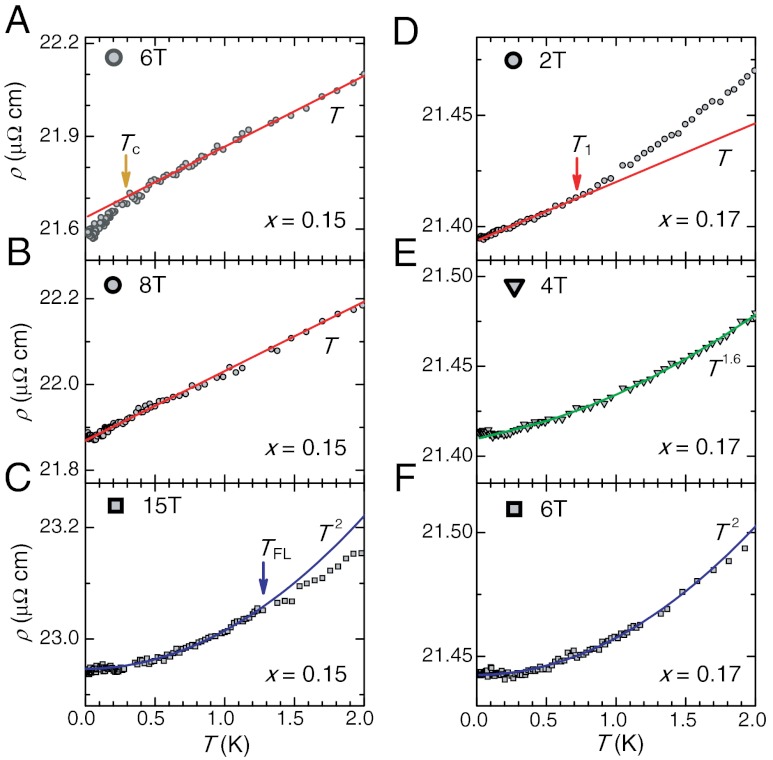
Fig. 3.
Contrasting non-Fermi liquid transport behaviors. The evolution of the zero-temperature limiting behavior of electrical resistivity ρ(T) for two characteristic superconducting films of La2-xCexCuO4 with x = 0.15 (A–C) and 0.17 (D–F) with applied magnetic field demonstrates the isolation of two distinct non-Fermi liquid power laws. The temperature-dependent change in ρ(T) is small compared to ρ0 in all cases. (A and B) For x = 0.15, the suppression of the superconducting state just above 6 T reveals the extension down to the T = 0 limit of the ubiquitous temperature-linear resistivity associated with spin fluctuation scattering (21). (C) This behavior is eventually displaced by a Fermi liquid ground state with conventional approximate T2 scattering behavior persisting up to a characteristic temperature TFL (blue arrows) at higher fields. In contrast, increasing doping closer to the critical endpoint of the superconducting phase at xc = 0.175 reveals a different anomalous scattering behavior. (D) For x = 0.17, the temperature-linear scattering that is present above Tc in a finite range of temperatures up to T1 (red arrows) in zero field is displaced by a more dominant scattering mechanism upon increase of field. (E) At 4 T, an approximate T1.6 power law (green line fit) is observed to extend down to zero temperature and is likely due to fluctuations associated with endpoint of the superconducting phase.
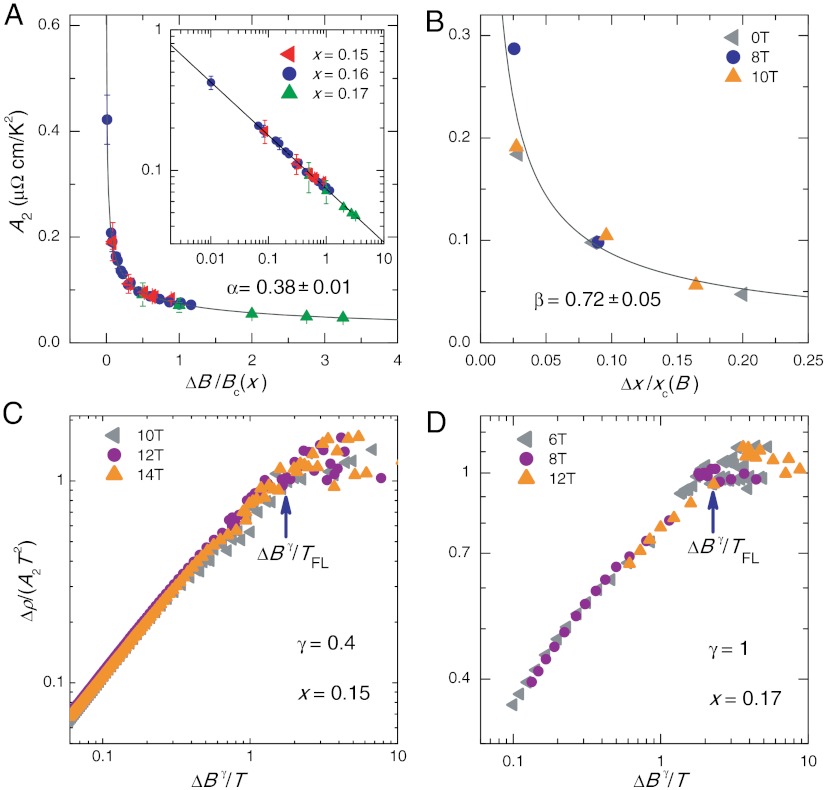
Fig. 4.
Signatures of magnetic field and charge doping-tuned quantum criticality. (A) A strong increase of the quasiparticle–quasiparticle scattering coefficient A2 (from fits of ρ = ρ0 + A2T2) as a function of magnetic field provides evidence for a field-tuned quantum critical point, with a critical divergence observed to occur at the quantum critical field Bc as a function of the field tuning parameter ΔB = B - Bc. Taken in the zero-temperature limit for three Ce concentrations spanning the overdoped region of superconducting LCCO, all of the data fit to one divergent function, A2 = A0(ΔB/Bc)-α with critical exponent α = 0.38 ± 0.01, indicating that the doping-dependent critical field Bc(x) constitutes a quantum phase transition. The normalizing field-independent factor A0 is equal to unity for x = 0.15, and scaled to unity for other samples to remove variations due to geometric factor uncertainties, and the inset presents the same data on a log–log plot with slope representative of the same exponent α. (B) A critical divergence in A2 is also witnessed to occur as a function of Ce concentration tuning parameter Δx = x - xc upon approach to the critical doping xc where the superconducting, Fermi liquid, and spin fluctuation phases terminate. Data for different magnetic field values are fitted by A2 = A0(Δx/xc)-β with critical exponent β = 0.72 ± 0.05, showing that A2 diverges via two orthogonal tuning parameters that both cooperate to direct the evolution of Bc(x) through the T = 0 field-doping plane (Fig. 1). The normalizing factor A0 is equal to unity for 10 T data and scaled to unity for 0 T and 8 T value for the same reasons as above. (C and D) Scaling plots of ρ(T) of LCCO for x = 0.15 and 0.17 in magnetic fields greater than Bc showing that resistivity Δρ data divided by A2T2 collapse onto the same curve with a suitable choice of scaling exponent γ. The blue arrows indicate ΔBγ/TFL, which delineates the Fermi liquid side with zero slope and ordinate equal to unity from the non-Fermi liquid behavior with positive slope. The success of this scaling over two orders of magnitude in ΔBγ/T indicates that the critical scaling of A2 and the approximate Tn resistivity have the same origin, and that magnetic field and temperature are the dominant energy scales in the system.
Strikingly similar divergences have been identified in several different systems exhibiting magnetic field-tuned quantum criticality, including the heavy-fermion materials CeCoIn5 (16), CeAuSb2 (17), YbRh2Si2 (18), and YbAlB4 (19), with critical exponents 1.37, 1.0, 1.0, and 0.50, respectively. In contrast to classical transitions, the sensitivity to effective dimensionality involved in a quantum phase transition can lead to nonuniversal critical exponents (15). In LCCO, the observation of a universal exponent at several doping levels is unprecedented but is limited to magnetic field tuning. When considering doping as a tuning parameter, the system can also be tuned to approach the critical field but with a distinct critical exponent. That is, A2 also scales as a function of reduced doping Δx/xc(B) for different constant magnetic field values, with a critical exponent β = 0.72 ± 0.05 (Fig. 4B). LCCO is a rare example of a material where both magnetic field and doping can drive the electronic system to quantum criticality in a similar but distinct manner. These two tuning parameters, one adding charge carriers and one breaking time reversal symmetry, likely alter the excitation spectrum in fundamentally different ways, as considered in the case of heavy-fermion systems with similar orthogonal tuning parameters (20). However, they also smoothly connect the ground state boundaries that define the phase diagram on the overdoped side.
In LCCO, resistivity data can be scaled as a function of ΔB/T as shown in Fig. 4, providing a second key signature of the reach of a quantum phase transition. First observed in heavy-fermion materials (21), this type of energy-temperature scaling not only indicates a quantum critical system below its upper critical dimension but also reflects the lack of an energy scale other than temperature itself (15). In such a case, the transport can be described generally as a function f(ΔBγ/T) of both field and temperature, with asymptotic limits in both FL (Δρ ∝ T2) and NFL (Δρ ∝ Tn) regions (SI Text). Through this approach, the anomalous Tn scattering and the magnetic field-tuned divergence of A2 with exponent α are shown to be two aspects of the same critical behavior, with a self-consistency given by α = γ(2 - n) that is derived in the SI Text (see Table 1 for summary of exponents). A scaling exponent γ is obtained for both x = 0.15 and 0.17, but with different values of 0.4 ± 0.1 for x = 0.15 (Fig. 4C) and 1.0 ± 0.02 for x = 0.17 (Fig. 4D). Given the same measured critical divergence exponent α = 0.38 for both dopings, self-consistency requires that the power law exponent n must be different for these two dopings. Upon inspection of the phase diagram of Fig. 1, one can see this correspondence is indeed verified: At finite temperatures immediately above the quantum critical point at Bc(x) for each doping, Δρ ∝ Tn is best fit with n = 1.0 for x = 0.15, and n = 1.6 for x = 0.17 (Fig. 1), confirming self-consistency.
Table 1.
Definition and range of transport power law and critical exponents
| Exponent | Determined by | Range of applicability | Value |
| n | power law fits to ρ(T) data | temperature range depends on (x,B) (Fig. 1) | 1 < n < 2 |
| α | divergence of A2 coefficients as Bc is approached from high B | all (x,B) exhibiting a Fermi liquid ground state | 0.38 ± 0.01 |
| β | divergence of A2 coefficients as xc is approached from high x | all (x,B) exhibiting a Fermi liquid ground state | 0.72 ± 0.05 |
| γ | collapse of ρ(T) data for constant x at different values of B | all (x,B) exhibiting a Fermi liquid ground state, from 20 mK to upper limit of Tn behavior | = α(2-n),β(2-n)= 0.4 ± 0.1(x = 0.15) = 1.00 ± 0.02(x = 0.17) |
The dynamical range of the fitted parameter over which each exponent has been determined is shown explicitly in Fig. 1 for the transport power law exponent n, where temperature ranges of best fit are dependent on doping and field values (e.g., for x = 0.15, n = 1 for three decades of T in the range 0.020 < T < 20 K). For the critical and scaling exponents, the dynamical ranges are shown explicitly in Fig. 4 and listed here for critical exponents α (0.01 < ΔB/Bc < 3) and β (0.025 < Δx/xc < 0.20), as well as the scaling exponent γ (0.06 < ΔBγ/T < 10 for γ = 0.4, and 0.1 < ΔBγ/T < 10 for γ = 1).
But what is the origin of these inherently different scattering rate behaviors, with n = 1.0 and n = 1.6? In LCCO, strong circumstantial evidence indicates that the temperature-linear scattering arises due to an antiferromagnetic quantum critical point that lies deep within the SC dome near xFS = 0.14 (22, 23), where the Fermi surface reconstructs as in other electron-doped cuprates (24, 25). Fluctuations emanating from this critical point are likely to be responsible for the n = 1.0 power law (26) [strong disorder is evidenced by a small temperature-dependent change in ρ(T) compared to ρ0 in all cases], spawning an extended spin fluctuation (SF) region defined by the n = 1.0 scattering behavior that dominates a substantial range of temperature, magnetic field, and doping. Of course, the inception of superconductivity likely consumes much of the entropy associated with such a state (27), filling in most of the SF phase space as shown in Fig. 2. However, as shown in Fig. 2B, a tantalizing glimpse of a possible non-Fermi liquid phase (NFL) may be present between the SC upper critical field Bc2 and Bc, where an extended range of T = 0 NFL behavior endures much like in other anomalous systems (28–30).
Thus, at x = 0.15, the n = 1.0 scattering mechanism is dominant, extending to the zero-temperature limit once Bc2 is surpassed, and the resultant ΔB/T scaling obeys the expected self-consistency in a wide range of fields and temperatures reaching up to the SF scale T1. However, upon increasing doping from x = 0.15, the SF energy scale is dramatically reduced both in temperature and in field, with both scales terminating at the critical doping xc = 0.175 where both T1 and B1 approach zero together with Tc and TFL. Given the intimate correlation between T1 and Tc in zero field (14), the discrepancy between their magnetic field dependence is all the more remarkable. It indicates that magnetic field does not destabilize superconductivity by destroying the mediating spin fluctuations, but rather through more mundane orbital effects. For instance, at x = 0.15, the upper temperature limit of the SF region, denoted as T1, is much more robust against magnetic field than Tc itself, extrapolating to a zero-temperature field scale B1 that far surpasses Bc2 (Fig. 2B). But at higher doping, T1 and Tc are both suppressed at an almost equal rate toward zero close to Bc, and the n = 1.6 power law characterizes the dominant scattering rate at temperatures directly above the quantum critical point. For instance, in the special case of x = 0.17 at 4 T (Fig. 2C and SI Text), this power law persists to at least 13 K, spanning at least three decades in temperature when it is the dominant scattering mechanism.
This correspondence underscores two major points. First, the magnetic field-induced divergence, critical scaling and the NFL scattering temperature dependence can be understood within a self-consistent framework. Second, the fact that this self-consistency adjusts according to which scattering is dominant is evidence for critical behavior arising from two origins—two sets of anomalous scattering, two forms of scaling and self-consistent critical exponents. Clearly, there are two distinct scattering behaviors that respond differently to doping and magnetic field, and the competition of these two scattering mechanisms is directly borne out in the temperature dependence of resistivity throughout the field-doping phase diagram. With the n = 1.0 power law likely arising from scattering with fluctuations associated with the antiferromagnetism of the parent compound, the n = 1.6 power law appears to be a distinct signature of a second type of quantum critical fluctuation. Interestingly, this power law is strikingly similar to that observed in the hole-doped cuprates La2-xSrxCuO4 (1) and Tl2Ba2CuO6+x (31) in the vicinity of xc, suggesting the quantum critical endpoint of the SC phase may give rise to fluctuations that cause this particular anomalous scattering behavior. In fact, recent measurements of both La2-xSrxCuO4 (32) and Tl2Ba2CuO6+x (33) indeed show quantum critical behavior originating from the end of the SC dome, pointing to a universal nature of the quantum phase transition separating the superconducting and Fermi liquid ground states. The possibility of calculating a nonperturbative critical theory of such fluctuations for a disorder-driven SC quantum critical point (34) shows promise for confirming such a scenario.
Clearly, quantum criticality plays a significant role in shaping the phase diagram of the electron-doped cuprates, both in optimizing the superconductivity as well as limiting its extent. The ensuing picture is that two proximal quantum critical points compete in the cuprate phase diagram. The first, positioned near optimal doping, gives rise to spin fluctuations that stabilize unconventional superconductivity. The second, at Bc(x), owes its very existence to the first because it is born of the suppression of superconductivity and the emergence of the normal FL state. The result is a complex but tractable interplay of competing quantum critical fluctuations that conspire to shape the phase diagram that has become the ubiquitous signature of high-temperature superconductivity.
Methods
Samples.
The c-axis-oriented LCCO films were deposited on (100) SrTiO3 substrates by pulsed laser deposition utilizing a KrF excimer laser. The annealing process for each Ce concentration was optimized such that samples showed the narrowest SC transition widths or metallic behavior down to the lowest measured temperature (20 mK), whereas nonoptimized samples usually showed an upturn at low temperature, as previously reported. The films were patterned into Hall bar bridges using photolithography and ion milling techniques. Several samples of each concentration were studied to ensure that the data are representative.
Measurements.
Electrical transport measurements at temperatures greater than 2 K were carried out in a commercial cryostat equipped with a 14 T magnet, whereas lower temperature measurements down to 20 mK were performed in a dilution refrigerator equipped with a 15 T magnet. Data from the two platforms were measured with overlapping temperature ranges. Current was applied in the ab plane while the magnetic field was applied along the c axis for all the measurements.
Supplementary Material
Acknowledgments.
We thank A. Chubukov, V. Galitski, J. Schmalian, L. Taillefer, and C. M. Varma for their discussions. This research was supported by the National Science Foundation under DMR-0952716 (to J.P. and K.K.) and DMR-1104256 (to R.L.G.) and the Maryland Center for Nanophysics and Advanced Materials (K.J. and N.P.B.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1120273109/-/DCSupplemental.
References
- 1.Cooper RA, et al. Anomalous criticality in the electrical resistivity of La2-xSrxCuO4. Science. 2009;323:603–607. doi: 10.1126/science.1165015. [DOI] [PubMed] [Google Scholar]
- 2.Taillefer L. Scattering and pairing in cuprate superconductors. Annu Rev Condens Matter Phys. 2010;1:51–70. [Google Scholar]
- 3.Tanatar MA, Paglione J, Petrovic C, Taillefer L. Anisotropic violation of the Wiedemann-Franz law at a quantum critical point. Science. 2007;316:1320–1322. doi: 10.1126/science.1140762. [DOI] [PubMed] [Google Scholar]
- 4.Maple MB, et al. Non-Fermi liquid regimes and superconductivity in the low temperature phase diagrams of strongly correlated d- and f-electron materials. J Low Temp Phys. 2010;161:4–54. [Google Scholar]
- 5.Sachdev S. Where is the quantum critical point in the cuprate superconductors? Phys Status Solidi B. 2010;247:537–543. [Google Scholar]
- 6.Aji V, Shekhter A, Varma CM. Theory of the coupling of quantum-critical fluctuations to fermions and d-wave superconductivity in cuprates. Phys Rev B. 2010;81:064515. [Google Scholar]
- 7.Broun DM. What lies beneath the dome? Nat Phys. 2008;4:170–172. [Google Scholar]
- 8.Doiron-Leyraud N, et al. Quantum oscillations and the Fermi surface in an underdoped high- Tc superconductor. Nature. 2007;447:565–568. doi: 10.1038/nature05872. [DOI] [PubMed] [Google Scholar]
- 9.Vignolle B, et al. Quantum oscillations in an overdoped high-Tc superconductor. Nature. 2008;455:952–955. [Google Scholar]
- 10.Matsui H, et al. Evolution of the pseudogap across the magnet-superconductor phase boundary of Nd2-xCexCuO4. Phys Rev B. 2007;75:224514. [Google Scholar]
- 11.Kartsovnik MV, et al. Fermi surface of the electron-doped cuprate superconductor Nd2-xCexCuO4 probed by high-field magnetotransport. New J Phys. 2011;13:015001. [Google Scholar]
- 12.Armitage NP, Fournier P, Greene RL. Progress and perspectives on electron-doped cuprates. Rev Mod Phys. 2010;82:2421–2487. [Google Scholar]
- 13.Sawa A, et al. Electron-doped superconductor La2-xCexCuO4: Preparation of thin films and modified doping range for superconductivity. Phys Rev B. 2002;66:014531. [Google Scholar]
- 14.Jin K, Butch NP, Kirshenbaum K, Paglione J, Greene RL. Link between spin fluctuations and electron pairing in copper oxide superconductors. Nature. 2011;476:73–79. doi: 10.1038/nature10308. [DOI] [PubMed] [Google Scholar]
- 15.Coleman P, Pépin C, Si Q, Ramazashvili R. How do Fermi liquids get heavy and die? J Phys Condens Matter. 2001;13:R723–738. [Google Scholar]
- 16.Paglione J, et al. Field-induced quantum critical point in CeCoIn5. Phys Rev Lett. 2003;91:246405. doi: 10.1103/PhysRevLett.91.246405. [DOI] [PubMed] [Google Scholar]
- 17.Balicas L, et al. Magnetic field-tuned quantum critical point in CeAuSb2. Phys Rev B. 2005;72:064422. [Google Scholar]
- 18.Gegenwart P, et al. Magnetic-field induced quantum critical point in YbRh2Si2. Phys Rev Lett. 2002;89:056402. doi: 10.1103/PhysRevLett.89.056402. [DOI] [PubMed] [Google Scholar]
- 19.Nakatsuji S, et al. Superconductivity and quantum criticality in the heavy-fermion system β-YbAlB4. Nat Phys. 2008;4:603–607. [Google Scholar]
- 20.Löhneysen Hv, Pfleiderer C, Pietrus T, Stockert O, Will B. Pressure versus magnetic-field tuning of a magnetic quantum phase transition. Phys Rev B. 2001;63:134411. [Google Scholar]
- 21.Aronson MC, et al. Non-Fermi liquid scaling of the magnetic response of UCu5-xPdx (x = 1,1.5) Phys Rev Lett. 1995;75:725–728. doi: 10.1103/PhysRevLett.75.725. [DOI] [PubMed] [Google Scholar]
- 22.Jin K, et al. Evidence for antiferromagnetic order in La2-xCexCuO4 from angular magnetoresistance measurements. Phys Rev B. 2009;80:012501. [Google Scholar]
- 23.Jin K, et al. Normal-state transport in electron-doped La2-xCexCuO4 thin films in magnetic fields up to 40 Tesla. Phys Rev B. 2008;77:172503. [Google Scholar]
- 24.Dagan Y, et al. Evidence for a quantum phase transition in Pr 2-xCexCuO4-δ from transport measurements. Phys Rev Lett. 2004;92:167001. doi: 10.1103/PhysRevLett.92.167001. [DOI] [PubMed] [Google Scholar]
- 25.Lin J, Millis AJ. Theory of low-temperature Hall effect in electron-doped cuprates. Phys Rev B. 2005;72:214506. [Google Scholar]
- 26.Rosch A. Magnetotransport in nearly antiferromagnetic metals. Phys Rev B. 2000;62:4945–4962. [Google Scholar]
- 27.Wu J, Zhu L, Si Q. Entropy accumulation near quantum critical points: Effects beyond hyperscaling. J Phys Conf Ser. 2011;273:012019. [Google Scholar]
- 28.Doiron-Leyraud N, et al. Fermi-liquid breakdown in the paramagnetic phase of a pure metal. Nature. 2003;425:595–599. doi: 10.1038/nature01968. [DOI] [PubMed] [Google Scholar]
- 29.Butch NP, Maple MB. Evolution of critical scaling behavior near a ferromagnetic quantum phase transition. Phys Rev Lett. 2009;103:076404. doi: 10.1103/PhysRevLett.103.076404. [DOI] [PubMed] [Google Scholar]
- 30.Custers J, et al. Evidence for a non-Fermi-liquid phase in Ge-substituted YbRh2Si2. Phys Rev Lett. 2010;104:186402. doi: 10.1103/PhysRevLett.104.186402. [DOI] [PubMed] [Google Scholar]
- 31.Shibauchi T, et al. Field-induced quantum critical route to a Fermi liquid in high-temperature superconductors. Proc Natl Acad Sci USA. 2008;105:7120–7123. doi: 10.1073/pnas.0712292105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lemberger TR, et al. Superconductor-to-metal quantum phase transition in overdoped La2-xSrxCuO4. Phys Rev B. 2011;83:140507(R). [Google Scholar]
- 33.Krusin-Elbaum L, et al. Interlayer magnetotransport in the overdoped cuprate Tl2Ba2CuO6+x: Quantum critical point and its downslide in an applied magnetic field. Phys Rev B. 2010;82:144530. [Google Scholar]
- 34.Galitski V. Nonperturbative microscopic theory of superconducting fluctuations near a quantum critical point. Phys Rev Lett. 2008;100:127001. doi: 10.1103/PhysRevLett.100.127001. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.