Triple resonance for a three-level system of a chiral molecule

Abstract

A new spectroscopic method of triple resonance is proposed for studying chirality of a molecule of C₁ symmetry. Each enantiomer of such a molecule is of mixed parity and thus exhibits all three a-, b-, and c-types of rotational spectra. The present study concludes, by using time-dependent perturbation theory, that the transition probability between two of the three rotational levels under triple resonance differs for different enantiomer. This result can thus be of some significance for enantiomer differentiation.

I. Introduction

Chirality is a fascinating phenomenon; its influence prevails in a number of fields, as described in many books and articles.¹⁾ At an early stage of quantum mechanics, Hund already noticed a serious paradox for this new theory, namely the optical activity would vanish in quantum mechanics for any molecule in a stationary state.^2,3) In order to solve this problem, he thought of a tiny perturbation term between enantiomers, which could mix the left-handed and right-handed molecules by the tunneling motion through a potential barrier caused by the perturbation, but the rate of the motion would be so slow that the optical activity would be preserved practically forever. In 1957 a new finding of parity violation was reported.^4,5) This result means that the R- and S-enantiomers are not degenerate in energy. Both Hund’s perturbation and parity violation terms are quite small for almost all the “stable” chiral molecules, in other words, the Hamiltonian of a chiral molecule is almost completely symmetric with respect to inversion, and the measurement of optical rotation has so far been nearly the only way to differentiate enantiomers. Even highly sophisticated spectroscopic methods such as the one with highly stabilized carbon dioxide lasers as sources⁶⁾ have achieved the resolution to Δν/ν = 10⁻¹³, which is still at least three orders of magnitude larger than theoretical estimates for the contribution of parity violation.^7–9)

In view of the importance of enantiomer differentiation, quite a large variety of spectroscopic methods have been proposed, but most of them have proven far from successful. It might be appropriate here to cite several attempts for enantiomer differentiation using molecular complexes combined with high-resolution spectroscopic methods. Le Barbu-Debus, Zehnacker-Rentien and their collaborators¹⁰⁾ employed UV and UV/IR double-resonance spectroscopy to record electronic and vibrational spectra of chiral complexes generated by supersonic expansion. Howard and his collaborators,^11,12) Xu and her associates,^13–15) and Caminati’s group¹⁶⁾ have applied Fourier-transform microwave spectroscopy to molecular complexes consisting of chiral-achiral and chiral-chiral molecules.

In these circumstances I decided to examine closely chiral molecules of C₁ symmetry, namely molecules without any symmetry operation, in order to trace the real origin of molecular chirality and to detect its consequences on spectra of chiral molecules. The other group of chiral molecules belong to C₂ group, which consists of a C₂ operation, but I shall treat this group of molecules separately, because they give only one type of rotational transitions, due to the permanent dipole moment being aligned to the C₂ axis. On the other hand, as has been well known, C₁ chiral molecules exhibit all three a-, b-, and c-type rotational transitions. This is certainly very surprising, but not many people have appreciated the significance of this important fact. It has been well established that any electric-dipole transitions take place between two levels of opposite parity, because the dipole moment is of odd parity, and certainly this rule should also apply to any pure rotational transitions of molecules. We have, however, many examples of C₁ chiral molecules in the literatures, for which all a-, b-, and c-types of rotational transitions were observed and reported. Thus the observations on these chiral molecules remained a puzzle for us for a long time. We may wonder how we can understand the rotational spectra of C₁ chiral molecules. This is the start of the present research; I suspected that this puzzle was closely related to Hund’s paradox. I keep in mind mainly pure rotational spectroscopy of molecules such as microwave spectroscopy as an experimental tool of the present study, because it is straightforward and yet amenable to various types of spectroscopic experiments such as double resonance quite easily. Of course, laser spectroscopy is very similar to it in many respects, and the present treatment may readily be extended to other wavelength regions, infrared, visible, and ultraviolet, and may thus be applicable to C₂ chiral molecules as well, for which two of the three types of transitions can be vibrational, for example.

As already stressed, one of the most crucial points of the present study lies in the characteristic feature of C₁ chiral molecules that all the three a-, b-, and c-types of rotational transitions take place simultaneously. Of course, they can be observed routinely one by one by using a conventional spectroscopic method, but such observations, even with highest resolution available at the present, have not provided us with any new information on molecular chirality. Obviously a fundamentally new approach is required to clarify the real essence of molecular chirality, and I have decided to focus the attention to the dynamical behavior of a three-level system of a C₁ chiral molecule by introducing a triple-resonance method, combined with time-dependent perturbation theory.

II. Time-dependent perturbation theory

We follow the formulation described by Landau and Lifshitz in their textbook,¹⁷⁾ and reproduce some essential part of the theory for the sake of convenience. The Hamiltonian of a three-level system is expressed as

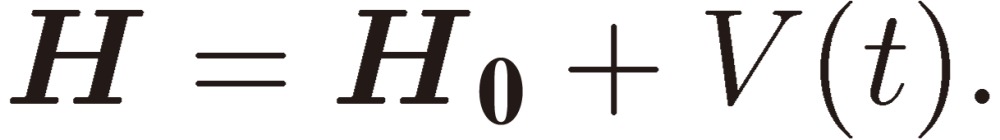[1]

The eigenfuction of the unperturbed time-independent Hamiltonian H₀ in a stationary state k is given by Ψ_k⁽⁰⁾ with the eigenvalue E_k⁽⁰⁾; Ψ_k⁽⁰⁾ = ψ_k⁽⁰⁾ exp(−iE_k⁽⁰⁾t/ℏ). When a time-dependent perturbation V(t) is added, the solution of the Schrödinger equation:

[2]

may be expressed by a sum of Ψ_k⁽⁰⁾ over k: Ψ = ∑_ka_k(t)Ψ_k⁽⁰⁾. Inserting Ψ in Eq. [2] leads to the following equation for the coefficient a_k(t):

[3]

where

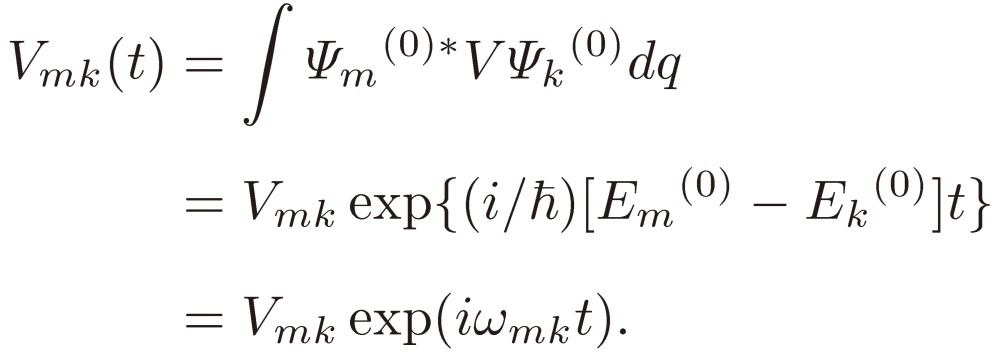[4]

We assume the perturbation periodic with the frequency ω, i.e. of the form:

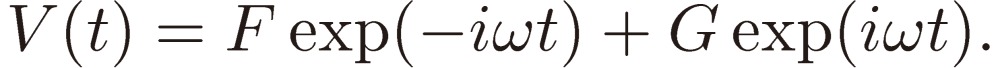[5]

Because V(t) is a Hermitian operator,

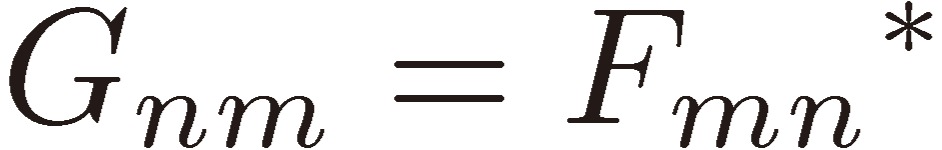[6]

holds, and Eq. [4] is given by

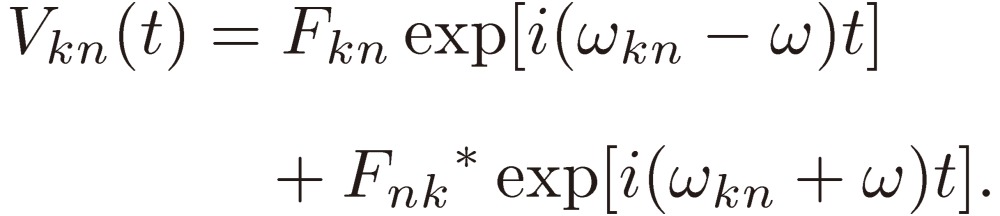[4a]

III. Application to two- and three-level systems

First we review the result on a two-level system worked out by Landau and Lifshitz,¹⁷⁾ which will allow us to make an important comparison with the results on a three-level system given below.

(1). Two-level system.

The frequency of the external perturbation ω is assumed to be very close to ω_mn: E_m⁽⁰⁾ − E_n⁽⁰⁾ = ħ(ω + ε), where ε represents a small frequency shift. Retaining only terms depending on the low frequency ω_mn − ω results in

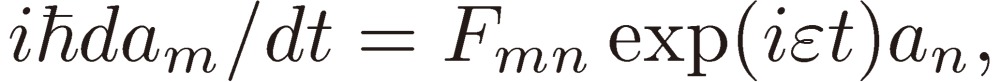[7a]

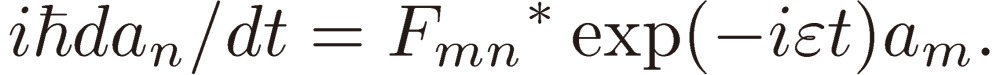[7b]

Because these equations involve the second time derivative of a_m, they yield two independent solutions for the coefficients, which are given by

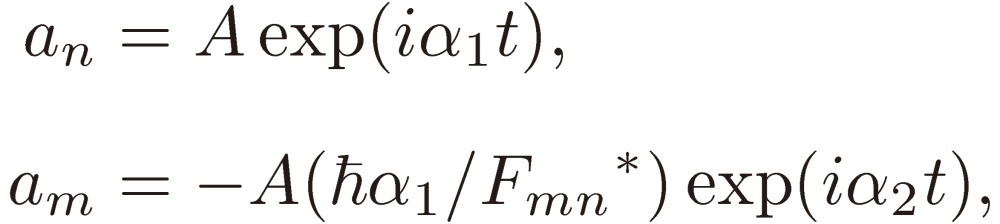[8a]

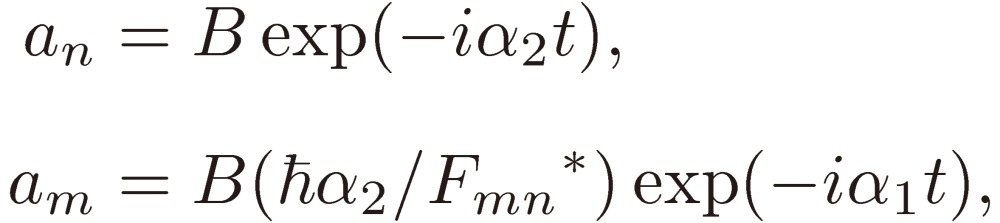[8b]

where

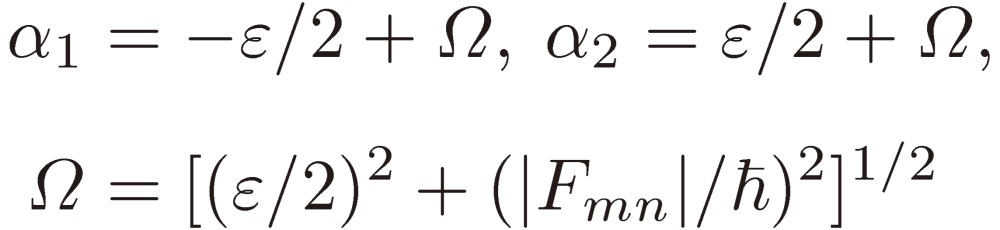[9]

and A and B are determined by the normalization condition. The system at time t is, in general, expressed by a linear combination of the two solutions Eqs. [8].

Suppose that the system lies in the m-th state Ψ_m⁽⁰⁾ at t = 0, then after t its wavefunction changes to

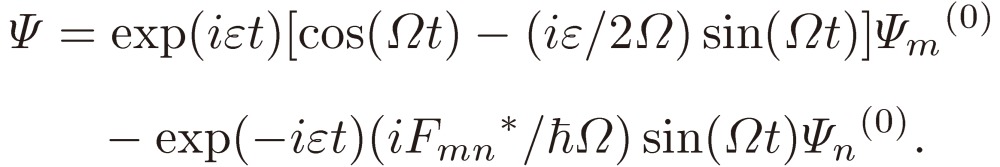[10]

The absolute square of the coefficient of Ψ_n⁽⁰⁾ in this equation is the probability for the state being in the n-th state after t, which is given by

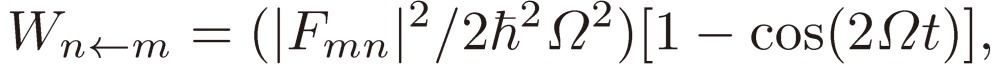[11]

which, at the exact resonance ε = 0, reduces to

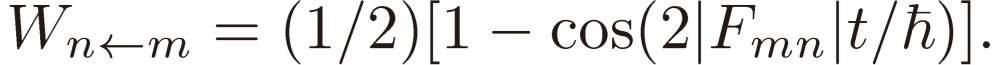[11a]

This varies between 0 and 1 as the time passes with the periodicity of πℏ/|F_mn| and, when multiplied by a damping factor exp(−t/τ) to account for the effect of intermolecular collision with the average collision time interval τ, gives a free induction decay signal function.

(2). Three-level system.

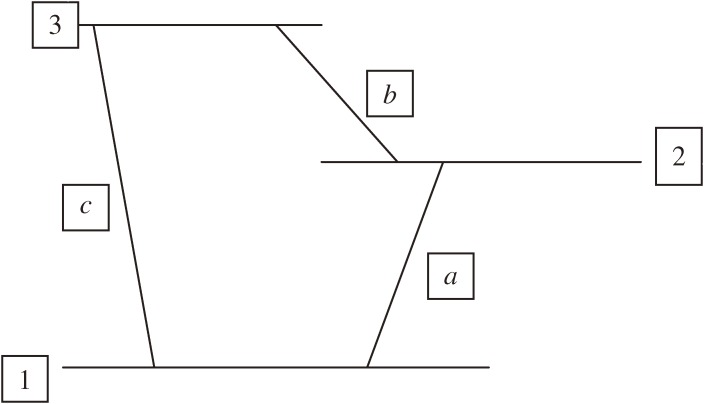
This treatment on the two-level system has been extended in the present study to a three-level system 1, 2, and 3, with the level separations given in frequency unit by ω_a = 2 − 1, ω_b = 3 − 2, and ω_c = 3 − 1 (the suffixes a, b, and c of the frequencies imply the types of rotational transitions). Here without loss of generality, the three levels are assumed to be arranged, as shown in Fig. 1. The equations for the coefficients, which correspond to Eqs. [7] in the case of the two-level system, are

[12a]

[12b]

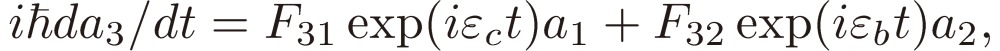[12c]

where

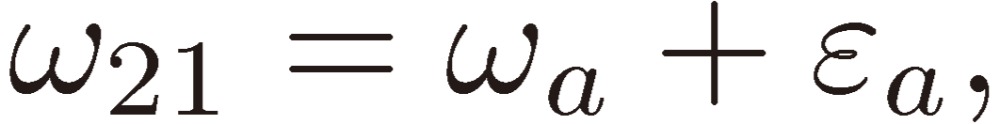[13a]

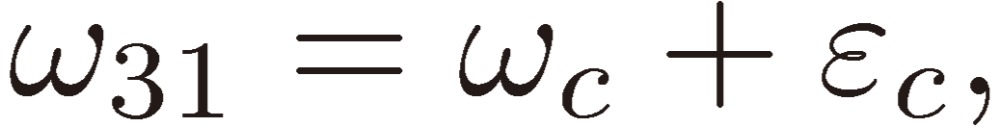[13b]

[13c]

Figure 1.

Three-level system.

In the following, for the sake of simplicity, the exact resonance is assumed for the three transitions. The coefficient a₁ satisfies the following equation:

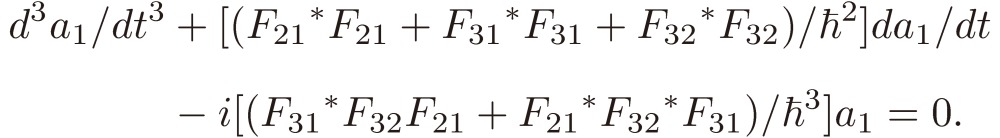[14]

We shall assume the following trial form for a₁:

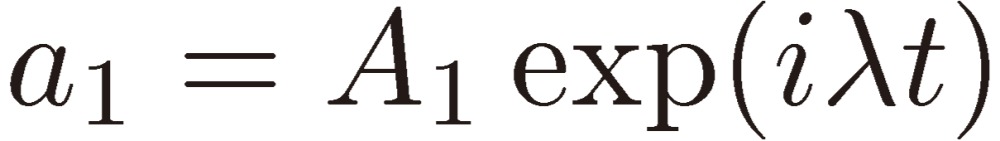[15]

and insert it in Eq. [14]. Then we obtain a third-order equation for λ given by

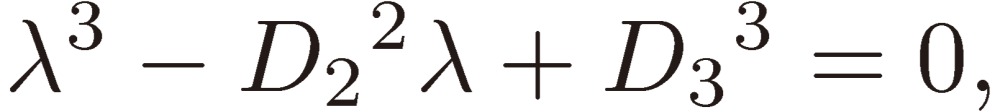[16]

where

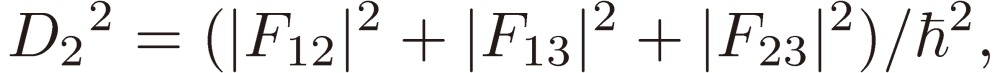[16a]

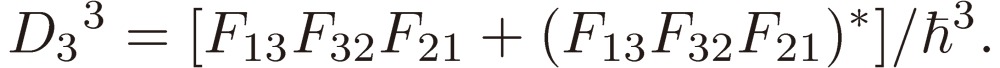[16b]

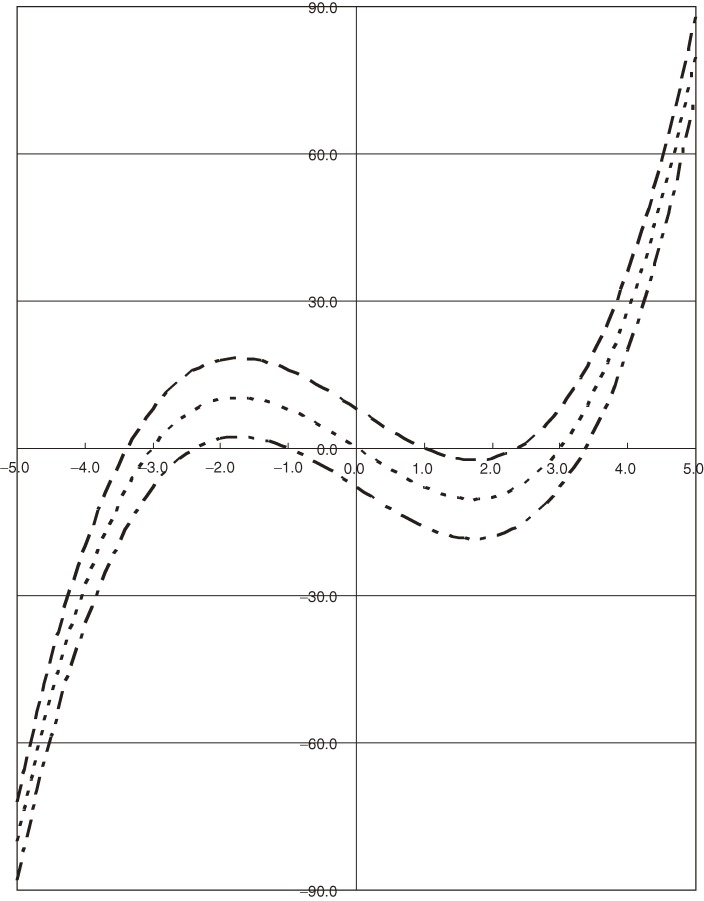
The left-hand side of Eq. [16] is plotted in Fig. 2 as a function of λ, where D₂ is arbitrarily chosen to be 3.0 and D₃ to take three values 2.0, 0.0, and −2.0.

Figure 2.

The left-hand side of Eq. [16] is plotted as a function of λ, assuming D₂ = 3.0 and D₃ = 2.0 (– – – –), 0.0 (- - - - -), and −2.0 (– - – -).

The properties of Eq. [16] may be summarized as follows:

• (1)
  There are three roots for λ: λ₁, λ₂, and λ₃, which are taken to satisfy the condition:

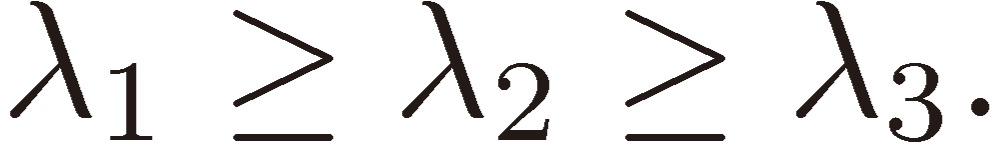
  [17]
• (2)
  The left-hand side of Eq. [16]: f(λ) = λ³ − D₂²λ + D₃³ reaches extremes at λ = +λ_x (minimum) and λ = −λ_x (maximum) with λ_x denoting D₂/√3. The values of f(λ) at these extremes are

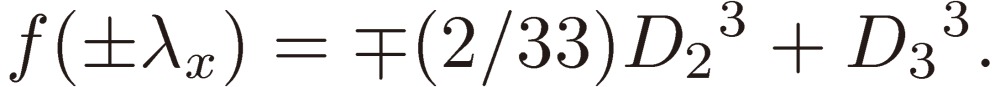
  [18]
• (3)-1 If D₃ > 0 and (2/3√3)D₂³ > D₃³, there are three roots: λ₁ and λ₂ > 0, λ₃ < 0and (2/3√3)D₂³ = D₃³, λ₁ = λ₂ = +D₂/√3, λ₃ < 0and (2/3√3)D₂³ < D₃³, only one root exists: λ₃ < 0.
• (3)-2 If D₃ = 0, λ₁ = −λ₃ = D₂ > 0, λ₂ = 0.
• (3)-3 If D₃ < 0 and (2/3√3)D₂³ > |D₃³|, there are three roots: λ₁ > 0, λ₂ and λ₃ < 0and (2/3√3)D₂³ = |D₃³|, λ₁ > 0, λ₂ = λ₃ = −D₂/√3and (2/3√3)D₂³ < |D₃³|, only the root is λ₁ > 0.

Equation [15] assumed for a₁ is then inserted in Eqs. [12b] and [12c] to derive the solutions for a₂ and a₃:

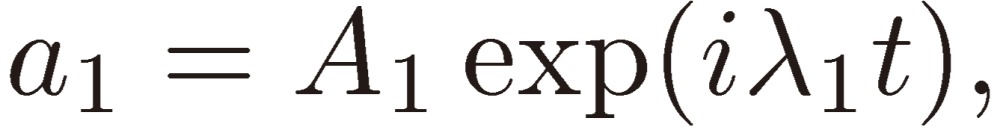[19a]

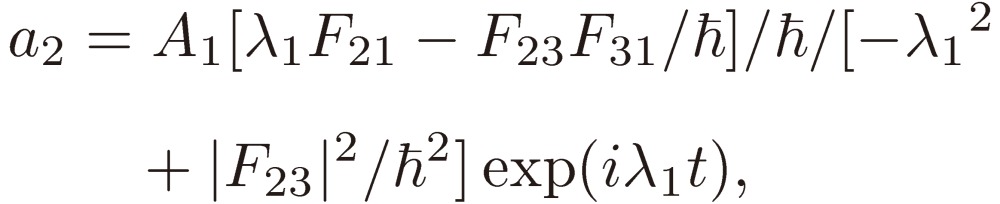[19b]

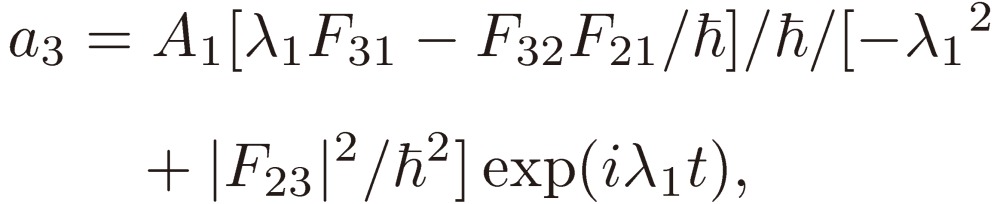[19c]

where λ = λ₁ is chosen. The other roots: λ₂ and λ₃, if available, are inserted in Eqs. [19] in place of λ₁ to derive the corresponding a₁, a₂, and a₃, respectively.

IV. Time-dependent behavior of the 2 ← 1 transition under a triple-resonance condition

Suppose that the three-level system under consideration lies in Ψ₁⁽⁰⁾ at t = 0. Using the results Eqs. [19], the system at t is expressed as

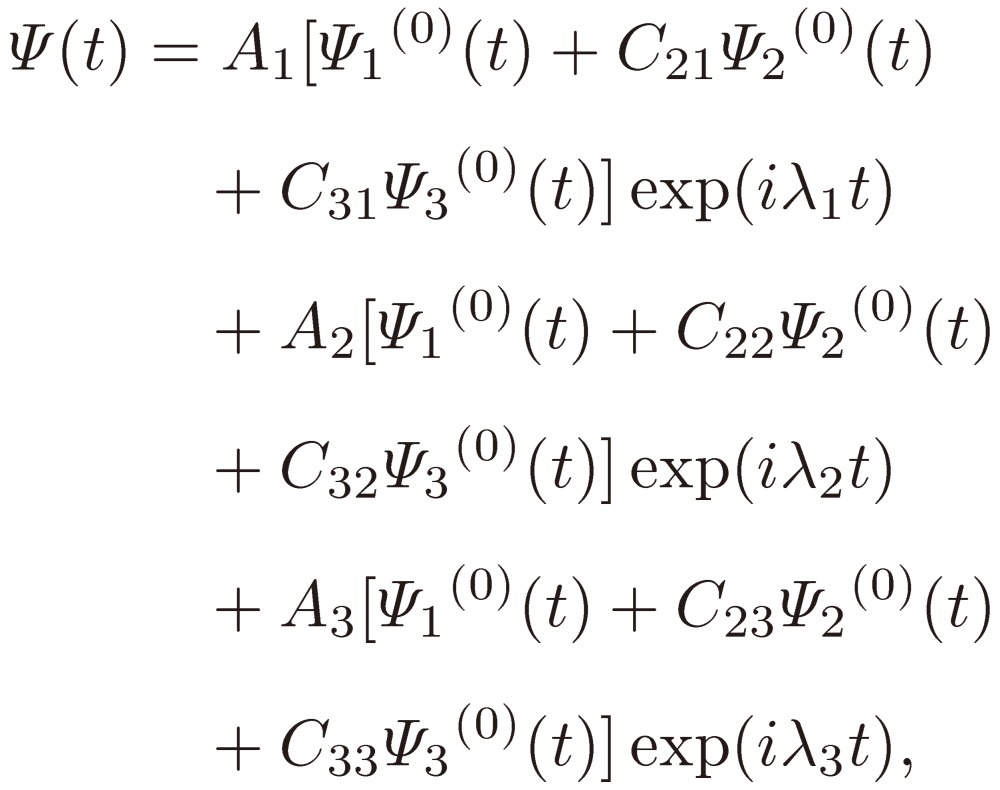[20]

where

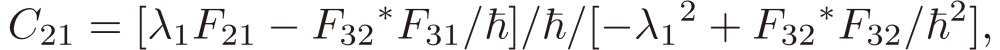[21a]

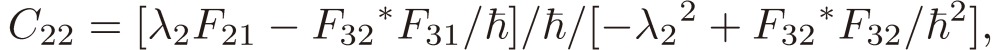[21b]

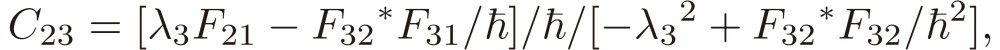[21c]

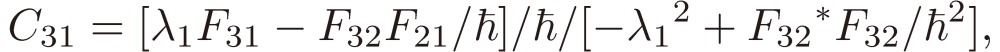[21d]

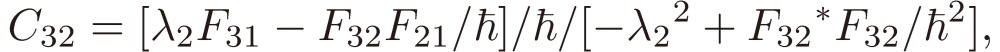[21e]

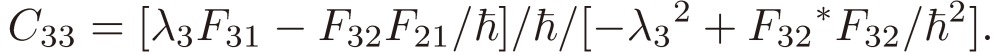[21f]

The initial conditions at t = 0, which we assumed, correspond to

[22a]

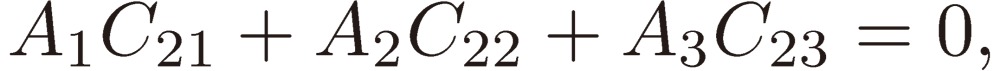[22b]

[22c]

Equations [22] are solved for A_i as follows:

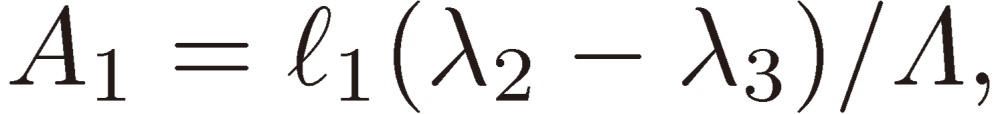[23a]

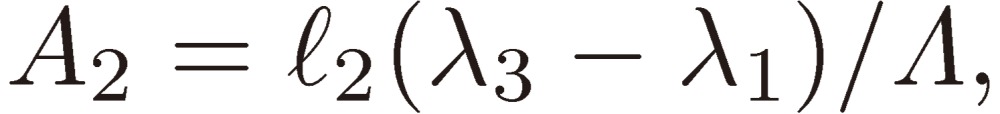[23b]

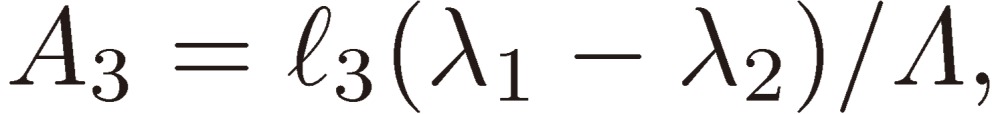[23c]

where

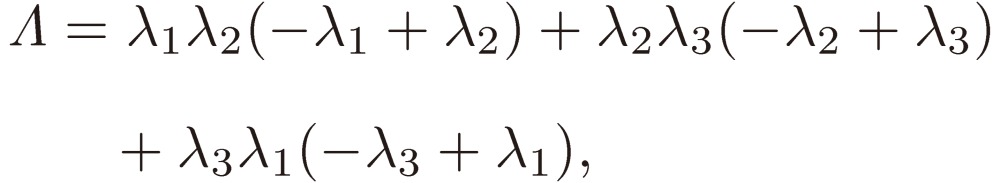[24]

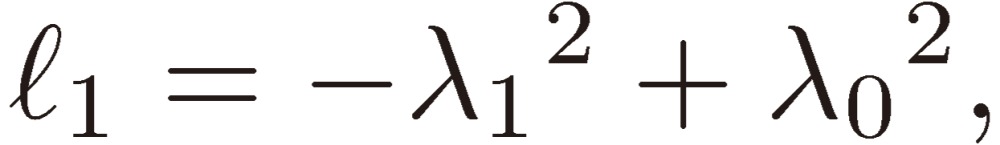[25a]

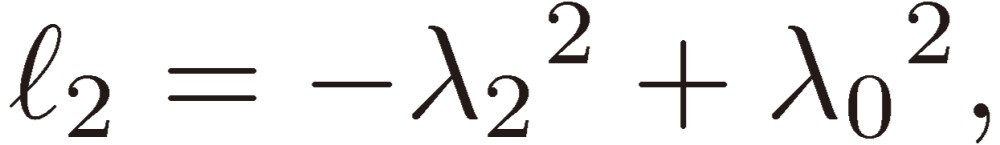[25b]

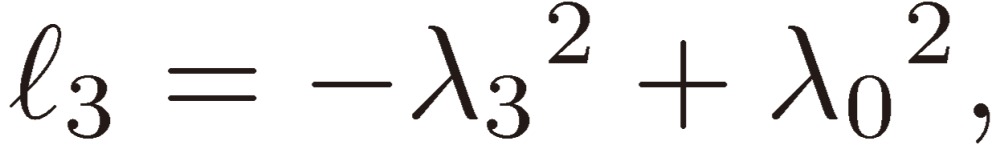[25c]

[26]

The probability of the state being in the state 2 at t is given by the absolute square of the coefficient of Ψ₂⁽⁰⁾(t) in Eq. [20], i.e.

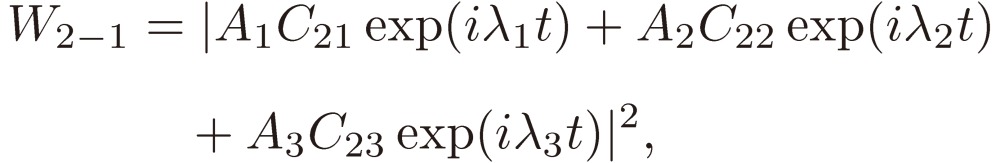[27]

which, when Eqs. [21a], [21b], and [21c] are inserted, reduces to

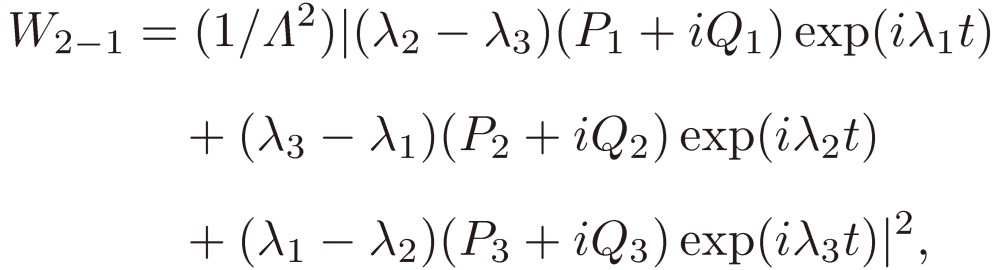[28a]

with the new definitions:

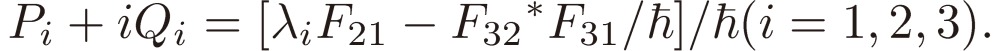[28b]

We thus finally obtain

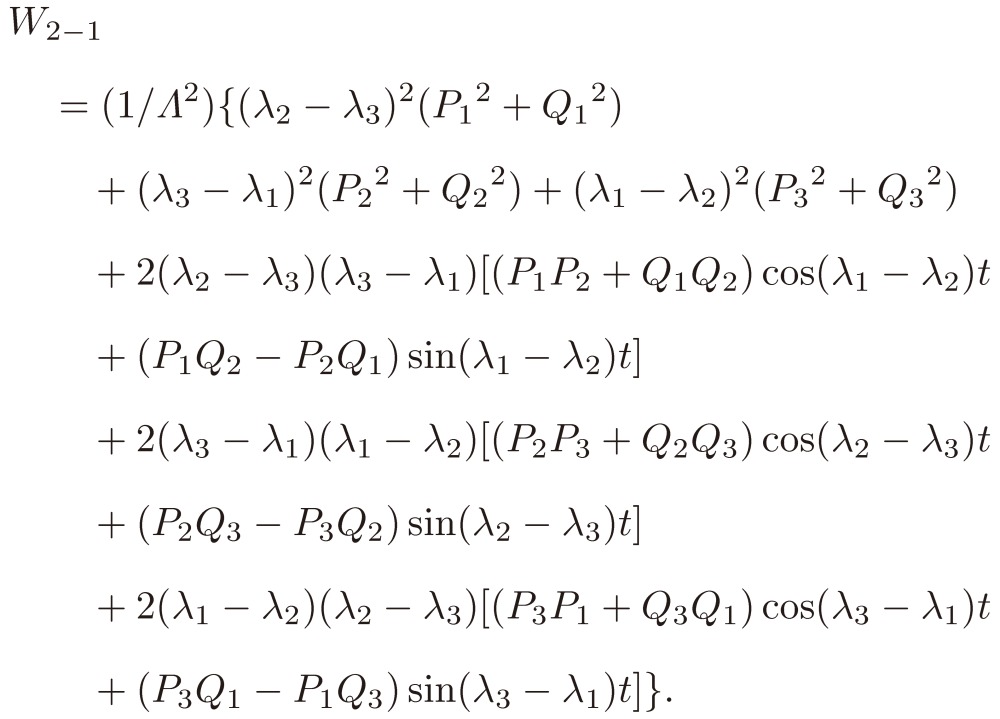[29]

V. Implications for enantio-differentiation

We shall focus attention to the rotational motion of a chiral molecule. The perturbation Eq. [4] is then ascribed to the interaction of the molecule with the external microwave electric field through the dipole moment of the molecule, namely due to the Stark effect. Because the dipole moment is a vector, it is reversed in sign when one enantiomer is transformed to the other, which means that all the matrix elements F_ij change sign. As shown in a previous section III, because D₃ as defined by Eq. [16b] changes its sign, the three characteristic frequencies λ₁, λ₂, and λ₃ will be transformed accordingly as follows:

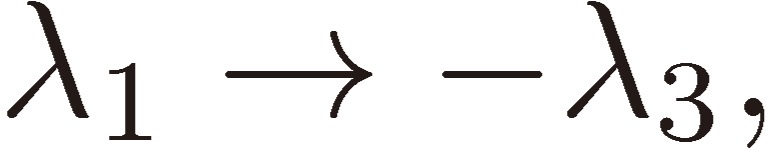[30a]

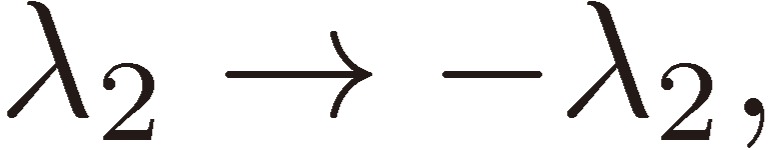[30b]

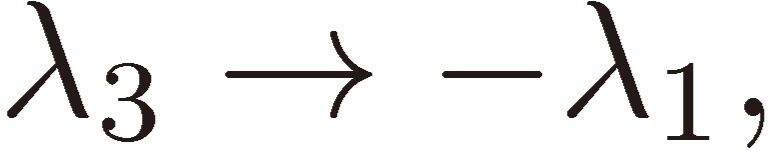[30c]

and P_i + iQ_i, as defined by Eq. [28b], varies as follows:

[31a]

[31b]

[31c]

and hence

[31d]

[31e]

[31f]

[31g]

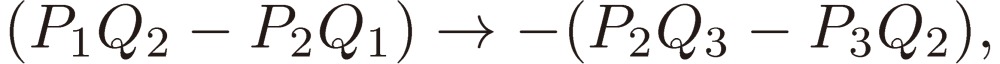[31h]

[31i]

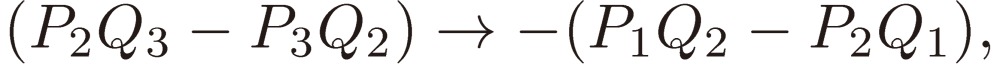[31j]

[31k]

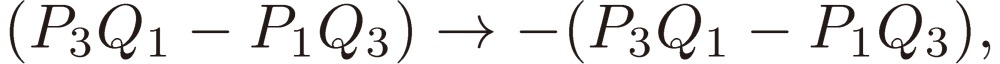[31l]

while the frequencies and their trigonometric functions in Eq. [29] are changed as follows:

[32a]

[32b]

[32c]

[32d]

[32e]

[32f]

[33a]

[33b]

[33c]

[33d]

[33e]

[33f]

As a result, the three sine terms in Eq. [29] will change their signs from one enantiomer to the other. Therefore, we may conclude that we might have a chance to differentiate two enantiomers through the observation of their time-dependent rotational spectra under a triple resonance condition.

VI. Discussion and conclusion

VI-1. The D₃ constant.

One of the most important results of the present study lies in the discovery of the D₃ constant, which, as defined by Eq. [16b], consists of products of three Stark matrix elements, each corresponding to a different-type transition between two of the three levels of the system, as illustrated in Fig. 1. This constant may thus be regarded to bear an essential feature of molecular chirality.

It should be pointed out that this constant is not compatible with conventional theory of molecular rotation (i.e. the rotation of a rigid body). The Stark effect for the molecular rotation is expressed by products of the components of the permanent dipole moment and the direction cosines between the dipole moment components and the space-fixed axis along which the external electric field is applied. For the pure rotation, the dipole moment is a constant, and the matrix elements of the three direction cosines are normally chosen such that two of them real and one imaginary. Therefore, the rotation theory concludes D₃ to be zero. We may generalize this treatment such that the three Stark matrices result in a real D₃, to be consistent with its definition, namely by choosing the Stark matrices to be either (i) all real or (ii) one real and two imaginary. Then we would arrive at an insignificant conclusion that P_i and Q_i defined by Eq. [28b] satisfy either P_i ≠ 0 and Q_i = 0 or P_i = 0 and Q_i ≠ 0, making all the sine terms in Eq. [29] vanish. The present study indicates that the rotational levels of a C₁ chiral molecule do not belong to any definite parity, rather to a mixed parity, and hence they do not follow the theory of molecular rotation.

In deriving Eq. [29], we implicitly assumed that there are three solutions of λ. This assumption, which is indispensable for chirality, looks plausible, namely the condition D₃ > 0 and (2/3√3)D₂³ > D₃³ or D₃ < 0 and (2/3√3)D₂³ > |D₃³| hold in most cases.

VI-2. The mixed parity.

Next we need clarify the meaning of parity mixing for the rotational levels of a C₁ chiral molecule. As mentioned in the Introduction, there are two terms known at the present time that give rise to molecular chirality or to parity mixing of rotational levels: Hund’s perturbation and parity violation. Here I shall derive a formal expression for the mixed parity, although the two terms originate from backgrounds quite different in physical nature (see Ref. 3, pp. 207–213 for the physical basis of the parity violation). We designate the two terms (in the energy unit) by E_F and E_PV, respectively, and write down the wavefunctions for the enantiomers: |R〉 and |S〉 in terms of the two basis sets of definite parity: |+〉 and |-〉 as follows:

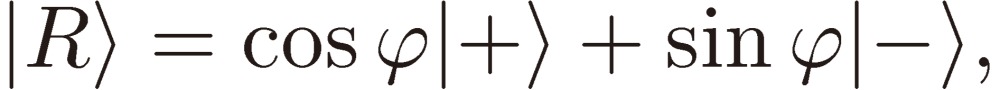[34a]

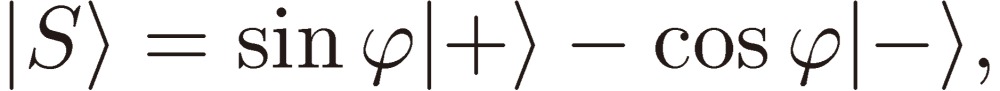[34b]

where

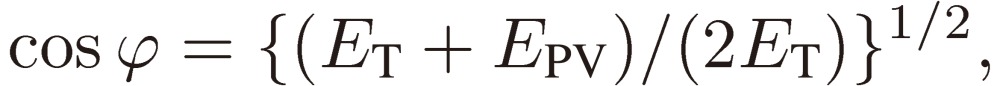[35a]

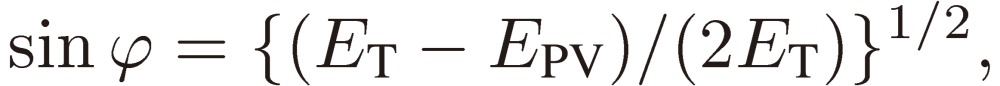[35b]

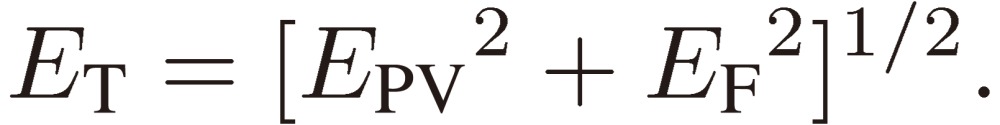[36]

If we assume E_PV susceptible to the inversion operation P as follows:

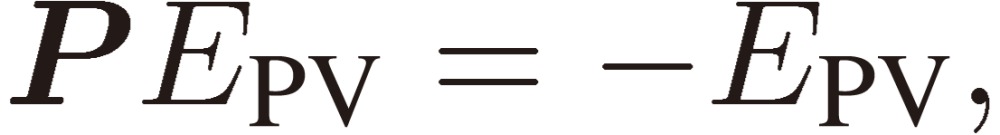[37]

we have

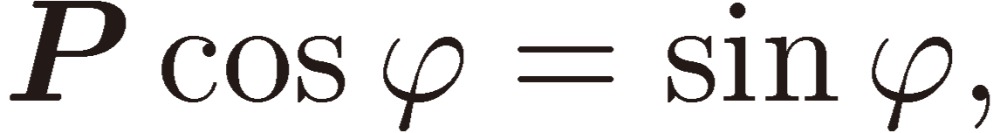[38a]

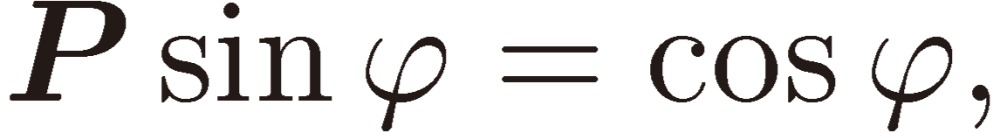[38b]

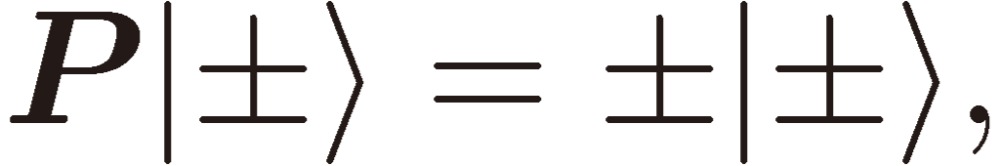[38c]

and arrive at

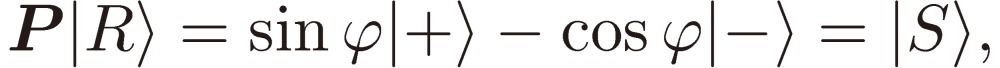[39a]

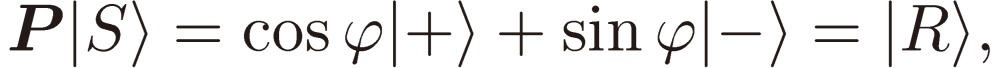[39b]

as we expected. Note that the assignment of |R〉 and |S〉 is immaterial here, in other words, they may be interchanged.

VI-3. The parity mixing of rotational levels of a chiral molecule.

The parity mixing expressed by Eqs. [34] is of great significance for enantiomer differentiation as represented by the sine terms in Eq. [29]. In order to make clear this point further, we examine the parity of pure rotational states in some detail.

In order to include the rotational motion in the discussion of chirality, we rewrite the inversion operation as follows:

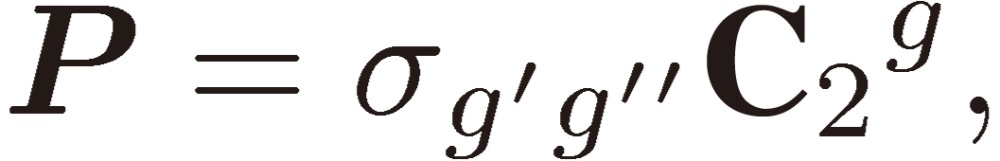[40]

where g, g′, and g″ denote the three different principal inertial axes, a, b, and c. The first factor σ_g′g″ of Eq. [40] denotes the reflection on the g′g″ plane and the second one the two-fold rotation about the g axis. We designate a rovibronic state as |+,r〉 or |-,r〉, where the vibronic part is of definite parity either + or −, as shown above, and r denotes the rotational part, which is one of the four group members for an asymmetric rotor: K_aK_c = ee, eo, oo, and oe.¹⁸⁾ The transition probability for the r₁–r₂ transition is the absolute square of the matrix element of the dipole moment component along the space-fixed Z axis μ_Z.

Let us consider two simple examples of chiral molecules, in order to illustrate the role of the rotational motion. The first example is the isopropanol molecule: (CH₃)₂CHOH, which has been confirmed to exist in two rotational isomers, trans and gauche, with respect to the dihedral angle between the C–O–H and the H–C–O planes.^19–23) There are two equivalent gauche forms, which may be regarded as a chiral pair, while we simply ignore trans, because it is well isolated from gauche. Hirota²⁴⁾ and Hirota and Kawashima²⁵⁾ found that the rotational spectra observed for gauche were well reproduced by assuming the a inertial axis antisymmetric, whereas the b and c axes symmetric, and established that the two gauche forms were split into a symmetric (+) and an antisymmetric (−) state with the energy separation of 46798.901(60) and 4431.4613(17) MHz, respectively, for (CH₃)₂CHOH and (CH₃)₂CHOD. Although the gauche forms of isopropanol are by no means optically stable in a conventional sense, as indicated by the large energy separations, they are of great use in discussing the role of rotational motion in chirality.

We may thus interpret the matrix elements of the dipole moment Z component of the gauche chiral pair of isopropanol using Eq. [40] as follows:

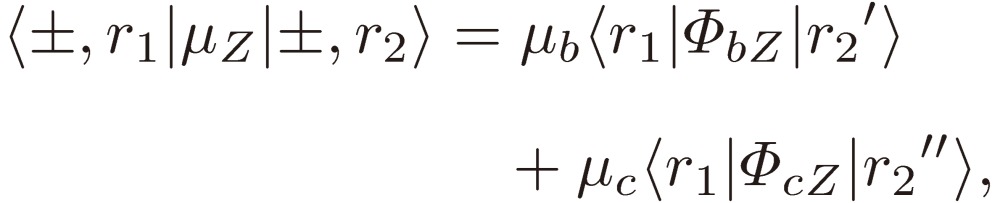[41a]

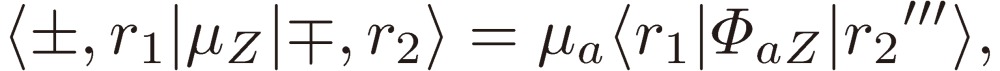[41b]

where the (r₁, r₂) pair in the 〈r₁|Φ_bZ|r₂^'〉 block, the matrix element of the direction cosine Φ_bZ, is either (ee, oo) or (eo, oe), that in the 〈r₁|Φ_cZ|r₂^”〉 block is either (ee, oe) or (oo, eo), and that in the 〈r₁|Φ_aZ|r₂^”'〉 block is either (ee, eo) or (oo, oe). Eqs. [41] exactly provide a basis for the theoretical framework, which Hirota employed to analyze the rotational spectra of gauche isopropanol.

We then derive the matrix element of the dipole moment in the enantiomer basis, provided that the enantiomer is optically stable, i.e. localized in a limited area of phase space, by employing Eqs. [34]:

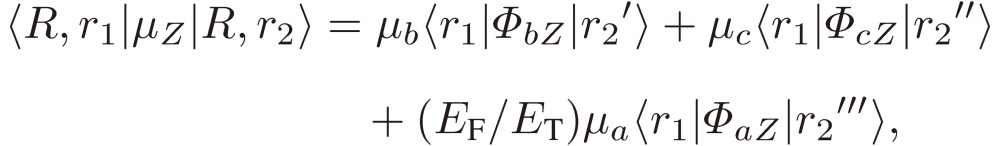[42a]

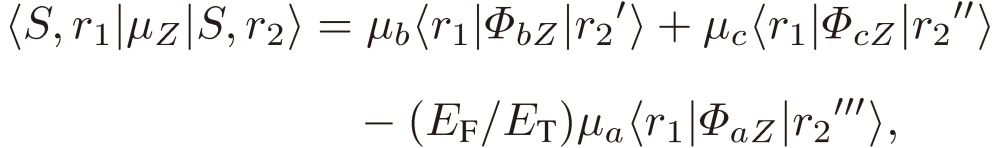[42b]

[42c]

Although the relative magnitudes of E_F and E_PV are different for different molecules, we may estimate E_F/E_T to be of the order of one, in view of the fact that the parity violation term is as small as 10⁻¹³ cm⁻¹. We may thus conclude that the rotational spectra of an enantiomer consist of all three a-, b-, and c-types transitions, with one component, a-type in the present example, opposite in sign for the two enantiomers, in agreement with what we found for D₃ and others. It is interesting to note that, when the parity violation is sizable compared with the Hund term, we may observe transitions between the two different enantiomers, as Eq. [42c] indicates.

The second example of the chiral molecule is propylene oxide, CH₃CH(O)CH₂. An optically pure sample of this molecule is available commercially, which means that the enantiomer of this molecule is optically stable, and in fact, all three types of rotational spectra were observed and analyzed in a conventional way; one trivial example of three transitions, which form a loop similar to that depicted in Fig. 1, is the c-type 1₁₁–1₀₁, the a-type 2₁₂–1₁₁, and the b-type 2₁₂–1₀₁ transitions.^26–28) The antisymmetric inertial axis of this molecule is the c axis, and thus all the results derived for isopropanol hold for propylene oxide as well, provided that the c axis plays the role in place of the a axis.

IV-4. Comments on enantio-differentiation experiments.

It should be noted that the observation of time-dependent microwave spectra based upon Eq. [29], if successful, tells us only the difference between the enantiomers; the assignment of the observed spectra to either R- or S-enantiomers individually needs additional information. It should also be noted that the level scheme depicted in Fig. 1 and the enantiomer-dependent signal might be correlated with each other.

The prediction of enantio-differentiation based upon Eq. [29] looks reasonable and an experiment based on this prediction is certainly worth being carried out. It requires three microwave radiations of different frequencies, and care must be taken to estimate an optimum power for these radiations. In recent years we employ molecular beams in a routine way, which eliminate the burden of pressure broadening to a considerable extent. Furthermore, the advances in electronics allow us to use microwave sources with a wide variety of power and frequency, and thus no serious limitations exist in this respect in conducting triple resonance experiments. There are two factors to which we should pay attention: the off-resonance terms ε_a, ε_b, and ε_c in Eqs. [13] and the relative phases of the three radiations. The former is deliberately ignored in the present study primarily to simplify the theoretical development, but would play significant roles when we are interested in the line shape of the triple resonance signals, as are the case for double resonance,²⁹⁾ where the intermolecular collisions will compete with the effects of multiple resonances. The phases of the three external radiations might affect triple resonance conditions to a considerable extent, but can be exploited to extract some further useful information from the triple resonance signals.

IV-5. The nature of “tunneling” in Hund’s paradox.

The mechanism leading to the tunneling in Hund’s paradox has not all been clarified in detail. The chiral molecule is normally “defined” in such a way that one must break at least one chemical bond of this chiral molecule to transform one enantiomer to the other, and thus the transformation and/or the racemization will resemble a sort of chemical reaction, although the reaction paths have not been identified clearly for most chiral molecules. The gauche forms of isopropanol briefly discussed in IV-2 are not considered as chiral molecules in light of this conventional definition of molecular chirality. However, as I demonstrate, the gauche forms certainly behave like chiral molecules, but the tunneling splitting is quite large and thus enantiomers are almost impossible to isolate one from the other. The tunneling motions in these cases are thought to approximate some known internal motions. In the example of isopropanol, the internal rotation about the CH–OH axis has been suspected to be the main “reaction” coordinate. However, it should be pointed out that the energy differences between the two gauche forms determined for the OH and OD species of isopropanol do not satisfy the relation expected from a simple internal-rotation model,²⁵⁾ indicating close examination of the “reaction coordinate” indispensable to clarify the real mechanism of tunneling in this molecule.

Presumably because the tunneling in Hund’s paradox remains ambiguous in nature, several investigations have recently been carried out, and here I cite a study of Trost and Hornberger³⁰⁾ as such an example. They treated a specific molecule D₂S₂ by assuming the dominant collisional decoherence mechanism to stabilize the configuration states, i.e. the enantiomer states, of the molecule. They stated that the chirally sensitive parts of the London dispersion interaction in their treatment consist of (ED-EQ)(ED-ED) van der Waals interaction, where ED denotes the electric dipole and EQ the electric quadrupole transitions, and that the associated dispersion term is proportional to r⁻⁷, rather than of the ordinary r⁻⁶ dependence on the distance r between the interacting atoms and/or molecules.

The mechanism proposed by Trost and Hornberger can play an important role in the tunneling problem. It should be pointed out, however, that most asymmetric chemical syntheses so far employed are based on chiral catalyzers, and we certainly have to carry out much more extensive researches in order to clarify how significant the collisional decoherence is in enormous number of chiral catalytic materials.