Abstract
In order to fully explore and utilize the advantages of droplet-based microfluidics, fast, sensitive, and quantitative measurements are indispensable for the diagnosis of biochemical reactions in microdroplets. Here, we report an optical detection technique using two-photon fluorescence lifetime imaging microscopy, with an aligning-summing and non-fitting division method, to depict two-dimensional (2D) maps of mixing dynamics by chaotic advection in microdroplets with high temporal and spatial resolution. The mixing patterns of two dye solutions inside droplets were quantitatively and accurately measured. The mixing efficiency in a serpentine droplet mixer was also quantified and compared with the simulation data. The mapped chaotic mixing dynamics agree well with the numerical simulation and theoretical prediction. This quantitative characterization is potentially applicable to the real-time kinetic study of biological and chemical reactions in droplet-based microfluidic systems.
INTRODUCTION
Droplet-based microfluidic devices have been exploited for various applications including fast kinetics measurement,1, 2, 3 protein crystallization,4, 5 synthesis of micro/nano particles,6, 7 DNA sequencing and amplification,8, 9 single-cell level gene expression10 and enzyme assays,11 octanol-water partition coefficient measurement,12 liquid-liquid extraction,13 etc. Rapid mixing is a critical step in these chemical and biological processes. Mixing inside droplets is not dominated by molecular diffusion but promoted by internal circulating flow. By introducing serpentine shape into microchannels, mixing is further enhanced by chaotic advection, which can be as fast as few milliseconds.14 The characterization of mixing is indispensable for appraisal of the performance of micromixers and microreactors. Quantification of the concentration field directly reflects the mixing and reaction conditions of reagents. In many chemical and biological assays, the analysis of chemical environment or distribution of species inside droplets is essential for monitoring the reactions. It has been reported that protein crystallization,5 as well as the yields and size distributions of the synthesized nanoparticles,15 was significantly affected by the mixing dynamics within droplets.
The hydrodynamics and chaotic mixing in microdroplets have been widely investigated in computational studies.16, 17, 18, 19, 20, 21, 22, 23 Stone and Stone16 labeled the fluid inside the droplet with two colors and visualized mixing with a “backtrace imaging” method to exhibit three-dimensional (3D) mixing flows inside a spherical droplet. Kashid et al.17 developed a particle tracing algorithm using multiphase computational fluid dynamics (CFD) to characterize 2D internal circulation flow within drops flowing through a straight channel. Muradoglu and Stone18 performed a 2D numerical study of chaotic mixing in a drop moving through a winding channel using a finite-volume and front-tracking method. Sarrazin et al.19 used a similar method to simulate the complete 3D dynamics inside the droplets and performed 2D computations with tracing particles to reveal the mixing inside the droplets. Tung et al.20 extended mixing analysis in droplets by considering the molecular diffusion and simulated the distribution of dye concentration inside droplets moving through a planar serpentine channel. Although numerical simulation has become a versatile and convenient method to analyze the mixing behaviors in various geometries, the accuracy of simulation results is yet to be validated by quantitative measurements.
In continuous microfluidics, the usage of pH sensitive fluorescein,24 dye quenching,25 or calcium-sensitive dyes26 to characterize mixing is very efficient. Indeed, using the reaction3, 27 between Fluo-4 and Ca2+ or pH sensitive fluorescein28 to characterize the mixing efficiency in a droplet mixer has been demonstrated. For example, the mixing in droplets flowing through a microchannel has been captured by time-averaged intensity images with extra long exposure and the mixing efficiency along the channel was quantified as a continuous evolution,27 but the detailed mixing patterns in droplets were missing. The challenges for direct measurements of mixing in droplets are due to the fact that the droplets flowing in a microchannel are typically at high frequency, and the signals in droplets are discrete, which is different from continuous laminar flow in microchannels. Coarse intensity images of chaotic mixing patterns can be obtained using a conventional CCD camera with short exposure, but the temporal and spatial resolutions are greatly scarified at high droplet generation rates. High-speed cameras can achieve frame rates in excess of 10 kHz but lack of high sensitivity in fast imaging. The microflow behavior in droplets has also been investigated by micro-particle image velocimetry (microPIV),29 which only provides indirect information for concentration fields. An elegant detection method for recording signals inside droplets applies laser induced fluorescence intensity measurement to achieve on-line detection of concentration fields in microchannels. Dittrich et al.30 first reported this technique and used it to study protein expression inside artificial cells. Srisa-Art et al.31, 32 developed a confocal fluorescence spectroscopy for online characterization of high-throughput droplet assays based on fluorescence resonance energy transfer (FRET). Using such developed system, droplet size, droplet formation frequencies, and droplet compositions were precisely measured and binding kinetics of biological assays were extracted at millisecond time resolution. However, the time-integrated fluorescence intensity measurements may not be reliable, since the intensity-based signal depends on experimental and optical conditions such as sample concentration, volume, excitation intensity, and optical collection efficiency. In contrast, the fluorescence lifetime, an intrinsic fluorescence feature of individual molecules, is free of these dependent factors. It has been employed to differentiate respective components of a mixture by applying fluorescence lifetime fitting model. Srisa-Art et al.33 and Solvas et al.34 applied the fluorescence lifetime imaging microscopy (FLIM) technique to record emission photons and used the maximum likelihood estimator method to extract fluorescence lifetimes for reconstruction of mixing patterns inside droplets with microsecond temporal resolution.
Inspired by the previous work, we have developed a two-photon excitation fluorescence lifetime imaging technique to accurately and quantitatively measure mixing fractions of two fluorescence dyes within microdroplets.35 The line scanning along the microfluidic channel was passively achieved via the droplets flowing through the excitation focal point. We stress here cross/autocorrelation was used to precisely align and magnify the line-scanning signal due to the high reproducibility of each droplet signal. A non-fitting method based on the ratio of fluorescence signals in two regions of a fluorescence decay curve was used to produce a calibration curve for mapping the mixing ratios. With the improved methodologies, chaotic mixing dynamics inside microdroplets were visualized with 5 μs time resolution, and mixing efficiency was evaluated along a serpentine channel. The patterns of two fluid mixing fraction and mixing efficiency were also investigated by numerical simulation of coupled laminar two-phase flow level set and convection-diffusion equations. The combined experimental and numerical investigations provide a direct comparative study of chaotic mixing inside microdroplets.
EXPERIMENTAL SECTION
Device fabrication and operation
The microfluidic device was fabricated in poly(dimethylsiloxane) (PDMS) (Sylgard 184 silicone elastomer, Dow Corning) using a micromolding process.36 The photolithographically patterned silicon microchannels were etched ∼40 μm in depth by deep reactive-ion etching and served as a mold for PDMS replica molding. The silicon mold was then put in a vacuum chamber with a few drops of trichloro(1 H,1 H,2 H,2 H-perfluorooctyl)silane (Sigma-Aldrich) to prevent the PDMS from sticking to the mold. A PDMS mixture (in a 10:1 ratio of monomer and curing agent) was poured over the mold, degassed in a vacuum chamber, and cured in an oven at 85 °C for 2 h. After the PDMS replica was removed from the mold, inlet and outlet holes were punched by a pan head needle. The PDMS replica was then bonded to a PDMS-hexane (volume ratio of 1:10) coated glass slide to ensure all the microchannel surfaces made of PDMS. Hexane was used to dilute the PDMS mixture so that the PDMS-hexane mixture has a much smaller viscosity than the original PDMS mixture for a thinner film coating. This PDMS coated glass slide served to seal the PDMS microchannel by curing PDMS-hexane in an oven at 85 °C for 2 h (hexane will be evaporated during the curing), and more importantly, kept all the microchannel surfaces hydrophobic.
Microdroplet generation and mixing were demonstrated using two-phase flow focusing in a microchannel of 50 × 40 μm2 in cross section as illustrated in Figure 1. Two aqueous streams, 25 μM Alexa Fluor 430 streptavidin conjugate (Invitrogen) in phosphate buffered saline (PBS, pH 7.4, Sigma-Aldrich, density: ρ1 = 1.008 g/ml, viscosity: μ1 = 1.02 mPa·s) and 200 μM Lucifer yellow CH lithium salt (Invitrogen) in PBS, were pumped into the mid two inlets at a flow rate of 1 μl/min each using syringe pumps (kd Scientific). The formed parallel streams were then focused by two mineral oil streams (Sigma-Aldrich, M5904, density: ρ2 = 0.84 g/ml, viscosity: μ2 = 30 mPa·s, surface tension between mineral oil and water: σ = 38 mN/m) from two side inlets at a flow rate of 1.5 μl/min each and pinched off into microdroplets suspended in the continuous oil phase. The two aqueous solutions were mixed in droplets flowing through the serpentine outlet channel. The Reynolds number and Capillary number based on the continuous fluid are 0.06 and 0.03, respectively. A highly sensitive CCD camera (EXi Blue, Q-IMAGING) was mounted on an inverted microscope (Eclipse Ti, Nikon) to capture the microdroplet size and shape, and a high speed digital camera (Phantom ir300, Vision Research) was also mounted on the same microscope to measure the generation frequency and flow velocity of microdroplets formed in the microchannel.
Figure 1.
A bright field image of water-in-oil droplets, generated from two aqueous solutions (labeled with Lucifer yellow and Alexa 430 dyes, respectively) flowing in parallel and intersected by two mineral oil flows in a 50 × 40 μm2 microchannel. An arrow shows the cross scanning direction is perpendicular to the microchannel.
Two-photon FLIM system
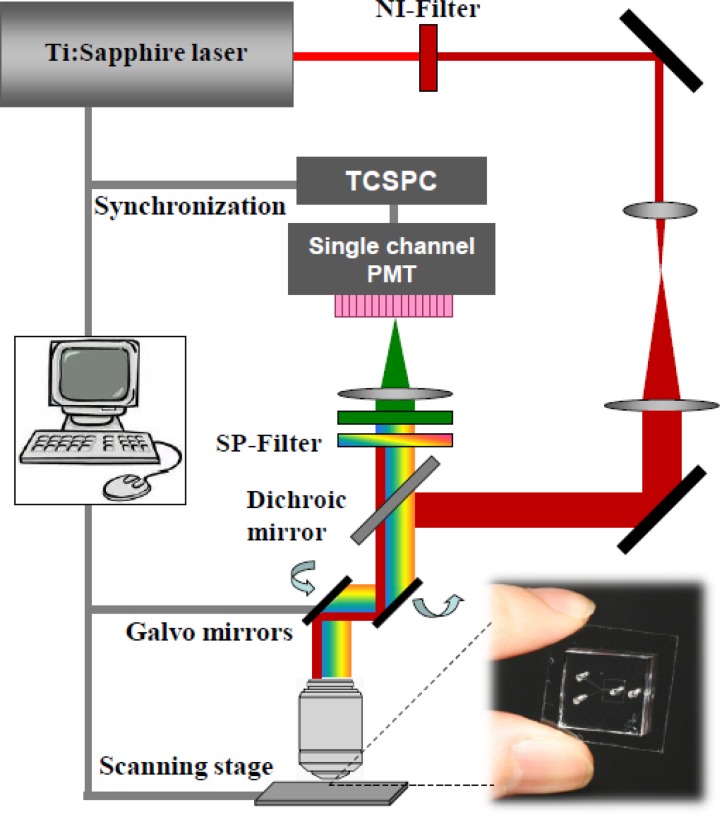
The fluorescence signals of the two probes inside microdroplets were detected using a home-built two-photon fluorescence lifetime microscopy system, modified from the previously reported FLIM,37 as shown in Figure 2. A tunable femtosecond Ti:sapphire laser (850 nm) operating at a repetition rate of 80 MHz (12.5 ns pulse separation) was employed as the excitation source. The collimated excitation beam was focused into the chip by a water immersion objective lens (60×, NA = 1.20 NA), and manipulated by an actuator for depth adjustment. The chip was mounted on a PC-controlled translation stage (V-102, Physik Instrument) with 0.1 μm positioning precision. The focal point was set at 20 μm above the bottom surface wall of the microchannel. The microscope imaging system produced lateral and axial resolutions of 0.5 μm and 1.5 μm, respectively. The backscattered fluorescence signal was separated by a dichroic mirror (730 nm Chroma) and passed a short pass filter (740 nm, Chroma) and a bandpass filter (550 ± 20 nm, Thorlabs). The photomultiplier tube (PMT) with a time-correlated single photon counting (TCSPC) module (PML-100-20 and SPC-150, Becker & Hickl GmbH) detects the photon arrival time with respect to the first excitation pulse with ∼50 ps time resolution, and the histogram of photon counts versus their arrival times represents a time-resolved fluorescence decay curve.38 All the collected data were analyzed using customer-built programs in matlab.
Figure 2.
A schematic of home-built two-photon fluorescence lifetime microscopy system.
Calibration of two dye solution mixing
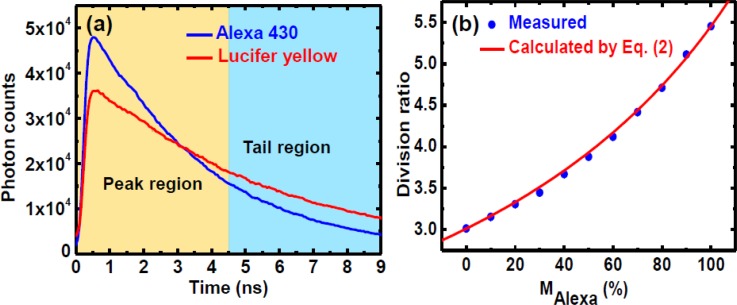
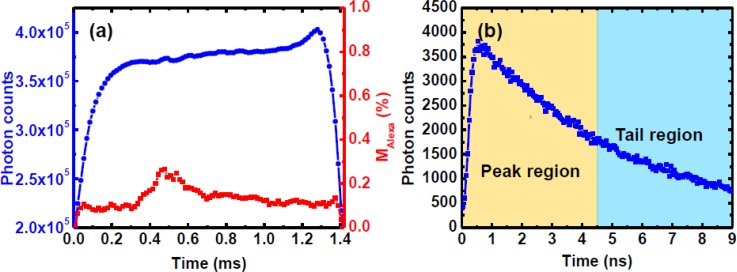
To map chaotic mixing patterns in microdroplets, we utilized two commercial probes of Alexa 430 and Lucifer yellow with similar absorption and emission spectra as the indicators for fluidic mixing. In our previous work,35 we developed a non-fitting division method to resolve the mixing fraction of one dye from the fluorescence decay curves of mixtures. We first measured the time-resolved fluorescence decay curves of the pure Alexa 430 and Lucifer yellow dye solutions using ∼20 mW excitation power, as shown in Fig. 3a. The lifetimes of pure Alexa 430 and Lucifer yellow are 3.1 ns and 5.0 ns, respectively. We define the division ratio as DR = IP/IT, where IP and IT are the integrated photon counts from the peak and tail regions as indicated in Fig. 3a. The widths of the two regions were set equal in order to balance the fluctuation of the photon counts such that the signal-to-noise ratio was significantly increased using the summed counts in the two time windows. In the calibration experiments, we measured the fluorescence decay curves of 11 pre-mixed Alexa 430 and Lucifer yellow solutions. The division ratio (DR) from measured decay curves versus the mixing fraction of Alexa 430 was plotted in Fig. 3b. Here, the mixing fraction of Alexa 430 was defined as
| (1) |
where and are normalized concentrations, = CAlexa/CAlexa,o and = CLucifer/CLucifer,o, C represents the real value of the dye concentration in the mixture, and Co represents the value of the initial concentration. Shown together is a theoretical curve calculated from Eq. 2, assuming that emission photon counts are proportional to the concentrations of two probes and there is no interaction between the two probes
| (2) |
where IP- and IT- are the photon counts in the peak and tail regions from the pure Alexa and Lucifer solutions under the same condition, respectively. The excellent agreement between the measured points and the theoretical curve ensures that no interaction between the two probes occurs, and Eq. 2 can serve as a calibration model for the DR versus the mixing fraction of Alexa (MAlexa) and be directly used to convert the DR measured from the fluorescence decay of a mixture to MAlexa. Compared with the conventional least squares approach,39 our division method to evaluate the fluorescence decay in the time-domain has shown much higher accuracy in processing the same number of photon counts.35
Figure 3.
(a) Fluorescence decays of Lucifer yellow (lifetime of 5.0 ns) and Alexa 430 (lifetime of 3.1 ns). The peak and tail regions are set in identical width to define the division ratio. (b) A calibration curve of two fluid mixing based on the division method: measured (circles) from 11 pre-mixed bulk solutions and theoretically calculated (solid line) using Eq. 2.
SIMULATION SECTION
Numerical method
The mixing dynamics in a microdroplet mixer was simulated using a commercial finite-element code, comsol multiphysics 4.1 (Comsol, Inc.), based on the laminar two-phase flow level set model coupling with the transport of diluted species model. We considered the water droplet contour evolution in the continuous oil phase by tracking the water-oil interface in two-phase flow and the mixing of diluted solutions in droplets by molecular diffusion and fluid convection. The mixing patterns are visualized by the distribution of mixture fraction at various locations along the microchannel.
First, the interface between the immiscible water and oil phases is tracked by using level set method, in which the interface is represented by a so called level set function φ.40 In this method, φ > 0.5indicates the continuous phase domain, and φ < 0.5 indicates the dispersed phase domain. The interface is implicitly represented by the points where φ = 0.5. The velocity field and pressure field of two-phase flow in the simulation are governed by the incompressible Navier-Stokes equations
| (3) |
| (4) |
| (5) |
where ρ1 and ρ2 are the fluid densities of dispersed phase and continuous phase, is the flow velocity, t represents time, p is the pressure, and μ1 and μ2 denote the dynamic viscosities of dispersed phase and continuous phase. The body force is caused by the surface tension, , where σ is the surface tension between two phases, κ is the curvature, δ is a Dirac delta function concentrated to the interface, and is the unit normal to the interface. And the motion of the water-oil interface can be tracked by solving the equation for φ
| (6) |
where γ determines the amount of reinitialization of the level set function and ɛ determines the thickness of the interface. In practice, a suitable value for γ is the maximum magnitude of the velocity filed and ɛ should be of the same order as the size of the mesh elements. In our simulations, γ = 0.3 and ɛ = 0.6 × 10−6 are used.
Second, the mixing of two aqueous solutions in droplets is achieved by adding the convection and diffusion equation in the dispersed phase (φ < 0.5), assuming there is no chemical reaction in the mixture
| (7) |
where ci and Di represent the concentration and diffusion coefficient of ith reagent, respectively.
Computational setup
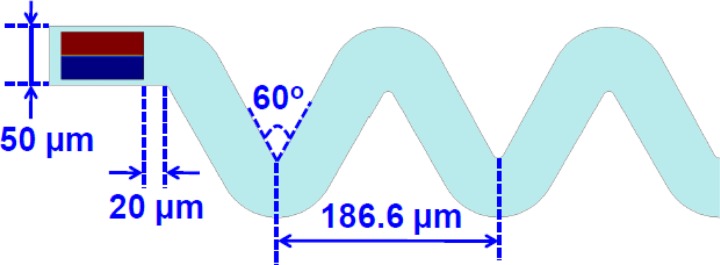
We investigated the chaotic mixing of two diluted Alexa 430 and Lucifer yellow solutions in microdroplets moving through a serpentine microchannel in a 2D numerical simulation. Figure 4 shows the geometry of the computational domain. The droplet was initially set in rectangular shape (75 × 40 μm2) with two parallel aqueous phases in the continuous oil phase. The initial geometry of the droplet was determined by keeping the droplet area (estimated from the CCD captured image) constant in the simulation and adjusting the droplet length and width until the fully developed droplet in the simulation matched the shape captured in the experiment. Triangular meshes with a maximum size of 0.8 μm were adopted and boundary layer meshing was used to refine the grids near the walls. An analysis of the mesh size independence was performed to ensure the mixing index variation was within 5%. A total number of 3.3 × 105 meshes were adopted in our typical simulations. The inlet velocity was set as 41.7 mm/s, calculated from the averaged velocity of the continuous and dispersed phases in our experiment. The physical parameters used in the simulation are summarized in Table TABLE I..
Figure 4.
2D computational domain and the initial dimension (75 × 40 μm2) of a droplet with two dyes in parallel arrangement.
TABLE I.
Physical properties of fluids.
| Density of water, ρ1 | 1008 kg/m3 |
| Density of mineral oil, ρ2 | 840 kg/m3 |
| Dynamic viscosity of water, μ1 | 1.02 mPa·s |
| Dynamic viscosity of mineral oil, μ2 | 30 mPa·s |
| Interfacial tension, σ | 38 mN/m |
| Diffusivity of Lucifer yellow (Ref. 41), D1 | 3.1 × 10−10 m2/s |
| Diffusivity of Alexa 430 (Ref. 42), D2 | 5.0 × 10−10 m2/s |
RESULTS AND DISCUSSION
Aligning-summing up periodic signals of microdroplets
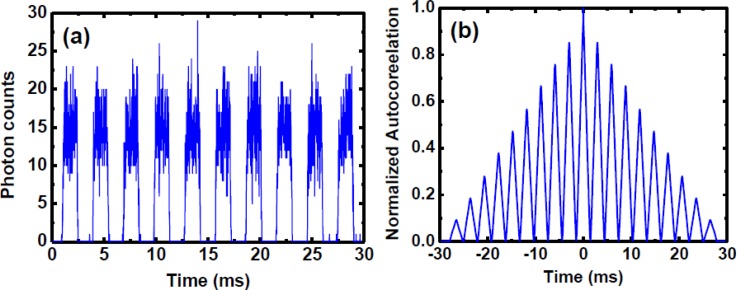
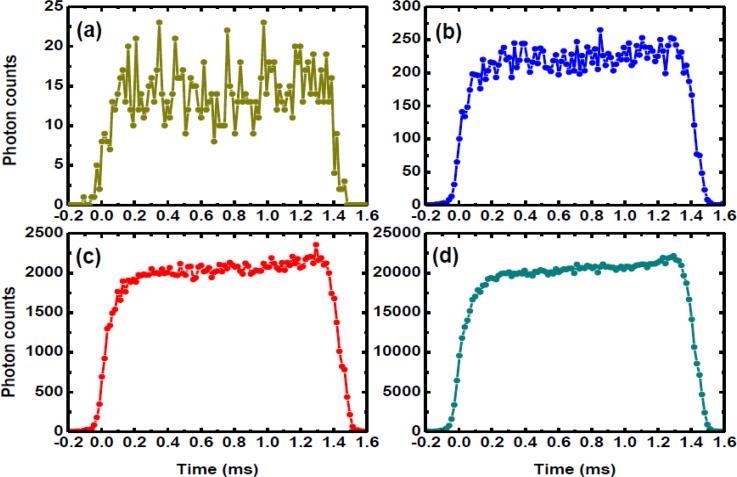
We firstly focused the detecting point at the middle (20 μm above of the low surface wall) of microchannel and 45 μm downstream from the droplet forming region. The two probes of the mixture inside microdroplets were excited when the droplets flowed through the focal point. The emitted photons were detected by the PMT and the arrival times of these photons were recorded by the TCSPC system with ∼50 ps resolution. The photon counts were further integrated at a time interval of 5 μs to form a time-tracking intensity signal. A line scanning time-tracking trajectory was passively achieved via the droplets flowing through the focal point. Figure 5a shows the time-tracking fluorescence signal for 10 droplets. Each periodic signal represents one microdroplet flowing through the focal point, and each data point was acquired by integrating the photons at 5 μs interval. However, the number of photon counts at each data point (typically 15 photons) is not sufficient for accurately representing a fluorescence decay curve. Due to the high structural reproducibility of microdroplets (as demonstrated by the autocorrelation function of the time-tracking fluorescence signal in Fig. 5b), the issue of low photon counts can be solved by aligning and summing up those periodic signals based on the cross/autocorrelation function. The period calculated from cross/autocorrelation function was used to divide the signal sequences in a data file and align the signal of each droplet for summing up.35 Figures 6a, 6b, 6c, 6d show the intradroplet time-tracking trajectories summed up using 1 droplet, 15 droplets, 150 droplets, and 1500 droplets.
Figure 5.
(a) A time-tracking fluorescence signal for 10 droplets. Each point is the total photon counts integrated for 5 μs, and each periodic signal represents one droplet flowing through the detection point. (b) The autocorrelation of the time-tracking fluorescence signal shows that the reproducible mixing pattern in the droplets can be aligned and summed up.
Figure 6.
Intradroplet time-tacking trajectories summed up using 1 droplet (a), 15 droplets (b), 150 droplets (c), and 1500 droplets (d).
In data processing, we aligned-summed up 2850 periodic droplet signals and did a 3× binning (3 data points added up to form a single data point) to obtain the final intradroplet time-tracking trajectory as shown in Fig. 7a (blue line with circles). The temporal and special resolutions after binning were 15 μs and ∼1.0 μm (calculated from the droplet velocity), which matched the 1.0 μm special resolution in the lateral direction (as described in Sec. 4B ). Normally, more than 200 k photons can be acquired at each data point in the trajectory, and the arrival times of these photons were precisely recorded by the FLIM system. We also plotted those photons at one data point (say at the data point of 0.9 ms in the trajectory shown in Fig. 7a) versus their arrival times. The time-resolved fluorescence decay of the mixture solution at that point is illustrated in Fig. 7b. The division ratio for this decay curve was calculated by its definition (i.e., Eq. 2), and the mixing fraction of Alexa 430 in the mixture at that point was obtained based on the calibration curve shown in Fig. 3b. In this way, mixing fractions of Alexa 430 at each data point in the trajectory were calculated as shown in Fig. 7a (red line with squares).
Figure 7.
(a) A time-tracking fluorescence signal (blue line with circles) after aligning-summing up 2850 periodic signals and 3× binning, and the corresponding mixing fractions of Alexa 430 (red line with squares) calculated from Eq. 2. (b) A demonstrated fluorescence decay of the mixture at the position of 0.9 ms in (a).
Chaotic mixing patterns inside microdroplets
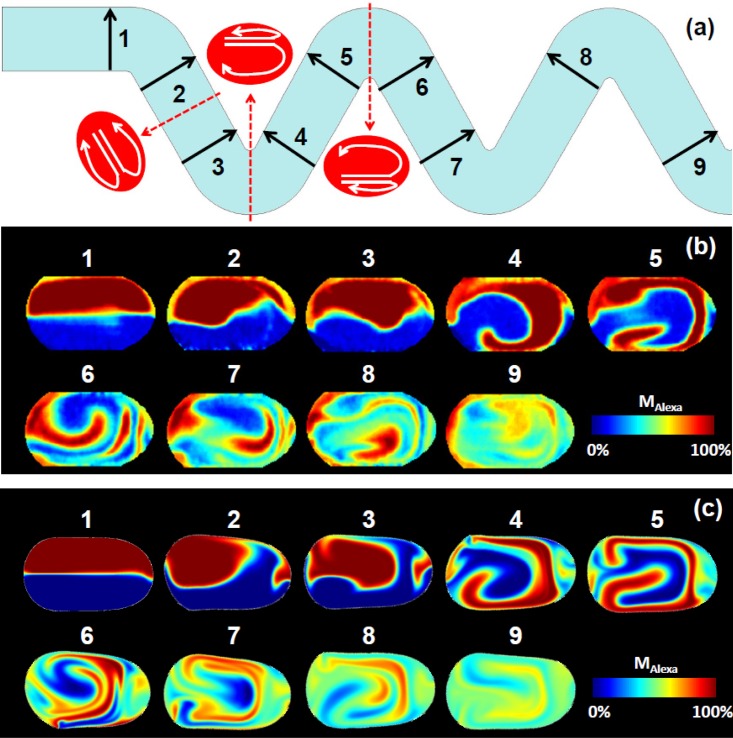
In order to obtain a two-dimensional image of mixing pattern in a microdroplet, we translocated the scanning detection point across the channel at 1.0 μm intervals (resulting in 1.0 μm resolution in the lateral direction) to obtain the periodic time-tracking fluorescence signals line by line. Using the aligning-summing method described above and matching the line signals into the droplet profile captured by the CCD camera (as shown in Fig. 1), we obtained a 2D intensity map of the horizontal cross-section of a droplet. The mixing pattern of MAlexa inside the droplet was further calculated using Eq. 2 for the fluorescence decay curve at each point. Figure 8b shows the mapped mixing patterns at various locations along the serpentine channel as indicated in Fig. 8a. The simulated concentration fields of Alexa 430 and Lucifer yellow, obtained from the 2D numerical simulation, were applied to calculate MAlexa with the same definition used in the experiments, i.e., Eq. 1. The results are shown in Fig. 8c. The corresponding measured and simulated patterns show a considerable similarity, despite the fact that the possible discrepancy may arise from the numerical simulation using a 2D model instead of 3D.
Figure 8.
(a) Schematics of asymmetric and symmetric vortices formed in droplets moving through the bent and straight microchannels, respectively. Two dye mixing patterns are shown at various locations indicated in (a): experimental results (b), and numerical simulation results (c).
It is well accepted that the reagents within microdroplets are mainly transported by chaotic advection when they move though a serpentine microchannel. Theoretical43 and computational18 studies suggest that the chaotic advection inside microdroplets is introduced by the periodic flow in terms of two symmetric or asymmetric vortices inside microdroplets moving through a serpentine channel. From this standpoint, our mapped and simulated chaotic mixing patterns (Figures 8b, 8c, 123456789) matched remarkable well with the flow behavior. When a microdroplet is generated, the two probes lie side-by-side in a parallel pattern (as the initial condition in the simulation). When it moves through the first turn which is relatively smooth (from position 1 to 2), the parallel pattern is broken by two slightly asymmetric vortices. Moving through straight channels (from 2 to 3, 4 to 5, and 6 to 7), the mixing follows the law that fluids inside droplets are transported by two symmetric vortices in the forms of stretching and folding as described by the barker’s transformation.43 Significant changes in mixing pattern arise from the microdroplet moving through the sharp turns (from 3 to 4 and 5 to 6). At a sharp turn, two asymmetric vortices are generated and the asymmetry is large enough that the large vortex is dominant within the droplet. As suggested by baker’s transformation, the large vortex can be viewed as the reorientation of the whole droplet after the sharp turn (e.g., from 3 to 4, the two fluid arrangement was changed from horizontal to vertical). When the sharp turns alternate along the winding channel, the large vortices are generated alternatively, and thus contributing to the enhanced chaotic mixing.
Figure 9.
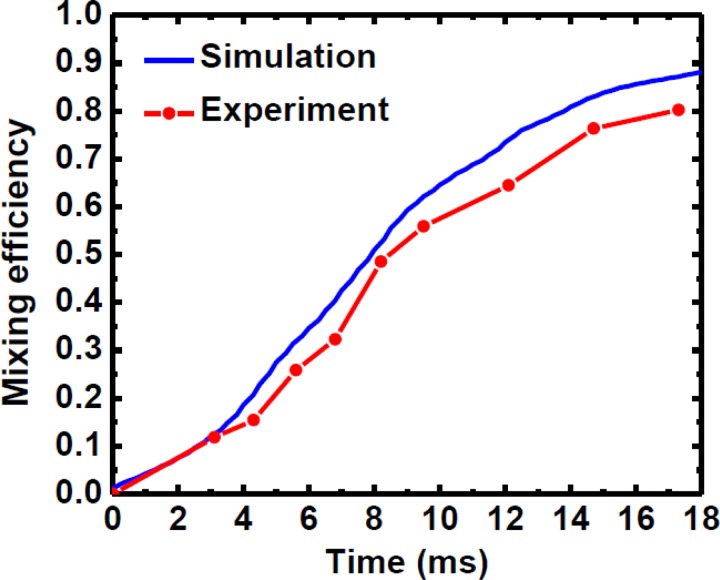
Mixing efficiency versus time for two dye mixing in droplets flowing through a serpentine microchannel: calculated from experiments (red line with circles) and from numerical simulations (blue line).
Quantification of mixing
In previous work,27 the mixing efficiency in droplet micromixers was quantified using a time-averaged intensity trace along the microchannel by long exposure imaging. It has been demonstrated that chaotic advection enables mixing of reagents inside microdroplets moving through a serpentine channel within a few milliseconds.14 Our experimentally mapped and numerically simulated images of mixing patterns allow us to more precisely calculate the mixing efficiency of chaotic mixing inside microdroplets at various locations. Here, we define the mixing efficiency Emixing as44
| (8) |
where and are the standard deviation of the mixing fraction and its maximum value, is the mixing fraction of Alexa 430 at point j, is the final mixing fraction of Alexa 430 ( = 0.5), is the initial mixing fraction of Alexa 430, and N is the total number of data points in a microdroplet. By this definition, Emixing equals 0 when no mixing happens ( equals 1 or 0) and Emixing equals 1 when the two probes are completely mixed inside a microdroplet. The red circles shown in Fig. 9 were calculated from experimentally mapped microdroplets at different locations along the microchannel. The time in x-axis was calculated based on the velocity of microdroplets measured by high speed photography. Shown together is the result calculated from time-dependent simulation (blue solid line). Our experimental and simulation results consistently show over 80% of mixing was completed in 18 ms in microdroplets moving through our designed serpentine microchannel in the set conditions.
CONCLUSION
We performed two-photon fluorescence lifetime imaging and 2D numerical simulation to directly visualize millisecond chaotic mixing dynamics inside microdroplets moving through a serpentine channel. The chaotic mixing patterns inside microdroplets were quantitatively measured with 5 μs time resolution and 1.0 μm spatial resolution. The mapped patterns compare well with the simulated patterns, both of which clearly indicate that the internal mixing within droplets is enhanced by alternatively generated asymmetric vortices when the droplets move through a winding channel with alternating sharp turns. The mixing efficiencies of chaotic mixing, calculated from both experimental and simulation results, also show a good agreement, indicating that the mixing of two probes achieves ∼80% after 18 ms. Our passive scanning FLIM with improved data analysis for characterization of mixing in microdroplets provides unprecedented insight into microflow and micromixing dynamics in droplet-based microfluidic devices and will serve as a promising diagnose tool for real-time monitoring of biochemical reactions in lab-on-a-chip systems.
ACKNOWLEDGMENTS
The authors thank the Nanoelectronics Fabrication Facility and Professor Baoling Huang’s group at HKUST for their technical support. This work was supported by HKUST Research Project Competition Grant (RPC10EG30).
References
- Song H. and Ismagilov R. F., J. Am. Chem. Soc. 125, 14613 (2003). 10.1021/ja0354566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huebner A. M., Abell C., Huck W. T. S., Baroud C. N., and Hollfelder F., Anal. Chem. 83, 1462 (2011). 10.1021/ac103234a [DOI] [PubMed] [Google Scholar]
- Liau A., Karnik R., Majumdar A., and Cate J. H. D., Anal. Chem. 77, 7618 (2005). 10.1021/ac050827h [DOI] [PubMed] [Google Scholar]
- Zheng B., Roach L. S., and Ismagilov R. F., J. Am. Chem. Soc. 125, 11170 (2003). 10.1021/ja037166v [DOI] [PubMed] [Google Scholar]
- Chen D. L., Gerdts C. J., and Ismagilov R. F., J. Am. Chem. Soc. 127, 9672 (2005). 10.1021/ja052279v [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C. H., Shah R. K., Abate A. R., and Weitz D. A., Langmuir 25, 4320 (2009). 10.1021/la900240y [DOI] [PubMed] [Google Scholar]
- Hung L. H., Choi K. M., Tseng W. Y., Tan Y. C., Shea K. J., and Lee A. P., Lab Chip 6, 174 (2006). 10.1039/b513908b [DOI] [PubMed] [Google Scholar]
- Kumaresan P., Yang C. J., Cronier S. A., Blazej R. G., and Mathies R. A., Anal. Chem. 80, 3522 (2008). 10.1021/ac800327d [DOI] [PubMed] [Google Scholar]
- Tewhey R., Warner J. B., Nakano M., Libby B., Medkova M., David P. H., Kotsopoulos S. K., Samuels M. L., Hutchison J. B., Larson J. W., Topol E. J., Weiner M. P., Harismendy O., Olson J., Link D. R., and Frazer K. A., Nat. Biotechnol. 27, 1025 (2009). 10.1038/nbt.1583 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mary P., Dauphinot L., Bois N., Potier M. C., Studer V., and Tabeling P., Biomicrofluidics 5, 024109 (2011). 10.1063/1.3596394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huebner A., Olguin L. F., Bratton D., Whyte G., Huck W. T. S., de Mello A. J., Edel J. B., Abell C., and Hollfelder F., Anal. Chem. 80, 3890 (2008). 10.1021/ac800338z [DOI] [PubMed] [Google Scholar]
- Marine N. A., Klein S. A., and Posner J. D., Anal. Chem. 81, 1471 (2009). 10.1021/ac801673w [DOI] [PubMed] [Google Scholar]
- Mary P., Studer V., and Tabeling P., Anal. Chem. 80, 2680 (2008). 10.1021/ac800088s [DOI] [PubMed] [Google Scholar]
- Song H., Tice J. D., and Ismagilov R. F., Angew. Chem. 115, 792 (2003). 10.1002/ange.200390172 [DOI] [PubMed] [Google Scholar]
- Hung L. H., Teh S. Y., Jester J., and Lee A. P., Lab Chip 10, 1820 (2010). 10.1039/c002866e [DOI] [PubMed] [Google Scholar]
- Stone Z. B. and Stone H. A., Phys. Fluids 17, 063103 (2005). 10.1063/1.1929547 [DOI] [Google Scholar]
- Kashid M. N., Gerlach I., Goetz S., Franzke J., Acker J. F., Platte F., Agar D. W., and Turek S., Ind. Eng. Chem. Res. 44, 5003 (2005). 10.1021/ie0490536 [DOI] [Google Scholar]
- Muradoglu M. and Stone H. A., Phys. Fluids. 17, 073305 (2005). 10.1063/1.1992514 [DOI] [Google Scholar]
- Sarrazin F., Bonometti T., Prat L., Gourdon C., and Magnaudet J., Microfluid. Nanofluid. 5, 131 (2008). 10.1007/s10404-007-0233-9 [DOI] [Google Scholar]
- Tung K. Y., Li C. C., and Yang J. T., Microfluid. Nanofluid. 7, 548 (2009). 10.1007/s10404-009-0415-8 [DOI] [Google Scholar]
- Blanchette F., Phys. Rev. E 80, 066316 (2009). 10.1103/PhysRevE.80.066316 [DOI] [PubMed] [Google Scholar]
- Che Z., Wong T. N., and Nguyen N. T., Int. J. Heat Mass Transfer 53, 1977 (2010). 10.1016/j.ijheatmasstransfer.2009.12.058 [DOI] [Google Scholar]
- Fries D. M. and von Rohr P. R., Chem. Eng. Sci. 64, 1326 (2009). 10.1016/j.ces.2008.11.019 [DOI] [Google Scholar]
- Munson M. S. and Yager P., Anal. Chem. Acta 507, 63 (2004). 10.1016/j.aca.2003.11.064 [DOI] [Google Scholar]
- Hertzog D. E., Michalet X., Jager M., Kong X., Santiago J. G., Weiss S., and Bakajin O., Anal. Chem. 76, 7169 (2004). 10.1021/ac048661s [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheat P. M. and Posner J. D., Phys. Fluids 21, 037101 (2009). 10.1063/1.3078247 [DOI] [Google Scholar]
- Song H., Bringer M. R., Tice J. D., Gerdts C. J., and Ismagilov R. F., Appl. Phys. Lett. 83, 4664 (2003). 10.1063/1.1630378 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarrazin F., Prat L., Di Miceli N., Cristobal G., Link D. R., and Weitz D. A., Chem. Eng. Sci. 62, 1042 (2007). 10.1016/j.ces.2006.10.013 [DOI] [Google Scholar]
- Kinoshita H., Kaneda S., Fujii T., and Oshima M., Lab Chip 7, 338 (2007). 10.1039/b617391h [DOI] [PubMed] [Google Scholar]
- Dittrich P. S., Jahnz M., and Schwille P., ChemBioChem 6, 811 (2005). 10.1002/cbic.200400321 [DOI] [PubMed] [Google Scholar]
- Srisa-Art M., deMello A. J., and Edel J. B., Anal. Chem. 79, 6682 (2007). 10.1021/ac070987o [DOI] [PubMed] [Google Scholar]
- Srisa-Art M., Dyson E. C., deMello A. J., and Edel J. B., Anal. Chem. 80, 7063 (2008). 10.1021/ac801199k [DOI] [PubMed] [Google Scholar]
- Srisa-Art M., deMello A. J., and Edel J. B., Phys. Rev. Lett. 101, 014502 (2008). 10.1103/PhysRevLett.101.014502 [DOI] [PubMed] [Google Scholar]
- Solvas X. C., Srisa-Art M., deMello A. J., and Edel J. B., Anal. Chem. 82, 3950 (2010). 10.1021/ac100055g [DOI] [PubMed] [Google Scholar]
- Zeng Y., Jiang L., Zheng W., Li D., Yao S., and Qu J. Y., Opt. Lett. 36, 2236 (2011). 10.1364/OL.36.002236 [DOI] [PubMed] [Google Scholar]
- McDonald J. C., Duffy D. C., Anderson J. R., Chiu D. T., Wu H., Schueller O. J. A., and Whitesides G. M., Electrophoresis 21, 27 (2000). [DOI] [PubMed] [Google Scholar]
- Li D., Zheng W., and Qu J. Y., Opt. Lett. 33, 2365 (2008). 10.1364/OL.33.002365 [DOI] [PubMed] [Google Scholar]
- Lakowicz J. R., Principles of Fluorescence Spectroscopy, 3rd ed. (Springer, New York, 2006). [Google Scholar]
- Maus M., Cotlet M., Hofkens J., Gensch T., De Schryver F. C., Schaffer J., and Seidel C. A. M., Anal. Chem. 73, 2078 (2001). 10.1021/ac000877g [DOI] [PubMed] [Google Scholar]
- Sussman M., Smereka P., and Osher S., J. Comput. Phys. 114, 146 (1994). 10.1006/jcph.1994.1155 [DOI] [Google Scholar]
- Brink P. R. and Ramanan S. V., Biophys. J. 48, 299 (1985). 10.1016/S0006-3495(85)83783-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham C. W., Mukhopadhyay A., Lushington G. H., Blagg B. S. J., Prisinzano T. E., and Krise J. P., Mol. Pharm. 7, 1301 (2010). 10.1021/mp100089k [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bringer M. R., Gerdts C. J., Song H., Tice J. D., and Ismagilov R. F., Philos. Trans. R. Soc. London, Ser. A 362, 1087 (2004). 10.1098/rsta.2003.1364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engler M., Kockmann N., Kiefer T., and Woias P., Chem. Eng. J. 101, 315 (2004). 10.1016/j.cej.2003.10.017 [DOI] [Google Scholar]