Abstract
This paper presents a numerical study of DC-biased AC-electrokinetic (DC-biased ACEK) flow over a pair of symmetrical electrodes. The flow mechanism is based on a transverse conductivity gradient created through incipient Faradaic reactions occurring at the electrodes when a DC-bias is applied. The DC biased AC electric field acting on this gradient generates a fluid flow in the form of vortexes. To understand more in depth the DC-biased ACEK flow mechanism, a phenomenological model is developed to study the effects of voltage, conductivity ratio, channel width, depth, and aspect ratio on the induced flow characteristics. It was found that flow velocity on the order of mm/s can be produced at higher voltage and conductivity ratio. Such rapid flow velocity is one of the highest reported in microsystems technology using electrokinetics.
INTRODUCTION
Dynamic manipulation of fluids in microchannel is crucial for the development of lab-on-a-chip (LOC) devices.1, 2 One key requirement for the actuation system in LOC devices is to avoid mechanical moving parts which can potentially complicate the fabrication and increase the size of the system.3, 4 Electrokinetics has been demonstrated as a viable approach to effectively manipulate fluids in microchannels through the use of an electrical driving force.5, 6 One key advantage lies in its ease of implementation which makes electroosmosis (i.e., the use of DC electric field to drive fluid flow, due to the Coulomb force on the diffuse double layer) one of the most widely used pumping approaches in microfluidics in addition to pressure-driven methods.7, 8
AC-electrokinetic (ACEK) makes use of AC electric fields acting on AC charge density to induce rectified flow; two important examples of ACEK are AC-electroosmotic (ACEO) and AC-electrothermal (ACET) flows.9, 10, 11, 12, 13, 14, 15, 16 ACEO flow is based on the Coulomb force acting on the induced charge in the double layer in the presence of a tangential AC electric field.10, 11, 12, 13 ACET flow is based on the interaction of AC electric fields with conductivity gradients in the fluid induced by a thermal gradient.14, 15, 16
More recently, a DC-bias AC voltage (Vapplied = VDC + VAC cos ωt) has been employed effectively to concentrate particles/cells17, 18, 19 and for pumping/mixing20, 21, 22, 23 applications in microfluidics. There has been several hypothesis on the driving mechanism of the flow induced by DC-bias AC voltage.6, 18, 19 Recently, we conducted experimental investigation to elucidate the driving mechanism of the DC-biased ACEK flow phenomenon.21, 24 In the publications, we demonstrated that the applied DC-bias voltage gives rise to incipient Faradaic reactions at the electrodes’ surface.21, 24 Indeed, it was tested that these reactions cause changes on the local pH due to the generation of co-ions above the electrodes. As a result, the region above the anode became acidic due to the increase of H+ ions, and the region above the cathode was basic due to the increase of OH– ions. In addition, it was measured that the basic region is ∼11%–12% more conductive than the acidic region.24
Hitherto, there is no existing theoretical model to describe the DC-biased ACEK flow. In this paper, we present a phenomenological model based on the actual conductivity difference between the anode and the cathode to give a description of the fluid flow. It should be noted that the effect of DC-bias could not be included by simply adding a DC-bias to the AC voltage in established ACEO model.12, 13 This is because we do not know with certainty all the electrochemical reactions taking place at the electrodes’ surface. Therefore, we take the value of the increment of conductivity from experiments.24 Moreover, since the DC voltage is just enough to generate the species, the applied DC voltage is dropped across the double layer and not in the bulk. A convection-diffusion equation is used here to describe the distribution of conductivity. The interaction of the electric field with the conductivity gradient leads to fluid flow. This paper will demonstrate that the developed model could predict well the experimental observations23, 24 namely the single and dominant flow vortex and the direction of vortex rotation. It is experimentally difficult to characterize the cross-sectional fluid velocity profiles; therefore a numerical simulation serves as a tool to better understand the various factors affecting the induced flow velocity. Parametric factors (voltage, conductivity ratio) and geometrical factors (width, depth, and aspect ratio) were varied in this study to understand their effects on the induced DC-biased ACEK flow velocity.
NUMERICAL ANALYSIS
DC-biased ACEK flow phenomenon was modeled using comsol multiphysics®. A phenomenological model was presented here to give a description of the DC-biased AC-electrokinetic fluid flow. The numerical model is based on the measured conductivity difference between the anode and the cathode and was used as the basis for the boundary conditions for the conductivity equation. It was determined that the liquid above the cathode is more conductive than the one on the anode side. AC impedance analysis was adopted to measure the conductivity level above the cathode and the anode. It was found that with a DC bias of 2 VDC, the cathode is more conductive than the anode by 11%–12%.24
We assume that the applied DC voltage is just above the threshold to generate Faradaic reactions at the electrodes. In this way, VDC is dropped at the electrode/electrolyte interface to drive the reactions and negligible DC voltage is dropped across the bulk electrolyte. Notice that the minimum voltage to produce electrolysis of water is about 1.23 V. Therefore, we can neglect VDC in the medium and solve only for the AC potential (Vapplied = VAC cos ωt). Moreover, since the frequency of the AC signal is much greater than the reciprocal RC time for charging the double layer,10 the AC voltage is dropped mainly across the bulk electrolyte and negligible AC voltage is dropped at the electrode/electrolyte double layers. In addition, the effect of joule heating is ignored since the conductivity used is low.
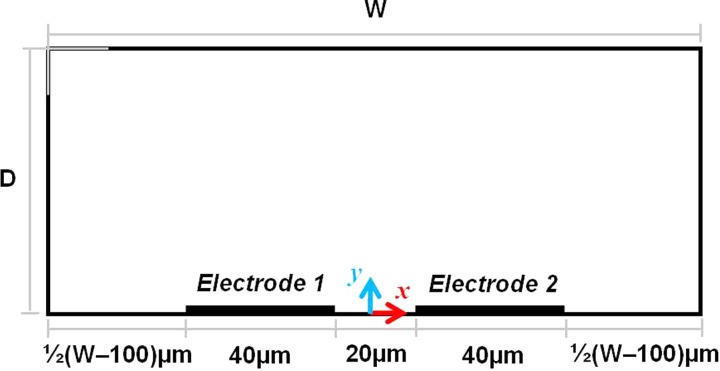
In this study, a 2D analysis was performed for a pair of coplanar and symmetrical electrodes enclosed by a microchannel as shown in Fig. 1. To limit the scope in this study, the electrode width and gap were fixed at 40 μm and 20 μm, respectively, but the microchannel width (W) and depth (D) were varied from 100 to 400 μm and 20 to 200 μm, respectively.
Figure 1.
Geometrical configuration and boundary conditions of the simulated DC-biased AC-electrokinetics problem. Boundary conditions for right electrode (conductivity: σRight, electrical: VGND, flow: no slip), left electrode (conductivity: σLeft, electrical: VAC, flow: no slip), and channel walls (conductivity: insulation/symmetry, electrical: electrical insulation flow: no slip).
Electrical equations
For an electrolyte, the electric potential (φ) distribution at any point in the solution can be related to the electric charge density () which is described by the Poisson equation
| (1) |
where ɛ is the permittivity and is the electric field. The movement of the ions in the solution will constitute to an electrical current
| (2) |
where (, with the ionic valence and e the elementary charge) is the ion charge, is the ion number density, () is the mobility, is the diffusion coefficient, and is the velocity. The first, second, and third terms represent, respectively, electromigration (i.e., conduction), diffusion, and convection. Typically for electrolytes, the convective current is usually smaller than the conduction current which is governed by the electrical Reynolds number.25 In microsystems, the electrical Reynolds number is very small for electrolyte. For semi-insulating liquids, a conductivity smaller than 10−9 S/m would be required in order to have a convective current of the same order than the conduction current. In addition, the ratio of diffusive current to electromigration is smaller than unity in the liquid bulk.25 Typically, for voltage drop in the bulk much greater than 0.025 V, diffusion is negligible as compared to electromigration. The ratio between these two currents is on the order of ∼0.025/V. In our experiments, we apply around 10 V ≫ 0.025 V. In this situation, we can write , where is the electrolyte conductivity. With these approximations, the charge conservation equation for the AC potential becomes25, 26, 27
| (3) |
where Φ is the phasor of the electrical potential. Consider a binary electrolyte ( = 1), assuming electroneutrality,16 the solution conductivity can be represented in the model with a convection–diffusion equation27, 28, 29
| (4) |
where the second and third terms represent, respectively, diffusion and convection.
Mechanical equations
In a microscale system, Reynolds number is usually small (<1) and flow is laminar in nature. The fluid velocity is governed by the Navier-Stokes equations, for steady-state solutions, we have
| (5) |
| (6) |
where is the fluid density, P is the pressure, η is the dynamic viscosity, and is the electrical body force. The electrical body force on the fluid is given by the time-average Coulomb force25, 26, 27
| (7) |
where is the charge density phasor, Re[...] represents the real part, is the complex conjugate of the electric field phasor. In this case, the time-average Coulomb force is used in the calculation. This is because the ac signals have periods much shorter than the typical mechanical time of variation of the system. Despite the electrolyte being quasi-electroneutral, the residual charge can lead to a significant force. The charge density () in the bulk can be obtained from Eqs. 1, 3 leading to a charge density phasor26, 27
| (8) |
Numerical method and settings
To solve for the DC-biased ACEK flow, “convection and diffusion,” “conductive media DC,” and “incompressible Navier-Stokes” modules in the comsol software were employed. comsol software employs the finite element method (FEM) in solving the partial differential equations (PDEs). The numerical scheme discretizes the defined spatial domain into triangular finite elements to approximate the solutions of the PDEs. Typical computation consists of approximately 1300 triangular elements and the minimum element quality is 0.86. Further investigation on the numerical convergence was conducted. With mesh refinement up to 5000 or even 20 000 triangular elements, the computed velocity does not change appreciably (less than 1%).
In the module of “convection and diffusion,” constant conductivities ( and ) were set on the two electrodes and insulation/symmetry on the channel walls. In the module of “conductive media DC,” various potentials were set on the two electrodes and electrical insulation was applied on the channel walls. In the module of “incompressible Navier-Stokes,” no slip boundary conditions were set for the electrodes and the channel walls.
In the solving process, an iterative approach was adopted where the problem was solved in three steps: First, the convection-diffusion equation was solved for the conductivity field, Eq. 4. Next, the computed conductivity solution was used to solve for the electrical potential field, Eq. 3. A parametric solver was adopted to set the voltage where the voltage was increased from zero to the set voltage level at a voltage step of 0.01 V. Lastly, the computed potential solution was used to solve for the electrokinetic flow velocity field, Eqs. 5, 6. The solving process was repeated until we obtained a converged solution where the relative tolerance is set at 10−3. The parameters used in the simulation are listed in Table TABLE I..
TABLE I.
Simulation parameters.
| Property | Value |
|---|---|
| Fluid density (ρ) | 1 × 103 kg/m3 |
| Fluid dynamic viscosity (η) | 1 × 10−3 kg/ms |
| Relative permittivity of KCl () | 80 |
| Permittivity of free space () | 8.85 × 10−12 F/m |
| Coefficient of diffusion (D) | 1 × 10−9 m2/s |
| Voltage amplitude (V) | 1–20 V |
| AC frequency (f) | 100 kHz |
| Conductivity at electrode 1 () | 1–10 mS/m |
| Conductivity at electrode 2 () | 1–10 mS/m |
RESULTS AND DISCUSSIONS
DC-biased AC-electrokinetic flow
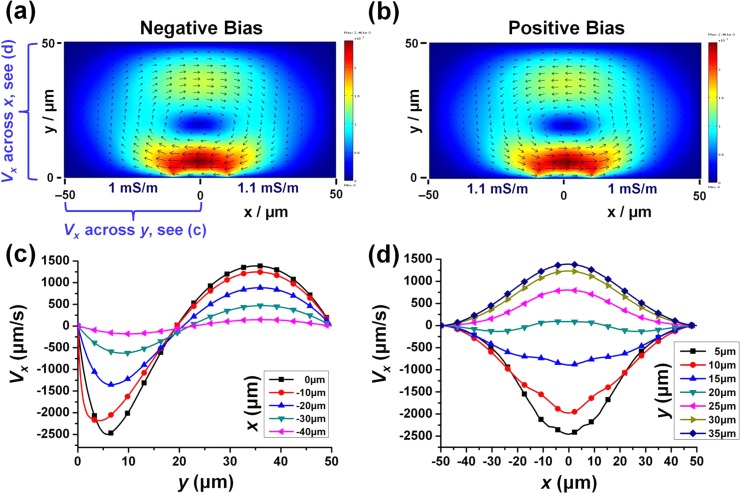
Figure 2 shows the simulated results for the velocity distribution in the 2D cross-section model (W = 100 μm, D = 50 μm, electrode width = 40 μm, and electrode gap = 20 μm) for both negative and positive DC-biased AC-electrokinetic flow. The voltage amplitude used was 10 V and the conductivity level at the two electrodes was set with a 10% difference. In both cases, a single and dominant flow vortex was obtained in the direction from higher conductivity (basic, cathode) to lower conductivity (acidic, anode). As explained, due to Faradaic reactions, a conductivity gradient is generated from the basic (higher conductivity, net negative electrode) to the acidic (lower conductivity, net positive electrode) domains. When an AC signal is applied, a horizontal force component is generated close to the electrode surface where the field is strongest. As such, the fluid is actuated from the higher conductivity to the lower conductivity domains close to the surface of the electrodes; this determines the direction of rotation and eventually results in a single and dominant vortex over the electrodes pair.24
Figure 2.
Simulated velocity distributions. (a) Negative DC-bias, < and (b) positive DC-bias, > . Conditions: voltage amplitude = 10 V, conductivity difference = 10%, W = 100 μm, D = 50 μm, electrode width = 40 μm, and electrode gap = 20 μm. For negative DC-bias of (a), plots of X-velocity (horizontal) across (c) channel depth at various locations along the left electrode, and (d) channel width at different channel heights.
For a negative DC-bias AC voltage case (see Fig. 2a), the fluid flows from right to left, i.e., from higher conductivity OH– ions rich cathode to lower conductivity H+ ions rich anode, at region near the electrodes’ surface. This flow produces a resultant clockwise (CW) vortex rotation. For a positive DC-bias AC voltage case (see Fig. 2b), the fluid flows from left to right, i.e., it is still flowing from higher conductivity OH– ions rich cathode to lower conductivity H+ ions rich anode, at region near the electrodes’ surfaces. This flow produces a resultant anti-clockwise (anti-CW) vortex rotation. As such, the predicted results on the vortex direction corroborate the reported experimental observations.23, 24
In general, the negative and the positive DC-bias simulated results are similar and symmetrical. The x-velocities () of the simulated results for the negative DC-biased case (Fig. 2a) were extracted and plotted. The horizontal velocities were plotted across the width and across the depth at different locations on the channel as shown in Figs. 2c, 2d, respectively. From Figs. 2c, 2d, it can be observed that are faster on the region nearer to the electrode surface. This is expected as the velocity is driven by the gradients of conductivity and the electrical potential, where the conductivity and the electric field are the strongest near the surface at the electrode gap.
Taking the point where = 0 along the center of the channel (y = 0) as the center of the vortex; the center of vortex is at a height of 20 μm. This corresponds to ∼40% (i.e., 20 μm/50 μm) of the total channel height. Defining Hv as the percentage of the vortex height to the channel depth (D), the Hv value computed is thus rather high at ∼40%. Similarly, we have previously reported an observed high Hv value (>30%) by experimental imaging the induced DC-biased ACEK flow vortex.24 This high center of vortex implies that the flow mechanism is bulk driven. In the literature, ACET flow which is bulk induced generally has a vortex center between 30% and 40% of the channel height.14, 15, 16
Effect of voltage and conductivity ratio
The applied voltage and the conductivity ratio affect the velocities of the flow induced in the system. Here, the conductivity ratio (γ) is defined as the ratio of the higher conductivity () to the lower conductivity (). To quantify the velocities of the flow at various conditions (voltage, conductivity ratio), the average velocity amplitude in the cross-section domain was computed and defined as27
| (9) |
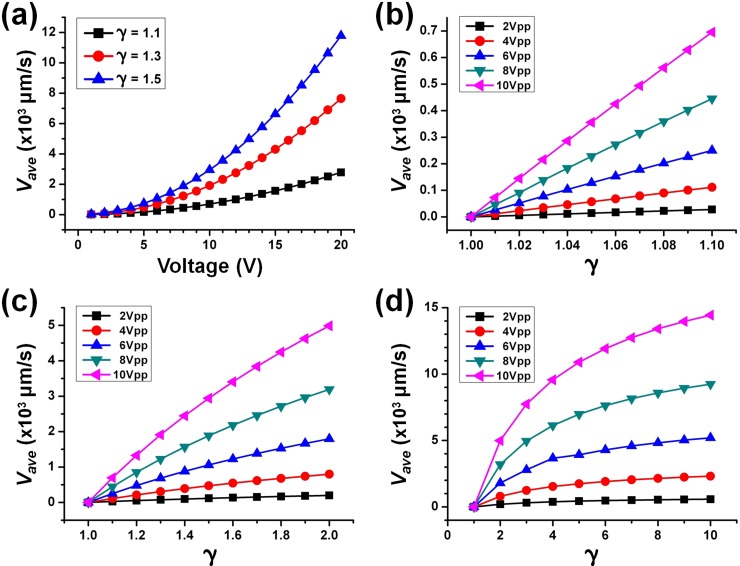
where is the velocity amplitude at and A (m2) is the area of the cross-section domain. Similarly, the adopted geometry to be study were W = 100 μm, D = 50 μm, electrode width = 40 μm, and electrode gap = 20 μm. The average velocity amplitudes for negative DC-bias at different parameters (voltage, conductivity ratio) were calculated and presented in Fig. 3.
Figure 3.
Average velocity amplitude at different (a) applied voltage, (b) conductivity ratio, up to 1.1, (c) conductivity ratio, up to 2, and (d) conductivity ratio, up to 10. Configurations: W = 100 μm, D = 50 μm, electrode width = 40 μm, and electrode gap = 20 μm.
Figure 3a shows that the average velocity amplitudes increase with the applied voltage at various conductivity ratios. The highest velocities obtained for γ = 1.1, 1.3, and 1.5 at 20 V were 2.78 mm/s, 7.64 mm/s, and 11.78 mm/s, respectively. Next, by fixing the voltage amplitude at 10 V, the effect of conductivity ratio on velocity was investigated. Figure 3 depicts results for various conductivity ratios. It indicates a clear trend that a higher applied voltage and/or higher conductivity ratio will result in a faster flow velocity. From Fig. 3a, the simulated velocity at 10 V and γ = 1.1 is ∼695 μm/s, which compares favorably with the experimental measured velocity of ∼700 μm/s.24
It should be noted that the conductivity gradient/ratio generated by the DC-bias Faradaic charging has a limitation. This is because electrolysis and electrodes degradation will occur at too high voltage. Therefore, the conductivity ratio via this method is limited by the level of DC-bias (i.e., <3 VDC). Nevertheless, to facilitate an understanding of mechanism, simulation is conducted for conductivity ratio up to 10 which is the typical ratio adopted in electrokinetic instability (EKI) flow phenomenon.30, 31, 32 From Fig. 3d, the achieved velocity at 20 V and γ = 10 was extremely fast, ∼14.44 mm/s. As a comparison with a more complex numerical model,33 it was reported that the achieved velocity was up to tens of mm/s (i.e., at 0.5 × 105 V/m and γ = 10). Their predicted velocity is of the same order of magnitude as obtained by the current model. In addition, this result implies that rapid induced flow can be achieved by incorporating a microelectrode (with applied AC voltage) with manually induced conductivity streams. Typically, the EKI configuration introduces the high AC voltage through bulk electrodes from the reservoirs. Integrated microelectrodes can indeed supply electric field of the same order of magnitude (∼104–105 V/m) due to the reduced electrodes gap.
Effect of channel width, depth, and aspect ratio
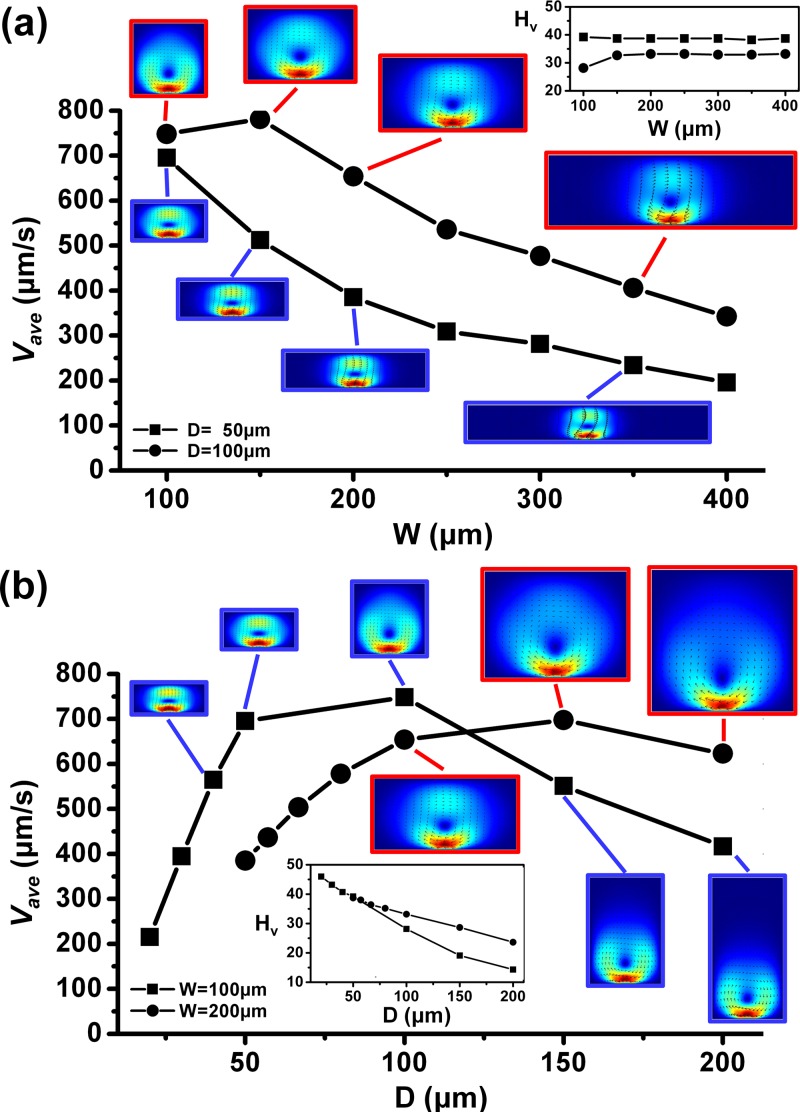
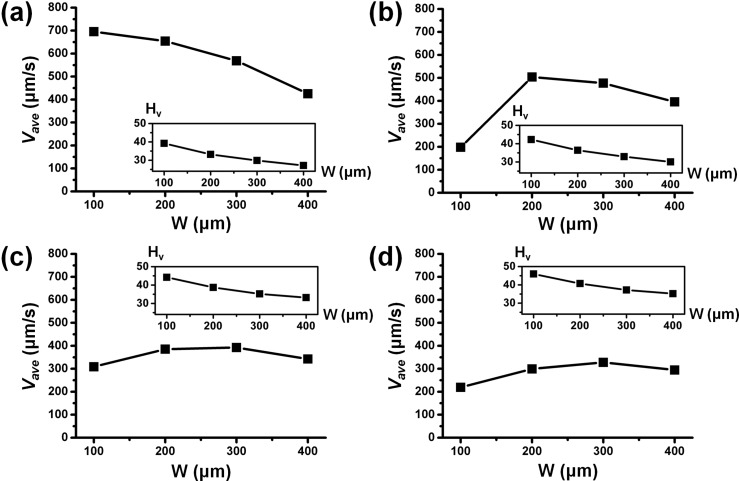
Channel dimensions can affect the effectiveness of fluid manipulation in the microchannel. As such, the effects of the channel width (W), depth (D), and aspect ratio (i.e., AR = D/W) on the average vortex flow velocity () were investigated. Similarly, the electrode width and gap were fixed at 40 μm and 20 μm, respectively. The voltage amplitude used was 10 V and conductivity ratio was at γ = 1.1. Figure 4a shows the average velocity amplitudes () as the width of the channel (W) varies from 100 μm to 400 μm, at fixed depth of either 50 μm or 100 μm. It can be observed that the generally decreases as the W increases. This is because there is a limit where the induced DC-biased ACEK flow can drag the surrounding fluids into motion.34 Therefore, there is an optimum range where the fluids can be effectively actuated, determined by the driving velocity (i.e., velocity near the surface of the electrodes). As W increases (see Fig. 4a), the velocities are only confined within the central region of the microchannel, and thus, the actuation efficient generally decreases. These findings have implication on the design of pump and mixer devices, as it would be preferred to locate the electrodes in close proximity of the pumping/mixing region. The inset in Fig. 4a shows the corresponding Hv percentage of the simulated data points. The trend indicates that the vortex center height stays relatively constant (28%–40%) for different channel width (100–400 μm) investigated. This is because of the fixed channel depths (50 μm, 100 μm) adopted.
Figure 4.
Average velocity amplitude with varying channel (a) width, for a fixed depth of 50 μm or 100 μm, and (b) depth, for a fixed width of 100 μm or 200 μm. Inset shows Hv value of each data point. Conditions: voltage amplitude = 10 V, conductivity difference = 10% (γ = 1.1), electrode width = 40 μm, and electrode gap = 20 μm.
Figure 4b shows the average velocity amplitudes () as the depth of the channel (D) varies from 20 μm to 200 μm, at a fixed width of either 100 μm or 200 μm. The average velocity increases to a maximum and then decreases with increasing channel depth. It can be observed that there is an optimal depth where a maximum average velocity is obtained. The maximum velocities were 748 μm/s (at W = 100 μm, D = 100 μm, AR = 1) and 698 μm/s (at W = 200 μm, D = 150 μm, AR = 3/4) for the fixed widths investigated. Note that when the cross-section is large, the fluid velocity does not extend very far from the gap between electrodes. This means that the average velocity should decrease, since regions far from the gap has very small velocity. If the cross-section is small (short height), the velocity is reduced because of viscous friction with the walls. Therefore, there is a maximum in between the two limits. In addition, the maximum average velocity generally occurs at channel AR close to 1, this gives us clue on designing the geometry of the pump with better efficiency. The result indicates that for large channel cross-section (AR ≫ 1) the induced flow would not extend far from the electrode surface, hence will not be efficient. For small channel cross-section (AR ≪ 1), the induced flow velocity is decreased from expected due to viscous friction.
Next, the inset in Fig. 4a shows the corresponding Hv percentage of the simulated data points. The Hv percentage generally decreases with increasing depth. Similarly, this is because the induced DC-biased ACEK flow also has a limit in setting the fluids in motion in the y-direction (depth-wise). In Fig. 4b, it should be noted that for the fixed width of 200 μm, the channel AR < 1, and the obtained Hv percentage is still considerably high (>23%). For the fixed width of 100 μm, as the geometrical configuration changes from a flat microchannel (AR < 1) to a tall microchannel (AR > 1), a dramatic drop in the Hv percentage is observed. This also suggests that the design of microchannel geometry should adopt a square (AR = 1) or flat (AR < 1) type of channel cross-section for electrokinetic flow actuation to be more effective.
As observed in Fig. 4b, the channel AR can affect the manipulation of fluid inside a microchannel. Here, we investigate the velocity of the induced flow in a channel of various ARs (1/2, 1/3, 1/4, and 1/5), but we restricted our study to AR < 1 (flat microchannel), the preferred channel configuration. Figure 5 shows the average velocity amplitudes in different channel widths for various constant channel ARs. Figs. 5a, 5b, 5c, 5d show the plots for AR of 1/2, 1/3, 1/4, and 1/5, respectively. With a decrease in AR from 1/2 to 1/5, the generally decreases. The AR measures the flatness of the microchannel, thus a lower AR indicates that W is much larger than the D. Note in Fig. 4a with fixed D, the computed average velocity is also found to decrease with increasing W. Therefore, the trend in Figs. 4a, 5 are the same depicting a decreasing AR with fixed D and increasing W.
Figure 5.
Average velocity amplitude at different channel aspect ratios (a) AR = 1/2, (b) AR = 1/3, (c) AR = 1/4, and (d) AR = 1/5. Inset shows Hv value of each data point. Conditions: voltage amplitude = 10 V, conductivity difference = 10% (γ = 1.1), electrode width = 40 μm, and electrode gap = 20 μm.
Typically in such configuration, the induced DC-biased ACEK flow has a limited actuation range as discussed previously for Fig. 4a. It should be noted that the Hv percentage remains relatively high at 27%–39%, 30%–42%, 33%–44%, and 35%–45% for AR of 1/2, 1/3, 1/4, and 1/5.
CONCLUSIONS
In this paper, a numerical model describing DC-biased AC-electrokinetic flow has been presented. “Convection and diffusion,” “conductive media DC,” and “incompressible Navier-Stokes” modules were adopted in the comsol software. The phenomenological model is based on experimentally measured conductivity gradient generated upon the application of a DC-bias to one of the electrode pairs. The simulated results indicate good correlation with reported experiments in terms of flow induced vortex characteristics, magnitude, and rotating direction. It was confirmed that the flow direction was from the higher conductivity to the lower conductivity regions near the surfaces of the electrodes and thus forming a single and unified vortex across the width of the microchannel. Parametric studies were conducted by varying the voltage, conductivity ratio, channel width, depth and aspect ratio. It was found that the flow velocity induced in DC-ACEK can reach values in the range mm/s by selecting an appropriated higher voltage and conductivity ratio. In addition, it was found that micro channels with square dimensions (AR = 1) are more efficient for optimum flow velocity.
ACKNOWLEDGMENTS
This work was performed at the Institute of Materials Research and Engineering, Agency for Science, Technology and Research (A*STAR).
References
- Stone H. A., Stroock A. D., and Ajdari A., Annu. Rev. Fluid Mech. 36, 381 (2004). 10.1146/annurev.fluid.36.050802.122124 [DOI] [Google Scholar]
- Squires T. M. and Quake S. R., Rev. Mod. Phys. 77, 977 (2005). 10.1103/RevModPhys.77.977 [DOI] [Google Scholar]
- Laser D. J. and Santiago J. G., J. Micromech. Microeng. 14, R35 (2004). 10.1088/0960-1317/14/6/R01 [DOI] [Google Scholar]
- Ramos A., “Electrohydrodynamic and magnetohydrodynamic micropumps,” in Microfluidic Technologies for Miniaturized Analysis Systems, edited by Hardt S. and Schonfeld F. (Springer, New York, 2007). [Google Scholar]
- Chang H.-C., Can. J. Chem. Eng. 84, 146 (2006). 10.1002/cjce.5450840202 [DOI] [Google Scholar]
- Chang H.-C. and Yeo L. Y., Electrokinetically Driven Microfluidics and Nanofluidics (Cambridge University Press, Cambridge, UK, 2010). [Google Scholar]
- Yang C., “Transport of Liquid in Rectangular Micro-Channels by Electroosmotic Pumping,” in Microfluidics and BioMEMS Applications, edited by Tay F. E. H. (Kluwer Academic, Boston, 2002). [Google Scholar]
- Li D., Electrokinetics in Microfluidics (Elsevier Academic, London, 2004). [Google Scholar]
- Morgan H. and Green N. G., AC Electrokinetics: Colloids and Nanoparticles (Research Studies, Hertfordshire, UK, 2003). [Google Scholar]
- Ramos A., Morgan H., Green N. G., and Castellanos A., J. Colloid Interface Sci. 217, 420 (1999). 10.1006/jcis.1999.6346 [DOI] [PubMed] [Google Scholar]
- Green N. G., Ramos A., Gonzalez A., Morgan H., and Castellanos A., Phys. Rev. E 61, 4011 (2000). 10.1103/PhysRevE.61.4011 [DOI] [PubMed] [Google Scholar]
- Gonzalez A., Ramos A., Green N. G., Castellanos A., and Morgan H., Phys. Rev. E 61, 4019 (2000). 10.1103/PhysRevE.61.4019 [DOI] [PubMed] [Google Scholar]
- Green N. G., Ramos A., Gonzalez A., Morgan H., and Castellanos A., Phys. Rev. E 66, 026305 (2002). 10.1103/PhysRevE.66.026305 [DOI] [PubMed] [Google Scholar]
- Green N. G., Ramos A., Gonzalez A., Castellanos A., and Morgan H., J. Phys. D: Appl. Phys. 33, L13 (2000). 10.1088/0022-3727/33/6/308 [DOI] [Google Scholar]
- Green N. G., Ramos A., Gonzalez A., Castellanos A., and Morgan H., J. Electrost. 53, 71 (2001). 10.1016/S0304-3886(01)00132-2 [DOI] [Google Scholar]
- Gonzalez A., Ramos A., Morgan H., Green N. G., and Castellanos A., J. Fluid Mech. 564, 415 (2006). 10.1017/S0022112006001595 [DOI] [Google Scholar]
- Wu J., Ben Y., and Chang H.-C., Microfluid. Nanofluid. 1, 161 (2005). 10.1007/s10404-004-0024-5 [DOI] [Google Scholar]
- Wu J., IEEE Trans. Nanotechnol. 5, 84 (2006). 10.1109/TNANO.2005.858592 [DOI] [Google Scholar]
- Gao J., Sin M. L. Y., Liu T., Gau V., Liao J. C., and Wong P. K., Lab Chip 11, 1770 (2011). 10.1039/c1lc20054b [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lian M. and Wu J., Appl. Phys. Lett. 94, 064101 (2009). 10.1063/1.3080681 [DOI] [Google Scholar]
- Ng W. Y., Lam Y. C., and Rodriguez I., Biomicrofluidics 3, 022405 (2009). 10.1063/1.3120273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ng W. Y., Goh S., Lam Y. C., Yang C., and Rodriguez I., Lab Chip 9, 802 (2009). 10.1039/b813639d [DOI] [PubMed] [Google Scholar]
- Ng W. Y., Lam Y. C., and Rodriguez I., Adv. Mater. Res. 74, 109 (2009). 10.4028/www.scientific.net/AMR.74.109 [DOI] [Google Scholar]
- Ng W. Y., Ramos A., Lam Y. C., Wijaya I. P. M., and Rodriguez I., Lab Chip 11, 4241 (2011). 10.1039/c1lc20495e [DOI] [PubMed] [Google Scholar]
- Castellanos A., Ramos A., Gonzalez A., Green N. G., and Morgan H., J. Phys. D: Appl. Phys. 36, 2584 (2003). 10.1088/0022-3727/36/20/023 [DOI] [Google Scholar]
- Garcia-Sanchez P., Ramos A., Gonzalez A., Green N. G., and Morgan H., Langmuir 25, 4988 (2009). 10.1021/la803651e [DOI] [PubMed] [Google Scholar]
- Ren Y., Jiang H., Yang H., Ramos A., and Garcia-Sanchez P., J. Electrost. 67, 372 (2009). 10.1016/j.elstat.2008.12.023 [DOI] [Google Scholar]
- Newman J. S. and Thomas-Alyea K. E., Electrochemical Systems (Wiley-IEEE, New Jersey, 2004). [Google Scholar]
- Chen C. H., Lin H., Lele S. K., and Santiago J. G., J. Fluid Mech. 524, 263 (2005). 10.1017/S0022112004002381 [DOI] [Google Scholar]
- Oddy M. H., Santiago J. G., and Mikkelsen J. C., Anal. Chem. 73, 5822 (2001). 10.1021/ac0155411 [DOI] [PubMed] [Google Scholar]
- Park J., Shin S. M., Huh K. Y., and Kang I. S., Phys. Fluids 17, 118101 (2005). 10.1063/1.2127873 [DOI] [Google Scholar]
- Tai C.-H., Yang R.-J., Huang M.-Z., Liu C.-W., Tsai C.-H., and Fu L.-M., Electrophoresis 27, 4982 (2006). 10.1002/elps.v27:24 [DOI] [PubMed] [Google Scholar]
- Lin H., Storey B. D., Oddy M. H., Chen C. H., and Santiago J. G., Phys. Fluids 16, 1922 (2004). 10.1063/1.1710898 [DOI] [Google Scholar]
- The energy in producing the flow is provided by the electrical source. The electrical body force acts on the fluids andtransfer to the flow momentum. The energy in this flow momentum is then dissipated through the fluids layers which moves with different velocities (according to shear stress = viscosity x velocity gradient). Assuming the energy in the system is ∼10 mJ, the fluids viscosity = 10−3 kg/ms, and the maximum velocity on the electrodes’ surface ∼100 μm/s, this makes the actuated distance to be ∼10−5 m. Tens of microns of distance is reasonable in our case.