The role of the sutures in biomechanical dynamic simulation of a macaque cranial finite element model: Implications for the evolution of craniofacial form

Abstract

The global biomechanical impact of cranial sutures on the face and cranium during dynamic conditions is not well understood. It is hypothesized that sutures act as energy absorbers protecting skulls subjected to dynamic loads. This hypothesis predicts that sutures have a significant impact on global patterns of strain and cranial structural stiffness when analyzed using dynamic simulations; and that this global impact is influenced by suture material properties. In a finite element model developed from a juvenile Rhesus macaque cranium, five different sets of suture material properties for the zygomaticotemporal sutures were tested. The static and dynamic analyses produced similar results in terms of strain patterns and reaction forces, indicating that the zygomaticotemporal sutures have limited impact on global skull mechanics regardless of loading design. Contrary to the functional hypothesis tested here, the zygomaticotemporal sutures did not absorb significant amounts of energy during dynamic simulations regardless of loading speed. It is alternatively hypothesized that sutures are mechanically significant only insofar as they are weak points on the cranium that must be shielded from unduly high stresses so as not to disrupt vitally important growth processes. Thus, sutural and overall cranial form in some vertebrates may be optimized to minimize or otherwise modulate sutural stress and strain.

INTRODUCTION

Besides being important loci of craniofacial growth (Opperman, 2000), sutures are mechanically “imperfecta” in an otherwise rigid body (a cranium), and their mechanical impact has been often discussed and investigated using various experimental and computer-aided techniques in both living and fossil species (Behrents et al., 1978; Bright and Gröning, 2011; Farke, 2008; Herring, 1993; Herring and Mucci, 1991; Herring and Rafferty, 2000; Herring and Teng, 2000; Jasinoski et al., 2010a,b; Jaslow and Biewener, 1995; Kupczik et al., 2009; Kupczik et al., 2007; Lieberman et al., 2004; Moazen et al., 2009a,b; Oudhof and Van Doorenmaalen, 1983; Porro et al., 2011; Rafferty and Herring, 1999; Rafferty et al., 2003; Rayfield, 2004; 2005; Reed et al., 2011; Smith and Hylander, 1985; Sun et al., 2004; Wang et al., 2008, 2010a). Experimental studies (Behrents et al., 1978; Herring and Mucci, 1991; Herring and Teng, 2000) have demonstrated that patent sutures affect strains locally (i.e., near the suture), but practical considerations limit the ability of purely experimental studies to assess the global influence of these joints across the entire cranium. Recently, finite element analysis (FEA) has been used to examine the mechanical behavior of sutures because sutures can be modeled and assigned varying sets of material properties, and the process of sutural fusion can be simulated (Jasinoski et al., 2010a,b; Wang et al., 2010a).

Using static simulations corresponding to incisor, premolar, and molar maximal biting conditions, a recent sensitivity analysis of the mechanical effect of sutures in FE models of a macaque cranium demonstrates that the presence of sutures does not profoundly influence global strain patterns, regardless of their material properties (Wang et al., 2010a). More specifically, strain patterns remained relatively unaffected away from the suture sites, and bite reaction force was likewise barely affected. Thus, the biomechanical significance of sutures in a global context would therefore appear to be limited. However, static analyses are insufficient to simulate the role sutures may play under physiological dynamic loading conditions. It has been proposed that cranial sutures in goats are able to absorb 16%–100% of energy during impact (Jaslow, 1990), but in static analysis, sutures do not have a high capacity to absorb energy, which may be a function of either their limited volume (Wang et al., 2010a), or model resolution and element size in in silico, or simplified morphology. Whether or not sutures provide a significant strain-dampening or shock absorbing function under dynamic loading conditions, as suggested by Jaslow and Biewener (1995), has yet to be tested. In this study, a finite element model (FEM) of a primate cranium was analyzed using dynamic simulations to assess the effect of a pair of sutures (zygomaticotemporal) on stress and strain patterns associated with feeding, a habitual behavior that has the potential to impose high and/or repetitive loads on the craniofacial skeleton. It is hypothesized that sutures act as energy absorbers protecting skulls subjected to dynamic loads. This hypothesis predicts that sutures have a significant impact on global patterns of strain and cranial structural stiffness when analyzed using dynamic simulations; and that this global impact is influenced by suture material properties.

MATERIALS AND METHODS

Model creation

The FEM used here was generated following the Biomesh protocol described in publications by Dumont, Grosse and colleagues (Dumont and Herrel, 2003; Dumont et al., 2005; Grosse et al., 2007) (www.biomesh.org). The FEM was built from a juvenile Macaca mulatta specimen (age 2.5 years, with full set of deciduous teeth and the first permanent molar) obtained from the Yerkes Primate Research Center (supported by NIH Base Grant RR000165) (Figure 1a). The specimen was scanned using iCAT cone-beam computed tomography (CBCT) facility (Imaging Sciences International, Hatfiled, PA) at Indiana University. CBCT is a recently developed technology used to evaluate 3D bone morphology at high resolution (Cho, 2009). Each volumetric image was obtained using iCAT CBCT for approximately 40 seconds with a voxel size of 0.25 mm, and saved in the Digital Imaging and Communications in Medicine (DICOM). Then, a tessellated surface model was constructed from these images in Mimics 13.1 (The Materialise Group, Leuven, Belgium). After the model was surface meshed in Mimics, it was transferred as a Binary STL file to Studio 11.0 (Geomagic, Inc., Research Triangle Park, NC), a digital shape sampling and processing software, to generate a clean and smooth polygon model. Then the model was brought back to Mimics to be converted into a 3D mesh of 173,936 solid 4-noded tetrahedral elements and exported as a NASTRAN file. The elements in this model varied in size, but typical edge lengths of elements were between 0.4 mm and 1.7 mm. The NASTRAN file was imported to Strand7 FEA software (v. 2.4.1) (Strand7 Pty Ltd, Sydney, Australia) for both static and dynamic analysis. Parts for sutures were created by grouping elements (around 3 elements in thickness) roughly along the profile of the zygomaticotemporal sutures at the zygomatic arch at both sides of the cranium. Sutures were approximately 1 mm to 2 mm in thickness, and the two sutures had 316 elements, occupying 0.08% of the total volume of the cranium. Several simplifying assumptions were employed to reduce model complexity and avoid lengthy calculation times during dynamic simulation. These include the lack of modeling of viscoelastic properties of bone, the omission of trabecular bone (trabeculae were modeled as cortical bone), teeth and periodontal ligaments, the lack of a complete set of muscle forces, the omission of all other soft tissues and organs (such as the brain and eyeballs), and the modeling of only one pair of sutures; only the zygomaticotemporal sutures on both left and right sides were modeled (at the age of 2.5 years, most craniofacial sutures are open in rhesus macaques [Wang et al., 2006b]). This model was not identical to the previous model with multiple sutures generated for static analysis (Wang et al., 2010a).

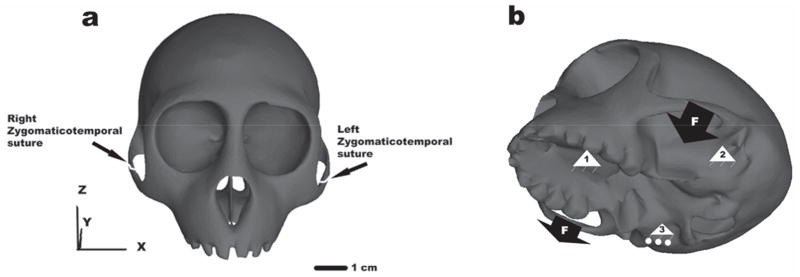
Figure 1.

a. Three-dimensional solid model of a M. mulatta cranium. b. Loading regime (cranium not scaled as in a). A node on the occlusal surface of the left dm¹ (1) and a node at the articular eminence of the left temporomandibular joint (TMJ) (2) were constrained for displacement in three (all) orthogonal directions axes; a node at the eminence of the right TMJ was constrained in the anteroposterior and inferosuperior directions (3). Force of 70 Newtons and 50 Newtons were distributed evenly as ten nodal forces (F) in the anterior two-thirds of the inferior surface of the left zygomatic arch (working side) and the right zygomatic arch (balancing side) respectively.

Elastic properties were the same for the bone yet five different sets of elastic material properties were assigned to the sutures (Table 1). Briefly, the elastic modulus (E) is a measure of material stiffness and is the amount of stress induced per unit of induced strain due to an applied load. Poisson’s ratio (ν) is a measure of the coupling effect of strain components in transverse directions; it is the negative of the ratio of the strain in the secondary direction (response direction) divided by strain in the primary direction (applied load direction). Coefficient of viscous damping measures the dissipation of energy with time in a dynamic mechanical system. For bone, the non-sutural parts of the cranium were assigned isotropic elastic properties based on an average of values obtained from all parts of the skull of adult macaques (Elastic modulus E = 17.3 GPa, Poisson’s ratio ν = 0.28) (1 GPa [GigaPascal] =10⁹N/m² ) (Wang and Dechow, 2006). For sutures, there is no consensus on the elastic modulus of sutural tissue, as indicated by widely varying published or used data (Wang et al., 2010a). For example, 1.2 MPa (Kupczik et al., 2009) (1 MPa [MegaPascal] =10⁶N/m²), 10 MPa (Moazen et al., 2009), 29 MPa (Compression) to 74 MPa (Tension) (Popowics and Herring, 2007), 46MPa (Bright and Gröning, 2011), 50 MPa (Odame et al., 2005), 0.4 GPa (Farke, 2008), and 0.5–2.5 GPa (Wang et al., 2008b) have each been reported or proposed as proper elastic moduli. Five sets of isotropic elastic material properties were generated based on based on in vivo and in silico experiments listed above and presumptions detailed as follows (Table 1). Models 4 and 5 applied a high Poisson’s ratio (ν = 0.49). This value assumes that sutural tissue is nearly incompressible (like a sealed fluid-filled volume) to ensure that bone fronts on opposite sides of the suture will not meet each other. Presumably, such contact would interfere with bone growth. In Models 2–5, a coefficient of viscous damping was assigned (C_v = 0.451Ns/m, Okazaki et al., 1996) to model the shock absorbing capacity of sutures associated with their internal friction. Elastic properties data designed for sutures were generated from multiple.

Table 1.

Material property values used for simulation models.

Model	Suture type	Elastic Modulus (E)	Poisson’s Ratio (ν)	Density (g/cm3)	Coefficient of Viscous Damping (Unit: Ns/m)
Model l	Suture I - Fused suture (bone)	17.3GPa1	0.281	2.061	-
Model 2	Suture II (Static FEA Theoretical value)	50 MPa2	0.402	1.063	0.4514
Model 3	Suture III (Experimental value )	1MPa2	0.402	1.063	0.4514
Model 4	Suture IV (High elasticity, high Poisson’s ratio)	50 MPa2	0.492	1.063	0.4514
Model 5	Suture V (Higher elasticity, high Poisson’s ratio)	1MPa2	0.492	1.063	0.4514

Note:

¹Values of bone elastic properties and density were calculated from Wang and Dechow (2006) (Strait et al., 2005).

²Values elastic properties for sutures were generated based on various in vitro and in silico experiments and further presumptions (see text).

³The value for the density of sutures was a round-up of the value 1.0597 g/cm³ measured from unfixed rabbit and canine muscle tissue (Mendez and Keys, 1960).

⁴Value of Coefficient of Viscous Damping was from Okazaki et al., (1996).

Simulation

A constraint regime, or reaction loading procedure, was applied to the model (Figure 1b). To examine the strain patterns of the skull incurred from dm¹ biting, a node at the articular eminence of the left temporomandibular joint (TMJ) was constrained for displacement in three (all) axes, and a corresponding node at the eminence of the right TMJ was constrained in the anteroposterior and inferosuperior directions (i.e., perpendicular to the line defined by the left and right TMJ nodes). A node on the occlusal surface of the left dm¹ (corresponds to the position of the first permanent premolar/P³ in an adult) was constrained from displacing in three (all) orthogonal directions.

Only two masticatory muscle forces were applied to the model, representing the right and left masseters (superficial and deep). As calculated from physiological cross sectional area, the maximum force generating capacity of the superficial and deep masseters in adult M. mulatta are 100.8 N and 39.0 N respectively (~140N in total) (Strait et al., 2005). In this study a resultant force of 70 (a coarse estimate for a skull of juvenile size) Newtons (x, y, z vector components: −13.7, 0, −68.6) was distributed evenly as ten nodal forces in the anterior two-thirds of the inferior surface of the left zygomatic arch (working side), and a force of 50 Newtons (9.8, 0, −49.0) was applied in a similar manner to the right zygomatic arch (balancing side). The asymmetrical loading pattern (70N vs. 50N) simulates different activity levels in the Working Side and Balancing Side muscles during unilateral tooth loading. Electromyographic data were not available for macaques of this age, so these values are coarse estimates. We have previously modeled Working-to-Balancing Side asymmetry to be as great as 2-to-1 for post canine teeth loadings (Strait et al., 2005; Wang et al., 2010a), but asymmetry is expected to decline in forceful bites, and the forces used here likely represent a forceful bite for a juvenile.

For each model, in addition to linear static simulations, two sets of linear transient dynamic simulations were run using Strand7. Forces were applied to the models at two different loading rates (Table 2). The first loading rate (Slow Loading) used ten time steps spread over 100 ms, with the peak loading force occurring at 30 ms. The second loading rate (Fast Loading) used ten time steps spread over 10 ms, with the peak force occurring at 3 ms. In adult rhesus monkeys, the time-to-peak of biting forces are reached from 31.0 ms (male) to 37.4 ms (female) (Dechow and Carlson, 1990). In this sense, the Slow Loading design adopted a loading speed comparable to the accumulation speed of normal biting forces, thus it could be viewed as a simulation of the normal biting speed (as a shorthand, we refer to this loading regime as “normal” biting), yet the Fast Loading was an order of magnitude faster, simulating a quick sudden force loading, in order to examine the capacity of the sutures to absorb energy at different loading rates.

Table 2.

Profiles of Fast and Slow dynamic transient linear simulations.

Step	Slow Loading (ms)	Fast Loading (ms)	Percentage of Total Peak Force
0	0	0	0%
1	10	1	40%
2	15	1.5	60%
3	20	2	80%
4	30	3	100%
5	40	4	100%
6	50	5	100%
7	60	6	80%
8	70	7	60%
9	80	8	40%
10	90	9	0%

Sutural integrity was assessed by examining the principal stresses within the elements assigned suture material properties. In the pig nasofrontal sutures, Popowics and Herring (2007) measured the peak failure stresses in pigs (5–6 months old) to be 0.9±0.5 MPa (Mean ± SD. n=4) in tension and 3.4±1.4MPa (Mean ± SD. n=4) in compression. Thus a principal stress bracket from −3.4 MPa (compressive) to 0.9 MPa (tensile) was used as a “safe zone” to represent the range of safe stress values for typical cranial sutures. Obviously, the boundaries of this safe zone are not meant to indicate that values outside of range will necessarily lead to suture failure, but rather that as one exceeds these limits the risk of suture failure might reasonably be expected to increase. Following the initial analyses, models whose principal stresses in the sutural elements fall in the safe zone were subjected to increased forces that simulate very powerful bites. In this case, forces were first doubled (140N left, 100N right), then maximum forces were applied at both sides (140N left, 140N right), and more loading cases were solved. The maximum forces were calculated from the muscle architecture of adult specimens, so they represent abnormally high loads for a juvenile.

RESULTS

Element principal stresses at the zygomaticotemporal sutures

Element principal stresses (both compressive and tensile) of all sutural elements were examined in all four models that include patent zygomaticotemporal sutures. The magnitude of the element principal stresses at some elements within the sutures fell outside the safe zone (from −3.4 MPa to 0.9 MPa) (Figure 2), indicating that these sutures are at varying degrees of risk of failure during “normal” biting. In Model 2, 104 of 632 sutural elements (16.5%) fell out of the safe zone. This number rose to 164 out of 632 (25.9%) in Model 4. These two models apply an elastic modulus of 50 MPa to sutural tissue. In contrast, Models 3 and 5 applied a modulus value of 1 MPa. In Model 5, 42 elements (6.6%) were outside of the safe zone, but in Model 3, which employed a lower Poisson’s ratio (0.40 vs. 0.49), only one element (0.1%) was slightly over 0.9 MPa in tensional stress. When the loading forces were doubled in magnitude in Model 3, 15 elements (2.4%) were out of the safe zone, and when a force of 140N was applied on both left and right sides, that number rose to 41elements (6.5%). These results were unaffected by the nature of the simulations (Static vs. Dynamic).

Figure 2.

Distribution of element principal stresses (Maximum and minimum combined) in right and left zygomaticotemporal sutures (Total number of element principal stresses: 632 = 316 x2) during Slow Loading Dynamic simulations. A “safe zone” was identified between −3.4 MPa and 0.9 MPa based on data from Popowics and Herring (2007).

Overall strain patterns

In general, global strain patterns on craniofacial bone surfaces are comparable for each FEA simulation regardless of assigned material property values or loading design (Figure 3). Suture patency affected strains locally insofar as decreasing sutural stiffness was associated with local reductions in strain on the zygomatic arch, an area that normally is highly strained owing to the fact that the muscle loads are applied there.

Figure 3.

Von Mises strain (mm/mm) in five suture models under simplified left dm¹ biting point with force of 70N in the left side and 50N in the right side. White areas on the zygomatic arch indicated von Mises strain values exceeds the scale minimum (500με).

Strain energy absorbed by the zygomaticotemporal sutures

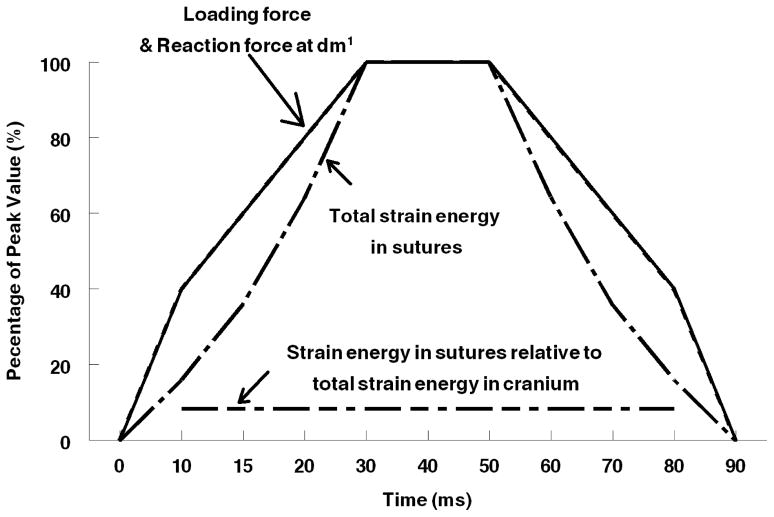
The percentages of strain energy absorbed by the zygomaticotemporal suture in dynamic simulations are identical to those in the static simulations for a given set of material properties. However, these absorbed strain energies are different depending on which suture model is being loaded, with Model 2 and Model 5 absorbing slightly more energy than Model 3 (Table 3). The increase in the amount of strain energy absorbed by the zygomaticotemporal sutures lagged behind the increase in force, as in the bone from the rest of the cranium (Table 4). Compared to bone, the zygomaticotemporal sutures do not play a greater role in absorbing energy at any stage during the loading process.

Table 3.

Percentage of total strain energy absorbed by the sutures during Static and Slow Loading simulations (Peak force – 70N left, 50N right) relative to the total strain energy in cranium at corresponding steps.

	Model 1 (17.3GPa,0.28)	Model 2 (50MPa,0.40)	Model 3 (1MPa,0.40)	Model 4 (50MPa,0.49)	Model 5 (1MPa,0.49)
Static	4.3%	9.9%	8.3%	6.5%	9.5%
DS1	4.4%	9.9%	8.2%	6.5%	9.6%
DS2	4.3%	9.8%	8.2%	6.4%	9.5%
DS3	4.4%	9.9%	8.2%	6.5%	9.6%
DS4	4.3%	9.8%	8.2%	6.4%	9.5%
DS5	4.4%	9.9%	8.3%	6.5%	9.6%
DS6	4.3%	9.8%	8.2%	6.4%	9.5%
DS7	4.3%	9.9%	8.3%	6.5%	9.6%
DS8	4.3%	9.9%	8.2%	6.5%	9.5%
DS9	4.3%	9.8%	8.2%	6.4%	9.5%
DS10	0.2%	0.7%	0.5%	0.3%	1.3%

Abbreviation: DS – Dynamic steps.

Table 4.

Stepwise energy absorption in bones and sutures relative to peak values during dynamic simulations in Model 3 (E=1MPa, ν=0.40) (Peak force – 70N left, 50N right). Peak forces were reached at Step 4 and remained unchanged at Steps 5 and 6. Forces were canceled completely at Step 10.

Dynamic Steps	Force relative to Peak Force	Model 3 (1MPa,0.40) Slow Loading		Model 3 (1MPa,0.40) Fast Loading
		Bone	Suture	Bone	Suture
Step 1	40%	16.0%	16.0%	15.7%	15.9%
Step 2	60%	36.0%	36.0%	36.0%	36.0%
Step 3	80%	64.0%	63.9%	62.5%	63.4%
Step 4	100%	100.0%	100.0%	100.0%	100.0%
Step 5	100%	100.0%	100.0%	97.8%	99.1%
Step 6	100%	100.0%	100.0%	99.8%	100.0%
Step 7	80%	63.9%	64.4%	62.8%	63.3%
Step 8	60%	36.0%	36.0%	35.8%	36.1%
Step 9	40%	16.0%	16.0%	15.8%	15.7%
Step 10	0%	0.00%	0.00%	0.02%	0.00%

Biting efficiency

In all five models, the reaction force stepwise profile is identical regardless of loading speed (Figure 4), and the differences in biting efficiency (= reaction forces divided by the loading forces along Z axis) due to the loading designs and material property values are small (Table 5), indicating insignificant or no effect on biting efficiency by the presence of the zygomaticotemporal sutures, as also observed in a previous analysis (Wang et al., 2010a).

Fig. 4.

Stepwise profile of loading forces (Peak force – 70N left, 50N right), reaction forces at the left dm¹ (almost indistinguishable from the profile of loading forces), strain energy absorbed in sutures, and the amount of strain energy in suture relative to the total strain energy in the cranium (last step was not demonstrated) in Model 3 dynamic simulation Slow Loading experiment.

Table 5.

Nodal reaction forces at the left dm¹ biting point in Z axis (up and down direction relative to the occlusal plane. See Figure 1) compared to total loading forces (Peak force – 70N left, 50N right) in Z axis.

	Static	Dynamic - Slow Loading	Dynamic - Fast Loading
Model 1 (17.3GPa,0.28)	42.1%	42.1%	43.2%
Model 2 (50MPa,0.40)	43.8%	43.8%	44.9%
Model 3 (1MPa,0.40)	45.1%	45.1%	46.2%
Model 4 (50MPa,0.49)	43.1%	43.1%	44.2%
Model 5 (1MPa,0.49)	44.8%	44.9%	46.0%

DISCUSSION

Limitations of the study

The FEM used in this analysis is limited in certain respects. First, it was simplified structurally to reduce model complexity and avoid lengthy calculation times during dynamic simulation; thus, it was impractical to model all of the sutures. Second, this FEM simplifies the viscoelastic properties of the sutures, which are normally a combination of several mechanical behaviors (including both elastic and viscous components), such that only a single coefficient of viscous damping was assigned in addition to a linear elastic modulus. Additionally, the sutural deformation behavior and capacity for absorbing energy would be different with inclusion of many factors not considered here, such as size of model elements, loading regimes more similar to a physiological reality, suture morphology (i.e., intra- and inter-species variations in terms of ontogeny and fusion patterns), and particularly an effective validation with consideration of microanatomical features in sutures (i.e., interdigitations and interactions with covering linings, such as dura matter or periosteom). Nonetheless, the models are usefully serve the purpose of examining the global effects of zygomaticotemporal sutures under dynamic simulation, since comparisons among results from different experiments (with suture or without suture) using identical loading regimes may provide a useful framework for understanding the biomechanical behavior and global influence of sutures in general.

Influence of zygomaticotemporal sutures on global skull mechanics

Results obtained here are inconsistent with the hypotheses that (1) simple sutures such as the zygomaticotemporal behave differently under dynamic rather than static loads, and (2) sutures have a profound impact on global strain patterns. It is unclear whether or not other craniofacial sutures or variation in morphological complexity would influence strain patterns during these dynamic simulations. Results of this analysis do not exclude the possibility that highly complex sutures (such as those seen in head-butting vertebrates), or those with proportionally large volumes may perform this role. It would appear that simple, linear, and butt-ended sutures do not possess advantageous properties in the context of feeding biomechanics.

Findings of this analysis differ from those of Moazen et al. (2008, 2009a,b), in which the presence/absence of sutures affected strains both near the suture site and at other regions across the cranium. Previously, a static study by Wang et al. (2010a) examining many sutures simultaneously, found that suture patency had only a limited effect on strain magnitudes at sites across the cranium. It is notable that the size and architecture of the lizard skull examined by Moazen et al. (2008, 2009a,b) differs from that of macaques. The lizard skull is at least an order of magnitude smaller in size and is composed primarily of bony struts. Although the macaque skull used here is a juvenile, it is still larger and composed of bony plates. These differences may affect the manner in which sutures mediate cranial strains. Findings of this analysis are also contrary to those by Kupczik et al. (2007) who also used macaque models and who observed that sutures had a global effect, but whose material property values may have been influenced by chemical preservative soaked into the tissues of the skulls examined by them. Moreover, Kupczik et al. (2007) modeled a loading regime corresponding to an in vitro experiment, and those loading conditions do not fully reproduce mastication. Assessment of the inconsistencies between Moazen et al. (2008, 2009a, b), Kupczik et al. (2007) and the present study requires detailed sensitivity studies focusing on bone material properties, constraints, and a consideration of strut vs. plate mechanics.

Sensitivity of sutural element stress to variation in material properties

The zygomaticotemporal sutures exhibited considerable sensitivity to variation in material properties. Under “normal” biting conditions that correspond to slightly elevated loads in juveniles, comparatively minor variations in elastic modulus and Poisson’s ratio led to stress levels that could have potentially threatened suture integrity. Generally speaking, the potential risk to integrity increased with increasing elastic modulus and Poisson’s ratio. Thus, as suture connective tissue grows stiffer, it is more likely to injure. This analysis does not allow one to conclude that the material properties employed in Model 3 are accurate, but it does imply that those used in the other models could be unrealistic. Another implication of this study is that suture connective tissue may not behave as a perfectly incompressible material.

Even when using the most favorable material properties, suture integrity still may be threatened during maximal biting conditions (Figure 3). Moreover, suture material properties almost certainly change during ontogeny, and those changes might influence the degree to which stress accumulates in the suture (Popowics and Herring, 2007). Thus, one might infer that sutures are mechanically vulnerable structures. Given that sutures are important loci of bone growth, it appears evident that natural selection should favor mechanisms to shield sutures from stress. This possibility has potentially broad implications.

Sutures and the evolution of craniofacial form

The primary function of sutures in young individuals is to allow the growth of the skull. The finding that elevated feeding loads have the potential to threaten suture integrity at certain material properties stands in contrast to experimental data demonstrating that the facial skeleton in several mammalian species normally experiences relatively low strains during feeding (the behavior that most regularly exposes the cranium to high or repetitive loads) (Lieberman et al., 2004; Ross and Metzger, 2004). This has led to the hypothesis that some aspects of the form of the facial skeleton in many clades may not be optimized to dissipate feeding loads (Ross and Metzger, 2004), despite the fact that comparative analyses seem to suggest a relationship between craniofacial form and feeding behavior (Antón, 1990, 1993; Bastir et al., 2007; Daegling, 1996; Gilbert et al., 2009; Hylander, 1977a,b; Rak, 1983; Ravosa, 1991a, b; Ross, 2001; Spencer and Demes, 1993; Strait et al., 2008, 2009; Trinkaus, 2003; Vinyard et al., 2003; Wang et al., 2010b; Williams et al., 2009; Wright, 2005).

One reason underlying this apparent contradiction may be that craniofacial form in many mammals and, perhaps, other vertebrates as well, might include design features that minimize or otherwise modulate stresses in sutures rather than in bone. We hypothesize that the primary function of cranial sutures in subadult individuals is intramembranous bone growth. Because sutures are zones of structural weakness, they must be shielded from high stresses so that the vertebrate cranium can grow a shape appropriate for proper functioning of sensory, respiratory and feeding systems. The result in this paper, that elevated feeding loads have the potential to damage sutures with certain material properties, suggests that craniofacial form in mammals, and perhaps other vertebrates, might include design features that reduce stresses in sutures rather than in bone. These design features might be found not only in high stress areas of the facial skeleton, but also in areas characterized by lower stresses (Hylander et al., 1991; Ross, 2001; Ross and Metzger, 2004).

Several overlapping predictions could be derived from this hypothesis: (1) Cranial sutures (via the guiding forces of natural selection) should, when possible, be found in areas where stresses do not concentrate in the vertebrate cranium; (2) When cranial sutures are found in areas that experience relatively high stress concentrations, suture complexity forms as a protective mechanism to preserve the growth center; (3) The facial skeleton should adapt by taking a form that minimizes stress across the face, or in particular facial regions. Consequently, craniofacial form may be optimized for feeding while growing throughout ontogeny, but not simply by minimizing stress and strain in bones.

Many of the components of the hypothesis described above can be found in prior studies, but to our knowledge, they have not previously been consolidated in a comprehensive framework. This hypothesis can be tested using comparative, experimental and modeling methods. For example, one mechanism being considered is an age-related increase in cranial suture complexity observed in mice (Byron, 2006) and humans (Saito et al., 2002) that helps to preserve flat bone growth fronts. Moreover, it will be important to establish the degree to which the hypothesis applies across vertebrates. It is conceivable that it applies only to certain vertebrate groups (e.g., mammals), body sizes, or that the hypothesis manifests itself differently in different groups. Craniofacial strain magnitudes recorded during in vivo experiments in alligators are approximately twice those observed during analogous experiments in primates, swine and hyraxes (Lieberman et al., 2004; Ross and Metzger, 2004), and strain magnitudes in FEA simulations of lizards resemble those of alligators (Moazen et al., 2008, 2009a), so it is possible that broad patterns of cranial biomechanics differ between mammals and non-mammal vertebrates. Moreover, some sutures in certain taxa may be specially adapted to accommodate movements (cranial kinesis), and in those taxa the above hypothesis might not apply.

Challenges in suture biology and biomechanics

Although the global impact of sutures is negligible in skulls of relatively large mammals such as monkeys and pigs (Wang et al., 2010a; Bright and Gröning, 2011), their local effect and interactions with bone fronts and covering tissues might be of special interest in studies of bone growth and adaptation, given that sutures are morphologically diverse in terms of complexity, location (i.e., cranial vs. facial), ontogeny, fusion, sexual dimorphism, and intra- and inter-species differences. The diversity in sutural morphology poses a tremendous challenge to analyses of suture biology and biomechanics.

Historically, important experimental work by Moss in the mid-twentieth century demonstrated that sutural morphologies are somewhat labile when the mechanical environment is perturbed, which led to a synthesis of suture concepts that defined intrinsic and extrinsic factors that direct the fate of cranial suture formation (Moss, 1961, 1962; Moss and Young, 1960). An important intrinsic factor that has been the focus of much research in the last 20 years is the outermost cranial mininx, the dura mater, which regulates significant suture growth events such as fusion or maintenance of patency (Opperman et al., 1998; Opperman et al., 1995; Opperman et al., 1993). Within the last ten years, Byron and colleagues (Byron, 2006; Byron et al., 2004) have hypothesized that small-scale suture growth events such as adding (or resorbing) bone mineral to (from) the leading edge of a suture front are influenced by extrinsic, mechanical events that often relate to masticatory biomechanics. This assertion is supported by comparative evidence in primates (Byron, 2009) and in caimans (Monteiro and Lessa, 2000) wheredurophagous feeders have enhanced cranial suture complexity.

Unlike cranial sutures, facial sutures do not overlie dura and thus do not receive the kinds of fate-determining cytokine secretions that the braincase sutures receive. This is a fundamental difference between two kinds of suture, which suggests that facial sutures may be more directed by extrinsic mechanical forces than calvarial sutures. Traditionally, suture complexities are normally modeled in two dimensions using fractal geometry (Byron, 2006; Byron et al., 2004; Hartwig, 1991; Long, 1985; Long and Long, 1992; Lynnerup and Jacobsen, 2003; Monteiro and Lessa, 2000; Skrzat and Walocha, 2003a, b; Yu et al., 2003). However, if facial sutures provide a more “pure” indication of biomechanical loading history, then a detailed study on sutural three-dimensional complexity measures will be necessary.

Ultimately, the competing interests of protection and growth, and their variation throughout ontogeny and phylogeny warrant more study at both macro- and micro-anatomical levels. Finite element analysis will continue to be a useful tool for addressing these challenges, along with advanced imaging modalities (such as micro-CT) and histological studies (i.e., Holliday et al., 2010; Payne et al., 2011; Reinholt et al., 2009; Smith et al., 2010; Stadler et al., 2006), growth, complexity and fusion patterns (i.e., Byron, 2006, 2009; Sun et al., 2004; Wang et al., 2006b; Yu et al., 2003;), genetics and evolution of sutural configuration patterns ( Sidor, 2001; Wang et al., 2006a), and in vivo and in vitro experiments ( i.e., Behrents et al., 1978; Henry and Teng, 2000;Wang et al., 2008).

CONCLUSION

Finite element analysis was used to evaluate the roles of zygomaticotemporal sutures in biomechanics of a macaque cranium. Static and dynamic analyses produced similar results in terms of strain patterns and reaction forces, indicating that zygomaticotemporal sutures play a limited role in modulating global skull mechanics regardless of loading design. The zygomaticotemporal sutures did not absorb significant amounts of energy during dynamic simulations, regardless of loading speed. It is thus hypothesized that sutures are mechanically significant only insofar as they are weak points on the cranium that must be shielded from unduly high stresses so as not to disrupt vitally important growth processes. Sutures are morphologically diverse in terms of location, ontogeny, fusion, sexual dimorphism, and intra-and inter-species variations. This hypothesis predicts that sutural protection is an important selective pressure that may have influenced diverse aspects of sutural and craniofacial form.