Simultaneous Inference For The Mean Function Based on Dense Functional Data

Abstract

A polynomial spline estimator is proposed for the mean function of dense functional data together with a simultaneous confidence band which is asymptotically correct. In addition, the spline estimator and its accompanying confidence band enjoy oracle efficiency in the sense that they are asymptotically the same as if all random trajectories are observed entirely and without errors. The confidence band is also extended to the difference of mean functions of two populations of functional data. Simulation experiments provide strong evidence that corroborates the asymptotic theory while computing is efficient. The confidence band procedure is illustrated by analyzing the near infrared spectroscopy data.

1. Introduction

In functional data analysis problems, estimation of mean functions is the fundamental first step; see Cardot (2000); Rice and Wu (2001); Cuevas, Febrero and Frainman (2006); Ferraty and Vieu (2006); Degras (2011) and Ma, Yang and Carroll (2011) for example. According to Ramsay and Silverman (2005), functional data consist of a collection of iid realizations 3-1 ${\{{\eta }_i(x)\}}_{i=1}^n$ of a smooth random function η(x), with unknown mean function Eη(x) = m(x) and covariance function G(x, x′) = cov {η(x), η(x′)}. Although the domain of η(·) is an entire interval 𝒳, the recording of each random curve η_i(x) is only over a finite number N_i of points in 𝒳, and contaminated with measurement errors. Without loss of generality, we take 𝒳 = [0, 1].

Denote by Y_ij the j-th observation of the random curve η_i(·) at time point X_ij, 1 ≤ i ≤ n, 1 ≤ j ≤ N_i. Although we refer to variable X_ij as time, it could also be other numerical measures, such as wavelength in Section 6. In this paper, we examine the equally spaced dense design, in other words, X_ij = j/N, 1 ≤ i ≤ n, 1 ≤ j ≤ N with N going to infinity. For the i-th subject, i = 1, 2, …,n, its sample path {j/N, Y_ij} is the noisy realization of the continuous time stochastic process η_i(x) in the sense that Y_ij = η_i (j/N)+σ (j/N) ε_ij, with errors ε_ij satisfying $E({\epsilon }_{\mathit{\text{ij}}})=0,E({\epsilon }_{\mathit{\text{ij}}}^2)=1$, and {η_i(x), x ∈ [0, 1]} are iid copies of the process {η(x), x ∈ [0, 1]} which is L², i.e., E ∫_[0,1] η²(x)dx < +∞.

For the standard process {η(x), x ∈ [0, 1]}, let sequences ${\{{\lambda }_k\}}_{k=1}^{\mathrm{\infty }},{\{{\psi }_k(x)\}}_{k=1}^{\mathrm{\infty }}$ be the eigenvalues and eigenfunctions of G(x, x′) respectively, in which λ₁ ≥ λ₂ ≥ ⋯ ≥ 0, ${\displaystyle {\sum }_{k=1}^{\mathrm{\infty }}}{\lambda }_k<\mathrm{\infty },{\{{\psi }_k\}}_{k=1}^{\mathrm{\infty }}$ form an orthonormal basis of L² ([0, 1]) and $G(x,x\prime )={\displaystyle {\sum }_{k=1}^{\mathrm{\infty }}}{\lambda }_k{\psi }_k(x){\psi }_k(x\prime )$, which implies that ∫ G(x, x′) ψ_k (x′) dx′ = λ_kψ_k(x). The process {η_i(x), x ∈ [0, 1]} allows the Karhunen-Loève L² representation ${\eta }_i(x)=m(x)+{\displaystyle {\sum }_{k=1}^{\mathrm{\infty }}}{\xi }_{\mathit{\text{ik}}}{\varphi }_k(x)$, where the random coefficients ξ_ik are uncorrelated with mean 0 and variance 1, and ${\varphi }_k=\sqrt{{\lambda }_k}{\psi }_k$. In what follows, we assume that λ_k = 0, for k > κ, where κ is a positive integer or ∞, thus $G(x,x\prime )={\displaystyle {\sum }_{k=1}^{\kappa }}{\varphi }_k(x){\varphi }_k(x\prime )$ and the model that we consider is

$$Y_{\mathit{\text{ij}}}=m(j/N)+{\displaystyle {\sum }_{k=1}^{\kappa }}{\xi }_{\mathit{\text{ik}}}{\varphi }_k(j/N)+\sigma (j/N){\epsilon }_{\mathit{\text{ij}}}.$$ (1)

Although the sequences ${\{{\lambda }_k\}}_{k=1}^{\kappa },{\{{\varphi }_k(·)\}}_{k=1}^{\kappa }$ and the random coefficients ξ_ik exist mathematically, they are unknown or unobservable respectively.

The existing literature focuses on two data types. Yao, Müller and Wang (2005) studied sparse longitudinal data for which N_i, i.e. the number of observations for the i-th curve, is bounded and follows a given distribution, in which case Ma, Yang and Carroll (2011) obtained asymptotically simultaneous confidence band for the mean function of the functional data, using piecewise constant spline estimation. Li and Hsing (2010a) established uniform convergence rate for local linear estimation of mean and covariance function of dense functional data, where min_1≤i≤n N_i ≫ (n/logn)^1/4 as n → ∞ similar to our Assumption (A3), but did not provide asymptotic distribution of maximal deviation or simultaneous confidence band. Degras (2011) built asymptotically correct simultaneous confidence band for dense functional data using local linear estimator. Bunea, Ivanescu and Wegkamp (2011) proposed asymptotically conservative rather than correct confidence set for the mean function of Gaussian functional data.

In this paper, we propose polynomial spline confidence band for the mean function based on dense functional data. In function estimation problems, simultaneous confidence band is an important tool to address the variability in the mean curve, see Zhao and Wu (2008); Zhou, Shen and Wolfe (1998) and Zhou and Wu (2010) for related theory and applications. The fact that simultaneous confidence bands have not been widely used for functional data analysis is certainly not due to lack of interesting applications, but to the greater technical difficulty to formulate such bands for functional data and establish their theoretical properties. In this work, we have established asymptotic correctness of the proposed confidence band using various properties of spline smoothing. The spline estimator and the accompanying confidence band are asymptotically the same as if all the n random curves are recorded over the entire interval, without measurement errors. They are oracally efficient despite the use of spline smoothing, see Remark 1. This provides partial theoretical justification for treating functional data as perfectly recorded random curves over the entire data range, as in Ferraty and Vieu (2006). Theorem 3 of Hall, Müller and Wang (2006) stated mean square (rather than the stronger uniform) oracle efficiency for local linear estimation of eigenfunctions and eigenvalues (rather than the mean function), under assumptions similar to ours, but provided only an outline of proof. Among the existing works on functional data analysis, Ma, Yang and Carroll (2011) proposed the simultaneous confidence band for sparse functional data. However, their result does not enjoy the oracle efficiency stated in Theorem 2.1, since there are not enough observations for each subject to obtain an good estimate of the individual trajectories. As a result, it has the slow nonparametric convergence rate of n^−1/3logn, instead of the parametric rate of n^−1/2 as this paper. This essential difference completely separates dense functional data from sparse ones.

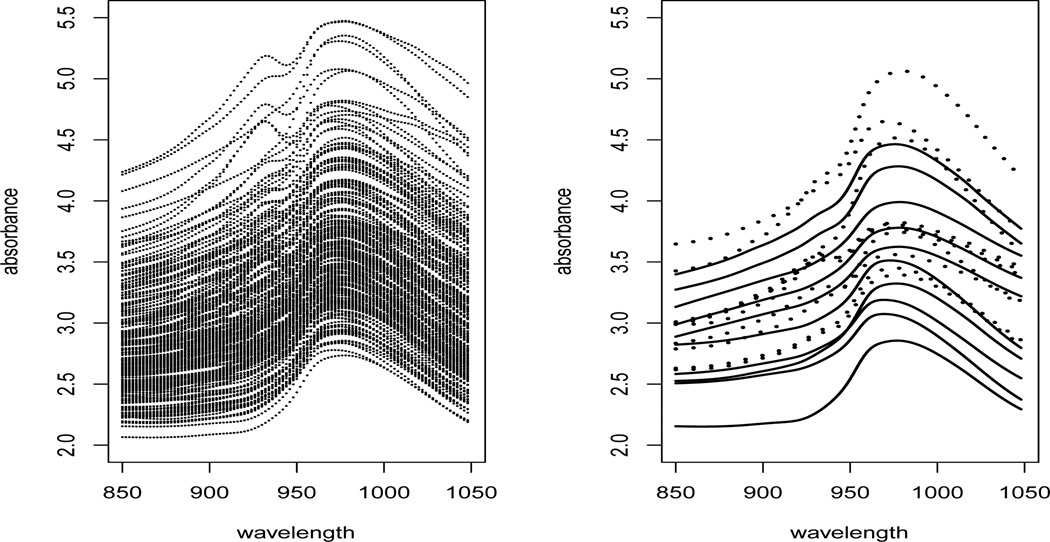
The aforementioned confidence band is also extended to the difference of two regression functions. This is motivated by Li and Yu (2008), which applied functional segment discriminant analysis to a Tecator data set, see Figure 3. In this data set, each observation (meat) consists of a 100-channel absorbance spectrum in the wavelength with different fat, water and protein percent. Li and Yu (2008) used the spectra to predict whether the fat percentage is greater than 20%. On the flip side, we are interested in building a 100 (1 − α) % confidence band for the difference between regression functions from the spectra of the less than 20% fat group and the higher than 20% fat group. If this 100 (1 − α) % confidence band covers the zero line, one accepts the null hypothesis of no difference between the two groups, with p-value no greater than α. Test for equality between two groups of curves based on the adaptive Neyman test and wavelet thresholding techniques were proposed in Fan and Lin (1998), which did not provide an estimator of the difference of the two mean functions nor a simultaneous confidence band for such estimator. As a result, their test did not extend to testing other important hypotheses on the difference of the two mean functions while our Theorem 2.3 provides a benchmark for all such testing. More recently, Benko, Häardle and Kneip (2009) developed two-sample bootstrap tests for the equality of eigenfunctions, eigenvalues and mean functions by using common functional principal components and bootstrap tests.

Figure 3.

Left: Plot of Tecator data. Right: Sample curves for the Tecator data. Each class has 10 sample curves. Dashed lines represent spectra with fact > 20% and solid lines represent spectra with fact < 20%.

The paper is organized as follows. Section 2 states main theoretical results on confidence bands constructed from polynomial splines. Section 3 provides further insights into the error structure of spline estimators. The actual steps to implement the confidence bands are provided in Section 4. A simulation study is presented in Section 5, and an empirical illustration on how to use the proposed spline confidence band for inference is reported in Section 6. Technical proofs are collected in the Appendix.

2. Main results

For any Lebesgue measurable function ϕ on [0, 1], denote ‖ϕ‖_∞ = sup_x∈[0,1] |ϕ(x)|. For any ν ∈ (0, 1] and nonnegative integer q, let C^q,ν [0, 1] be the space of functions with ν-Häolder continuous q-th order derivatives on [0, 1], i.e.

$$C^{q,\nu }[0,1]=\{\varphi :{\Vert \varphi \Vert }_{q,\nu }=\underset{t\ne s,t,s\in [0,1]}{\text{sup}}\frac{|{\varphi }^{(q)}(t)-{\varphi }^{(q)}(s)|}{|t-s{|}^{\nu }}<+\mathrm{\infty }\}.$$

To describe the spline functions, we first introduce a sequence of equally-spaced points ${\{t_J\}}_{J=1}^{N_m}$, called interior knots which divide the interval [0, 1] into (N_m + 1) equal subintervals I_J = [t_J, t_J+1), J = 0, ….,N_m − 1, I_Nm = [t_Nm, 1]. For any positive integer p, introduce left boundary knots t_1−p, …,t₀, and right boundary knots t_Nm+1, ….,t_Nm+p,

$$\begin{array}{cc}\hfill t_{1-p}=& \cdots =t_0=0<t_1<\cdots <t_{N_m}<1=t_{N_m+1}=\cdots =t_{N_m+p},\hfill \\ \hfill t_J=& {\mathit{\text{Jh}}}_m,0\le J\le N_m+1,h_m=1/(N_m+1),\hfill \end{array}$$

in which h_m is the distance between neighboring knots. Denote by ℋ^(p−2) the space of p-th order spline space, i.e., p − 2 times continuously differentiable functions on [0, 1] that are polynomials of degree p − 1 on [t_J, t_J+1], J = 0,…, N_m. Then ${\mathscr{H}}^{(p-2)}=\{{\displaystyle {\sum }_{J=1-p}^{N_m}}{b}_{J,p}{B}_{J,p}(x),b_{J,p}\in ℛ,x\in [0,1]\}$, where B_J,p is the J-th B-spline basis of order p as defined in de Boor (2001).

We propose to estimate the mean function m(x) by

$${\widehat{m}}_p(x)=\underset{g(·)\in {\mathscr{H}}^{(p-2)}}{\text{argmin}}{\displaystyle {\sum }_{i=1}^n}{\displaystyle {\sum }_{j=1}^N}{\{Y_{\mathit{\text{ij}}}-g(j/N)\}}^2.$$ (2)

The technical assumptions we need are as follows:

• (A1)The regression function m ∈ C^p−1,1 [0, 1], i.e., m^(p−1) ∈ C^0,1 [0, 1].
• (A2)The standard deviation function σ(x) ∈ C^{0, μ} [0, 1] for some μ ∈ (0, 1].
• (A3)As n → ∞, N⁻¹n^1/(2p) → 0 and N = O (n^θ) for some θ > 1/ (2p); the number of interior knots N_m satisfies ${\mathit{\text{NN}}}_m^{-1}\to \mathrm{\infty },N_m^{-p}{n}^{1/2}\to 0,N^{-1/2}{N}_m^{1/2}\text{log}n\to 0$ or equivalently Nh_m → ∞, $h_m^p{n}^{1/2}\to 0,N^{-1/2}{h}_m^{-1/2}\text{log}n\to 0$.
• (A4)There exists C_G > 0 such that G(x, x) ≥ C_G, x ∈ [0, 1], for k ∈ {1, …, κ}, ϕ_k (x) ∈ C^0,μ [0, 1], ${\displaystyle {\sum }_{k=1}^{\kappa }}{\Vert {\varphi }_k\Vert }_{\mathrm{\infty }}<\mathrm{\infty }\mathit{\text{ and as }}n\to \mathrm{\infty },h_m^{\mu }{\displaystyle {\sum }_{k=1}^{{\kappa }_n}}{\Vert {\varphi }_k\Vert }_{0,\mu }=o(1)$ for a sequence ${\{{\kappa }_n\}}_{n=1}^{\mathrm{\infty }}$ of increasing integers, with lim_n→∞ κ_n= κ and the constant μ ∈ (0, 1] as in Assumption (A2). In particular, ${\displaystyle {\sum }_{k={\kappa }_n+1}^{\kappa }}{\Vert {\varphi }_k\Vert }_{\mathrm{\infty }}=o(1)$.
• (A5)
  There are constants C₁,C₂ ∈ (0,+∞), γ₁, γ₂ ∈ (1,+∞), β ∈ (0, 1/2) and iid N(0, 1) variables ${\{Z_{\mathit{\text{ik}},\xi }\}}_{i=1,k=1}^{n,\kappa },{\{Z_{\mathit{\text{ij}},\epsilon }\}}_{i=1,j=1}^{n,N}$ such that

  $$\underset{1\le k\le \kappa }{\text{max}}P[\underset{1\le t\le n}{\text{max}}|{\displaystyle {\sum }_{i=1}^t}{\xi }_{\mathit{\text{ik}}}-{\displaystyle {\sum }_{i=1}^t}{Z}_{\mathit{\text{ik}},\xi }|>C_1{n}^{\beta }]<C_2{n}^{-{\gamma }_1},$$ (3)

  $$P\{\underset{1\le j\le N}{\text{max}}\underset{1\le t\le n}{\text{max}}|{\displaystyle {\sum }_{i=1}^t}{\epsilon }_{\mathit{\text{ij}}}-{\displaystyle {\sum }_{i=1}^t}{Z}_{\mathit{\text{ij}},\epsilon }|>C_1{n}^{\beta }\}<C_2{n}^{-{\gamma }_2}.$$ (4)

Assumptions (A1)–(A2) are typical for spline smoothing, see Huang and Yang (2004), Xue and Yang (2006) and Wang and Yang (2009a). Assumption (A3) concerns the number of observations for each subject, and the number of knots of B-splines. Assumption (A4) ensures that the principal components have collectively bounded smoothness. Assumption (A5) provides Gaussian approximation of estimation error process, and is ensured by the following elementary assumption:

• (A5’)There exist η₁ > 4, η₂ > 4+2θ such that E |ξ_ik|^η₁+E |ε_ij|^η₂ < +∞, for 1 ≤ i < ∞, 1 ≤ k ≤ κ, 1 ≤ j < ∞. The number κ of nonzero eigenvalues is finite or κ is infinite while the variables {ξ_ik}_{1≤i<∞,1≤k<∞} are iid.

Degras (2011) makes a restrictive assumption (A.2) on the Hölder continuity of the stochastic process $\eta (x)=m(x)+{\displaystyle {\sum }_{k=1}^{\mathrm{\infty }}}{\xi }_k{\varphi }_k(x)$. It is elementary to construct examples where our Assumptions (A4) and (A5) are satisfied while assumption (A.2) of Degras (2011) is not.

The part of Assumption (A4) on ϕ_k’s holds trivially if κ is finite and all ϕ_k (x) ∈ C^0,μ [0, 1]. Note also that by definition, ${\varphi }_k=\sqrt{{\lambda }_k}{\psi }_k,{\Vert {\varphi }_k\Vert }_{\mathrm{\infty }}=\sqrt{{\lambda }_k}{\Vert {\psi }_k\Vert }_{\mathrm{\infty }},{\Vert {\varphi }_k\Vert }_{0,\mu }=\sqrt{{\lambda }_k}{\Vert {\psi }_k\Vert }_{0,\mu }$, in which ${\{{\psi }_k\}}_{k=1}^{\mathrm{\infty }}$ form an orthonormal basis of L² ([0, 1]), hence, Assumption (A4) is fulfilled for κ = ∞ as long as λ_k decreases to zero sufficiently fast. Following one Referee’s suggestion, we provide the following example. One takes λ_k = ρ^2[k/2], k = 1, 2, … for any ρ ∈ (0, 1), with ${\{{\psi }_k\}}_{k=1}^{\mathrm{\infty }}$ the canonical orthonormal Fourier basis of L² ([0, 1])

$$\begin{array}{cc}\hfill {\psi }_1(x)\equiv \hfill & 1,{\psi }_{2k+1}(x)\equiv \sqrt{2}\text{cos }(k\pi x)\hfill \\ \hfill {\psi }_{2k}(x)\equiv \hfill & \sqrt{2}\text{sin }(k\pi x),k=1,2,\dots ,x\in [0,1].\hfill \end{array}$$

In this case, ${\displaystyle {\sum }_{k=1}^{\mathrm{\infty }}}{\Vert {\varphi }_k\Vert }_{\mathrm{\infty }}=1+{\displaystyle {\sum }_{k=1}^{\mathrm{\infty }}}{\rho }^k(\sqrt{2}+\sqrt{2})=1+2\sqrt{2}\rho {(1-\rho )}^{-1}<\mathrm{\infty }$, while for any ${\{{\kappa }_n\}}_{n=1}^{\mathrm{\infty }}$ with κ_n increasing, odd and κ_n → ∞, and Lipschitz order μ = 1

$$h_m{\displaystyle {\sum }_{k=1}^{{\kappa }_n}}{\Vert {\varphi }_k\Vert }_{0,1}=h_m{\displaystyle {\sum }_{k=1}^{({\kappa }_n-1)/2}}{\rho }^k(\sqrt{2}k\pi +\sqrt{2}k\pi )\le 2\sqrt{2}\pi h_m\rho {\displaystyle {\sum }_{k=1}^{\mathrm{\infty }}}{\rho }^{k-1}k=2\sqrt{2}\pi h_m{(1-\rho )}^{-2}=O(h_m)=o(1).$$

Denote by ζ (x), x ∈ [0, 1] a standardized Gaussian process such that Eζ (x) ≡ 0, Eζ² (x) ≡ 1, x ∈ [0, 1] with covariance function

$$E\zeta (x)\zeta (x\prime )=G(x,x\prime ){\{G(x,x)G(x\prime ,x\prime )\}}^{-1/2},x,x\prime \in [0,1]$$

and define the 100 × (1 − α)-th percentile of the absolute maxima distribution of ζ (x), ∀x ∈ [0, 1], i.e., P [sup_x∈[0,1] |ζ (x)| ≤ Q_1−α] = 1 − α, ∀α ∈ (0, 1). Denote by z_1−α/2 the 100 (1 − α/2)-th percentile of the standard normal distribution. Define also the following “infeasible estimator” of function m

$$\overline{m}(x)=\overline{\eta }(x)=n^{-1}{\displaystyle {\sum }_{i=1}^n}{\eta }_i(x),x\in [0,1].$$ (5)

The term “infeasible” refers to the fact that m̄(x) is computed from unknown quantity η_i(x), x ∈ [0, 1], and it would be the natural estimator of m(x) if all the iid random curves η_i(x), x ∈ [0, 1] were observed, a view taken in Ferraty and Vieu (2006).

We now state our main results in the following theorem.

Theorem 2.1 : Under Assumptions (A1)–(A5), for ∀α ∈ (0, 1), as n → ∞, the “infeasible estimator” m̄(x) converges at the $\sqrt{n}$ rate

$$\begin{array}{c}P\{{\text{sup}}_{x\in [0,1]}{n}^{1/2}|\overline{m}(x)-m(x)|G{(x,x)}^{-1/2}\le Q_{1-\alpha }\}\to 1-\alpha ,\hfill \\ P\{n^{1/2}|\overline{m}(x)-m(x)|G{(x,x)}^{-1/2}\le z_{1-\alpha /2}\}\to 1-\alpha ,\forall x\in [0,1],\hfill \end{array}$$

while the spline estimator m̂_p is asymptotically equivalent to m̄ up to order n^1/2, i.e.

$${\text{sup}}_{x\in [0,1]}{n}^{1/2}|\overline{m}(x)-{\widehat{m}}_p(x)|=o_P(1).$$

Remark 1 : The significance of Theorem 2.1 lies in the fact that one does not need to distinguish between the spline estimator m̂_p and the “infeasible estimator” m̄ in (5), which converges with $\sqrt{n}$ rate like a parametric estimator. We therefore have established oracle efficiency of the nonparametric estimator m̂p.

Corollary 2.2: Under Assumptions (A1)–(A5), as n → ∞, an asymptotic 100 (1 − α) % correct confidence band for m(x), x ∈ [0, 1] is

$${\widehat{m}}_p(x)\pm G{(x,x)}^{1/2}{Q}_{1-\alpha }{n}^{-1/2},\forall \alpha \in (0,1)$$

while an asymptotic 100 (1 − α) % pointwise confidence interval for m(x), x ∈ [0, 1], is m̂_p(x) ± G(x, x)^1/2 z_1−α/2n^−1/2.

We next describe a two-sample extension of Theorem 2.1. Denote two samples indicated by d = 1, 2, which satisfy

$$Y_{\mathit{\text{dij}}}=m_d(j/N)+{\displaystyle {\sum }_{k=1}^{{\kappa }_d}}{\xi }_{\mathit{\text{dik}}}{\varphi }_{\mathit{\text{dk }}}(j/N)+{\sigma }_d(j/N){\epsilon }_{\mathit{\text{dij}}},1\le i\le n_d,1\le j\le N$$

with covariance functions $G_d(x,x\prime )={\displaystyle {\sum }_{k=1}^{{\kappa }_d}}{\varphi }_{\mathit{\text{dk}}}(x){\varphi }_{\mathit{\text{dk}}}(x\prime )$ respectively. We denote the ratio of two sample sizes as r̂ = n₁/n₂ and assume that lim_n1→∞ r̂ = r > 0.

For both groups, let m̂_1p(x) and m̂_2p(x) be the order p spline estimates of mean functions m₁(x) and m₂(x) by (2). Also denote by ζ₁₂ (x), x ∈ [0, 1] a standardized Gaussian process such that Eζ₁₂ (x) ≡ 0, $E{\zeta }_{12}^2(x)\equiv 1$, x ∈ [0, 1] with covariance function

$$E{\zeta }_{12}(x){\zeta }_{12}(x\prime )=\frac{G_1(x,x\prime )+{\mathit{\text{rG}}}_2(x,x\prime )}{{\{G_1(x,x)+{\mathit{\text{rG}}}_2(x,x)\}}^{1/2}{\{G_1(x,x\prime )+{\mathit{\text{rG}}}_2(x,x\prime )\}}^{1/2}},x,x\prime \in [0,1].$$

Denote by Q_12,1−α the (1 − α)-th quantile of the absolute maxima deviation of ζ₁₂ (x), x ∈ [0, 1] as above. We mimic the two sample t-test and state the following theorem whose proof is analogous to that of Theorem 2.1.

Theorem 2.3 : If Assumptions (A1)–(A5) are modified for each group accordingly, then for any α ∈ (0, 1), as n₁ → ∞, r̂ → r > 0,

$$P\{{\text{sup}}_{x\in [0,1]}\frac{n_1^{1/2}|({\widehat{m}}_{1p}-{\widehat{m}}_{2p}-m_1+m_2)(x)|}{{\{(G_1+{\mathit{\text{rG}}}_2)(x,x)\}}^{1/2}}\le Q_{12,1-\alpha }\}\to 1-\alpha .$$

Theorems 2.3 yields uniform asymptotic confidence band for m₁(x)−m₂(x), x ∈ [0, 1].

Corollary 2.4: If Assumptions (A1)–(A5) are modified for each group accordingly, as n₁ → ∞, r̂ → r > 0, a 100 × (1 − α) % asymptotically correct confidence band for m₁(x)−m₂(x), x ∈ [0, 1] is $({\widehat{m}}_{1p}-{\widehat{m}}_{2p})(x)\pm n_1^{-1/2}{Q}_{12,1-\alpha }{\{(G_1+r{G}_2)(x,x)\}}^{1/2}$, ∀α ∈ (0, 1).

If the confidence band in Corollary 2.2 is used to test hypothesis

$$H_0:m(x)=m_0(x),\forall x\in [0,1]\leftrightarrow H_a:m(x)\ne m_0(x),\text{ for some }x\in [0,1],$$

for some given function m₀(x), as one referee pointed out, the asymptotic power of the test is α under H₀, 1 under H₁ due to Theorem 2.1. The same can be said for testing hypothesis about m₁(x) − m₂(x) using the confidence band in Corollary 2.4.

3. Error Decomposition For the Spline Estimators

In this section, we break the estimation error m̂_p(x) − m(x) into three terms. We begin by discussing the representation of the spline estimator m̂p(x) in (2).

The definition of m̂_p(x) in (2) means that

$${\widehat{m}}_p(x)\equiv {\displaystyle {\sum }_{J=1-p}^{N_m}}{\widehat{\beta }}_{J,p}{B}_{J,p}(x),$$

with coefficients {β̂_1−p,p, …, β̂_Nm,p }^T solving the following least squares problem

$${\{{\widehat{\beta }}_{1-p,p},\dots ,{\widehat{\beta }}_{N_m,p}\}}^{\mathrm{T}}=\underset{\{{\beta }_{1-p,p},\dots ,{\beta }_{N_m,p}\}\in R^{N_{m+p}}}{\text{argmin}}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^N}{\{Y_{\mathit{\text{ij}}}-{\displaystyle \sum _{J=1-p}^{N_m}}{\beta }_{J,p}{B}_{J,p}(j/N)\}}^2.$$ (6)

Applying elementary algebra, one obtains

$${\widehat{m}}_p(x)=\{B_{1-p,p}(x),\dots ,B_{N_{m,p}}(x)\}{({\mathbf{X}}^{\mathrm{T}}\mathbf{X})}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{Y}$$ (7)

where Y = (Ȳ_.1,…, Ȳ_.N)^T, ${\overline{Y}}_{․j}=n^{-1}{\displaystyle {\sum }_{i=1}^n}{Y}_{\mathit{\text{ij}}},1\le j\le N$, and the design matrix X is

$$\mathbf{X}={\left(\begin{array}{ccc}\hfill B_{1-p,p}(1/N)\hfill & \hfill \cdots \hfill & \hfill B_{N_m,p}(1/N)\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill B_{1-p,p}(N/N)\hfill & \hfill \cdots \hfill & \hfill B_{N_m,p}(N/N)\hfill \end{array}\right)}_{N\times (N_m+p)}.$$

Projecting via (7) the relationship in model (1) onto the linear subspace of R^N_m+p spanned by (B_J,p (j/N)}_{1≤j≤N,1−p≤J≤Nm}, we obtain the following crucial decomposition in the space ℋ^(p−2) of spline functions:

$${\widehat{m}}_p(x)={\tilde{m}}_p(x)+{\tilde{e}}_p(x)+{\tilde{\xi }}_p(x),$$ (8)

where

$$\begin{array}{cc}\hfill {\tilde{m}}_p(x)\hfill & ={\displaystyle {\sum }_{J=1-p}^{N_m}}{\tilde{\beta }}_{J,p}{B}_{J,p}(x),{\tilde{\epsilon }}_p(x)={\displaystyle {\sum }_{J=1-p}^{N_m}}{\tilde{a}}_{J,p}{B}_{J,p}(x),\hfill \\ \hfill {\tilde{\xi }}_p(x)& ={\displaystyle {\sum }_{k=1}^{\kappa }}{\tilde{\xi }}_{k,p}(x),{\tilde{\xi }}_{k,p}(x)={\displaystyle {\sum }_{J=1-p}^{N_m}}{\tilde{\tau }}_{k,J,p}{B}_{J,p}(x).\hfill \end{array}$$ (9)

The vectors {β̃_1−p, …,β̃N_m}^T, {ã_1−p, …, ãN_m}^T and {τ̃_k,1−p, …,τ̃_k,Nm}^T in (9) are solutions to (6) with Y_ij replaced by m(j/N), σ (j/N) ε_ij and ξ_ikϕ_k (j/N) respectively.

Alternatively,

$$\begin{array}{cc}\hfill {\tilde{m}}_p(x)\hfill & =\{B_{1-p,p}(x),\dots ,B_{N_m,p}(x)\}{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{m}\hfill \\ \hfill {\tilde{e}}_p(x)& =\{B_{1-p,p}(x),\dots ,B_{N_m,p}(x)\}{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{e}\hfill \\ \hfill {\tilde{\xi }}_{k,p}(x)& ={\overline{\xi }}_{.k}\{B_{1-p,p}(x),\dots ,B_{N_m,p}(x)\}{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}{\varphi }_k,1\le k\le \kappa \hfill \end{array}$$

in which m = (m(1/N),…m(N/N))^T is the signal vector, $\mathbf{e}={(\sigma (1/N){\overline{\epsilon }}_{.1},\dots ,\sigma (N/N){\overline{\epsilon }}_{.N})}^{\mathrm{T}},{\overline{\epsilon }}_{.j}=n^{-1}{\displaystyle {\sum }_{i=1}^n}{\epsilon }_{\mathit{\text{ij}}},1\le j\le N$ is the noise vector and ϕ_k = (ϕ_k (1/N),…, ϕ_k (N/N))^T are the eigenfunction vectors, and ${\overline{\xi }}_{.k}=n^{-1}{\displaystyle {\sum }_{i=1}^n}{\xi }_{\mathit{\text{ik}}},1\le k\le \kappa$.

We cite next an important result from de Boor (2001), p. 149.

Theorem 3.1 : There is an absolute constant C_p−1,μ > 0 such that for every ϕ ∈ C^p−1,μ [0, 1] for some μ ∈ (0, 1], there exists a function g ∈ ℋ^(p−1) [0, 1] for which ${\Vert g-\varphi \Vert }_{\infty }\le C_{p-1,\mu }{\Vert {\varphi }^{(p-1)}\Vert }_{0,\mu }{h}_m^{\mu +p-1}$.

The next three propositions concern m̃_p(x), ẽ_p(x) and ζ̃_p(x) given in (8).

Proposition 3.2: Under Assumptions (A1) and (A3), as n → ∞

$${\text{sup}}_{x\in [0,1]}{n}^{1/2}|{\tilde{m}}_p(x)-m(x)|=o(1).$$ (10)

Proposition 3.3: Under Assumptions (A2)–(A4), as n → ∞

$${\text{sup}}_{x\in [0,1]}{n}^{1/2}|{\tilde{e}}_p(x)|=o_P(1).$$ (11)

Proposition 3.4: Under Assumptions (A2)–(A4), as n → ∞

$${\text{sup}}_{x\in [0,1]}{n}^{1/2}|{\tilde{\xi }}_p(x)-(\overline{m}(x)-m(x))|=o_P(1)$$ (12)

also for any α ∈ (0, 1)

$$P\left\{{\text{sup}}_{x\in [0,1]}{n}^{1/2}\right|{\tilde{\xi }}_p(x)|G{(x,x)}^{-1/2}\le Q_{1-\alpha }\}\to 1-\alpha .$$ (13)

Equations (10), (11) and (12) yield the asymptotic efficiency of the spline estimator m̂_p, i.e. sup_x∈[0,1] n^1/2 |m̄(x) − m̂_p(x)| = o_P (1). The Appendix contains proofs for the above three propositions, which together with (8), imply Theorem 2.1.

4. Implementation

This section describes procedures to implement the confidence band in Corollary 2.2.

Given any data set ${(j/N,Y_{\mathit{\text{ij}}})}_{j=1,i=1}^{N,n}$ from model (1), the spline estimator m̂_p (x) is obtained from (7), the number of interior knots in estimating m(x) is taken to be N_m = [cn^1/(2p)log (n)], in which [a] denotes the integer part of a. Our experiences show that the choice of constant c = 0.2, 0.3, 0.5, 1, 2 seems quite adequate, and that is what we recommend. When constructing the confidence bands, one needs to estimate the unknown functions G(·, ·) and the quantile Q_1−α and then plug in these estimators: the same approach is taken in Ma, Yang and Carroll (2011) and Wang and Yang (2009a).

The pilot estimator Ĝ_p (x, x′) of covariance function G(x, x′) is

$${\widehat{G}}_p=\underset{g(·,·)\in {\mathscr{H}}^{(p-2),2}}{\text{argmin}}{\displaystyle {\sum }_{j\ne j\prime }^N}{\{C_{.\mathit{\text{jj}}\prime }-g(j/N,j\prime /N)\}}^2,$$

with $C_{.\mathit{\text{jj}}\prime }=n^{-1}{\displaystyle {\sum }_{i=1}^n}\{Y_{\mathit{\text{ij}}}-{\widehat{m}}_p(j/N)\}\{Y_{\mathit{\text{ij}}\prime }-{\widehat{m}}_p(j\prime /N)\},1\le j\ne j\prime \le N$ and the tensor product spline space ${\mathscr{H}}^{(p-2),2}=\{{\displaystyle {\sum }_{J,J\prime =1-p}^{N_G}}{b}_{\mathit{\text{JJ}}\prime }{B}_{J,p}(t)B_{J\prime ,p}(s),b_{\mathit{\text{JJ}}\prime }\in ℛ,t,s\in [0,1]\}$ in which N_G = [n^1/(2p)log(log(n))].

In order to estimate Q_1−α, one first does the eigenfunction decomposition of Ĝ_p (x, x′), i.e. $N^{-1}{\displaystyle {\sum }_{j=1}^N}{\widehat{G}}_p(j/N,j\prime /N){\widehat{\psi }}_k(j/N)={\widehat{\lambda }}_k{\widehat{\psi }}_k(j\prime /N)$, to obtain the estimated eigenvalues λ̂_k and eigenfunctions ψ̂_k. Next, one chooses the number κ of eigenfunctions by using the following standard and efficient criterion, i.e. $\kappa ={\text{argmin}}_{1\le l\le T}\{{\displaystyle {\sum }_{k=1}^l}{\widehat{\lambda }}_k/{\displaystyle {\sum }_{k=1}^T}{\widehat{\lambda }}_k>0.95\},\text{where }{\{{\lambda }_k\}}_{k=1}^T$ are the first T estimated positive eigenvalues. Finally, one simulates ${\widehat{\zeta }}_b(x)={\widehat{G}}_p{(x,x)}^{-1/2}{\displaystyle {\sum }_{k=1}^{\kappa }}{Z}_{k,b}{\widehat{\varphi }}_k(x),\text{where }{\widehat{\varphi }}_k=\sqrt{{\widehat{\lambda }}_k}{\widehat{\psi }}_k,Z_{k,b}$ are i.i.d standard normal variables with 1 ≤ k ≤ κ and b = 1, …, b_M, where b_M is a preset large integer, the default of which is 1000. One takes the maximal absolute value for each copy of ζ̂_b (x) and estimates Q_1−α by the empirical quantile Q̂_1−α of these maximum values. One then uses the following confidence band

$${\widehat{m}}_p(x)\pm n^{-1/2}{\widehat{G}}_p{(x,x)}^{1/2}{\widehat{Q}}_{1-\alpha },x\in [0,1],$$ (14)

for the mean function. One estimates Q_12,1−α analogous to Q̂_1−α and computes

$$({\widehat{m}}_{1p}-{\widehat{m}}_{2p})(x)\pm n_1^{-1/2}{\widehat{Q}}_{12,1-\alpha }{\left\{\right({\widehat{G}}_{1p}+\widehat{r}{\widehat{G}}_{2p})(x,x)\}}^{1/2},$$ (15)

as confidence band for m₁(x) − m₂(x). Although beyond the scope of this paper, as one referee pointed out, the confidence band in (14) is expected to enjoy the same asymptotic coverage as if true values of Q_1−α and G(x, x) were used instead, due to the consistency of Ĝ_p (x, x) estimating G(x, x). The same holds for the band in (15).

5. Simulation

To demonstrate the practical performance of our theoretical results, we perform a set of simulation studies. Data are generated from model

$$Y_{\mathit{\text{ij}}}=m(j/N)+{\displaystyle {\sum }_{k=1}^2}{\xi }_{\mathit{\text{ik}}}{\varphi }_k(j/N)+\sigma {\epsilon }_{\mathit{\text{ij}}},1\le j\le N,1\le i\le n,$$ (16)

where ξ_ik ~ N(0, 1), k = 1, 2, ε_ij ~ N(0, 1), for 1 ≤ i ≤ n, 1 ≤ j ≤ N, m(x) = 10+sin {2π (x − 1/2)}, ϕ₁(x) = −2 cos {π (x − 1/2)} and ϕ₂(x) = sin {π (x − 1/2)}. This setting implies λ₁ = 2 and λ₂ = 0.5. The noise levels are set to be σ = 0.5 and 0.3. The number of subjects n is taken to be 60, 100, 200, 300 and 500, and under each sample size the number of observations per curve is assumed to be N = [n^0.25log²(n)]. This simulated process has a similar design as one of the simulation models in Yao, Müller and Wang (2005), except that each subject is densely observed. We consider both linear and cubic spline estimators, and use confidence levels 1 − α = 0.95 and 0.99 for our simultaneous confidence bands. The constant c in the definition of N_m in Section 4 is taken to be 0.2, 0.3, 0.5, 1 and 2. Each simulation is repeated 500 times.

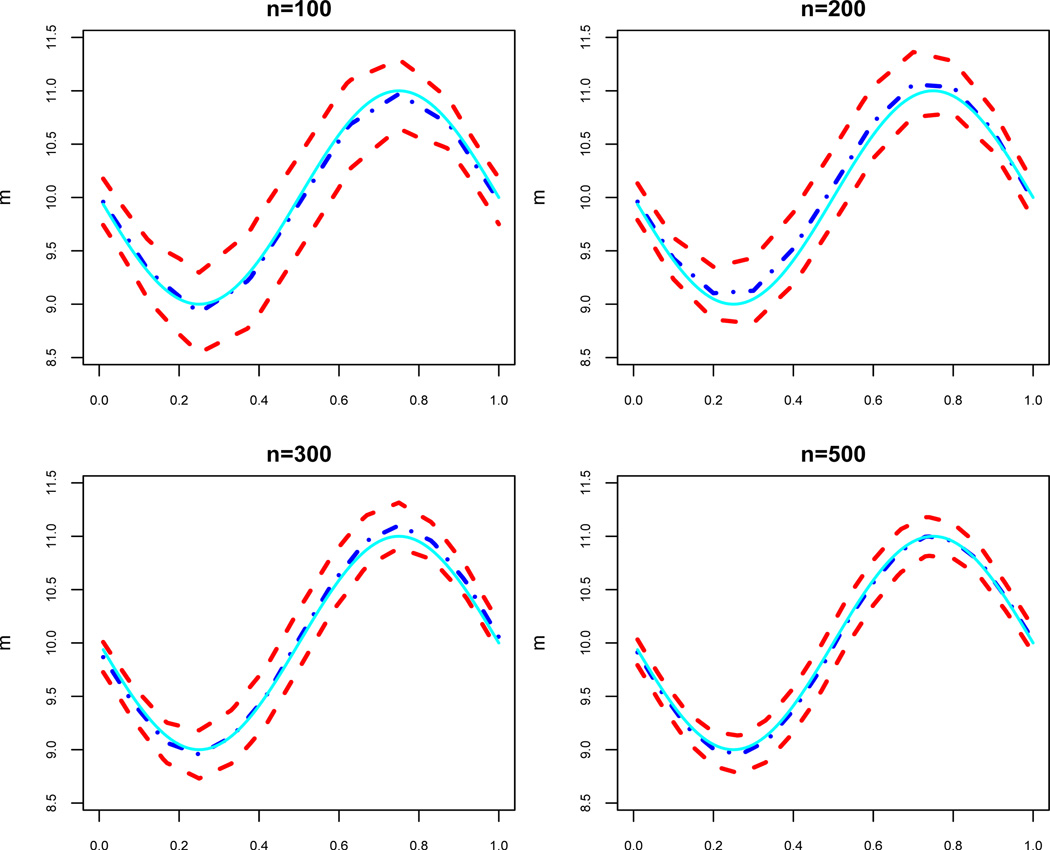
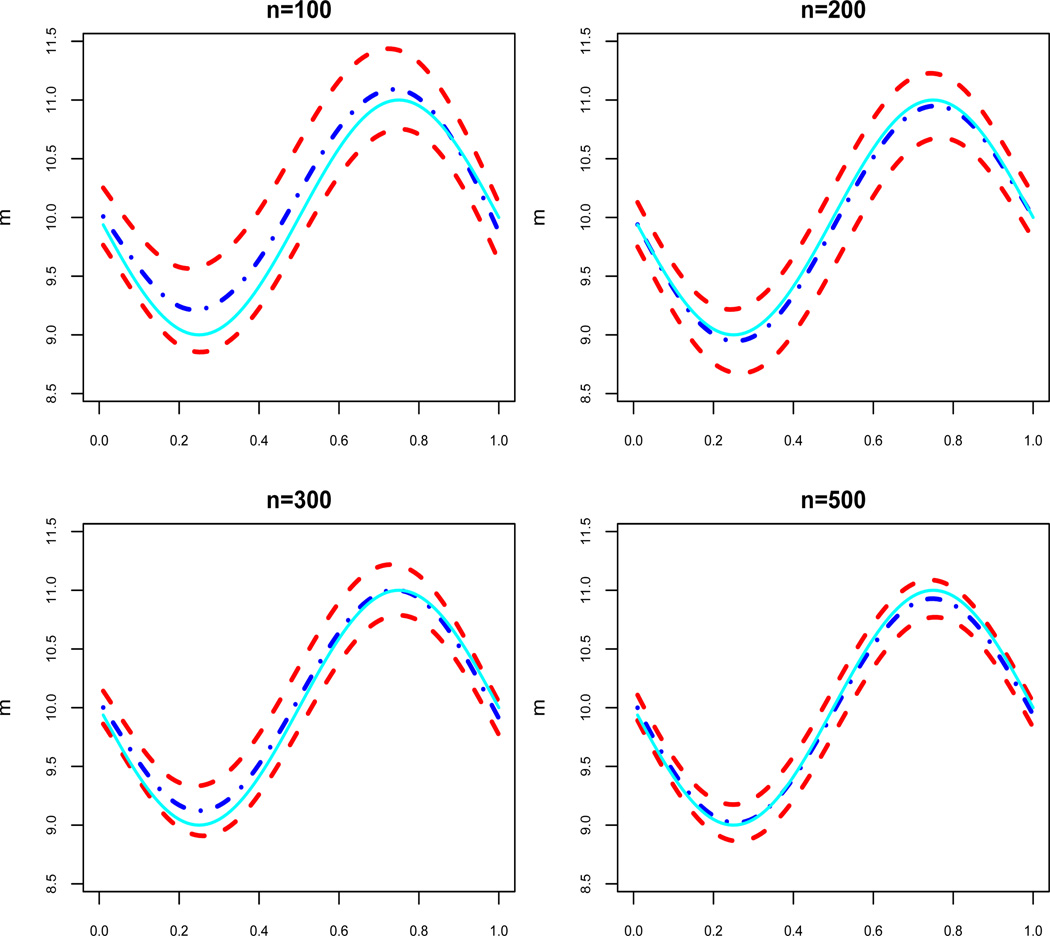
Figures 1 and 2 show the estimated mean functions and their 95% confidence bands for the true curve m(·) in Model (16) with σ = 0.3 and n = 100, 200, 300, 500 respectively. As expected when n increases, the confidence band becomes narrower and the linear and cubic spline estimators are closer to the true curve.

Figure 1.

Plots of the linear spline estimator (2) for simulated data (dashed-dotted line) and 95% confidence bands (14) (upper and lower dashed lines) (14) for m(x) (solid lines). In all panels, σ = 0.3.

Figure 2.

Plots of the cubic spline estimator (2) for simulated data (dashed-dotted line) and 95% confidence bands (14) (upper and lower dashed lines) (14) for m(x) (solid lines). In all panels, σ = 0.3.

Tables 1 and 2 show the empirical frequency that the true curve m(·) is covered by the linear and cubic spline confidence bands (14) at 100 points {1/100, …, 99/100, 1} respectively. At all noise levels, the coverage percentages for the confidence band are close to the nominal confidence levels 0.95 and 0.99 for linear splines with c = 0.5, 1 (Table 1), and cubic splines with c = 0.3, 0.5 (Table 2) but decline slightly for c = 2 and markedly for c = 0.2. The coverage percentages thus depend on the choice of N_m, and the dependency becomes stronger when sample sizes decrease. For large sample sizes n = 300, 500, the effect of the choice of N_m on the coverage percentages is negligible. Although our theory indicates no optimal choice of c, we recommend using c = 0.5 for data analysis as its performance in simulation for both linear and cubic splines is either optimal or near optimal.

Table 1.

Coverage frequencies from 500 replications using linear spline (14) with p = 2 and N_m = [cn^1/(2p)log(n)].

n	1 − α	Coverage frequency σ = 0.5					Coverage frequency σ = 0.3
		c = 0.2	c = 0.3	c = 0.5	c = 1	c = 2	c = 0.2	c = 0.3	c = 0.5	c = 1	c = 2
60	0.950	0.384	0.790	0.876	0.894	0.852	0.410	0.786	0.930	0.914	0.884
	0.990	0.692	0.938	0.970	0.976	0.942	0.702	0.950	0.972	0.966	0.954
100	0.950	0.184	0.826	0.886	0.884	0.838	0.198	0.822	0.916	0.916	0.896
	0.990	0.476	0.936	0.964	0.966	0.944	0.496	0.940	0.974	0.974	0.968
200	0.950	0.418	0.856	0.914	0.922	0.862	0.414	0.862	0.946	0.942	0.926
	0.990	0.712	0.966	0.976	0.990	0.972	0.720	0.966	0.984	0.984	0.980
300	0.950	0.600	0.888	0.920	0.932	0.874	0.602	0.896	0.940	0.934	0.926
	0.990	0.834	0.978	0.976	0.980	0.972	0.840	0.982	0.984	0.986	0.980
500	0.950	0.772	0.880	0.922	0.886	0.894	0.768	0.888	0.954	0.950	0.942
	0.990	0.902	0.964	0.984	0.976	0.976	0.906	0.968	0.992	0.994	0.988

Table 2.

Coverage frequencies from 500 replications using cubic spline (14) with p = 4 and N_m = [cn^1/(2p)log(n)].

n	1 − α	Coverage frequency σ = 0.5					Coverage frequency σ = 0.3
		c = 0.2	c = 0.3	c = 0.5	c = 1	c = 2	c = 0.2	c = 0.3	c = 0.5	c = 1	c = 2
60	0.950	0.644	0.916	0.902	0.890	0.738	0.672	0.922	0.940	0.940	0.916
	0.990	0.866	0.980	0.958	0.964	0.888	0.884	0.986	0.986	0.984	0.982
100	0.950	0.596	0.902	0.904	0.876	0.846	0.610	0.916	0.914	0.914	0.896
	0.990	0.786	0.970	0.968	0.956	0.952	0.798	0.980	0.974	0.970	0.964
200	0.950	0.928	0.942	0.932	0.936	0.904	0.938	0.952	0.950	0.948	0.934
	0.990	0.978	0.992	0.982	0.992	0.978	0.982	0.984	0.992	0.982	0.984
300	0.950	0.920	0.948	0.926	0.948	0.898	0.922	0.956	0.948	0.942	0.938
	0.990	0.976	0.986	0.986	0.988	0.980	0.982	0.984	0.988	0.984	0.982
500	0.950	0.928	0.922	0.954	0.902	0.898	0.928	0.928	0.936	0.932	0.916
	0.990	0.980	0.982	0.990	0.976	0.978	0.980	0.982	0.990	0.990	0.992

Following the suggestion of one referee and the Associate Editor, we compare by simulation the proposed spline confidence band to the least squares Bonferroni and least squares bootstrap bands in Bunea, Ivanescu and Wegkamp (2011) (BIW). Table 3 presents the empirical frequency that the true curve m(·) for model (16) is covered by these bands at {1/100, …, 99/100, 1} respectively as Table 1. The coverage frequency of the BIW Bonferroni band is much higher than the nominal level making it too conservative. The coverage frequency of the BIW bootstrap band is consistently lower than the nominal level by at least 10%, thus not recommended for practical use.

Table 3.

Coverage frequencies from 500 replications using least squares Bonferroni band and least squares Bootstrap band.

n	1 − α	Coverage frequency least squares Bonferroni		Coverage frequency least squares bootstrap
		σ = 0.5	σ = 0.3	σ = 0.5	σ = 0.3
60	0.950	0.990	0.988	0.742	0.744
	0.990	0.994	0.994	0.856	0.864
100	0.950	0.996	0.998	0.678	0.712
	0.990	0.998	1.000	0.860	0.870
200	0.950	0.988	0.992	0.710	0.734
	0.990	1.000	1.000	0.856	0.888
300	0.950	0.988	0.998	0.704	0.720
	0.990	1.000	1.000	0.868	0.870
500	0.950	0.996	0.998	0.718	0.732
	0.990	1.000	1.000	0.856	0.860

Following the suggestion of one referee and the Associate Editor, we also compare the widths of the three bands. For each replication, we calculate the ratios of widths of the two BIW bands against the spline band at {1/100, …, 99/100, 1} and then average these 100 ratios. Table 4 shows the five number summary of these 500 averaged ratios for σ = 0.3 and p = 4. The BIW Bonferroni band is much wider than cubic spline band, making it undesirable. While the BIW bootstrap band is narrower, we have mentioned previously that its coverage frequency is too low to be useful in practice. Simulation for other cases (e.g. p = 2, σ = 0.5) leads to the same conclusion.

Table 4.

Five number summary of ratios of confidence band widths.

n	1 − α	least squares Bonferroni/cubic spline					least squares bootstrap/cubic spline
		Min.	Q1	Med.	Q3	Max.	Min.	Q1	Med.	Q3	Max.
60	0.950	0.964	1.219	1.299	1.397	1.845	0.522	0.667	0.716	0.770	0.967
	0.990	0.907	1.114	1.188	1.285	1.730	0.527	0.662	0.715	0.770	1.048
100	0.950	0.995	1.263	1.331	1.415	1.684	0.565	0.675	0.714	0.754	0.888
	0.990	0.910	1.148	1.219	1.295	1.603	0.536	0.665	0.708	0.752	0.925
200	0.950	1.169	1.326	1.383	1.433	1.653	0.600	0.683	0.715	0.743	0.855
	0.990	1.045	1.197	1.250	1.300	1.507	0.557	0.668	0.702	0.740	0.888
300	0.950	1.169	1.363	1.412	1.462	1.663	0.574	0.690	0.717	0.742	0.838
	0.990	1.067	1.228	1.277	1.322	1.509	0.587	0.676	0.707	0.739	0.850
500	0.950	1.273	1.395	1.432	1.476	1.601	0.620	0.691	0.714	0.737	0.818
	0.990	1.132	1.243	1.288	1.334	1.465	0.607	0.674	0.707	0.734	0.839

To examine the performance of the two-sample test based on spline confidence band, Table 5 reports the empirical power and type I error for the proposed two-sample test. The data were generated from (16) with σ = 0.5 and m₁(x) = 10+sin {2π (x − 1/2)}+δ (x), n = n₁ for the first group, and m₂(x) = 10 + sin {2π (x − 1/2)}, n = n₂ for the another group. The remaining parameters, ξ_ik, ε_ij, ϕ₁(x) and ϕ₂(x) were set to the same values for each group as in (16). In order to mimic the real data in Section 6, we set N = 50, 100 and 200 when n₁ = 160, 80 and 40 and n₂ = 320, 160 and 80 accordingly. The studied hypotheses are:

$$H_0:m_1(x)=m_2(x),\forall x\in [0,1]\leftrightarrow H_a:m_1(x)\ne m_2(x),\text{for some }x\in [0,1].$$

Table 5.

Empirical power and type I error of two-sample test using cubic spline.

δ (x)	n1 = 160, n2 = 320		n1 = 80, n2 = 160		n1 = 40, n2 = 80
	Nominal test level		Nominal test level		Nominal test level
	0.05	0.01	0.05	0.01	0.05	0.01
0.6t	1.000	1.000	0.980	0.918	0.794	0.574
0.7sin(x)	1.000	1.000	0.978	0.910	0.788	0.566
0	0.058	0.010	0.068	0.010	0.096	0.028
Monte Carlo SE	0.001	0.004	0.001	0.004	0.001	0.004

Table 5 shows the empirical frequencies of rejecting H₀ in this simulation study with nominal test level equal to 0.05 and 0.01. If δ(x) ≠ 0, these empirical powers should be close to 1, and for δ(x) ≡ 0, the nominal levels. Each set of simulations consists of 500 Monte Carlo runs. Asymptotic standard errors (as the number of Monte Carlo iterations tends to infinity) are reported in the last row of the table. Results are listed only for cubic spline confidence bands, as those of the linear spline are similar. Overall, the two-sample test performs well, even with a rather small difference (δ(x) = 0.7 sin(x)), providing a reasonable empirical power. Moreover, the differences between nominal levels and empirical type I error do diminish as the sample size increases.

6. Empirical Example

In this section, we revisit the Tecator data mentioned in Section 1, which can be downloaded at http://lib.stat.cmu.edu/datasets/tecator. In this data set, there are measurements on n = 240 meat samples, where for each sample a N = 100 channel near-infrared spectrum of absorbance measurements was recorded, and contents of moisture (water), fat and protein were also obtained. The Feed Analyzer worked in the wavelength range from 850 nm to 1050 nm. Figure 3 shows the scatter plot of this data set. The spectral data can be naturally considered as functional data, and we will perform a two-sample test to see whether absorbance from the spectrum differs significantly due to difference in fat content.

This data set has been used for comparing four classification methods (Li and Yu, 2008), building a regression model to predict the fat content from the spectrum (Li and Hsing, 2010b). Following Li and Yu (2008), we separate samples according to their fat contents being less than 20% or not. The right panel of Figure 3 shows 10 samples from each group. Here, hypothesis of interest is:

$$H_0:m_1(x)=m_2(x),\forall x\in [850,1050]\leftrightarrow H_a:m_1(x)\ne m_2(x),\text{for some }x\in [850,1050],$$

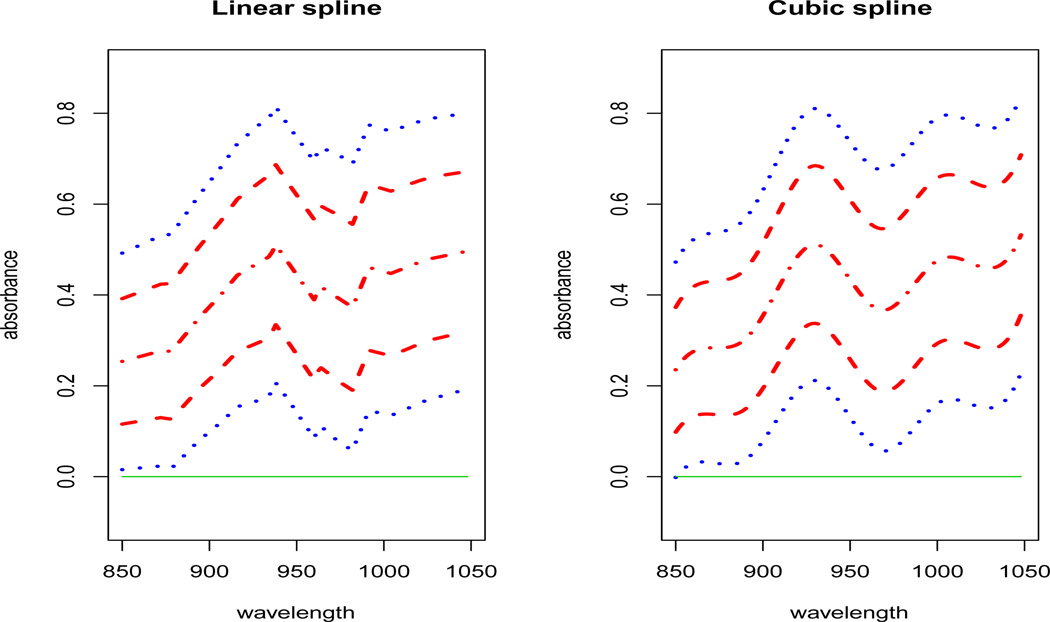
where m₁(x) and m₂(x) are the regression functions of absorbance on spectrum, for samples with fat content less than 20% and great than or equal to 20% respectively. Among 240 samples, there are n₁ = 155 with fat content less than 20%, the rest n₂ = 85 no less than 20%. The numbers of interior knots in (2) are computed as in Section 3 with c = 0.5 and are N_1m = 4 and N_2m = 3 for cubic spline fit and N_1m = 8 and N_2m = 6 for linear spline fit. Figure 4 depicts the linear and cubic spline confidence bands according to (15) at confidence levels 0.99 (upper and lower dashed lines) and 0.999995 (upper and lower dotted lines), with the center dashed-dotted line representing the spline estimator m̂₁(x)− m̂₂(x) and a solid line representing zero. Since even the 99.9995% confidence band does not contain the zero line entirely, the difference of low fat and high fat populations' absorbance was extremely significant. In fact, Figure 4 clearly indicates that the less the fat contained, the higher the absorbance is.

Figure 4.

Plots of the fitted linear and cubic spline regressions of m₁(x)−m₂(x) for the Tecator data (dashed-dotted line), 99% confidence bands (15) (upper and lower dashed lines), 99.9995% confidence bands (15) (upper and lower dotted lines) and the zero line (solid line).

APPENDIX

In this appendix, we use C to denote a generic positive constant unless otherwise stated.

A.1. Preliminaries

For any vector ζ = (ζ₁, …, ζ_s) ∈ R^s, denote the norm ‖ζ‖_r = (|ζ₁|^r + ⋯ + |ζ_s|^r)^1/r, 1 ≤ r < +∞, ‖ζ‖_∞ = max (|ζ₁|, …, |ζ_s|). For any s × s symmetric matrix A, we define λ_min (A) and λ_max (A) as its smallest and largest eigenvalues, and its L_r norm as ${\Vert \mathbf{A}\Vert }_r={\text{max}}_{\mathit{\zeta }\in R^s,\mathit{\zeta }\ne \mathbf{0}}{\Vert \mathbf{A}\mathit{\zeta }\Vert }_r{\Vert \mathit{\zeta }\Vert }_r^{-1}$. In particular, ‖A‖₂ = λ_max (A), and if A is also nonsingular, ${\Vert {\mathbf{A}}^{-1}\Vert }_2={\lambda }_{\text{min}}^{-1}(\mathbf{A})$.

For functions ϕ, φ ∈ L₂[0, 1], one denotes the theoretical and empirical inner products as $\langle \varphi ,\phi \rangle ={\displaystyle {\int }_0^1}\varphi (x)\phi (x)\mathit{\text{ dx and }}{\langle \varphi ,\phi \rangle }_{2,N}=N^{-1}{\displaystyle {\sum }_{j=1}^N}\varphi (j/N)\phi (j/N)$. The corresponding norms are ${\Vert \varphi \Vert }_2^2=\langle \varphi ,\varphi \rangle ,{\Vert \varphi \Vert }_{2,N}^2={\langle \varphi ,\varphi \rangle }_{2,N}$.

We state a strong approximation result, which is used in the proof of Lemma A.6.

Lemma A.1: [Theorem 2.6.7 of Csőrgő and Révész (1981)] Suppose that ξ_i, 1 ≤ i < ∞ are iid with E(ξ₁) = 0, $E({\xi }_1^2)=1$ and H(x) > 0 (x ≥ 0) is an increasing continuous function such that x^−2−γH(x) is increasing for some γ > 0 and x⁻¹logH(x) is decreasing with EH (|ξ₁|) < ∞. Then there exist constants C₁, C₂, a > 0 which depend only on the distribution of ξ₁ and a sequence of Brownian motions ${\{W_n(l)\}}_{n=1}^{\mathrm{\infty }}$, such that for any ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ satisfying H⁻¹ (n) < x_n < C₁ (nlogn)^1/2 and $S_l={\displaystyle {\sum }_{i=1}^l}{\xi }_i$

$$P\left\{\underset{1\le l\le n}{\text{max}}|S_l-W_n(l)|>x_n\right\}\le C_{2}n{\{H({\mathit{\text{ax}}}_n)\}}^{-1}.$$

The next lemma is a special case of Theorem 13.4.3, Page 404 of DeVore and Lorentz (1993). Let p be a positive integer, a matrix A = (a_ij) is said to have bandwidth p if a_ij = 0 when |i − j| ≥ p, and p is the smallest integer with this property.

Lemma A.2: If a matrix A with bandwidth p has an inverse A⁻¹ and d = ‖A‖₂‖A⁻¹‖₂ is the condition number of A, then ‖A⁻¹‖_∞ ≤ 2c₀ (1 − η)⁻¹, with c₀ = ν^−2p‖A⁻¹‖₂, η = ((d² − 1)/(d² + 1))^1/(4p).

One writes ${\mathbf{X}}^{\mathrm{T}}\mathbf{X}=N{\widehat{\mathbf{V}}}_p,{\mathbf{X}}^{\mathrm{T}}\mathbf{Y}={\{{\displaystyle {\sum }_{j=1}^N}{B}_{J,p}(j/N){\overline{Y}}_{.j}\}}_{J=1-p}^{N_m}$, where the theoretical and empirical inner product matrices of ${\{B_{J,p}(x)\}}_{J=1-p}^{N_m}$ are denoted as

$${\mathbf{V}}_p={(\langle B_{J,p,}{B}_{J\prime ,p}\rangle )}_{J,J\prime =1-p}^{N_m},{\widehat{\mathbf{V}}}_p={\left({\langle B_{J,p,}{B}_{J\prime ,p}\rangle }_{2,N}\right)}_{J,J\prime =1-p}^{N_m}.$$ (A.1)

We establish next that the theoretical inner product matrix V_p defined in (A.1) has an inverse with bounded L_∞ norm.

Lemma A.3: For any positive integer p, there exists a constant M_p > 0 depending only on p, such that ${\Vert {\mathbf{V}}_p^{-1}\Vert }_{\mathrm{\infty }}\le M_p{h}_m^{-1}$, where h_m = (N_m + 1)⁻¹.

Proof. According to Lemma A.1 in Wang and Yang (2009b), V_p is invertible since it is a symmetric matrix with all eigenvalues positive, i.e. $0<c_p{N}_m^{-1}\le {\lambda }_{\text{min }}({\mathbf{V}}_p)\le {\lambda }_{\text{max }}({\mathbf{V}}_p)\le C_p{N}_m^{-1}<\mathrm{\infty }$, where c_p and C_p are positive real numbers. The compact support of B-spline basis makes V_p of bandwidth p, hence one can apply Lemma A.2. Since d_p = λ_max (V_p) /λ_min (V_p) ≤ C_p/c_p, hence

$${\eta }_p={(d_p^2-1)}^{1/4p}{(d_p^2+1)}^{-1/4p}\le {(C_p^2{c}_p^{-2}-1)}^{1/4p}{(C_p^2{c}_p^{-2}+1)}^{-1/4p}<1.$$

If p = 1, then ${\mathbf{V}}_p^{-1}=h_m^{-1}{\mathbf{I}}_{N_m+p}$, the lemma holds with M_p = 1. If p > 1, let ${\mathbf{u}}_{1-p}={\left(1,{\mathbf{0}}_{N_m+p-1}^{\mathrm{T}}\right)}^{\mathrm{T}},{\mathbf{u}}_0={\left({\mathbf{0}}_{p-1}^{\mathrm{T}},1,{\mathbf{0}}_{N_m}^{\mathrm{T}}\right)}^{\mathrm{T}}$, then ‖u_1−p‖₂ = ‖u₀‖₂ = 1. Also lemma A.1 in Wang and Yang (2009b) implies that

$$\begin{array}{cc}{\lambda }_{\text{min}}({\mathbf{V}}_p)\hfill & ={\lambda }_{\text{min}}({\mathbf{V}}_p){\Vert {\mathbf{u}}_{1-p}\Vert }_2^2\le {\mathbf{u}}_{1-p}^{\mathrm{T}}{\mathbf{V}}_p{\mathbf{u}}_{1-p}={\Vert B_{1-p,p}\Vert }_2^2,\hfill \\ \hfill {\mathbf{u}}_0^{\mathrm{T}}{\mathbf{V}}_p{\mathbf{u}}_0& ={\Vert B_{0,p}\Vert }_2^2\le {\lambda }_{\text{max}}({\mathbf{V}}_p){\Vert {\mathbf{u}}_0\Vert }_2^2={\lambda }_{\text{max}}({\mathbf{V}}_p),\hfill \end{array}$$

hence $d_p={\lambda }_{\text{max }}({\mathbf{V}}_p)/{\lambda }_{\text{min }}({\mathbf{V}}_p)\ge {\Vert B_{0,p}\Vert }_2^2{\Vert B_{1-p,p}\Vert }_2^{-2}=r_p>1$ where r_p is an absolute constant depending only on p. Thus ${\eta }_p={(d_p^2-1)}^{\frac{1}{4p}}{(d_p^2+1)}^{-\frac{1}{4p}}\ge {(r_p^2-1)}^{\frac{1}{4p}}{(r_p^2+1)}^{-\frac{1}{4p}}>0$. Applying Lemma A.2 and putting the above bounds together, one obtains

$${\Vert {\mathbf{V}}_p^{-1}\Vert }_{\mathrm{\infty }}{h}_m\le 2{\eta }_p^{-2p}{\Vert {\mathbf{V}}_p^{-1}\Vert }_2{(1-{\eta }_p)}^{-1}{h}_m\le 2{\left(\frac{r_p^2+1}{r_p^2-1}\right)}^{1/2}{\lambda }_{\text{min}}^{-1}({\mathbf{V}}_p)\times {\left\{1-{\left(\frac{C_p^2{c}_p^{-2}-1}{C_p^2{c}_p^{-2}+1}\right)}^{1/4p}\right\}}^{-1}{h}_m\le 2{\left(\frac{r_p^2+1}{r_p^2-1}\right)}^{1/2}{c}_p^{-1}{\left\{1-{\left(\frac{C_p^2{c}_p^{-2}-1}{C_p^2{c}_p^{-2}+1}\right)}^{1/4p}\right\}}^{-1}\equiv M_p.$$

The lemma is proved.

For any function ϕ ∈ C [0, 1], denote the vector ϕ = (ϕ (1/N), …, ϕ (N/N))^T and function

$$\tilde{\varphi }(x)\equiv \{B_{1-p,p}(x),\dots ,B_{N_m,p}(x)\}{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}\varphi .$$

Lemma A.4: Under Assumption (A3), for V_p and V̂p defined in (A.1), ‖V_p − V̂_p‖_∞ = O (N⁻¹) and ${\Vert {\widehat{\mathbf{V}}}_p^{-1}\Vert }_{\mathrm{\infty }}\le 2h_m^{-1}$. There exists c_ϕ,p ∈ (0,∞) such that when n is large enough, ‖ϕ̃‖_∞≤ c_ϕ,p ‖ϕ‖_∞ for any ϕ ∈ C [0, 1]. Furthermore, if ϕ ∈ C^p−1,μ [0, 1] for some μ ∈ (0, 1], then for C̃_p−1,μ = (c_ϕ,p + 1)C_p−1,μ

$${\Vert \tilde{\varphi }-\varphi \Vert }_{\mathrm{\infty }}\le {\tilde{C}}_{p-1,\mu }{\Vert {\varphi }^{(p-1)}\Vert }_{0,\mu }{h}_m^{\mu +p-1}.$$ (A.2)

Proof. We first show that ‖V_p−V̂_p‖_∞ = O (N⁻¹). In the case of p = 1, define for any 0 ≤ J ≤ N_m, the number of design points j/N in the J-th interval I_J as N_J, then

$$N_J=\{\begin{array}{c}\#\{j:j\in [\mathit{\text{NJ}}/(N_m+1),N(J+1)/(N_m+1))\},0\le J<N_m\hfill \\ \#\{j:j\in [\mathit{\text{NJ}}/(N_m+1),N(J+1)/(N_m+1)]\},J=N_m\hfill \end{array}.$$

Clearly max_0≤J≤Nm |N_J − Nh_m| ≤ 1 and hence

$${\Vert {\mathbf{V}}_1-{\widehat{\mathbf{V}}}_1\Vert }_{\mathrm{\infty }}=\underset{0\le J\le N_m}{\text{max}}\left|{\Vert B_{J,1}\Vert }_{2,N}^2-{\Vert B_{J,1}\Vert }_2^2\right|=\underset{0\le J\le N_m}{\text{max}}\left|N^{-1}{\displaystyle {\sum }_{j=1}^N}{B}_{J,1}^2(j/N)-h_m\right|=\underset{0\le J\le N_m}{\text{max}}|N^{-1}{N}_J-h_m|=N^{-1}\underset{0\le J\le N_m}{\text{max}}|N_J-{\mathit{\text{Nh}}}_m|\le N^{-1}.$$

For p > 1, de Boor (2001), Page 96, B-spline property ensures that there exists a constant C_1,p > 0 such that

$$\underset{1-p\le J,J\prime \le N_m}{\text{max}}\underset{1\le j\le N}{\text{max}}\underset{x\in [(j-1)/N,j/N]}{\text{sup}}|B_{J,p}(j/N)B_{J\prime ,p}(j/N)-B_{J,p}(x)B_{J\prime ,p}(x)|\le C_{1,p}{N}^{-1}{h}_m^{-1},$$

while there exists a constant C_2,p > 0 such that max_{1−p≤J,J′≤Nm} N_J,J′≤C_2,pNh_m where N_J,J′ = #{j : 1 ≤ j ≤ N,B_J,p (j/N)B_J′,p (j/N) > 0}. Hence

$${\Vert {\mathbf{V}}_p-{\widehat{\mathbf{V}}}_p\Vert }_{\mathrm{\infty }}=\underset{1-p\le J,J\prime \le N_m}{\text{max}}\left|N^{-1}{\displaystyle {\sum }_{j=1}^N}{B}_{J,p}(j/N)B_{J\prime ,p}(j/N)-{\displaystyle {\int }_0^1}{B}_{J,p}(x)B_{J\prime ,p}(x)\mathit{\text{dx}}\right|\le \underset{1-p\le J,J\prime \le N_m}{\text{max}}{\displaystyle {\sum }_{j=1}^N}{\displaystyle {\int }_{(j=1)/N}^{j/N}}|B_{J,p}(j/N)B_{J\prime ,p}(j/N)-B_{J,p}(x)B_{J\prime ,p}(x)|\mathit{\text{dx}}\le C_{2,p}{\mathit{\text{Nh}}}_m\times N^{-1}\times C_{1,p}{N}^{-1}{h}_m^{-1}\le {\mathit{\text{CN}}}^{-1}.$$

According to Lemma A.3, for any (N_m + p) vector γ,${\Vert {\mathbf{V}}_p^{-1}\mathit{\gamma }\Vert }_{\mathrm{\infty }}\le h_m^{-1}{\Vert \mathit{\gamma }\Vert }_{\mathrm{\infty }}$. Hence, ‖V_pγ‖_∞ ≥ h_m ‖γ‖_∞ : By Assumption (A3), N⁻¹ = o (h_m) so if n is large enough, for any γ, one has

$${\Vert {\widehat{\mathbf{V}}}_p\mathit{\gamma }\Vert }_{\mathrm{\infty }}\ge {\Vert {\mathbf{V}}_p\mathit{\gamma }\Vert }_{\mathrm{\infty }}-{\Vert {\mathbf{V}}_p\mathit{\gamma }-{\widehat{\mathbf{V}}}_p\mathit{\gamma }\Vert }_{\mathrm{\infty }}\ge h_m{\Vert \mathit{\gamma }\Vert }_{\mathrm{\infty }}-O(N^{-1}){\Vert \mathit{\gamma }\Vert }_{\mathrm{\infty }}=\frac{h_m}{2}{\Vert \mathit{\gamma }\Vert }_{\mathrm{\infty }}.$$

Hence ${\Vert {\widehat{\mathbf{V}}}_p^{-1}\Vert }_{\mathrm{\infty }}\le 2h_m^{-1}$.

To prove the last statement of the lemma, note that for any x ∈ [0, 1] at most (p + 1) of the numbers B_1−p,p (x), …, B_Nm,p (x) are between 0 and 1, others being 0, so

$$\left|\tilde{\varphi }(x)\right|\le (p+1)\left|{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}\varphi \right|=(p+1)\left|{\widehat{\mathbf{V}}}_p^{-1}\left({\mathbf{X}}^{\mathrm{T}}\varphi N^{-1}\right)\right|\le (p+1){\Vert {\widehat{\mathbf{V}}}_p^{-1}\Vert }_{\mathrm{\infty }}\left|{\mathbf{X}}^{\mathrm{T}}\varphi N^{-1}\right|\le 2(p+1)h_m^{-1}\left|{\mathbf{X}}^{\mathrm{T}}{\mathbf{I}}_N{N}^{-1}\right|{\Vert \varphi \Vert }_{\mathrm{\infty }}$$

in which I_N = (1, …, 1)^T. Clearly |X^TI_NN⁻¹|≤Ch_m for some C > 0, hence |ϕ̃(x)|≤ 2 (p + 1)C ‖ϕ‖_∞ = c_ϕ,p ‖ϕ‖_∞. Now if ϕ ∈ C^p−1,μ [0, 1] for some μ ∈ (0, 1], let g ∈ ℋ^(p−1) [0, 1] be such that ${\Vert g-\varphi \Vert }_{\infty }\le C_{p-1,\mu }{\Vert {\varphi }^{(p-1)}\Vert }_{0,\mu }{h}_m^{\mu +p-1}$ according to Theorem 3.1, then g̃ ≡ g as g ∈ ℋ^(p−1) [0, 1] hence

$${\Vert \tilde{\varphi }-\varphi \Vert }_{\mathrm{\infty }}={\Vert \tilde{\varphi }-\tilde{g}-(\varphi -g)\Vert }_{\mathrm{\infty }}\le {\Vert \tilde{\varphi }-\tilde{g}\Vert }_{\mathrm{\infty }}+{\Vert \varphi -g\Vert }_{\mathrm{\infty }}\le (c_{\varphi ,p}+1){\Vert \varphi -g\Vert }_{\mathrm{\infty }}\le (c_{\varphi ,p}+1)C_{p-1,\mu }{\Vert {\varphi }^{(p-1)}\Vert }_{0,\mu }{h}_m^{\mu +p-1}$$

proving (A.2).

Lemma A.5: Under Assumption (A5), for $C_0=C_1(1+\beta C_2{\displaystyle {\sum }_{s=1}^{\mathrm{\infty }}}{s}^{\beta -1-{\gamma }_1})$ and n ≥ 1

$$\underset{1\le k\le \kappa }{\text{max}}E\left|{\overline{\xi }}_{.,k}-{\overline{Z}}_{.k,\xi }\right|\le C_0{n}^{\beta -1},$$ (A.3)

$$\underset{1\le j\le N}{\text{max}}\left|{\overline{\epsilon }}_{.,j}-{\overline{Z}}_{.j,\epsilon }\right|=O_{a.s.}\left(n^{\beta -1}\right)$$ (A.4)

where ${\overline{Z}}_{.k,\xi }=n^{-1}{\displaystyle {\sum }_{i=1}^n}{Z}_{\mathit{\text{ik}},\xi },{\overline{Z}}_{.j,\epsilon }=n^{-1}{\displaystyle {\sum }_{i=1}^n}{Z}_{\mathit{\text{ij}},\epsilon },1\le j\le N,1\le k\le \kappa$. Also

$$\underset{1\le k\le \kappa }{\text{max}}E\left|{\overline{\xi }}_{.,k}\right|\le n^{-1/2}{(2/\pi )}^{1/2}+C_0{n}^{\beta -1}.$$ (A.5)

Proof. The proof of (A.4) is trivial. Assumption (A5) entails that F̄_n+t,k < C₂ (n + t)^−γ₁, k = 1, …, κ, t = 0, 1, …, ∞, in which ${\overline{F}}_{n+t,k}=P\left[|{\displaystyle {\sum }_{i=1}^n}{\xi }_{\mathit{\text{ik}}}-{\displaystyle {\sum }_{i=1}^n}{Z}_{\mathit{\text{ik}},\xi }|>C_1{(n+t)}^{\beta }\right]$. Taking expectation, one has

$$E\left|{\displaystyle {\sum }_{i=1}^n}{\xi }_{\mathit{\text{ik}}}-{\displaystyle {\sum }_{i=1}^n}{Z}_{\mathit{\text{ik}},\xi }\right|\le C_1{(n+0)}^{\beta }+{\displaystyle {\sum }_{t=1}^{\mathrm{\infty }}}{C}_1{(n+t)}^{\beta }({\overline{F}}_{n+t-1,k}-{\overline{F}}_{n+t,k})\le C_1{n}^{\beta }+{\displaystyle {\sum }_{t=0}^{\mathrm{\infty }}}{C}_1{C}_2{(n+t)}^{-{\gamma }_1}\beta {(n+t)}^{\beta -1}\le C_1\{n^{\beta }+\beta C_2{\displaystyle {\sum }_{t=0}^{\mathrm{\infty }}}{(n+t)}^{\beta -1-{\gamma }_1}\}\le n^{\beta }{C}_1[1+\beta C_2{n}^{-1-{\gamma }_1}{\displaystyle {\sum }_{s=1}^{\mathrm{\infty }}}{\displaystyle {\sum }_{t=\mathit{\text{sn}}-n}^{\mathit{\text{sn}}-1}}{(1+t/n)}^{\beta -1-{\gamma }_1}]\le n^{\beta }{C}_1[1+\beta C_2{n}^{-1-{\gamma }_1}\times n{\displaystyle {\sum }_{t=1}^{\mathrm{\infty }}}{t}^{\beta -1-{\gamma }_1}]\le C_0{n}^{\beta },$$

which proves (A.3) if one divides the above inequalities by n. The fact that Z̄_,k,ξ ~ N (0, 1/n) entails that E |Z̄_.k,ξ| = n^−1/2 (2/π)^1/2 and thus max_1≤k≤κE|ξ̄_.,k|≤ n^−1/2 (2/π)^1/2 + C₀n^β−1.

Lemma A.6: Assumption (A5) holds under Assumption (A5’).

Proof. Under Assumption (A5’), E |ξ_ik|^η₁ < +∞, η₁ > 4, E |ε_ij |^η₂ < +∞, η₂ > 4+2θ, so there exists some β ∈ (0, 1/2) such that η₁ > 2/β, η₂ > (2 + θ) /β.

Now let H(x) = x^η₁, then Lemma A.1 entails that there exists constants C_1k, C_2k, a_k which depend on the distribution of ξ_ik, such that for $x_n=C_{1k}{n}^{\beta },\frac{n}{H(a_k{x}_n)}=a_k^{-{\eta }_1}{C}_{1k}^{-{\eta }_1}{n}^{1-{\eta }_1\beta }$ and iid N(0, 1) variables Z_ik,ξ such that

$$P[\underset{1\le t\le n}{\text{max}}\left|{\displaystyle {\sum }_{i=1}^t}{\xi }_{\mathit{\text{ik}}}-{\displaystyle {\sum }_{i=1}^t}{Z}_{\mathit{\text{ik}},\xi }\right|>C_{1k}{n}^{\beta }]<C_{2k}{a}_k^{-{\eta }_1}{C}_{1k}^{-{\eta }_1}{n}^{1-{\eta }_1\beta }.$$

Since η₁ > 2/β, γ₁ = η₁β − 1 > 1. If the number κ of k is finite, so there are common constants C₁,C₂ > 0 such that $P[{\text{max}}_{1\le t\le n}|{\displaystyle {\sum }_{i=1}^t}{\xi }_{\mathit{\text{ik}}}-{\displaystyle {\sum }_{i=1}^t}{Z}_{\mathit{\text{ik}},\xi }|>C_1{n}^{\beta }]<C_2{n}^{-{\gamma }_1}$ which entails (3) since κ is finite. If κ is infinite but all the ξ_ik's are iid, then C_1k, C_2k, a_k are the same for all k, so the above is again true.

Likewise, under Assumption (A5’), if one lets H(x) = x^η₂, Lemma A.1 entails that there exists constants C₁, C₂, a which depend on the distribution of ξ_ij, such that for $x_n=C_1{n}^{\beta },\frac{n}{H(a_k{x}_n)}=a^{-{\eta }_2}{C}_1^{-{\eta }_2}{n}^{1-{\eta }_2\beta }$ and iid N(0, 1) variables Z_ij,ε such that

$$\underset{1\le j\le N}{\text{max}}P\{\underset{1\le t\le N}{\text{max}}\left|{\displaystyle {\sum }_{i=1}^t}{\epsilon }_{\mathit{\text{ij}}}-{\displaystyle {\sum }_{i=1}^t}{Z}_{\mathit{\text{ij}},\epsilon }\right|>C_1{n}^{\beta }\}\le C_2{a}^{-{\eta }_2}{C}_1^{-{\eta }_2}{n}^{1-{\eta }_2\beta },$$

now η₂β > 2+θ implies that there is γ₂ > 1 such that η₂β −1 > γ₂ +θ and (4) follows.

Proof of Proposition 3.2. Applying (A.2), ${\Vert {\tilde{m}}_p-m\Vert }_{\mathrm{\infty }}\le C_{p-1,1}{h}_m^p$. Since Assumption (A3) implies that $O(h_m^p{n}^{1/2})=o(1)$, equation (10) is proved.

Proof of Proposition 3.3.

Denote by Z̃_p,ε (x) = {B_1−p,p (x), …, B_Nm,p (x)} (X^TX)⁻¹X^T Z, where Z = (σ (1/N) Z̄_.1,ε, …, σ (N/N) Z̄_.N,ξ)^T. By (A.4), one has ‖Z − e‖_∞ = O_a.s.(n^β−1), while

$${\Vert N^{-1}{\mathbf{X}}^{\mathrm{T}}(\mathbf{Z}-\mathbf{e})\Vert }_{\mathrm{\infty }}\le {\Vert \mathbf{Z}-\mathbf{e}\Vert }_{\mathrm{\infty }}\underset{1-p\le J\le N_m}{\text{max}}{\langle B_{J,p},1\rangle }_{2,N}\le C{\Vert \mathbf{Z}-\mathbf{e}\Vert }_{\mathrm{\infty }}\underset{1-p\le J\le N_m}{\text{max}}\#\{j:B_{J,p}(j/N)>0\}{N}^{-1}\le C{\Vert \mathbf{Z}-\mathbf{e}\Vert }_{\mathrm{\infty }}{h}_m.$$

Also for any fixed x ∈ [0, 1], one has

$${\Vert {\tilde{\mathbf{Z}}}_{p,\epsilon }(x)-{\tilde{e}}_p(x)\Vert }_{\mathrm{\infty }}={\Vert \{B_{1-p,p}(x),\dots ,B_{N_m,p}(x)\}{\widehat{\mathbf{V}}}_p^{-1}{N}^{-1}{\mathbf{X}}^{\mathrm{T}}(\mathbf{Z}-\mathbf{e})\Vert }_{\mathrm{\infty }}\le C{\Vert {\widehat{\mathbf{V}}}_p^{-1}\Vert }_{\mathrm{\infty }}{\Vert \mathbf{Z}-\mathbf{e}\Vert }_{\mathrm{\infty }}{h}_m=O_{a.s.}(n^{\beta -1}).$$

Note next that the random vector ${\widehat{\mathbf{V}}}_p^{-1}{N}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{Z}\text{ is }(N_m+p)$-dimensional normal with covariance matrix $N^{-2}{\widehat{\mathbf{V}}}_p^{-1}{\mathbf{X}}^{\mathrm{T}}\text{var }(\mathbf{Z})\mathbf{X}{\widehat{\mathbf{V}}}_p^{-1}$, bounded above by

$$\underset{x\in [0,1]}{\text{max}}{\sigma }^2(x){\Vert n^{-1}{N}^{-1}{\widehat{\mathbf{V}}}_p^{-1}{\widehat{\mathbf{V}}}_p{\widehat{\mathbf{V}}}_p^{-1}\Vert }_{\mathrm{\infty }}\le {\mathit{\text{CN}}}^{-1}{n}^{-1}{\Vert {\widehat{\mathbf{V}}}_p^{-1}\Vert }_{\mathrm{\infty }}\le {\mathit{\text{CN}}}^{-1}{n}^{-1}{h}_m^{-1},$$

bounding the tail probabilities of entries of ${\widehat{\mathbf{V}}}_p^{-1}{N}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{Z}$ and applying Borel-Cantelli Lemma leads to

$${\Vert {\widehat{\mathbf{V}}}_p^{-1}{N}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{Z}\Vert }_{\mathrm{\infty }}=O_{a.s.}(N^{-1/2}{n}^{-1/2}{h}_m^{-1/2}{\text{log}}^{1/2}(N_m+p))=O_{a.s.}\left(N^{-1/2}{n}^{-1/2}{h}_m^{-1/2}{\text{log}}^{1/2}n\right).$$

Hence, ${\text{sup}}_{x\in [0,1]}|n^{1/2}{\tilde{\mathbf{Z}}}_{p,\epsilon }(x)|=O_{a.s.}\left(N^{-1/2}{h}_m^{-1/2}{\text{log}}^{1/2}n\right)$ and

$$\underset{x\in [0,1]}{\text{sup}}\left|n^{1/2}{\tilde{e}}_p(x)\right|=O_{a.s.}(n^{\beta -1/2}+N^{-1/2}{h}_m^{-1/2}{\text{log}}^{1/2}n)=o_{a.s.}(1).$$

Thus (11) holds according to Assumption (A3).

Proof of Proposition 3.4.

We denote ζ̃_k(x) = Z̄_.k,ξϕ_k (x), k = 1, …, κ and define

$$\tilde{\zeta }(x)=n^{1/2}{\left[{\displaystyle {\sum }_{k=1}^{\kappa }}{\{{\varphi }_k(x)\}}^2\right]}^{-1/2}{\displaystyle {\sum }_{k=1}^{\kappa }}{\tilde{\zeta }}_k(x)=n^{1/2}G{(x,x)}^{-1/2}{\displaystyle {\sum }_{k=1}^{\kappa }}{\tilde{\zeta }}_k(x).$$

It is clear that ζ̃ (x) is a Gaussian process with mean 0, variance 1 and covariance Eζ̃ (x) ζ̃ (x′) = G(x, x)^−1/2 G(x, x′)^−1/2 G(x, x′), for any x, x′ ∈ [0, 1]. Thus ζ̃ (x), x ∈ [0, 1] has the same distribution as ζ (x), x ∈ [0, 1].

Using Lemma A.4, one obtains that

$${\Vert {\tilde{\varphi }}_k\Vert }_{\mathrm{\infty }}\le c_{\varphi ,p}{\Vert {\varphi }_k\Vert }_{\mathrm{\infty }},{\Vert {\tilde{\varphi }}_k-{\varphi }_k\Vert }_{\mathrm{\infty }}\le {\tilde{C}}_{0,\mu }{\Vert {\varphi }_k\Vert }_{0,\mu }{h}_m^{\mu },1\le k\le \kappa .$$ (A.6)

Applying the above (A.6), (A.5) and Assumptions (A3), (A4), one has

$${\mathit{\text{En}}}^{1/2}{\text{sup}}_{x\in [0,1]}G{(x,x)}^{-1/2}\left|{\displaystyle {\sum }_{k=1}^{\kappa }}{\overline{\xi }}_{.k}\{{\varphi }_k(x)-{\tilde{\varphi }}_k(x)\}\right|\le {\mathit{\text{Cn}}}^{1/2}\{{\displaystyle {\sum }_{k=1}^{{\kappa }_n}}E\left|{\overline{\xi }}_{.k}\right|{\Vert {\varphi }_k\Vert }_{0,\mu }{h}_m^{\mu }+{\displaystyle {\sum }_{k={\kappa }_n+1}^{\kappa }}E\left|{\overline{\xi }}_{.k}\right|{\Vert {\varphi }_k\Vert }_{\mathrm{\infty }}\}\le C\{{\displaystyle {\sum }_{k=1}^{{\kappa }_n}}{\Vert {\varphi }_k\Vert }_{0,\mu }{h}_m^{\mu }+{\displaystyle {\sum }_{k={\kappa }_n+1}^{\kappa }}{\Vert {\varphi }_k\Vert }_{\mathrm{\infty }}\}=o(1),$$

hence

$$n^{1/2}{\text{sup}}_{x\in [0,1]}G{(x,x)}^{-1/2}\left|{\displaystyle {\sum }_{k=1}^{\kappa }}{\overline{\xi }}_{.k}\{{\varphi }_k(x)-{\tilde{\varphi }}_k(x)\}\right|=o_P(1).$$ (A.7)

In addition, (A.3) and Assumptions (A3), (A4) entail that

$${\mathit{\text{En}}}^{1/2}{\text{sup}}_{x\in [0,1]}G{(x,x)}^{-1/2}\left|{\displaystyle {\sum }_{k=1}^{\kappa }}({\overline{Z}}_{.k,\xi }-{\overline{\xi }}_{.k}){\varphi }_k(x)\right|\le {\mathit{\text{Cn}}}^{\beta -1/2}{\displaystyle {\sum }_{k=1}^{\kappa }}{\Vert {\varphi }_k\Vert }_{\mathrm{\infty }}=o(1).$$

hence

$$n^{1/2}{\text{sup}}_{x\in [0,1]}G{(x,x)}^{-1/2}\left|{\displaystyle {\sum }_{k=1}^{\kappa }}({\overline{Z}}_{.k,\xi }-{\overline{\xi }}_{.k}){\varphi }_k(x)\right|=o_P(1).$$ (A.8)

Note that

$$\begin{array}{cc}\hfill \overline{m}(x)-m(x)-{\tilde{\xi }}_p(x)& ={\displaystyle {\sum }_{k=1}^{\kappa }}{\overline{\xi }}_{.k}\{{\varphi }_k(x)-{\tilde{\varphi }}_k(x)\},\hfill \\ \hfill n^{-1/2}G{(x,x)}^{1/2}\tilde{\zeta }(x)-\{\overline{m}(x)-m(x)\}& ={\displaystyle {\sum }_{k=1}^{\kappa }}({\overline{Z}}_{.k,\xi }-{\overline{\xi }}_{.k}){\varphi }_k(x)\hfill \end{array}$$

hence

$$\begin{array}{c}\hfill n^{1/2}\underset{x\in [0,1]}{\text{sup}}G{(x,x)}^{-1/2}\left|\overline{m}(x)-m(x)-{\tilde{\xi }}_p(x)\right|=o_P(1),\\ {\text{sup}}_{x\in [0,1]}\left|\tilde{\zeta }(x)-n^{1/2}G{(x,x)}^{-1/2}\{\overline{m}(x)-m(x)\}\right|=o_P(1).\hfill \end{array}$$

according to (A.7) and (A.8), which leads to both (12) and (13).