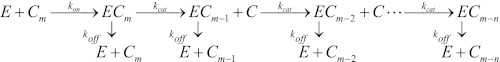Pre-steady-state Kinetics for Hydrolysis of Insoluble Cellulose by Cellobiohydrolase Cel7A

Background: The molecular understanding of factors that limit enzymatic hydrolysis of cellulose remains incomplete.

Results: Pre-steady-state analysis of cellulolytic activity provides rate constants for basic steps of the overall reaction.

Conclusion: Slow dissociation of inactive enzyme-cellulose complexes governs the hydrolytic rate at pseudo-steady state.

Significance: Kinetic constants elucidate molecular mechanisms and structure-function relationships for cellulases.

Abstract

The transient kinetic behavior of enzyme reactions prior to the establishment of steady state is a major source of mechanistic information, yet this approach has not been utilized for cellulases acting on their natural substrate, insoluble cellulose. Here, we elucidate the pre-steady-state regime for the exo-acting cellulase Cel7A using amperometric biosensors and an explicit model for processive hydrolysis of cellulose. This analysis allows the identification of a pseudo-steady-state period and quantification of a processivity number as well as rate constants for the formation of a threaded enzyme complex, processive hydrolysis, and dissociation, respectively. These kinetic parameters elucidate limiting factors in the cellulolytic process. We concluded, for example, that Cel7A cleaves about four glycosidic bonds/s during processive hydrolysis. However, the results suggest that stalling the processive movement and low off-rates result in a specific activity at pseudo-steady state that is 10–25-fold lower. It follows that the dissociation of the enzyme-substrate complex (half-time of ∼30 s) is rate-limiting for the investigated system. We suggest that this approach can be useful in attempts to unveil fundamental reasons for the distinctive variability in hydrolytic activity found in different cellulase-substrate systems.

Introduction

Kinetic analysis in the pre-steady-state regime is an important avenue to mechanistic understanding of enzyme action (1). In contrast to steady-state measurements, studies of this transient stage provide direct insight into fast (non-rate-limiting) steps of the catalytic cycle, and upon appropriate modeling, this may elucidate rate constants for basic steps of the overall enzymatic process. Pre-steady-state measurements have been widely used for different enzyme classes, including β-glycosyl hydrolases acting on soluble substrates and substrate analogs (2–5), but so far, no pre-steady-state investigations have addressed the activity of cellulases on their natural substrate, insoluble cellulose. Information of this type appears relevant for the molecular understanding of factors and processes that limit cellulase activity, particularly so in light of the extensive current efforts to develop better cellulolytic enzymes for the industrial breakdown of plant biomass.

The absence of pre-steady-state data is probably the result of the distinctive difficulties of working with cellulose as substrate, and we propose that there are three particular challenges that must be addressed. First, there is a scarcity of quantitative assay techniques, particularly real-time methods, that are sensitive and fast enough to monitor product accumulation in the brief pre-steady-state phase. Second, it has proven difficult to establish if and when steady state is reached for cellulolytic reactions and hence to identify the pre-steady-state period. Experimental investigations addressing time scales from seconds (6) to days (7) have shown gradually declining rates as the reaction progresses even if the substrate remains abundant. If a constant reaction rate is taken as a necessary (but not sufficient) criterion for steady state, this implies that enzymatic hydrolysis of insoluble cellulose may in fact never reach a steady state, and this is clearly a challenge for conventional pre-steady-state analyses. The third challenge is the requirement of an explicit model that specifies relevant steps of the process. Thus, explicit modeling of cellulolytic activity remains controversial, and most published models are not suitable for pre-steady-state analysis, as they address effects that occur later in the hydrolysis (e.g. product inhibition or substrate modification) and/or rely on steady-state assumptions as in Michaelis-Menten kinetics (see Ref. 8 for a recent review).

In this work, we address these three issues using the exo-acting cellulase Cel7A (formerly CBH1) from Trichoderma reesei and amorphous cellulose. Specifically, we have implemented a rapid continuous assay based on amperometric biosensors (9–11) and used this together with an explicit kinetic model (12). The results provide insight into the rates of separate reaction steps, including formation of a threaded enzyme complex, catalysis, and desorption.

EXPERIMENTAL PROCEDURES

Materials

We used T. reesei Cel7A (TrCel7A)² and regenerated amorphous cellulose (RAC) for comparisons with the comprehensive material published for this system. TrCel7A was obtained from a strain with deletion of the cel6A gene. Desalted and concentrated culture broth was purified by column chromatography as described previously (12). The purified enzyme showed a single band in SDS-PAGE (see supplemental data), and the absence of cellobiase activity was confirmed as the lack of detectable activity against the chromogenic substrate analog p-nitrophenyl β-d-glucopyranoside. RAC was prepared from Sigmacell 20 (Sigma) using a slight modification of the method of Zhang (13) as described elsewhere (14). The disappearance of the crystal C-4 peak in ¹³C cross-polarization/magic angle spinning NMR (14, 15) was interpreted as nearly completely amorphous substrate. All experiments were conducted in standard buffer with 50 mm sodium acetate and 2 mm CaCl₂ (pH 5.0).

Kinetics of Hydrolysis

The concentration of cellobiose was measured in real time with a benzoquinone-modified carbon paste electrode with surface-adsorbed and cross-linked cellobiose dehydrogenase from Phanerochaete chrysosporium. Preparation of biosensors and the electrochemical setup followed previously established principles (11) with some modifications as described in the supplemental data. Kinetic measurements were made on 5-ml RAC samples in a water-jacketed glass cell, which was temperature-controlled (Julabo F12 water bath) to 25.0 ± 0.1 °C and stirred at 600 rpm with a magnetic bar. Enzyme was injected from a Chemyx Fusion 100 syringe pump at variable rates so that the total injection time was always 1.0 s. The sensor was calibrated between each hydrolysis experiment by consecutive titration of 1–5-μl aliquots of 1 mm degassed cellobiose solution into the substrate suspension. All hydrolysis data were analyzed with respect to two “neighboring” calibrations and corrected for the background current. Cellobiose dehydrogenase is essentially inactive against the α-anomer (16, 17), and the sensor therefore specifically detects β-cellobiose (and the β-form of higher cello-oligosaccharides). TrCel7A is a retaining cellulase and therefore produces solely the β-anomer, and as the half-time of mutarotation is several hours at the temperature and pH used here (18, 19), the electrode signal can be used directly as a measure of hydrolytic activity in short (∼1 min) hydrolysis experiments. Conversely, mutarotation equilibrium has to be taken into account for the calibrations. To this end, we allowed a minimum of 24 h of equilibration of the standards and corrected their nominal concentration by the equilibrium composition (64.4% β-d-cellobiose at pH 5 and 24.8 °C) (18).

Kinetics of Adsorption

A standard quench-flow setup was made with two 20-ml syringes mounted in parallel in a Chemyx Fusion 100 syringe pump. The syringes contained 200 nm TrCel7A and 2 g/liter RAC suspension, respectively, in standard buffer supplemented with 0.1 g/liter BSA (95%; Sigma) and 50 ppm Triton X-100 (Sigma) to minimize nonspecific adsorption to the filter and tubing. To maintain a uniform suspension, the RAC sample was continuously stirred with a small magnetic bar inside the syringe. Flows of 0.375 ml/s from both syringes were combined in a mixing piece and aged as they moved down a piece of polytetrafluoroethylene tubing (1.5-mm inner diameter). Free and substrate-bound enzymes were separated in a filter (polyethersulfone syringe filter, 0.45-mm pore size, 0.25-cm diameter; Frisenette ApS, Knebel, Denmark) mounted at the end of the polytetrafluoroethylene tubing. To elucidate the early time course of adsorption, the concentration of free enzyme was determined in filtrates from continuous runs with different lengths of polytetrafluoroethylene tubing (covering 1–7 s of aging). For longer mixing times, the flow was stopped for the mixed sample to age in the tubing before restarting the pump and separating the sample by filtration.

Enzyme concentrations in the filtrates were determined from the activity against the synthetic substrate p-nitrophenyl lactocide (systematic name, 4-nitrophenyl β-d-lactopyranoside; Sigma). The procedure was a slight modification of the one used by Jalak and Väljamäe (20). To avoid inhibition by cellobiose, the filtrates were added 30 nm (final concentration) Aspergillus fumigatus β-glucosidase, cloned, and purified as described previously (21). 500 μl of filtrate was mixed with 55 μl of 5 mm p-nitrophenyl lactocide, incubated at 50 °C, and quenched after 3 h with 150 μl of 2 m Na₂CO₃. The concentration of product was determined by light adsorption at 410 nm, and the enzyme concentration was derived by comparisons with standard curves made daily, also with 30 nm A. fumigatus β-glucosidase. As in any quench-flow method, the “age” of the sample is determined by the length of the tubing. However, quenching by filtration poses the special challenge that the thickness of the filter cake increases with time (and hence, a disproportional amount of enzyme could be removed in the passage of the cake). To assess this, we measured the enzyme concentration in three consecutive samples (650 μl) retrieved during continuous flow, but no systematic changes in the enzyme concentration could be detected in these samples. We concluded that passage through the filter cake does not induce measurable changes in enzyme concentration for the dilute systems studied here and used the average of the three measurements in the analysis.

RESULTS

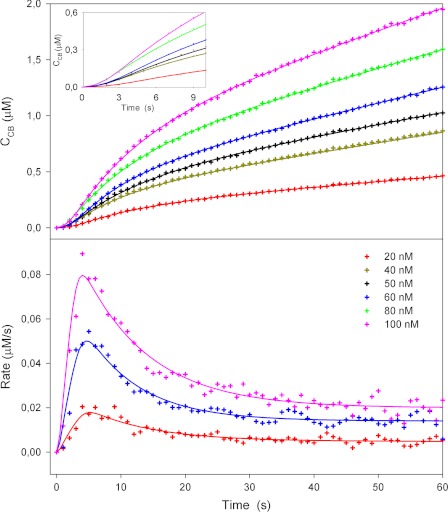
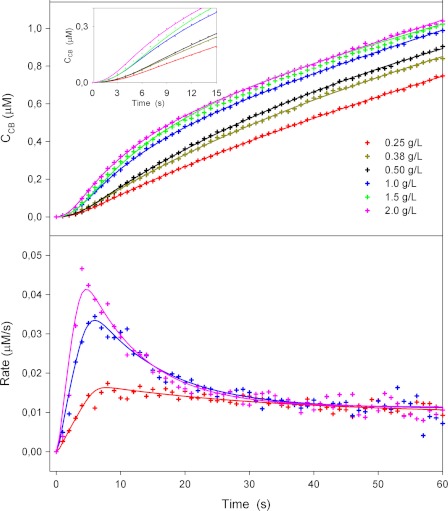
Figs. 1 and 2 show typical results from the biosensor measurements. In these series, the initial kinetics of TrCel7A was studied as a function of the load of enzyme (Fig. 1) and substrate (Fig. 2), respectively. Symbols represent experimental data, and lines are model fits discussed in detail below. The cellobiose concentrations measured directly with the cellobiose dehydrogenase electrode at 1-s intervals are in the upper panels of both figures, whereas the lower panels show the rates derived from the slope of the concentration traces. All results follow a general pattern of a rapid initial increase in the rate of hydrolysis with an apex at 5–8 s, followed by a conspicuous slowing down. For the higher substrate concentrations (>1 g/liter), the data in both figures show a 3-fold reduction in the reaction rate over just 20 s (from t = 5 s to t = 25 s). At lower cellulose concentrations (Fig. 2), this effect lessened, and the overshoot in reaction rate for 0.25 g/liter RAC was only slightly larger than the experimental noise. The location of the maximum in the reaction rate was independent of the enzyme concentration (4–5 s in Fig. 1) but shifted slightly to longer times when the RAC concentration was lowered (maximum at 8–9 s for 0.25 g/liter) (Fig. 2). The reaction rate scaled proportionally to the enzyme load when the concentration of RAC was constant (Fig. 1). Conversely, the rate of hydrolysis did not depend on the amount of substrate after the initial burst (∼20 s) in experiments with constant enzyme load (Fig. 2). The latter two observations together show that the substrate was in excess under the investigated conditions and hence that the reaction was limited by the amount of enzyme. We note that the maximal cellobiose concentration in these experiments was ∼2 μm. This is orders of magnitude lower than the cellobiose inhibition constant for TrCel7A hydrolyzing insoluble cellulose (22), and it is safe to assume that the kinetic behavior in Figs. 1 and 2 was unaffected by product inhibition.

FIGURE 1.

Hydrolysis of amorphous cellulose (2 g/liter RAC) by different concentrations of TrCel7A studied using cellobiose dehydrogenase biosensor. The upper panel shows measured cellobiose concentrations (symbols) as a function of time (enzyme injected into substrate at t = 0). The best fit of the kinetic model is indicated by the lines. The inset shows an enlargement of the first 10 s. In the lower panel, data for three enzyme concentrations are expressed as the rate of reaction (i.e. the slopes of the curves in the upper panel).

FIGURE 2.

Hydrolysis of amorphous cellulose at different concentrations by 50 nmTrCel7A. The upper and lower panels show the time dependence of the cellobiose concentration and the rate of reaction, respectively. The inset is an enlargement of the first 10 s of the concentration curve.

To analyze these results, we now turn to the two other issues raised in the Introduction. TrCel7A is a processive enzyme (i.e. it conducts several catalytic cycles without dissociation from one cellulose strand), and to model the temporal development of its activity, we previously proposed Reaction 1 (12).

REACTION 1.

In Reaction 1, the enzyme (E) first combines with a cellulose strand (C_m) to form a productive complex (EC_m), where the enzyme is “threaded” with the cellulose strand. This simplified description neglects that the association process is likely to include several distinguishable states. Such states were recently documented by Kostylev et al. (23), who showed that the most common form of the processive endoglucanase Cel9A in suspension with crystalline cellulose was adsorbed enzyme with an unoccupied active site. In contrast to this, Jalak and Väljamäe (20) found that for the system studied here (Cel7A and amorphous cellulose), adsorbed enzyme did not contribute measurably to the activity against a small soluble substrate. This suggests that adsorbed enzyme is predominantly threaded. In any case, this level of complexity (i.e. distinction of free and adsorbed unthreaded enzymes) is not readily captured by product accumulation data as in Figs. 1 and 2 because conversion between these states does not release product. It follows that k_on is a composite rate constant that specifies the rate of forming a threaded complex without providing separate information of these underlying steps. The catalytic cycle and dissociation are described by the first-order rate constants k_cat and k_off. Again, these are composite apparent rate constants that specify the kinetics of more steps. For k_cat, these steps include chain ablation from the substrate particle, chain relocation in the active tunnel, and product expulsion as discussed in detail by Beckham et al. (24). For simplicity, the rate constants are assumed to be independent of the length of the cellulose strand and the local environment of the scissile glycosidic bond. It follows that the parameters will define average values. The strand is initially composed of m cellobiose units, and it is assumed that an average of n units, counting from the attack point of the enzyme, is available for enzymatic hydrolysis. At the nth unit (i.e. when the strand has been reduced to a length of m-n cellobiose units), there is some kind of obstacle that prevents further processive movement, and the EC_m-n complex therefore has to dissociate before the enzyme can continue hydrolysis on a different strand. This model picture is in accord with recent experimental work on the processivity of TrCel7A (20, 25). The ordinary differential equations for Reaction 1 can be solved to obtain an expression for the time-dependent cellobiose concentration, C_CB(t), without resorting to any steady-state assumptions (see supplemental data).

The expression for C_CB(t) was fitted to the experimental data using nonlinear regression routines in Mathematica 8 (Wolfram Research, Champaign, IL). The simplest approach is to analyze each experimental curve separately, and results from this are illustrated in Figs. 1 and 2. It appears that the model accounts well for the measurements, and more importantly, the parameters obtained for different enzyme and substrate concentrations are consistent (Table 1), i.e. the model is able to account for variations in enzyme and substrate concentrations on the basis of a single set of parameters. To test the consistency of the regression procedure, particularly with respect to parameter dependence, we also implemented a global analysis approach in which all trials in a series with different enzyme concentrations were analyzed simultaneously in a three-dimensional space. The parameters derived from the global analysis were identical to those found in the simple analysis, and the parameter dependence was moderate in both cases (see supplemental data). We conclude that the molecular picture in Reaction 1 and a single set of parameters (Table 1) reproduce the experimental data well.

TABLE 1.

Maximum likelihood values for parameters in Reaction 1 based on analysis of all data in Figs. 1 and 2

Parameter	Value
kon (g/liter)−1 s−1)	0.06 ± 0.02
kcat (s−1)	4 ± 1
koff (s−1)	0.022 ± 0.005
n	13 ± 2

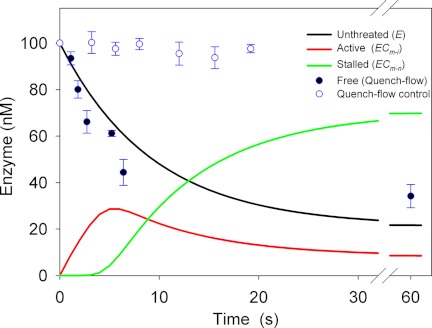
As shown in the supplemental data, the time-dependent distribution between the three states of enzyme in Reaction 1 may be calculated from the parameters in Table 1. An example of such a calculation (with 1 g/liter RAC and 100 nm enzyme) is shown in Fig. 3. The concentration of free enzyme was also measured experimentally by the quench-flow method, and these results are included in Fig. 3. The theoretical data show that the concentration of active enzyme (red line) increases over the first 5 s and reaches a maximum of ∼28 nm, i.e. less than one-third of the total enzyme pool. Around this stage (3–4 s), the first enzymes encounter an obstacle, which terminates their first processive run, and the population of the (slowly dissociating) inactive EC_m-n complex starts to build up (green line). As discussed above, the cellulase population denoted E in Reaction 1 comprises all unthreaded enzyme (i.e. both free and adsorbed/unthreaded), and its calculated time course (black line in Fig. 3) decreased to half of its initial value in ∼8 s. This theoretical value is comparable with the adsorption measurements, which showed a 50% reduction in free enzyme in 5 ± 2 s. The model predicts a steady-state condition after 30–40 s in which the concentrations of unthreaded, active, and stalled enzymes are 23, 10, and 67 nm, respectively. The value for unthreaded enzyme is in reasonable accord with 34 nm free TrCel7A found in the quench-flow experiments.

FIGURE 3.

Experimental adsorption data from quench-flow measurements (filled circles) and calculated concentrations of three enzyme species defined in Reaction 1 (lines). The experimental results are averages with error bars of 2 S.D. for duplicate measurements, and details of the calculations are given in the supplemental data. Open symbols show data from control experiments without substrate.

DISCUSSION

In the Introduction, we sketched out three issues (assay technology, modeling, and identification of steady state) that were particularly challenging for studies of the transient kinetics of cellulases hydrolyzing insoluble cellulose. Regarding the first, we found that the detection limit of the cellobiose dehydrogenase-based biosensor (∼25 nm) was low enough to monitor the pre-steady-state concentration range. The time resolution of the sensor (τ ∼ 1 s) was also sufficiently short to capture the initial time course, although a slight smearing of the burst phase may occur. Mathematical correction of this smearing suggested that it had a marginal effect on the values of k_on, k_off, and n but may cause an underestimation of k_cat. However, the magnitude of this effect was quite small and not critical for the current discussion (see supplemental data). The regression analysis showed that the reaction scheme in Reaction 1 accounted well for the measurements. Thus, a good fit to experimental data covering a broad range of enzyme (Fig. 1) and substrate (Fig. 2) loads was obtained with a single set of parameters (Table 1). Also, qualitative features in the experiments such as the disappearance of the initial burst at low substrate concentration and the mutual independence of the steady-state rate and the substrate load (Fig. 2) were captured well by the model. As discussed in more detail below, the parameters in Table 1 also compared favorably with independent experimental analysis of the different reaction steps. Regarding the last and possibly most important challenge (the question of steady state), we suggest that the linear range observed between ∼25 and 60 s in the concentration traces of Figs. 1 and 2 represents a pseudo-steady-state condition. Closer inspection shows that the slope of C_CB(t) does not become fully constant, and longer trials with the biosensor confirmed that the rate of hydrolysis decreased continuously (data not shown). We interpret this as a sign of a second inactivation process, which progresses much more slowly than the one defined in Reaction 1 (i.e. enzymes temporarily stalled in front of an obstacle). The mechanism underlying this slower inactivation is beyond the current scope, but a possible explanation could be irreversible adsorption to the substrate (26). The apparent rate constant for this slower inactivation is several orders of magnitude less than k_cat (12, 27), and it follows that only a negligible enzyme population will experience this over short experimental times as studied here. Therefore, a possible (pseudo-) steady state for TrCel7A and feasibly other cellulolytic enzymes should be sought not by waiting for the reaction rate to become as constant as possible, but in an intermediate time range. The lower boundary of this range is the time required to get a stable distribution of enzyme between the different free and bound states (cf. Fig. 3). The upper boundary is reached when an appreciable fraction of the enzyme has been inactivated by the slower process. Beyond this point, problems of describing the inactivated population will complicate model analyses. For the current system, these criteria appear to be largely fulfilled (to within the experimental errors) from ∼25 to 60 s, and we conclude that the transient kinetics of the RAC/TrCel7A system may be analyzed along the lines of Reaction 1 using ∼60-s biosensor measurements.

The concordance of model and experiment in Figs. 1 and 2 obviously supports the validity of the molecular picture in Reaction 1, but its suitability must also be tested against independent experimental assessments of one or more of the model parameters. One approach to this is to compare the populations of enzyme forms defined in Reaction 1 with results from adsorption measurements. As no earlier adsorption study has provided sufficient time resolution (∼1 s) to allow comparison with Figs. 1 and 2, we tested the adsorption using a novel quench-flow method. The results in Fig. 3 show that the unthreaded E form calculated from the kinetic model and the free enzyme measured directly by quench flow show similar time courses. This provides support of the kinetic picture in Reaction 1 and the parameters in Table 1, with the important caveat that that “free” enzyme is detected differently in the two approaches. Thus, adsorbed unthreaded enzyme will appear as bound in the quench-flow measurements (it is trapped in the filter), but as it is catalytically inactive, it will belong to the E form in Reaction 1 (see “Results”). This difference hampers comparisons in Fig. 3, but unlike earlier observations of much slower cellulase adsorption (28–31), the rapid decline in free enzyme found for this system (half-time of 3–5 s) is in line with the kinetic parameters in Table 1. Another test of the model is the comparison of the k_cat value derived here and in earlier kinetic studies of TrCel7A. Igarashi et al. used high-speed atomic force microscopy to show that TrCel7A moved at a rate of 3.5 ± 1.1 nm/s (32) to 7.1 ± 3.9 nm/s (33) on the surface of crystalline cellulose at ambient temperatures. As one cellobiose unit is 1.0 nm long, this corresponds to a turnover of 3.5–7.1 catalytic cycles/s, in excellent accord with k_cat in Table 1. Other studies have used biochemical assays to elucidate the initial kinetics of TrCel7A (20, 22, 25) and reported k_cat values of ∼2 s⁻¹. This is slightly lower than the value found here. This difference could rely on the inactive pool of bound enzyme (EC_m-n in Fig. 3), which is substantial even early in the hydrolysis. Väljamäe and co-workers used a combination of labeling and activity measurements to show that that the obstacle-free path was between 10 (20) and 21 (25) for the hydrolysis of amorphous cellulose by TrCel7A, and this also compares favorably with the n values found here. Like the present study, these latter works also emphasized that the dissociation rate constant (k_off) was much lower than k_cat and hence that release of stalled enzyme was the rate-limiting step for the hydrolysis. The value reported by Kurasin and Väljamäe (k_off = 0.0032 s⁻¹) (25) was somewhat lower that the off-rate constant found here. These comparisons support the view of an obstacle-based interpretation of the transient kinetics, although other contributions cannot be ruled out. Other origins of a rapid slowing down could be the depletion of particularly reactive substrates such as small cello-oligosaccharides or frayed cellulose ends. Such parameters appear, however, to be of minor importance for the current system, as injection of a second enzyme dose generates essentially the same burst as the first (see Ref. 12 and supporting information).

The molecular understanding of factors that limit enzymatic hydrolysis of cellulose remains incomplete (8, 34), and interest in this area has been strongly enhanced, as the enzymatic conversion of cellulosic biomass has been claimed to be a key industrial challenge for the 21st century (35). We suggest that analyses of the pre-steady-state regime provide one avenue to such information. For the specific system investigated here, we found that even at the peak of the burst phase (t ∼ 5 s), only about one-third of the enzyme population is hydrolytically active, and after a half-minute, when the system approaches pseudo-steady state, the active fraction has fallen to ∼10%. It follows that although the enzyme is capable of conducting about four catalytic cycles/s, the specific activity (i.e. the rate normalized with respect to the total enzyme concentration) at pseudo-steady state is over an order of magnitude lower (0.23 ± 0.02 s⁻¹ for the measurements in Fig. 2). The results also suggest that a half-minute into the reaction, the majority of the enzyme (∼70% of the total enzyme pool) is stalled on the insoluble substrate (EC_m-n in Fig. 3). It follows that the rate-limiting step is the dissociation of the EC_m-n complex, which in turn recruits free enzyme for the attack of a new cellulose strand. The (first-order) rate constant found here for the dissociation of EC_m-n was k_off = 0.022 s⁻¹ (Table 1), and this implies that the half-life of a stalled enzyme is ∼30 s, a time span in which an active enzyme produces >100 cellobiose molecules. This interim “parking” of cellulase in an inactive position is pertinent to the interpretation of specific activities for cellulases. Reported specific activities for Cel7A typically fall in the 0.1–1 s⁻¹ range (see Ref. 36 and references therein), and if the substrate is in excess, this is often taken as a measure of maximal turnover of the enzyme and is expressed as an “apparent k_cat.” The present results suggest that this specific activity relies on the output from a small population of active enzymes with a much higher turnover, whereas a larger population is inactive. If so, this clearly hampers mechanistic interpretations of specific activities measured at pseudo-steady state.

We conclude that the transient kinetics of TrCel7A can be studied by biosensor measurements and that a theory based on putative obstacles for processive movements accounts well for experimental data over a wide range of enzyme and substrate loads. Obstacle-based kinetic interpretations have been repeatedly suggested for cellobiohydrolases (12, 20, 25, 37–39) and recently also for processive endoglucanases (40), and the present results support the general validity of this approach. We emphasize, however, that obstacles have not yet been directly identified and that their structural origin remains obscure. It is also evident that at longer time scales, other mechanisms, including irreversible enzyme adsorption (26) and surface erosion (6), may contribute to the nonlinear kinetics consistently found for insoluble cellulose, and more detailed experimental information appears to be necessary to assess the relative importance of these parameters during continued hydrolysis. The current analysis provides insight into the kinetics of different steps underlying the hydrolytic reaction, including rapid steps that have little or no influence on product release rates at steady state. We found a rapid association and initiation of activity for TrCel7A and amorphous cellulose: at t ∼ 5 s, about half of the enzyme is adsorbed, and maximal activity is observed. Processive hydrolysis proceeds at a rate of about four glycosidic bonds/s, and the processive movement is terminated after an average of 13 steps. This is much less than the theoretical value, k_cat/k_off ≈ 180, which would be expected for an unhindered processive progression (Reaction 1), and we conclude that the movement is terminated by some morphological obstacle. A similar conclusion was reached on the basis of long-term (100 h) hydrolysis trials of crystalline cellulose (38). However, the latter work suggested that the hydrolysis was limited by a low on-rate. This is hard to reconcile with the observation of a pronounced maximum in the hydrolytic activity already after 5 s, and it appears that the rate-limiting step may shift as the hydrolysis progresses, perhaps as a result of substrate modifications. We found that the first enzymes encounter a hindrance a few seconds into the hydrolytic reaction, and as the off-rate is low, the population of stalled enzymes rapidly increases to ∼70%. This in turn drives the hydrolytic rate down, and after about a half-minute, it has fallen to a third or a fourth of its maximal value. Hence, the balance between rapid association and processive movement on one hand and slow dissociation of enzyme on the other is suggested to generate the distinctive burst in the activity seen in Figs. 1 and 2.