Beyond noise power in 3D computed tomography: The local NPS and off-diagonal elements of the Fourier domain covariance matrix

Abstract

Purpose: To investigate the correlation and stationarity of noise in volumetric computed tomography (CT) using the local discrete noise-power spectrum (NPS) and off-diagonal elements of the covariance matrix of the discrete Fourier transform of noise-only images (denoted Σ_DFT). Experimental conditions were varied to affect noise correlation and stationarity, the effects were quantified in terms of the NPS and Σ_DFT, and practical considerations in CT performance characterization were identified.

Methods: Cone-beam CT (CBCT) images were acquired using a benchtop system comprising an x-ray tube and flat-panel detector for a range of acquisition techniques (e.g., dose and x-ray scatter) and three phantom configurations hypothesized to impart distinct effects on the NPS and Σ_DFT: (A) air, (B) a 20-cm-diameter water cylinder with a bowtie filter, and (C) the cylinder without a bowtie filter. The NPS and off-diagonal elements of the Σ_DFT were analyzed as a function of position within the reconstructions.

Results: The local NPS varied systematically throughout the axial plane in a manner consistent with changes in fluence transmitted to the detector and view sampling effects. Variability in fluence was manifest in the NPS magnitude—e.g., a factor of ∼2 variation in NPS magnitude within the axial plane for case C (cylinder without bowtie), compared to nearly constant NPS magnitude for case B (bowtie filter matched to the cylinder). View sampling effects were most prominent in case A (air) where the variance increased at greater distance from the center of reconstruction and in case C (cylinder) where the NPS exhibited correlations in the radial direction. The effects of detector lag were observed as azimuthal correlation. The cylinder (without bowtie) had the strongest nonstationarity because of the larger variability in fluence transmitted to the detector. The diagonal elements of the Σ_DFT were equivalent to the NPS estimated from the periodogram, and the average off-diagonal elements of the Σ_DFT exhibited amplitude of ∼1% of the NPS for the experimental conditions investigated. Furthermore, the off-diagonal elements demonstrated fairly long tails of nearly constant amplitude, with magnitude somewhat reduced for experimental conditions associated with greater stationarity (viz., lower Σ_DFT tails for cases A and B in comparison to case C).

Conclusions: Volumetric CT exhibits nonstationarity in the NPS as hypothesized in relation to fluence uniformity and view sampling. Measurement of the NPS should seek to minimize such changes in noise correlations and include careful reporting of experimental conditions (e.g., phantom design and use of a bowtie filter) and spatial dependence (e.g., analysis at fixed radius within a phantom). Off-diagonal elements of the Σ_DFT similarly depend on experimental conditions and can be readily computed from the same data as the NPS. This work begins to check assumptions in NPS analysis examine the extent to which NPS is an appropriate descriptor of noise correlations, and investigate the magnitude of off-diagonal elements of the Σ_DFT. While the magnitude of such off-diagonal elements appears to be low, their cumulative effect on space-variant detectability remains to be investigated—e.g., using task-specific figures of merit.

INTRODUCTION

Characterization of image noise is critical in 3D x-ray computed tomography (CT) because the performance of many diagnostic tasks is governed by underlying image noise, which in turn is governed directly by the radiation dose to the patient. Since noise is reduced by increasing patient dose, characterizing the noise magnitude and correlations is important in choosing imaging techniques that minimize radiation dose while maintaining an acceptable noise level. There is a large body of research characterizing the noise in x-ray CT in two and three dimensions^{1, 2, 3, 4, 5, 6, 7, 8} both in the Fourier and the spatial domain, and standards for fully 3D NPS evaluation are rapidly evolving [for example, the American Association of Physicists in Medicine (AAPM) Task Group No. 169, “Measurements of the 3D Image Noise-Power Spectrum in Computed Tomography,”³⁹].

Proper characterization of the noise is an important step in task-based assessment of image quality^{9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19} since the dose should be appropriate to the clinical task for which the images are taken. Simple measures of the noise level (e.g., the standard deviation and the contrast-to-noise ratio) fail to account for the importance of noise correlation in clinical tasks. These correlations can be characterized under conditions of wide-sense stationarity (i.e., spatial invariance in the moments of the noise distribution) in the frequency domain using the noise-power spectrum (NPS) or in the spatial domain using the autocovariance function (ACF).

Images in 3D CT are nonstationary for reasons including the discrete nature of the reconstructed images, variable fluence in x-rays transmitted to the detector, angular sampling, detector defects, detector nonlinearity, etc. In this work, we investigate the changes imparted upon Fourier descriptors of the 3D image noise under experimental conditions purposely varied in a manner that affects such considerations. We restrict analysis in the current work to a volumetric “slab” 1.6 cm thick and centered on the central axial plane to minimize the effect of the “missing cone” at greater distance (z) from the central plane in cone-beam CT reconstructions from a circular trajectory. The missing cone is an important consideration in fully 3D CT and the subject of significant research.^{6, 20} It also presents yet another source of noise nonstationarity in cone-beam CT—viz., a null cone in the 3D spatial-frequency response that increases with greater distance from the central axial plane and precesses about the vertical (f_z) axis as a function of (f_x, f_y), where (f_x, f_y, f_z) are Fourier domain coordinates. Nonstationarity in z is important because the fully 3D noise characteristics [i.e., the NPS(f_x, f_y, f_z)] are expected to reflect the missing cone in 3D filtered backprojection from a circular source-detector trajectory, but emphasis herein is on the factors affecting noise stationarity that are more physically intrinsic to photon statistics, system configuration, and a finite number of projections, with focus on analysis of 3D noise characteristics near the central axial plane.

Common methods for evaluating CT image noise in the Fourier domain typically compute the location-averaged NPS. The NPS can be interpreted as the variance of the Fourier coefficients of the noise. These variance terms are the diagonal components of the covariance matrix of the discrete Fourier transform of “noise-only” images (denoted as Σ_DFT).^{13, 21, 22, 23, 24} In this work, we conduct an experimental study in which different phantoms were imaged to explore both the spatial variability of the local 3D NPS as well as the magnitude of the off-diagonal elements of the Σ_DFT which are typically ignored. We emphasize analysis in real physical phantoms under various imaging conditions to identify practical implications of noise characterization for engineers and practicing medical physicists for whom noise and NPS analysis are increasingly part of system development, acceptance testing, and quality assurance (QA) in CT. The motivation for this work comes from the need both to understand how the local NPS varies in space and to investigate the off-diagonal elements of the covariance matrix of the discrete Fourier transform which are typically ignored by the current methodology. The latter begins to answer a long-standing challenge²⁴ to check assumptions regarding the extent to which NPS represents an appropriate noise characterization and to examine the Σ_DFT more completely (not just the diagonal) in characterizing image noise.

THEORY

Definitions

In the characterization of noise from real measurements, it is important to clearly define what is meant by “noise.” A reasonable definition of noise is the component of the data that change stochastically when image acquisition is repeated under otherwise identical conditions

$$\mathbf{n}=\mathbf{I}-H(O)$$ (1)

where n is the discrete noise in the reconstructed images, I are the reconstructed images, and H is the deterministic continuous-to-discrete operator that maps the object O to the reconstructed image I. In the absence of Poisson quantum noise and electronic noise, the discrete noise n would be the zero image. Artifacts in the image due to finite sampling, missing data, or aliasing would not be considered noise by this definition and would be reproducible under repeated measurement. However, these artifacts could affect the noise, for example, by applying a multiplicative spatially varying mask. The analysis below includes both the purely stochastic quantum noise in combination with such sampling effects.

The digital NPS which is often computed for experimental characterization of noise is an estimate of the variance of the DFT of the noise^{21, 23}

$$\mathrm{NPS}(f_i)\approx \frac{1}{N}\sum _{k=1}^N{|\mathrm{DFT}\{{\mathbf{n}}_k\}(f_i)|}^2=\frac{1}{N}\sum _{k=1}^N\mathrm{DFT}\{{\mathbf{n}}_k\}(f_i)\overline{\mathrm{DFT}\{{\mathbf{n}}_k\}(f_i),}$$ (2)

where ${\mathbf{n}}_k$ is a reconstructed noise volume and $\overline{\mathrm{DFT}\{{\mathbf{n}}_k\}(f_i)}$ is the complex conjugate of the discrete Fourier transform of the ${\mathbf{n}}_k$ volume evaluated at the spatial frequency f_i. Considering the noise image as a random vector, the elements of the full Σ_DFT would be given by

$${\Sigma }_{\mathrm{DFT}\mathrm{,}\mathit{ij}}\approx \frac{1}{N}\sum _{k=1}^N\mathrm{DFT}\{{\mathbf{n}}_k\}(f_i)\overline{\mathrm{DFT}\{{\mathbf{n}}_k\}(f_j).}$$ (3)

Hence, we see that common methodology for noise characterization assumes that this matrix is diagonal by only computing the NPS (the diagonal elements). The relationship between the Fourier domain covariance matrix (Σ_DFT) and the spatial domain covariance matrix (K_x) illustrates how the DFT approximately diagonalizes the covariance matrix under the stationary assumption:

$${\Sigma }_{\mathrm{DFT}}=⟨\mathrm{DFT}\{\mathbf{n}\}{(\mathrm{DFT}\{\mathbf{n}\})}^H⟩=\mathrm{DFT}⟨\mathbf{nn}⟩{\mathrm{DFT}}^H=\mathrm{DFT}{K}_x{\mathrm{DFT}}^H,$$ (4)

where DFT^H is the conjugate transpose of the DFT. This assumption is natural if one thinks of the image as a sample of an underlying stationary random process, but for real data, the assumption is violated. For example, the discrete nature of the data ensures that the assumption cannot formally hold.

The spatially varying NPS

The NPS of CT images is expected to exhibit variations in magnitude and correlation across the spatial domain—i.e., nonstationarity—due to well-known effects of varying quantum noise (nonuniform x-ray fluence transmitted to the detector), view aliasing effects (discrete sampling from a finite number of projection views), and detector lag (spatiotemporal blur).^{1, 2, 6, 7, 25, 26} A detailed treatment of the variability of the 3D NPS from an analytic and experimental perspective is given in Refs. ^{6, 7}. An estimate of the NPS in CT should therefore be recognized as a “local” estimate of the noise magnitude and correlation. Despite such systematic variability, the image NPS is an important factor in image quality assessment and system QA as mentioned above, and it is useful to study not only the manner in which the NPS varies but also systematic variations in the off-diagonal elements of the covariance matrix of the DFT as a check on the implicit assumptions. While we will primarily focus in this paper on variability with radius, we anticipate at least three sources of systematic variation of the NPS (and Σ_DFT) in the axial spatial domain.

Variability with radius (i.e., distance from the center of reconstruction)

Under conditions in which the x-ray fluence transmitted to the detector is nonuniform, the noise in CT reconstructions is expected to vary accordingly. The most common, simple example is a water cylinder imaged without a bowtie filter, for which the fluence at the detector is lower along more highly attenuated rays (through the center of the cylinder), and the image noise (NPS magnitude) is correspondingly higher in the center of reconstruction. Detector lag arising from temporal correlation of successive projections imparts spatiotemporal blur in the reconstructed image, which will also lead to an overall decrease in NPS. For cases of uniform exposure at the detector (e.g., an air scan or a cylinder imaged with a perfectly matched bowtie filter), the noise in CT reconstructions is expected to be more uniform as a function of radius. View sampling effects, on the other hand, are anticipated to result in the converse dependence on radius—i.e., image noise increasing at greater radius due to a finite number of projection views.

Variability with angle

Finite view sampling is furthermore anticipated to result in an angular dependence of noise correlation. For filtered backprojection reconstruction, view sampling is evident as “streaks” emanating from the center of reconstruction, with intensity of the streaks related to both the number of projection views (greater for fewer views) and radius (greater at increased radius). The effect of image lag is an azimuthal correlation which is perpendicular to that caused by view sampling.

Variability with height (i.e., distance from the central axial plane)

As mentioned above, although outside the scope of the current work, the NPS for CBCT images is expected to vary in z due to the “null cone” associated with the “cone-beam artifact” of incomplete sampling from a circular source-detector orbit.^{6, 20} Specifically, a null cone about the f_z axis is expected within the 3D NPS, increasing at greater distance from the central axial plane.

These sources of systematic variation in the NPS (and presumably the Σ_DFT) pose important considerations for image quality evaluation, system QA, and ultimately task-based performance assessment. They immediately suggest methods by which one might hope to minimize NPS nonstationarities in such assessment: (i) operate under conditions providing uniform x-ray fluence to the detector; (ii) restrict analysis to a given radius (or explicitly analyze radial dependence); (iii) incorporate analysis that accounts for angular variation (e.g., a rotating reference frame); and (iv) restrict analysis to a given height (e.g., z ∼ 0 or explicitly analyze z dependence). Such factors were analyzed in their effect upon NPS and Σ_DFT under a variety of experimental conditions below, with the aim of quantifying the degree of such nonstationarity and elucidating practical considerations for CT noise measurement.

Connection between the Σ_DFT and detectability

In this paper, we focus on the characterization of CT noise in and of itself, motivated by the growing use of NPS as a more standardized quality metric, and with an underlying theoretical motivation coming from the connection between the Σ_DFT and detectability. This connection arises from expressing the SNR (detectability) for the Hotelling observer in the continuous domain^{9, 11, 15}

$${\mathrm{SNR}}^2=\int \frac{{|H(f)|}^2}{\mathrm{NPS}(f)}{|W(f)|}^2\mathit{df},$$ (5)

where H(f) is the Fourier transform of the point spread function of the imaging system and W(f) is the Fourier transform of the object being detected.

For discrete data, this equates to

$${\mathrm{SNR}}^2={\mathbf{W}}^t{\Sigma }_{\mathrm{DFT}}^{-1}\mathbf{W},$$ (6)

where W is the DFT of the discrete signal (i.e., discrete approximation of the continuous signal W).^{21, 23, 27} The use of the digital noise-power spectrum to compute the SNR is based on the assumption that the continuous-to-discrete imaging system has a covariance matrix that is diagonalized by the DFT. Under the assumption that Σ_DFT is a diagonal matrix, the SNR expression in Eq. 6 becomes

$${\mathrm{SNR}}^2=\sum _i\frac{{\left|{\mathbf{W}}_i\right|}^2}{{\mathbf{NPS}}_i},$$ (7)

where NPS_i is Σ_DFT,ii.

With characterization of imaging systems based on the NPS becoming more prevalent, several researchers have questioned the underlying stationarity assumption and its effect on the off-diagonal elements of the covariance matrix of the DFT which are currently ignored.^{21, 24} This work begins to address that question by measuring the off-diagonal elements of a 3D CT system.

EXPERIMENTAL METHODS

CBCT imaging bench and experimental conditions

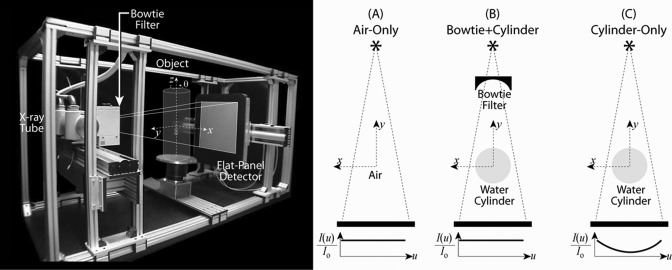
An imaging bench for CBCT reported in previous work²⁸ was used for experiments described below. Briefly, the bench includes an x-ray tube (Rad94 in Sapphire housing; W anode, 14° anode angle, 0.4 mm focal spot; Varian, Inc., Salt Lake City, UT) and flat-panel detector (PerkinElmer RID1640; 250 mg/cm² CsI:Tl x-ray converter, 0.4 mm pixel pitch, 1024 × 1024 pixel format; PerkinElmer, Inc., Palo Alto, CA) implemented on linear translation stages (406XR series; Parker-Hannifin, Irwin, PA) for precise adjustment of system geometry. In this case, the geometry was approximate to that of systems for image-guided radiation therapy (SAD = 93.5 cm, SDD = 144.0 cm, magnification = 1.54). An antiscatter grid was not used. The longitudinal (z) extent of the beam was limited by collimators, ranging from ∼1 to ∼25 cm at isocenter, corresponding to a longitudinal field-of-view (FOV_z) ranging from narrow (low-scatter conditions) to the full FOV (broad cone-beam, high scatter conditions). The phantom (in configurations detailed below) was placed on a rotation stage (Dynaserv; Parker-Hannifin, Irwin, PA) as shown in Fig. 1. The entire system was operated under computer control under pulsed-fluoroscopy in step-and-shoot mode. The data are therefore expected to be free of motion artifacts (i.e., azimuthal blur due to object rotation during exposure) but are expected to contain realistic correlations associated with image lag^{5, 7, 26} (i.e., residual signal carried over between projection frames).

Figure 1.

Experimental setup for CBCT imaging. Left, photograph of the imaging bench, with position of the bowtie filter and cylinder indicated. Right, three phantom configurations hypothesized to yield varying degrees of noise stationarity: (A) air-only; (B) bowtie filter + water cylinder; and (C) water cylinder (without a bowtie filter). The (x, y, z) coordinates of image reconstruction are shown. The relative fluence at the detector is illustrated by [I(u)/I_o] for the three configurations.

Nominal CBCT image acquisition involved 320 projections acquired at 1 frame per second across a 360° rotation, where the technique for each projection was 120 kVp (with 2.1–5.1 mm Cu added filtration, described below) and exposure varied across four levels spanning the sensitive range of the detector—specifically, four exposure levels—0.4, 0.8, 1.6, and 3.2 mAs, corresponding to 0.13, 0.26, 0.52, and 1.0 mR in-air exposure per projection at the detector, respectively. The corresponding dose to the center of a 20 cm cylindrical water phantom at isocenter was computed from the in-air exposure (per projection) at the detector as in Ref. 29; the in-air exposure per projection was scaled to isocenter by the inverse-square law and attenuated (Beer–Lambert law) by the radius of the cylinder (10 cm) assuming a 120 kVp beam for computing the effective attenuation coefficient of water;³⁰ the result was multiplied by the number of projections (320), the experimentally determined backscatter factor (∼3), and f-factor (0.9). The resulting dose levels were ∼0.4, 0.7, 1.5, and 2.8 mGy, respectively. Projections were dark-flood corrected by the mean of 50 dark-field and 50 flood-field images acquired at ∼30% of sensor saturation (∼1.0 mAs). Volume images were reconstructed using the FDK algorithm using a Hann filter in combination with the ramp filter as typical in soft-tissue imaging applications.³¹ Voxel size was (0.25 × 0.25 × 0.25) mm³, giving (1024 × 1024) voxels in the axial (x, y) plane and longitudinal extent up to 1024 voxels (but typically ∼128 for purposes of experiments below).

Three distinct phantom configurations illustrated in Fig. 1 were examined to investigate conditions hypothesized to represent varying levels of noise stationarity in 3D reconstructions: (A) air, (B) bowtie, and (C) cylinder. The first, referred to as configuration “A,” involved air-only scans (no phantom) with added filtration of 5.1 mm Cu, corresponding approximately to the attenuation of 20 cm water. Configuration A was hypothesized to yield the most stationary noise characteristics, owing to the most uniform x-ray fluence at the detector. The second, referred to as configuration “B,” involved a 20 cm diameter water cylinder placed at isocenter, with an aluminum bowtie filter placed near the collimator as in Fig. 1. The bowtie was uniform in the z-direction and machined to a smooth cosh shape varying from ∼3 mm Al thickness at the center to ∼30 mm Al thickness at the position corresponding to the projected edge of the water cylinder. The bowtie was placed through careful trial and error along the source-to-detector axis at a position that yielded the most uniform x-ray fluence at the detector—i.e., optimally matching the attenuation of the bowtie and water cylinder to give a nearly uniform detector signal. This configuration was hypothesized to yield noise stationarity approaching that of configuration A. The third configuration (C) involved the same 20-cm-diameter water cylinder but without the bowtie filter, hypothesized to give the least stationary noise characteristics, owing to the nonuniform x-ray fluence at the detector, and expected to result in high quantum noise at the center of reconstruction and lower quantum noise near the edge of the reconstruction. For both configurations B and C, added filtration of 2.1 mm Cu was used.

Estimating Σ_DFT from sample measurements

The ideal method to estimate the off-diagonal elements of Σ_DFT is to collect many realizations of the noise and to average over noise realizations for each subvolume. This procedure would avoid assumptions of local stationarity and would provide a spatially varying estimate of Σ_DFT. In this work, we have taken a different approach arising from methodology that is closer to current experimental methods for estimating the NPS. Specifically, two images were collected and subtracted from each other to estimate a zero mean image of the noise (with twice the variance; because of this we divided the resulting NPS by 2). From these noise images, we obtained 21 subvolumes (realizations) per radius of size 63³ voxels placed along 3 radii ranging from 40 to 80 mm. The subvolumes were obtained by placing the center of each equally spaced on circles with radii of 40, 60, and 80 mm, as illustrated in Fig. 4a. At 80 mm, this resulted in no overlap between subvolumes, but at 40 mm there was a maximum overlap of 20% [see Fig. 4a]. Consistent with the methods of Bartlett (nonoverlapping) and Welch (overlapping with a rect window), no correction was applied for the overlap in the realizations. Note that the overlap (or nonoverlap) in subvolumes does not affect the mean of the NPS estimate; rather, it affects the relationship between the number of subvolumes and the variance in the resulting measurements (inversely proportional for the case of nonoverlapping ROIs).³² The implicit assumptions are that the off-diagonal elements at a fixed radius have local wide-sense stationarity and that realization overlap has minimal effect on covariance estimation. The NPS and the off-diagonal elements of the Σ_DFT were computed from exactly the same data by simply summing over different indices [Eqs. 2, 3].

Figure 4.

Download video file ^{(1.4MB, wmv)}

Download video file ^{(1.6MB, wmv)}

Download video file ^{(1.4MB, wmv)}

(a) One quadrant of acquisitions at the three radii (40, 60, and 80 mm). The angular spacing between each acquisition was 18° leading to a total of 21 subvolumes per radius. (b) The change of the NPS with radius and angle is clearly visualized in movies available as electronic content associated with this paper. The NPS is seen to vary both radially and in angle, with large horns arising in the NPS at large radii due to angular sampling and small horns due to lag. The composite frame shown above is from case (C), cylinder without bowtie and shows several characteristics of the images. Detector lag and view aliasing effects are visible in the noise at large radii. The axial space-frequency plot shows reduction in the NPS as a function of radius. The surface plots of the axial, sagittal, and coronal slices show the structure of the 3D NPS, including horns that “rotate” depending on the position of the noise realization along the spiral trajectory seen in the axial NPS (enhanced online) .

Estimation of the NPS from periodograms is always accompanied by a choice of window (or tapering) function—e.g., a rectangular window if none is explicitly applied. We hypothesized that the choice of window function has distinct effect not only on the NPS estimate (usually a small effect, since quantum noise NPS is typically free of sharp correlations that may be subject to “leakage”) but also on off-diagonal elements (ODEs) of the Σ_DFT. Specifically, since application of a window function in the spatial domain implies convolution of the Σ_DFT with the Fourier transform of the window function, we anticipated the usual effects of “window carpentry” in analysis of off-diagonal elements. The Fourier transform of the rectangular window in three dimensions has a narrow central peak and long tails. An alternate window (e.g., Hann) has a broader central peak but short tails. We performed a complete analysis based on both windows, and results below are reported for the rectangular window, as it better estimated ODEs close to the NPS.^{33, 34}

To study the variability in NPS and Σ_DFT associated with angular direction (which is typically averaged out in the procedure described above), we alternatively rotated the subvolume realizations using cubic interpolation such that the coordinate system was always in the radial (and perpendicular-to-radial—i.e., azimuthal) direction. Although this alternative reference frame/coordinate system was not the focus of this study, a representative result is shown in the Appendix to illustrate the effect on correlations that can arise in the NPS.

Off-diagonal elements of Σ_DFT

Investigating the off-diagonal elements of Σ_DFT is a challenging task for three-dimensional images, introducing not only a potentially large computational load but also a variety of ways in which the complex Σ_DFT can be visualized and analyzed. One way of constructing the covariance matrix for an individual subvolume realization with 63³ elements would be to arrange the elements in a 1D vector. This leads to a covariance matrix of size 63³× 63³ (∼6.3 × 10¹⁰ elements) for each subvolume. Instead of following that approach, we pursued a simpler, more computationally tractable approach in order to more simply gauge and quantify the magnitude of off-diagonal elements of the Σ_DFT in comparison to the diagonal (NPS). We computed the first off-diagonal elements in each of the three frequency directions and performed the same processing as done to obtain the NPS. We then analyzed the absolute value of each of these off-diagonal elements and divided by the NPS to obtain the relative magnitude of the first off-diagonal elements: (|K_x| + |K_y| + |K_z|)/3NPS, where K_x, K_y, and K_z are the radially averaged first off-diagonal elements [for example, K_x = K(f_x,  f_x + df_x)] in each of the three directions. The results were plotted as a function of spatial location and spatial frequency, showing the dependence of the magnitude of ODEs on various factors affecting stationarity and probing the extent to which the diagonal of the covariance matrix of the DFT (i.e., the NPS) captures a complete description of the noise characteristics.

RESULTS

Variance maps

A simple characterization of the noise in reconstructed images is a map of the variance. In Fig. 2, we see the anticipated behavior in the variance maps for the three phantom configurations due to the variability in the transmitted x-ray fluence. Namely, the more x-ray photons pass through a region to the detector, the smaller the variance in the reconstructed images.¹ The change in the variance across the field of view is a characterization of the nonstationarity of the system. The variance maps for (A) air and (B) bowtie + cylinder exhibit a similar degree of (low) variability as a function of radius, with air having a lower overall variance. The water cylinder case (C) exhibits the most pronounced decrease in variance as a function of radius. The effect is due to both the increased fluence transmitted to the detector and increased image lag (which tends to increase with detector signal²⁶), and careful inspection of the variance map in case (C) shows the expected correlation in the angular direction. A third factor in the variance maps is related to view sampling, most evident in case (A), where the variance at the edge of the field of view is increased by streak artifacts.

Figure 2.

Variance maps for three phantom configurations: (A) air, (B) bowtie + cylinder, and (C) cylinder alone (without bowtie). Images correspond to high-scatter conditions (full FOV in the z-direction) at a dose level of 1.6 mAs per projection. As expected, the variance maps demonstrate the highest uniformity for (A) air and (B) bowtie + cylinder compared to (C) cylinder. The radially averaged variance plotted at left is normalized to the value near the center of the phantom (i.e., at R = 40 mm, where noise is reasonably uniform and uncorrupted by ring artifacts that can arise near the center of reconstruction). The dotted line of the radially averaged variance represents the edge of the cylinder.

3D noise-power spectrum

The Fourier domain analog of the variance is the NPS (the variance of the DFT coefficients). We collected sample realizations at fixed radii to obtain a radially averaged estimate of the NPS. As seen in Fig. 3, the same type of nonstationarity seen in the variance maps of Fig. 2 is evident in the 3D NPS. Specifically, for (A) air and (B) bowtie + cylinder, the NPS are nearly equivalent at radii of 40, 60, and 80 mm. For the cylinder case (C), however, the NPS decreases with radius due to a greater transmission of x-rays to the detector (higher exposure at greater radius).

Figure 3.

Download video file ^{(1.4MB, wmv)}

Download video file ^{(1.6MB, wmv)}

Download video file ^{(1.4MB, wmv)}

The axial NPS for three phantom configurations shows that noise magnitude and correlation vary radially in a manner consistent with the variance maps of Fig. 2. The water cylinder [case (C)] has significantly larger variability than (A) air or (B) bowtie + cylinder, with the NPS amplitude decreasing as a function of radius (enhanced online).

Illustration and visualization of the change in the axial NPS throughout the central axial plane is illustrated in videos available as electronic content associated with this paper. Each movie shows the axial, sagittal, and coronal NPS as a function of position in a spiral trajectory in the axial plane. The videos illustrate not only the reduction in NPS at greater radius as in case (C) of Fig. 3 but also the angular dependence of noise correlations evident as “horns” in the NPS. A composite frame of the movie is shown in Fig. 4.

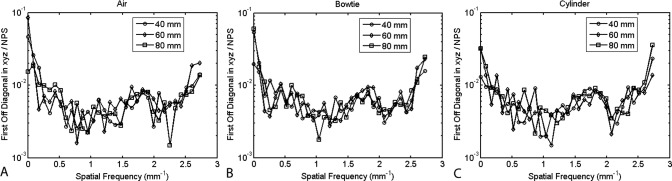
Off-diagonal elements of Σ_DFT

The magnitude of the first ODE in the x, y, and z directions quantifies in part the extent to which the NPS (i.e., the diagonal) describes the image noise. As shown in Fig. 5, plotting this quantity as a function of radius and spatial frequency shows that the average relative magnitude of the ODEs is found to be less than ∼1% of that for the NPS for all three phantom configurations. The relative error is independent of location and object, meaning that the relative error in the covariance matrix estimation is fairly constant. Although the NPS depends strongly on position as illustrated in previous figures, the relative size of the first off-diagonal elements does not appear to vary as strongly with radius or with the type of object. To justify that 21 subvolumes were enough to estimate the off-diagonal elements, Fig. 5 was reproduced (not shown) with 11 subvolumes resulting in similar results (but increased statistical error in the spectral estimate).

Figure 5.

The average relative magnitude of the first off-diagonal element in all three spatial frequency directions. For each phantom configuration, the average first ODE is less than about 1% of the NPS at that frequency.

A more complete picture of the off-diagonal elements can be seen in the axial slices of Σ_DFT in Fig. 6 and coronal slices of Fig. 7, each showing the NPS (diagonal) as well as first, second, and tenth ODE. In these figures, we see that the structure of the ODEs mimics that of the NPS with a decrease in magnitude by a factor of 10. The decrease is 1 order of magnitude instead of the two seen in Fig. 5 because the radial averaging of the ODEs further reduces their size compared to the NPS since the real and imaginary parts of the ODEs change signs. This implies that there are multiple ways of looking at the relative size of the off-diagonal elements.

Figure 6.

Slices of representative off-diagonal elements in the axial plane at a fixed radius of 80 mm (the radius at which the highest nonstationarity in the NPS was observed). The images to the left are the axial NPS for each of the three objects (air, bowtie, and cylinder). For each object, we show slices of the first, second, and tenth off-diagonal elements in the x-direction. For example, the images of the first off-diagonal elements show the correlation between that frequency and a frequency one bin higher in the x-direction. Note that the images are zero-padded to be the same size. (i.e., the images for the tenth off-diagonal elements do not contain data for the last 10 frequencies in the x-direction.) The grayscale is the magnitude of an element of the NPS or off-diagonal elements of the Σ_DFT. The scales for the NPS are the same for each phantom configuration, and the scales for the ODEs are all 1 order of magnitude smaller to enhance visibility but allow comparison with the NPS.

Figure 7.

Slices of off-diagonal elements of the Σ_DFT in the coronal plane at a fixed radius of 80 mm. Details are the same as in Fig. 6.

Finding a simple summary metric that captures the relative size of the off-diagonal elements with respect to the NPS is challenging. From a task-based perspective the appropriate metric should involve the task.^{9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19} A simple metric describing the relative size of the off-diagonal elements of the Σ_DFT is

$${\Omega }_{\mathit{xyz}}(n)=\frac{1}{3}[\frac{\left|⟨K_{x,n}⟩\right|}{⟨\mathrm{NPS}⟩}+\frac{\left|⟨K_{y,n}⟩\right|}{⟨\mathrm{NPS}⟩}+\frac{\left|⟨K_{z,n}⟩\right|}{⟨\mathrm{NPS}⟩}],$$ (8)

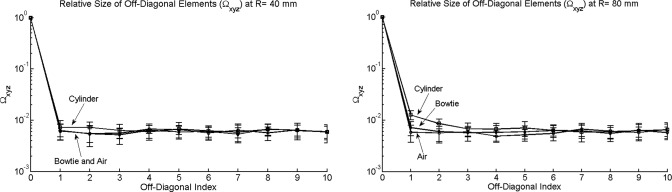
where Ω_xyz(n) is a measure of the relative size of the nth off-diagonal elements (in x, y, and z directions) with respect to the NPS. The expected values are interpreted as the sample mean over all frequencies in the subvolume realization. Figure 8 plots Ω_xyz as a function of n, where each point is the average over the 21 realizations at a particular radius. At the smaller radius (R = 40 mm), we observe a steep decline by 2 orders of magnitude from the diagonal [Ω_xyz(n = 0) = NPS] to the first off-diagonal element [Ω_xyz(n = 1)] for all three phantom configurations. At the higher radius (R = 80 mm), we again see a steep decline between the diagonal and the first ODE, but there is a measurable, systematic difference between the three phantom configurations. Specifically, Ω_xyz is highest for the cylinder (case C), followed by the bowtie + cylinder (case B) and air (case A)—which follows the rank order of nonstationarity observed in the local NPS results above. This systematic trend is strongest at the first ODE and persists out to the second or third ODE. While all cases demonstrate that the magnitude of the off-diagonal elements is fairly small (less than ∼1% of the NPS), the trends are consistent with the hypothesis that various phantom configurations imparting different levels of noise stationarity impart different magnitudes of off-diagonal elements in Σ_DFT.

Figure 8.

The relative size of the off-diagonal elements with respect to the NPS. (a) Ω_xyz(n) at a radius of 40 mm. (b) Ω_xyz(n) at a radius of 80 mm. The error bars represent 1 standard deviation based on 21 sample realizations at a fixed radius. In each case, we observe a steep drop between the diagonal and first off-diagonal element. The magnitude of Ω_xyz(n) for the three phantom configurations agrees with the hypothesized effect of the three phantom configurations on the Σ_DFT.

Although not investigated directly, the effects of image lag are also evident in the measured NPS and Σ_DFT. As noted above and in Refs. ^{5, 7}, image lag is expected to impart two primary effects on the NPS—a reduction in NPS magnitude (owing to temporal correlation and modulation by the bandwidth integral associated with the temporal MTF) and correlation of the noise in the azimuthal direction (i.e., perpendicular to radial, as in the “comet” artifact of Ref. 26). To the extent that image lag exhibits a dependence on detector signal (which is usually the case, typically increasing at higher signal level), one may expect nonstationarity in the NPS magnitude and correlation associated with variations in image lag throughout the image. This effect can be observed as horns in the axial NPS that are seen to rotate in the movies associated with Fig. 4 in relation to the position (angle) of the ROI for case A and in Fig. 9.

Figure 9.

NPS and off-diagonal elements of the Σ_DFT analyzed from subvolume realizations rotated as a function of angle to align with the radial direction. We used 21 subvolumes averaged at the radius of 80 mm. Analysis in the rotated coordinate system better distinguishes the horns of the NPS associated with radial correlation that is washed out in Fig. 3. These correlations are evident in the movie files (electronic content associated with Fig. 4), but the horns are seen to rotate in the axial NPS exactly with the angle of the realization. The large peaks appearing in the NPS for the cylinder are in the ±f_φ direction which is consistent with the streak artifact arising from view sampling effects.

The large horns effect seen in the movie and in Fig. 9 for case C are explained by the streak artifacts caused by view sampling. The radial correlations in the noise are dominant in the cylinder with no bowtie because of the large difference in fluence for views at different angles (say 0° and 90°). The pattern of spokes manifests itself as peaks in the azimuthal (angular) frequency.

As mentioned in Sec. 3, additional experiments were performed in which images of the three phantoms were acquired as a function of dose and level of x-ray scatter. At various dose levels, the results were consistent with those reported above, and over the range of linear detector response, the level of stationarity reflected by the local NPS and off-diagonal elements of Σ_DFT was consistent with expectations and the results summarized above. Specifically, the NPS varied in inverse proportion to mAs (dose) and did not change in shape or degree of (non)-stationarity. At various levels of x-ray scatter (controlled through adjustment of the longitudinal field), images exhibited distinct nonstationarity in the mean voxel value—viz., shading artifacts at higher levels of x-ray scatter.³⁵ However, because the NPS and Σ_DFT concern the second-order statistics of the image distribution, and because the image subtraction technique was effective in removing background “trends,” there was no significant effect on the stationarity characteristics as described by the local NPS or ODEs of the Σ_DFT.

DISCUSSION AND CONCLUSIONS

Characterization of the noise correlations for 3D CT from experimental measurement of the full Σ_DFT is currently a computationally daunting task because of the high dimensionality of the problem. Methods for dimensionality reduction, such as the use of a discrete Fourier transform, carry inevitable assumptions and limitations but have nonetheless proven very useful in a broad spectrum of work in CT image quality analysis, including new and evolving standards for CT image quality, acceptance testing, and QA. The work reported above begins to investigate those limitations through analysis of the Σ_DFT “neighborhood” about the diagonal while also seeking to identify experimental methods and system configurations that improve the validity of NPS-based analysis techniques. Analysis of changes in the local NPS as a function of location in 3D CT reconstruction demonstrates the dependence of such assumptions on the system configuration—specifically in terms of the phantom and bowtie configuration. It is hoped that such investigation will help promote methodologies that make simple, practical Fourier methods of characterizing noise correlations more practical and valid while also beginning to answer the challenge to look beyond the diagonal of the Σ_DFT and explore more complete spatial domain methods which may avoid some of the assumptions of Fourier domain methods.

The variability of the NPS in characterizing noise properties of reconstructed images is dependent on the reconstruction algorithm. While the results above pertain to filtered backprojection (FBP), a broad variety of nonlinear reconstruction algorithms becoming more prevalent in CT would almost certainly involve noise (and NPS) characteristics that are different from what we have shown. Depending on freely variable parameters governing the regularization of spatial resolution and variance within such nonlinear reconstruction techniques, the noise characteristics may be more stationary or less stationary than in FBP. The methods described above for analyzing the stationarity of noise characteristics, the off-diagonal elements of Σ_DFT, and the local NPS may be useful tools in understanding the noise behavior of such reconstruction methods. With the increased clinical implementation of iterative reconstruction algorithms, therefore, one could add a fourth bullet point to our list of sources of nonstationarity—viz., the reconstruction algorithm. Investigation of the experimental variability of the NPS for different reconstruction algorithms is an interesting area for future study.

Perhaps the best estimate of the local NPS would be gained from acquisition of a large number of noise volumes—for example, to match the statistical error of results reported above: 42 volumes subtracted to give 21 noise-only images, or alternatively 21 volumes subtracted by the mean over the same 21. Alternatively, one could envision N volumes from which the mean volume is subtracted from each individual volume (and a correction applied depending on N). For a large number of volumes, we would be able to obtain NPS estimates for each location of the field of view with a variance in the estimates that would be inversely proportional to the number of images. This would allow for both more accurate and location-specific assessment of the variability of the NPS. In the work reported here, we simply used two volumes, subtracted to give a single noise-only image from which the local NPS and Σ_DFT were analyzed from subvolume realizations as a function of location within the volume. Practical considerations of image acquisition time and file storage motivated this conservative approach. The manner in which one should average over subvolumes for NPS and Σ_DFT estimation depends somewhat on the noise correlations of primary interest. If the primary interest is to characterize the noise at a fixed radius, it makes sense to average over angle. Of the various forms and directionality of nonstationarity in cone-beam CT (namely, radius, angle, and height), averaging over the angle at a fixed radius (R) and height (z) is a reasonable approach. On the other hand, if angular correlations are of primary interest, then rotating the subvolume realizations as shown in the Appendix is a better method. For a proper quantification, one should correct for the associated interpolation/resampling. Finally, if nonstationarity in z is the effect of primary interest (e.g., the null cone “cone-beam” artifact), then realizations at fixed R and/or angle but varying in distance from the central axial plane are appropriate. Recognition that all of these choices yield a local estimate of the NPS is equally important.

The choice of window function for the periodogram estimates of the Σ_DFT was made primarily focusing on the first few ODEs. A rectangular window was chosen in the work reported above, since it has the highest spectral resolution close to the rapidly declining region of spectral density near the diagonal. Analysis with the Hann window gave results similar to Figs. 67, but the results analogous to Fig. 8 showed clear leakage from the NPS to the first few ODEs—i.e., the Fourier domain convolution associated with the spatial domain tapering window “blurred” the diagonal across the first few ODEs (washing out the rank order among the three phantoms). The choice of window therefore depends somewhat on what “region” of the Σ_DFT is of interest. For the work herein, we were primarily concerned with the ODEs immediately adjacent to the diagonal; for ODEs farther from the diagonal, a Hann or similar data tapering window may be the appropriate choice.

An interesting aspect in our results suggested by Fig. 5 is that the relative size of the first off-diagonal elements with respect to the NPS does not depend on the radius or type of object. This highlights how different metrics can lead to different conclusions of stationarity based on Σ_DFT. The Σ_DFT is a high-dimensional object which is difficult to characterize and summarize in terms of simple metrics. The Ω_xyz metric in Fig. 8 demonstrates the expected rank order consistent with the experimental hypothesis of noise stationarity for various phantom configurations. This metric characterizes the magnitude of the nth off-diagonal element of the Σ_DFT relative to the NPS by averaging over the ODEs at a distance of n elements from the diagonal in the x, y, and z directions. Other metrics could certainly be derived. For example, the choice of the order of the absolute value is somewhat arbitrary—i.e., taken of the expectation value of K_xyz,n as in Eq. 8 or taken of the quotient of K_xyz,n/NPS—and would not necessarily yield the same trends observed in Fig. 8. While the Ω_xyz metric demonstrates the magnitude of off-diagonal elements of the Σ_DFT and supports the hypothesis of nonstationarity under various experimental conditions, it is not intended as a standard measure of the off-diagonal elements. Such lies to future work in probing the Σ_DFT, and the most meaningful way to understand the relative importance of the off-diagonal elements is ultimately by relating to a task-based approach.

The work reported above highlights a number of practical considerations for CT system design, evaluation, and image quality QA.

• Phantoms. Air is a reasonable phantom for NPS analysis in a laboratory CT system and best obeys assumptions of noise stationarity. Recognizing that air scans can be problematic for diagnostic CT scanners that may behave in unexpected (proprietary) ways under high fluence (i.e., in the unattenuated beam), the next best choice is a water cylinder well matched to a bowtie filter. The water phantom also offers more straightforward relation to dose and noise-equivalent quanta. A water cylinder without a bowtie filter (or a water cylinder of diameter poorly matched to the shape of the bowtie) is subject to strong NPS nonstationarity.

• Bowtie filters. The degree of noise stationarity depends on how well matched the bowtie filter is to a particular diameter of water cylinder. Since different CT scanners have bowtie filters that differ in shape and material, a single water cylinder diameter will not perform equally well on various scanners. A given cylinder may demonstrate a high degree of stationarity on one make of scanner but exhibit poorer stationarity on a different scanner solely due to the different bowtie. The same caveats hold for NPS analysis at different kVp (on the same or different scanners), since a given bowtie is not expected to give ideal matching to a given cylinder phantom at all kVp.

• Nonstationarity. The 3D NPS varies throughout the 3D image. The central portion of the axial plane tends to be dominated by quantum noise, whereas the edge is dominated by view sampling and detector lag effects. For detectors with appreciable lag (and dependence of lag on detector signal), effect on both the NPS magnitude and azimuthal correlation can be expected. The very center of the axial plane is often cluttered by ring artifacts, and although clinical scanners likely have superior ring artifact correction than the prototype scanner in this work, such artifacts will have a major effect on the local NPS. For most purposes of NPS characterization (i.e., evaluation of quantum noise and noise-equivalent quanta), the very center of the reconstruction is probably best avoided, with ROIs selected at a specified radius.

• NPS reporting. For NPS characterization across various systems, it may be most useful to analyze the NPS at a fixed, specified radius in a region between those dominated by quantum noise and view aliasing—the “sweet spot” evident in the region R = 40–60 mm in images above. The NPS for volumetric CT is intrinsically a 3D quantity, and methods seeking to simplify representation of such to 2D surfaces and 1D plots must consider the correlations intrinsic to the data. Analysis of the NPS from 2D slices “extracted” from the 3D volume is fraught with error: it yields incorrect units for a fully 3D image NPS, and it is not simply related to the 3D NEQ.⁵ While one may consider correcting such correlations in 2D analysis (i.e., dividing by the bandwidth integral associated with out-of-plane correlation), the most straightforward analysis is to employ a 3D Fourier transform of the 3D data to yield a 3D NPS. Reduction to 2D axial or sagittal/coronal representations of the NPS or 1D plots is then a matter of data simplification/visualization, for example, 2D central axial, sagittal, and coronal slices of the full 3D NPS; and reduction to 1D plots by a radial average of the axial NPS to yield NPS(f_r), as above.

• So… is the NPS an appropriate metric? The work reported here was motivated in part by the challenge issued by prominent practitioners of spatial domain image quality characterization^{8, 21, 22, 23, 24, 36} to check assumptions on NPS analysis, balanced by the recognition of the utility of the NPS and related Fourier metrics to practitioners of CT system design and practical, clinical medical physics. The work suggests that the NPS is the dominant feature of the Σ_DFT and that the first off-diagonal element is lower by 2 orders of magnitude. Note that this observation pertains to uniform objects (with no anatomical variability) for assessment of the NPS in relation to quantum noise; characteristics of the Σ_DFT for “anatomical clutter” [for example, following a power-law noise characteristic as invoked in mammography and breast CT (Refs. ^{37, 38})] are yet to be investigated. However, the results also suggest broad tails in the ODEs, such that the tenth off-diagonal element has nearly the same magnitude as the first—namely, ∼1% of the NPS and the results are likely to be different for objects with anatomical structure.^{14, 17, 18} There are many ways in which one could quantify the error in the underlying assumption that the noise is stationary in CBCT. For example, one could compute the detectability of an object or quantify the difference in the spatial covariance matrix at various locations in the imaging volume. We have examined off-diagonal elements of the Fourier domain covariance matrix primarily to understand the magnitude of the elements of Σ_DFT currently ignored in NPS analysis under different experimental conditions. A better understanding of the local nature of the NPS will hopefully lead to more accurate estimates of noise correlation and more standardized reporting in prevalent Fourier methods. Since such metrics are tied directly to metrics such as NEQ (e.g., in system design and optimization) and also to radiation dose (the importance of which cannot be overstated), the importance of such improved understanding is clear. Looking beyond the NPS to a fuller appreciation of the complete Σ_DFT could shed additional understanding with only the tip of the iceberg suggested in the analysis of the first through tenth off-diagonal elements and various summary metrics in this work. Ultimately, such characterization can be tied to spatial domain methods for characterization of the noise and, ultimately, to task-based detectability in helping to identify the factors that govern image quality.

APPENDIX: NPS AND Σ_DFT IN A ROTATED COORDINATE SYSTEM

To reduce statistical error in the measurements, the NPS reported in imaging system characterization is typically an average over NPS estimates obtained from ROI realizations—e.g., at a fixed radius). When performed in the (x, y) coordinate system, this leads to averaging out structures which may be present in the angular (azimuthal) direction (i.e., perpendicular to the radial direction). We consider a rotated coordinate system (r, φ) where each subvolume realization is rotated to align with the radial direction. Because the data are discrete, this method requires interpolation and resampling, but it preserves the correlations in the angular direction that may be otherwise averaged over (i.e., “washed out”). Figure 9 shows that in the rotated coordinate system, the streaking effects (and “horns of the NPS” of Fig. 4) clearly appear in the NPS of the cylinder image (case C) as enhanced side lobes of the NPS. These effects were not apparent in the off-diagonal elements of the Σ_DFT. In the NPS image for air (case A), we observe small peaks in the ±f_r direction representing azimuthal correlations (comet artifact) which we attribute to detector lag. These small horns can also be seen in the NPS movies.