Knowledge-based Potential for Positioning Membrane-Associated Structures and Assessing Residue Specific Energetic Contributions

Abstract

The complex hydrophobic and hydrophilic milieus of membrane-associated proteins pose experimental and theoretical challenges to their understanding. Here we produce a non-redundant database to compute knowledge-based asymmetric cross-membrane potentials from the per-residue distributions of C_β, C_γ and functional group atoms. We predict transmembrane and peripherally associated regions from genomic sequence and position peptides and protein structures relative to the bilayer (available at http://www.degradolab.org/ez). The pseudo-energy topological landscapes underscore positional stability and functional mechanisms demonstrated here for antimicrobial peptides, transmembrane proteins, and viral fusion proteins. Moreover, experimental effects of point mutations on the relative ratio changes of dual-topology proteins are quantitatively reproduced. The functional group potential and the membrane-exposed residues display the largest energetic changes enabling to detect native-like structures from decoys. Hence, focusing on the uniqueness of membrane-associated proteins and peptides, we quantitatively parameterize their cross-membrane propensity thus facilitating structural refinement, characterization, prediction and design.

Introduction

While membrane proteins account for over a quarter of the proteome and most drug targets, they constitute only 2% of deposited structures (Fagerberg et al., 2010; White, 2009). Computational structural analysis (Arinaminpathy et al., 2009; Frishman, 2010; Pellegrini-Calace and Thornton, 2009), prediction (Barth et al., 2009; Elofsson and von Heijne, 2007; Fleishman and Ben-Tal, 2006; Hurwitz et al., 2006; Kernytsky and Rost, 2003; Michino et al., 2009) and design (Ghirlanda, 2009; Samish et al., 2010; Senes, 2011) provide a way to bridge this gap. The five distinct environments of membrane proteins (a hydrocarbon core surrounded by asymmetric polar head groups and aqueous milieus) present experimental and theoretical challenges in their biophysical dissection (Bill et al., 2011; Bowie, 2005; Dowhan and Bogdanov, 2009; Langosch and Arkin, 2009; Moore et al., 2008; White, 2009). The need for functional plasticity within a hydrophobic setting requires weak and intricate helix-helix interaction motifs. The corresponding conformational changes facilitate functions such as transport, channeling and signal transduction. Other membrane-associated proteins disrupt the bilayer: SNARE proteins mediate eukaryotic cell vesicular fusion (Langosch et al., 2007), while viral fusion proteins merge the viral envelope and the target cell membrane (Harrison, 2008).

While transmembrane (TM) domains vary in length and composition according to their organelle association (Sharpe et al., 2010), the basic properties of TM helices follow simple rules. Hydrophobicity is pivotal in TM helix insertion via the translocon (White and von Heijne, 2008) as demonstrated by per-residue scales derived from experimental measurements of transfer energy to the membrane (Bowie, 2005; Elofsson and von Heijne, 2007; White, 2009). Still, charged residues can be located in the hydrophobic core of the membrane with their side chains snorkeling to the membrane surface (Chamberlain et al., 2004). Positively charged residues prefer the cytoplasm (the “positive-inside” rule (Nilsson et al., 2005; von Heijne, 1984)) significantly affecting topology. The clustering of Trp and Tyr at membrane interfaces (Yau et al., 1998) contributes to protein positioning in the membrane, and is biased to the outer leaflet for reasons that are not well understood (Nakashima and Nishikawa, 1992; Nilsson et al., 2005). Likewise, Gly exhibits preference for the outer leaflet, partially due to asymmetric helix-to-coil unwinding (Jin and Takada, 2008). Helix-helix interfaces are generally lined by small residues, which is key to the limited number of helix-assembly geometries (Walters and DeGrado, 2006). Thus, while some structural biases of membrane proteins are known, the full biophysical parameterization of these discrete phenomena and related energetics is, unfortunately, still unclear.

Surface helices, lying nearly parallel to the membrane, serve as structural supports or play functional roles, defining specific microenvironments, gating channels, or interacting with other proteins (Orgel, 2006). They may also be independent peptides such as antimicrobial peptides (Wimley, 2010; Zasloff, 2002), which are part of the innate immune system. Often, these amphiphillic segments have adjacent TM regions, making sequence context and hydrophobic moment key parameters for their prediction (Phoenix et al., 2002). Yet, there is currently no publicly-available tool for quickly docking such peptides onto the membrane.

To overcome the lack of biophysical understanding, statistical approaches have been applied to position proteins in the membrane (Senes et al., 2007; Ulmschneider et al., 2005, 2006). The knowledge-based E_z potential (Senes et al., 2007) uses an inverse Boltzmann potential (statistical potential or log-odds score (Saven, 2003)) to convert observed depth (z-coordinate) propensities into amino acid pseudo-energies. However, this symmetric algorithm was limited by the small size and limited diversity of the database on which it relied. It was unable to discriminate between the inner and outer leaflets of the membrane, let alone resolve higher-resolution phenomena such as rotamer preference. Moreover, the search and sampling procedure was unable to address large structures. Ulmschneider et al. evaluated the membrane insertion of six TM proteins and nine antimicrobial peptides using a gaussian set derived as an effective potential of mean force (Ulmschneider et al., 2005, 2006). They found that while hydrophobic matching is pivotal, it is the polar, charged, and aromatic residues that determine the orientation. Lomize et al. produced a dataset (OPM (Lomize et al., 2011)) for calculating an all-atom transfer energy using a planar hydrophobic slab and a solvation model.

Importantly, current methods lack the ability to robustly extend the conceptual framework from full TM proteins to the effect of numerous mutations as required for structure prediction and design. Further, a topological energy landscape is required to unravel characteristics such as stability and multiple positional minima, as found in dual topology proteins as well as in fusion and lytic peptides. Hence, while the study of membrane proteins has yielded significant insights, general rules for the intricate relationships between sequence, structure, and environment remain to be discovered and used for new analysis, prediction and design applications.

Here we utilize the growing number of structurally diverse, high resolution helical membrane protein structures to assemble a non-redundant, representative dataset from which we compute an asymmetric E_z potential for C_β, and C_γ atoms, as well as functional group centers. In addition to orienting full-sized TM proteins accurately in the membrane we analyze pseudo-energy landscapes to examine biological systems like antimicrobial peptides (Wimley, 2010) and membrane fusion proteins. Likewise, we investigate higher-resolution phenomena such as rotameric preferences, topological stabilities, and the effects of point mutations on positional stability. We demonstrate that the new potential can predict and characterize membrane-associated proteins and peptides from genomic sequences and accurately position them relative to the membrane. It is also sufficiently sensitive to quantitatively assess the energetic effect of point mutations on the relative population ratio of dual topology TM proteins as well as accurately score and rank competing models. These features facilitate the prediction, refinement and design of TM protein structures.

Results

From Biophysical Insight to a Knowledge-Based Potential and Back

We trained our model on a representative experimental dataset of 76 proteins, which is over three times larger relative to the previous symmetric version (Senes et al., 2007) and, more importantly, has increased diversity (Figure 1A, Table S1a).

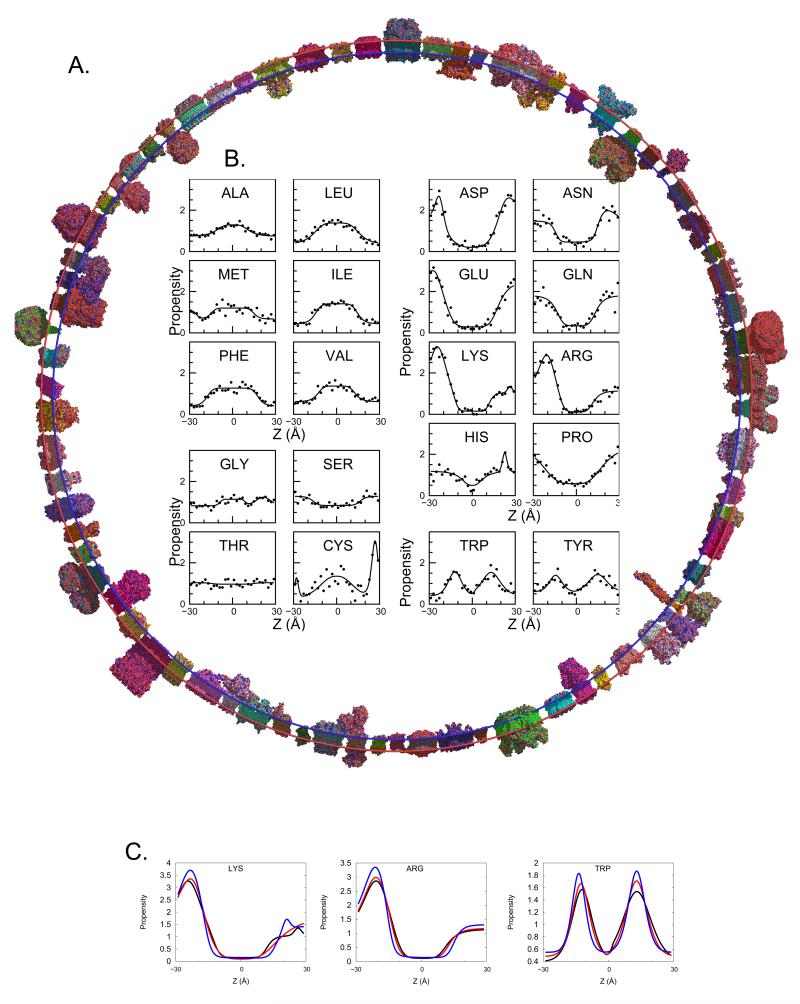
Figure 1.

Asymmetric E_z. The 76 protein database (A) is used to derive plots of amino acid propensity as a function of depth (Z) in the membrane. (B) Amino acid propensities (i.e. normalized frequencies, see Supplementary Methods) are grouped to hydrophobic residues, which prefer to be in the core of the bilayer; hydrophillic residues, which prefer to be in an aqueous environment; small, moderately polar residues; and aromatic residues, which prefer to partition in the head groups. (C) Comparison of the C_β (black), C_γ (red), and functional group (blue) propensities for Lys, Arg, and Trp. Unlike hydrophobic residues in hydrophilic amino acids (Figure S1d) transitions get sharper as the atoms in question get further from the backbone. See also Figure S1 and Table S1.

The cross-membrane distributions of residues are treated using reverse Boltzmann statistics, resulting in pseudo-energy profiles (Figure 1B, Figure S1a). The position-dependent potentials are modeled as gaussians or sigmoids, with added features at the edges when appropriate (Table S1b). For polar and charged side chains, the steepness of the transition into the hydrocarbon core depends on side chain length. For example, Asp and Asn have a steeper transition compared to Glu and Gln, respectively. The latter residues have an extra methylene group in their side chains, allowing them to snorkel more than the former ones. Overlaying the symmetric and asymmetric fits shows that many residues display significant asymmetries (Figure S1b). Lys and Arg show the largest asymmetry, following the positive-inside rule (Nilsson et al., 2005; von Heijne, 1984). The negatively charged residues Asp and Glu show a mild preference for the inner leaflet. This may facilitate salt bridges to Arg and Lys that follow the positive-inside rule. Pro, Tyr, and Trp exhibit mild asymmetric preferences for the outer leaflet. Gly and His show clear clusters just outside of the outer leaflet of the membrane. For His, this is mainly due to metal ligation, with the majority of counts in this cluster originating from respiratory and photosynthetic proteins. Interestingly, Cys favors the extracellular region where disulfide bonds are more easily formed compared to the reducing environment of the cytoplasm. Forty occurrences of Cys from sixteen proteins form an outer cluster facilitating disulfide bonds (28 residues) and metal ligation (12 residues), the latter mainly due to iron sulfur clusters. Notably, Cys is the main outlier of the otherwise excellent agreement between existing experimental scales and our computed transfer energy from the aqueous medium to the membrane center (Figure S1c).

Next, we focused on side chain orientation by deriving potentials using the location of C_γ or functional atoms (Tables S1c,d). Figure 1C demonstrates that functional group location drives the cross-membrane variation for some residues: polar and charged side chains display the sharpest transitions into the hydrophobic region, with features that are more clearly defined. An important possible application is the energetic scoring of rotamers.

Positioning and Orienting Proteins in the Membrane

With the sensitivity derived from the rich database, the algorithm should capture TM and surface-active helices from sequence information alone. E_Z-Profile in TM-mode threads a 26 sliding residue sequence onto an ideal helix to assess whether the sequence is TM and if so, in what topology. The potential finds 484 of the 539 (90%) unique TM helices in the structural database. Interestingly, 80% of the predicted TM helices are predicted with the correct topology (Table S2a). This is comparable to the six leading machine learning methods (Table S2b). The comparison utilizes a standardized benchmark database (Kernytsky and Rost, 2003) circumventing the inherent bias of comparing to our database that was used to parameterize our potential.

For structures, E_z-3D uses a quick grid search (Figure 2), accurately positioning proteins to within the published error of OPM (Lomize et al., 2011), regardless of which potential (C_β, C_γ or functional group) is applied (Table S2c and Figure S2). A similar result was obtained with a database of 185 membrane proteins positioned in the membrane using coarse-grained molecular dynamics simulations (Sansom et al., 2008), with the average difference in tilt being 9.5 ± 12°.

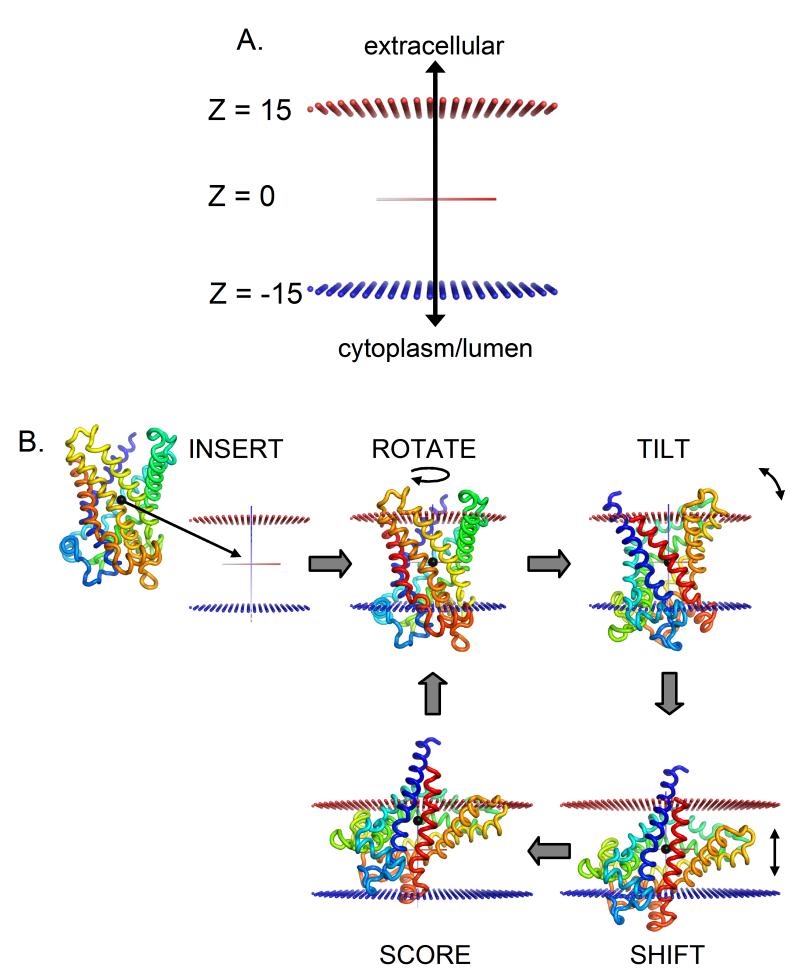
Figure 2.

Illustration of E_z-3D search protocol. (A) The Z-axis is defined so as to coincide with the membrane normal. Z=0 at the center of the bilayer, so the membrane head groups end at approximately Z=±15Å. Blue spheres represent the inner leaflet of the membrane (negative Z) and red spheres represent the outer leaflet (positive Z). (B) A schematic of one step of the E_z-3D exhaustive grid search using bovine mitochondrial ADP/ATP carrier (PDB ID: 1okc). When orienting a structure, an initial guess as to the protein’s TM segments is made using E_z-Profile. The protein is inserted into the membrane so that the center of mass of these segments is at the membrane center and their average helical axis is aligned to the Z axis. If a sequence is input instead of a structure, the sequence is threaded onto a single ideal helix and aligned with the N-terminus inside the cell. To conduct the search, the protein is sequentially rotated around the Z-axis, tilted away from the Z-axis, and shifted along the Z-axis. The E_z score is calculated in each configuration and the process is iterated through all possible configurations (e.g. with N-terminus outside the cell) in order to find the global minimum. See also Figure S2 and Table S2.

As a more stringent test, we applied E_z-3D to newly released structures that became available after the derivation of our potentials (Table S2b). The results are within the experimental error of OPM. For example for the cbb₃ cytochrome oxidase (PDB ID 3mk7) and the FucP fucose transporter (PDB ID 3o7q) the tilt and shift relative to OPM are 3.9° / 2.7 Å and 0.9° / 1.0 Å for the two proteins, respectively.

To ensure that E_z-3D compares well with experimental data, two structures crystallized in a membrane (rather than a detergent) were analyzed. Compared to the experimental structure, the shift and tilt that E_z-3D assigns to bacteriorhodopsin (PDB ID 2brd) and aquaporin (PDB ID 3m9i) are 170° / 0Å and 169° / −1Å, respectively. As the input file is not z-aligned, the center of mass was used as a reference state with respect to shift. The z-axis definition for the aquaporin file is defined in a flipped conformation for the experimental structure relative to our definition, namely E_z assigns the correct topology. For bacteriorhodopsin, E_z-3D gives a flipped structure, however with an energy landscape showing a small energetic change between the two orientations. This is possibly due to buried charged residues such as the retinal-binding Arg.

Finally, to ameliorate the few cases in which TM helices are misidentified, we provided an option to manually identify one or more TM segments in place of the automatic assignment. For five structures annotated incorrectly, the average tilt decreased from 23.7° to 16.8° and the average shift is decreases from 17.4 Å to 3.5 Å (Table S2d).

Full Genome Residue Biases

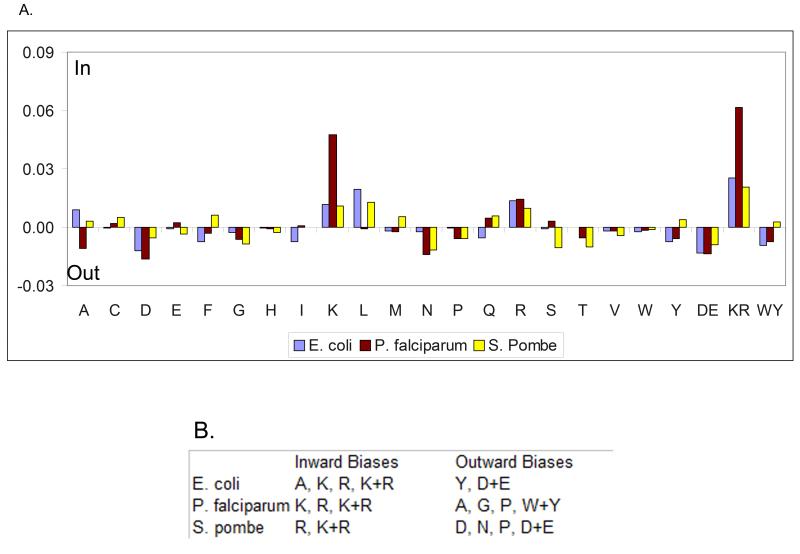
To exemplify how our general method can recapitulate inside/outside sequence biases previously found by artificial intelligence techniques specifically trained for the task (Nilsson et al., 2005) we scanned the genomes of E. coli, P. falciparum, and S. pombe (Figure 3, Table S3a). Following the positive-inside rule, statistically significant biases are observed for Lys and Arg in all species, including P. falciparum, where the bias was not previously detected (Nilsson et al., 2005). More intriguing are species-specific biases on the outer leaflet, e.g., S. pombe preferentially places the polar residues Asp and Asn in the outer leaflet, while P. falciparum places the small residues Ala and Gly there. Thus, species-specific biases may be biologically important and partly due to different structure and composition of the translocon machinery.

Figure 3.

Asymmetric bias across the membrane for single residues, as well as negative (Asp and Glu, denoted DE), positive (Lys and Arg, denoted KR) and aromatic Trp and Tyr (denoted WY). (A) Inside/outside amino acids biases detected from membrane proteins in three genomes. (A) The average bias of each amino acid type for E. coli (blue), P. falciparum (red) and S. pombe (yellow). (B) Amino acids for which the detected bias is statistically significant (p ≤ 0.1, see Supplementary Methods). See also Table S3.

More challengingly, we applied the TM-protein-derived parameterization to the medically important surface-anchored proteins. Three viruses were tested, and most known surface-anchored proteins were found (Table S3b). For example, E_z-Profile successfully predicts the positively charged residues near the N-terminus of HIV Nef protein (Gerlach et al., 2010) as being involved in membrane binding. Likewise, it picks out the C-terminal region of the HIV Env protein, which is known as LLP-1 and modulates fusion kinetics (Wyss et al., 2005). In the parainfluenza virus 5 matrix protein, the surface helix adjacent to and including the FPIV viral budding (Schmitt et al., 2005) motif is predicted as surface anchored.

Topology Characterization: Pseudo-Energy Landscapes of TM, Antimicrobial, Lytic and Fusion Peptides

E_z-3D provides pseudo-energy landscapes illuminating the energetic effect of changing tilt and orientation (Figure S4). For instance, TM peptides can easily be distinguished by eye from surface active helices and sequences that prefer to orient at an oblique angle (Figure 4). Likewise, the positive-inside rule manifests an energy well bias to the positive-inside conformation (Figure 4A). An amphiphillic peptide such as mastoparan exhibits a strong preference to the interfacial region of the inner leaflet (Figure 4B). In contrast, a TM peptide stabilized mainly by aromatic residues displays a more disperse energy well compared to a well stabilized TM peptide (Figure 4C). Finally, a lytic peptide e.g. Melittin, forms pores in the cell membrane and displays a dynamic equilibrium between a surface-bound conformation and a fully-inserted TM one (Figure 4D). Notably, Melittin places its positively charged residues at the C-terminus allowing for a TM configuration.

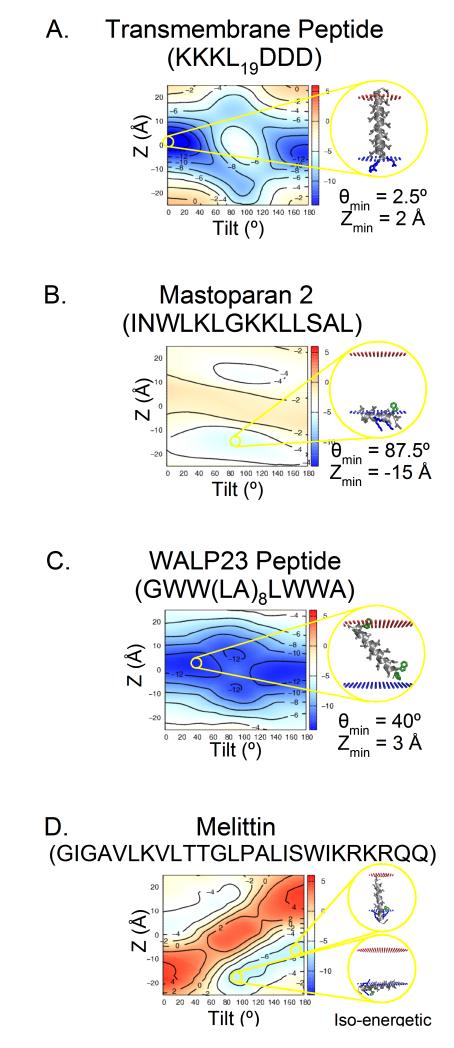
Figure 4.

An E_z-3D pseudo-energy landscape computed with the C_β potential. Theoretically, and as further justified by comparison to experimental scales (Figure S1c), the pseudo-energy is in units of kT. (A) A typical TM peptide, which prefers to be nearly parallel with the bilayer normal. The Z=0Å minimum corresponds to a peptide well centered in the bilayer. The primary θ=0° minimum corresponds to the N-terminus being inside the cell. This asymmetry is driven by the Lys (blue). A secondary minimum is observed at θ=180° with the C-terminus inside the cell. (B) The minimum for an amphiphillic peptide, is near θ=180°. The Z minimum at −15Å indicates that mastoparan prefers the interfacial region of the inner leaflet. The secondary minimum at Z=15Å is much smaller and somewhat shallower, indicating an asymmetric preference for the inner leaflet. (C) A peptide containing Trp (green) tilts (θ_min=40°) to place that residue in the headgroup region of the membrane. Secondary minima in deeply inserted (∣Z∣<10Å) surface configurations also accommodate this preference. (D) The E_z-3D landscape of the pore-forming lytic Melittin peptide suggests a dynamic equilibrium between a surface-bound conformation and a fully-inserted TM one. See also Figure S4.

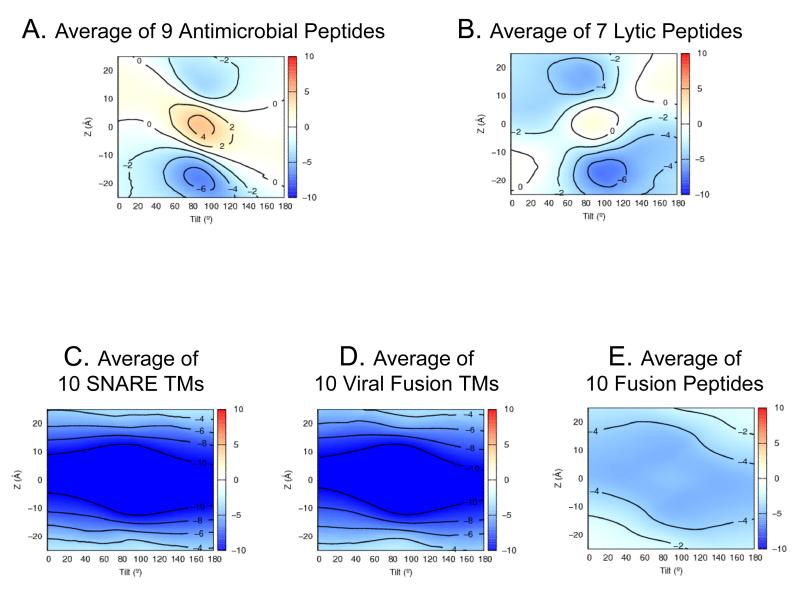
A more stringent test is the generation of mechanistic hypotheses for proteins that function dynamically. Figure 5 compares averaged pseudo-energy landscapes from antimicrobial, lytic, and fusion peptides (listed in Table S5). Antimicrobial peptides are amphiphillic sequences capable of penetrating and killing prokaryotic cells and play a role in the innate immune system. Such peptides depend on electrostatic interactions and thus are less effective against neutral eukaryotic membranes. Lytic peptides are similar but can also lyse eukaryotic cells. The latter have a weaker preference for the inner leaflet and a smaller barrier toward crossing the membrane core, possibly due to increased hydrophobicity and a reduced dependence on electrostatic interactions. Indeed, antimicrobial peptides are more charge dependent and are less accessible to non-microbial membranes. Both groups have a preference for forming inner leaflet helices parallel to the bilayer. This supports the “interfacial activity” model (Wimley, 2010), suggesting that the peptides partition to the head group region and eventually translocate to the inner leaflet, causing membrane disruption.

Figure 5.

Averaged E_z-3D landscapes computed with the Cβ potential for different classes of peptide demonstrate the types of mechanistic insights that can be obtained. Comparing averaged E_z-3D landscapes for (A) nine antimicrobial peptides (Table S5) and (B) seven lytic peptides shows that lytic peptides are more symmetrically distributed and have a lower barrier against crossing the membrane. The second comparison shows (C) ten viral fusion protein C-terminal TM segments (Table S5), (D) ten viral fusion protein “fusion peptides”, and (E) ten SNARE protein TM segments. While TMs from fusion proteins and SNAREs share nearly identical E_z-3D landscapes, the fusion peptides are less stable (~ −5.5 kT) in the bilayer, compared to TMs (~ −12 kT), possibly reflecting the insertion dynamics that may be required for fusion function. See also Table S5.

Similarities can also be observed among three classes of peptides which facilitate fusion. These display broad minima that encompass a range of orientations, from a modestly oblique TM segment to a surface-bound helix to being completely buried in the hydrocarbon layer. The extensive plasticity is unique to this class of proteins as compared to most multi or single-span helices and comes from the need to stabilize and adapt to multiple lipidic intermediates along the fusion pathway (Donald et al., 2011). Interestingly, viral fusion protein TMs exhibit nearly identical landscapes to SNARE TMs, while viral fusion peptides (which start the viral life-cycle buried in the protein core) tend to be less stable than the permanent TM segments.

Quantitative Recapitulation of Experimental Mutation Effects on Dual Topology Protein Topology

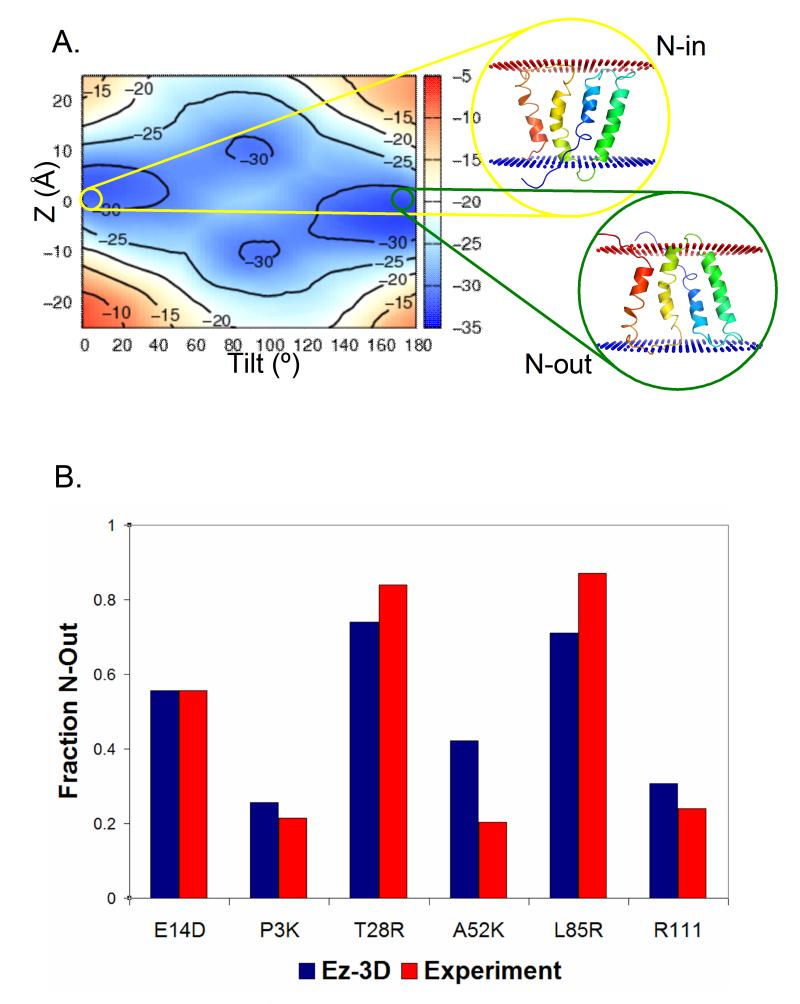
High resolution landscapes can demonstrate when a structure is topologically unstable, allowing investigation of the effects of single mutations. The EmrE transporter is a naturally-occurring dual-topology transporter found both with the N terminus facing the cytoplasm (N_in) and in the opposite orientation (N_out). The population ratio between topologies changes following even single point mutations (Seppala et al., 2010). Strikingly, these experimentally-determined effects are fully recapitulated by our potentials (Figure 6). The potential not only captures the trend of the relative topological change but also the precise division between the two topologies as measured by the relative E_z energy of each conformation (see Supplemental Methods).

Figure 6.

The E_z-3D landscape reflects the dual-topology nature of EmrE. (A) The E_z-3D energy landscape describing the burial and tilt of the EmrE monomer supports a low barrier dual topology protein with shallow energy minima. Cartoon representations of the two topologies are shown. (B) A comparison of calculated and experimental topologies for EmrE variants. The fraction of each EmrE mutant predicted by E_z-3D to assume the N_out topology (y-axis) recapitulates recent experimental work (Seppala et al., 2010). The experimental value of E14D was used to calibrate the predictions for the other mutations (see methods).

Decoy Scoring: Knowledge-based vs. Energy-based Approach

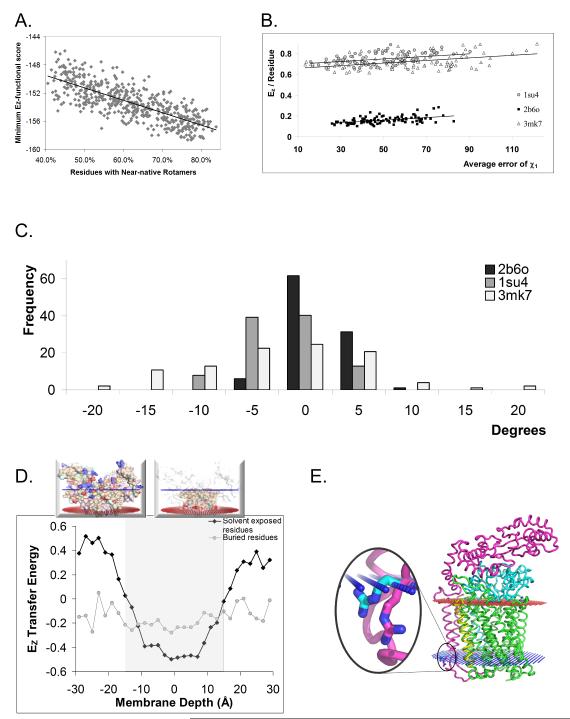
Next, we assessed the capability of the functional group potential to score side chain conformations, e.g. select the native-like conformation from different rotameric states, a task pivotal to mutational analysis, structure prediction, refinement, and design. Using the high-resolution bacteriorhodopsin as a test case (Figure 7A) and other examples (Figure S7a) decoy structures were tested. These were produced by randomly rotating the side chain around the χ₁ angle and tested by “near-nativeness,” defined as the percent of residues with χ₁ angles within 30^o of the native structure. The E_z-3D functional score is well correlated with the near-nativeness of the decoy structures. The R² of the linear trend line is inversely correlated with the resolution and positively correlated with the protein size (Figure S7). To ensure that this correlation was not due solely to violations of stereochemistry, we used MESHI (Kalisman et al., 2005) to remove steric violations using an energy function trained on water soluble proteins (Amir et al., 2008; Summa and Levitt, 2007). The correlation between near-nativeness and E_z score was, indeed, maintained (Figure S7). Moreover, subjecting these decoys to minimization using the ROSETTA-membrane (Rohl et al., 2004) scoring function maintained this correlation (Figure S7).

Figure 7.

High-resolution side-chain orientation and energetics. (A) 1,000 decoy models of the high resolution bacteriorhodopsin structure (1.55Å, PDB ID 1c3w) were produced by rotating side-chains randomly around the χ₁ dihedral angle. (B) For several example structures tested, the per residue contribution of snorkeling residues correlates with the average error in their χ₁ angle. (C) Rosetta Membrane does not significantly optimize snorkeling residues (see methods for definition) achieving an overall small change in the χ₁ dihedral angle relative to the change required to shift the decoy side-chains to their snorkeled experimental position. (D) The relative contribution of transfer energy to the potential is dominated by exposed residues spanning 10> ∣z∣ > 30Å. As an example, the insert shows exposed (top) and buried (bottom) residues for PDB ID 1orq (E) An example (PDB ID 3mk7) for a rotamer optimized by standard minimization (magenta) which is directed counter snorkeling and compared to a rotamer selected by E_Z (cyan) as the one with the lowest energy among a set of decoys.

Since the membrane milieu dictates conformational preferences, we hypothesized that E_z will be most powerful for the protein region that interacts with the complex headgroup region of the membrane. To test this hypothesis we looked at polar and charged residues (Asp, Asn, Glu, Gln, Lys, and Arg) that are on the surface of the protein but within the membrane. Such residues are known to snorkel their side chains from the hydrophobic region toward the aqueous solvent. Snorkeling involves a changing microenvironment making rotamer optimization via a local energy function challenging. The per residue contribution of the snorklers correlates with the average error of their χ₁ angle (Figure 7B). Note that different residue types carry different penalties for membrane insertion; Asn and Gln have a lower penalty compared to charged residues. Further, the positive-inside rule means that insertion of Lys and Arg into the inner leaflet is energetically advantageous compared to the outer leaflet. Combined with structure resolution large difference are apparent in per residue contributions among the various structures. Strikingly, once these are accounted for the slope of the correlation with χ₁ error is the same for all three proteins. Consequently, it is not surprising that while ROSETTA-membrane optimizes the decoys overall (Figure S7), it is not successful in optimizing snorkeling residues (Figure 7C) – in 89% of the decoys tested, the average χ₁ deviation either decreases by less than 10° or actually increases. Indeed, our knowledge-based pseudo-energetic potential derives the transfer energy mainly from membrane exposed residues (Figure 7D) resulting in an ability to distinguish between a rotamer that is selected by a regular minimization routine to a snorkeling rotamer as exemplified in Figure 7E. Hence, the membrane protein designated functional group potential is superior to local energy minimization for rotamer optimization.

Discussion

The updated database presented here has enabled rigorous positioning and analysis of membrane protein helical structures using an exclusively knowledge-based potential. The potential focused on helical structures, which are the largest and most important membrane-associated protein group. Recently a similar approach was applied to beta-barrel proteins (Hsieh et al., 2011). The conceptual core method has been published by the DeGrado lab (Senes et al., 2007) and by others (Ulmschneider et al., 2005, 2006). We have extended those works to encompass assymmetry of residue spread, improved server reliability, accuracy and speed. More importantly, the new method can carry out a detailed analysis of the specific interactions between individual residues or helices and the membrane environment. These advantages are demonstrated for (a) the quantitativly precise detection of shifts in the relative topology of dual topology proteins, (b) the inference of mechanistic hypotheses from topological energy landscapes of short peptides, and (c) the detection of native-like rotamers within a decoy set. Taken together, the accuracy of our method along with the detailed topological energy landscape and the speed of the output can enable thorough analysis, prediction and design of membrane proteins.

Other methods for positioning proteins within a membrane include atomic-level, long-range molecular dynamics. Due to computational constraints, coarse-grain molecular dynamics have been used with overall satisfactory results (Sansom et al., 2008). However, molecular dynamics cannot be used to regularly produce full range energy landscapes required for thorough analysis or to systematically scan numerous mutations as required, e.g. for protein design. Notably, the pseudo-energy lanscape represents the topological aspect of backbone or side-chain energetics for a given rigid structure, rather than a full search for all side-chain conformations. As shown for several decoy sets, focusing on the difficult task of scoring alternative models and understanding the energetics of protein-membrane interaction provides a structure prediction and design capability when combined with an existing model generating tool.

The increased resolution of our results comes from the data’s coverage and representativeness (Samish, 2009), drawing on the exponential growth of the high resolution structural data (White, 2009) and the shift to more difficult-to-crystallize, wild-type, and mesophilic structures. While some applications require non-redundant datasets, others benefit from including all possible data. For membrane proteins, few and often extremophile structures, e.g. photosynthetic bacterial reaction centers, have been structurally elucidated resulting in highly redundant structural data. Including such data will bias the overall potential to the unique properties of specific families of structures. Such biases are beyond the recently characterized organelle specific biases (Sharpe et al., 2010). For this study, we required that subunits with two or more TM helices share less than 30% sequence identity with other such subunits in the database and gave preference to high-resolution, wild-type, ground-state mesophile structures.

The biogenesis of TM proteins requires insertion into the membrane via the translocon, which is thought to operate as a hydrophobicity sensor (Hessa et al., 2007). The determination of whether a sequence will become TM is captured by the E_z potential in great detail. For example, it enables the recapitulation of genomic sequence biases previously found by far more advanced artificial intelligence methods. As a follow-up study, it would be interesting to assess sequence-structure relationships by examining sequence biases not found by the E_z potential. Structurally, pseudo-energetic landscapes are rich in information that provides insight on conformational stability and can be used to generate mechanistic hypotheses or, alternatively, stabilize membrane proteins.

Current state of the art modeling relies on local energetics parameterized from soluble proteins. In contrast, this study emphasizes the unique cross-membrane distribution of each residue’s functional group specifically capturing the difference between soluble and membrane proteins. Consequently, the new method can improve existing tools for selecting preferred residues based on location and refining side chain orientations and rotamers.

The potential provides extraordinary power, especially considering its simple, biophysically-based structure. Despite using a fixed window and no machine learning or hierarchical characterization, E_z-Profile detects membrane-associated segments from primary sequence with results comparable to the most sophisticated methods and, further, can correctly determine their topologies. Indeed, since our scale agrees with experimental scales of position-specific amino acid contributions to the free energy of membrane proteins (Figure S1c), such scales can also predict membrane protein topology on par with the most sophisticated prediction methods (Bernsel et al., 2008). Thus, E_z helps bridge the gap through its ability to quickly scan sequences of TM helices and examine rotamer tendencies. No less important is the computational speed up compared to the previous, symmetric version. For instance, a medium-sized structure (1pw4, 434 residues) is oriented in 30 seconds (2.8 GHz Intel Core i7, 8 GB RAM). The speed-up increases rapidly with protein size, e.g. a 3,550-residue protein (PDB ID 1v54) runs in 5 minutes instead of days, making it now possible to run the program on an online server.

Our results show that the solvent exposed residues have the greatest dependency on membrane depth. The average transfer energy of buried residues is flatter than previously thought (Ulmschneider et al., 2005), since the packing and interior electrostatics of membrane and soluble protein interiors are similar (Joh et al., 2009). Consequently, TM protein interiors are well optimized via routine minimization. In contrast, the average transfer energy of exposed residues is highly dependent on the changing charge densities of the microenvironment. As such, utilization of this characterization, as done in the knowledge-based potential presented here, paves the way for a new membrane-protein-specific rotamer minimization routine.

Future directions will be possible following additional increase in the size and resolution of the database. These include the derivation of different scales for different subgroups of interest: different protein types with unique characteristics (e.g. transporters or photosynthetic systems), and different membrane types (e.g. specific organelles or different membrane thicknesses), as well as different organism types, such as eukaryotic vs. prokaryotic. Future applications include a membrane protein specific rotamer library, which will account for the relative distribution of lipid-facing rotamers in a cross-membrane specific manner, thus accounting for phenomena such as snorkeling. Finally, integrating this work into a protein design algorithm that produces alternative models will enable the implementation of a quick protein design focused on making proteins or peptides with specific topological stabilities or tendencies.

Hence, the newly derived biophysical parameterizations and the resulting toolbox offer benefits for the analysis, prediction and design of membrane-associated proteins. The community wide assessment of membrane protein structural prediction has shown that the field lags far behind the success for soluble structures and is highly dependent on expert input (Michino et al., 2009). Despite few computational design success stories (Yin et al., 2007), membrane protein computational design has yet to become widespread. Finally, beyond shedding light on membrane protein structure-function relationships, our approach may be used routinely for applications ranging from de novo design to assessing the energetics of side chain locations. It will also prove useful for mutagenesis efforts, as in stabilizing membrane proteins for biochemistry, industry, or crystallization. Current membrane protein design efforts in the lab are already employing these capabilities.

Experimental Procedures

Database

The dataset includes all TM alpha-helical structures available as of June 2010 with resolution better than 3.5Å and a maximum sequence identity of 30% for subunits with two or more TM segments. Preference was given to structural quality (resolution and R_free), wild-type, mesophile, ground-state and non-engineered structures (Figure 1A and Table S1a). Proteins in the OPM (Lomize et al., 2011) database have an average TM helix tilt of θ=0° and thus were used ‘as is’ in the E_z parameterization. Proteins not found in this database were aligned to a related structure. E_z-3D tilts are defined as difference compared to OPM positioning. Separate databases were computed for buried and exposed residues by rolling a 1.9 Å-radius lipid methylene probe on the TM protein complex and defining residues in contact with the probe as ‘exposed’ (see Supplementary Methods)

Data Fitting

One subunit was retained from homooligomeric structures except 2j7a, for which two chains in different configurations were retained. Residues were divided into 2Å bins along the membrane normal, with Z=0 at the bilayer center and positive Z toward the exoplasm. Residue position was defined by using C_β (C_α for glycine) and as in Table S1e for the advanced potentials. The propensity (P_z) and effective energy (E_z) were calculated as in the symmetric version (Senes et al., 2007) (Supplementary Methods and Table S1f) but separately for positive and negative Z. ΔE_z was fit to a sigmoid, a guassian, or a combination of the two, depending on what best described the data (Table S1b and Supplementary Methods).

E_z-Profile

E_z-Profile follows an approach previously applied to a test case (Bissonnette et al., 2009). In TM helix mode, each 26-residue sliding window was threaded on an ideal helix, for which C_β coordinates (pseudo-C_β for glycine) had been precomputed. Three flanking residues on each side were included to help determine topology. Pseudo-energy was calculated with the center of mass positioned at the bilayer center. Topology was determined by a majority vote of all windows below the threshold (-4.9) in that local minimum. Consecutive TM segments were forced to alternate topology. Flipped helices were chosen to minimize the number of flips and avoid flipping segments for which the initial vote overwhelmingly favored a particular orientation (Supplementary Methods).

In surface helix mode, E_z-Profile examined regions less than 17 residues from chain termini and TM segments. A 7-residue window was threaded onto an ideal helix placed parallel to the plane of the membrane at a distance of +/−15Å. The helix was rotated about its axis in 10° steps, and the score for the same window, rotated by 180° around the helical axis, was subtracted so that,

$$S_{\mathit{final}}(i,z,\stackrel{`}{e})=S_{\mathit{Orginal}}(i,z,\stackrel{`}{e})-S_{\mathit{orginal}}(i,z,\stackrel{`}{e}+180)$$

where i is a sequence window, and z and θ are the depth and rotation of the helix, respectively. Thus, non-amphiphillic sequences tend to have an Sfinal~0. Windows for which the minimum of Sfinal(i)≥−1.25 were discarded. For greater specificity, a second, slower, step used E_z-3D to orient each remaining window; those with a preferred depth of −22.0≤Z≤−11.5 and E_z<2.0 were empirically determined to be those most likely to be surface helices.

Amino Acid Biases

Each chain in the proteome was scanned using E_z-Profile. Those for which TM segments were found and for which the topology could be assigned with a confidence score >0.95 (see Supplementary Methods) were analyzed for inside-outside amino acid biases, following von Heijne (Nilsson et al., 2005) (Supplementary Methods).

E_z-3D

E_z-Profile identified the TM segments, and HELANAL (Bansal et al., 2000) was used to find the helical axis of each one. These were averaged in order to estimate the protein axis, which was initially aligned to the Z-axis. The center of mass of the detected TM segments was positioned at Z=0 (Figure 2A). Translation along the Z-axis was carried out in 0.5Å increments and rotation was carried out in 5° and 2.5° steps around the Z and Y axes, respectively (Figure 2B). Large step sizes, restricted search space, and a precalculated lookup table of E_z values were used to reduce runtime without sacrificing accuracy (Figure S1e). Notably, while membrane proteins are found in membranes of diverse content and thickness, within the framework of our knowledge-based potential, scaling the potential to different membrane thicknesses did not affect our result significantly. Pseudo-energy landscapes were drawn with Gnuplot 4.2.5 (http://gnuplot.sourceforge.net/).

Overall, solvent-exposed residues contribute the most to the pseudo-energy and these contributions are centered on the membrane region (Figure 7D). However, applying our potential over solvent exposed residues alone did not show a significant improvement in the results with 5.5 ± 15Å change in shift and 4.7 ± 8.7Å change in tilt, both averaging over all proteins relative to the OPM database (Figure S7b). The increased spread of results possibly stems from considering far fewer residues and from considering residues beyond the depth that affect the potential the most. Thus, the correlation between near-nativeness and E_z score is most pronounced for the membrane exposed residues and contributes the most to the correlation coefficient.

Decoys

Decoys were generated using a random rotation of the χ₁ dihedral angle from the native structure, allowing for a high variation of rotameric states among the decoy set. Notably, these decoys included large clashes and thus were not usable in standard minimization schemes. To compensate, the decoys were minimized using a designated protocol (Supplementary Methods) within MESHI (Kalisman et al., 2005). The “near-nativeness” of each decoy is defined as the number of residues for which the side chain χ₁ angle is within 30^o of the native structure, and was neither significantly affected by the application of MESHI nor by ROSETTA (Figure 7A) and ROSETTA-membrane (Figures 7 and S7).

To look specifically at snorkeling, we isolated highly polar or charged residues (Asp, Asn, Glu, Gln, Lys, and Arg) that were designated by VOLBL (see below) as lying on the protein surface. We excluded residues for which the C_β atom had ∣Z∣ > 15 Å, since those are already in the aqueous solvent and do not snorkel. We also excluded residues that are involved in ion coordination, since their rotamers are determined by the geometry of the coordination. This left 5 residues in 3mk7, 14 residues in 1su4, and 32 in 2b6o that are considered to be snorkeling. The average deviation of χ₁ from the native structure for these residues was calculated before and after minimization with ROSETTA-membrane.

EmrE models

The C_α EmrE structure (PDB ID 3b5d) was used as a template for the dual-topology mutation analysis. Geometric constraints were used for backbone reconstruction (Gront et al., 2007). Missing residues at each terminus and all side chains were added and minimized using Rosetta (Rohl et al., 2004) with an mutations as in (Seppala et al., 2010). To determine the relative ratios of N_in and N_out, we assumed a Boltzmann distribution for the probability of finding the model in a given topology. The two configurations were delimited by −5Å≤Z≤5Å with θ ≤10° and θ≥170° for N_in and N_out, respectively. For this area the Boltzman probability (back-calculated from the reported Ez energy) was computed for each grid point. We then took the Boltzman probability ratio P(N_in)/P(N_out) (Supplementary methods) to eliminate the constant and further normalized so that the ratio for E14D was equal to that reported by Seppala et al. (Seppala et al., 2010).

Highlights.

• A statistical potential accurately positions proteins and peptides in the membrane.

• Topological energy landscapes present structure-function-stability relationships.

• Side-chain functional-atom parameters allow modeling of rotameric preferences.

• Experimental effects of point mutations on topology are quantitatively reproduced.