Abstract
Malaria resulting from Plasmodium falciparum infection is a major cause of human suffering and mortality. Red blood cell (RBC) deformability plays a major role in the pathogenesis of malaria. Here we introduce an automated microfabricated “deformability cytometer” that measures dynamic mechanical responses of 103–104 individual RBCs in a cell population. Fluorescence measurements of each RBC are simultaneously acquired, resulting in a population-based correlation between biochemical properties, such as cell surface markers and dynamic mechanical deformability. This device is especially applicable to heterogeneous cell populations. We demonstrate its ability to mechanically characterize a small number of P. falciparum-infected (ring stage) RBCs in a large population of uninfected RBCs. Furthermore, we are able to infer quantitative mechanical properties of individual RBCs from the observed dynamic behavior through a dissipative particle dynamics (DPD) model. These methods collectively provide a systematic approach to characterize the biomechanical properties of cells in a high-throughput manner.
Introduction
RBC deformability may be pathologically altered due to inherited genetic disorders (e.g. sickle cell anemia and hereditary spherocytosis), and both non-infectious 1 and infectious 2 diseases. Decreased human RBC deformability is both a cause of and biomarker for disease states 3. Malaria, a disease threatening approximately 2.2 billion people globally, and causing about 250 million clinical episodes and 1 million deaths annually 4, is an important example of an infectious disease process that drastically decreases RBC deformability. The most virulent human malaria parasite, Plasmodium falciparum, invades and develops within RBCs, and transitions through morphologically-distinct ring, trophozoite and schizont stages during the 48-hour maturation period within the RBC 5. While ring stage parasite-infected RBCs are less deformable than uninfected RBCs by only several-fold, late (trophozoite and schizont) stage parasite-infected RBCs are stiffer by a factor of up to 50 or more 2, 6.
Altered RBC deformability has important implications for disease pathophysiology. In traversing a blood capillary, the biconcave disc-shaped RBC must deform dramatically, as its unconstrained diameter exceeds that of a capillary. The reticuloendothelial system (RES) plays an important role in eliminating parasite-infected RBCs from the circulation, and achieves this in part by sensing increases in RBC membrane rigidity 7. While the RES can efficiently deplete rigid late stage parasite infected RBCs from the circulation, the less rigid ring-stage-parasite infected RBCs are inefficiently removed 7. Thus, ring but not late stage parasite infected RBCs can be found in the peripheral circulation and measured for diagnostic purposes. Additionally, increased stiffness of late stage parasite infected RBCs, together with their enhanced adherence to endothelial cells, leads to their sequestration in the microvasculature of various organs. This is believed to be a key event precipitating potentially fatal malaria complications such as cerebral malaria 8. As such, characterizing parasite infected RBC deformability in a quantitatively rigorous manner will be important for better understanding the basic mechanisms underlying host clearance of parasite-infected RBCs and overall malaria pathophysiology. To this end, robust laboratory methods for quantitatively analyzing cell deformability in high throughput over heterogeneous cell populations and at low cost are desirable.
Existing high-throughput methods for analyzing and quantifying cell deformability typically overlook cell population heterogeneity, and quantitative single-cell measurements are generally labor and skill-intensive. While methods for studying cell biochemical characteristics (e.g. fluorescence-activated cell sorting (FACS)) are common, there is a paucity of techniques for investigating dynamic mechanical properties of cells. Commonly used methods for studying RBC deformability include filtration 9 and laser diffraction ellipsometry 10, which both measure bulk properties of a cell population. Therefore, these methods are not applicable in situations where the target cells constitute a small fraction of the entire cell population 11, as would routinely be the case for minimally processed laboratory or clinical samples containing P. falciparum-infected RBCs. Furthermore, past work involving filtration typically involves a sheet of pores, resulting in only a single pore-transit measurement for each cell 11–14.
Examining cells individually is an important strategy for characterizing inherently heterogeneous cell populations. Micropipette aspiration is one such method, and it has been applied to quantitatively study infected RBC deformability 15. However, it is laborious and limited in its throughput 16. More recent techniques include atomic force microscopy 17, optical stretching 18, and optical tweezers 19. Still, these methods are labor-intensive, expensive, and time-consuming. Furthermore, the relevance of these essentially static mechanical responses to what the RBC experiences in the circulation of a living organism may be limited.
Improvements in microfabrication techniques have enabled the creation of pores comparable in size to the smallest human capillaries 20. Studies using these devices are similar in nature to those involving micropipette aspiration 21, 22. However, less time and effort are required due to the well-controlled dimensions of the pores and the ability to simultaneously examine many cells. Furthermore, studies using microfabricated pores arguably simulate more closely the movement of individual RBCs through capillaries in vivo. Along these lines, a microfabricated device similar to a single micropipette aspirator has been created to examine the rigidity of P. falciparum infected RBCs 22. However, this single micropore design significantly limits overall throughput, and cell-cell interactions resulting in clogging at the pore inlet complicate obtaining quantitative and statistically significant data for cell populations.
Here we introduce an automated, microfabricated ‘deformability cytometer’ that measures dynamic mechanical responses of about 103–104 individual RBCs in a population. Fluorescence measurements on each RBC are simultaneously acquired, resulting in a population-based correlation between biochemical properties (e.g. cell surface markers) and dynamic mechanical deformability. Significantly extending past work 20, 22, we propose a novel method relying on low Reynolds number fluid mechanics to evaluate the effect of entrance architecture on the sensitivity of cell deformability measurements. Custom software was written to automate video processing and facilitate easy analysis of thousands of RBCs, which is rarely accomplished in microfluidic systems. This higher throughput enabled us to measure statistically significant differences in deformability between two cell populations. Lastly, a Dissipative Particle Dynamics (DPD) model was built to translate the experimental measurements into quantitative data describing the mechanical properties of individual RBCs. This is the first study to systematically design and implement a microfluidic device capable of measuring cell deformability in high throughput and is sufficiently simple and inexpensive such that it can potentially be tailored for use with many different cell types.
Results
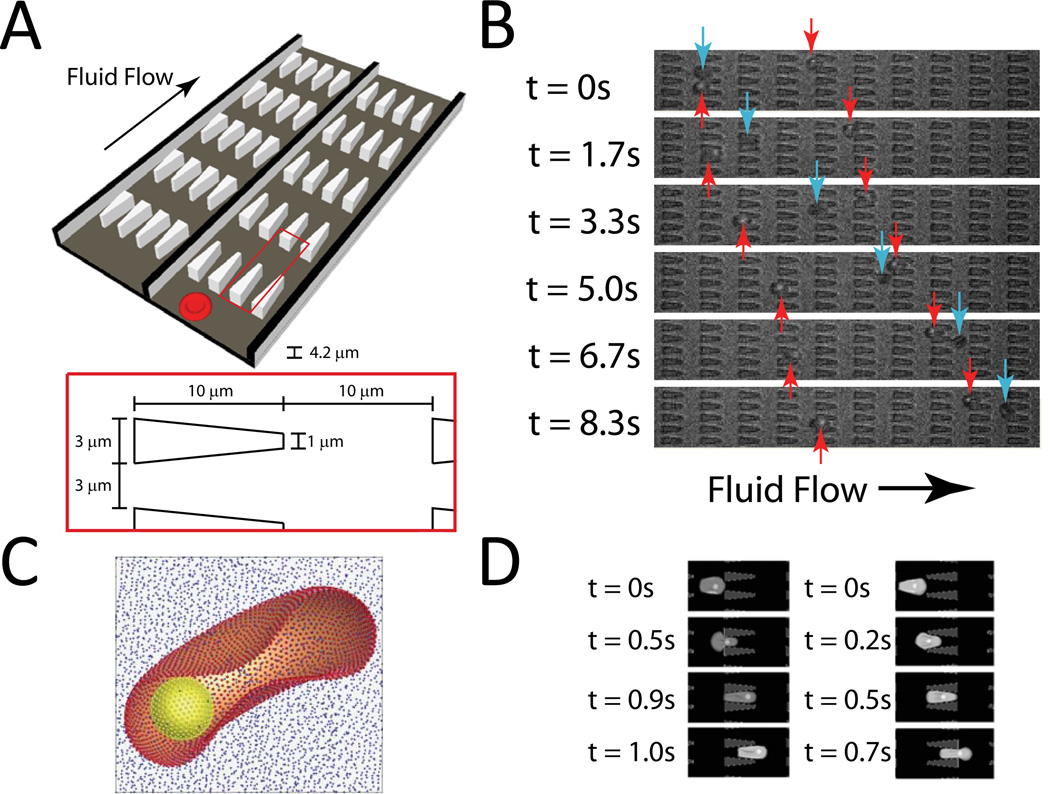
Our device design involves periodically spaced, triangle-shaped pillars. The gaps between these pillars result in well-controlled constrictions for RBCs to pass. The height of the device was set to 4.2 µm to encourage RBCs to assume a flat orientation before entering each constriction. This height, in addition to filters at the reservoirs (10 µm diameter pillars spaced 10 µm apart), prevents white blood cells from entering the device, permitting diluted whole blood to be used directly. As in any of these types of microfluidic devices, this device will eventually clog after a long term operation. However, the device can be operated until approximately 104 cells are analyzed before significant clogging occurs, resulting in the ability to generate statistically-significant results using a single device. Further increasing the parallelism of the device will result in the ability to expand the number of cells analyzed by 1–2 orders of magnitude. Still, in any design where objects are forced to enter a pore clogging is inevitable; in another approach, we forced cells to travel at an oblique angle to slits, which avoids the clogging problem 23. In our experiments, the concentration of RBCs is sufficiently low such that there is minimal interaction between cells and that transit times are independent. The constrictions in parallel across the width of the channel allow higher throughput, and the constrictions in series along the length of the channel enable repeated measurements of the same cell, increasing precision. Typically, the velocity of the cell is tracked across 10 such constrictions. Figure 1A and B illustrate the device design and demonstrate infected and uninfected RBCs moving at different velocities.
Figure 1.
A. Illustration of device design; each channel of the actual device is 10 pores wide and 200 pores long. B. Experimental images of ring-stage P. falciparum-infected (red arrows) and uninfected (blue arrows) RBCs in the channels at a pressure gradient of 0.24 Pa/µm. The small fluorescent dot inside the infected cell is the GFP-transfected parasite. At 8.3 s, it is clear that the uninfected cell moved about twice as far as each infected cell. C. The computational RBC model consists of 5000 particles connected with links. The P. falciparum parasite is modeled as a rigid sphere inside the cell. D. DPD simulation images of P. falciparum-infected RBCs traveling in channels of converging (left) and diverging (right) pore geometry at 0.48 Pa/µm.
In past studies involving microfabricated pores, there has not been a determined effort to examine the influence of the pore shape on the ability of a cell to enter. For example, some studies use 90-degree angles for the walls of the pores 20, while others use angled or curved entrances 21, 22. In addition, most previous studies rely on the passage of many cells through a single pore, rendering the device susceptible to clogging and other confounding factors during the critical trapping and escape process at the bottleneck. These differing shapes naturally leads to the question of whether the geometry of constriction affects the amount of force required for cell herniation and traversal for openings of the same eventual cross-sectional area. Given the complicated nature of a cell’s deformation process through the pore, we believe it may be possible to determine an optimized geometry ideally suited for “deformability selection.”
To address these questions, we built a device to compare pairs of pore entrance geometries (Figure 1A). In this device are two channels in parallel with pores of different rates of constriction. According to low Reynolds number laminar flow, the forward and backward flow velocities and resistances will be identical 24. When we introduce low concentrations of cells, we are able to simultaneously observe control and experiment in the same microscope field of view. The difference in velocity of cells moving in the two channels indicates the role that entrance effects play in cell deformation through the pores with different entrance geometries, as confounding effects caused by temperature 19, cell age 25, buffer conditions 26, pressure, and device variability are obviated.
Verification of indistinguishable fluid velocities in two channels
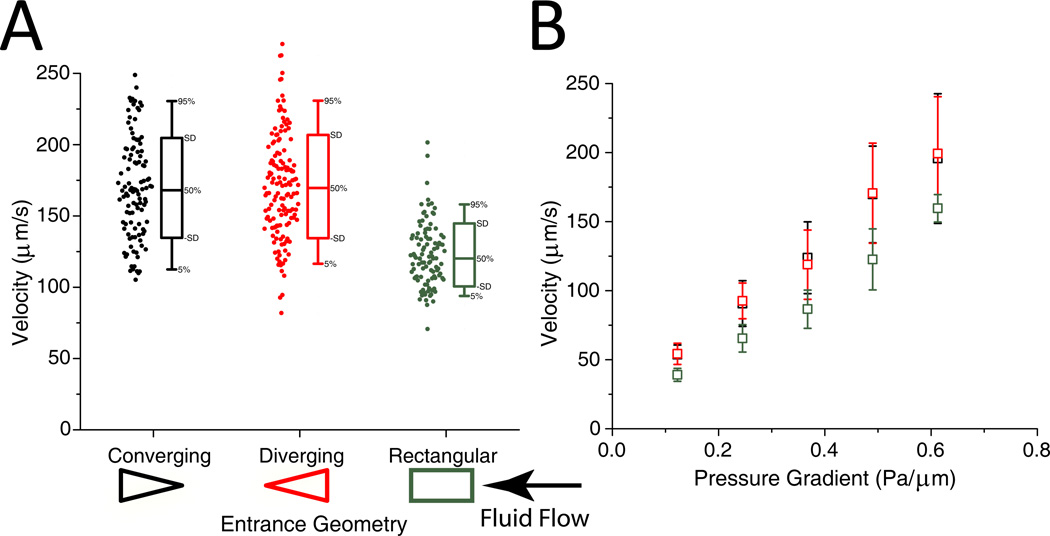
To verify indistinguishable fluidic resistance in, and flow rate through, the two parallel channels, we introduced 200 nm non-deformable polystyrene beads into the fluid to track velocity. In the range of pressures and fluid velocities that are relevant both physiologically and in our experiments, we found that there were no statistically significant differences in bead velocity through the channels (Figure 2). The spread in bead velocities is mostly attributable to non-constant fluid velocities across a cross section of the channel, due to the viscous nature of the fluid.
Figure 2.
A. Velocity of individual 200-nm-diameter beads at a pressure difference of 0.49 Pa/µm. There is no statistically significant difference in the velocity of beads travelling through the converging and diverging geometries. The beads travelling through the channel with rectangular obstacles move slower on average. B. Velocity vs. Pressure for the different obstacle geometries.
DPD simulations confirmed this result. The difference in fluid flow velocity was found to be less than 0.3%, confirming that the fluidic resistance does not depend on the orientation of the obstacles. Streamlines were also examined to confirm almost complete reversibility of the flow.
Effect of fluid velocity and obstacle orientation on velocity of RBCs
We performed all of the experiments using RBCs diluted to approximately 1% hematocrit. At high hematocrit, cell-cell interactions would dominate in the channels, as fluidic resistances and velocities would be affected by nearby cells. However, at very low hematocrit, experiments would take an unreasonably long time to run. We found that at ~1% hematocrit, cell-cell interactions were negligible and approximately 1000 cells could be analyzed in 10 minutes.
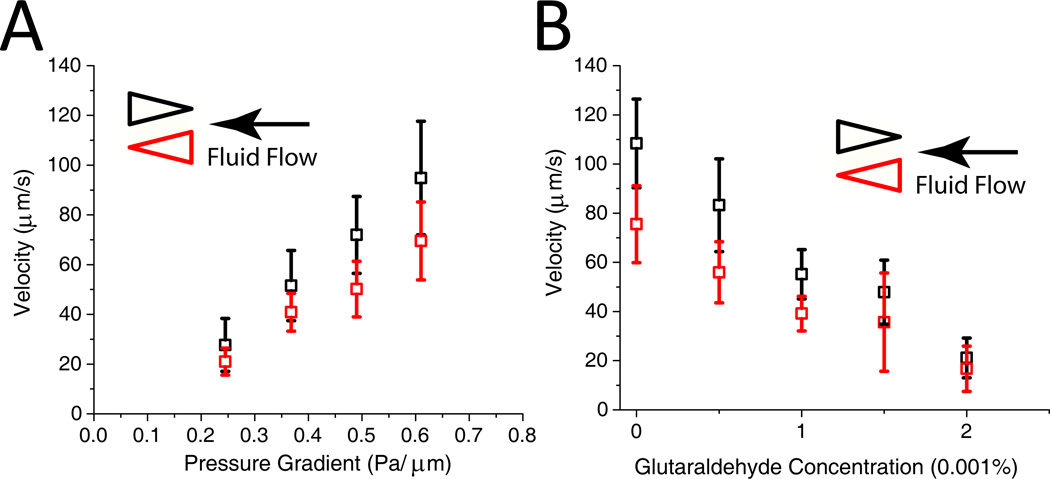
At all of the pressure gradients, RBCs exhibited faster velocity in the channel with converging entrance geometries (Figure 3A). On average, RBCs traveled 25.5 % slower in the channels with diverging geometries. The large standard deviation of velocities is consistent with experimental results presented by others 20. Consistent with the results of Brody et al., the velocity is independent of projected cell size and is confirmed by our computational simulations. The large variation in velocity may be caused by the increasing stiffness of the RBCs over their 120-day lifespan.
Figure 3.
A Velocity vs. pressure for RBCs moving through the two pore geometries. Error bars indicate standard deviation for each measurement. B. Velocity vs. glutaraldehyde concentration (v/v). RBCs were treated with the indicated concentration of glutaraldehyde for 30 minutes in PBS and then washed 3 times. The pressure difference/length was approximately 0.61 Pa/µm.
Effect of RBC stiffness on velocity through different constriction geometries
Treatment with increasing concentrations of glutaraldehyde for a limited period of time results in cells of increased stiffness 27. At concentrations of glutaraldehyde less than 0.002% and treatment for 30 minutes, more than 95% of the RBCs moved through the device. As we increased the glutaraldehyde concentration in the treatment solution, RBCs became progressively stiffer. As shown in Figure 3B, there is an inverse correlation between the degree of artificial stiffening and the velocity of the RBCs through the channels. At a glutaraldehyde concentration greater than 0.003%, the majority of RBCs became immobilized toward the entrance of the device. These experiments demonstrate that decreased deformability alone can cause RBCs to travel with slower velocity in this device, as cell shape and size are preserved during glutaraldehyde treatment27.
Deformability of late ring-stage P. falciparum-infected RBCs
We performed this set of experiments using late ring-stage P.falciparum-infected RBCs that were transfected with a gene encoding green fluorescent protein (GFP) (Figure 4). It is believed that treatment with cell dyes influences the deformability of the cells 28. By using cells that express GFP, we overcome this concern. Our image analysis program tracked a shadow without a bright dot inside as an uninfected RBC and a shadow with a bright dot inside as an infected RBC. Around 1000 RBCs were tracked for each pressure gradient. The parasitemia in this set of experiments was around 1–2%. In all of these experiments, we observed negligible pitting, expulsion of the parasite from the RBC.
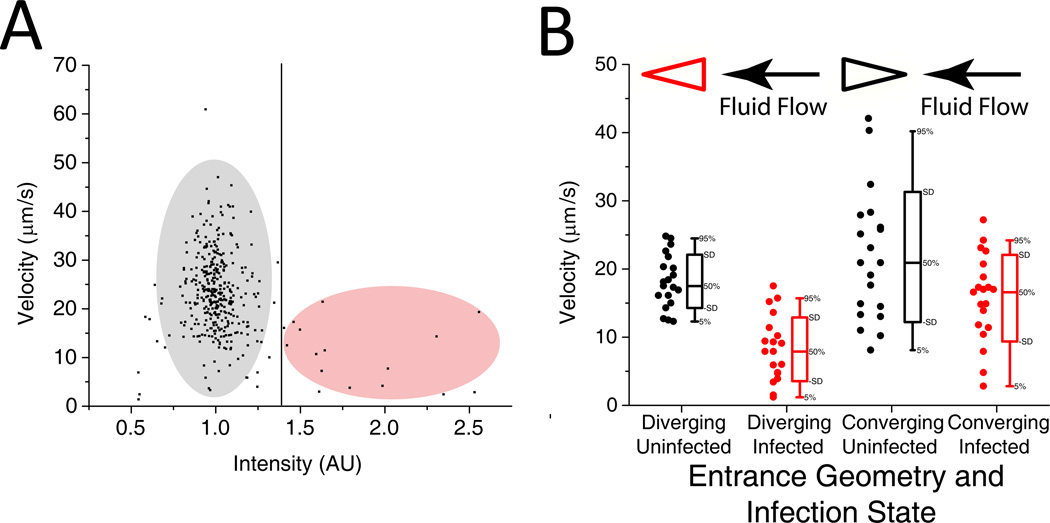
Figure 4.
A. FACS-like plot of velocity vs. intensity for ring-stage P. falciparum infected RBCs at a pressure gradient of 0.24 Pa/µm travelling in the converging geometry. Points to the right of the vertical line represent velocities of infected RBCs, while those to the left represent velocities of uninfected RBCs. The velocities of 381 RBCs were tracked. B. Velocity vs. infection state for RBCs infected with late ring-stage parasites at a pressure gradient of 0.24 Pa/µm. For each infected cell that was tracked, the next uninfected cell was tracked. Twenty cells were tracked for each measurement.
We determined that optimal pressure gradients for device operation are around 0.24 and 0.37 Pa/µm. For both the converging and diverging geometries, at pressure gradients of 0.24 and 0.37 Pa/µm, infected RBCs exhibited lower average velocities than uninfected RBCs. A p-value less than 0.01 at these pressure gradients leads us to conclude that the mean velocities for the infected and uninfected cells are different with statistical significance. These results are consistent with those involving micropipette aspiration 15. In those experiments, ring-stage infected RBCs required around 1.5–2 times the pressure and around 1.5 times the time to enter single pipette pores of around 3–3.5 µm. At higher pressures, mean velocities of infected and uninfected RBCs moving through the device converged. At a pressure gradient of 0.48 Pa/µm, uninfected and infected RBCs moved through the converging geometry at approximately the same velocity (about 50 µm/s).
In Figure 4B, we show that the diverging geometry is better able to accentuate differences in deformability between ring-stage infected cells and uninfected cells. The median velocity of infected cells in the diverging geometry is 44% of that of the uninfected cells, compared to 80% in the converging geometry.
Deformability of reticulocytes contained in whole blood
Reticulocytes are immature RBCs and typically account for around 1% of RBCs in whole blood. In contrast to mature RBCs, reticulocytes contain residual amounts of RNA. In our experiments, we diluted whole blood in phosphate-buffered saline (PBS) containing thiazole orange, a nucleic acid stain for reticulocytes. Then, the diluted blood was used directly in our device, without any further pre-treatment. White blood cells are removed at the inlet region of the device due to the 4.2 µm device height and filtration pillars and therefore do not interfere with the operation of the device.
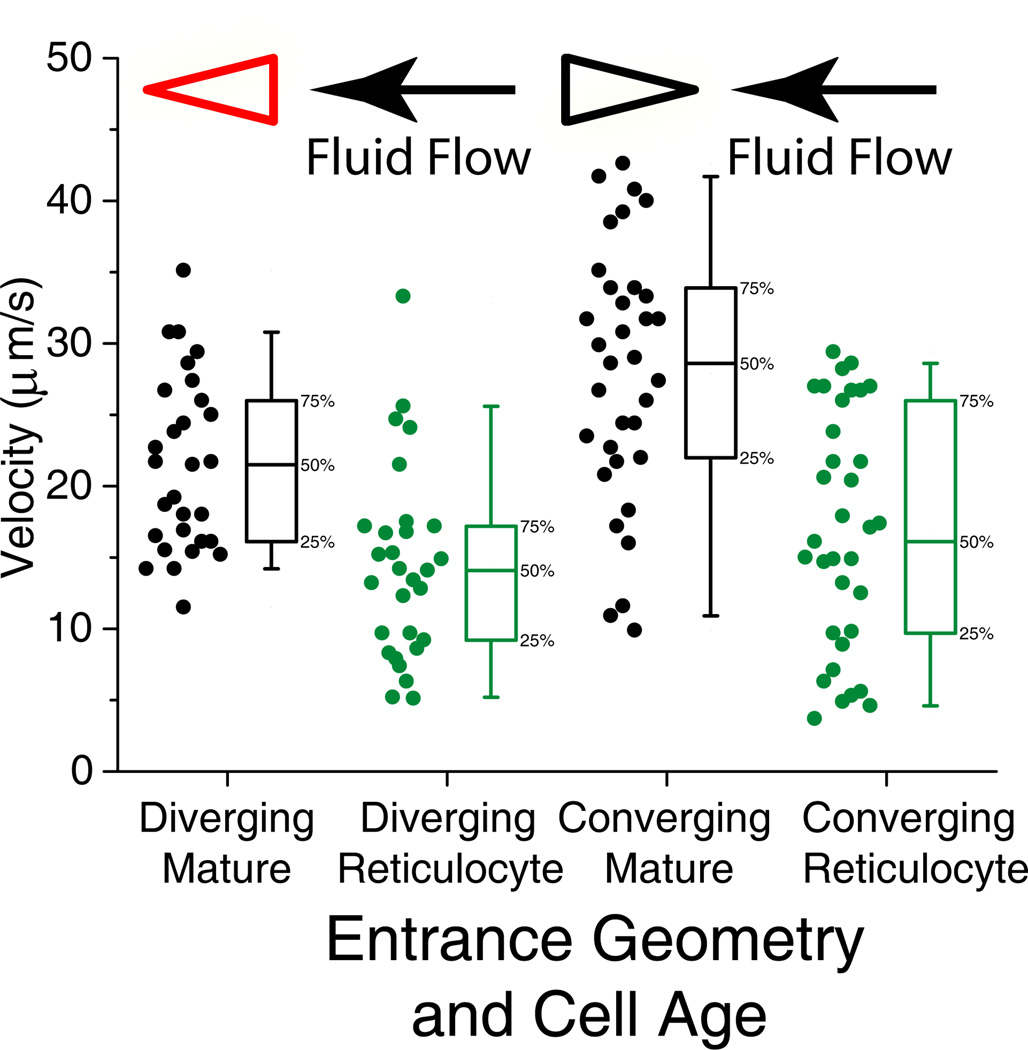
Reticulocytes are larger than mature RBCs, on average having 44 µm2 more surface area and 29 fL greater volume than mature RBCs 29. Additionally, reticulocytes are more rigid than mature RBCs. Reticulocytes take a substantially longer time to enter a single pore 30, and much higher pressure is necessary to bend the reticulocyte membrane and to force it to enter a pipette 28. The membrane shear elastic modulus of reticulocytes is almost double that of mature RBCs 31. In our experiments, reticulocytes exhibited velocity on average 67% that of mature RBCs in the diverging geometry, and 61% that of mature RBCs in the converging geometry (Figure 5).
Figure 5.
Velocity vs. cell maturation state. All experiments were run simultaneously, at a pressure gradient of 0.24 Pa/µm. Whole blood RBCs was stained for nucleic acid content with thiazole orange. Cells homogeneously fluorescesing under the GFP filter set were identified as reticulocytes. For every reticulocyte that was identified and tracked for 200 µm, the next cell appearing in the field of view was also tracked.
Dissipative Particle Dynamics (DPD) simulation of cell deformation through different constriction geometries
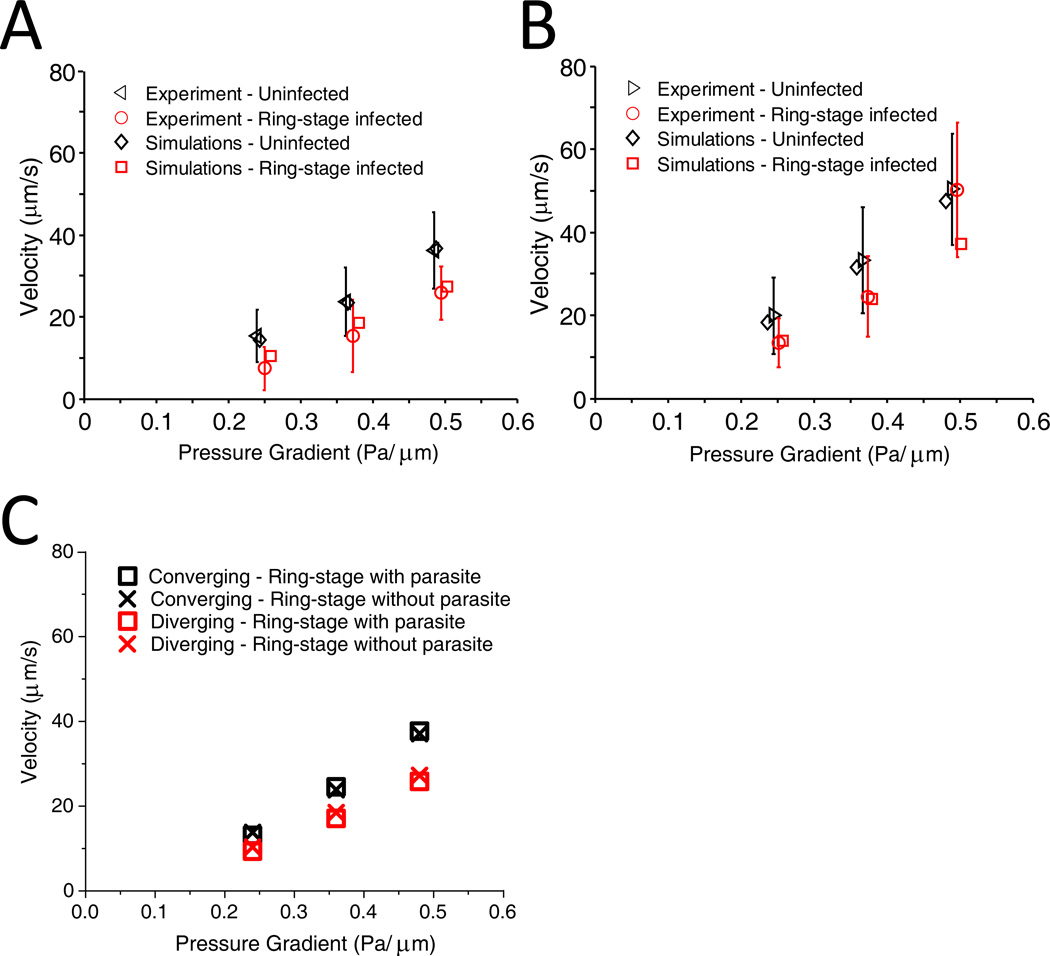
We performed three-dimensional simulations of uninfected and P. falciparum-infected cells using the DPD method. Infected cells were modeled with increased shear modulus and membrane viscosity values obtained from quantitative experimental measurements performed by recourse to optical tweezers stretching of the parasitized RBCs 19. We modeled the parasite as a rigid sphere, 2 microns in diameter 32, placed inside the cell (Figure 1C). Snapshots from simulations showing passage of an infected RBC through channels with converging and diverging pore geometries are shown in Figure 1D. Simulations were able to capture the effects of pore geometry and changes of RBC properties arising from parasitization quite well. Quantitative comparison of simulation results with experimental data for uninfected and infected cell velocity as a function of applied pressure gradient is shown in Figure 6A and B.
Figure 6.
A. Velocity vs. pressure for uninfected and ring-stage-infected RBCs in diverging pore geometry: comparison of simulation and experimental results. For experimental data, mean values are shown. The error bars correspond to one standard deviation. B. Velocity vs. pressure in converging pore geometry. C. Effect of intracellular parasite presence on the velocity of ring-stage infected cells. The parasite is modeled in simulations as a rigid sphere, 2 microns in diameter, placed inside the cell.
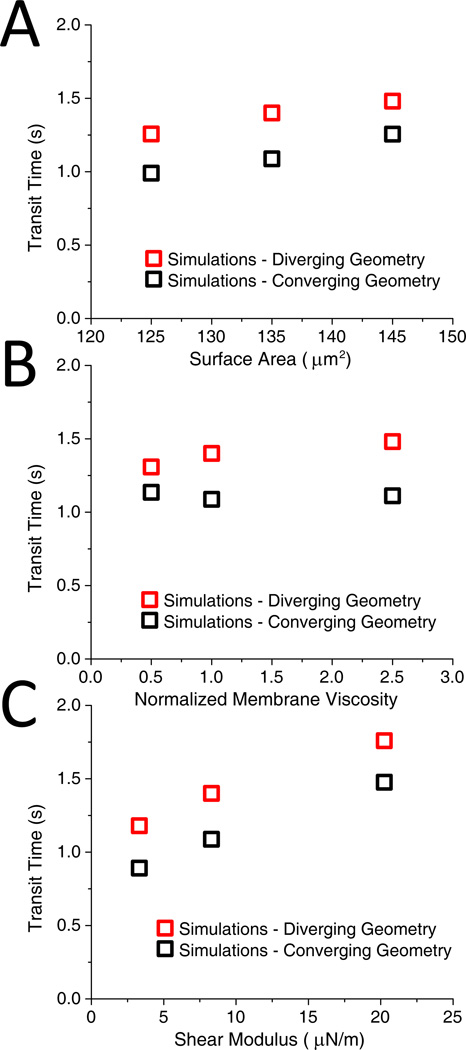
In order to evaluate contributions of individual mechanical properties of the cell to overall dynamic behavior, we performed additional simulations. The DPD model provides a unique opportunity to perform this analysis, since experimental evaluation of these contributions is laborious or impossible. We found that the flow behavior of infected RBCs in the device was not affected by the presence of the parasite inside the cell (Figure 6C). Larger cells were found to travel with lower velocities; however, the velocity variation due to cell size was not significant (Figure 7A). Therefore, decrease of the traverse velocity of infected RBCs was mainly due to the increase of membrane shear modulus and/or membrane viscosity. Additional simulations were performed in which membrane shear modulus and membrane viscosity were varied independently of each other. The results showed that shear modulus was a dominant factor, while variation of membrane viscosity did not contribute significantly to the decrease of velocity of infected cells.
Figure 7.
Dissipative particle dynamics (DPD) simulations. A. Effect of RBC size variation on transit time at a pressure gradient of 0.24 Pa/µm. Cells with surface area of 125, 135 and 145 µm2 are modeled with corresponding volumes of 85, 94 and 103 µm3. B. Effect of membrane viscosity variation on RBC transit time at a pressure gradient of 0.24 Pa/µm. The membrane viscosity is normalized by the uninfected cell membrane viscosity value. C. RBC transit time vs. membrane shear modulus at 0.24 Pa/µm.
Increased membrane viscosity should increase the time it takes for a RBC to traverse an individual pore. However, it also slows down the recovery of RBC shape when the cell is traveling between pores, making it easier to enter the next pore. As a result, the particular design of our device lessens the dependence of the cell velocity on membrane viscosity (Figure 7B). Increased membrane shear modulus increases the transit time for an individual pore and also accelerates shape recovery, making it more difficult to enter the next pore. In Figure 7C we plot the variation of time it takes a cell to travel from one set of obstacles to the next at a pressure gradient of 0.24 Pa/µm as a function of membrane shear modulus. To a first approximation, the time increases linearly with shear modulus within the range considered in simulations. This simple dependence can be an advantage if the device is used to estimate the average shear modulus of a cell population based on the average velocity. For higher values of shear modulus, the transit time is likely to become a non-linear function; however, stiffer cells (e.g. shear modulus greater than 30 µN/m, 19) are presumably cleared by the spleen and therefore not typically present in free circulation.
Discussion
We have developed a versatile tool to measure cells’ deformability in a quantitative, high-throughput manner, along with other optical (fluorescence) characteristics of the cells. We applied our deformability cytometer to malaria research, by measuring dynamic deformability of low-abundance (1–2%) ring-stage infected RBC population out of a much larger number of uninfected RBCs. Common methods for assessing cell deformability involve bulk measurements 3. Therefore bulk measurements do not offer the sensitivity required to measure the mechanical properties of only the infected RBCs. Furthermore, bulk measurements require relatively large volumes of precious cultured cells. Our device also overcomes many of the limitations inherent in traditional single-cell measurements, such as low throughput and measurement artifacts that decrease physiological relevance. Additionally, diluted whole blood can be directly used in our device, without the need for centrifugation or other separation steps. It is straightforward to combine our device with other microfluidic methods to assess cell properties, such as the surface area-to-volume measurement parallel microchannels33 and the oxygen perfusion-approach of Higgins et al. 34.
Quantitative measurement of dynamic cell deformability for various stages of P. falciparum-infected RBCs (both asexual and sexual stages) and other types of blood cells would be significant, both scientifically and clinically. P. falciparum-infected RBC deformability could be used as a biophysical marker for enriching infected RBCs for improving the sensitivity of microscopy-based malaria diagnostics35. In addition, dynamic deformability measurement in this work essentially measures the cell’s susceptibility to the splenic biofiltration process, which has a significant role in clearing both malaria parasites and other bloodborne pathogens in general36.
In our results, deformability measurement of ring-stage P. falciparum infected RBCs and uninfected RBCs shows significant overlap in terms of their dynamic deformability, even though the average dynamic deformability (measured as the cell velocity) are clearly different for the two populations. One confounding issue is the low abundance of infected cells (typically less than 2%) compared with uninfected cells. This means that extreme outliers of Gaussian-like cell velocity distribution of uninfected cells could still overwhelm the minority population of infected RBCs in our measurement, which is a ubiquitous problem in low-abundance detection. In addition, the normal RBC population is inherently diverse, due to cells’ age and other factors 25. Because the spleen removes some of the older RBCs and not all of the ring-stage P. falciparum-infected RBCs, as demonstrated by Safeukui et al.7, it can be inferred that the rigidities of ring-stage P.falciparum-infected RBCs and uninfected but older RBCs must overlap to some extent. We suspect that a rather large distribution of deformability for the uninfected RBC population may come from this diversity. When any single modality alone (e.g. cell deformability or cell surface marker status) cannot be used due to its limited specificity, multi-modal analysis provide more precise discrimination between different cell populations, as we have demonstrated. Our ability to differentiate reticulocytes from P. falciparum-infected cells is an example of such a multi-modal analysis. In Figures and 5, we observe that the velocities of reticulocytes and P. falciparum-infected cells are similar compared to those of uninfected cells. As cell rigidity alone cannot differentiate the two populations, staining with fluorescent dyes that distinguish RNA and DNA content provides another level of resolution. Reticulocytes contain uniformly dispersed RNA remnants and P. falciparum-infected cells contain localized DNA within the parasite. Therefore, a combination of cell deformability and fluorescence cytometry allows differentiation of these cell populations, and quantitative measurement of their respective dynamic deformability properties. Additionally, the ability of our deformability cytometer to clearly distinguish reticulocytes in a large population of RBCs points to its potential for studying other human malarial parasites, such as Plasmodium vivax malaria, which preferentially invades reticulocytes.
We have also shown experimentally, for the first time, that entrance geometry of the constriction has a significant impact on RBC transit time, which has not been fully appreciated before. We have also experimentally demonstrated that geometries with sharper corners are better able to discriminate differences in RBC deformability for a given pressure difference. Using this tool, we measured the dynamic deformability of ring-stage P. falciparum-infected RBCs quantitatively and statistically significantly. Using the advanced DPD modeling and simulation, it should be possible to further optimize the entrance geometries for better selectivity of infected versus uninfected RBCs. Currently, there is some disagreement regarding which aspect of pore traversal causes the distribution in velocities. Brody et al. assert that pore entrance time is insignificant compared to kinetic friction between the RBC membrane and device walls for differences in RBC velocity 20. However, Secomb and Hsu propose that the time taken for RBCs to enter pores is more than one half of the transit time for a single pore 37. In addition to the distribution in velocities, the effect of the entrance shape on traversal time has not been experimentally examined. Computational simulations examining the impact of entrance radius of curvature on the neutrophil transit time indicate that larger radii of curvature result in decreased transit time 38. However, to the best of our knowledge, no controlled experimental studies have been presented. In our experiments, we found that converging geometries resulted in RBCs exhibiting faster velocities on average when moving through the channels. We also found that an entrance geometry with a more abrupt transition from an open region to a pore is better at discerning differences in RBC deformability, as shown by our experiments with late ring-stage P. falciparum-infected RBCs. Whole blood is known to be a non-Newtonian fluid, with viscosity decreasing with shear rate. However, in the context of our experiments, this large-scale effect does not play a major role, since in our experiments the hematocrit was approximately 1%, while it is between 33% and 49% in whole blood. What is relevant in our experiments is the relaxation time of an individual RBC (approximately 0.2 seconds) 39. When an individual RBC does not have enough time to recover its original shape before crossing from one constriction to the next, that RBC may assume a more favorable shape upon encountering the second constriction. This more favorable shape may then decrease the amount of time required for the RBC to deform and traverse the next pore than what would be predicted had the RBC assumed its original shape. Computer simulations by Shirai et al. of neutrophils passing through a succession of two cylindrically-symmetrical pores showed reduced transit time through the second pore under certain flow conditions 40. Groisman et al. applied this phenomenon in the context of polyacrylamide polymers to create microfluidic flux stabilizers 41. When the RBC relaxation time is substantially greater than the inter-pore travel time (e.g. at high pressure gradients), the ability of our device to discriminate differences in rigidity will be diminished. More generally, when the pore-traversal time is substantially shorter than the relaxation time of the RBC, the sensitivity of the measurement to deformability may be compromised. Therefore, we believe there is a maximum throughput for pore-based deformability measurement methods.
The device that we present may be applicable to drug efficacy screening and cancer diagnostics. In P. falciparum malaria, only ring-stage infected RBCs are found in the circulation, while later-stage infected RBCs are either removed by the spleen (due to their increased stiffness) or adhere to the vascular endothelium (due to their cytoadherent properties). In fact, the subtle deformability increase of ring-stage infected RBCs and their ability to pass through the spleen are critical for P. falciparum survival in an infected host. One obvious and interesting application of this device would be screening for drug compounds that increase ring-stage infected RBC rigidity to improve splenic clearance, or decrease late-stage parasite infected RBC rigidity to prevent capillary blockage. It has also been shown that primary cancer cells exhibit different deformabilities compared to normal cells42. Often cells from primary tumors detach and circulate in the bloodstream. Although the concentration of these circulating tumor cells (CTCs) is very low, we believe that with appropriate pre-processing steps, our device may be able to further enrich for these CTCs and aid in their detection. Overall, we believe the microfluidic deformability-based flow cytometer will provide unexplored opportunities in drug efficacy screening and cancer detection.
Materials and Methods
Device Fabrication
A mold of the device was made on a silicon wafer using photolithography and reactive-ion etching techniques. A 5x reduction step-and-repeat projection stepper (Nikon NSR2005i9, Nikon Precision) was used for patterning. The spacing between pillars was 3 µm, and the depth of the device was 4.2 µm. Devices with other depths were also created, however those with depths less than 3 µm resulted in RBCs not being able to satisfy their surface-area to volume constraints and the device clogging up within minutes. Devices with depths greater than 5 µm resulted in RBCs not substantially deforming while passing through the pores, which led to a loss of sensitivity. Details regarding the device structure are presented in Figure 1A. The device was made using standard PDMS casting protocols and bonded to a glass slide.
Parasite culture
P. falciparum was cultured in leukocyte-free human RBCs (Research Blood Components, Brighton, MA) under an atmosphere of 5% O2, 5% CO2 and 95% N2, at 5% hematocrit in RPMI culture medium 1640 (Gibco Life Technologies) supplemented with 25 mM HEPES (Sigma), 200 mM hypoxanthyne (Sigma), 0.20% NaHCO3 (Sigma) and 0.25% Albumax II (Gibco Life Technologies). Parasites were synchronized by treatment with 5% sorbitol at least 12 hours before sample collection. The strain FUP-GFP, expressing a GFPmut2-neo fusion protein, was constructed by transfecting P. falciparum strain FUP with the plasmid pFGNr (Malaria Research and Reference Reagent Resource Center). Parasites expressing GFPm2:neo were selected with 350 mg/L G-418. Transfection was performed by the spontaneous DNA uptake method 43.
Experimental Protocol
PBS was mixed with 0.2 % w/v Pluronic F-108 (BASF, Mount Olive, NJ) and 1 % w/v Bovine Serum Albumin (BSA) (Sigma-Aldrich, St. Louis, MO) as a stock solution to prevent RBC adhesion to the device walls. This was the stock solution used in all of the experiments. For the fluorescent bead experiments, 200 nm FluoSpheres europium luminescent microspheres (Molecular Probes, Eugene, OR) diluted to a final concentration of 1.25×10−5 percent solids were used.
In experiments involving blood, 1 µl of whole blood (~50% hematocrit) was diluted in 100 µl of the PBS-pluronic-BSA solution for all of the experiments. In experiments involving parasites that express GFP, no further treatment was performed. These cells appear as shadows with a small fluorescent circle inside, as shown in Figure 1B. In experiments involving uninfected RBCs, 1 µl of whole blood (Research Blood Components, Brighton, MA), 1 µl of 50 µg/ml of Cell Tracker Orange (Invitrogen, Carlsbad, CA), and 98 µl of PBS were mixed with the indicated concentration of glutaraldehyde and allowed to sit for 30 minutes. The sample was then washed 3 times with the PBS-Pluronic-BSA solution. In experiments involving reticulocytes, 1 µl of whole blood, 89 µl of the PBS-Pluronic-BSA solution, and 10 µl of 1×10−6 M thiazole orange were mixed and allowed to sit for 20 minutes before starting experiments. In our videos, reticulocytes appear as uniformly fluorescent cells under the GFP filter set, while mature RBCs appear as shadows.
The PBS-Pluronic-BSA solution was pumped through the device for 30 minutes to coat the device walls with Pluronic and BSA. The RBC-PBS-Pluronic-BSA suspension was then injected into the device. Differences in pressure between the two reservoirs were generated hydrostatically by a difference in water column height. Liquid columns were connected to 60-ml plastic syringes lacking plungers to minimize surface tension effects. A Hamamatsu Model C4742-80-12AG CCD camera (Hamamatsu Photonics, Japan), connected to an inverted epi-fluorescent Olympus IX71 microscope (Olympus, Center Valley, PA) was used for imaging. IPLab (Scanalytics, Rockville, MD) was used for video acquisition, resulting in an .avi file.
Data Analysis
A custom-written MATLAB program tracked the RBCs and generated data used for velocity histograms. This program first applies a high-pass filter to the video frames and then identifies RBCs based on areas of intensity above a certain threshold and within a preset size. After identifying the RBCs in a particular frame, it first attempts to match the RBCs in the current frame to RBCs in the previous frame based on proximity. The program then takes the location and velocity of RBCs in the previous frame to confirm the match to RBCs in the current frame. The end result of this program is a video with RBCs identified by number and a spreadsheet of each RBC’s velocity. The video was then checked for RBC identification accuracy.
Simulation Setup
The Dissipative particle dynamics (DPD)44 method was employed in simulations. In DPD, the fluid, solid walls, and RBC membrane are represented by collections of particles. The particles interact with each other through soft pairwise forces: conservative, dissipative, and random force. The latter two form the DPD thermostat and are linked through the fluctuation-dissipation theorem. The viscosity of the DPD fluid can be varied by changing the functional form and magnitude of these forces45. The solid walls were assembled from randomly distributed DPD particles whose positions were fixed during the simulations. In addition, bounce-back reflections were used to achieve no-slip conditions and prevent fluid particles from penetrating the walls46. A portion of the microfluidic device with dimensions 200 by 120 by 4.2 microns containing 5 rows of pillars (10 pillars in each row) was modeled. The fluid region was bounded by four walls while periodic boundary conditions were used in the flow direction. The RBC was simulated using 5000 DPD particles connected with links47. The model took into account bending, in-plane shear energy, and membrane viscosity. The effect of membrane viscosity was modeled by adding frictional resistance to each link. The total area and volume were controlled through additional constraints. Parameters of the uninfected cell model were derived from RBC spectrin network properties47–49. In addition, membrane fluctuation measurements and optical tweezers experiments were used to define simulation parameters. Specifically, we required that the amplitude of thermal fluctuations of the membrane at rest to be within the range of experimental observations50. We also required that the characteristic relaxation time of the RBC model in simulations to be equal to the experimentally measured value of 0.18 seconds. For P. falciparum infected cells, the membrane shear modulus and viscosity were increased 2.5 times19. The P. falciparum parasite was modeled as a rigid sphere, 2 microns in diameter. The RBC model was immersed into the DPD fluid. The membrane particles interacted with internal and external fluid particles through the DPD forces. The viscosity of the internal fluid was 9 times higher than external fluid viscosity. The flow was sustained by applying a body force to the DPD particles. By changing the direction of the body force, the motion of the cell through channels with converging and diverging pores was simulated using the same channel geometry.
Acknowledgments
This work was supported by Interdisciplinary Research Groups on Infectious Diseases and BioSyM, which are funded by the Singapore-MITAlliance for Research and Technology (SMART) Center and from the National Institutes of Health (Grants R01 HL094270-01A1 and 1-R01-GM076689-01). We thank D.J. Quinn for background experimental work that was helpful in the initial calibrations of the DPD modeling. We thank A. Benson for help with statistical analysis. All simulations were performed on the Cray XT5 (Kraken) at NICS. S.J.G. was supported by NIEHS Training Grant 5-T32-ES007020, and MIT Startup Funds were used otherwise.
Footnotes
Disclosure
H. Bow, I. Pivkin, M. Diez-Silva, S. Suresh, and J. Han filed two US provisional patents based on a portion of the contents of this paper.
References
- 1.McMillan D, Utterback N, La Puma J. Diabetes. 1978;27:895–901. doi: 10.2337/diab.27.9.895. [DOI] [PubMed] [Google Scholar]
- 2.Cranston H, Boylan C, Carroll G, Sutera S, Williamson J, Gluzman I, Krogstad D. Science. 1983;233:400–403. doi: 10.1126/science.6362007. [DOI] [PubMed] [Google Scholar]
- 3.Mokken FC, Kedaria M, Henny CP, Hardeman M, Gleb A. Ann. Hematol. 1992;64:113–122. doi: 10.1007/BF01697397. [DOI] [PubMed] [Google Scholar]
- 4.WHO. World Malaria Report 2008. 2008
- 5.Maier A, Cooke B, Cowman A, Tilley L. Nature Reviews Microbiology. 2009;7:341–354. doi: 10.1038/nrmicro2110. [DOI] [PubMed] [Google Scholar]
- 6.Suresh S, Sptaz J, Mills J, Micoulet A, Dao M, Lim C, Beil M, Sefferlein T. Acta Biomaterialia. 2005;1:16–30. doi: 10.1016/j.actbio.2004.09.001. [DOI] [PubMed] [Google Scholar]
- 7.Safeukui I, Correas J, Brousse V, Hirt D, Deplaine G, Mule S, Lesurtel M. Blood. 2008;112:2520–2528. doi: 10.1182/blood-2008-03-146779. [DOI] [PubMed] [Google Scholar]
- 8.van der Heyde J, Nolan J, Combes V, Gramaglia I, Grau G. Trends in Parasitology. 2006;22:503–508. doi: 10.1016/j.pt.2006.09.002. [DOI] [PubMed] [Google Scholar]
- 9.Reid J, Barnes A, Lock P, Dormandy J, Dormandy T. J. Clin. Pharmacol. 1976;29:855–858. doi: 10.1136/jcp.29.9.855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bessis M, Mohandas N. Blood Cells. 1977;1:307–313. [PubMed] [Google Scholar]
- 11.Nash GB. Proceedings, Seventh International Congress of Biorheology. 1990;III:873–882. [Google Scholar]
- 12.Fisher TC, Wenby RB, Meiselman HJ. Biorheology. 1992;29:185–201. doi: 10.3233/bir-1992-292-301. [DOI] [PubMed] [Google Scholar]
- 13.Drochon A, Barthes-Biesel D, Bucherer C, Lacombe C, Lelievre JC. Biorheology. 1993;30:1–8. [PubMed] [Google Scholar]
- 14.Skalak R, Impelluso T, Schmalzer EA, Chien S. Biorheology. 1983;20:41–56. doi: 10.3233/bir-1983-20104. [DOI] [PubMed] [Google Scholar]
- 15.Nash G, O'Brien O, Gordon-Smith E, Dormandy J. Blood. 1989;74:855–861. [PubMed] [Google Scholar]
- 16.Chien S. Blood Cells. 1977;3:71–99. [Google Scholar]
- 17.Lekka M, Fornal M, Pyka-Fosciak G, Lebed K, Wizner B. Biorheology. 2005;42:307–317. [PubMed] [Google Scholar]
- 18.Guck J, Ananthakrishnan R, Mahmood J, Moon T, Cunningham C, Kas J. Biophysical Journal. 2001;81:767–784. doi: 10.1016/S0006-3495(01)75740-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mills JP, Diez-Silva M, Quinn DJ, Dao M, Lang MJ, Tan K, Lim C, Milon G, David P. PNAS. 2007;104:9213–9217. doi: 10.1073/pnas.0703433104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Brody JP, Han Y, Austin RH, Bitensky M. Biophysical Journal. 1995;68:2224–2232. doi: 10.1016/S0006-3495(95)80443-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Abkarian M, Faivre M, Stone H. PNAS. 2006;103:538–542. doi: 10.1073/pnas.0507171102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shelby JP, White J, Ganesan K, Rathod PK, Chiu DT. PNAS. 2003;100:14618–14622. doi: 10.1073/pnas.2433968100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bow H, Hou HW, Goldfless S, Abgrall P, Tan K, Niles J, Lim C, Han J. Proceedings of microTAS. 2009:1219–1221. [Google Scholar]
- 24.Deen W. Analysis of Transport Phenomena. New York: Oxford University Press; 1998. [Google Scholar]
- 25.Chien S. Ann. Rev. Physiol. 1987;49:177–192. doi: 10.1146/annurev.ph.49.030187.001141. [DOI] [PubMed] [Google Scholar]
- 26.Rand RP, Burton AC. Biophysical Journal. 1964;4:115–135. doi: 10.1016/s0006-3495(64)86773-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tong X, Caldwell KD. Journal of Chromatography B. 1995;674:39–47. doi: 10.1016/0378-4347(95)00297-0. [DOI] [PubMed] [Google Scholar]
- 28.Leblond P, LaCelle P, Weed R. Blood. 1971;37:40–46. [PubMed] [Google Scholar]
- 29.Gifford S, Derganc J, Shevkoplyas S, Yoshida T, Bitensky M. British Journal of Haematology. 2006;135:395–404. doi: 10.1111/j.1365-2141.2006.06279.x. [DOI] [PubMed] [Google Scholar]
- 30.Waugh R. Blood. 1991;78:3037–3042. [PubMed] [Google Scholar]
- 31.Xie L, Jiang Y, Yao W, Gu L, Sun D, Ka W, Wen Z, Chien S. Journal of Biomechanics. 2006;39:530–535. doi: 10.1016/j.jbiomech.2004.11.032. [DOI] [PubMed] [Google Scholar]
- 32.Enderle T, Ha T, Ogletree D, Chemla D, Magowan C, Weiss S. PNAS. 1997;94:520–525. doi: 10.1073/pnas.94.2.520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gifford SC, Frank MG, Derganc J, Gabel C, Austin RH, Yoshida T, Bitensky MW. Biophysical Journal. 2003;84:623–633. doi: 10.1016/S0006-3495(03)74882-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Higgins J, Eddington D, Bhatia S, Mahadevan L. PNAS. 2007;104:20496–20500. doi: 10.1073/pnas.0707122105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hou HW, Bhagat AAS, Chong AGL, Mao P, Tan KSW, Han J, Lim CT. Lab Chip. 2010;10:2605–2613. doi: 10.1039/c003873c. [DOI] [PubMed] [Google Scholar]
- 36.Mebius RE, Kraal G. Nature Reviews Immunology. 2005;5:606–616. doi: 10.1038/nri1669. [DOI] [PubMed] [Google Scholar]
- 37.Secomb T, Hsu R. Biophysical Journal. 1996;71:1095–1101. doi: 10.1016/S0006-3495(96)79311-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bathe M, Shirai A, Doerschuk C, Kamm R. Biophysical Journal. 2002;83:1917–1933. doi: 10.1016/S0006-3495(02)73955-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hochmuth R, Worthy P, Evans E. Biophysical Journal. 1979;26:101–114. doi: 10.1016/S0006-3495(79)85238-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Shirai A, Fujita R, Hayase T. JSME International Journal. 2003;46:1198–1207. [Google Scholar]
- 41.Groisman A, Enzelberger M, Quake S. Science. 2003;300:955–958. doi: 10.1126/science.1083694. [DOI] [PubMed] [Google Scholar]
- 42.Cross SE, Jin Y-S, Rao J, Simzewski JK. Nature Nanotechnology. 2007 doi: 10.1038/nnano.2007.388. [DOI] [PubMed] [Google Scholar]
- 43.Deitsch K, Driskill C, Wellems T. Nucleic Acids Res. 2001;29:850–853. doi: 10.1093/nar/29.3.850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Groot RD, Warren PB. J Chem Phys. 1997;107:4423–4435. [Google Scholar]
- 45.Fan XJ, Phan-Thien N, Chen S, Wu XH, Ng TY. Phys Fluids. 2006;18:063102. [Google Scholar]
- 46.Pivkin IV, Karniadakis GE. Journal of Computational Physics. 2005;207:114–128. [Google Scholar]
- 47.Pivkin IV, Karniadakis GE. Phys Rev Lett. 2008;101:118105. doi: 10.1103/PhysRevLett.101.118105. [DOI] [PubMed] [Google Scholar]
- 48.Discher DE, Boal DH, Boey SK. Biophysical Journal. 1998;75:1584–1597. doi: 10.1016/S0006-3495(98)74076-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Li J, Dao M, Lim CT, Suresh S. Biophysical Journal. 2005;88:3707–3719. doi: 10.1529/biophysj.104.047332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Park Y, Diez-Silva M, Popescu G, Lykotrafitis G, Choi W, Feld M, Suresh S. PNAS. 2008;105:13730–13735. doi: 10.1073/pnas.0806100105. [DOI] [PMC free article] [PubMed] [Google Scholar]