Slow Motions in The Hydrophobic Core of Chicken Villin Headpiece Subdomain and their Contributions to Configurational Entropy and Heat Capacity from Solid-State Deuteron NMR measurements

Abstract

We have investigated microsecond to millisecond time scale dynamics in several key hydrophobic core methyl groups of chicken villin headpiece subdomain protein (HP36) using a combination of single-site labeling, deuteron solid-state NMR line shape analysis, and computational modeling. Deuteron line shapes of hydrated powder samples are dominated by rotameric jumps and show a large variability of rate constants, activation energies, and rotameric populations. Site-specific activation energies vary from 6 to 38 kJ/mol. An additional mode of diffusion on a restricted arc is significant for some sites. In dry samples, the dynamics is quenched. Parameters of the motional models allow for calculations of configurational entropy and heat capacity, which, together with the rate constants, allow for observation of interplay between thermodynamic and kinetic picture of the landscape. Mutations at key phenylalanine residues at both distal (F47L&F51L) and proximal (F58L) locations to a relatively rigid side-chain of L69 have a pronounced effect on alleviating the rigidity of this side chain at room temperature and demonstrate the sensitivity of the hydrophobic core environment to such perturbations.

Introduction

It has been long recognized that protein structures are not static, but can rather be viewed as an ensemble of conformations (sub-states) with somewhat different free energies within the free energy “landscape”.(1) The hydrophobic core of proteins plays a major role in protein stability, folding pathways, and biological function.(2) It is a complex, dynamic medium reflecting the existence of the conformational ensemble.

Many groups have studied the dynamics of hydrophobic cores in solution by NMR, all showing considerable extent of motions.(3–13) It is very interesting that mutations in the core regions affect not only neighboring groups, but also distant sites, as, for example, was found to be the case for chymotrypsin inhibitor 2,(7) the B1 domain of protein L, (11) and homologous fibronectin type III domains.(14)

While solution NMR techniques are very useful in describing general dynamical features of the protein, studies in solid-state can offer significant advantages. These include(15) a) freedom from constraints imposed by protein solubility; b) investigations of the effects of controlled hydration on dynamics, and thus the importance of protein-solvent interactions on biomolecular flexibility; c) an expanded temperature range, which allows for more accurate determination of the potential energy function that governs thermodynamic properties such as the contributions of dynamics to the configurational entropy and heat capacity; d) an expanded range of time scales of motions that can be characterized, since overall tumbling of the molecule masks time scales slower than the tumbling in a conventional solution NMR approach based on laboratory frame relaxation rates; and e) solid-state NMR data combined with single-site labeling techniques permits the design and testing of detailed motional models that depict the details of molecular motions. Skrynnikov and coworkers(4) showed that essential features of dynamics probed by solution and solid-state NMR are similar, thus allowing us to extend the results obtained in the solid state to physiologically relevant conditions.

Our main experimental technique is deuteron NMR line shape analysis. This technique is very sensitive to the mechanisms of motion on μs-ms time scales and allow for construction of precise motional models.(16, 17) Dynamics on these time scales have been shown important in many biological functions.(18, 19)

In this work we combine solid-state deuteron NMR spectroscopy with single-site labeling techniques and computational modeling to analyze the details of side-chain dynamics of several key hydrophobic methyl groups in a small thermostable helical protein, chicken villin headpiece subdomain (HP36).

HP36 is one of the smallest known examples of a cooperatively folded domain of a naturally occurring protein and has been a subject of numerous experimental and computational investigations.(20–39) The villin headpiece subdomain is a 35-residue motif at the extreme C-terminus of villin(28), which is an F-actin bundling protein involved in the maintenance of the microvilli of the absorptive epithelia.(40, 41) This subdomain spans residues 42–76 (residues 791–825 of intact chicken villin) of the full-length 76 amino acid residue villin headpiece. The recombinant form of the sub-domain, HP36, has an additional N-terminal methionine residue designated arbitrarily as residue 41. The structure of HP36 (Figure 1), as determined by X-ray and NMR spectroscopy,(42, 43) consists of three short helices (residues 44–51, 54–60, and 64–74) surrounding a tightly packed hydrophobic core.

Figure 1.

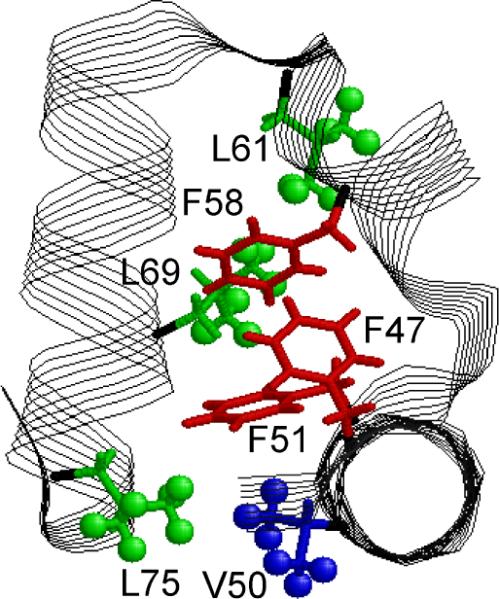
Ribbon diagram of HP36 with key hydrophobic core residues labeled.

Three phenylalanine side chains, F47, F51, and F58, form the basis of the core.(21, 42, 43) Frank, et al.(32) and Xiao et al.(33) identified the stability of several mutants with changes in the hydrophobic core region. They concluded that, out of three key phenylalanine residues, F58 is most important for protein stability. In addition, analysis of the double mutant demonstrated that F47 and F51 make the strongest pairwise interaction. All three helices contribute additional residues to the hydrophobic core. The third helix is disordered in isolation, whereas the subdomain lacking the third helix retains residual structure.(30) Tycko and coworkers(20, 24) studied local conformational distributions of HP36 in frozen glycerol/water solutions by solid-state NMR. In particular, they have analyzed line shapes of C_α/C_β cross-peaks as a function of denaturant concentration in selected residues in each of the helices: V50, A57, and L69. L69, which belongs to the third helix, was found to become most disordered at high concentrations of denaturant.

In a previous work(44) we have characterized the dynamics of L69 in wild-type HP36 in a hydrated powder sample and concluded that a three-mode motional model was necessary to account for the observed deuteron line shapes: a) fast 3-site rotational jumps about the pseudo C₃ methyl spinning axis, b) slower reorientation of the spinning axis, described by diffusion along a restricted arc and c) large angle jumps between traces of rotameric conformers. This study will compare the methyl group dynamics at several hydrophobic core sites (L61, L75, L69, and V50), as well as at a site outside of the core (L63) and also in a peptide corresponding to the third longest helix (residues 61–76 of intact protein) with deuterated methyl groups at L69 position. The latter peptide can be viewed as unfolded state analog. For each of the sites we find the parameters of the motional model, investigate how these parameters change with temperature, and obtain activation energies, configurational entropy contributions and heat capacities. These characteristics, which reflect the local free energy landscapes, indicate a striking variability among the residues. We also look at the effects of hydration, which has a profound effect on μs-ms time scale motions for most of these sites.

In addition, we investigate the effects of F58L and F47L&F51L mutation on the methyl dynamics of the key core residue L69. The former mutation is at the phenylalanine which makes a contact with one of the L69 methyl groups, while the latter mutation involves two phenylalanine which are not in close proximity to L69 (Figure 1). Both of these mutations render L69 considerably more mobile.

Materials and Methods

Sample preparation

Powdered 5,5,5-d₃ FMOC-Leucine and d₈-FMOC-Valine were purchased from Cambridge Isotopes Laboratories (Andover, MA). All protein samples were synthesized commercially by solid-state peptide synthesis with incorporation of the deuterated leucine or valine at selected sites. The samples were purified by Reverse-Phase HPLC. The identity and purity of the samples were confirmed by mass-spectroscopy and Reverse-Phase HPLC. Lyophilized powders were dissolved in water and pH was adjusted to about 6 using NaOH/HCl. All wild-type and mutant samples are expected to be folded in this range. We have previously confirmed the refolding procedure for the wild-type HP36 by measuring ¹⁵N chemical shifts of F58 and F51 and obtaining values that agree with the shifts reported for a folded protein in solution. The sample hydration was performed by exposing re-lyophilized powder to vapor diffusion in a dessicator until the water content reached about 35–40% by weight.

Deuteron Solid-state NMR spectroscopy

Experiments were performed on a 17.6T spectrometer equipped with a static probe operating at temperatures between 145 and 380K. Line shape experiments were performed with a quadrupole echo pulse sequence based on an eight-step phase cycle(16), with a delay of 31μs between 90° pulses. The duration of the 90° pulses was 2.0μs. Data acquisition was initiated prior to the echo maximum. The number of scans varied from 8 × 1024 to 64 × 1024, depending on the signal to noise ratios. Higher temperatures required more scans. Relaxation delays were set to two times the longitudinal relaxation rates of methyl deuterons, which were determined by inversion recovery experiments using either quadrupole echo(45, 46) or multiple echo detection schemes.(47) The later scheme is advantageous in increasing signal-to-noise ratio and does not suppress anisotropy of the relaxation rates,(48) although some mixing of the contributions from neighboring frequencies sill exists. Therefore, as described in detail in Supporting Information S1, the quadrupole echo acquisition scheme was used in the case of valine-labeled samples in order to see a clear distinction between the relaxation times of D^β versus D^γ. Time domain data were left-shifted and apodized with 1000 Hz broadening. Temperature calibration was done by recording static lead nitrate line shapes(49) and using the freezing point of D₂O, 3.8°C, as the fixed point for the calibration.

Modeling

Theoretical discussions and computational approaches for computing deuteron line shapes have been presented elsewhere.(16, 17, 50) Systems with multi-modal motions require extensive numerical simulations. In this work we utilize freely available EXPRESS program,(51) which is ideally suited for computation of the deuteron line shapes for multimodal motions as described in Vold et al.(51) This computational tool has been previously used for the motional modes considered in this paper for the line shape data of L69.(44)

We use a three-mode motional model, depicted in Figure 2. The first mode (Figure 2A) consists of three-site methyl group jumps around the methyl axis. Because the rate of these jumps is several orders of magnitude higher than the deuteron quadrupole splitting, the only effect of this mode of motion on the line shape is through averaging of the quadrupole tensor. The averaged tensor has a quadrupole splitting constant 1/3 of the original one and is symmetrical along the methyl axis. The second and third modes of motion are related to fluctuations of the dihedral angles of the side chain. The second mode (Figure 2B) describes small fluctuations of the dihedral angle adjacent to the methyl groups (χ₂ for leucine side chains and χ₁ for the valines). These fluctuations occur around the equilibrium position for each rotamer and can be modeled by the motion of the methyl carbon on an arc on a side of the cone with the axis along C^βC^γ bond for leucines and C^αC^β bond for valines. The apex angle of the cone is 141° in accordance with the tetrahedral geometry. We refer to this mode of motion as motion along the arc. In general, the motion along the arc should be described through a local potential for this degree of freedom. We found(44) that for the purposes of line shape modeling a good assumption is a constant potential on a restricted arc. The size of the arc may be temperature dependent. The motion along the arc is a free diffusion. Technically, the motion is computed through a series of equally spaced (Δφ = 5°) sites along the arc with jumps allowed between neighboring sites. The rate constant of the jumps is directly related to the diffusion constant for the arc motion, D = Δφ² k^arc.

Figure 2.

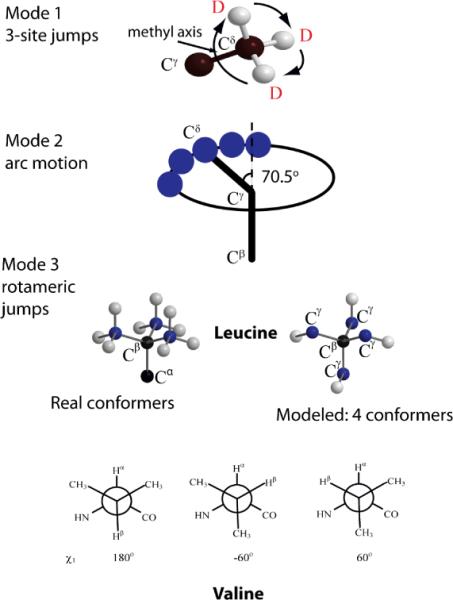
Schematic representation of the motional model which is used to fit the line shape data. Mode 1: fast 3-site hops of the methyl group. Mode 2: restricted diffusion on an arc approximated by small nearest neighbor jumps of the methyl axis demonstrated here for leucine side chain. Mode 3: rotameric jumps correspond to hops between four non-equivalent positions of leucine side chain out of 9 possible configurations and between three rotamers for valine.

The third mode of motion consists of large angle jumps between different rotamers of the side chain (Figure 2B). For leucine side chains with tetrahedral bond angles, there are nine distinct conformations corresponding to different combinations of χ₁ and χ₂ dihedral angles. These nine rotamers lead to four distinct directions for the methyl axis, which can be described geometrically as pointing from the center to the four corners of a tetrahedron. Therefore, we model leucine side chain motion in the third frame through the jumps between four sites corresponding to these directions. Each of the four sites is connected to the other three and all jump rates are equal. Generally, the rotamers have unequal populations, which change with temperature according to the Boltzmann law. For the valine side chain, all three values of χ₁ angle (−60°, 60°, 180°) lead to distinct directions of the methyl axis and the jumps between these positions are modeled by 3 sites. Examples of Euler angles used for the second and third modes are shown in Supporting Information S2.

Best-fit parameters were obtained using visual comparison of experimental and modeled line-shapes in an iterative procedure. The values of the rotameric populations were fixed at the highest temperature and calculated for the lower temperatures according to the Boltzmann law. The errors were estimated as ranges of the parameters within which there is no sensitivity to the quality of the fits. The values of the activation energies of rotameric motions and their corresponding errors were calculated from Arrhenius plots.

Results and Discussion

Deuteron quadrupole echo line shapes of core residues

We have looked at several essential hydrophobic core methyl groups of HP36, which belong to the side chains of V50, L61, L69, and L75 (Figure 1). L69 is in close proximity to F58, L61 is on the opposite side of F58 and further away from it, and L75 and V50 are packed against F51.(42)

All leucine side chains had a single CD₃ label with a 50%/50% ratio for the two methyl groups. Commercially available Valine-d₈ has all α-, β-, and γ-deuterons labeled. As we demonstrated in detail in the Supporting Information S1, the contribution of beta and alpha deuterons to the quadrupole echo line shapes can be filtered out by employing short recycle delays, as the longitudinal relaxation time of gamma deuterons is significantly shorter than that of either beta or alpha for the range of temperatures studied. Note that in both valine and leucine the two methyl groups participate in identical μs-ms motions due to constraints imposed by the tetrahedral geometry. An additional source of signal is a trace contribution from water (HOD), which manifests itself as a narrow peak at zero frequency.

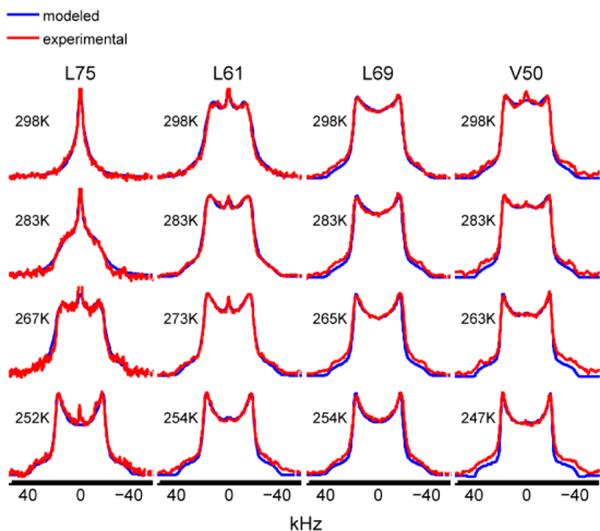
The extent of variability in the dynamics of the core residues is immediately apparent looking at the solid-state deuteron NMR line shapes of hydrated samples (red line in Figure 3). The hydration level of all samples was ~35–40%, which corresponds roughly to one layer of water molecules and is a typical threshold at which most globular proteins are fully hydrated(52, 53), so that their internal dynamics is similar to those in solution state.(54)

Figure 3.

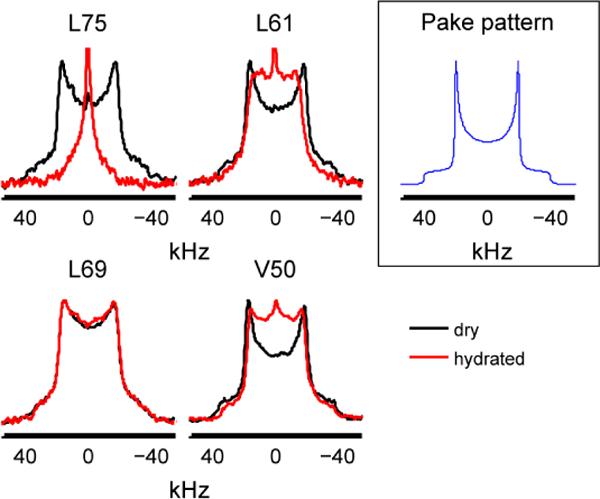
Experimental deuteron quadrupole echo line shapes for hydrophobic core methyl groups in hydrated (red) and dry (black) samples at 298K. The graph in black frame represents simulated spectrum for a methyl group with the 3-site hops in fast limit in the absence of μs-ms motions.

L69 exhibits a relatively rigid Pake-like pattern, while L75 appears to be the most mobile (largest extent of motional averaging). By contrast, in the dry (lyophilized) state, all of the sites show nearly rigid line shapes (black line in Figure 3), indicating that large-amplitude motions on μs-ms time scales are quenched under conditions. Thus, our data provide direct evidence on the importance of the hydration shell for the existence of biologically-relevant μs-ms time scale mobility in the solvent-protected hydrophobic core residues at site-specific resolution. While we have not investigated the mechanism leading to these changes, the result suggests that the landscape of the core is adjusted in response to the free energy changes of surface residues occurring upon an introduction of interactions with water. A cross-talk between surface and core residues has been also indicated by mutagenesis studies, such as for example by Billings et al.(14) Interestingly, solvent-accessibility does not correlate with the dynamical characteristics, as all three of the leucine residues have about 17% solvent-accessibility(42) and yet their dynamics in the hydrate state are clearly very different.

The dependence of the line shapes on temperature is also very different among the residues (Figure 4), with L69 line shapes showing the smallest change and L75 the largest change with temperature. The variability in the dynamics of the core residues must reflect fine details of the free-energy landscape of the core, which is not easily accessible from structural studies. To characterize these features quantitatively, motional modeling and thermodynamics analysis was employed, which we describe in the following sections.

Figure 4.

Representative experimental (red) and simulated (blue) quadrupole echo line shapes for hydrophobic core methyl groups in hydrated samples. The variability in the line-shapes reflects the differences in mobility on the μs-ms time scale. Simulated line-shapes were generated according to the motional model depicted in Figure 2 with the values of model parameters discussed in the text.

Motional models and their parameters

The procedure for modeling the motions is described in detail in the Materials and Methods section. As illustrated in Figure 2, three modes of motion are necessary to adequately simulate the experimental data (simulated line shapes are shown in blue line in Figure 4). The 3-site jumps of the methyl group, which occur on a fast ps time scale, are responsible for overall narrowing of the line shapes and reduce the effective quadrupole constant by a factor of 1/3. Thus, if this were the only mode of motion, the line shape would be a 3-fold narrowed Pake-pattern (Figure3 insert). The value of the effective quadrupole constant was taken from the previous work as 53.3 kHz,(44) in which we analyzed the line shapes of L69 down to temperatures at which the μs-ms time scale dynamics is frozen. We assumed that this value remains the same for all methyl groups.

The mode of restricted diffusion on an arc is responsible for introducing an effective asymmetry in the electric field gradient tensor, with major visual effect reflected in broadening of the horns. Besides our previous paper on the dynamics of L69, this mode of restricted diffusion has been previously observed by Meints et al.(55) in DNA oligomers.

The third mode, which consists of large angle rotameric jumps, accounts for major motional narrowing features in the room-temperature spectra of L75, L61, and V50, as well as leading to flattening of the shoulders compared to the rigid-like pattern. Rotameric motional modes are frequently used to explain deuteron line shapes of methyl bearing side chains. In particular relevance to our results are the works of Batchelder et al.(56) with applications to collagen fibrils and Weidner et al.(57), who looked at the dynamics of leucine side chains adsorbed on polysterene surfaces.

The parameters of the restricted diffusion mode consist of the rate of jumps and length of the arc, while those of the rotameric jumps consist of jump rates and populations of the rotamers.

Simulations show that it is sufficient to model all four non-equivalent rotameric conformations for leucine side chain in w:1:1:1 proportions, where w >1 stands for the relative weight of a single major conformer. Introduction of non-equivalent populations for the minor conformers did not lead to significant improvement of simulated data. We note that this scenario produced significantly better fits compared with modeling by two or three non-equivalent rotamers. For the side chain of valine, there are three non-equivalent conformers and the fits were performed using the w:1:1 assumption. Similarly to leucine, introduction of non-equivalent populations for the two minor conformers did not lead to significant improvement in the fits. Also, attempts to model the line shapes with two conformers produced significantly worse line shapes.

We have also checked that the relaxation delays of 2 times the longitudinal relaxation times used for most of the spectra are sufficiently long. First, we compared experimental normalized spectra of L75 and L69 at 283K obtained with relaxation delays of 2 versus 4 times T_1Z and found no differences. Second, normalized simulated line shapes for L75 and L69 with the best-fit parameters corresponding to 298K were calculated either assuming thermal equilibrium or using the relaxation delay of 2 times T_1Z and yielded identical results.

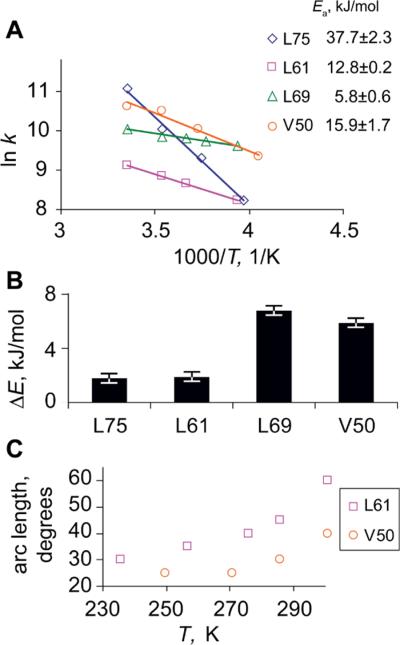
Fitted rotameric rate constants, activation energies, and rotameric populations are presented in Figure 5. Rotameric rate constants at room temperature vary from (6.5±0.3) ·10⁴ s⁻¹ (L75) to (2.3±0.1)·10⁴ s⁻¹ (L69), and the activation energies span the range from 38±2 (L75) to 5.8±0.6 kJ/mol (L69). Large variability in rotameric populations is also apparent from Figure 6B, which displays the energy differences between major and minor conformers. We note that the value of the activation energy 6 kJ/mol shown for L69 represents an upper limit for this residue, as its rotameric and arc modes rate constants are in the regime in which there is an interplay between the two, leading to a certain extent of ambiguity. The lower limit for this value is zero(44). L75 is the only methyl-bearing side chain that has been implicated in F-actin binding. It is possible that its comparatively large rate constant for rotameric jumps combined with a small energy difference between the rotamers facilitates the existence of conformational sub-states compatible with the F-actin binding form.

Figure 5.

Parameters of the motional modes for core residues. A) Fitted rotameric rate constants and activation energies. Error estimates for individual rate constants are within the size of the symbols. B) Energy difference between the major and minor forms of rotamers. C) Temperature dependence of the arc length for the restricted diffusion mode.

Figure 6.

(A) Representative experimental (red) and simulated (blue) quadrupole echo line shapes for solvent-exposed methyl groups in hydrated samples. B) Fitted rotameric rate constants and activation energies. Error estimates for individual rate constants are within the size of the symbols. C) Energy difference between the major and minor forms of rotamers. D) Temperature dependence of the arc length for the restricted diffusion mode.

The arc length for restricted diffusion showed temperature dependence only for V50 and L61 (Figure 5C). L61 has the largest arc length at room temperature of 60°. L75 was fitted with the arc length of 40° for all temperatures, except for 298K, at which the line-shape was not sensitive to the changes of the arc length. Based on the lower temperatures, we decided to use the value of 40° arc length for this temperature. L69 indicated a constant arc length of 35° for all temperatures. All values of the arc length have an error estimate of 5°. In most instances, the rate of the restricted diffusion could not be fixed unambiguously due to proximity to the fast regime in which the line shapes do not depend on the rate constant.

The range of variability in the parameters of the two modes parallels the distribution of generalized NMR order parameters for methyl groups found in calmodulin protein by Wand and coworkers (6, 58). In these studies, residues were grouped according to the amplitudes of the motions within a rotameric well and in-between the wells, which in our model corresponds to the restricted diffusion and rotameric jumps modes, respectively. These motions were detected by solution NMR techniques sensitive to sub-nanosecond time scales, while we have focused on much slower time scales visible due to the absence of overall molecular tumbling. The hydration level of one shell of water molecules does not reintroduce the molecular tumbling, which is evident from the variability of the hydration effect on the hydrophobic core sites and almost complete absence of hydration dependence for the methyl groups of L69. It is possible that the time scale of motions that we observe is somewhat slowed compared to those found in solution due to solvent-slaving(59). Studies of side-chain dynamics of HP36 in solution with techniques sensitive to a variety of time scales would be useful to probe the extent of this effect.

Comparison with solvent-exposed regions

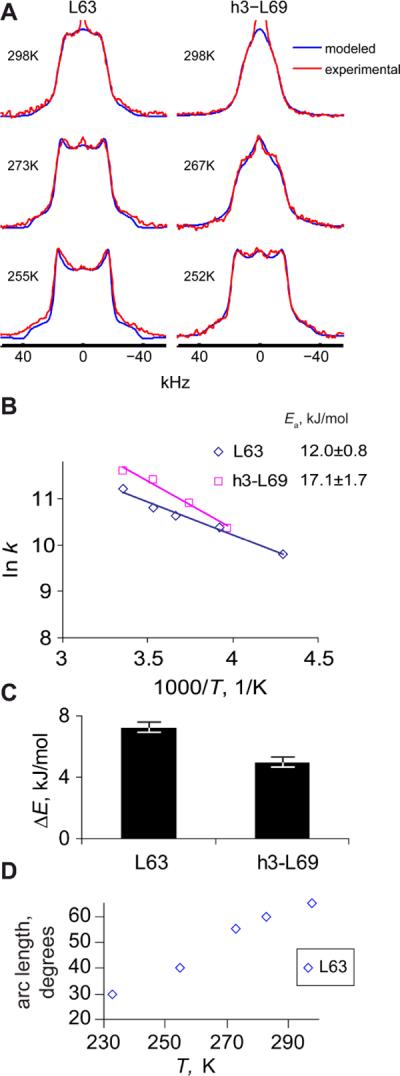
In order to obtain a further insight into dynamical features unique to the hydrophobic core we have looked at two leucine residues which do not belong to the core region. The first of these, L63, lies in the loop between the second and third helix and its side chain is pointing outside the core. The second leucine belongs to a peptide comprising only the third helix of HP36 and the loop in front of it (residues 61–76). The deuteron label was placed on L69 position. This peptide could be considered an unfolded state analog. In the dry samples these unstructured sites do not show considerable μs-ms dynamics, in similarity to what we observe in the core region. In the hydrated state the motions are clearly present, as seen from the line shapes in Figure 6A. They are dramatically enhanced in the L69 site in the isolated helix compared to the same site in the intact folded protein.

The line shapes (Figure 6A) were fitted with the same motional model as the one developed for the core region and its parameters are presented in Figure 6B–D. Both the activation energies for rotameric motions and the energy difference between the conformers are comparable to those found for the methyls in the core region. However, there is a clear shift for L69 from a very low value of E_a and a large value of ΔE in the folded state of HP36 to more moderate values in the isolated helix peptide. The fitted value of arc length was 45–50° for all temperatures for L69 in the peptide, compared to a smaller value of 35° for the intact protein. Thus, the diffusive arc motions are also enhanced. L63 gave a temperature-dependent value of the arc length in the range of 60° for 298K to 30° for 233K.

Interpretation of the data for the solvent-exposed residues in the solid-state is complicated by the uncertainty in the role of the inter-molecular contacts. Nevertheless, our comparison suggests the solvent-exposed regions can exhibit motional characteristics similar to the more mobile parts of the core. However, the mobility of a site that displays rigidity in the core can be greatly affected upon unfolding.

Configurational Entropies and Heat Capacities

The parameters of motions for the modes of restricted diffusion on an arc and rotameric jumps can be used to calculate residue-specific contributions of configurational entropies and heat capacities corresponding to these modes. The calculations assume that these contributions are independent from all other contributions into the total partition function. Also, in our motional model the modes of the rotameric and restricted diffusion modes are independent of each other and therefore give independent contributions to configurational entropy: S_tot = S_rot + S_arc.

Configurational molar entropy as defined for discrete states is $S=-R{\sum }_i{p}_i\ln p_i$, where p_i is the probability to occupy a particular spatial location. For rotameric motions with the relative weight of the most probable conformer w and number of minor conformers defined by n (n=3 for leucine and n=2 for valine), p for the major conformer is given by w/(w+n), while for minor conformers it is 1/(w+n). This leads to the rotameric contribution to the configurational entropy of

$$S_{rot}=R\left(\ln (w+n)-\frac{w\ln w}{w+n}\right)$$ (1)

For continuous motions of the restricted diffusion mode we use a probability distribution of P (ϕ) = 1/α, where α is the length of the arc and ϕ is an integration variable representing the angle along the arc. This distribution is consistent with the constant potential on a restricted arc. The contribution of this mode to the configurational entropy is then given by

$$S_{arc}=R\ln \alpha \left(T\right)$$ (2)

Heat capacities are in general derived from the temperature-dependence of the configurational entropy as C = TdS / dT. This gives the rotameric

$$C_{rot}=\frac{\Delta E^2}{R{T}^2}\frac{nw}{{(w+n)}^2}$$ (3)

where the temperature-dependence of the rotameric populations is taken from the Boltzmann Law as w = exp(ΔE / RT). The contribution of the restricted arc mode is given by

$$C_{arc}=RT\frac{{\alpha }^{\prime }\left(T\right)}{\alpha \left(T\right)}$$ (4)

This implies that this mode will give a non-zero value only for those residues that have a temperature-dependent arc length. For numerical computation of the heat capacity values, we used a linear fit to the temperature dependence of the α(T).

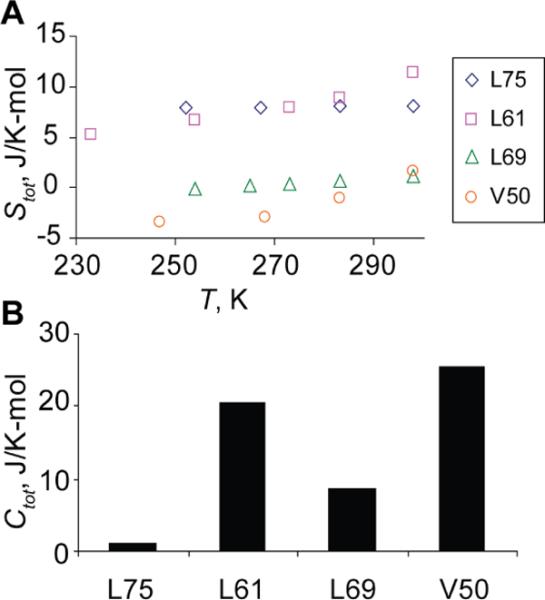
Figure 8A presents the values of S_tot for the four hydrophobic core residues, while the results for C_tot = C_rot + C_arc are given in Figure 8B for 298K.

Figure 8.

Comparison of the dynamics of L69 methyl groups in wild-type protein with F58L and F47LF51L mutants. (A) Representative experimental (red) and simulated (blue) quadrupole echo line shapes. B) Fitted rotameric rate constants and activation energies. Error estimates for individual rate constants are within the size of the symbols. C) Energy difference between the major and minor forms of rotamers. D)Temperature dependence of the arc length for the restricted diffusion mode.

It is important to note that the extent of motional averaging in the deuteron line shape is given primarily by the magnitude of the rotameric rate constant and the energy difference between the major conformers. The length of the arc has a relatively minor effect. In contrast, the length of the arc gives a large contribution toward the configurational entropy, while there is no dependence on the rate constants. For example, L75 appears to be most motionally averaged, however it does not have the largest configurational entropy due to its modest arc length. Similarly, the strong temperature dependence of the line shapes for these residues is governed by a large activation energy for the rotameric motion, but because the arc length is temperature-independent and the energy difference between rotameric conformers is minor, this residue has a small heat capacity. L61 shows the largest configurational entropy and heat capacity at room temperature due to its relatively large arc length. V50 has the largest heat capacity due to a combination of a relatively large difference in the rotameric energies and the temperature-dependent length of the arc. L69 has relatively low configurational entropy and heat capacity values. As usual, the thermodynamic description is derived from the amplitude of fluctuations, while the rate constants provide a kinetic picture. Lastly, we would like to caution that slow motions of methyl groups of different residues could be correlated, and in this case their contributions to the overall configurational entropy would not be simply additive.

More traditional thermodynamic analysis is based on the model-independent approach using the generalized NMR order parameters.(60–63) We present a brief comparison with this approach in the Supporting Information S3. While qualitative views arising from both approaches are similar, the quantitative results can have substantial model-dependence.

The thermodynamic results presented in this work ca}n be useful in refining force-field potentials for prediction of methyl groups dynamics(64) and construction of rotameric libraries(65).

Effect of Mutation on the Dynamics of L69 side chain

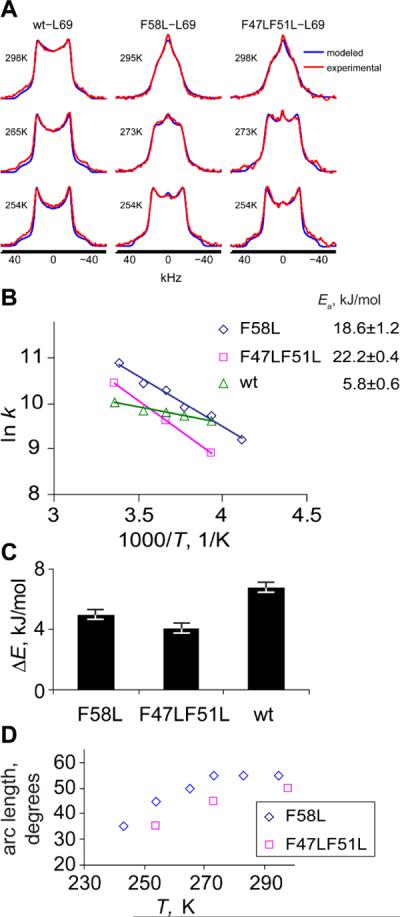
In order to gain an insight how sensitive the hydrophobic core dynamics are to perturbations that significantly affect the core region, we have compared the dynamics of methyl groups of L69 in the wild-type protein with those in two mutants. Both of these mutations leave the protein in the folded state. The first mutant contains a F58L substitution which significantly alters the environment in the close proximity to the methyl groups. As mentioned in the introduction, this phenylalanine is most important for protein stability(32, 33) even though the protein lacking this residue is still folded. The second mutation F47L&F51L introduces a profound change in the core region which is not in immediate proximity to L69. This is the only double-mutant of the core phenylalanines which is folded. Xiao et al.(33) have estimated the free energy difference of unfolding of both mutants compared to the native protein to be decreased by about 2.5 kcal/mol.

Characteristic temperature-dependent line shapes for the three proteins in a hydrated state are shown in Figure 8A. It is immediately apparent that both of the mutations lead to a significant increase in the motional averaging of the spectra and their temperature dependence. At room temperature the rate constants for rotameric jumps are significantly larger for both of the mutants and their rotameric conformers are more equally populated. (Figure 8B, C) The extent of the arc motions is also larger for the mutants, in which the arc length increases to 50–55° compared with 35° for the native protein (Figure 8D). In addition, temperature dependence is also more pronounced in the mutants with the activation energies of 18.5±1.2 and 22.2±0.4 kJ/mol for F58L and F47LF51L compared to the value of 5.8±0.6 kJ/mol for the wild-type protein. Overall, the effect of mutation on the dynamics is small at low temperatures but is very much evident at room temperature.

Our results demonstrate that the hydrophobic core environment of hydrated proteins is very sensitive to perturbations in both proximal and remote sites of the core. In the native protein L69 shows the most rigid kinetic behavior of all sites probed both in the core and the solvent exposed sites, as well as a very modest value of configurational entropy, while the mutations in the core region have a dramatic effect of alleviating this rigidity and raising configurational entropy (Figure 9). An increased entropic contribution upon Phe to Leu and Phe to Val mutations in the core region has also been found for the hydrophobic core methyl groups in SH3 domain from the FYN tyrosine kinase.(10) Additionally, we see an interesting parallel to the mutagenesis studies by Whitely et al.,(7) in which the authors have observed that the chymotrypsin inhibitor 2 mutants with substitutions in the core region are more dynamically similar to each other than to the more rigid wild-type protein. They have proposed that the dynamic environment of its core has been optimized for its biological function as a serine protease inhibitor. The optimization of the hydrophobic core environment to facilitate biologically relevant dynamical features could be a more general property of proteins.

Figure 9.

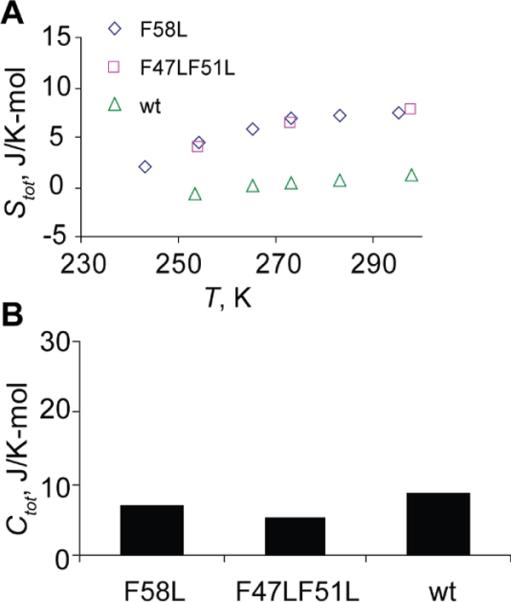
Contributions to configuration entropy S_tot (A) and heat capacity at room temperature C_tot (B) for the methyl groups of L69 in wild-type HP36 and its F58L and F47LF51L mutants.

Conclusion

One of the main results of this paper is a very substantial variability in the μs-ms dynamics of the core methyl groups in the hydrated powder state, reflecting the sensitivity of the hydrophobic core to fine details of the free energy landscape. This is reinforced by investigations of the mutants which significantly alter the environment of the core, yet still yield folded variants of the protein. The relatively rigid side chain of L69 undergoes a very significant overall increase in mobility upon mutations at both proximal and distal sites. We have also seen that motions are practically quenched in all of the dry samples and thus our results stress the importance of the hydration shell for the existence of μs-ms dynamics in the solvent-protected core residues.

Modeling procedures have allowed fixing the parameters of the motional model and their temperature dependence, which, in turn, allowed for the determination of contributions of the motional modes to configurational entropy and heat capacity. We have seen an interesting interplay between the thermodynamic and kinetic pictures of the landscape. For example, the F-actin binding residue L75 displays the most motionally narrowed line shape, which is reflected in the high rate constant for the rotameric jumps and low energy difference between the rotameric populations. Yet, due to its relatively small and temperature-independent length of the arc, this residue shows a modest contribution to configurational entropy and a small contribution to heat capacity.

Figure 7.

Contributions to configuration entropy S_tot (A) and heat capacity at room temperature C_tot (B) for core methyl groups.