Statistical analysis for identifying mediating variables in public health dentistry interventions

Abstract

Objective

This article provides an overview of statistical mediation analysis methods in the evaluation of public health dentistry interventions.

Methods and Results

First, reasons for conducting mediation analysis are outlined, followed by a discussion of the link between the mediation model and theoretical bases of interventions. Second, the basic statistical procedures in mediation analysis are presented. An example application to data from a hypothetical intervention is provided in Appendix A. Third, interpretation of the results from statistical mediation analysis is described along with additional information pertinent to identifying true mediation relations.

Conclusions

Guidelines for describing mediation analyses in research articles related to public health dentistry intervention studies are outlined.

Introduction

If parents are taught to model appropriate dental health practices, then their children will demonstrate better dental health behavior.

If dental health professionals are encouraged to routinely screen for oral cancer, then oral cancer deaths will be reduced.

If athletes are coached to know the importance of wearing mouth guards, then they will have fewer dental injuries. If children consume fluoridated water instead of bottled water, then dental cavities will be reduced.

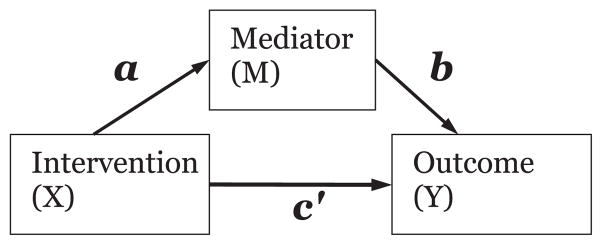
Statements like these suggest that public health dental problems can be reduced by changing intermediate behavioral, biological, psychological, or social factors. These intermediate constructs (italicized in the abovementioned examples) are called mediating variables or mediators, and represent a variable that transmits the intervention activities to changes in an outcome variable. Figure 1 displays the underlying idea of mediation wherein the intervention (X) causes the mediator (M), which then causes the outcome (Y). Mediators help explain how an intervention works. For example, an intervention that seeks to improve child dental health may theorize that increasing parental modeling of dental practices will improve children’s dental health. In this example, parental modeling would be hypothesized to mediate the intervention effect on child dental health. Mediation analysis can test that hypothesis, and is useful for improving interventions and making them more cost-effective. Intervention programs are designed to change mediators under the theoretical proposition that changing the mediating variable will lead to a subsequent change in the outcome variable. If the mediating variable causes the outcome variable, then changing the mediating variable will lead to a change in the outcome variable. Evidence for a mediator is obtained if the intervention changes the mediator and if changes in the mediator is related to changes in the outcome variable (1–3).

Figure 1.

Single mediator model.

A wide range of constructs may serve as potential mediators, such as biological (e.g., inflammation), psychological (e.g., attitudes), behavioral (e.g., flossing), or environmental (availability of dental clinics) variables. Mediation examples in public health dentistry include interventions to target maternal attitudes about dental health and permissiveness with oral health as a way to improve children’s dental health (4,5). In other interventions, dental health care providers have discussed quitting tobacco with patients in order to increase tobacco cessation (6), emphasized healthy diets to promote overall and dental health (7), and educated persons to improve dental health (8). In each of these examples, the intervention targets one or more mediating variables thought to change an outcome variable.

Mediators are easily confused with moderators and confounders, which also represent third variable effects that can help explain how two variables are related. There are important differences between these types of variables, however, that are worth considering. Mediation can be simply defined as a relation such that an independent variable causes a mediating variable, which then causes a dependent variable (3). Thus, a mediator (M) is in a causal sequence from X to M to Y. A moderator variable is one in which the relation between two variables is different at different values of the moderator variable. An important difference from a mediator is that a moderator is not intermediate in the causal sequence from X to Y. A third variable effect called a confounder may also explain why two variables are related because it is related to the two variables. A confounding variable changes the relation between an independent and dependent variable because it is related to both variables, but is not theoretically in a causal sequence (9). In short, the main characteristic of a mediator that differentiates it from other third variable effects is that it is in a causal sequence such that the relation of X to Y is transmitted by the mediator M (9,10).

The success of intervention programs is determined appropriately by effects on outcome variables, such as behavior, death, or disease. The first step in the analysis of any intervention program is the estimation of size of the program effect on the outcome variable along with a measure of the variability of that program effect. The measure of variability of the program effect is used to decide whether an observed difference between program and control groups is likely to be a real difference or is more likely a chance result. In most cases, the evaluation of direct program effects on outcomes is the statistical test of primary interest to intervention researchers. However, if the research design also includes measures of the mediating variables selected for change, then considerably more information can be obtained from a research study, namely the evidence for how the program achieved its effects through mediating processes.

The purpose of this article is to describe the use of mediation analyses for addressing theoretical and empirical questions in the development of dental interventions. First, motivations for conducting mediation analysis are outlined. Second, we describe a theoretical framework for intervention mediators. Third, we describe statistical analyses to investigate whether one variable is a mediator of an intervention. In Appendix A, a hypothetical example is used to demonstrate the statistical analyses. Extensions of the method for multiple mediators, moderators, multilevel, and longitudinal data are briefly outlined. Finally, guidance for how to report mediation analyses in research articles is provided.

Why do analyses of mediation in intervention research?

Vital information regarding program design can be obtained by evaluating whether the program changed the theorized mediators, and whether the mediators were related to the outcome. The results of these analyses may lead to strikingly divergent conclusions regarding program redesign (e.g., deciding to strengthen a component of the intervention versus removing it). The following are seven overlapping benefits of conducting mediation analyses in intervention studies [see also (3,11)]:

• Manipulation check: mediation analyses provide a check on whether the intervention produced a change in the constructs it was designed to change (e.g., if the intervention was designed to increase parental modeling, then program effects on parental modeling should be evident). If the program did not change the mediator, it is unlikely to have the desired effects on the targeted outcome. Failure to change mediating variables may occur because the program was ineffective, the measure of the mediating variable was inadequate, or by chance.

• Program improvement: mediation analyses can be used to identify successful and unsuccessful program components. If a program component did not change the mediator, then the actions used to change the mediator require improvement. For example, if no program effects on parental modeling are found, the program may need to reconsider the strategies used to change parental modeling. If the program increases parental modeling but parental modeling does not affect dental health, the parental modeling component of the program may be ineffective and/or unnecessary.

• Measurement improvement: lack of a program effect on a mediating variable can suggest that the measures of the mediator were not reliable or valid enough to detect changes. If no program effects are found on parental modeling, for example, it may be that the method being used to evaluate parental modeling is not reliable.

• Possibility of delayed program effects: if the intervention does not have the desired effect on the outcome variable but does significantly affect theorized mediating variables, it is possible that program effects on outcomes will emerge later in time. For example, the effects of a parental modeling intervention to improve child dental health may not be evident until the children are older.

• Evaluating the process of change: mediation analysis provides information on the processes by which the intervention program achieved its effects. For example, if intervention program effects on dental health are found, it is possible to study whether the changes in mediators like parental modeling or another mediator were responsible for the improvements.

• Building and refining theory: one of the greatest strengths of mediation analysis is the ability to test the theories upon which intervention programs are based. Many theories are based on results of cross-sectional studies with little or no experimental verification. Mediation analysis in the randomized design often used in intervention research is ideal for testing theories. Competing theories of contributors to child dental health, for example, may suggest alternative mediators that can be tested in an experimental design.

• Practical implications: the vast majority of intervention programs have limited resources for implementation and dissemination. Intervention programs will cost less and provide greater benefits if mediation analyses are used to hone in on the most important program components and weed out ineffective components. Mediation analyses can also help determine when to abandon an intervention approach or persist despite a nonsignificant overall program effect.

Theory and selection of intervention mediators

Theory is critical to selecting mediators and, accordingly, intervention program components. Intervention programs are designed to change mediating variables that are theorized to be causally related to the desired outcome. The assumption of a causal relation between the mediator and the outcome is critical, as is the assumption that the mediator can be changed by the program. If these assumptions are correct, a program that substantially changes the mediating variables will, in turn, change the outcome. Mediation also requires the assumption of temporal precedence such that change in the theorized mediator occurs before change in the targeted outcome.

The two links in the mediation model in Figure 1, labeled “a” and “b,” are informed by two different types of theory. The first is “action” theory, which informs the “a” path, and is the theory for how the intervention will change the mediating variables. Action theory provides the background for determining the manipulations that will be used in efforts to change the targeted mediators. For example, specific strategies such as education or role playing may be used by a program to teach and encourage parents to model good dental hygiene for their children. The second is the “conceptual” theory, which informs the “b” path, and is the theory for how the mediating variables are related to the dependent variable (12). For example, theory might suggest that children are motivated to imitate their parents’ behavior, so viewing parental dental hygiene behavior will improve their own dental health behaviors. Conceptual theory typically relies on past theory and empirical research for selection of variables expected to be causally related to the outcome.

Both action and conceptual theory are critical for intervention research because both must be accurate for the intervention to successfully change the outcome variable. If the action theory is inaccurate and the intervention does not change a mediator that is causally related to the outcome variable, then the intervention would not alter the outcome variable. If the conceptual theory for how the mediators are related to the outcome is inaccurate then any intervention change in the mediator will not lead to change in the outcome because the mediator is not causally related to the outcome.

Theoretical and practical considerations limit the mediators that realistically can be changed in an intervention study. Personality is likely more difficult to change than knowledge or attitudes, for example. The amount of resources required, the time required for change to be observed, and the ability to accurately measure variables are important factors when selecting mediators. A researcher may choose a mediator that is easier to change (e.g., public knowledge), even though it may have a weaker relation to the outcome than a mediator with a stronger relation to the outcome (e.g., impulsivity), because it can be more realistically targeted in a resource-limited intervention.

There are additional decisions that must be made regarding mediation of interventions. Most mediating processes reflect a long sequence of activities. For example, an intervention to increase parental modeling may involve a string of mediating processes, from exposure to an intervention component, to comprehension of the component, to short-term attitude change, to long-term attitude change, to actually applying material learned in the component when behaving. With a few exceptions, researchers generally consider individual mediators rather than hypothesizing or analyzing a long chain of mediation. Empirical research and theory can provide rationale for which mediators are most important and which to select.

Specification of the exact outcome measure of interest can also be complicated. For example, an outcome measure in one study might be whether an athlete wears a mouth guard or not even though the critical outcome of interest is actually dental trauma. In some cases, it is unrealistic to use certain outcomes because the low frequency of the event makes it prohibitive to study without a large sample size or extended follow up. In such a situation, researchers have used outcome variables as surrogates for the primary outcome measures. Theory or empirical data regarding the relation between the surrogate and the actual outcome of interest is used to justify the use of the surrogate. For example, intervention effects on precancerous mouth lesions may be a surrogate for oral cancer, which may require a longer follow up or larger sample size than is practical given limited resources.

Steps in statistical mediation analysis

Statistical mediation analysis is: a) the test of the effect of an independent variable X, such as an intervention program, on mediating variables (M); and b) the test of the link between program effects on mediators to effects on outcomes (Y). As shown in Figure 1, for a single mediator model, there are coefficients that reflect the relation of the intervention X to the mediator M, represented by coefficient a, and the relation of to M to Y adjusted for the X variable, represented by the b coefficient. A c′ coefficient represents the relation of X on the outcome Y that is not through the mediator M.

There are several tests for mediation [see (13) or (3) for more information on these tests] but each of these tests use information from some or all of the three regression equations shown in the following. The parameter estimates (and standard errors) from Equations 1 to 3 provide information for a statistical mediation analysis for the case of one mediator and one outcome variable:

$$Y=i1+cX+e1$$ Equation 1

$$Y=i3+c^{\prime }X+bM+e2$$ Equation 2

$$M=i2+aX+e3$$ Equation 3

As described earlier, Y is the outcome variable, X is the independent variable (intervention program), and M is the mediator. The coefficient c quantifies the relationship between the program and the outcome; c′ is the coefficient quantifying the program to the outcome adjusted for the mediator; a is the coefficient quantifying the program to the mediator; b is the coefficient quantifying the mediator to the outcome variable, adjusted for the program; e1, e2, and e3 represent unexplained residual variability; and the intercepts are represented by i1, i2, and i3. In practice, only two of these equations are necessary for investigation of statistical mediation analysis but information from all three equations can be used in mediation analysis.¹ Seven steps in conducting mediation analysis are described in the following. The first three steps correspond to the information obtained from the three regression equations described earlier. Appendix A applies the following steps to a hypothetical example of an intervention to increase fluoride exposure among children.

• Intervention effect on the outcome: the estimate c reflects the change in Y for a one unit change in X. Typically X will represent exposure to an intervention so the estimate is the difference between the means in the program and control groups. With random assignment of participants to conditions, the program effect of the intervention on the outcome can be interpreted as a causal effect (3). In one of the most widely used tests of mediation based on a series of statistical tests (1,14) a statistically significant program effect is deemed necessary for mediation to exist. However, mediation can exist even when there is not a statistically significant program effect for several reasons. First, the significance test is a test of the overall program effect and not a test for mediation. Like any statistical test it is subject to error when the entire population of data is not available. Second, in some situations the test for mediation can have more power than the test for the overall program effect. A third reason requires consideration of a multiple mediator model that will be discussed later in the article. In this case, there may be program effects on mediators that have opposing effects. That is, if some mediators reduce the problem behavior and others increase the problem behavior there may be a nonsignificant overall program effect when mediation actually exists albeit through two opposing mediators [see (3) and (15) for examples].

• Intervention effect on the mediator. The estimate a quantifies the change in the mediator for a 1-unit change in X, so for an intervention (coded 0 and 1), the a coefficient is the mean difference between intervention and control groups. The test of the a path provides a test of the X to M link, which is required for mediation to exist. With random assignment of participants to conditions, the program effect of the intervention on the mediator can be interpreted as a causal effect.

• Relation of the mediator to the outcome variable when adjusted for the intervention. The effect of the mediator on the outcome variable (b path) represents the estimate of change in the outcome variable for a one unit change in M adjusted for X. The c′ coefficient represents the estimate of change in the outcome for a one unit change in X, adjusted for M. The remaining steps use information from the first three steps described earlier.²

• Estimation of the mediated effect: the mediated effect can be calculated in two ways based on the above equations. One way to estimate the mediated or indirect effect equals the difference in the intervention effect with and without the mediator (c − c′). A second method that yields identical mediated-effect estimates for the case of ordinary least-squares regression originates in path analysis. The estimator of the mediated effect is the product of the a and b parameter estimates (ab). The rationale of this method is that mediation depends on the extent to which the intervention changes the mediator (path a) and the extent to which the mediator affects the outcome variable (path b).

• Significance testing and confidence limit estimation. In order to test the significance of the mediated effect, it is necessary to calculate the sample standard error of the indirect or mediated effect ab (16,17), which equals

  $$s_{ab}=\sqrt{s_a^2{b}^2+s_b^2{a}^2}$$ Equation 4
  where a and b are estimated regression coefficients and s_a² and s_b² are the squared standard error of a and b from Equations 2 and 3 shown earlier. The standard error (s_ab) is used to form confidence limits for the mediated effect represented by UCL and LCL for the upper and lower confidence limits, respectively:

  $$\mathit{UCL}=\text{mediated}\text{effect}+z({\text{s}}_{\text{ab}})$$ Equation 5

  $$\mathit{LCL}=\text{mediated}\text{effect}-z({\text{s}}_{\text{ab}})$$ Equation 6

  If the confidence limit does not include the 0 value, then the mediated effect is considered statistically significant.

  Alternatively, the mediated effect can be divided by the standard error and compared with the z distribution, e.g., if the absolute value of the ratio is equal to or larger than 1.96, then it would be statistically significant at the P = 0.05 level. More accurate confidence intervals and tests of significance can be obtained by using a method based the distribution of the product using a computer program called PRODCLIN, available at http://www.public.asu.edu/~davidpm/ripl/Prodclin/ or a type of analysis called bootstrapping [(3), Chapter 12].

  If the mediated effect is statistically significant and the c′ coefficient is nonsignificant, then there is evidence for complete mediation, i.e., all of the relation of X on Y is through the mediator M. If the mediated effect is statistically significant and the c′ coefficient is statistically significant then this would suggest partial mediation such that there are additional variables that may mediate the relation.

• All of these statistical tests are subject to Type I error (saying an effect is significant when it is not present in the population) and Type II error (failing to say a real effect is statistically significant). Studies of the statistical power to detect mediated effects (13,18,19) suggest that substantial sample sizes are required to detect effects. For example, if the relation of X to M and M to Y corresponds to a medium effect (about a correlation of 0.3 or 9 percent variance explained) then a sample of about 70 subjects is needed. However, if the two effects are small, a sample of around 500 is needed.

• Calculate measures of effect size. The estimates calculated earlier are useful for interpretation and incorporating chance in the statistical analysis. It is also useful to compute effect size for the mediated effect relations as described in MacKinnon [(3); Chapter 4]. The correlation effect size measure is useful for the a and b paths, where the partial correlation is used for the b path. Standardized beta coefficients are also useful to provide an indication of relations in standard deviation units. There are several additional quantities that are useful for interpreting the mediated effect. These quantities include the direct effect, c′, the total effect, ab + c′ = c, and the proportion mediated ab/c = 1 − c′/c = ab/(c′ + ab).

• Consider alternative explanations of an observed mediation effect. As described earlier, the relation of X to M has a causal interpretation when X represents random assignment to groups and reflects the change in M with exposure to an intervention. The randomization of X clarifies interpretation of the a and c coefficients. But the mediator is not directly randomized, so the interpretation of the b and c′ coefficients often requires additional information to make the case for mediation. We focus on the b coefficient here as it is part of the mediated effect. The relation between M and Y represents an association because M is not directly randomized; participants select their own value of M. As a result, the interpretation of the b coefficient merits additional scrutiny in the evaluation of interventions (3). There are at least six aspects of this relation that should be considered. First, is there a variable not included in the analysis that predicts both M and Y, so that the observed relation between M and Y is solely caused by this omitted variable? Second, is the mediator the correct mediator or is it really a variable that is related to the true critical mediator? Third, is the mediator really the same as the outcome measure? Fourth, is the true temporal relation from M to Y or from Y to M? Fifth, is the relation between M and Y a linear or nonlinear relation? Sixth, what additional studies are needed to build the case for the mediator?

Guidance in interpreting the results of a mediation analysis

Four common results based on the significance of the a and b paths are outlined in the following, along with an interpretation for each situation.

• Nonsignificant intervention effect on the mediator and nonsignificant relation from the mediator to the outcome (the a and b paths are both not statistically significant). An intervention may not significantly change the mediator or the outcome variable. The lack of a significant X to M relation (a path) implies action theory failure – the intervention activities did not significantly change the mediator. There is also conceptual theory failure because the relation of M to Y (b path) is nonsignificant. If there is an intervention effect on the outcome (i.e., the c path is significant), then there may be other mediators that were changed by the intervention that are also related to the outcome. If the intervention effect is nonsignificant, however, then there were no significant relations in the study, suggesting that the study may have had low power to detect effects or the theory for the intervention needs to be reconsidered. As in any study where the null hypothesis is not rejected, these results do not prove that the theory or the mediators targeted by the program are wrong, only that the results are consistent with the null hypothesis of no intervention effects. The results do, however, raise questions about the theory, intervention approach, and implementation of the program that must be seriously addressed before continuation of the existing program or the development of a new program.

• Intervention effect on the mediator but no significant relation for the mediator to the outcome (the a path is statistically significant but the b path is not statistically significant). In this situation, there is evidence for action theory as the intervention significantly changed the mediator (a path) but there is not evidence for conceptual theory because the mediator was unrelated to the outcome (b path). The program changed the mediator as intended, but the mediator may not be causally related to the outcome measure. The researcher may decide to remove the component in future studies. If the overall intervention effect on the outcome (path c) is statistically significant, it implies that there are other mediators that may explain the intervention effect. Similarly, if there is not an overall intervention effect on the outcome, then there is evidence that the conceptual theory on which the intervention is based may be questioned. It is also possible that the effects of the mediator on the outcome may emerge at some future measurement or the overall program effect on the outcome may be nonsignificant because of the presence of mediation effects as planned and counterproductive mediation effects (i.e., program component effects that oppose the mediated effects).

• No intervention effect on the mediator but significant relation for the mediator to the outcome (the a path is not statistically significant, but the b path is statistically significant). This pattern of effects is commonly observed in a mediation analysis of intervention programs. There is evidence for conceptual theory because the mediator is significantly related to the outcome (the b path). There is action theory failure because the intervention was not able to significantly change the mediator (the a path). The mediator may have been a reasonable one to target but the intervention activities were not sufficient to change the mediator. If there is also a significant overall intervention effect, then there may be other mediators that led to the significant overall intervention effect.

• Program effects on the mediator and a significant relation of the mediator to the outcome (both the a and b paths are statistically significant). This result is evidence of a successful intervention program because it yielded a statistically significant effect on the mediator supporting the action theory of the program and statistically significant relation between the mediator and the outcome supporting the conceptual theory of the mediator. If the direct effect is also statistically significant, then there is evidence that the mediator partially mediated the relation of X to Y. If the direct effect is nonsignificant, then there is evidence for complete mediation. However, like any other study where the null hypothesis is rejected, such results must be treated with some caution. If the sample size is large, the mediated effect may be small (i.e., not clinically significant), even though the mediated effect is statistically significant. Alternative explanations of observed mediation effects should be considered as described earlier.

Extensions of the single mediator model

Multiple mediator model

Many interventions are designed to change multiple mediators rather than a single mediator. The multiple mediator model provides a way to organize the analysis of data when there are measures of more than one mediator. The single mediator model described above can be easily extended to model multiple mediators [(3,20), Chapters 5 and 6]. For the hypothetical example of an intervention to increase children’s fluoride exposure (described in Appendix A), it may be useful to measure changes in dental hygiene practices including dentist visits, flossing, and tooth brushing, which may also be theorized to act as mediators of the intervention. Similarly, additional mediators may be theorized to act in a sequence of mediating processes. In the hypothetical study, a mediation model with four variables could be tested, such as intervention (X) to parental attitudes about tap water (M1), to child’s exposure to tap water (M2), to dental caries (Y). In general, it is useful to estimate single mediator models as well as multiple mediator models, as the single mediator models require considerable interpretation alone.

Moderators

The mediation relations of X to M and M to Y may differ across groups [(3): Chapter 10]. These grouping variables are known as moderators and can be incorporated in mediation analysis. For example, for the hypothetical study, socioeconomic status may serve as a moderator; that is, mediation relations may differ for high versus low socioeconomic status children. Perhaps higher socioeconomic status families are more likely to consume bottled water, reducing exposure to fluoride from tap water. In this case the program effect on M may be larger for the higher socioeconomic status groups. Other potential moderating variables in public health dentistry include sex, age, ethnicity, geographic location, and availability of dental care.

Multilevel models

Another important consideration in public dentistry interventions are that data are collected in groups and groups are often used in delivering interventions. Examples of these grouping variables are communities, clinics, schools, and families. Collecting data from participants in these types of groups often introduces a dependency among observations from the same group, e.g., because they talk with each other and tend to have the same health practices. Multilevel mediation models have been developed to handle the statistical issues involved with data in groups [(3): Chapter 9].

Longitudinal models

Most interventions also include longitudinal data, whereby measures are taken before and after participants are randomly assigned to conditions. For the common two-wave case, the difference score model and the residualized change scores can be used to form one measure of M and one measure of Y in addition to the X variable coding intervention status. In this case, the same models described for the hypothetical tap water example can be applied. For a difference score, M is the difference between the mediator scores for each participant and Y is the difference between the outcome scores for each participant. For residualized change the baseline score is used to predict the time two score and then the predicted time two score is subtracted from the actual time two score providing one measure for M and one measure of Y. In an analysis of covariance model, the baseline for M and Y is included in the mediation equations in order to partial out the effects of baseline level from analyses. If more than two waves are available, then an ideal test of mediation is whether the intervention changed the mediator at time 2 and whether the time 2 change in the mediator is related to time 3 change in the outcome, thereby providing some evidence for temporal precedence among X, M, and Y. In longitudinal models, there can be many different types of mediated effects because change at an early time may predict change at later times (3,11). There are several sources for more information on longitudinal mediation models (3,21–24).

Describing mediation analysis in research articles

Nine overlapping aspects of mediation analyses are ideally described in research articles (11):

• Link theory and the mediators targeted by the program. One critically important aspect of mediation analysis is that it forces the researcher to consider the theoretical basis for how the intervention program leads to changes in an outcome measure. Experimental comparison of mediators suggested by competing theories provides an ideal test of the theories. As described earlier, such a intervention study will provide information on how to prevent a problem behavior as well as information on competing theories.

• Link intervention program components with targeted mediators, providing a background for action theory. A table with the specific program components and the mediators targeted by each component clarifies the link.

• Provide evidence that selected mediators can be changed. Build an argument for the importance of the mediators based on prior empirical and theoretical research on the proposed outcome and related outcomes. If personality mediators or other mediators that may not be easily modifiable are included, justify their role as mediators as well as how the program will be intense enough to change them.

• Provide evidence that mediators are related to the outcome measure. Prior theoretical and empirical research should suggest that the mediator is causally related to the outcome measure.

• Describe a program of research. The identification of mediators requires a program of study beginning with the identification of the mediators that are related to the outcome, the development of a intervention program to change the mediators, and the evaluation of the intervention program (3,25). Replication of previous research results and experimental studies provide the most convincing evidence for mediators.

• Include information on the psychometric properties of reliability and validity of mediators and outcome measures. The match between the content of the measures and the targeted construct should be described.

• Report estimated coefficients in the mediation analysis, c, a, b, c′, ab, their standard errors and confidence intervals. Estimate effect size measures of the partial correlation, standardized betas, and proportion mediated. Investigate linear and nonlinear relations among variables.

• Investigate assumptions of mediation analysis. Test whether there is an interaction between X and M that would imply that the relation of M to Y differs across levels of X. Test linear and nonlinear relations among variables. Provide detailed investigation for whether there may be an omitted variable that may explain results and discuss whether the observed mediator is likely to be the critical ingredient of the intervention.

• Describe the next steps to provide scientific evidence for mediation relations investigated in the research article. Describe randomized experiments that may more accurately test hypothesized mediation relations suggested in the research article. Describe the variety of information that would add more evidence for the mediators including qualitative studies, laboratory studies, and intervention studies with other measures of the mediators or outcomes.

Summary

Mediation analysis is useful for testing the theoretical and empirical foundations of dental health interventions. Studies of mediation investigate how intervention programs work (or fail to work), providing a scientific basis to develop successful programs, thereby reducing the cost and enhancing the impact of intervention programs. The long-term goal of mediation analysis is the development of the most efficient and most effective interventions. The application of these methods requires the specification of mediating variables and their measurement as part of the design of research studies. The development of successful interventions is best served by programs of research with attention to identifying the consistency of intervention effects in different samples and locations and the specificity of mediation relations. Information from many sources is useful for this endeavor, including qualitative and clinical insight as well as the statistical mediation analyses described in this report.

Appendix A: Hypothetical study of an intervention to increase fluoride exposure among children

Mediation analysis of an intervention program for parents of 5-year-old children to increase intake of tap water with fluoride is used to illustrate the statistical mediation analysis. Hypothetical data for 100 children were generated. Children were randomized to either an intervention or a control group (X). Prior to assignment to the intervention, each parent–child pair was measured for the amount of tap water consumed in the year before the intervention and a continuous measure of dental caries was recorded. After the baseline measurement half of the parents were assigned to an intervention where the importance of fluoride in water was emphasized and parents were shown how to increase the amount of fluoridated water that their child consumed. For example, use of tap versus bottle water was emphasized. After 1 year, the amount of dental caries in the child was measured again, as was a measure of tap water consumed during the previous year. The change in tap water consumption was the mediator measure (M) and the change in dental caries was the outcome measure (Y). The researchers were interested in the extent to which the intervention changed the amount of tap water consumption and the relation of tap water consumption to the outcome of change in dental caries. The conceptual theory basis of the intervention was based on the known relation between consumption of fluoridated water and reduced dental caries (26). The action theory postulated that involving parents in controlling exposure to tap water would increase the amount of fluoridated tap water consumed. The intervention was delivered in three 1-hour sessions with parents. To simplify this illustrative analysis, the amount of tap water consumed was the single mediator. The regression estimates and standard errors (below the coefficient and in parentheses) for the three equations are presented in the following:

$$Y=-0.1119+\underset{(0.1717)}{0.8145X}$$ Equation A1

$$\text{Y}=-12.7962-\underset{(0.1189)}{0.1397X}+\underset{(0.0716)}{1.0188M}$$ Equation A2

$$M=12.45+\underset{(0.1386)}{0.9366X}$$ Equation A3

Intervention condition (X) was significantly related to water consumption (Y) (c = 0.8145, s_c = 0.1717, t_c = 4.7435), providing evidence that there is a statistically significant intervention effect of 0.8145 units. There was a statistically significant intervention effect on tap water consumption (a = 0.9366, s_a = 0.1386, t_a = 6.7571). The intervention led to a 0.9366 increase in tap water consumption after the intervention. The effect of the water consumption mediator was statistically significant (b = 1.0188, s_b = 0.0716, t_b = 14.2373) controlling for intervention condition. A 1 unit change in tap water consumed was associated with an increase of 1.02 in the change in child dental caries. The adjusted effect of the intervention was not statistically significant (c′ = −0.1397, s_c′ = 0.1189, t_c′ = −1.1750).

The estimate of the mediated effect is equal to ab = (0.9366) (1.0188) = c−c′ = 0.8145−(−0.1397) = 0.9542. The mediated effect of the intervention through change in tap water consumption was equal to 95 units of change in dental caries. Using Equation 4 equals 0.1563 for the standard error of the mediated effect estimate as shown in the following:

$$0.1563=\sqrt{{(0.9366)}^2{(0.0716)}^2+{(1.0188)}^2{(0.1386)}^2}$$

The 95 percent confidence limits for the mediated effect based on normal theory are equal to:

$$\begin{array}{l}\text{Lower}\text{confidence}\text{limit}(\mathit{LCL})=0.9542-1.96(0.1563)\\ =0.6478\\ \text{Upper}\text{confidence}\text{limit}(\mathit{UCL})=0.9542+1.96(0.1563)\\ =1.2606\end{array}$$

The asymmetric confidence limits based on the distribution of the product program (PRODCLIN) were equal to LCL = 0.6587 and UCL = 1.2715. The normal theory and the distribution of the product confidence intervals do not include zero so the conclusion would be that the mediated effect is larger than expected by chance alone, or statistically significant. The effect size for the a path was 0.4321 and the effect size for b path corresponded to a partial correlation of 0.8224, and standardized regression coefficients of 0.5637 and 0.8980, respectively.

There is evidence for action theory because there is a program effect on tap water consumed and there is evidence for conceptual theory because the change in tap water consumed was associated with the change in caries. An assumption of the analysis is that the relation of M to Y does not differ in each condition. If there is evidence that this interaction exists, it implies that the conceptual theory may not apply equally in each intervention condition. A test of whether the relation between the mediator and outcome changed across intervention conditions was tested with these data by adding the interaction of X times M in the regression Equation A2. This interaction was not statistically significant.

There are several additional considerations regarding a statistically significant mediation effect in a research study. Is there some other variable besides the amount of tap water that may be related to both tap water and caries that may explain the results? For example, were families in the intervention condition more likely to go to the dentist or learn proper dental hygiene and these measures are the actual mediators of the intervention? If measures of these other potential mediators were available, significant mediated effects might also be obtained. Comprehensive interpretation of mediation analysis includes consideration of these and other alternative explanations as well as possible additional studies that would help clarify evidence for mediation relations. The goal is that the results of replication studies combined with other data including qualitative data, clinical observations, and theoretical development leads to the identification of critical mediating variables.