Thermodynamic Origins of Monovalent Facilitated RNA Folding

Abstract

Cations have long been associated with formation of native RNA structure and are commonly thought to stabilize the formation of tertiary contacts by favorably interacting with the electrostatic potential of the RNA, giving rise to an “ion atmosphere”. A significant amount of information regarding the thermodynamics of structural transitions in the presence of an ion atmosphere has accumulated and suggests stabilization is dominated by entropic terms. This work provides an analysis of how RNA–cation interactions affect the entropy and enthalpy associated with an RNA tertiary transition. Specifically, temperature-dependent single-molecule fluorescence resonance energy transfer studies have been exploited to determine the free energy (ΔG°), enthalpy (ΔH°), and entropy (ΔS°) of folding for an isolated tetraloop–receptor tertiary interaction as a function of Na⁺ concentration. Somewhat unexpectedly, increasing the Na⁺ concentration changes the folding enthalpy from a strongly exothermic process [e.g., ΔH° = −26(2) kcal/mol at 180 mM] to a weakly exothermic process [e.g., ΔH° = −4(1) kcal/mol at 630 mM]. As a direct corollary, it is the strong increase in folding entropy [Δ(ΔS°) > 0] that compensates for this loss of exothermicity for the achievement of more favorable folding [Δ(ΔG°) < 0] at higher Na⁺ concentrations. In conjunction with corresponding measurements of the thermodynamics of the transition state barrier, these data provide a detailed description of the folding pathway associated with the GAAA tetraloop–receptor interaction as a function of Na⁺ concentration. The results support a potentially universal mechanism for monovalent facilitated RNA folding, whereby an increasing monovalent concentration stabilizes tertiary structure by reducing the entropic penalty for folding.

Over the past 10 years, the number of structures and functions attributed to specific noncoding RNA sequences has grown significantly¹ and radically advanced the field of RNA biology. These structures are the result of a number of smaller molecular interactions (e.g., tertiary interactions), which stabilize the global conformation of RNAs.² However, it is important to note that these structures, although extremely helpful, represent only static images of RNA in a near-minimal energy conformation. Under more physiological conditions, these molecules can be richly dynamic and occupy a broad ensemble of thermally accessible structures.^3–5 The conformational dynamics of RNA tertiary interactions contribute to the diverse array of functionality.⁶

Because RNA molecules are anionic biopolymers, they are always accompanied by counterions in solution regardless of conformation. These counterions interact favorably with the electrostatic potential of the RNA, giving rise to an “ion atmosphere”. For RNA to achieve a specific three-dimensional conformation, it must undergo any number of structural transitions, most of which result in a more compact structure. Additional uptake of cations into the ion atmosphere can help alleviate the enhanced intramolecular columbic repulsion associated with a more compact conformation. A number of studies suggest that entropic considerations are largely responsible for the stabilization of folded nucleic acid structures being facilitated by increasing cation concentration.^7–9 One explanation for this entropic promotion is as follows. As nucleic acids undergo a structural transition to a more charge-dense state, additional counterions are brought from the bulk solution to the preexisting ion atmosphere as a result of the elevated charge density. This restricts the translational freedom of those ions and thus gives rise to an entropic penalty associated with “unmixing” the solution. At higher bulk concentrations, it is less entropically costly to unmix counterions that were taken up during the folding transition, thus reducing the entropic cost of the folding transition. Single-molecule experiments provide a relatively unexplored technique that can be used to quantitatively measure the salt dependence of RNA folding thermodynamics and represents the major focus of this work.

The cytosol contains cations of multiple valencies, each of which can interact with the electrostatic potential of the RNA and thus facilitate folding.^4,10–12 A number of RNAs are capable of adopting stable, native, tertiary structures in solutions consisting solely of monovalent ions.^13–16 Focusing on monovalent facilitated folding provides a crucial conceptual simplification for both experiment and theory, by avoiding complications associated with mixed solutions of monovalent, divalent, and higher-valence cations. In turn, these simple models serve as critical benchmarks for accurately testing our ability to predict thermodynamics of RNA folding under realistic cellular conditions.

Much work has been directed at understanding the role that monovalent ions play in the folding of structured RNAs.^17–20 Generally, monovalents are capable of interacting with RNAs through a variety of distance-dependent modes, ranging from totally diffuse to completely chelated. The most direct mode of interaction is chelation of an ion,^21,22 whereby the ion loses multiple water molecules in its primary sphere of hydration to make direct, stabilizing contact with the electronegative atoms of the RNA. These specific ion interactions are not dominant and therefore have an only minimal effect on net charge neutralization for a single RNA in solution,²³ though with potentially more significant effects on enzymatic activity.²¹ Diffuse ions have the most indirect mode of interaction with RNA. These ions interact only with the electrostatic potential of the RNA, giving rise to the ion atmosphere mentioned above.²⁴ Of course, many other ways in which ions can interact with the RNA exist (e.g., indirect hydrogen bonding via the hydration layers associated with the solvated ion), but all of them fall between the extremes of chelated and diffuse ions. This work contributes to the understanding of how the various monovalent cation–RNA interactions alter the thermodynamics associated with formation of an isolated tetraloop–receptor tertiary interaction.

MOLECULAR MODEL

RNAs are well-known to fold in a hierarchical manner, with secondary structure forming on a relatively rapid time scale (microseconds to milliseconds), followed by slower folding of the tertiary structure (milliseconds to minutes). Thus, a commonly proposed framework in which to view equilibrium folding of RNA is

$$\text{U}\iff \text{I}\iff \text{F}$$

where the unfolded state (U) corresponds to an RNA without extensive secondary interactions and the intermediate state (I) describes an RNA with well-formed secondary structure.^25–27 The I state then proceeds to form tertiary interactions on much longer time scales, resulting in the final folded state, F. This work focuses exclusively on tertiary interactions by making two additional assumptions. (i) Secondary structure formation (U ⇔ I) is rapid relative to formation of tertiary contacts, and (ii) experimental conditions are such that equilibrium constant between U and I is much greater than unity. These assumptions allow for further simplification of the kinetic framework to

$$\text{I}\iff \text{F}$$

where the equilibrium constant (K_eq) is defined as the ratio of k_fold (I ⇒ F) to k_unfold (I ⇐ F). In this two-state equilibrium, both macroscopic states I and F are likely composed of an ensemble of microscopic states. The Boltzmann-weighted averages of the ensembles are used to describe the macroscopic states, thus allowing for interpretations based on the two-state unimolecular equilibrium. This simplified two-state model proves to be sufficient for describing the formation of an individual tertiary interaction for the RNA construct in this study.

The model RNA used to explore tertiary interactions in monovalent ion atmospheres is a synthetic RNA construct that isolates the GAAA tetraloop–receptor interaction (Figure 1),²⁸ as observed in the P4–P6 domain of the Tetrahymena ribozyme.²⁹ The construct is built from a three-piece oligonucleotide assembly that allows the GAAA tetraloop (green), tethered by a flexible poly-A₇ linker, to freely dock into or undock from the 11-nucleotide receptor domain (red). This tertiary interaction^30,31 has undergone extensive biochemical and biophysical characterization,^32–36 making it a prime RNA folding motif for detailed kinetic and thermodynamic investigation. A significant amount of structural data for this RNA folding motif from a variety of RNA systems also exists.^{21,32,37–40} Most relevantly, the tetraloop–receptor interaction is stably formed in solutions containing only monovalent ions,¹⁰ thus eliminating the complications associated with mixed monovalent and divalent ions in solution and therefore making it an ideal RNA model for addressing the effect of monovalent cations on the formation of tertiary interactions. Additionally, the “binary” (folded–unfolded) nature of this tertiary interaction (Figure 2a) makes the isolated construct used in this study particularly useful, by eliminating potential complications caused by cooperative folding effects between multiple tertiary interactions. Lastly, the simplicity of the construct allows for the use of synthetic modifications (e.g., biotin and fluorescent dyes) necessary for single-molecule fluorescence resonance energy transfer (smFRET) experiments (Figure 1).^10,28,35,36 See Materials and Methods for details.

Figure 1.

Schematic of the three-piece donor–acceptor label RNA construct. The isolated GAAA tetraloop–receptor structure serves as a model system for investigating the thermodynamics and kinetics of monovalent facilitated formation of tertiary interactions in structured RNAs.

Figure 2.

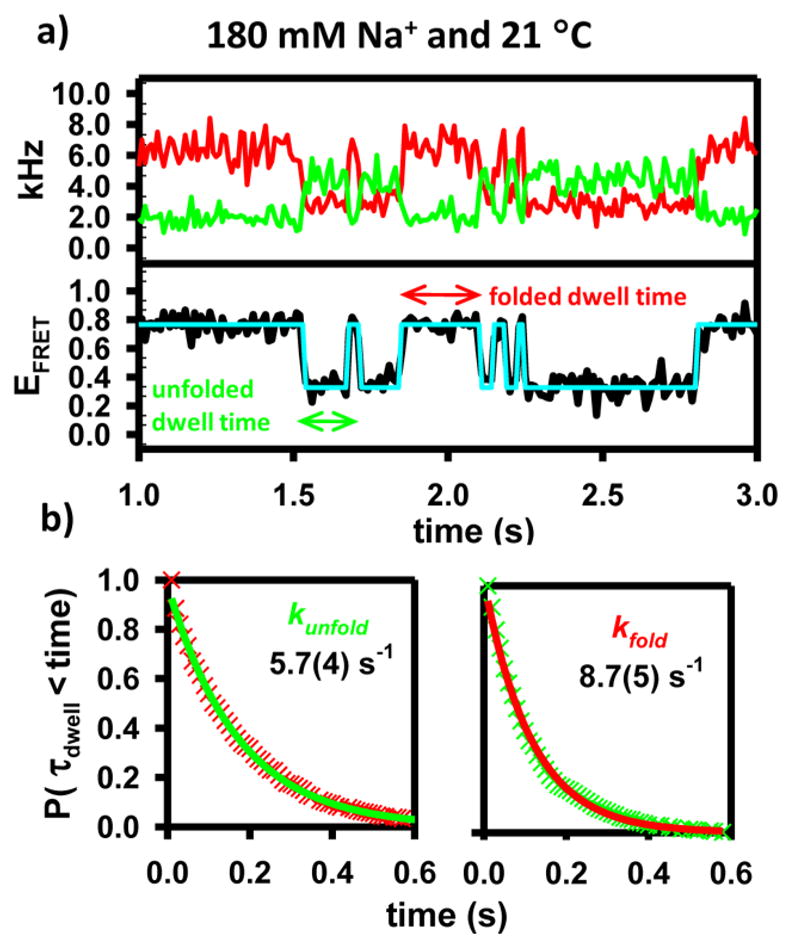
(a) Sample time trajectories for the model construct. A hidden Markov fit to the FRET trajectory is used to demonstrate the two-state behavior of the folding process.⁶⁷ (b) Cumulative distribution functions (CDFs) of the dwell times demonstrate single-exponential behavior and are used to extract unimolecular rate constants for folding and unfolding.^43–45

The smFRET experiments used throughout this work were conducted using a confocal fluorescent microscope equipped with time-correlated, two-color detection of single photons. This techniques provides the ability to measure, in real time and under equilibrium conditions, the amount of time that a single molecule spends in a given conformation (Figure 2a).^41,42 In the framework of the previously described two-state model, the cumulative distribution function (CDF) of durations spent in either state (τ_dwell) will be exponentially distributed, determined by the characteristic decay constant k_unfold or k_fold (Figure 2b).^43–45 At a specific monovalent concentration and temperature, therefore, smFRET can be used to measure k_fold, k_unfold, and K_eq for the GAAA tetraloop–receptor interaction. In this work, analysis of the equilibrium constants as a function of both temperature and Na⁺ concentration is used to extract standard state thermodynamics (ΔG°, ΔH°, and ΔS°) for this isolated tertiary interaction. Additionally, the temperature dependence of the forward and reverse rate constants (k_fold and k_unfold) is used to obtain information about the enthalpic (ΔH^‡) and entropic (ΔS^‡) components of the free energy barrier (ΔG^‡) as a function of Na⁺ concentration.

MATERIALS AND METHODS

Experimental Apparatus

Excitation of fluorescent molecules is accomplished by focusing light from a pulsed (20 MHz, 10 ps) 532 nm laser to a diffraction-limited spot in the sample with a 1.2 NA water emersion objective. The same objective collects the photons from the sample and directs them to a detection system using a dichroic mirror. A small pinhole rejects fluorescence from outside the confocal volume, thereby reducing the magnitude of the background signal. Photons from donor and acceptor fluorescence are separated by wavelength and polarization using dichroic filters and polarization beam splitters. The photons are then detected on single-photon avalanche photodiodes (see ref 36 for details). Photon arrival time information is sent to a time-correlated single-photon counting module where the fluorescence microtime (i.e., delay with respect to the laser pulse) and macrotime (time with respect to the start of the experiment) of each incoming photon are recorded.

Temperature Control

Two methods are used to provide temperature control of smFRET samples. The first involves the use of a microscope stage heater and a heated objective collar to uniformly heat the entire sample (see ref 36 and 50 for details), while the second involves the use of a newly adapted IR laser absorption-based heating technique (see ref 46 for details). This technique provides the ability to control the local temperature of an aqueous sample using focused light from a fiber-coupled 1440 nm continuous-wave laser. While the stage heating method is used for a majority of the data collection, IR laser-based heating is also explored at all reported Na⁺ concentrations. The two heating methods used here produce kinetic and thermodynamics results that have previously been determined to be indistinguishable from one another.⁴⁶

RNA and Sample Preparation

All nucleic acid sequences for the tetraloop–receptor constructs were purchased commercially. The full construct consisted of three strands of oligonucleotides (Figure 1): (i) a 5′ Cy3-labeled RNA strand containing the GAAA tetraloop sequence, (ii) a 5′ Cy5-labeled RNA strand with a 3′ overhang, and (iii) a 5′ biotinylated DNA strand complementary to the 3′ overhang of the Cy5 strand. The three strands were annealed and purified using solutions and buffers described previously.¹⁰ Thermodynamic and kinetic data were collected using solutions consisting of 50 mM hemisodium HEPES, 5.0 mM PCA, 100 nM PCD, 2.0 mM Trolox, and 0.1 mM EDTA (pH 7.5) with varying concentrations of NaCl (100–800 mM) to achieve the desired Na⁺ concentration. Note the Na⁺ concentration comes from added NaCl, buffer, and the oxygen scavenging system (PCA/PCD).⁴⁷

RESULTS

Folding Kinetics and Standard State Free Energy of Folding

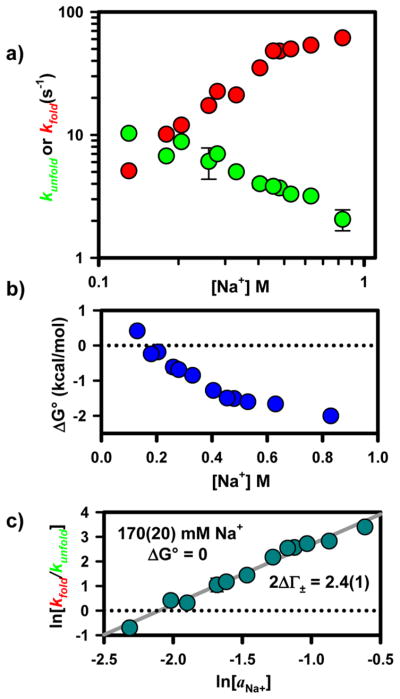
As shown in the titration data in Figure 3a, an increasing Na⁺ concentration both accelerates k_fold and decelerates k_unfold, which clearly favors formation of products (F) over reactants (I) and therefore increases K_eq. In terms of free energy, addition of Na⁺ increases the favorability of forming the tertiary interaction, i.e., Δ(ΔG°) < 0 (Figure 3b). At 130 mM Na⁺, the reaction is slightly unfavorable [ΔG°(298 K) = 0.4(1) kcal/mol], whereas at 830 mM Na⁺, folding becomes appreciably favored [ΔG°(298 K) = −2.0(1) kcal/mol]. Clearly, the free energy, and therefore ln(K_eq), has a nonlinear dependence on Na⁺ concentration. These data, when considered in the context of the physically motivated theoretical framework provided by preferential interaction coefficients, can be used to create a more informative depiction of the Na⁺ dependence of K_eq.^7,48 On the basis of this model-free description of RNA–ion interactions, the logarithm of the equilibrium constant [ln(K_eq)] should scale linearly with the logarithm of the thermodynamic activity of the monovalent ion [ln(a_Na⁺)]. From such an analysis, the slope (2ΔΓ _±) corresponds to the net change in the number of ion pairs associated with the ion atmosphere as a result of the folding transition. This is well demonstrated by a linear fit of ln(K_eq) versus ln(a_Na⁺), where the slope yields a net uptake of approximately 2.4(1) ion pairs (Figure 3c). This plot also demonstrates that at 170(20) mM Na⁺ formation of the tertiary interaction results in no free energy change. It should be noted that because ln(K_eq) is proportional to the Gibbs free energy (ΔG° = ΔH° − TΔS°) it seems reasonable to anticipate that both ΔH° and TΔS° might also scale linearly with ln(a_Na⁺).

Figure 3.

(a) Na⁺-dependent kinetics for the formation of the GAAA tetraloop–receptor interaction. An increasing Na⁺ concentration yields a significant enhancement of the folding rate constant (k_fold) and a subtle reduction in the rate constant for the unfolding process (k_unfold). (b) Dependence of the free energy on Na⁺ concentration. (c) Preferential interaction coefficient analysis for the formation of the tertiary interaction, which yields an ion pair uptake (2ΔΓ _±) of 2.4(1) and no change in free energy at 170(20) mM Na⁺.

The purpose of this work is to investigate the thermodynamics associated with the formation of the GAAA tetraloop–receptor interaction as a function of monovalent salt concentration. Therefore, it will be useful to develop the language used to describe the range of experimental Na⁺ concentrations. Specifically, this work will refer to RNA molecules in 180 mM Na⁺ as being under “free energy neutral” conditions where ΔG° ≈ 0 kcal/mol. Progressively higher concentrations of Na⁺ (i.e., 330, 480, and 630 mM) correspond to progressively more “free energy favorable” conditions as ΔG° decreases below zero with addition of Na⁺.

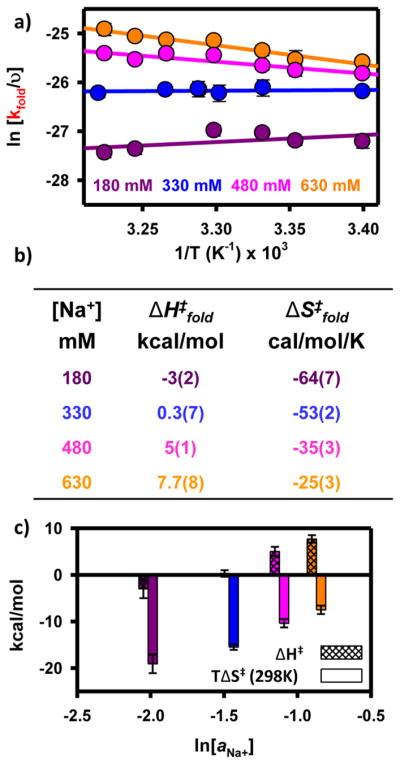
Standard State Enthalpy and Entropy of Folding

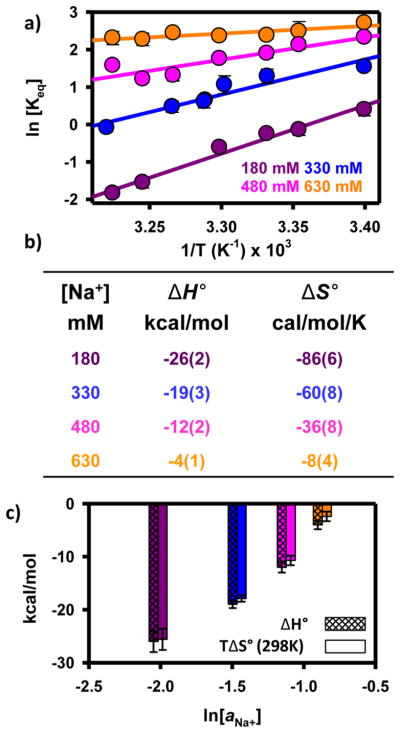
The observed increase in k_dock and the observed decrease in k_undock represent the fundamental kinetic basis for Na⁺-promoted folding (Figure 3a). However, to provide a more insightful description of the free energy folding pathway from I to F, it is also important to understand the thermodynamic contributions (i.e., enthalpic and entropic) to monovalent facilitated folding. This can be best accomplished by temperature-dependent van’t Hoff analysis of K_eq,³⁶ which allows the free energy (ΔG°) to be partitioned into the enthalpy (ΔH°) and entropy (ΔS°) changes associated with folding at a particular Na⁺ concentration (Figure 4a). Specifically, in a plot of ln(K_eq) versus 1/T, the slope and intercept are equal to −ΔH°/R and ΔS°/R, respectively.

Figure 4.

(a) van’t Hoff analysis of tetraloop–receptor interaction at four Na⁺ concentrations. An increasing Na⁺ concentration increases both ΔH° (decreasing slope) and ΔS° (increasing vertical intercept) for the formation of the tertiary interaction. (b) Table of thermodynamic parameters from van’t Hoff analysis. (c) Bar graph to visually display the change in ΔH° and ΔS° as a function of ln(a_Na+).

Under free energy neutral conditions at 180 mM, the van’t Hoff plot in Figure 4a reveals the folding process to be quite exothermic [ΔH° = −26(2) kcal/mol]. This is entirely consistent with (i) an increase in the extent of base stacking and (ii) the formation of hydrogen bonds upon formation of the F state.^29,32,36,37 In principle, an additional source of exothermicity could be the site-specific chelation of a monovalent ion in the folded conformation. Indeed, there is some structural evidence that supports a proposed monovalent binding site within the tetraloop-bound receptor domain.²¹ However, these chelation interactions are considerably stronger and thus likely already saturated well below the working conditions described here. Therefore, changes in Na⁺ concentration over the range of 180–630 mM will not significantly affect how monovalent chelation contributes to the folding thermodynamics. Under the same free energy neutral experimental conditions, the van’t Hoff analysis reveals a folding process that is entropically penalized [ΔS° = −86(6) cal mol⁻¹ K⁻¹]. This loss of disorder associated with formation of the F state is quite reasonable given that the noncanonical hydrogen bonds within the receptor domain are more conformationally restricted after the formation of tertiary contacts. Furthermore, formation of the tertiary interaction restricts the conformational freedom of the poly-A₇ linker. Lastly, the large entropic cost to folding is also the result of ion uptake as the RNA undergoes a structural transition. On the basis of these experimentally measured values of ΔH° and ΔS°, the calculated Gibbs free energy for the folding process at 180 mM Na⁺ is nearly zero [ΔG°(298 K) = −0.4(9) kcal/mol], which is consistent with the predictions from the preferential interaction coefficient analysis (Figure 3c).

These three thermodynamic parameters (i.e., ΔG°, ΔH°, and ΔS°) at 180 mM establish a baseline with respect to increasing monovalent concentrations. If the effect of Na⁺-facilitated folding were purely related to the uptake of ions from solution (e.g., unmixing), one would predict that increasing the Na⁺ concentration would have no effect on the enthalpy of folding [i.e., Δ(ΔH°) = 0]. Surprisingly, both the folding entropy and the enthalpy increase with an increasing Na⁺ concentration (Figure 4). The van’t Hoff plot for the equilibrium folding reaction at 330 mM Na⁺ (and higher) demonstrates a less positive slope [Δ(ΔH°) > 0] when compared to free energy neutral conditions. Specifically, the exothermicity of folding continues to diminish with further increases in Na⁺ concentration. Indeed, under the most free energy favorable conditions, formation of the tertiary interaction is much less exothermic [ΔH = −4(1) kcal/mol]. A similar and slightly overcompensating trend is also apparent when probing changes in the standard state entropy of folding (i.e., intercepts of the van’t Hoff plot) as a function of Na⁺ concentration. An increasing Na⁺ concentration gives rise to a large increase in the entropy change [Δ(ΔS°) > 0] for folding. At 630 mM Na⁺, the entropic penalty for folding is greatly reduced [ΔS° = −8(4) cal mol⁻¹ K⁻¹]. As seen in Figure 4c, both ΔH° and TΔS° scale linearly with ln(a_Na⁺).

Finally, the van’t Hoff analysis in Figure 4a demonstrates that increasing the Na⁺ concentration systematically increases both ΔH° and ΔS° but that at a fixed temperature, increasing the Na⁺ concentration increases the equilibrium constant and thus decreases ΔG°. To have a decreasing free energy [Δ (ΔG°) < 0] with an increasing Na⁺ concentration, the rate of increase for TΔS° must be larger than the rate of increase for ΔH° (Figure 4c). This implies that an increase in the monovalent cation concentration enhances tetraloop–receptor folding via a reduction of the entropic penalty that slightly overcompensates for the loss of exothermicity. In simple terms, the well-known increase in the stability of the tetraloop–receptor tertiary interaction with an increasing monovalent cation concentration is in fact dominated by entropic considerations. It is also interesting to note that rather large changes in ΔH° and ΔS° give rise to relatively small changes in ΔG°. This nearly compensatory nature of Δ (ΔH°) and Δ (ΔS°) is intriguing and may provide a way to tune the temperature sensitivity of biochemically relevant processes (e.g., RNA folding) without significantly perturbing the equilibrium constant.

Transition State Thermodynamics

This trend of increasing ΔH° and ΔS° values with increasing Na⁺ concentration clearly provides surprising information about thermodynamic changes between reactants (I) and products (F). If we take it one step further, a parallel investigation of the transition state barrier can provide additional insight into how the monovalent ion atmosphere affects the GAAA tetraloop–receptor interaction. Specifically, the temperature dependence of k_fold and k_unfold can be analyzed in the context of transition state theory (TST) to provide thermodynamic details about access to the transition state from the intermediate (I) and folded (F) states, respectively.^49,50 Although more sophisticated treatments exist in the literature,⁵¹ for our purposes we consider TST in its simplest form of activated complex theory. This treatment invokes two key assumptions: (i) a well-defined transition state dividing surface, beyond which the reactants proceed toward products without recrossing, and (ii) a transition state in quasi-equilibrium with the reactants. The transition state expression for the folding rate constant can then be rigorously written as

$$k_{\text{fold}}=\frac{k_{\text{b}}T}{h}\frac{q_{\text{perp}}^{‡}}{q_{\text{perp}}^{\text{I}}{q}_{\text{para}}^{\text{I}}}{\text{e}}^{-\mathrm{\Delta }{U}_{\text{fold}}^{‡}/(k_{\text{b}}T)}$$ (1)

where k_b, T, and h are Boltzmann’s constant, the temperature, and Planck’s constant, respectively.

In eq 1, $q_{\text{perp}}^{\text{I}}$ and $q_{\text{para}}^{\text{I}}$ represent partition functions for the I state in all degrees of freedom (i.e., both perpendicular and parallel to the reaction coordinate), whereas $q_{\text{perp}}^{‡}$ represents the corresponding partition function at the transition state, including only degrees of freedom perpendicular to the reaction coordinate. Additionally, $\mathrm{\Delta }{U}_{\text{fold}}^{‡}$ corresponds to the potential energy barrier between the I state and the transition state. Equation 1 can be conveniently expressed in terms of the Gibbs free energy barrier ( $\mathrm{\Delta }{G}_{\text{fold}}^{‡}$) by rewriting the ratio of the partition functions associated with the perpendicular degrees of freedom as $q_{\text{perb}}^{‡}/q_{\text{perp}}^{\text{I}}={\text{e}}^{\mathrm{\Delta }{S}_{\text{fold}}^{‡}/(k_{\text{b}}T)}$. If pressure–volume work is assumed to be negligible (i.e., ΔH = ΔU) and $q_{\text{para}}^{\text{I}}$ to be in the high-temperature limit [i.e., (k_bT)/(hν)], the TST equation reduces to the simple activated complex expression

$$k_{\text{fold}}=\nu {\text{e}}^{-\mathrm{\Delta }{G}_{\text{fold}}^{‡}/(k_{\text{b}}T)}$$ (2)

where ν corresponds to the attempt frequency, parallel to the reaction coordinate, for approaching the transition state. Equation 2 can be readily expressed as an Eyring plot, ln(k_fold/ν) versus 1/T, whose slope and intercept correspond to the transition state enthalpy ( $-\mathrm{\Delta }{H}_{\text{fold}}^{‡}/R$) and entropy ( $\mathrm{\Delta }{S}_{\text{fold}}^{‡}/R$), respectively. Though it is commonly misinterpreted as such, note that the attempt frequency (ν) is not the same as (k_bT)/h, and in fact, an accurate determination of ν requires far more detailed knowledge of the true folding potential surface versus what is currently available. Our analysis uses a ν of ≈1 × 10¹³ s⁻¹ as an approximate order of magnitude for hydrogen bond formation and breaking rates. However, it is important to stress that the choice of ν only introduces a constant offset to the barrier entropy ( $\mathrm{\Delta }{S}_{\text{fold}}^{‡}$) and has no effect on the barrier enthalpy ( $\mathrm{\Delta }{H}_{\text{fold}}^{‡}$). Furthermore, the choice of ν also has no effect on the change in barrier entropy [ $\mathrm{\Delta }(\mathrm{\Delta }{S}_{\text{fold}}^{‡})$] as a function of Na⁺ concentration, which is of particular interest for the analysis and interpretation of our results.

Temperature Dependence of k_fold

An Eyring plot of the folding rate constants (Figure 5a) at 180 mM Na⁺ depicts a slightly positive slope, indicating that formation of the transition state in a free energy neutral ion atmosphere is slightly exothermic [ $\mathrm{\Delta }{H}_{\text{fold}}^{‡}=-3(2)\text{kcal}/\text{mol}$], which is consistent with recent studies of a similar RNA construct under similar conditions.⁵² The lack of an endothermic component of the free energy barrier suggests the transition state is structurally similar to the I state; i.e., the transition state is “early” with respect to reactants. Again, if monovalent facilitated folding were solely a result of entropic terms associated with unmixing of the solution, one would expect the enthalpic component of the free energy barrier to be insensitive to Na⁺ concentration. Surprisingly, for increasing Na⁺ concentrations, the slope of the Eyring plot becomes significantly more negative [ $\mathrm{\Delta }(\mathrm{\Delta }{H}_{\text{fold}}^{‡})>0$], indicating the emergence of an endothermic barrier, which is often associated with formation of a less early transition state. This is best demonstrated at 630 mM Na⁺, where the enthalpy for forming the transition state is significantly positive [ $\mathrm{\Delta }{H}_{\text{fold}}^{‡}=7.7(8)\text{kcal}/\text{mol}$]. One source of an endothermic folding barrier at elevated Na⁺ concentrations could be associated with preferential stabilization of non-native contacts that must break prior to formation of the transition state.

Figure 5.

(a) Transition state theory (TST) analysis of the rate constant associated with formation of the tetraloop–receptor interaction (k_fold) as a function of temperature. (b) Table of thermodynamic parameters from TST analysis. (c) Bar graph depicting the change in $\mathrm{\Delta }{H}_{\text{fold}}^{‡}$ and $\mathrm{\Delta }{S}_{\text{fold}}^{‡}$ at four values of ln(a_Na⁺).

Additionally, the intercepts of the Eyring plot (Figure 5a) demonstrate that the entropy change associated with formation of the transition state also increases [ $\mathrm{\Delta }(\mathrm{\Delta }{S}_{\text{fold}}^{‡})>0$] with Na⁺ concentration. For example, at 180 mM Na⁺, transition state formation is a heavily penalized process [ $\mathrm{\Delta }{S}_{\text{fold}}^{‡}=-64(7)\text{cal}{\text{mol}}^{-1}{\text{K}}^{-1}$]. By 630 mM Na⁺, however, this penalty is dramatically reduced [ $\mathrm{\Delta }{S}_{\text{fold}}^{‡}=-25(3)\text{cal}{\text{mol}}^{-1}{\text{K}}^{-1}$]. These combined results suggest that (i) folding in a free energy neutral ion atmosphere is predominantly rate-limited by a conformational search (e.g., $-T\mathrm{\Delta }{S}_{\text{fold}}^{‡}>\mathrm{\Delta }{H}_{\text{fold}}^{‡}\approx 0\text{kcal}/\text{mol}$) and (ii) while under free energy favorable conditions, folding is rate-limited by an increased amount of structural rearrangement and reduced conformational search (e.g., $-T\mathrm{\Delta }{S}_{\text{fold}}^{‡}\approx \mathrm{\Delta }{H}_{\text{fold}}^{‡}>0\text{kcal}/\text{mol}$). Again, it should be noted that both $\mathrm{\Delta }{H}_{\text{fold}}^{‡}$ and $T\mathrm{\Delta }{S}_{\text{fold}}^{‡}$ appear to scale linearly with ln(a_Na⁺) (Figure 5c).

On the basis of the simple relationship among Gibbs free energy, entropy, and enthalpy, we can now describe the free energy barrier as a function of monovalent ion concentration. Increasing the “energetic favorability” of the experimental conditions gives rise to a strong increase in the entropic and enthalpic components of the free energy barrier. Similar to what was noted above for the standard state folding thermodynamics, these large changes yield a much more subtle effect on the transition state free energy barrier. Specifically, $\mathrm{\Delta }{G}_{\text{fold}}^{‡}(298\text{K})$ decreases by only ≈0.9 kcal/mol [from 16.1(8) to 15.2(7) kcal/mol] between free energy neutral and most free energy favorable conditions. This decrease in barrier height is the result of a dramatic increase in entropic rewards (≈11.6 kcal/mol at 298 K) that slightly outweighs the increase in enthalpic cost (≈10.7 kcal/mol) associated with formation of the transition state [i.e., $\mathrm{\Delta }(T\mathrm{\Delta }{S}_{\text{fold}}^{‡})>\mathrm{\Delta }(\mathrm{\Delta }{H}_{\text{fold}}^{‡})$]. As a central result, this implies that the Na⁺-accelerated k_fold of the GAAA tetraloop–receptor interaction (Figure 3a) occurs via a subtle reduction in the folding free energy barrier, which results from entropic facilitation barely overcoming enthalpic suppression.

To determine if the poly-A₇ linker has any appreciable effect on the thermodynamics of tetraloop–receptor folding, a poly-U₇ linker is used to replace the poly-A₇ linker of the original construct (Figure 1 of the Supporting Information). As was the case with the original poly-A₇ construct, addition of Na⁺ resulted in an acceleration of k_fold and a deceleration of k_unfold. A simple van’t Hoff analysis (Figure 2 of the Supporting Information) with the poly-U₇ RNA construct reveals the same trends as the poly-A₇ RNA construct; i.e., increasing the Na⁺ concentration from 80 to 330 mM increases ΔH° from −26 to −13 kcal/mol. This reduction in exothermicity was subtly overcompensated by an increase in ΔS° from −88 to −38 cal mol⁻¹ K⁻¹. Furthermore, a corresponding Eyring analysis of the forward rate constant indicates that increasing the Na⁺ concentration also increases both $\mathrm{\Delta }{H}_{\text{fold}}^{‡}$ and $\mathrm{\Delta }{S}_{\text{fold}}^{‡}$ (Figure 3 of the Supporting Information), the same trend observed for the poly-A₇ construct. The additional analysis of the poly-U₇ construct suggests that, although the linker may subtly change the thermodynamics of folding at a given Na⁺ concentration, the observed trends in the A₇ linker-based construct are dominated by the GAAA tetraloop–receptor tertiary interaction.

DISCUSSION

Folding Pathways and Ion Atmospheres

The free energy barrier thermodynamic data can be used in conjunction with the previously extracted standard state thermodynamic data to provide additional insight into the “reaction coordinate” for tetraloop–receptor folding as a function of Na⁺ concentration. As summarized schematically in Figure 6, the reaction coordinate follows the folding pathway from left to right, where the horizontal distance between the I state and the transition state qualitatively represents how “early” or “late” the free energy barrier is along the reaction coordinate. For all F states in the plot, the absolute energies are referenced to 0 kcal/mol. This choice is made because the F state is least likely to be influenced by Na⁺ concentration and will therefore more clearly demonstrate changes to the folding pathway.⁵³ First, the implications of the 180 mM reaction coordinate will be considered.

Figure 6.

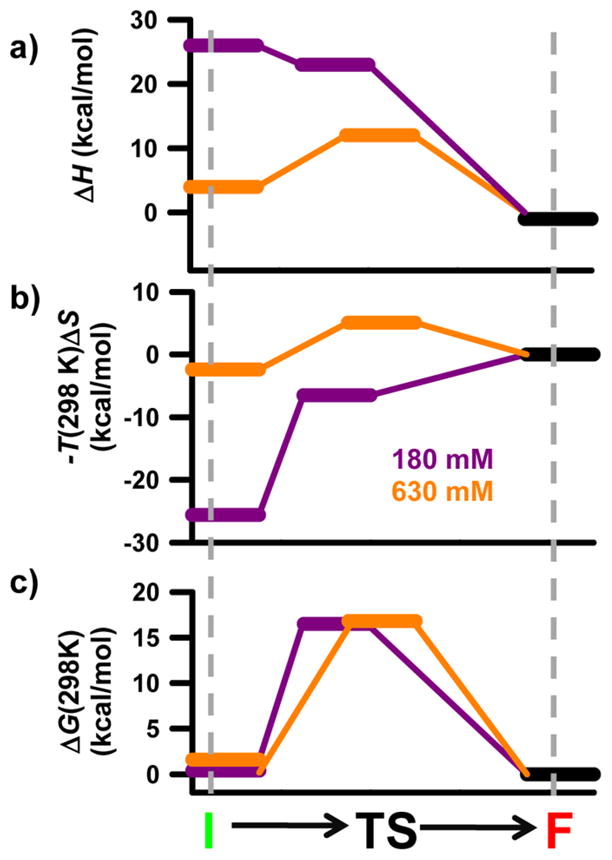
Complete thermodynamics reaction coordinates for the formation of the GAAA tetraloop–receptor tertiary interaction. The three panels depict the (a) enthalpy, (b) entropy, and (c) free energy along the reaction coordinate at 180 and 630 mM Na⁺. The horizontal distance between states qualitatively represents how early or late they are along the reaction coordinate. See the text for details.

Folding in a Free Energy Neutral Monovalent Ion Atmosphere

The path of the reaction coordinate under free energy neutral conditions (Figure 6, purple) is easily interpreted and serves as a baseline for comparison to the 630 mM Na⁺ reaction coordinate. Formation of a number of tertiary contacts in the F state, and perhaps specific chelation of a monovalent ion, makes the folding process strongly exothermic. Furthermore, the measured ΔH° values reported herein are in reasonable agreement with previously reported values using a complementary technique.⁵² Specifically, the measured exothermicity of the poly-U₇ construct at 180 mM Na⁺ is almost exactly half of the published values for a dual tetraloop–receptor construct at 200 mM KCl; the poly-A₇ construct is slightly more than half as exothermic.

The absence of any significant endothermic component of the free energy barrier suggests most of the standard state enthalpic gains occur as the transition state forms the F state (Figure 6a, purple), which is again supported by previous work.⁵² The strong entropic component of the free energy barrier at 180 mM Na⁺ suggests that a significant conformational search of the receptor by the tetraloop represents the rate-limiting step in transition state formation. Structural studies of the receptor domain have identified a high degree of conformational disorder within the free receptor, which is absent once the full tertiary interaction has formed.³⁷ Therefore, the loss of entropy associated with the formation of the transition state, and subsequently the F state, can in part be attributed to the restricted orientation of the base pairs within the 11-nucleotide receptor (Figure 6b, purple). Other contributions to the loss of entropy for folding under free energy neutral conditions come from (i) localizing the tetraloop near the receptor and (ii) the subsequent uptake of ions from the bulk to the ion atmosphere to compensate for the increased charge density of both the transition state and the F state. This leads to a proposed compact transition state in which the tetraloop is proximal to the receptor and a few additional monovalent ions have been localized around the RNA. Furthermore, the nucleotides within the receptor must have transiently adopted a conformation from the ensemble of unfolded microstates that is “aligned” for the formation of hydrogen bonds with the GAAA tetraloop.

Our identification of (i) an early transition state and (ii) a large entropic barrier in the GAAA tetraloop–receptor interaction supports two emerging paradigms for RNA folding. First, our findings under free energy neutral conditions support the observation that transition states for tertiary interactions are often early;^{44,49,50,52,54,55} in other words, there is little to no enthalpic component to the free energy barrier ( $\mathrm{\Delta }{H}_{\text{fold}}^{‡}\approx 0$). The second paradigm supported by the thermodynamic observations under free energy neutral conditions is that RNA folding is accompanied by a large entropic component of the free energy barrier ( $\mathrm{\Delta }{S}_{\text{fold}}^{‡}<0$) resulting from a conformational search. This idea was first proposed with regard to the slow folding of ribozymes from group I⁵⁵ and group II⁵⁶ introns, where the notion of contact order was used to explain the large entropic barrier to folding. The idea of a rate-limiting conformational search and a large $\mathrm{\Delta }{S}_{\text{fold}}^{‡}$ has since been supported by experiments with various RNA systems.^50,52,57 Most importantly, however, this work provides a quantitative framework for understanding how the entropic and enthalpic components of the free energy barrier change with increasing monovalent cation concentrations.

Folding in an Energetically Favorable Monovalent Ion Atmosphere

Increasing the Na⁺ concentration dramatically alters the folding pathway associated with formation of the tertiary interaction (Figure 6, orange). At elevated Na⁺ concentrations, the standard state entropy and enthalpy for folding are significantly increased as well as the entropic and enthalpic components of the free energy barrier. Mg²⁺-induced increases in ΔS° and ΔH° have been observed in both the P4–P6 domain of the Tetrahymena ribozyme and various GAAA tetraloop–receptor constructs.^50,52,58 However, support for the same trend with monovalent ions is less apparent in the literature. A great deal of work has concluded that for duplex denaturation there is little to no monovalent dependence of ΔH°,^8,59 concluding that entropy is the only thermodynamic term that is dependent on monovalent ion concentration. However, others have seen significant increases in ΔH° for helix formation with an increasing monovalent salt concentration,⁶⁰ suggesting that both entropy and enthalpy must be changing upon addition of a monovalent salt. With regard to the formation of the GAAA tetraloop–receptor interaction, recent studies of a bimolecular, dual tetraloop–receptor RNA construct were not able to unambiguously determine whether the observed monovalent induced stability was the result of entropic or enthalpic considerations.⁵² However, they note that over the range of 100–300 mM KCl Δ (ΔS°) accounts for 134–166% of the overall Δ (ΔG°), which clearly implies that the increase in ΔH° must be 34–66% of the overall Δ (ΔG°), which is certainly qualitatively consistent with our observations that both enthalpy and entropy change and that the increase in ΔS° slightly overcomes the increase in ΔH°.

These results, perhaps, suggest that addition of salt may indeed increase the observed ΔH° of formation. Although these bimolecular, dual tetraloop–receptor constructs do contain the GAAA tetraloop–receptor interaction from the Tetrahymena ribozyme, the context of the interaction is quite different. The duality of the construct and the significantly enhanced degree of helical packing upon formation of the interaction make truly rigorous comparisons with the construct used for this study challenging at best. The degree to which ΔH° for various RNA folding motifs is affected by monovalent salt concentrations is likely a result of how many alternative conformations are easily accessible in the ensemble of microstates associated with the I state. Nevertheless, in most examples described above, addition of a monovalent salt increases the overall favorability of folding by increasing the ΔS° of formation.

In conjunction with this work, these observations support a potential paradigm fundamental to tertiary interactions and perhaps even RNA folding, whereby additional monovalent cations facilitate folding by reducing the entropic penalty [Δ (ΔS°) > 0] at the potential cost of reducing the folding exothermicity [Δ (ΔH°) > 0]. The qualitatively established free energy barrier thermodynamics for the GAAA tetraloop–receptor interaction are used to further support this paradigm by providing a physical picture based on the molecular structure of the tertiary interaction, as described below.

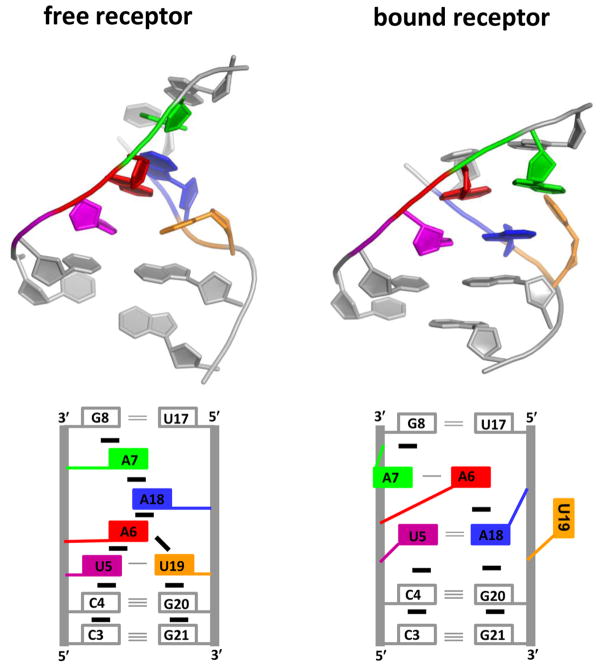
It is important to remember that discussion of structural changes pertains primarily to either of the Boltzmann-weighted macroscopic states; it is likely that these structural changes reflect a shift in the energetic distribution of the ensemble of microscopic states. As illustrated by the orange traces in panels a and b of Figure 6, formation of the transition state under the most free energy favorable conditions is accompanied by an enthalpic cost and an entropic penalty. The enthalpic cost associated with transition state formation is attributed to preferentially stabilized non-native intramolecular contacts within the unbound receptor domain (I) that must be broken prior to the formation of the transition state. One such contact from structural models of the free tetraloop–receptor domain is that of base U19 (numbering from ref 37). A nuclear magnetic resonance solution structure of the free receptor domain³⁷ depicts a conformation in which U19 participates in one hydrogen bonding interaction with U5 and is base stacked between G20 and A6 (Figure 7). Structural models of the bound receptor domain show that in the presence of the GAAA tetraloop the U19–U5 hydrogen bond and all of the base stacking interactions with U19 are absent as U19 is flipped outside of the receptor to accommodate the tetraloop.²⁹ The reduction of the entropic barriers results from the I state being preorganized by non-native contacts, thus removing the entropic cost associated with forming an aligned receptor conformation. The remaining entropic penalty for forming the transition state at 630 mM Na⁺ is likely associated with the tetraloop moving into the proximity of the receptor and ion uptake associated with the increased charge density. Taken together, these conclusions can be used to portray a more detailed image of the transition state. Specifically, the tetraloop is (i) proximal to the receptor, which (ii) is in a conformation aligned for formation of the tertiary interaction and (iii) has U19 flipped outside of the receptor to accommodate the GAAA tetraloop.

Figure 7.

Structural representation of the free and bound receptor domains. Bases that undergo significant structural rearrangement upon formation of the tetraloop–receptor interaction are color-coded. Bases of the GAAA tetraloop are not shown to emphasize changes within the receptor domain. See the text for details.

This putative model of the transition state is also in accord with the observed changes in $\mathrm{\Delta }{H}_{\text{fold}}^{‡}$ and $\mathrm{\Delta }{S}_{\text{fold}}^{‡}$ with increasing Na⁺ concentration. At 180 mM Na⁺, the interactions involving U19 in the free receptor are only poorly stabilized. Addition of Na⁺ preferentially stabilizes these interactions within the free receptor (I), which gives rise to an increase in $\mathrm{\Delta }{H}_{\text{fold}}^{‡}$ associated with hydrogen bond breakage, unstacking of bases, and base flipping, all prior to the formation of the transition state. The increase in $\mathrm{\Delta }{S}_{\text{fold}}^{‡}$ comes from the fact that stabilizing the non-native interactions preorganizes the receptor, thus reducing the amount of organization (i.e., entropy loss) required to form the transition state. An additional source of increasing $\mathrm{\Delta }{S}_{\text{fold}}^{‡}$ could be global compaction of the RNA at elevated Na⁺ concentrations, which is supported by a Na⁺-dependent undocked FRET position.³⁵ As additional support for this molecular model, recent electron paramagnetic resonance experiments with spin-labeled nucleotides have demonstrated that increasing the cation concentration by itself does not promote the un-base-stacked conformation of U19.⁶¹ Indeed, only in the presence of the GAAA tetraloop is the U19 base able to adopt a stable conformation where it is flipped outside of the receptor domain, which further supports the proposed origin of monovalent facilitated folding of the GAAA tetraloop–receptor interaction.

The tertiary contacts within the unbound receptor associated with U19 are used to explain the observed changes in the free energy barrier to folding. However, it is possible that interactions with solution may also contribute. Recent experiments have highlighted the importance of phosphate backbone dehydration in RNA folding transitions.⁶² With this in mind, solvent rearrangement may serve as a potential explanation for the monovalent induced changes to the folding thermodynamics. However, one must have a detailed understanding for how changing the monovalent concentration affects the entropic and enthalpic components of phosphate backbone dehydration. Fortunately, the total amount of buried phosphate surface area for the tetraloop–receptor interaction used in this study (≈67 Ų) is much smaller than those of more biologically relevant RNAs, making the energetics associated with desolvation much smaller in magnitude than it may have otherwise been.⁶²

One last explanation for the strong salt dependence of both the enthalpic and entropic terms pertains to the polynucleotide linker used to create the unimolecular tetraloop–receptor construct. Theoretically, increasing the monovalent concentration could preferentially stabilize a rigid, base-stacked conformation within the poly-A₇ linker.⁶³ If so, elevated monovalent concentrations could result in an additional enthalpic loss (and entropic reward), arising from the need to disrupt this rigid base-stacked linker.

Control experiments can be performed to test and rule out this alternative explanation. The poly-U₇ single-strand RNA linker is thought to be rigid and structured only at low ionic strengths (e.g., < 50 mM monovalent)⁶⁴ or low temperatures (<10 °C).⁶⁵ As a result, the poly-U₇ linker should act as a more flexible, passive, linker that is less susceptible to Na⁺-facilitated base stacking. A comparison of the results of the poly-U₇ construct with the rigorously determined values of the poly-A₇ construct clearly suggests the polynucleotide linker has an only minimal contribution to the absolute thermodynamic values, and that the observed changes in all measured thermodynamic values (ΔH°, ΔS°, $\mathrm{\Delta }{H}_{\text{fold}}^{‡}$, and $\mathrm{\Delta }{S}_{\text{fold}}^{‡}$) follow the same trend with an increasing Na⁺ concentration.

Dependence on Monovalent Cation Identity

One issue with RNA folding studies is the potential role of monovalent identity. For example, the use of K⁺ versus Na⁺ cations has been shown to affect rates of RNA catalysis and has been attributed to specific binding of K^+.21 We can easily test for monovalent identity effects with parallel folding studies as a function of K⁺ concentration. Interestingly, the corresponding K⁺ versus Na⁺ titrations reveal completely negligible differences in the folding kinetics of the GAAA tetraloop–receptor construct as summarized in Figure 8,⁶⁶ which is consistent with existing studies of a GAAA tetraloop–receptor construct.¹⁸ Furthermore, temperature-dependent kinetic experiments identical to those described for Na⁺ reveal that all thermodynamic parameters for Na⁺- and K⁺-promoted folding are identical within experimental uncertainty (Figure 9). The insensitivity to monovalent identity suggests that the observed effects are common to both Na⁺ and K⁺, thus demonstrating the broader applicability of the proposed model for monovalent facilitated RNA folding.

Figure 8.

Monovalent identity and folding kinetics for the formation of the GAAA tetraloop–receptor interaction. An increasing monovalent concentration provides a significant enhancement of the folding rate constant (k_fold) and a subtle reduction in the rate constant for the unfolding process (k_unfold). No significant difference is observed between Na⁺ and K⁺.

Figure 9.

(a) van’t Hoff analysis of tetraloop–receptor interaction comparing Na⁺ and K⁺ concentrations. (b) Eyring analysis of tetraloop–receptor interaction comparing Na⁺ and K⁺ concentrations. (c and d) Tables of thermodynamic parameters from the van’t Hoff and Eyring analyses. As depicted, folding behavior is largely independent of monovalent cation identity.

SUMMARY AND CONCLUSION

This work describes the use of smFRET experiments to improve our understanding of the origins of monovalent facilitated formation of an RNA tertiary interaction. The kinetic origin of this enhanced folding is a large acceleration of k_fold and a subtle deceleration of k_unfold at elevated Na⁺ concentrations. The large 14-fold change in the forward folding rate constant is the result of a modest [ $\mathrm{\Delta }(\mathrm{\Delta }{G}_{\text{fold}}^{‡})\approx 1\text{kcal}/\text{mol}$] decrease in the height of the free energy barrier associated with the folding reaction. This reduction in the free energy barrier is relatively small compared to the much larger changes in both the enthalpic [ $\mathrm{\Delta }(\mathrm{\Delta }{H}_{\text{fold}}^{‡})\approx 11\text{kcal}/\text{mol}$] and entropic { $\mathrm{\Delta }[T(298\text{K})\mathrm{\Delta }{S}_{\text{fold}}^{‡}]\approx 12\text{kcal}/\text{mol}$} components. Indeed, the growth of a strong enthalpic component to the free energy barrier with an increasing Na⁺ concentration is in surprising opposition to what would be predicted if the monovalent enhanced stability of tertiary interactions were solely the result of a reduction in the entropic penalty associated with ion uptake or unmixing. Nevertheless, the growth of an endothermic barrier makes entropy the thermodynamic parameter responsible for the increased favorability of folding at high monovalent concentrations. We postulate that these rather dramatic changes in the entropic and enthalpic components of the free energy barrier may result from monovalent induced structural changes within the receptor domain. Specifically, we propose base unstacking and flipping of U19, along with the resulting structural changes, as one possible explanation worthy of further exploration.

The results described here support the emerging paradigm that suggests RNA folding is predominately rate-limited under free energy neutral conditions by a conformational search (e.g., $-T\mathrm{\Delta }{S}_{\text{fold}}^{‡}>\mathrm{\Delta }{H}_{\text{fold}}^{‡}\approx 0\text{kcal}/\text{mol}$) and that addition of monovalent cations reduces the conformational search of RNAs at the potential cost of stabilizing alternative conformations (e.g., $-T\mathrm{\Delta }{S}_{\text{fold}}^{‡}\approx \mathrm{\Delta }{H}_{\text{fold}}^{‡}>0\text{kcal}/\text{mol}$). A thorough examination of other tertiary interactions such as H-type pseudoknots, larger noncoding RNAs (e.g., riboswitches), and perhaps even duplex formation would be useful to demonstrate the universality of such a paradigm. Additionally, this work provides detailed experimental benchmarks for the thermodynamics associated with formation of tertiary interactions in RNA. These benchmarks can be used to test rigorous theoretical modeling of simple but ubiquitous RNA tertiary interactions in the presence of monovalent ions. Finally, this work clearly highlights important directions for future investigations of the more complex effects associated with mixed-valence cation solutions more relevant to that of the cellular environment.

ABBREVIATIONS

PCA

protocatechuic acid

PCD

protocatechuate-3,4-dioxygenase