The effect of neural adaptation on population coding accuracy

Abstract

Most neurons in the primary visual cortex initially respond vigorously when a preferred stimulus is presented, but adapt as stimulation continues. The functional consequences of adaptation are unclear. Typically a reduction of firing rate would reduce single neuron accuracy as less spikes are available for decoding, but it has been suggested that on the population level, adaptation increases coding accuracy. This question requires careful analysis as adaptation not only changes the firing rates of neurons, but also the neural variability and correlations between neurons, which affect coding accuracy as well. We calculate the coding accuracy using a computational model that implements two forms of adaptation: spike frequency adaptation and synaptic adaptation in the form of short-term synaptic plasticity. We find that the net effect of adaptation is subtle and heterogeneous. Depending on adaptation mechanism and test stimulus, adaptation can either increase or decrease coding accuracy. We discuss the neurophysiological and psychophysical implications of the findings and relate it to published experimental data.

1 Introduction

Adaptation is a reduction in the firing activity of neurons to prolonged stimulation. It is a ubiquitous phenomenon that has been observed in many sensory brain regions, such as auditory (Shu et al. 1993; Ulanovsky et al. 2004), and somatosensory (Ahissar et al. 2000) cortices, as well as in primary visual cortex (V1) (Ohzawa et al. 1982; Carandini and Ferster 1997; Gutnisky and Dragoi 2008). In addition to response reduction, adaptation has been observed to deform the tuning curves (Muller et al. 1999; Dragoi et al. 2000; Ghisovan et al. 2008a, b), which is thought to lead to perceptual after-effects, such as the tilt after-effect (Jin et al. 2005; Schwartz et al. 2007, 2009; Kohn z2007; Seriès et al. 2009).

Adaptation is hypothesized to be functionally important for coding sensory information (Kohn 2007; Schwartz et al. 2007). On the single neuron level, the reduction in firing rate should reduce coding accuracy, since it will typically become harder to discriminate two similar stimuli when firing rates are lowered. However, on the population level the accuracy is determined not only by the firing rates, but also by the correlations between neurons. In primary visual cortex it has been observed that adaptation reduces correlations, which can improve population coding accuracy (Gutnisky and Dragoi 2008). However, it is currently unknown how accuracy is affected when both changes in firing rates and changes in the correlations are taken into account.

The coding accuracy of a population response can be analyzed using Fisher Information, which gives an upper bound to the accuracy that any decoder can achieve. Importantly, the Fisher Information takes the effects of correlations in neural variability (so called noise correlations) into account. Depending on the exact structure of the correlations, the Fisher Information can either increase or decrease with correlation strength (Oram et al. 1998; Abbott and Dayan 1999; Sompolinsky et al. 2002; Seriès et al. 2004; Averbeck et al. 2006). Therefore a precise determination of the correlation structure is required, which is difficult to accomplish experimentally since vast amounts of data are required. Moreover, experimental probe stimuli that measure coding before and after adaptation can induce additional adaptation, possibly obscuring the effect of the adaptor.

Here we study this issue using a computational model of primary visual cortex. We implement a variety of possible adaptation mechanisms and study coding accuracy before and after adaptation. We find that the precise adaptation mechanism and its parameters lead to diverse results: accuracy can decrease but under certain conditions also increase after adaptation. The changes in information due to tuning curves changes resulting are typically opposite from the changes in information due to correlations changes.

2 Methods

2.1 Network setup

The model of V1, Fig. 1(a), was a rate-based version of the ring model (Ben-Yishai et al. 1995; Somers et al. 1995; Teich and Qian 2003). The model did not pretend to be a full model of the visual system, but included essential cortical mechanisms that can produce adaptation. In the model, each of the N = 128 neurons was labeled by its preferred orientation θ, which ranged between −90 and 90 degrees. The instantaneous firing rate R̄_θ (spikes per second) was proportional to the rectified synaptic current.

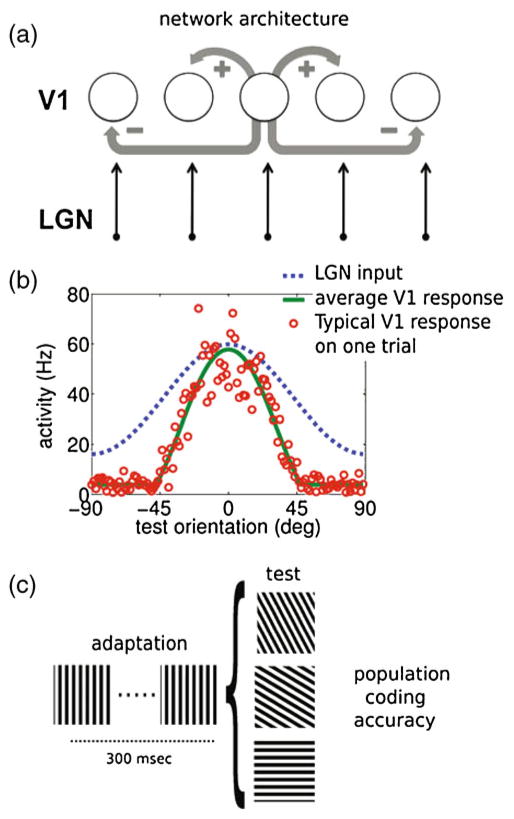
Fig. 1.

Network architecture, response and adaptation protocol. (a) The network architecture consists of a recurrent network in which neurons receive feedforward input from the LGN and lateral input with short range excitation and long range inhibition (Mexican hat profile). Periodic boundary conditions (not shown) ensured a ring topology of the network. (b) Model behavior: the cortical neurons (green line) sharpened the input from LGN (blue line; scaled 15 times for clarity). On a single trial the multiplicative noise leads to substantial variability (red dots). (c) Schematic of the adaptation protocol. During 300 ms the network is adapted to a stimulus with orientation ψ = 0, followed by a test phase with stimulus with orientation φ during which no further adaptation takes place

$${\overline{R}}_{\theta }=\kappa {[I]}_{+}+b,$$ (1)

where [x]₊ = max(x, 0). The constant b is the background firing rate and κ represents the gain to produce the firing rate R̄_θ for a given input I. Parameter values can be found in Table 1. We also used smoother rectification functions (van Rossum et al. 2008); however, this did not affect the results. The above firing rate model had the advantage of being much more efficient than a spiking model, while Fisher information in spiking models (Seriès et al. 2004) and rate models (Spiridon and Gerstner 2001) have been found to be qualitatively similar. Moreover, implementation of realistic variability across a wide range of firing rates is challenging in spiking models (for a review see e.g., Barbieri and Brunel 2008).

Table 1.

Symbols and parameters used in simulations. The parameters for SD and SFA were chosen to achieve the same control conditions, and a similar response reduction after adaptation for the neuron maximally responding at the adapter orientation. Finally all parameters were restricted to be in the physiologically plausible range

Meaning	Symbol	Value
Neuron’s preferred orientation	θ	(−90, 90) degrees
Adapter orientation	ψ	0 degrees
Test orientation	φ	(−90, 90) degrees
Time decay of synaptic current	τ	10 ms
Amplitude of thalamocortical input	aff	4.0
Gaussian width of thalamocortical input	σff	45.0
Gain for excitatory intracortical input	gexc	0.2
Interaction power for excitatory connections	Aexc	2.2
Gain for inhibitory intracortical input	ginh	2.5
Interaction power for inhibitory connections	Ainh	1.4
Probability of excit. transmitter release	U	0.02
Recovering time for synaptic depression	τ	600 ms
Background firing rate	b	4 Hz
Input current to firing rate gain	κ	4.0 Hz
Fano Factor	FF	1.5
Time decay for spike frequency adaptation (SFA)	τsfa	50 ms
Gain for spike frequency adaptation	gsfa	0.05

For each neuron the synaptic current had a triple angular dependence and evolved in time according to

$$\tau \frac{\partial I(\theta ,\phi ,\psi ,t)}{\partial t}=-I(\theta ,\phi ,\psi ,t)+I_{\text{ff}}(\theta ,\phi )+I_{\text{exc}}(\theta ,\phi ,\psi ,t)-I_{\text{inh}}(\theta ,\phi ,\psi ,t)-I_{\text{sfa}}(\theta ,\phi ,\psi ,t)$$ (2)

where ψ is the adapter angle, φ is the test stimulus angle, and τ is the synaptic time constant (Dayan and Abbott 2001). The current consisted of (1) feed-forward excitatory input I_ff from the LGN, (2) excitatory I_exc and inhibitory I_inh input mediated by lateral connections with a center-surround (Mexican-hat) profile subject to short-term synaptic depression, and (3) an adaptation current I_sfa which described spike frequency adaptation.

2.1.1 Network connections

The input I_ff represented feed-forward excitatory input from LGN. Except for Fig. 8 it was assumed not to be subject to adaptation (Boudreau and Ferster 2005). It was modeled as a Gaussian profile with periodic boundary conditions:

$$I_{\text{ff}}(\theta ,\phi )=a_{\text{ff}}\left[exp\left(-\frac{{(\theta -\phi )}^2}{2{\sigma }_{\text{ff}}^2}\right)+exp\left(-\frac{{(\theta -\phi +180)}^2}{2{\sigma }_{\text{ff}}^2}\right)+exp\left(-\frac{{(\theta -\phi -180)}^2}{2{\sigma }_{\text{ff}}^2}\right)\right]$$ (3)

where σ_ff represents the Gaussian width of stimulus profile and a_ff its amplitude.

Fig. 8.

The effect of input adaptation on tuning curve properties and Fisher Information. In this simulation the input current was adapted. The strength of adaptation was adjusted to have a similar amount of reduction in the peak response. No other adaptation mechanism was active. The changes in tuning curve and Fisher Information are very similar to the changes seen with SD

Lateral connections mediated the excitatory (I_exc) and inhibitory (I_inh) inputs to neuron i according to

$$\begin{array}{l}{I}_{\text{exc}}({\theta }_i,\phi ,\psi ,t)=g_{\text{exc}}\sum _j\mathcal{E}({\theta }_i,{\theta }_j)x_{\text{exc}}({\theta }_j,\phi ,\psi ,t)R_{{\theta }_j}(\phi ,\psi ,t)\\ I_{\text{inh}}({\theta }_i,\phi ,\psi ,t)=g_{\text{inh}}\sum _j\mathcal{I}({\theta }_i,{\theta }_j)x_{\text{inh}}({\theta }_j,\phi ,\psi ,t)R_{{\theta }_j}(\phi ,\psi ,t)\end{array}$$ (4)

where θ_j and θ_i represented respectively the pre- and postsynaptic neurons, the constants g were recurrent gain factors, and R_θ (φ, ψ, t) was a noisy realization of the firing rate (see below). The variables x in Eq. (4) represented the efficacy of the synapses subject to short-term plasticity (see below as well).

The functions 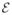and 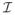in Eq. (4) define the connection strength between cells θ_i and θ_j. We use (Teich and Qian 2003)

$$\mathcal{E}({\theta }_i,{\theta }_j)={[CK(\mid {\theta }_i-{\theta }_j\mid )]}_{+}$$ (5)

and

$$\mathcal{I}({\theta }_i,{\theta }_j)={[-CK(\mid {\theta }_i-{\theta }_j\mid )]}_{+}$$ (6)

where

$$K(\theta )={[cos(2\theta )+1]}^{A_{\text{exc}}}-{[cos(2\theta )+1]}^{A_{\text{inh}}},$$ (7)

The functions 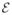and 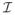were normalized with the constant C so that the sum of connections from any cell to the rest equals 1, that is 1/C = Σ_i|K(θ_i)|.

The exponents A_exc and A_inh control the range of interaction; the smaller they are, the flatter and wider the connection profile. We used a center-surround or Mexican-hat profile for the connection, satisfying A_exc > A_inh, as in previous studies (Ben-Yishai et al. 1995; Teich and Qian 2003; Seriès et al. 2004). The precise profile of lateral inhibition is not well known. However, we found that in order to obtain sharpening (from a broad thalamocortical input to a sharp cortical neuron response, Fig. 1(b)) the shape of inhibition was not critical, i.e. both long range inhibition or a flat profile gave similar results.

2.1.2 Synaptic short-term plasticity model

In the model cortical synaptic short-term depression affected the lateral connections only; the afferents from the LGN did not depress as observed experimentally (Boudreau and Ferster 2005). We used a phenomenological model of short-term depression (Tsodyks and Markram 1997): The fraction of available neurotransmitter x of a synapse of a presynaptic neuron with orientation θ was

$$\frac{\partial x(\theta ,\phi ,\psi ,t)}{\partial t}=\frac{1-x(\theta ,\phi ,\psi ,t)}{{\tau }^{\text{rec}}}-Ux(\theta ,\phi ,\psi ,t)R_{\theta }(\phi ,\psi ,t)$$

where U is the release probability. The variable x ranged between zero and one, with zero corresponding to a fully depleted synapse and one to a non-depressed synapse. Before stimulation and in the control condition, all x were set to one. The constant τ^rec was the recovery time from depletion to resting conditions. During prolonged stimulation, the steady state of the depression variable is smaller when the recovery time is slower, because $x_{\infty }=\frac{1}{1+U{\tau }^{\text{rec}}R}$. We only included depression in the excitatory connections (Galarreta and Hestrin 1998; Teich and Qian 2003; Chelaru and Dragoi 2008). We found that the opposite situation, namely stronger depression of inhibitory connections, lead to a unstable network activity.

2.1.3 Spike frequency adaptation

Spike frequency adaptation was implemented using a standard first-order model (Benda and Herz 2003)

$${\tau }_{\text{sfa}}\frac{\partial I_{\text{sfa}}(\theta ,\phi ,\psi ,t)}{\partial t}=-I_{\text{sfa}}(\theta ,\phi ,\psi ,t)+g_{\text{sfa}}{R}_{\theta }(\phi ,\psi ,t).$$

The time constant τ_sfa was set to 50 ms and the gain g_sfa was chosen so that the firing-rate reduction of the neuron to the adapter stimulus is comparable to that produced by synaptic depression.

2.2 Single neuron variability model

The responses of cortical neurons are typically highly variable, e.g. Tolhurst et al. (1983). To fit our noise model we used extra-cellular single unit recordings from neurons in area V1 of macaque presented with 300 ms stimuli (Oram et al. 1999). For each recorded cell, the grating orientation that elicited the maximal response was labeled as the “preferred orientation” (peak), and all orientations were given relative to the peak (22.5, 45, 67.5 and 90 degrees). For n = 19 different cells, 8 different orientations were tested with 3 stimulus types: gratings, bars lighter than background, bars darker than background. The spike rate was counted in 50 ms bins. The firing rate for each orientation was calculated as the arithmetic mean across the different stimulus types. In addition, symmetric orientations (e.g. peak at +22.5 degrees and peak at −22.5 degrees) were collapsed, yielding 60 trials for the peak and the orthogonal orientation and 20 trials for all other orientations. The variability was expressed in terms of the Fano Factor (FF), which is the spike count variance across trials divided by the mean spike count. We found that the FF was to a good approximation constant across time and independent of stimulus orientation, nor did the Fano Factor depend on the firing rate, implying that the noise was multiplicative.

To model this variability we added multiplicative noise to each neuron’s activity. The noise is added after its input current is converted to the firing rate Eq. (1), and noise reflects the stochastic nature of spikes generation. We set

$$R_{\theta }={\overline{R}}_{\theta }+\sigma ({\overline{R}}_{\theta })\eta (t),$$

where the noise η was Gaussian white noise, i.e. 〈η(t)〉 = 0, and 〈η(t)η(t′)〉 = δ_t,t′, and R̄_θ denotes the average over all the trials. To achieve a given Fano Factor the required amplitude of the noise was set according to $\sigma ({\overline{R}}_{\theta })=\sqrt{\text{FF}}\sqrt{{\overline{R}}_{\theta }}$. The added noise is temporally uncorrelated, reflecting the approximate Poisson-like nature of cortical activity.

A sample trial is illustrated in Fig. 1(b) (red dots). To study how the trial-to-trial variability of the single cell affects the population coding, we ran simulations using FF = 0.50, 1.00, 1.50, Fig. 5(c) and (d). In addition, to further investigate the generality of our results we used two alternative noise models: (1) Poisson distributed firing rates with mean R̄ (unity Fano Factor), and (2) additive Gaussian white noise. We found that, although the absolute scale of the Fisher Information differed, the adaptation affected the information exactly identically for all test angles. In other words the effect of the adaptation was independent of exact noise model.

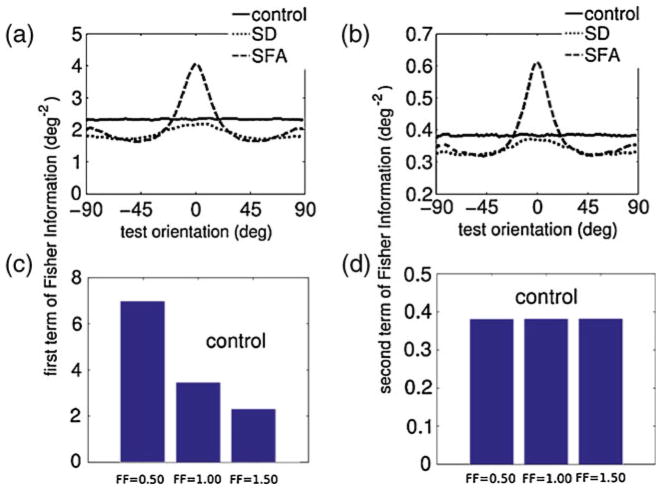
Fig. 5.

Contributions to the constituents of the Fisher Information. The Fisher Information is the sum of the term FI₁ (left) and FI₂ (right), see Eqs. (8) and (9). A–B: FI₁ and FI₂ for the adaptation scenarios compared to the control situation. The effect of the adaptation dependence was similar, although the second term was an order of magnitude smaller. (c)–(d) Dependence of FI₁ and FI₂ on the Fano Factor (FF), using Gaussian multiplicative noise. Only the control situation (before adaptation) is plotted, as the scaling before and after adaptation is identical

For the common input noise model, Fig. 7, the feed-forward input was corrupted with a multiplicative noise source that was identical on a given trial for all neurons I_ff(θ, φ) = (1 +η)Ī_ff(θ, φ), where η was a Gaussian random number with zero mean and unit variance.

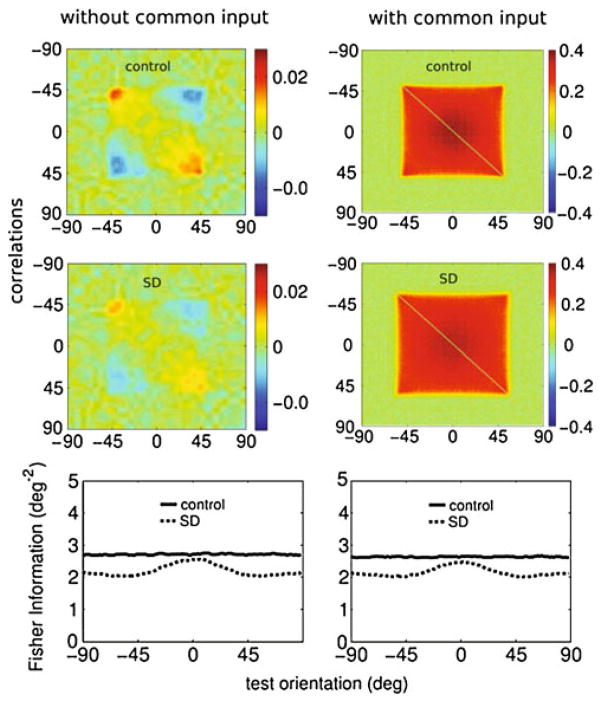
Fig. 7.

Effect of common input noise on correlation and coding. Compared to the situation without common noise (first column), after the inclusion of common noise input (second column) the correlation structures changed significantly. With common input the correlations increased from less than 0.1 to 0.4, and the correlations became weakly dependent on the stimulus orientation. Because the LGN input did not depress, changes in the correlations were practically unaffected by adaptation. However, the common noise did not modify the information (bottom panels). For clarity, only adaptation trough SD is shown; the same holds for SFA

2.2.1 Correlated variability

In the visual cortex the response variability is correlated (Nelson et al. 1992; Gawne et al. 1996; Kohn and Smith 2005). Although the noise in the model is temporally and spatially uncorrelated, the lateral synaptic coupling between the neurons will mix the noise from different neurons, resulting in correlated noise in the network (Seriès et al. 2004). The covariance matrix, Fig. 3 (top row), across trials was defined as

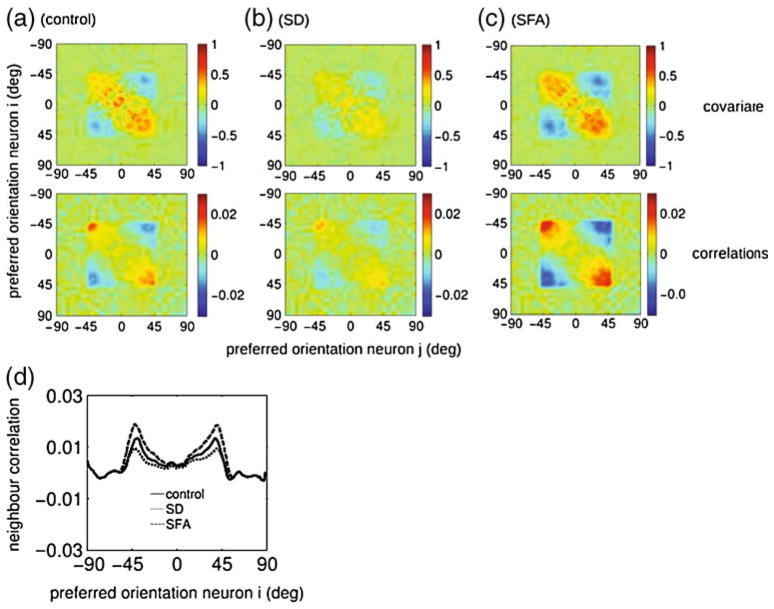
Fig. 3.

Effects of adaptation on the noise correlations. On top row, the covariance matrices are plotted such that each point at the surface represents the noise covariance between two neurons with preferred orientation given by x and y-axis. On bottom row, the covariance matrices were normalized to the noise (Pearson-r) correlations coefficients. The principal diagonal was omitted for clarity. Compared to the control condition (panel a), synaptic depression (SD) reduced noise correlations (panel b), while spike frequency adaptation (SFA) increased them (panel c). (d) The noise correlations coefficients depicted between neighboring cells (i.e. c_i,i+1), for the three conditions. Adaptation through SD reduces the correlations, SFA increases them. In all panels the adaptor and test orientation were set to 0 degrees

$$q_{ij}(\phi ,\psi )\equiv {\langle [R_i(\phi ,\psi )-{\overline{R}}_i(\phi ,\psi )]\times [R_j(\phi ,\psi )-{\overline{R}}_j(\phi ,\psi )]\rangle }_{\text{trials}},$$

where R_i = R_θi was the firing rate of neuron i and R̄ the average across trials. Although only the q-matrix enters in the Fisher Information, experimental data is often reported using normalized correlation coefficients. The (Pearson-r) correlation coefficient c_ij was obtained by dividing the covariance matrix by the variances, $c_{ij}=q_{ij}/[\sqrt{var(R_i)}\sqrt{var(R_j)}]$, Fig. 3 (bottom row).

The Mexican-hat connectivity produced a covariance matrix with both positive and negative correlation, corresponding to excitatory (short range) and inhibitory (long range) lateral connections, similar to other models (Spiridon and Gerstner 2001; Seriès et al. 2004).

2.3 Quantifying population coding accuracy

To quantify the accuracy of the population code we used the Fisher Information, which is a function of the tuning of individual neurons and the noise correlations.

$$\text{FI}(\phi ,\psi )=\int d\mathbf{R}P(\mathbf{R}\mid \phi )\frac{d^{2}lnP(\mathbf{R}\mid \phi )}{d{\phi }^2}$$

where R is the population response vector. For Gaussian distributed responses it equals (Wu et al. 2004; Abbott and Dayan 1999)

$$\text{FI}(\phi ,\psi )={\text{FI}}_1(\phi ,\psi )+{\text{FI}}_2(\phi ,\psi ).$$

Note that in contrast to population coding studies with homogeneous tuning curves where the FI is constant, here the FI depends both on the stimulus angle of adapter ψ and the stimulus angle of the probe φ. The first term is given by

$${\text{FI}}_1(\phi ,\psi )=\sum _i\sum _j{\overline{R}}_i^{\prime }(\phi ,\psi )q_{ij}^{-1}(\phi ,\psi ){\overline{R}}_j^{\prime }(\phi ,\psi )$$ (8)

where R̄′ denotes first derivative of R̄ with respect to the stimulus orientation φ, and $q_{ij}^{-1}$ is the inverse co-variance matrix. This term governs the discrimination performance of the optimal linear estimator and provides an upper bound to any linear estimator (Shamir and Sompolinsky 2004).

The second term equals

$${\text{FI}}_2(\phi ,\psi )=\frac{1}{2}\sum _{i,j,k,l}{q}_{ij}^{\prime }(\phi ,\psi )q_{jk}^{-1}(\phi ,\psi )q_{kl}^{\prime }(\phi ,\psi )q_{li}^{-1}(\phi ,\psi )$$ (9)

For a covariance matrix independent of the stimulus orientation q′(φ, ψ) = 0, so that FI₂(φ, ψ) = 0.

To calculate the derivatives appearing in Eqs. (8) and (9), we discretized the stimulus space with a resolution of h = 180/N, with N the number of neurons. The first derivative of the tuning curve of the neuron i was computed as $R_i^{\prime }(\phi ,\psi )=[R_i(\phi +h,\psi )-R_i(\phi -h,\psi )]/(2h)$, and similar for the derivative of the correlation matrix in Eq. (9). To accurately estimate the Fisher Information we used 12,000 trials for each data point, as too few trials lead to an overestimate of the Fisher Information (by some 5% when using only 4,000 trials).

The Fano Factor dependence for both terms can be analytically calculated; applying the Fano Factor definition, the covariance matrix is $q_{ij}(\phi ,\psi )={\text{FF}}_i{\overline{R}}_i(\phi ,\psi ){\delta }_{i,j}+c_{ij}(\phi ,\psi )\sqrt{{\text{FF}}_i}\sqrt{{\text{FF}}_j}\sqrt{R_i(\phi ,\psi )}\times \sqrt{R_j(\phi ,\psi )}$, where c_ij are pairwise correlations. For a population of neurons with the identical FF (as is the case here), FI₁ scales with 1/FF, while FI₂ is independent of FF for our noise model; this is illustrated for the control condition in Fig. 5 (bottom row).

The above calculation of the Fisher Information, Eqs. (8) and (9), assume Gaussian distributed responses. Due to the rectification in our model, Eq. (1) this won’t hold for the smallest firing rates. Unfortunately, there are no known results for the Fisher Information of correlated, non-Gaussian distributed responses, and a full sampling of the response probability distribution is computationally prohibitive. However, most of the information is coded where the tuning curve is steep. In these regions the firing rates are about half the maximum rate (Fig. 2(d)), and the Gaussian approximation is appropriate.

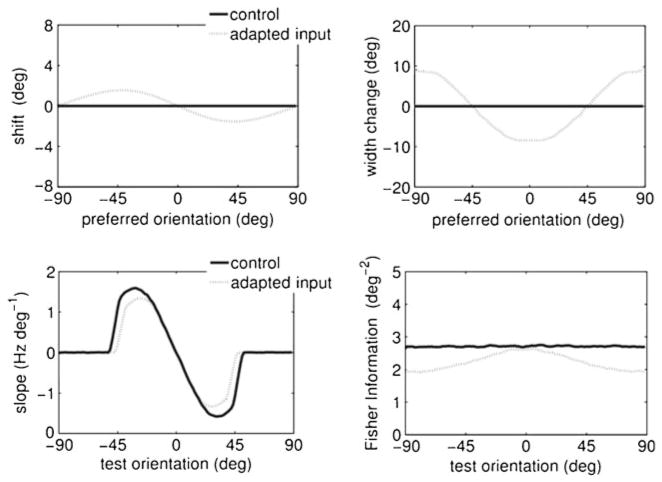
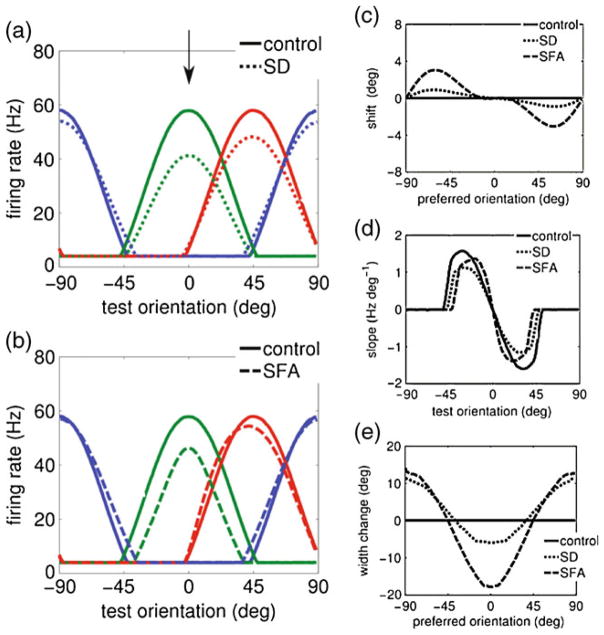
Fig. 2.

Effect of adaptation on the tuning curves of individual neurons. (a–b) Tuning curve properties for the different adaptation mechanisms: synaptic depression (SD) and spike-frequency-adaptation (SFA). Individual neuron tuning curves before and after adaptation. The tuning curves are shown for neurons with a preferred orientation of 0 (green), 45 (red) and 90 (blue) degrees, before (solid lines) and after adaptation (dashed lines). The adapter orientation was set to zero degrees (marked with an arrow in panel (a)). (c–e) Changes in tuning curves properties after adaptation. (c) Postadaptation tuning curve shift (center of mass) for all neurons. Both SD and SFA yielded an repulsive shift towards the adapter. (d) The slope of the tuning curve of a neuron with preferred orientation of zero degrees (green curve in panels (a–b)) as a function of the test orientation. The absolute value of the slope at small test angles increased with SFA, whilst the slope decreased with SD adaptation. (e) The change in the tuning curve width for the neurons in the population with respect to the control condition. For both SD and SFA the tuning curves narrowed for neurons with a preferred angle close to the adapter orientation, and widened far from the adapter orientation

2.3.1 Simulation protocol

The adaptation protocol is illustrated in Fig. 1(c). For each trial, we ran the network without input until the neural activity stabilized (~150 ms), after which an adapter stimulus with orientation ψ was presented for 300 ms during which the network adapted. After this adaptation period, the adaptation state of the network was frozen, i.e. no further adaptation took place. The response to a stimulus with orientation φ was tested using equilibration of the network activity of 450 ms. The activity at the end of this period corresponded to a single trial response.

2.4 Decoders of the population activity

We measured how adaptation modified the performances of two decoders or estimators: a Population Vector decoder and a winner-take-all decoder (Jin et al. 2005). For winner-take-all decoding the estimate was simply the (non-adapted) preferred orientation of the neuron with highest firing rate. For the population vector decoder the responses of all neurons were vector summed with an orientation equal to the neuron’s preferred orientation before adaptation.

For each decoder, we computed both the bias b(θ) and the discrimination threshold T(θ). The bias is the difference between the mean perceived orientation and the actual presented stimulus orientation. The discrimination threshold follows from the trial-to-trial standard deviation in the estimate, σ (θ) as

$$T(\theta )=\frac{D\sigma (\theta )}{1+b^{\prime }(\theta )}$$ (10)

where D is the discrimination criterion, chosen to be 1, corresponding to an error rate of ~76%. The Cramer–Rao bound on the discrimination threshold is given by (Seriès et al. 2009)

$$T(\theta )\ge \frac{D}{\sqrt{FI(\theta )}}.$$ (11)

3 Results

To study how adaptation affects coding, we used a well studied recurrent network model of area V1, the so called ring model (Ben-Yishai et al. 1995; Somers et al. 1995; Teich and Qian 2003). Neurons in the network were described by their firing rate and received feedforward input from the LGN and lateral input via a center-surround profile, Fig. 1(a) and (b) and Section 2. The noise model of the neurons was based on extra-cellular single unit recordings from neurons in area V1 recorded using a variety of visual stimuli (see Section 2). The variability was modelled by a Gaussian, stimulus independent, multiplicative noise with a Fano Factor of 1.5.

Neural adaptation occurs through multiple mechanisms. Here we focused on two distinct mechanisms both believed to contribute significantly to the adaptation of the neural responses to prolonged stimulation: (1) Spike frequency adaptation (SFA), in which the neuron’s firing rate decreases during sustained stimulation (Sanchez-Vives et al. 2000a, b; Benda and Herz 2003), and (2) short-term synaptic depression (SD) of the excitatory intra-cortical connections, so that sustained activation of the synapses reduces synaptic efficacy (Finlayson and Cynader 1995; Varela et al. 1997; Chung et al. 2002; Best and Wilson 2004). Synaptic depression is comparatively strong in visual cortex as compared to other areas (Wang et al. 2006).

In the adaptation protocol, Fig. 1(c), an adaption inducing stimulus with an angle ψ was presented for 300 ms, after which the population response to a test stimulus with orientation φ was measured. To insure that the models were comparable, the parameters were set such that the adaptation mechanisms reduced the firing rates of neurons tuned to the adapter orientation equally, see Fig. 2(a) and (b).

3.1 Effect of adaptation on single neuron tuning

First we studied how the different adaptation mechanisms changed the single neuron tuning curves. Note that in homogeneous ring networks the response of a neuron before adaptation is a function of a single variable only, namely the difference between the stimulus angle φ and the neuron’s preferred angle θ. Adaptation, however, renders the system in-homogeneous and the responses were characterized by three angles: The angle of the adapter stimulus ψ, always set to 0 degrees, the angle of the test stimulus, and the preferred orientation of the neuron. (The preferred orientation of a neuron refers to its preferred orientation before adaptation).

Both SD and SFA reduced the responses of neurons at the adapter orientation, in addition the tuning curves deformed, see Fig. 2(a) and (b). We characterized the effect of adaptation on preferred orientation shift, tuning curve slope and tuning curve width:

Tuning curve shift (Fig. 2(c))

Adaptation shifts the tuning curve (characterized by the center of mass). For both SD and SFA the tuning curves shifted towards the adapter stimulus. Attractive shifts after adaptation have been reported before in V1 (Ghisovan et al. 2008a, b), and in area MT (Kohn and Movshon 2004), although repulsive shift have been observed in V1 as well (Muller et al. 1999; Dragoi et al. 2000).

Tuning curve slope (Fig. 2(d))

The derivative of the firing rate with respect to stimulus angle, or slope, is an important determinant of accuracy. In the absence of correlations the Fisher information is proportional to the slope (see Eq. (8), Section 2). We plotted the slope of the tuning curve as a function of the test orientation for a neuron responding preferentially to the adapter orientation. For test angles close to the adapter orientation (<20 degrees), SD reduced the absolute value of slope relative to the control condition (solid line), but SFA increased the slope. Thus, for this neuron the increase in the slope occurring for SFA increases the coding accuracy around those orientations. For test angles further from the adapter orientation (ranging from 45 to 57 degrees) both SD and SFA showed a decreasing slope.

Tuning curve width (Fig. 2(e))

The width was computed as the angular range for which the neuron’s response exceeded the background firing rate. (Similar results were obtained using the width at half height). For both SD and SFA the width narrowed close to the adapter orientation and widened at orthogonal angles.

3.2 Effects of adaptation on noise correlations

Coding accuracy is not only determined by the properties of the single neuron tuning curves, but also critically depends on the noise in the response and the correlations in the noise between the neurons (Abbott and Dayan 1999; Sompolinsky et al. 2002; Gutnisky and Dragoi 2008). These noise correlations describe the common fluctuations from trial to trial between two neurons. The noise was modeled by independent multiplicative noise to the firing rates of the individual neurons, mimicking the Poisson-like variability observed in vivo (Section 2). In the model direct and indirect synaptic connections lead to correlations in the activity and its variability. For instance, if a neuron is by chance more active on a given trial, neurons which receive excitatory connections from it will tend to be more active as well.

We first studied the correlations in the control condition. Figure 3(a) top illustrates them for a stimulus angle of zero degrees. In analogy with experiments we also characterized them by the Pearson-r correlation coefficients. The correlation coefficients in the control condition are shown in Fig. 3(a) (bottom). Only neurons with a preferred angle between approximately −45 and +45 degrees were activated by this stimulus (the square region in the center of the matrix), and could potentially show correlation.

The correlations were strongest for neurons with similar preferred angles but that responded quite weakly to the stimulus, while neurons that had approximately orthogonal tuning (−45 and +45 degrees) showed negative correlation, as observed previously (Spiridon and Gerstner 2001; Seriès et al. 2004). The reason is that the noise causes fluctuations in the position of the activity bump (the attractor state) in the network, while its shape is approximately preserved. In nearby neurons for which the stimulus was at the edge of their receptive fields, such fluctuation lead to large, common rate fluctuations and hence strong correlation. In contrast, the responses of neurons in the center of the population, although noisy, were only weakly correlated as the precise position of the attractor state hardly affected their firing rates. The correlations might appear weak in comparison to experimental data. This is further discussed below (‘Effect of common input noise’).

Adaptation led to changes in the noise correlation, Fig. 3(b) and (c) (bottom row). Spike frequency adaptation (SFA) increased noise correlations, whilst synaptic depression (SD) decreased them. The latter is easy to understand. Synaptic depression weakens the lateral connections, and thus reduces correlations, shifting the operation of the network toward a feedforward mode. Figure 3(d) shows the correlations between neighboring neurons, showing the shape of the correlations and the effect of the adaptation in one graph.

3.3 Effect of adaptation on coding accuracy

Next we combined the effects of adaptation on tuning curves and correlations to calculate population coding accuracy as measured by the Fisher Information, see Section 2. The Fisher Information before and after adaptation is plotted as a function of test orientation in Fig. 4(a). Before adaptation the information is independent of the test angle as the network is homogeneous (solid line). After adaptation, the information becomes dependent on test angle (dashed curves).

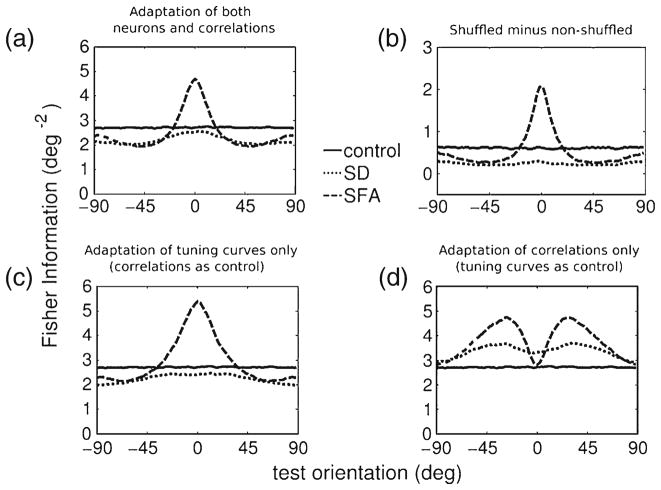
Fig. 4.

Effect of adaptation on population coding accuracy. (a) Fisher Information as a function of test orientation, in the control condition, i.e. before adaptation, and after adaptation through synaptic depression (SD) and spike frequency adaptation (SFA). Compared to the control condition the Fisher Information increases for SFA, provided the test stimulus orientation was similar to the adapter orientation. In all others cases a slight reduction of the accuracy is seen. (b) The additional information when the noise correlation is removed by shuffling the responses. The difference of Fisher Information using original responses (as panel (a)) and shuffled responses is shown. In all cases, including control, shuffling increases the information. For SD as after adaptation the population response is partially de-correlated, less information is gained by shuffling than in the control condition. For SFA the effect is heterogeneous, indicating that adaptation effects of the noise correlations for SFA were high for orientations close to the adapter orientation and less dominant far from it. (c) Fisher Information using adapted tuning curves and non-adapted correlations. (d) Adapted correlations with nonadapted tuning curves. Using non-adapted tuning curves, the decorrelation for SD adaptation increased Fisher Information

Only for SFA and only for test angles close to the adapter, the Fisher Information and hence accuracy increased. This peak was caused by the sharpening of the tuning curves near the adapter angle (see below). For all other combination of test orientation and adaptation mechanism the Fisher Information was slightly reduced. Interestingly, the shapes of the curves for SD and SFA are similar in that the Fisher Information peaked at the adapter angle.

Next, we explored the effect of the correlations on the information. We shuffled responses effectively removing any correlations. We subtracted the full Fisher Information from the Fisher Information using shuffled responses, Fig. 4(b). That this difference was always positive indicates that correlations always reduced the accuracy. After SD adaptation shuffling led to smaller increase than in control, consistent with the de-correlation caused by synaptic depression. For SFA the effect of correlations was more dominant for orientations close to the adapter angle, consistent with Fig. 3(c), and decreased for orientations far from the adapter angle.

As both individual tuning curves and the correlations change under adaptation, we further distinguished their contributions to the Fisher Information. First, we calculated the Fisher Information using adapted tuning curves and non-adapted correlations, Fig. 4(c). Because the correlations were now fixed to the control condition, changes in the Fisher Information are a consequence of the changes in tuning curves only. The Fisher Information resembled Fig. 4(a), indicating that the deformations of the tuning curves are important. For SFA, the tuning curve slope increased near to the adapter angle, Fig. 2(d), resulting in a prominent peak in the Fisher Information.

Finally we calculated the Fisher Information using non-adapted tuning curves but adapted correlations to reveal the information changes due to changes in correlations only, Fig. 4(d). Consistent with Fig. 3(b) and (c), with synaptic depression the Fisher Information increased for most orientations as the correlations are reduced. Also for SFA, the Fisher Information increased at almost all stimulus angles, except at a stimulus angle of zero degrees. In summary, when only adaptation of the correlations was taken into account, the information increased for most conditions. This finding is consistent with recent experimental data (Gutnisky and Dragoi 2008), where adaptation of the noise correlations were shown to increase population accuracy.

Although we typically observed opposite effects of changes in tuning curves and changes in correlation on the information (Fig. 4(c) and (d)), the total effect of the adaptation on coding is not simply the linear sum of the two. They interact non-linearly and therefore the total adaptation induced change of the Fisher Information in Fig. 4(a) is different from the sum of Fisher Information changes from Fig. 4(c) and (d).

The Fisher Information can be split in two terms, FI₁ and FI₂ (see Section 2). Interestingly, both contributions to the Fisher Information, Eqs. (8) and (9), were affected almost identically by adaptation, Fig. 5(a) and (b). The FI₂ is much smaller than FI₁ for the given number of neurons, but it should be noted that the second term is extensive in the number of neurons, even in the presence of correlations, while the FI₁ term saturates when correlations are present and the population is homogeneous (Shamir and Sompolinsky 2004). Because the almost identical effects of adaptation on the two terms, the effect of adaptation on the sum of the two terms will be independent on their relative contribution, suggesting that our results will be valid for a wider range of neuron numbers. In heterogeneous populations this saturation of FI₁ dissolves (Wilke and Eurich 2002; Shamir and Sompolisnky 2006), opening the possibility of an interesting interplay between adaptation and heterogeneity, where for instance adaptation yields a heterogeneous response. However, the readout has to be optimized for the heterogeneity (Shamir and Sompolisnky 2006), which is inconsistent with our decoding set-up (below) and we don’t examine this possibility here any further.

3.4 Reading out the population code

Because it is not known how populations of neurons are read-out by the nervous system, we analyzed how two well-known decoders, the winner-take-all and the Population Vector decoder, are affected by adaptation (see Section 2). Importantly, if the decoder does not have access to the state of adaptation, as we assumed here, its estimate will typically be biased (Seriès et al. 2009). For the two decoders, the bias profile was virtually identical, Fig. 6(a) and (b). Both SD and SFA led to strong tilt after-effects (repulsive shift away from the adapter orientation). As observed before, the tuning of individual neurons can behave differently from the population tuning (Teich and Qian 2003). The population bias can be opposite from the individual tuning curve shift, cf. Fig. 6 to Fig. 2(c). The reason is that the population vector weights the individual responses according to their firing rate. Therefore, although a neural tuning curve could shift towards the adapter orientation, if the rate is sufficiently reduced, the population vector shifts away from the adapter orientation.

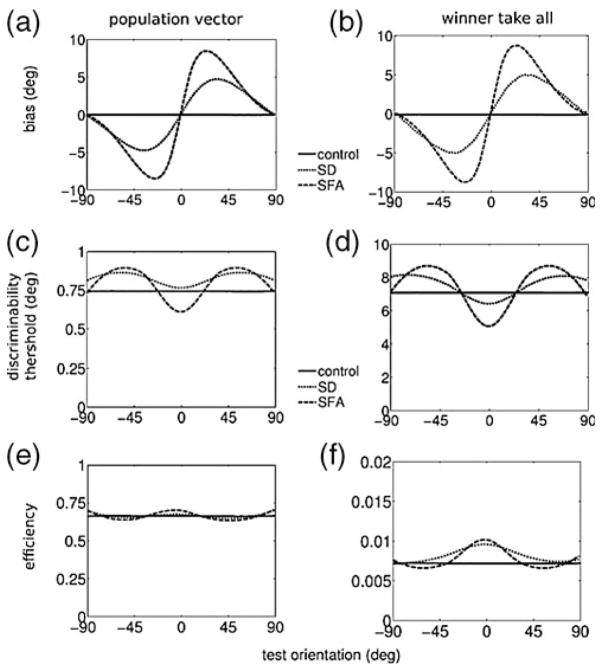
Fig. 6.

Decoding bias and variance. (a)–(b) The bias (average estimated orientation minus actual orientation) for two decoders: the population vector and winner-take-all decoder. SD and SFA adaptation induced a positive bias for estimations of positive orientations and negative bias for negative estimations (i.e. a repulsive shift of the population). (c)–(d) The discrimination threshold of the decoders is inversely proportional to the inverse of the Fisher Information, Fig. 4(a). (e)–(f) The discrimination threshold relative to the Fisher Information

For unbiased estimators the Cramer–Rao bound dictates that the minimum obtainable variance is given by the Fisher Information. For biased estimators where the bias is non-uniform this is no longer true. Instead, for biased estimators, the Fisher Information forms a bound on the decoder’s discrimination threshold (see Section 2 and Seriès et al. (2009)). Conveniently this is also the quantity that is typically assessed psychophysically. The discrimination threshold in the angle estimate in the two decoders is shown in Fig. 6(c) and (d). The threshold is inversely proportional to the Fisher information. Interestingly, for the winner-take-all decoder not only SFA but also SD increase performance at zero degrees. This is further illustrated in panel (e)–(f), where the threshold is plotted relative to the Fisher Information. This ratio is a measure of the biased decoder efficiency, a value of one indicating a perfect decoder. Unsurprisingly the population vector decoder (Fig. 6(e)) is more efficient than the winner-take-all (Fig. 6(f)), which, unlike the population vector, does not average over neurons to reduce fluctuations.

The population vector readout has a decent efficiency across conditions, perhaps suggesting that using a linear readout is sufficient to study the effects of adaptation on coding. However even under the Gaussian noise assumption an optimal linear discriminator can not extract all information from a correlated, heterogeneous (i.e. adapted) population (Shamir and Sompolisnky 2006), necessitating the calculation of the full Fisher Information to analyze the effect of adaptation on coding.

3.5 Effect of common input noise on correlations and coding accuracy

In our model the correlations were typically weak (<0.03) and neurons with orthogonal preferred angles were anti-correlated. There is a current debate about the strength of correlations in experimental data. A recent study in monkey V1 found average correlations coefficients of value 0.010 ± 0.002 (SEM), while there was a weak but significant relation between tuning curve similarity and correlation, so that more similar neurons show a higher correlation (Ecker et al. 2010). Negative correlations occurred in a substantial fraction of pairs. These findings are in line with our model.

In contrast, however, most other (older) studies show much stronger correlations in spike counts. Among nearby neurons with similar preferred orientations it is ≈ 0.2 (range 0.1 … 0.4) (Nelson et al. 1992; Gawne et al. 1996; DeAngelis et al. 1999; Smith and Kohn 2008). Again the correlations are generally somewhat less for neurons with different preferred orientations, but typically still above 0.1. Pairwise correlations between neurons with similar tuning were found to be only weakly dependent on stimulus orientation (Kohn and Smith 2005).

One possible explanation for this discrepancy is that there is an additional source of correlation in those data that is not present in the model. In particular, common input noise in the LGN could be the source of this missing correlation. We implemented LGN noise in the model that introduced common fluctuations in V1, enhancing the noise correlation and giving them a large offset, Fig. 7 (right column). Although the common input noise substantially increased the correlations to values compatable to the above cited works, the effect on the Fisher Information is negligible, cf. Fig. 7 (bottom row). The limited effect of common input noise on the coding accuracy can be understood from the fact that common input noise can be extracted away by a decoder (Sompolinsky et al. 2002). A simple algorithm would be to first calculate the population averaged activity on each trial, subtract it from the activity in all neurons and then decode relative to the average activity.

3.6 Effect of input adaptation on coding accuracy

Although there is evidence that in the LGN input does not adapt (Boudreau and Ferster 2005), we also tested the case where the input did adapt through synaptic depression. Parameters were adjusted so that the same response reduction after adaptation was achieved as SD and SFA. The adaptation reduces the drive to the V1 network. The adaptation effects on tuning curves and Fisher Information are shown in Fig. 8. These results are very similar to those found for synaptic depression. However, in contrast to SD, the correlations before and after adaptation were virtually identical (not shown), as adapting the input did not affect the lateral connections.

4 Discussion

We built a recurrent network model of primary visual cortex to address how adaptation affects population coding accuracy. Although a variety of models have modeled adaptation by imposing changes in the tuning curves, e.g. Jin et al. (2005), our model is the first to model the adaptation biophysically, thus directly relating biophysical adaptation to coding. From the adaptation mechanism, it predicts the concurrent changes in tuning curves, correlations, and coding. For synaptic depression (SD), we observed at the adapter orientation a strong reduction of tuning curve width, attractive shifts of the individual tuning curves, and strong repulsive population shifts. The case of spike frequency adaptation (SFA) was qualitatively comparable to SD with regards to tuning curves, but the changes in the coding accuracy were distinct (see below).

Experimental data on adaptation-induced tuning curves changes are unfortunately diverse and contradictory. Increased widths at the adapter orientation and repulsive shifts have been reported in V1 (Dragoi et al. 2000), while other studies in V1 reported a width reduction to the adapter stimulus and repulsive shifts (Muller et al. 1999). Yet another study reported typically attractive shifts for longer adaptation times (12 min) and repulsive shifts for short adaptation times, with no explicit quantification of width variations of the tuning curves (Ghisovan et al. 2008a, b). Finally, electrophysiological data from direction selective cells in area MT show a strong narrowing at the adapter orientation and attractive shifts, but that same study observed no shift in V1 tuning (Kohn and Movshon 2004).

Next, we examined the effect of adaptation on coding accuracy by means of the Fisher Information. We studied how Fisher Information depends on test orientation and precise adapting mechanism. The Fisher Information represented in Fig. 4(a) showed larger Fisher Information for orientations close to the adapter orientation in the case of SFA. This was due to the increased slope of the tuning curves after adaptation. The increase in information occurred despite increased noise correlations. In the case of SD the accuracy decreased, despite a reduction in the correlations, Fig. 3, which was however not enough to counter the decrease in accuracy due to tuning curve changes, Fig. 4(c). The changes in coding accuracy can partly be understood from the changes in the tuning curve slopes. But our results also show explicitly that both changes in the tuning curves and in the correlations need to be taken into account to determine the net effect of adaptation on coding.

We also considered the case where the input connections are adapting. It should be noted that whether the LGN-V1 connections are subject to short term synaptic depression is matter of debate (Boudreau and Ferster 2005; Jia et al. 2004). Inclusion of synaptic depression in the LGN-V1 connections reduced the drive of V1 for neurons close to the adapter. The results for both the tuning curve and Fisher Information changes is very comparable to SD, Fig. 8.

To compare these findings to psychophysics we implemented two common decoders which yield adaptation-induced biases and accuracy. Both decoders showed repulsive tilt after-effects. Both attractive and repulsive have been reported experimentally, typically showing repulsion close to the adapter and weak attraction far away (Schwartz et al. 2007, 2009; Clifford et al. 2000). Although we do find repulsion close to the adapter, the weak attraction for orthogonal orientation is not reproduced here. This could be due either to differences in the activity or to a different readout mechanism.

Data on orientation discrimination performance after adaptation is limited, Two studies found a slight improvement for orientation discrimination around 0 degrees, but a higher (worse) threshold for intermediate angles (Regan and Beverley 1985; Clifford et al. 2001). More data is available for motion adaptation which has been argued to resemble orientation data (Clifford 2002). The overall pattern is similar: no or small improvement at the adapter and worse performance for intermediate angles, see Seriès et al. (2009) and references therein. These results match our result for the SFA adaptation model. One study found a lower (better) threshold for angles close to 90 degrees (Clifford et al. 2001), never present in our model.

4.1 Model assumptions and extensions

Like any model, our model has certain limitations and is based on a number of assumptions; we discuss them here. First, the model is not spiking, but rate based. Of course a spiking model is in principle more realistic and could lead to different results, but apart from the difficulty tuning a spiking network model, in particular obtaining the right noise and correlations is far from trivial, such a model would be computationally challenging given the number of trials required to calculate the Fisher Information. Encouragingly however, in studies of non-adapting networks, a rate model with phenomenological variability lead to a similar covariances as a network with spiking neurons (Spiridon and Gerstner 2001; Seriès et al. 2004).

We assumed that the noise stems either from the neurons in the network or from common LGN modulation. Additional sources of noise do probably exists, including correlated noise sources such as other common input, common feedback, or common modulation, both stationary and adapting. Although such noises could be included in the model but too little is known about noise sources and their correlations to allow for strong conclusions on this point.

Our model focuses on brief adaptation paradigms of up to a few hundred ms, as cellular and synaptic adaptation is best characterized on those time scales. We have used simple phenomenological models of synaptic and cellular adaptation. As a result the dynamics of the observed changes in coding are simple as well (longer adaptation will give stronger effects). However, although the used models are well supported by empirical data, adaptation processes are known to be much more complicated biophysically and manifest multiple nonlinearities and timescales. For longer adaptation periods, other adaptation processes might be activated, e.g., Sanchez-Vives et al. (2000a), Wark et al. (2007), and Ghisovan et al. (2008b), which would require modified adaptation models. Despite these limitations, one could in principle consider cases where the network is continuously stimulated, as would occur under natural stimulation. Our results suggest that the coding accuracy would show a strong history dependence. Furthermore, the net effect of the synaptic depression is expected to be less, as the synapses will be in a somewhat depressed state already. Unfortunately, a detailed analysis of this scenario seems currently computationally prohibitive.

Finally, we assumed a model in which the tuning curves are sharpened by the recurrent connections. Previous studies, without adaptation, have contrasted coding in such networks with coding in feedforward networks with no or much less recurrence and found that the recurrence induces correlations that strongly degrade the coding (Spiridon and Gerstner 2001; Seriès et al. 2004), but see also Oizumi et al. (2010). Inline with those findings, we find that the correlations induced by the recurrent connections, severely reduce the information, see Fig. 4(c). Whether the primary visual cortex is recurrently sharpened or dominated by feed-forward drive is a matter of debate (Ferster and Miller 2000). In the feedforward variant of our model without any recurrence, noise correlations will be absent. Thus the tuning curves and the noise determine the information content and the changes caused by adaptation. This situation is comparable to calculating the information using uncorrelated (i.e. shuffled) responses, Fig. 4(b).

4.2 Conclusion

This study shows how various single neuron adaptation mechanisms lead to changes in the tuning curves and it shows how this then translates to shifts in the population properties and changes in coding accuracy. Our results explicitly show that both changes in the tuning curves and in the correlations need to be taken into account to determine the net effect of adaptation on coding. The experimentally observed biases and accuracies are more consistent with our model that has spike frequency adaptation on the single neuron level rather than with the synaptic depression model.