A Coupled Biventricular Finite Element and Lumped Parameter Circulatory System Model of Heart Failure

Abstract

Numerical modeling of the cardiovascular system is becoming an important tool for assessing the influence of heart disease and treatment therapies. In the current study we present an approach for modeling the interaction between the heart and circulatory system. This was accomplished by creating animal specific biventricular finite element models, which characterize the mechanical response of the heart, and coupling them to a lumped parameter model that represents the systemic and pulmonic circulatory system. In order to minimize computation time, the coupling was enforced in a weak (one-way) manner, where the ventricular pressure-volume relationships were generated by the finite element models and then passed into the circulatory system model to ensure volume conservation and physiological pressure changes. The models were first validated by tuning the parameters, such that the output of the models matched experimentally measured pressures and volumes. Then the models were used to examine cardiac function and the myofiber stress in a healthy canine heart and a canine heart with dilated cardiomyopathy. The results show good agreement with experimental measurements. The stress in the case of cardiomyopathy was found to increase significantly, while the pump function was decreased, compared to the healthy case. The total run time of the simulations is less than many fully-coupled models presented in the literature. This will allow for a much quicker evaluation of possible treatment strategies for combating the effects of heart failure, especially in optimization schemes that require numerous finite element simulations.

1. Introduction

Recent statistics from the American Heart Association (2011) indicate that Congestive Heart Failure (CHF) affects 5.7 million Americans. CHF is characterized by the hearts inability to pump blood efficiently into the body, due to either impaired myocardial contraction and global dilation of the ventricles (systolic heart failure), or decreased relaxation of the ventricles (diastolic heart failure). Several treatment strategies have been investigated to combat the adverse remodeling that leads to the progression of CHF (Gorman et al. 2004, Thompson et al. 2010a, Thompson et al. 2010b). Some of these treatments involve the improvement of blood flow to damaged regions of the heart, while others include reshaping the heart by means of surgical procedures and implantation of medical devices. Examples of implantable medical devices include the Acorn CSD and Copasys (Acker et al. 2006, Grossi et al. 2010). These devices were designed to improve pump function by reducing ventricular volume and thus reduce wall stress. The effect of these devices on regional ventricular mechanics and global ventricular function, however, is currently not fully understood.

The mechanics of the heart have been widely studied using the finite element (FE) method. Left ventricular (LV) FE models, which incorporate myocardial contractility, have been described and used to determine the influence of myocardial infarction on structure and function (Dang et al. 2005a, Guccione et al. 2001, Walker et al. 2005a). Additionally, the efficacy of various surgical procedures has been simulated (Dang et al. 2005b, Walker et al. 2005b), as well as the effect of cardiac support devices (Jhun et al. 2010, Wenk et al. 2009). Models that include volumetric growth (Kroon et al. 2009a) and myofiber remodeling (Kroon et al. 2009b) have also been implemented with the FE method, and coupled to lumped-parameter models of the circulatory system. Most recently, a non-invasive method for determining myocardial material properties was developed using magnetic resonance imaging (MRI), FE modeling, and optimization (Sun et al. 2009, Wenk et al. 2011), which can be used to characterize weakly contracting regions of the heart. These single ventricle models have provided much insight on cardiac mechanics, but do not account for the interaction between the left and right ventricles.

To enhance LV models, biventricular FE models have been developed to simulate the effects of ventricular dilation and electrical dyssynchrony on ventricular function and regional mechanics (Kerckhoffs et al. 2010), as well as the effects of external defibrillation on heart function (Rodriguez et al. 2006). In addition, biventricular FE models have been used as a framework in which to incorporate multiscale models for eccentric and concentric cardiac growth (Goktepe et al. 2010). The effects of surgical procedures for pulmonary valve and patch replacement in patients with tetrology of Fallot were also investigated with a biventricular FE model (Tang et al. 2008). Kerckhoffs et al. (2007b) developed a coupled biventricular FE and lumped systems model to evaluate the effects of ischemia on pump function, using an implicit scheme to simulate the results. These models, however, are computationally expensive and have not been used to simulate the effect of cardiac devices including surgical ventricular remodeling and passive constraint.

In the current study, we present a method to weakly couple a biventricular finite element model and a lumped parameter model of the circulatory system. To achieve this end, we used the biventricular FE model to represent the mechanical response of the heart, and then input the response into the circulatory system model to ensure physiological pressure changes and continuity of the total system volume during the cardiac cycle. By using a weak (one-way) coupling scheme, the simulations were conducted in much less time than previous approaches described in the literature. This is an important aspect of this work, since it allows for numerous simulations to be conducted in a short period of time. This is essential for the computational efficiency of optimization schemes, which require a large number of simulations to evaluate an objective function (Sun et al. 2009). In order to validate our method, two FE models were constructed, based on MRI and experimental hemodynamic measurements in a normal healthy dog and the same dog with pacing tachycardia-induced dilated cardiomyopathy. The primary goal of the current study is to evaluate the effects of heart failure on stress and pump function in the heart. In the near future, this approach will be used to optimize the design of devices used to treat systolic heart failure. Specifically, the method will be used to simulate the effect of passive constraint devices, such as the Acorn CSD and Coapsys device.

2. Methods

In this study, we developed a weakly coupled FE/lumped-parameter system to model the cardiovascular system. The model consists of two separate units: a biventricular FE model for the heart and a lumped parameter model for the cardiovascular tree. The coupling between the two units is based on previous experimental observations indicating that the ventricular output is well characterized by the end-systolic pressure-volume relationship (ESPVR) and end-diastolic pressure-volume relationship (EDPVR) (Suga and Sagawa 1974). We characterized the mechanical response of the heart to various pressure loads using the biventricular FE model and then, used this data to drive the circulatory system model (to ensure that pressure changes in each ventricle were coupled and physiologically realistic). A flow chart of the coupling scheme is shown in Figure 1. The key features of each model component are described in the following sections.

Figure 1.

Flow chart of the model validation and model application. Note that the exchange of data between models, used to represent the coupling, is indicated by the dashed boxes labeled weak coupling. (EDP = end-diastolic pressure, ESP = end-systolic pressure, EDV = end-diastolic volume, ESV = end-systolic volume, IVC = inferior vena cava)

2.1 Animal model and experimental data

The details of the animal model and data acquisition have been described previously (Potter et al. 2007). In brief, a single mongrel dog underwent a 4 week rapid pacing protocol to induce dilated cardiomyopathy. Magnetic resonance images were acquired before implantation of the pacemaker, as a baseline, and within 15 hours of termination of the pacing. Right ventricular pressure was measured using a Cook Swan-Ganz catheter via the pulmonary artery and left ventricular pressure was measured via direct cardiac puncture into the LV apex with an 18 gauge needle. Both pressures were taken under general anesthesia prior to surgical manipulation. The measured pressures were then used as boundary conditions in the FE models (Table 1).

Table 1a.

Experimentally determined hemodynamic data taken at the time of MRI, which was used to calibrate the normal baseline FE and circulatory system models.

	EDP (mmHg)	ESP (mmHg)	EDV (mL)	ESV (mL)	SV (mL)
LV	7	104	66.3	36.6	29.7
RV	2	24	66.3	36.5	29.8

LV, Left ventricle; RV, Right ventricle; EDP, End-diastolic pressure; ESP, End-systolic pressure; EDV, End-diastolic volume; ESV, End-systolic volume; SV, Stroke volume

2.2 Image analysis

A customized version of the MRI post-processing software, FindTags (Laboratory of Cardiac Energetics, National Institutes of Health, Bethesda, MD) was used to contour each short-axis image of the endocardial and epicardial surfaces in both the LV and right ventricle (RV) (Figure 2). Geometric surfaces (Rapidform, INUS Technology, Inc., Sunnyvale, CA) of the endocardium were created at end-diastole and end-systole, in order to calculate the experimentally observed ventricular volumes (Table 1). Then, geometric surfaces of the endocardium and epicardium were created at early diastole, which was assumed to be the zero stress state of the heart, since pressure is at a minimum.

Figure 2.

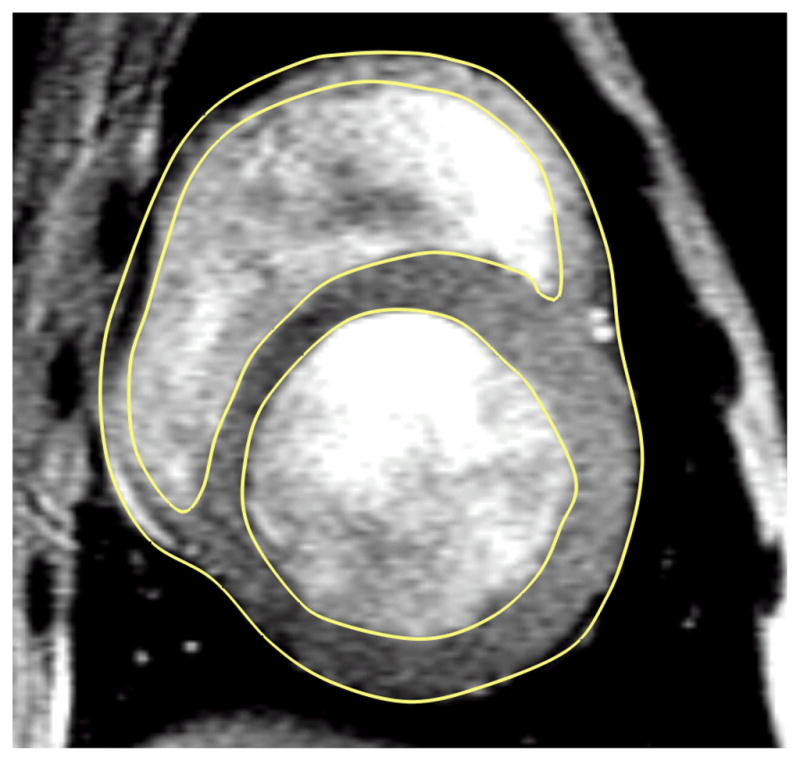
An equatorial MR image of a canine heart with dilated cardiomyopothy. The yellow lines are the contours used to generate to 3D geometry.

2.3 Finite Element Models

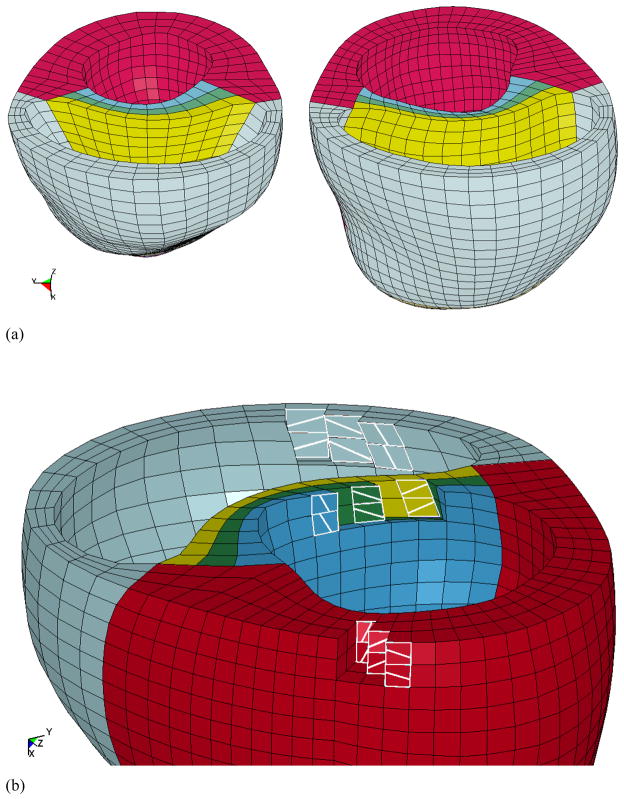
Biventricular FE models were created for the healthy canine heart (baseline) and for the globally dilated canine heart using the animal-specific surface geometries and the mesh generator TrueGrid (XYZ Scientific, Inc., Livermore, CA) (Figure 3a). The ventricular walls of each model were meshed with approximately 4150 8-node trilinear elements. The transmural mesh density was adjusted until the ventricular volume changed by less than 5% for a given load. It was found that 3 elements are sufficient for accurate ventricular volume calculations and computational efficiency (Sun et al 2009). The basic construction of the mesh involved a continuous ring (3 elements wide) of elements around the perimeter of both ventricular chambers, which was tangent to the epicardium of the heart. Then, three layers of elements were generated to represent the septum. The myofiber angles were assigned to each element using a custom in-house script that was created in MATLAB. Myofiber angles were first assigned to the continuous ring of elements, moving from base to apex. The angles varied transmurally, in a linear fashion, and were assigned to be −37 deg at the epicardium and 83 deg at the endocardium, relative to the circumferential direction (Figure 3b) (Omens et al. 1991). This fiber distribution was used throughout the entire LV, including the septum, and RV free wall. The endocardium of each ventricle was lined with shell elements in order to create an airbag for computing the cavity volume. The shell elements were modeled as being extremely soft (Young’s modulus of 1×10⁻¹⁰ kPa and Poisson’s ratio of 0.3), and thus had no influence on the mechanical response of the ventricles.

Figure 3.

(a) The biventricular finite element models. The normal heart is on the left and the cardiomyopathy heart is on the right. The red elements represent the LV myocardial wall, the light blue elements represent the RV myocardial wall, and the septum is represented by the 3 colored layers in between the ventricles. (b)The LV free wall, septum, and RV free wall have fiber angles of −37 deg at the epicardium, 23 deg at mid-wall, and 83 deg at the endocardium, relative to the circumferential direction..

2.4 Boundary and Loading Conditions

The boundary conditions of the heart were assigned to fully constrain the displacement at the epicardial-basal edge, while allowing the remaining nodes at the base to move in the circumferential-radial plane. Additionally, the nodes along the LV endocardial-basal edge of the septum were fully constrained. The inner endocardial walls of the LV and RV were loaded with the experimentally measured pressures (Table 1), in order to simulate the end-diastolic (ED) and end-systolic (ES) states. It should be noted that the pressure boundary conditions were applied by quickly ramping the load to the measured value, and then holding the load constant as the simulation reached a steady state solution at ED and ES. In order to save time, these simulations were conducted independently, since the ES state is not dependent on the ED state.

2.5 Material Properties of the heart

Nearly incompressible, transversely isotropic, hyperelastic constitutive laws for passive (Guccione et al. 1991) and active myocardium (Guccione et al. 1993a) were modeled with a user-defined material subroutine in the explicit FE solver, LS-DYNA (Livermore Software Technology Corporation, Livermore, CA). Passive material properties were represented by the strain energy function:

$$W=\frac{C}{2}\left\{exp\left[b_f{E}_{11}^2+b_t(E_{22}^2+E_{33}^2+E_{23}^2+E_{32}^2)+b_{fs}(E_{12}^2+E_{21}^2+E_{13}^2+E_{31}^2)\right]-1\right\}$$ (1)

where E₁₁ is fiber strain, E₂₂ is cross-fiber strain, E₃₃ is radial strain, E₂₃ is shear strain in the transverse plane, and E₁₂ and E₁₃ are shear strain in the fiber-cross fiber and fiber-radial planes, respectively. Values for the material constants b_f, b_t, and b_fs were chosen as 18.5, 3.58, and 1.63, respectively, based on previous studies of canine myocardium (Guccione et al. 1991). In order to validate the models, the material constant C was adjusted until the LV and RV end-diastolic volumes matched the experimentally measured values. It should be noted that the myocardial material properties (Guccione et al. 1991) have been used in previous biventricular FE simulations of the canine heart (Kerckhoffs et al. 2007a, Kerckhoffs et al. 2007b).

Active contraction was modeled by defining total stress as the sum of the passive stress derived from the strain energy function and an active fiber directional component, T₀, which is a function of time, t, peak intracellular calcium concentration, Ca₀, sarcomere length, l, and maximum isometric tension achieved at the longest sarcomere length, T_max (Guccione et al. 1993b),

$$\mathbf{S}=pJ{\mathbf{C}}^{-1}+2J^{-2/3}\text{Dev}\left(\frac{\partial \stackrel{\sim }{W}}{\partial \mathbf{C}}\right)+{\mathbf{T}}_{\mathbf{0}}\{t,{Ca}_0,l,T_{max}\}$$ (2)

where S is the second Piola-Kirchoff stress tensor, p is the hydrostatic pressure introduced as the Lagrange multiplier needed to ensure incompressibility, J is the Jacobian of the deformation gradient tensor, C is the right Cauchy-Green deformation tensor, Dev is the deviatoric projection operator,

$$\text{Dev}(•)=(•)-\frac{1}{3}([•]:\mathbf{C}){\mathbf{C}}^{-1}$$ (3)

and W̃ is the deviatoric contribution of the strain energy function, W (Eq. 1). The assumption of near incompressibility of the myocardium requires the decoupling of the strain energy function into dilational and deviatoric components,

$$W=U(J)+\stackrel{\sim }{W}(\stackrel{\sim }{\mathbf{C}})$$ (4)

where U is the dilatational (volumetric) contribution (Wenk et al. 2010).

The active fiber-directed stress component is defined by a time-varying elastance model, which at end-systole, is reduced to (Tozeren 1985),

$$T_0=\frac{1}{2}{T}_{max}\frac{{Ca}_0^2}{{Ca}_0^2+{\mathit{ECa}}_{50}^2}\left(1-cos\left(\frac{0.25}{m{l}_R\sqrt{2E_{11}+1}+b}+1\right)\pi \right)$$ (5)

with m and b as constants, and the length-dependent calcium sensitivity, ECa₅₀, is given by,

$${\mathit{ECa}}_{50}=\frac{{({Ca}_0)}_{max}}{\sqrt{exp\left[B\left(l_R\sqrt{2E_{11}+1}-l_0\right)\right]-1}}$$ (6)

where B is a constant, (Ca₀)_max is the maximum peak intracellular calcium concentration, l₀ is the sarcomere length at which no active tension develops and l_R is the stress-free sarcomere length. The material constants for active contraction were taken to be (Guccione et al. 1995a): Ca₀ = 4.35 μmol/L, (Ca₀)_max = 4.35 μmol/L, B = 4.75 μm⁻¹, l₀ = 1.58 μm, m = 1.0489 sec μm⁻¹, b = −1.429 sec, and l_R was set at 1.85 μm, the sarcomere length in the unloaded reference configuration. Based on biaxial stretching experiments (Lin and Yin 1998) and FE analyses (Usyk et al. 2000, Walker et al. 2005a), cross-fiber, in-plane stress equivalent to 40% of that along the myocardial fiber direction was added. In order to further validate the models, the parameter T_max was determined such that the LV and RV end-systolic volumes matched the experimental values.

2.6 Calculation of the EDPVR and ESPVR

The diastolic compliance and systolic elastance of both the normal and dilated cardiomyopathy cases were characterized by means of the pressure-volume relationship. The EDPVR was determined for both the left and right ventricle using the FE models to compute the volume at several end-diastolic pressures. In order to account for ventricular interaction during the FE simulations, the following procedure was used:

1. The RV EDP was fixed at a constant value.

2. The LV EDP was varied over a physiological range in order to generate a single EDPVR curve.

3. The RV EDP was incrementally increased and fixed at the new constant value.

4. Steps 2 and 3 were repeated until a family of curves was generated for the LV EDPVR.

5. In order to generate a family of curves for the RV EDPVR, steps 1 through 4 were repeated holding the LV EDP fixed at several points while varying the RV EDP.

The resulting data was fit to an exponential equation (Eq. (7)) using a nonlinear least squares regression analysis,

$$\mathit{EDP}=P_d(e^{K(\mathit{EDV}-V_d)}-1)$$ (7)

where P_d, K, and V_d are the parameters that characterize the diastolic compliance of the ventricle.

The ESPVR for the left and right ventricle was generated using a procedure similar to the one described above. It should be noted that changes in the ESP of the adjacent ventricle did not significantly affect the ESPVR of the ventricle of interest. Thus, each ventricle was characterized with a single curve for the ESPVR. The results from the end-systolic FE simulations were fit to the following linear equation by means of least square regression analysis,

$$\mathit{ESP}=E_{ES}(\mathit{ESV}-V_0),$$ (8)

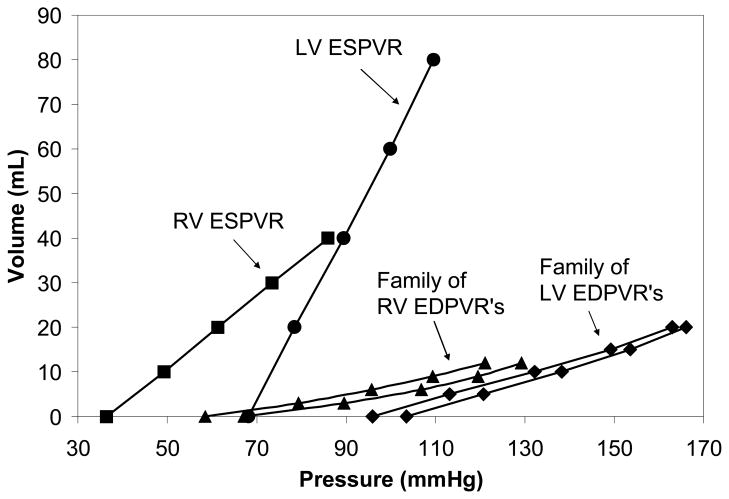
where V₀ is the volume intercept and E_ES is the slope of the left ventricle elastance. The family of curves that were generated for the cardiomyopathy case is shown in Figure 4.

Figure 4.

These are the EDPVR and ESPVR for the cardiomyopathy case. The EDPVR and ESPVR of each ventricle were determined with different pressures in the adjacent ventricle, in order to assess ventricular interaction. This generated a family of curves for each ventricle. Only two of the curves in each family are shown for brevity. The ESPVR was unaffected by the changes in pressure in the other ventricle.

2.7 Circulatory system modeling

In order to couple the biventricular FE model and the vascular system, we implemented a lumped-parameter circulatory model following the classic model PHYSBE using Simulink (The Mathworks, Natick, MA) (McLeod 1966). The PHYSBE model was chosen for its simplicity and, more importantly, its separation of flows through the superior vena cava (from head and arms) and inferior vena cava (from trunk and legs). This separation allows us to measure the Starling relationship through inferior vena cava (IVC) occlusion, accomplished by blocking IVC flows from entering the RV. The full details of the PHYSBE model are outlined in McLeod (1966)

Briefly, vascular resistance and compliance were modeled as analog resistance and capacitance components in a closed loop to ensure volume conservation. The key components of the vascular tree are shown in Figure 5. A description of the components and the parameters used for each component are given in the Supplemental Material. It should be noted that the original PHYSBE model approximates the LV and RV chambers with a linear time-varying compliance model, which does not account for the physiological ESPVR. The ESPVR is a pre-load independent parameter characterizing ventricular contractile function (Suga and Sagawa 1974). In the present work, we implemented a lumped-parameter model for the ventricles using the approach proposed by Ursino (1998). The RV and LV were modeled in the same fashion, using the family of curves generated from the FE simulations (Figure 4), with the only difference being a set of parameters governing the end-systolic and end-diastolic ventricular properties. In what follows the subscript LV is used to describe the left ventricular model. However, the same equations were used to model the RV as well, which can be written by switching the subscript LV for RV. The LV pressure within a cardiac cycle is governed by

Figure 5.

Lumped parameter model used to represent the cardiovascular system. The LV and RV were used to were modeled with the EDPVR and ESPVR, while the remaining components were modeled with resistance and capacitance components.

$$P_{LV}(V_{LV},t)=\varphi (t)P_{\mathit{act},LV}(V_{LV})+\left[1-\varphi (t)\right]P_{\mathit{pas},LV}(V_{LV})$$ (9)

where ϕ(t) is a squared half-sine wave that controls the activation of the ventricle, i.e., ϕ(t) = 1 at maximum contraction and ϕ(t) = 0 at complete relaxation (Ursino 1998). A description of the activation function can be found in the Supplemental Material. The term P_act,LV is the component of LV pressure generated by the active contraction of myofibers, while P_pas,LV is the passive component of LV pressure. The active pressure component is governed by applying (Eq. (8)) to the LV, such that

$$P_{\mathit{act}}\left(V_{LV}\right)=E_{ES,LV}\left(V_{LV}-V_{0,LV}\right)$$ (10)

It can be seen from the FE simulations that the passive properties which govern the LV EDPVR, for a fixed value of RV EDP, can be modeled by applying (Eq. (7) to the LV

$$P_{\mathit{pas}}(V_{LV})=P_{d,LV}\left(e^{K_{LV}(V_{LV}-V_{d,LV})}-1\right)$$ (11)

where changing the RV EDP leads to a different EDPVR curve, as shown in Figure 4. The interaction between the LV and RV was implemented into the circulatory model as follows. First, a set of LV EDPVR curves was generated at several prescribed RV pressure levels. In the case of the cardiomyopathy model, for example, three of those values in the RV were 5 mmHg, 8 mmHg, and 11 mmHg; i.e., the passive responses were given by P _pas,LV^5mm(V_LV), P _pas,LV^8mm(V_LV), and P_pas,LV^11mm(V_LV), respectively. Each of these pressure values is within the physiological range of pressures that could occur in the RV. The final pressure response of the LV was determined by using linear interpolation between adjacent curves in the family set. For example, if the RV pressure falls between 5 mmHg and 8 mmHg, or between 8 mmHg and 11 mmHg, the pressure in the LV is computed such that

$$P_{\mathit{pas},LV}=\{\begin{array}{ll}{P_{\mathit{pas},LV}}^{8mm}+\alpha ·\left({P_{\mathit{pas},LV}}^{11mm}-{P_{\mathit{pas},LV}}^{8mm}\right)\hfill & \alpha >0\hfill \\ {P_{\mathit{pas},LV}}^{8mm}-\alpha ·\left({P_{\mathit{pas},LV}}^{5mm}-{P_{\mathit{pas},LV}}^{8mm}\right)\hfill & \alpha \le 0\hfill \end{array},$$ (12)

where $\alpha =\frac{{\mathit{EDP}}_{RV}-8}{3}$. This approach was used to model both ventricles for the baseline and cardiomyopathy cases. In each case, the fixed ventricular pressure values were selected to give a physiologically realistic range and interpolation occurred between adjacent curves.

2.8 Calculation of Stroke Volume/EDP (Starling) Relationship

We generated the Starling relationship for the baseline and cardiomyopathy cases by conducting virtual inferior vena cava (IVC) occlusion experiments with the analog circulatory model. We started each simulation of the analog circulatory model with zero initial flows in the system and ran the simulation until it reached a steady state. Shortly after this, a virtual IVC occlusion was conducted by inserting a very large resistance component between the outlets of lower body circulation components (trunk and legs) and the inlet of vena cava (Figure 5). The virtual IVC occlusion led to a transient reduction in the preload of the LV in our model. The pressure-volume loops after IVC occlusion were recorded and the Starling curve was constructed using corresponding pairs of LV EDP and stroke volume data from selected heart beats during the transient preload reduction phase.

3. Results

3.1 Material Parameter Estimation

The passive material parameter, C, and the active material parameter, T_max, were varied until the volumes in the FE simulations matched the experimentally measured values at ED and ES. Unfortunately, no other time point data was available. For the healthy case, C was determined to be 0.455 kPa in the LV and 0.153 kPa in the RV. For the dilated cardiomyopathy case, C was determined to be 2.83 kPa in the LV and 1.63 kPa in the RV. It has been shown by Sacks and Chuong (1993a, b) that the LV and RV have different passive responses to biaxial tensile loading. The RV tends to be more anisotropic, but this was not taken into account in the present study. Rather, the effective difference in stiffness is determined through the parameter, C, keeping the b_f, b_t, and b_fs parameters constant.

For the normal heart case T_max was found to be 350 kPa and 59.2 kPa in the LV and RV, respectively. In the dilated cardiomyopathy case the values were found to be 204 kPa and 58.5 kPa in the LV and RV, respectively. It has been shown by Maughan et al. (1979, 1985) that the LV is less compliant than the RV during contraction. In those studies, the slope of the ESPVR was found to be steeper for the LV.

3.2 Comparison of Numerical Models and Experimental Measurements

The material properties in the FE models were determined such that the ventricular volumes matched those of the experimental measurements taken at the time of MRI to within 0.1%. This was also the case for the resistance and capacitance properties of the lumped parameter model. Thus, the biventricular FE and circulatory system models give equivalent volumes for the same set of pressures, using the measured data.

To ensure that the biventricular FE and circulatory system models match one another at physiological states other than the experimentally measured state, the circulatory system model was used to simulate the cardiac cycle for a heart rate that was 20% higher, for both the normal and cardiomyopathy cases. This caused the ventricular pressures to change by 10% to 30%. The pressures generated from these simulations were then used as boundary conditions in the FE models. A comparison of the resulting volumes is shown in Table 2a and 2b, for the normal and cardiomyopathy cases, respectively. There was good agreement between the biventricular FE and circulatory system models. The difference in volume calculations ranged from 0.0% to 2.0%.

Table 2a.

Comparison of the normal baseline FE and circulatory system models at a state of elevated heart rate.

	EDP (mmHg)	ESP (mmHg)	EDV (mL) circulatory model	EDV (mL) FE model	% diff	ESV (mL) circulatory model	ESV (mL) FE model	% diff
LV	5.25	98.65	62.3	61.5	−2.0%	37.1	36.5	−1.6%
RV	1.5	25.5	62.7	62.9	+0.3%	37.5	37.6	+0.2%

LV, Left ventricle; RV, Right ventricle; EDP, End-diastolic pressure; ESP, End-systolic pressure; EDV, End-diastolic volume; ESV, End-systolic volume; SV, Stroke volume

Table 2b.

Comparison of the cardiomyopathy FE and circulatory system models at a state of elevated heart rate.

	EDP (mmHg)	ESP (mmHg)	EDV (mL) circulatory model	EDV (mL) FE model	% diff	ESV (mL) circulatory model	ESV (mL) FE model	% diff
LV	6.65	63.16	121.7	123.43	+1.4%	101.1	101.1	0.0%
RV	4.1	27.2	91.3	90.0	−1.4%	70.6	70.4	−0.2%

LV, Left ventricle; RV, Right ventricle; EDP, End-diastolic pressure; ESP, End-systolic pressure; EDV, End-diastolic volume; ESV, End-systolic volume; SV, Stroke volume

3.3 Simulation Run Time

The FE simulations that were used to generate the families of EDPVR and ESPVR curves were run as batch jobs on a Dell Precision T7400 with dual 3.2 GHz Quad Core Xeon processors and 16 GB of RAM. The family of EDPVR curves required 56 simulations, while the ESPVR required 10. The total run time for all 66 simulations was approximately 330 minutes for the normal healthy case and 390 minutes for the cardiomyopathy case. The run time of the circulatory system model was roughly 5 minutes for the virtual IVC or increased heart rate simulations.

3.4 EDPVR, ESPVR, and Starlings Relationship

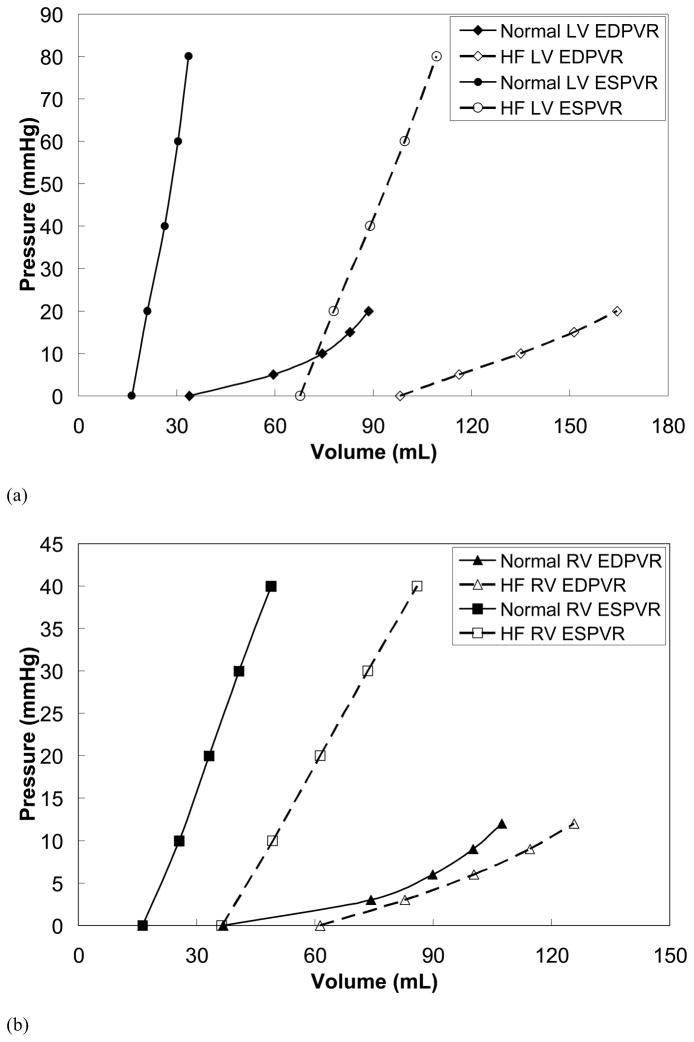
The EDPVR and ESPVR were generated using the validated FE models, and are shown in Figure 6. The induction of cardiomyopathy caused both the LV and RV to dilate significantly, which can be seen as rightward shifts of the EDPVR and ESPVR, shown in Figure 6. In addition, the diastolic compliance of the myocardium decreased as a result of the dilation. This is indicated by the increased slope of the EDPVR, and an increase in the passive stiffness parameter, C, described in the Methods section.

Figure 6.

(a) The EDPVR and ESPVR are shown for the LV of the normal and cardiomyopathy cases. (b) The EDPVR and ESPVR are shown for the RV of the normal and cardiomyopathy cases. The curves are shifted to the right due to CHF. This effect is more pronounced in the LV.

The slope of the ESPVR in the cardiomyopathy case decreased in both the LV and RV, relative to the healthy case. For the LV, E_ES,LV decreased from 4.96 mmHg/mL to 1.91 mmHg/mL. For the RV, E_ES,RV decreased from 1.24 mmHg/mL to 0.81 mmHg/mL. The intercept of the LV, V_0,LV, was found to nearly quadruple from 17.16 mL to 67.78 mL, for the healthy and cardiomyopathy cases, respectively. The intercept for the RV, V_0,RV, was found to nearly double from 16.82 mL to 36.65 mL. This is due to the significant dilation. It should be noted that the fit of the experimental data to the linear equation was in good agreement (R² > 0.9919 for the healthy case and R² > 0.9996 for the HF case).

The Starling relationship was generated using the circulatory system model, and is shown in Figure 7. The dilated heart shows an 18% decrease in stroke volume, leading to a downward shift of the Starling curve. This implies that the dilated heart is unable to pump as much blood into the body as the normal heart for a given EDP.

Figure 7.

The Starling relationship is shown for the normal and cardiomyopathy cases. It can be seen that the pump function is decreased due to CHF.

3.5 Myofiber Stress Distributions

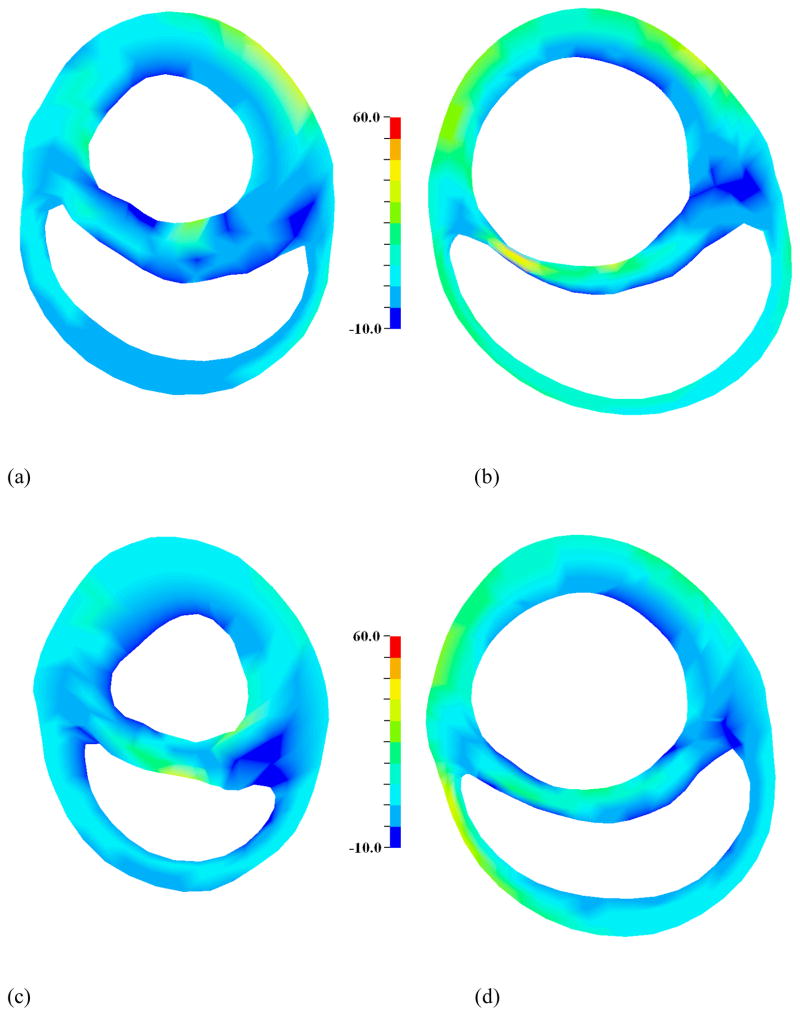
It was observed from the FE simulations that the average stress in the myofiber direction increased from the normal case to the cardiomyopathy case, as shown in Table 3. Stress distributions in the myocardial wall are reported at short-axis slices taken 9 mm and 33 mm below the base, shown in Figures 8 and 9. It can be seen that the stress is elevated globally in the cardiomyopathy case, relative to the normal case, but the stress is elevated the most in the posterior wall of the heart and in the septum.

Table 3.

Comparison of average stress in the myofiber direction, at end-diastole and end-systole, for the normal and cardiomyopathy cases based on pressures taken at time of MRI. It should be noted that the volume average of the myofiber stress was taken over all of the elements defined in each of the regions.

	Average ED fiber stress (kPa)		Average ES fiber stress (kPa)
	Normal	CHF	Normal	CHF
LV free wall	1.10 ± 0.59	2.21 ± 0.76	14.5 ± 6.40	19.9 ± 7.69
RV free wall	0.80 ± 0.43	2.81 ± 1.45	13.4 ± 6.01	18.1 ± 8.52
Septum	1.26 ± 0.75	1.61 ± 0.94	10.5 ± 6.21	15.2 ± 8.78

Values are reported as Mean ± SD.

Figure 8.

Stress in the myofiber direction at end-diastole for slices taken 10 mm below the base for (a) normal and (b) CHF, and 25 mm below the base for (c) normal and (d) CHF. Stress is elevated in the CHF case, relative to normal. Scale bar is in kPa. It should be noted that stress is calculated as constant within each element and then smoothed for the graphical presentation.

Figure 9.

Stress in the myofiber direction at end-systole for slices taken 10 mm below the base for (a) normal and (b) CHF, and 25 mm below the base for (c) normal and (d) CHF. Stress is elevated in the CHF case, relative to normal. Scale bar is in kPa. It should be noted that stress is calculated as constant within each element and then smoothed for the graphical presentation.

4. Discussion

A computationally efficient method for weakly coupling a biventricular FE model and lumped parameter model was developed and tested on animal-specific models of a normal canine and a canine with dilated cardiomyopathy. There was good agreement between the model simulations and experimentally measured volumes for both the normal and diseased case. The biventricular FE model and circulatory model were found to be in good agreement for a state of elevated heart rate, which was not directly measured during experiments. This indicates that the coupling scheme is able to represent the ventricular response over a range of physiological states.

One of the advantages of this approach is the relatively short total run times of the simulations. Once biventricular mechanics have been characterized with the FE models, via the pressure-volume relationships, this information can be used directly in the circulatory system model, which takes only minutes to run. This is mainly due to the fact that the FE simulations are set up to model only the end-diastolic and end-systolic states. Using this information, the circulatory model is able to simulate the entire cardiac cycle in a short period of time. Other studies have reported simulation times that take on the order of 100 hours (Kerckhoffs et al. 2007b), due to the fully coupled nature of the model. These long run times would make it extremely cumbersome to evaluate multiple simulations during an optimization. We have utilized a computationally efficient finite element formulation in previous optimization studies in which we determined the contractile properties of myocardium in animal-specific models of anteroapical and posterobasal infarction (Sun et al. 2009, Wenk et al. 2011).

In the present study, there is no need to assume a non-physiological preload (McLeod 1966), which allows us to capture the nonlinear effects of the ventricular mechanics. The lumped parameter model ensures that the pressure and volume changes in the circulatory system are properly coupled and conserve the total system volume. Once a particular state of interest is calculated with the circulatory system model, these pressures can be passed back to the FE model in order to calculate the stress and strain in the myocardial wall.

It can be seen from the results that the diastolic compliance decreases due to CHF (i.e., the wall becomes stiffer). As the heart dilates it becomes more difficult to fill, as evidenced by the increase in the passive stiffness parameter, C. Increased wall stiffness due to CHF has also been found in experimental studies by Wu et al. (2002) and Nagueh et al. (2004). In this case, canines underwent rapid pacing to induce dilated cardiomyopothy, similar to the present study, which causes myocardial stiffening, which were modulated by altered Titin expression. At sarcomere lengths comparable to those computed in the present study, the passive stiffness was increased by 5–6 times.

During the systolic phase of the cardiac cycle the strength of contraction is weaker in the LV due to CHF. The values of E_ES and V₀ are in close agreement with those found in experimental measurements with canines (Maughan et al. 1979, Maughan et al. 1985). Weaker contraction is indicated by a decrease in the active contraction parameter, T_max, as well as a decrease in E_ES. This is a primary characteristic of CHF (Gorman et al. 2004, Potter et al. 2007). As the heart dilates further, and myofiber stress increases, this will lead to further dysfunction of the contracting myocytes until the heart is no longer able to pump enough blood to the body to maintain even a resting metabolic state. As the heart becomes weaker, higher end-diastolic pressures are required to produce a stroke volume that is equivalent to that in a healthy heart, as seen in Figure 7.

The magnitude of average myofiber stress calculated in the current study is in close agreement with values calculated for canine ventricles in other FE studies. In Guccione et al. (1995b), an FE model of a healthy canine was validated with experimental strain at mid-ventricle. The average ED myofiber stress was found to be approximately 1.5 kPa, compared to 1.10 ± 0.59 kPa in the current study. In Kerckhoffs et al. (2010), stress was reported for a healthy baseline and dilated canine heart. The average ES myofiber stress in the healthy heart was approximately 12 ± 5.3 kPa, compared to 14.5 ± 6.4 kPa in the current study, and was approximately 20.4 ± 9.9 kPa in the dilated heart, compared to 19.9 ± 7.69 kPa in the current study. In both studies, the stress in the myofiber direction was found to be elevated in the entire heart due to cardiomyopathy.

There are a few limitations associated with the current study. Only a single animal data set was used to develop the coupled FE/circulatory system model. Focused animal experiments are needed to confirm the results at several physiological states, as well as multiple times during the cardiac cycle. Only cine MRI data was available for this study. In the future, tagged MRI will be obtained to further validate the FE models by matching the predicted deformation to experimentally measured strains. The one-way coupling may not be as accurate as a fully-coupled model. This is primarily due to the fact that the coupling does not happen at every time step. Both fully-coupled and weakly coupled methods will be bounded by the same EDPVR and ESPVR, which means the ED and ES states should be in close agreement. However, the exact path of the pressure-volume loop may differ between the two methods for a given heart beat. Depending on the application, the tradeoff of fast runtimes could outweigh the need for higher accuracy, especially when conducting computationally intensive optimization simulations. The active constitutive model does not contain strain rate dependence. The current model represents the steady state response at ES. There are numerous finite element models of regional ventricular mechanics that have focused only on the LV end-diastole and end-systole, which have been sufficient to quantify the efficacy of novel surgical procedures or medical devices for treating dilated or ischemic cardiomyopathy or heart failure (Dang et al. 2005a, Walker et al. 2005a, Sun et al. 2009, Wenk et al. 2011). The purpose of the present work is to describe a methodology for adding the RV, and ensuring volume conservation between ventricles. However, we are in the process of adding strain rate dependence in a new LV material model that is being developed in LS-DYNA.

In summary, the coupling approach presented in this work showed good agreement with experimentally measured pressures and volumes. The one-way scheme was able to characterize both a normal and dilated cardiomyopathy heart, in a relatively shorter runtime. In the future, this approach will be used to evaluate the effects of a passive constraint device, which wraps around the heart, to prevent dilation and help remodel the heart towards a normal state. It is anticipated that the fast runtime will allow for computationally efficient optimization of the key attributes of the constraint device.

Table 1b.

Experimentally determined hemodynamic data taken at the time of MRI, which was used to calibrate the cardiomyopathy FE and circulatory system models.

	EDP (mmHg)	ESP (mmHg)	EDV (mL)	ESV (mL)	SV (mL)
LV	8	66	127.7	102.4	25.3
RV	5	26	93.8	68.5	25.3

LV, Left ventricle; RV, Right ventricle; EDP, End-diastolic pressure; ESP, End-systolic pressure; EDV, End-diastolic volume; ESV, End-systolic volume; SV, Stroke volume