DNA looping by FokI: the impact of twisting and bending rigidity on protein-induced looping dynamics

Abstract

Protein-induced DNA looping is crucial for many genetic processes such as transcription, gene regulation and DNA replication. Here, we use tethered-particle motion to examine the impact of DNA bending and twisting rigidity on loop capture and release, using the restriction endonuclease FokI as a test system. To cleave DNA efficiently, FokI bridges two copies of an asymmetric sequence, invariably aligning the sites in parallel. On account of the fixed alignment, the topology of the DNA loop is set by the orientation of the sites along the DNA. We show that both the separation of the FokI sites and their orientation, altering, respectively, the twisting and the bending of the DNA needed to juxtapose the sites, have profound effects on the dynamics of the looping interaction. Surprisingly, the presence of a nick within the loop does not affect the observed rigidity of the DNA. In contrast, the introduction of a 4-nt gap fully relaxes all of the torque present in the system but does not necessarily enhance loop stability. FokI therefore employs torque to stabilise its DNA-looping interaction by acting as a ‘torsional’ catch bond.

INTRODUCTION

In many genetic processes, DNA-binding proteins interact with multiple target sites on the DNA, trapping the DNA between the specific sites as loops (1). Such processes include DNA replication and repair, site-specific recombination, transcription regulation and DNA cleavage by many restriction endonucleases (REases) (2,3). The ability of proteins to bridge two sites depends on the amount of elastic energy necessary to form a loop in the DNA. When the two recognition sites are spaced by an integral number of full helical turns, only the bending energy of the DNA plays a role. However, when one of the two sites is shifted away from the other by part of a helical turn, the twisting energy of the DNA loop also has to be paid. The ability to loop DNA is thus influenced by its lateral and torsional stiffness, which in turn is influenced by the length of DNA between the target sites (4). The latter becomes an increasingly important factor when the sites are separated by less than a persistence length (1,4).

DNA looping has been studied extensively by biochemical methods (2,5,6) but in recent years, biophysical single-molecule techniques have also become available to study protein–DNA dynamics (7–11). One method has proved to be especially useful for investigating DNA looping is tethered-particle motion (TPM) (12–16). In a typical TPM setup, a linear DNA with two copies of the target sequence is immobilized at one end on a glass slide, while a polystyrene bead is covalently attached to the other end of the DNA. The movement of the bead, governed by Brownian motion, is monitored using a CCD camera attached to a microscope: up to 50 beads can be tracked simultaneously (14). Upon addition of a protein that interacts with both target sites, the effective tether length is shortened due to DNA looping, restricting the Brownian motion of the bead (12,15). Recent advances in this technique allow the observation and dissection of every step in the looping pathway of proteins: protein association, loop capture, loop release and protein dissociation (14,16).

Among the best systems to study DNA looping are the Type II REases, as many of these have to bind two copies of their recognition sequence before they become fully active (2,3,17,18). While most Type II REases recognise palindromic sequences, a subset of these enzymes, the Type IIS systems, recognise non-palindromic sequences that possess a directionality. A synaptic complex with two asymmetric sites held together in parallel with each other is distinctly different from that with the sites in an anti-parallel arrangement (19). No such distinction between parallel and anti-parallel alignments can be made with palindromic sites. Perhaps the best known of the Type IIS endonucleases is FokI, the subject of the preceding paper (19). As noted in that paper (19 and references therein), FokI exists in solution as a monomer and is composed of two domains: an N-terminal DNA-binding domain that makes all of the contacts to its 5-bp recognition sequence; and a C-terminal catalytic domain that cuts the DNA on one side of the asymmetric site, 9 and 13 nt away from the site in top and bottom strands, respectively. The catalytic domain contains only one active centre so, to cut both strands, the monomer at the recognition site has to recruit a second monomer to form a dimer (17,20). Dimerization occurs through the catalytic domains to yield a unit with two active sites that each cleave one strand of the DNA (20,21): the monomer bound to the recognition site cuts the bottom strand while the second monomer cuts the top strand (22). However, the enzyme at the cognate site has to engage its target phosphodiester bond 13 nt away from the recognition sequence before it can associate with the second monomer (23). The latter can come in trans, bound to a separate DNA molecule or more favourably in cis, bound to another site on the same molecule (17,19,24). In both cases, the two DNA sites are bridged by the protein dimer not at the recognition sequences but rather at the cleavage locus downstream of one of the sites.

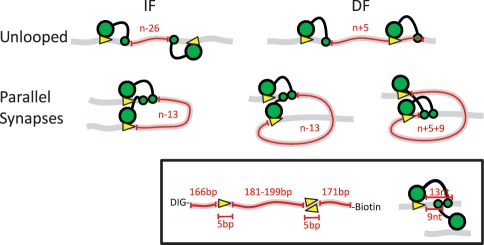
On a DNA with two FokI sites, the assembly of the FokI dimer spanning the sites in cis traps the intervening DNA in a loop. The rate-limiting step in trapping the DNA loop is the loop formation step itself; i.e. the juxtaposition and the association of the protein monomers at the individual sites (24). The stability of the loop is governed by the protein–protein interaction, and this was shown to vary cyclically with a periodicity roughly matching the helical repeat of DNA (17). The non-palindromic nature of the FokI recognition site means that two sites in cis can be in either inverted (IF) or directly repeated (DF) orientations along the DNA contour (Figure 1). (Our notation also records the number of base pairs between the sites: namely IF181 denotes a DNA with two inversely oriented FokI sites 181 bp apart: see Materials and Methods). The accompanying paper in this issue shows that in either arrangement, the two sites become juxtaposed in a parallel alignment (19), resulting in a unique DNA loop topology for each orientation: a 180° loop for the IF arrangement and a 360° loop for the DF case [Figure 1; see also Figure 1 in (19), the preceding paper].

Figure 1.

Schematic representation of the possible orientations of two recognition sites for FokI in cis and the resulting loop topologies. The FokI restriction endonuclease recognizes a 5-bp non-palindromic sequence and cuts 9 and 13-nt downstream of the site, in top and bottom strands, respectively (insert). The DNA molecules are shown as grey ribbons with two recognition sites for FokI (yellow arrowheads) in cis, in either inverted (IF) or directly repeated (DF) orientations (as indicated by the direction of the arrowheads): ‘n’ is the absolute distance in base pairs between the recognition sites, measured from the base pairs immediately following the upstream recognition site to that immediately before the downstream. The FokI monomer is shown as a large green circle (the DNA recognition domain bound to its target sequence) connected to a small green circle (the catalytic domain that before dimerization binds to the scissile bond 13 nt away). Hence, in the unlooped state, the length of DNA between the two catalytic domains (noted in red) is n − 26 bp in the IF construct and n + 5 bp in the DF construct: these lengths denote the length of DNA involved in the loop capture process (i.e. the ‘loop size’ for capture). When the catalytic domains of two monomers on the DNA associate to the dimer, the sites become aligned in a parallel arrangement, giving rise to two different loop topologies: a DNA loop with a 180° bend from the IF DNA (left), or a more extended loop with a 360° bend from the DF DNA (right: note that the latter has two alternative configurations, depending on whether the dimer is assembled at the upstream or the downstream recognition site). In each case, the number of base pairs trapped between the two protein monomers (noted in red) differs from the absolute separation of the sites (n) as shown: the lengths of the trapped segments correspond to ‘loop size’ for the release process.

DNA-looping proteins that recognise rotationally symmetric sites are unable to distinguish between parallel and anti-parallel synapses so they can potentially trap either 180° or 360° loops, (8,25,26). Therefore, the FokI system with its asymmetric sites gives us a significant advantage over all of the previous single molecule experiments analysing proteins recognizing symmetrical sites. In those cases, the different DNA loop topologies are generated purely as a result of stochastic processes waiting to happen (15,27). Here, we examine the influences of both DNA bending and twisting rigidities on protein-induced looping dynamics. The twisting rigidity was examined by varying the DNA loop size, while keeping the site orientation fixed, thereby changing the angle between the two recognition sites. The bending rigidity was examined by changing the relative orientation of the two sites so as to produce either a simple 180° bend or a convoluted 360° loop.

MATERIALS AND METHODS

Proteins and plasmids

The FokI endonuclease was purified and its concentration assessed as described before (17,19). The BbvCI restriction enzyme and its variants that cut only top or bottom strands, nt.BbvCI and nb.BbvCI, respectively (28), were gifts from G. Wilson (New England Biolabs). All other enzymes were purchased from New England Biolabs and used as advised.

The current study employed a range of plasmids with two FokI sites, in either head-to-head (inverted: IF) or head-to-tail (directly repeated: DF) orientations (17,19), with varied lengths of DNA between the sites. The plasmids are named pIF and pDF, to denote the relative orientation of the sites, followed by an integer, to record the number of base pairs between the two recognition sequences (Figure 1). For example, a plasmid with inverted sites 190 bp apart is named pIF190. The plasmids pIF181–pIF199 and pDF190 were described before, as was also an isogenic plasmid with one FokI site, pF1 (17,19). Similar procedures were used to create further plasmids with two FokI sites in directly repeated orientation, pDF181 and pDF185 (A. Welsh and L. Catto, personal communication). For experiments on nicked DNA, selected plasmids from the pIF and pDF series, with inter-site spacings of 181, 185 or 190 bp, were modified by introducing a BbvCI site between the FokI sites without altering their separation: the segment 127–133 bp downstream of the first FokI site was converted to the recognition sequence for BbvCI. These are named as before but with the subscript n following the name: i.e. pIF190_n. For experiments on gapped DNA, the plasmids carrying the BbvCI site were modified further by replacing the segment 119–123 bp downstream of the first FokI site with a BsmAI site, again leaving unaltered the distance between the FokI sites. This time an identifying letter g is added to the original name: i.e. pIF190_g. In all cases, the plasmids carried the same flanking sequences at each FokI site, for ≥5 bp upstream of the site and for all the downstream sequence to ≥6 bp beyond the cleavage points: changes to the intervening sequence were also kept to a minimum.

DNA constructs

To generate the linear constructs, the region of the above plasmids that encompassed the FokI recognition site(s) was amplified using forward and reverse primers tagged at their 5′ ends with either a biotin or DIG label. These constructs are named from the parental plasmids: i.e. pIF190 generates the PCR product IF190, an intact DNA with two FokI sites in inverted orientation 190 bp apart, while pDF185_n yields (after cutting one strand at its BbvCI site: see below) DF185_n, a nicked DNA with directly repeated sites 185 bp apart. The constructs from both IF and DF series carried the two FokI sites at fixed positions 166 and 170 bp from their proximal ends, approximately equidistant from the midpoint of the DNA, and had overall lengths of 528–546 bp depending on the inter-site spacing. PCR products were purified as before (19).

To prepare the nicked constructs, the top strand of the BbvCI site in each of the relevant PCR products was cut using the nt.BbvCI enzyme: the nick follows nucleotide 128 downstream from the first FokI site (i.e. from 53 to 62 nt upstream of the second FokI site, depending on the inter-site separation). To confirm that the material had been nicked, an aliquot of the DNA that had been treated with nt.BbvCI was digested for 2 h at 37°C with nb.BbvCI, which cuts only the bottom strand (28). Analysis of this aliquot by electrophoresis through agarose showed that all of the DNA now carried a double-strand break at the BbvCI site (Supplementary Figure S1A). Further confirmation that the nicking reaction had proceeded to completion was obtained during the course of the TPM experiments: the addition of nb.BbvCI to the slide carrying a nicked DNA tether resulted in the release of the bead while its addition to an intact DNA failed to release the bead.

To create the gapped constructs, the PCR products were digested successively with the nt.BbvCI and Nt.BsmAI enzymes, each for 2 h at 37°C. Both enzymes cleave only the top strand of their respective recognition sites and excise a 4-nt segment from this strand, to leave a gap between positions 125–129 bp downstream of the first FokI site. After purification, the product was heated to 65°C for 30 min to remove the 4-nt segment. The requisite gap spans part of the BbvCI recognition site, so the gapped DNA ought to be resistant to cleavage by BbvCI. An aliquot of the DNA that had been treated with both nt.BbvCI and nt.BsmAI was therefore subjected to a reaction with native BbvCI, in parallel with a control sample of intact DNA. BbvCI cleaved the intact DNA but failed to cleave the DNA that had been processed with both nicking enzymes, indicating that the latter carried the desired gap (Supplementary Figure S1B). If either one of the nicking enzymes had failed, BbvCI would still have been able to cleave the DNA.

Single-molecule assay and analysis

We studied the dynamics of protein induced looping by TPM. In these experiments, the DIG label at one end of each construct was linked to a glass cover slip coated with anti-DIG antibodies (Roche), immobilizing the DNA molecules. The remaining free end was attached via its biotin label to a 440-nm streptavidin-coated bead (Kisker Biotechnology). The surface of the glass was coated with a layer of α-casein to prevent sticking of the DNA, proteins and beads to the glass (10). All TPM studies apart from the bead release assays (Supplementary Figure S2) were undertaken in 20 mM Tris–acetate (pH 7.9), 50 mM potassium acetate, 2 mM CaCl₂ 1 mM DTT, 100 µg ml⁻¹ BSA and 100 µg ml⁻¹ α-casein [CC-buffer (19)]. To observe DNA cleavage by bead release, the CaCl₂ was replaced with 10 mM magnesium acetate (M-buffer). All TPM experiments reported in this study were conducted at room temperature (20°C).

All data acquisition and processing was done using a self written-image acquisition and analysis programme, described in detail elsewhere (14). The motions of up to 50 beads were imaged using a CCD camera at a frame rate of 50 Hz. The measurements were done on a Nikon TI-e inverted microscope (100× objective), using the Nikon perfect focus feature to prevent the sample from drifting out of focus during a measurement, which typically lasted for 30–60 min. The positions of the beads in the sample were obtained from the images in real time, allowing for on-the-spot analysis. After a measurement was complete, the root mean square motion (RMS) of each bead was calculated from the expression 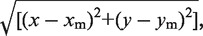where x_m and y_m are the mean values averaged over 100 frames. The histogram of this motion was fitted to a double Gaussian to find the RMS values of the looped and unlooped state [see Figure 5 in the accompanying paper (19)]. The intersection of the two Gaussians sets a threshold for the RMS data and the dwell times of both states were extracted (Figure 2A).

Figure 5.

DNA bending. Looping dynamics were measured for three DF constructs with inter-site spacings of 181, 185 and 190 bp and compared to their IF counterparts: both loop capture (A) and loop release (B) rates are plotted as a function of the number of base pairs between the recognition sites. In both panels, rates for the DF constructs are shown in dark grey and their IF counterparts in light grey: error bars indicate SEMs. In (A), the histograms for the loop capture rates demonstrate that the IF and DF substrates are out of phase with each other. Loop capture rates for IF181 and IF190 are both slow, while that for IF185 is fast while the DF constructs display the reverse behaviour, fast capture for DF181 and DF190 and slow for DF185. In contrast, the loop release rates in (B) show the same trends for the IF and the DF substrates. In both the IF and the DF constructs, the 185-bp spacing gave a faster loop release rate than either the 181- or the 190-bp site separations.

Figure 2.

TPM experiments in Ca²⁺. (A) The RMS motions for a single IF190 tether (inverted FokI sites 190 bp apart) in the presence of 5 nM FokI is plotted as a function of time (black trace). The trace shows clear dynamics between an unlooped (high RMS) and a looped (low RMS) state. To find the RMS value of these two states, a threshold was set to divide the data into the two states (step function shown in red) and the dwell times in each state extracted (marked by black arrows). (B) A plot of the cumulative distribution function of the dwell times extracted from the trace in (A) (i.e. the probability of remaining in the looped or the unlooped state as a function of time). The red circles show the dwell times of the looped state and are fitted with a single exponent to obtain the loop release rate (the lifetime of the looped state is unaffected by the protein dissociation step since this has no impact on the RMS values). Since dwell times in the unlooped state are a combination of the protein associating with the recognition sites and the actual loop capture process, the dwell times show a bi-exponential behaviour and are fitted accordingly. The protein dissociation rate can be obtained, despite the fact that it does not give a signal in the RMS trace, by calculating the intersection of the two exponentials in the bi-exponential fit.

To obtain from the TPM experiments the kinetic rates for protein association, for loop capture, for loop release and for protein dissociation in a single measurement, the dwell times of the looped and unlooped states were fitted to exponential functions (Figure 2B). The dwell times for the looped state were fitted to a single exponent to yield directly the loop release rate, while the dwell times for the unlooped state were fitted to a double exponential to give the loop capture and protein association. Moreover, the protein dissociation rates can be extracted from the relative occurrence of association and loop capture (14). However, the theory to obtain all four rates was developed for a tetramer binding two recognition sites at the same time. In the current study, the loop is induced by the association of two DNA-bound monomers. Nevertheless, above a particular protein concentration (on the order of the K_d for the binding of the protein to a single individual site on the DNA), one of the two sites are occupied most of the time, which reduces the problem to just a single monomeric protein associating with the remaining free recognition site. This was found to be the case for the FokI concentrations used in this study, by observing the equilibrium distribution as described in (16). [The K_d for the initial binding FokI to DNA containing a single FokI site is ∼4 nM (24).]

RESULTS

Loop dynamics

Before we studied the loop topology induced by the assembly of the FokI dimer and its effect on the kinetics of protein-induced looping, we first demonstrated that the system is active in our TPM set-up. We examined the cleavage activity of FokI (in a buffer containing Mg²⁺) by recording bead release from tethers formed by DNA substrates carrying one or two FokI sites. This can only occur if both top and bottom strands of at least one site are cut by the protein and that the protein lets go of the DNA ends (14). We observed no systematic variation in bead release rates for substrates with inverted (IF) or directly repeated (DF) FokI sites, regardless of inter-site spacing (∼2 × 10⁻² s⁻¹, Supplementary Figure S2). Previously, products from the reactions of FokI on all of the plasmids in the pIF series (pIF181–pIF199) had been analysed by gel electrophoresis: no significant differences in cleavage rates were observed, in accord with the bead release assay (17). However, the release rate from cutting a DNA with only one FokI site was much slower (∼1 × 10⁻³ s⁻¹) than that from any of the two-site substrates. Efficient cleavage thus requires protein-induced DNA looping, in agreement with previous biochemical data (2,24).

To prevent hydrolysis but still allow for DNA-binding dynamics and protein–protein interactions, we replaced the Mg²⁺ in the buffer with Ca²⁺. The Brownian motion, restricted by the DNA tether, was recorded over time and the RMS motion over ∼0.5 s was calculated. A typical record is shown in Figure 2A: this particular example was with an IF construct carrying 190 bp between the sites. A threshold value was set in the RMS data and values above and below the threshold assigned, respectively, to the unlooped and looped states, which in turn yielded the dwell times in both states. The dwell times obtained by this procedure were subsequently fitted to exponential functions (Figure 2B) as described before (14).

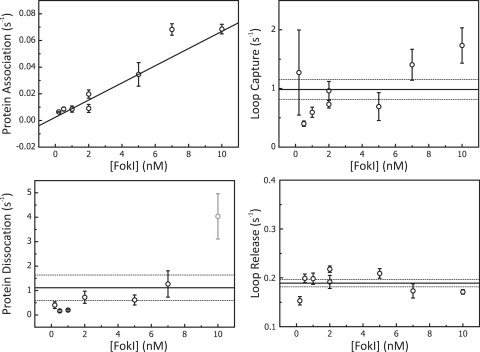
With this method, it is possible to evaluate from a single measurement rates for all four processes in protein-induced loop formation (protein association, loop capture, loop release and protein dissociation) and to characterise them as a function of the protein concentration (representative data from one DNA construct, IF190, is shown in Figure 3). The protein association rate that we find, 6 ± 1 × 10⁶ M⁻¹ s⁻¹, is a factor of 10 below the rates previously reported by TPM measurements on other REases (14,16). We find a protein dissociation rate of 1.1 ± 0.5 s⁻¹, and rates for loop capture and loop release on IF190 of 1.0 ± 0.2 s⁻¹ and 0.19 ± 0.01 s⁻¹, respectively, all independent of protein concentration (Figure 3, N > 25 DNA molecules). FokI thus captures loops and dissociates from this DNA more rapidly than any REase studied previously by TPM (14,16). The resulting K_d is, however, higher than obtained by biochemical studies. Such systematic difference was also reported for other REases studied by TPM (14,16).

Figure 3.

Concentration dependence of kinetic rates determined by TPM. Protein association, dissociation, loop capture and loop release rates were determined at various concentrations of FokI (0.2, 0.5, 1, 2, 5, 7 and 10 nM) on a DNA construct containing two FokI sites in inverted orientation separated by 190 bp (IF190). Each data point represents the average value from at least 25 DNA molecules. Error bars on the data points denote the SEM. The graphs, apart from that for protein association, show the average rate across the range of FokI concentrations (solid black line) and the SEs (the dotted lines above and below the averages). Rates calculated for protein dissociation (1.1 ± 0.5 s⁻¹), loop capture (1.0 ± 0.2 s⁻¹) and loop release (0.19 ± 0.01 s⁻¹) all showed no systematic variation with the enzyme concentration. In contrast, rates calculated for protein association varied linearly with FokI concentrations to yield from the slope a second order rate constant (6 ± 1 × 10⁶ M⁻¹ s⁻¹). Above 8 nM FokI, DNA looping between non-specific sequences, i.e. DNA condensation, was sometimes observed, making it hard to extract certain rates (namely the grey data point for the protein dissociation rate).

Next, we set out to study the effects of DNA twisting rigidity on the looping dynamics. For these experiments, we used the IF constructs, which were shown by FRET to form loops with the 180° topology (19), and varied the distance between the two recognition sites. The lengths of DNA between the recognition sites, the values for n (Figure 1), were converted into actual loop sizes for the loop capture and for the loop release events by the procedures shown in Figure 1. The loop capture and loop release rates, measured for each site separation essentially as above, were plotted as a function of the relevant loop size (Figure 4A and C, respectively). Both rates vary strongly with loop length. In previous studies, DNA cleavage reactions on the supercoiled form of the plasmid pIF185 at 37°C had yielded a loop capture rate of 3.0 s⁻¹ (24), while the same inter-site spacing gave here a capture rate of 2.2 s⁻¹ at 20°C, in strikingly good agreement considering the temperature difference and the supercoiled nature of the plasmid substrate. [The 185-bp inter-site separation is recorded in Figure 3 as a loop capture size of 159 bp (from n − 26; Figure 1).]

Figure 4.

DNA twisting. The loop capture and release rates from the IF series of constructs are plotted as functions of: (i) the loop size [(A) and (C), respectively]; (ii) the change in torque [(B) and (D)]. Black circles denote data from the intact DNA substrates; blue triangles, the nicked IF_n constructs; green squares, the gapped IF_g constructs. For the loop release rates, the data is separated for positive and negative torque (filled and unfilled circles, respectively). The variations of the rates with torque (C and D) are fitted with an Arrhenius law: the best fits are shown as red lines in all four panels. Introducing a nick between the sites did not release any torque within the loop: the IF_n constructs (blue triangles) behaved like the intact constructs. But, the introduction of a gap between the two sites released all torque effects: the rates with the IF_g substrates were invariant with inter-site spacing [green squares (A) and (C), grey band shows the confidence intervals of a linear fit]. This data shows that loop capture is fastest when there is zero torque [grey band in (A) and (B)], but loop release rates are not necessarily minimized by the absence of torque [grey band in (C) and (D)]: the latter indicates that a limited amount of negative torque stabilizes the protein–protein synapse. Moreover, it also explains why the capture and release rates are out of phase with respect to the loop size [(A) and (C)]. The arrow in (C) marks the loop size at which there is zero torque on the protein–protein interface (see text).

To capture a DNA loop, the catalytic domains of two FokI monomers need to be aligned. However, due to the helical periodicity of the DNA, the two domains might not be on the same side of the DNA. Therefore, aligning the catalytic domains requires the DNA to be torqued by an angle θ. This angle is set by the rotation required, in addition to the integral number of full helical turns in the DNA between the sites, to bring the two sites into the requisite alignment. Thus, it is directly related to 2π times the fraction of a full helical turn that remains after dividing the loop length (L) by the helical pitch (HP). The HP was independently determined by a global fit to all the capture and release rates, which gave a value of 10.6 ± 0.1 bp per helical turn (Supplementary Figure S3), in good agreement with many previous studies (29). The amount of torque (τ) that builds up in the loop due to twisting by the angle θ can be then calculated using the determined HP, if we assume that the twist is distributed uniformly along the DNA with a certain twisting rigidity [C = 300 pN nm² (30)]. In addition, we add a preferred docking angle (ξ) to the twisting angle (the independent variable) because the catalytic domains might dock with a well defined angle between the interacting proteins. The resulting equation for the torque on the protein-induced DNA loop is then given by:

(1)

Figure 4B shows the measured capture rates versus the calculated torques fitted to the Arrhenius equation [k = k₀ e^(ΔG/KT)]. The good fit indicates that the capture rate represents a single step across an energy barrier. The height of the energy barrier is determined by the amount of torque multiplied by an angle (ΔG = φ × τ), where the angle represents the position of the energy barrier with respect to the unlooped state, when plotting the potential landscape as a function of torque. This torque angle was found to be φ_capture = 0.34 ± 0.06 rad. The fit gives a preferred docking angle for loop capture (ξ) of zero rad, indicating that the two catalytic domains dock straight onto each other. Finally, we find that the loop capture rate with zero torque on the DNA is 1.9 ± 0.2 s⁻¹ (k₀), while the capture rate with maximum torque is 0.6 ± 0.1 s⁻¹, a 3-fold decrease.

Unlike loop capture, where the torque acts directly on the DNA to affect the rate at which the two binding sites come into proper alignment, the loop release rate is influenced mainly by the torque felt at the protein dimer interface, since loop stability is determined by the protein–protein interaction. The measured release rates were analysed as a function of loop length, which was subsequently converted to torque as above. Even though the DNA itself responds identically to small changes in either positive or negative torque (30), the protein–protein interface may not. Instead, positive and negative torque may have different effects on the stability of the protein-protein synapse, depending on the rotational symmetry of the protein dimer relative to the direction of the twist induced by the external torque. Therefore, the release rates for over- and under-wound DNA were treated separately and fitted to individual Arrhenius equations (Figure 4D). The plot shows clearly that negative and positive torque have different effects on the stability of the looped DNA complex, and this is reflected in the parameters of the Arrhenius fits. The amount of twist that the protein can handle before it is forced from the looped to the unlooped state is obtained from the fit as φ_release+ = 0.35 ± 0.07 rad for positive torque and as φ_release− = 0.5 ± 0.1 rad for negative torque, with a preferred docking angle for release (ξ) of ∼1.8 ± 0.1 rad. The clear difference shows that the distance to the energy barriers for unlooping are indeed not symmetric with regard to the direction of the experienced torque. The protein–protein synapse can handle negative torque better than positive torque.

Dynamics without torque

According to the Arrhenius fits and from an energetic point of view, the fastest loop capture will occur when there is no torque on the DNA, and this should also result in the most stable loop (the lowest release rate). Yet, this appears not to be the case as the dotted line drawn through a local maximum in the loop capture rates (Figure 4A) intersects with the curve for the loop release rates (Figure 4C) not at the expected minimum but instead at a point well above the minimum, almost halfway to the next maximum. To solve this paradox, we identified how the system behaves in the absence of torque. Using three substrates from the IF series with different inter-site spacings, we introduced into each first a nick in the DNA between the FokI sites and subsequently a 4-nt gap, to allow the DNA to swivel and release any torsional effects. The nicked and the gapped constructs were tested to confirm that they were indeed nicked or gapped as anticipated (Supplementary Figure S1).

The insertion of a nick had, surprisingly, no effect on either the loop capture or the loop release rates of any of the three IF constructs tested: they were all the same as their equivalent intact counterparts (Figure 4A and C, blue data points). A nicked form of a DF species, DF185_n, was also compared to its intact counterpart: again, loop capture and release rates with the nicked DNA were indistinguishable from those on the same DNA in its intact state. On the other hand, the introduction of a gap removed the periodical dependencies of both loop capture and release rates on loop size, and gave instead invariant dependencies that fitted to horizontal lines (grey bands in Figure 4A and C: capture and release rates at 1.52 ± 0.12 s⁻¹ and 0.43 ± 0.03 s⁻¹, respectively). On a gapped DNA with directly repeated sites, DF190_g, the rates for both loop capture and release matched, within experimental limits, the invariant capture and release rates observed across the gapped IF series, even though the looping dynamics with the intact DF190 DNA differed considerably from those with the intact IF substrate at the same inter-site spacing (see below, Figure 5).

As expected, the capture rate for DNA without torsional constraint lies close to the capture rate on the intact DNA when there are an integral number of helical turns between the two sites, i.e. at the ideal spacing where there is no torque on the DNA as the synapse is formed (dotted line in Figure 4A). The same effect was found for the DF constructs. However, the uniform release rates for the gapped DNA constructs, regardless of the orientation of the sites, do not correspond to the expected minimum rate. Instead, the release rates on the gapped DNA lie between the minimal and maximal rates found for the intact DNA. This result thus shows that the absence of torque actually decreases the stability of the looped state.

Next, we sought to deduce the loop size at which there is zero torque on the protein–protein synapse. From Figure 4C, this happens at the intersection between the grey band and the Arrhenius fit (in red) on either the left or the right of the local minimum. Strikingly, the dotted line drawn through the zero torque point for loop capture, the local maximum in the capture rates in Figure 4A, crosses the right-hand intersection between the rates on the gapped and the rates on the intact DNA (marked by the arrow in Figure 4C). Therefore, the arrow in Figure 4C marks the loop size at which there is zero torque on the protein–protein interface. This zero torque point is ∼3 bp away from the adjacent minimum in the observed release rates. This matches the phase shift ξ of 1.8 rad related to the preferred docking angle found for the relapse of the synapse which in fact equals ∼3 bp (10.6 bp turn⁻¹ = 2π rad). All in all, these results suggest that the protein–protein interaction is stabilized by applying some negative torque to the synapse.

With these results, we can now determine directly how much positive and negative torque the protein complex is able to handle in a looped configuration, by tracing the change in torque along the contours of the Arrhenius fits in Figure 4D. When the system is in the looped state with zero torque (arrow Figure 4C and grey band), it can handle a positive torque of ∼5 pN nm before the peak on the right of the zero torque point is reached. After that, it becomes energetically more favourable to release half a helical turn. If instead we apply a negative torque of ∼6 pN nm, the DNA loop is fastened into its most stable position, the adjacent minimum in the loop release rates. Twisting the protein complex even further, we find that the system can handle a total negative torque of ∼24 pN nm before it would be energetically more favourable to shorten the DNA loop by half a helical repeat and so reverse the sign of the torque.

Bending topology of DNA

Following the above analysis of the influence of the twisting rigidity on DNA looping, we now report on the role of DNA bending via alternative topologies (Figure 1). Here, we study the phase relationship of the capture and release rates between the IF and the DF constructs, with inverted and directly repeated recognition sites, respectively, as a function of the spacing between the sites. Loop capture and release rates were measured for three DF constructs varying in inter-site spacing by approximately one full helical turn, and compared to their IF counterparts (Figure 5).

The loop capture rates with the IF and DF constructs are out of phase with each other (Figure 5A): spacings that gave low capture rates with the IF species gave high rates with the DF forms, and vice versa. Hence, there should be a difference in loop size of (n + ½) helical turns between the two constructs. Due to the different orientations of the recognition sites, the catalytic domains of the FokI monomers at the cleavage loci on the DF constructs are 31 bp further apart prior to loop capture than on the IF constructs (Figure 1). However, these 31 bp add 3 helical turns (31/10.6) to the loop and thus do not explain the out-of-phase behaviour. The phase difference can, however, be explained by differences in loop topology. The DF construct forms the 360° DNA loop topology, which induces an additional half helical turn upon loop capture. In contrast, the 180° DNA loop topology captured by the IF construct does not induce any additional turns in the DNA. This difference in phase again confirms our previous findings (19) that FokI prefers a uniform recognition site alignment regardless of the orientation of the sites along the DNA.

In contrast to the out-of-phase capture rates, the release rates of the IF and DF loops are in phase with each other when plotted against inter-site spacing (Figure 5B): spacings that gave low high release rates with the IF constructs did likewise with the DF constructs. We therefore expect the difference in loop size between the IF and DF constructs to be an integral number of helical turns. The parallel 360° topology of the DF constructs can result in loop lengths that are either the same as that for the IF counterpart or 27 bp longer, depending on which of the two FokI sites the synapse is formed at (Figure 1). The difference in loop size therefore accounts for either zero or 2.5 extra helical turns. When added to the half helical turn due to the 360° topology, these alternate loops for the DF forms carry either 0.5 or 3 additional turns compared to the equivalent IF loop. The observed phase match of the release rates between the IF and DF constructs as a function of loop length thus suggests that FokI generally traps the longer of the alternate loops on the DF constructs. Though both configurations should be accessible, longer loops are energetically favoured over shorter loops, which probably accounts for the preference for FokI selecting the synapse that traps the longer loop size.

DISCUSSION

The ability of proteins to loop DNA is influenced by the bending and twisting rigidity of DNA. Several studies have examined the effect of twisting by varying the length of DNA between specific binding sites. Looping ability was shown to vary cyclically, with a periodicity corresponding to the helical repeat (3,17,27,31). These studies have so far focused on proteins that exist pre-assembled in solution and contain separate surfaces for binding each site on DNA (14,27,32). Here, we examine the restriction endonuclease FokI, which first binds as a monomer to an individual site with a high affinity (K_d ≈ 4 nM), before associating to a higher-order assembly with a lower affinity (K_d ≈ 100 nM), preferably in cis thus trapping a DNA loop (17,24). The dynamic nature of the FokI binding allowed us to investigate how torque on the DNA influences loop formation (the capture rate) and how torque on a protein–protein interface has an impact on its dissociation (the loop release rate). In both cases, the rates varied with the loop size, with a periodicity directly related to the helical repeat of the DNA (Figure 4). Converting the loop sizes to torques allowed us to examine the free energy needed for loop capture (ΔG ∼ 1.5kT, the maximal torque obtained from the Arrhenius fit). For comparison, we calculate the energy stored in the twisting of length L of our DNA molecule, given a twisting rigidity C of 300 pN nm² (30), as a function of the amount of twist (θ in radians) by a simple theoretical estimation,

(2)

For our constructs, this gives a ΔG of the same order of magnitude (∼6kT) as the experimental value. Previous studies on the Lac repressor showed a similar difference between measured and theoretical values of the free energy for looping. It was suggested that the difference might be due to contributions from different loop topologies and/or from the flexibility of the DNA or the protein (27). Here, however, we force the FokI system to adopt a unique topology by setting the orientation of the two recognition sites, which eliminates the first problem. Furthermore, we show that the protein prefers a dimerization angle of zero degrees, leaving the second option, the structural flexibility of the protein and/or the DNA, as a potential explanation for the discrepancy between theory and experiment.

The loop capture rate of FokI under maximum torque is 0.6 ± 0.1 s⁻¹. Interestingly, NaeI, SfiI and EclK18I all have slower loop capture rates of ∼0.1 s⁻¹ (13,14,16). The torque conditions in these published experiments were not known, so it is unlikely that the observed capture rates reflect the lowest values at maximum torque. The reason for their relative slow capture rates is probably due to the fact that both SfiI and NaeI act as a single functional unit that binds first one site and then searches for the second site while remaining bound to the initial site. The enzyme Ecl18KI binds DNA as a dimer and forms a loop by associating to a tetramer. The tetramerization interface is also responsible for flipping out bases from the DNA (16) and might thus be a more complex and more rigid interface than the FokI interface that holds together its DNA loop. Thus, FokI-induced looping, even under torque, seems to be a very efficient process. One possible rationalization is that FokI consists of two domains connected by a flexible linker (21), which might confer greater freedom on the positioning of the dimerization surface (in the smaller of its domains) than would be the case with a structurally rigid protein.

Previous studies had demonstrated that torque on DNA is influenced by introducing nicks in the DNA substrate (33–35). However, much to our surprise, the introduction of a nick in our FokI substrates had no effect on either loop capture or release rates. This stands in contrast to some theoretical (34) and experimental data (33,35) that suggest that a nick fully releases all torque in the system. It is also known that the introduction of a nick in supercoiled DNA relaxes any perturbation in twist and so yields the open-circle structure. However, the torque needed to induce supercoils in DNA, by magnetic tweezers for example, and therefore the torque present in supercoiled DNA is higher than the values found in this study (>30 pN nm) (33). The maximum twist generated by FokI dimerization is half a helical turn, which apparently does not generate enough torque to overcome base stacking interactions. The introduction of a gap of 4 nt in the DNA loop resulted in the release of all of the torque on the DNA molecule. The isotropic bending rigidity of gapped DNA is 13 times smaller than intact duplex DNA (36). Without torque, the capture rate is maximized but, surprisingly, the release rate is not minimized. The FokI synapse is thus actively stabilized by some torque. A bond that increases its strength as the force on it increases is already employed in biology: the catch bond (37). However, this is to our knowledge the first report of a ‘torsional’ catch bond.

The directionality of the FokI recognition site enabled us to characterise the impact of different bending topologies on both loop capture and release. The typical bending energy involved in a circular DNA loop of lengths used in this study is around ∼15kT (38). Despite the different loop topologies (180° and 360° bends), the maximum rate to capture a loop remained the same. However, the release rate for the 360° bend topology of the DF constructs is increased by roughly a factor of two. So, it seems that the additional bending destabilises the protein–protein synapse but does not alter the probability of the two recognition sites coming into close contact, at least on the linear DNA substrates used here.

To conclude, we show that the loop capture and release rate depend on the amount of torque on the DNA and on the protein synapse. FokI even employs the torque induced by the DNA to stabilise the loop and thus enhance the lifetime of the protein–DNA synapse, possibly acting as a torsional catch bond.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Figures 1–3.

FUNDING

Physics of the Genome of Stichting voor Fundamenteel Onderzoek der Materie (FOM) (partial); Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO) (to N.L. and G.J.L.W.); VICI grant of NWO (to G.J.L.W.); Wellcome Trust (grant 078794 to D.A.R. and S.E.H.) and EU Marie Curie Studentship (to C.P.). Funding for open access charge: Wellcome Trust.

Conflict of interest statement. None declared.