Greater Running Speeds Result in Altered Hippocampal Phase Sequence Dynamics

Abstract

Hebb (1949) described a “phase sequence” to be the sequential activation of sets of cell assemblies. Within the hippocampus, cell assemblies have been described as groups of coactive neurons whose place fields overlap. Membership of assemblies in a phase sequence changes systematically as a rat travels through an environment, serving to accelerate the temporal order that place fields are encountered during a single theta cycle. This sweeping forward of network activity (‘look ahead’), results in locations in front of the animal being transiently represented. In the current experiment, a population vector-based reconstruction method was used to capture the look ahead and reveals that the composition of the phase sequence changes with velocity, such that more cell assemblies are active within a theta cycle at higher running speeds. These results are consistent with hypotheses suggesting that hippocampal networks generate short-time scale predictions of future events in order to optimize behavior.

Introduction

In the seminal publication, The Organization of Behavior, Hebb (1949) provided a framework for understanding neural plasticity by describing the concepts of the cell assembly and the phase sequence. One aspect of this theory is that cell assemblies are groups of neurons that tend to be excited by similar input. As sensory input changes, the activity within the network transitions across multiple assemblies linking together these populations into a phase sequence (Harris, 2005; Hebb, 1949). Principal cells of the hippocampus exhibit patterned neural activity that is highly correlated with the rat’s position in space (the “place field” of the cell) (e.g., O'Keefe and Conway, 1978; O'Keefe and Dostrovsky, 1971; O'Keefe and Nadel, 1978) and cells that are members of the same assembly therefore have overlapping place fields (e.g., Harris et al., 2003; Maurer et al., 2006a). Thus, in the hippocampus, as the rat moves through space the order that place cells are activated comprises a phase sequence (Harris, 2005). These sequences have been proposed to be capable of storing a series of spatial locations (e.g., Lisman and Idiart, 1995).

The development and maintenance of phase sequences is facilitated by the timing of spikes relative to the hippocampal local field potential. In 1993, O’Keefe and his colleagues made the fundamental observation that the spikes of hippocampal principal neurons systematically shift relative to the theta rhythm, as a rat traverses a place field (O'Keefe and Recce, 1993; Skaggs et al., 1996). This fundamental relationship between place-specific firing of hippocampal cells and the phase at which the cell fires relative to the hippocampal theta rhythm, is referred to as “theta phase precession”. In CA1, the first spikes in the field occur late in phase, near phase 360°, whereas the spikes that fire as the rat exits the place field occur early in phase, near phase 0°. Therefore, these cells “precess” up to, but no more than, a full cycle of theta (360°), implying that the neurons in a given cell assembly have a similar theta phase relationship (Harris et al., 2003). This phenomenon has been hypothesized to facilitate the linking together of adjacent cell assemblies, which could serve as a mechanism for storing a succession of place fields in a route.

Skaggs and colleagues (1996) demonstrated that when a rat passes through a sequence of place fields, portions of this sequence are replicated in a compressed form within individual theta cycles. The phase sequence is then apparently initiated at the beginning of a theta cycle, transitioning across multiple assemblies until the activity is terminated at the end of the theta cycle. Moreover, each portion of the sequence is repeated several times as the rat traverses the environment. If each cell represents a specific point in space, then the rat’s location can be reconstructed based on brief epochs of CA1 neuronal activity (Harris et al., 2002; Samsonovich and McNaughton, 1997; Wilson and McNaughton, 1993; Zhang et al., 1998). Moreover, the compression of place fields within a single theta cycle can be observed in short time-scale reconstructions of hippocampal firing patterns as a sweeping forward of network activity (Samsonovich and McNaughton, 1997). Thus, locations ahead of the animal are transiently represented, and the net distance of this forward shift is the approximate size of a place field (Skaggs et al., 1996). Assuming that place field size is maintained across velocities (see Supplemental Figure 1), the network must “look-ahead” a greater distance as velocity increases. This would require more distinct cell assemblies to be activated within a theta cycle, and a decrease in the time required for network activity to shift from one assembly to the next (See Figure 1). Such changes in hippocampal network dynamics with velocity have not been shown empirically, however.

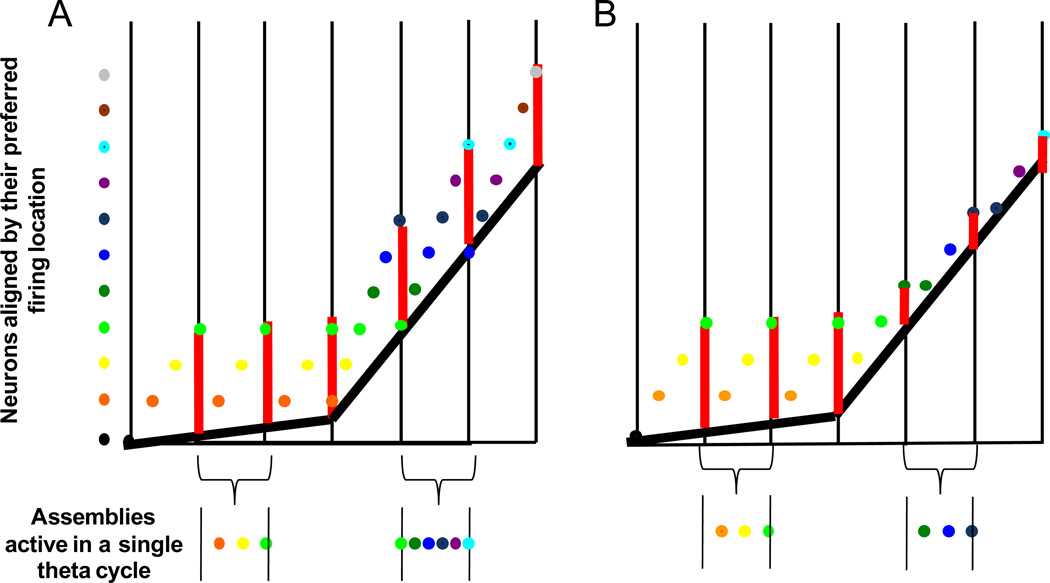
Figure 1.

A schematic of the ‘look ahead’ of CA1 cell assembles when there is an increase sequence compression of active cell assemblies at faster running velocities (A) and when the number of assemblies is constant (B). The Y dimension is spatial location and the X dimension is time in theta cycles. The vertical back lines delineate different theta cycles and the dots on the left represent different CA1 cell assemblies sorted by the location of their place fields. For example, the black cell assembly is active before the orange cell assembly, which is active before the yellow and so on. The current position of the rat is indicated by the thick black line. Notice that at faster velocities, this line has a steeper slope. Finally, the vertical red lines represent the size of place fields (and “jump-back”, Tsodyks et al., 1996). In A, at slower velocities only three cell assemblies (orange, yellow, green) are active within a theta cycle. At faster velocities, for place field size to be maintained, six cell assemblies (green, dark green, blue, dark blue, purple, cyan) need to be active within a theta cycle for the distance between the rat’s current location and the position of the hippocampal network to remain constant with increases in running speed. This results in an increase in sequence compression (i.e., the temporal offset between cell assemblies decreases as running speed increases). In B, when there is no increase in sequence compression, three cell assemblies are active within a theta cycle regardless of the rat’s velocity. In this case, the jump-back is smaller at higher running velocities. Therefore, the result of no increase in change in the composition of the phase sequence is a decrease in place field size at higher velocities, which is not observed empirically (see Supplemental Figure 1).

The current experiment used short-time scale reconstructions of CA1 network activity to investigate the composition of the phase sequence (the hippocampal look-ahead) across a range of velocities. Moreover, the rate that activity transitioned from one cell assembly to the next was examined by measuring the temporal offset of activity between pyramidal cell pairs (Dragoi and Buzsaki, 2006) at different running speeds. A change in these parameters with velocity would suggest the existence of a mechanism within the hippocampal formation (as defined by Amaral and Witter, 1995) that acts to optimize the serial processing of spatial locations.

Research Design and Methods

Animals and Surgical Procedures

Three Brown Norway-Fisher⁻344 hybrid male rats between 8 and 12 months old were used in this study. The rats were housed individually and maintained on a 12 h light-dark cycle. Recordings took place during the dark phase of the cycle. Surgery was conducted according to National Institutes of Health guidelines for rodents and approved Institutional Animal Care and Use Committee protocols. Before surgery, the rats were administered Bicillin (30,000 U, i.m., in each hindlimb). The rats were implanted, under isofluorane anesthesia, with an array of 14 separately moveable microdrives ("hyperdrive"). This device, implantation methods, and the parallel recording technique have been described in detail previously (Gothard et al., 1996). Briefly, each microdrive consisted of a drive screw coupled by a nut to a guide cannula. Twelve guide cannulae contained tetrodes (McNaughton et al., 1983b; Recce and O'Keefe, 1989), four-channel electrodes constructed by twisting together four strands of insulated 13 µm nichrome wire (H. P. Reid, Neptune, NJ). Two additional tetrodes with their individual wires shorted together served as an indifferent reference and an EEG recording probe. A full turn of the screw advanced the tetrode 318 µm. For all three rats, hippocampal recordings were made from the dorsal CA1 region (3.0 posterior, 1.4 lateral to bregma). The implant was cemented in place with dental acrylic anchored by dental screws. A ground lead was connected to one of the jeweler’s screws placed in the skull. After surgery, rats were orally administered 26 mg of acetaminophen (Children's Tylenol Elixir; McNeil, Fort Washington, PA). They also received 2.7 mg/ml acetaminophen in the drinking water for 1–3 d after surgery and oral ampicillin (Bicillin; Wyeth Laboratories, Madison, NJ) on a 10 d on 10 d off regimen for the duration of the experiment. Data from these animals have been used in other unrelated analyses that have been published previously (Maurer et al., 2006a; Maurer et al., 2006b; Maurer et al., 2005), drawing from a database of approximately 900 well-isolated pyramidal neurons.

Electrophysiological Recording

Twelve tetrodes were lowered after surgery into the hippocampus, allowed to stabilize for several days just above the CA1 hippocampal subregion, and then gradually advanced into the CA1 stratum pyramidale. Another probe was used as a neutral reference electrode, and was located in or near the corpus callosum. The final probe was used to record theta field activity from the vicinity of the hippocampal fissure. Each tetrode was each attached to 4 separate channels of a 50-channel unity-gain head stage (Neuralynx, Tucson, AZ). A multiwire cable connected the head stage to digitally programmable amplifiers (Neuralynx). The spike signals were amplified by a factor of 1000–5000, bandpass filtered between 600 Hz and 6 kHz, and transmitted to the Cheetah Data Acquisition system (Neuralynx). Signals were digitized at 32 kHz, and events that reached a predetermined threshold were recorded for a duration of 1 msec. Spikes were sorted off-line on the basis of the amplitude and principal components from the four tetrode channels, by means of a semiautomatic clustering algorithm [BBClust (P. Lipa, University of Arizona, Tucson, AZ); KlustaKwik (K. D. Harris, Rutgers University, Newark, NJ)]. The resulting classification was corrected and refined manually with custom-written software (MClust; A. D. Redish, University of Minnesota, Minneapolis, MN), resulting in a spike-train time series for each of the well-isolated cells. No attempt was made to match cells from one daily session to the next, and, therefore, the numbers of recorded cells reported does not take into account possible recordings from the same cells on consecutive days; however, because the electrode positions were adjusted from one day to the next, recordings from the same cell over days were probably relatively infrequent. Putative pyramidal neurons were identified by means of the standard parameters of firing rate, burstiness, spike waveform shape characteristics (Ranck, 1973), as well as the first moment of the autocorrelation (Csicsvari et al., 1998). As noted by Csicsvari et al. (1998), pyramidal neurons exhibit a faster decay in their autocorrelation compared with interneurons.

Theta activity in the EEG was recorded from a separate probe that was positioned 0.5 mm below the CA1 pyramidal layer, near the hippocampal fissure. EEG signals were bandpass filtered between 1 and 300 Hz and sampled at 2.4 kHz, were amplified on the head stage with unity gain, and then again with variable gain amplifiers (up to 5000).

Several light-emitting diodes were mounted on the head stage to allow position tracking. The position of the diode array was detected by a television camera placed directly above the experimental apparatus and recorded with a sampling frequency of 60 Hz. The sampling resolution was such that a pixel was 0.3 cm.

Behavior

The animals were food deprived to 85% of their ad libitum weight. During this time period, the rats were trained to run on a circular track (382 cm in circumference) for food reinforcement. Rats ran bi-directionally around the track, which was partitioned by a barrier at one point. Food was given on either side of the barrier and at the 180° opposite point. Rats ran on the track for 20 min, resulting in a variable number of laps per session. Each running session was flanked by a rest period in the "nest”. Data from the rest periods were used to assess baseline firing and cell stability.

Analyses

Spatial population vector construction

Spatial population vectors were constructed in the same manner as in Maurer et al. (2005) with the exception that spatial bins were reduced to 0.7 cm (compared to 12 cm previously using in Maurer et al., 2005) in size to increase resolution. Briefly, to generate this matrix, the spatial firing rate distributions (0.7 cm bin size) of all recorded pyramidal neurons in a given region or condition were combined into a single, two-dimensional array: Cell number in rows and linearized location in the columns. Each column thus represents an estimate of the composite population vector for the corresponding location. For bidirectional running, the vectors for the clockwise and counterclockwise directions were computed separately, because the firing patterns during running in opposite directions are only weakly correlated (e.g., Battaglia et al., 2004; Markus et al., 1995; Maurer et al., 2005; Muller et al., 1994).

Temporal population vector construction

The temporal population vector was constructed in a manner similar to the position population vector, with n cells by t temporal bins. Time was binned into 20° of a theta cycle with 126 bins over 7 consecutive theta cycles centered on a single theta trough (i.e., the theta time population vector; see also (Georgopoulos et al., 1989; McNaughton, 1998). The LFP was digitally filtered, bidirectionally in time to avoid phase shifts, with a 6–11 Hz Chebyshev bandpass filter. The phase of firing relative to theta time t was 360° (t – t₀)/(t₁ – t₀), where t₀ and t₁ are the times of the preceding and following peaks of the filtered reference EEG signal (Skaggs et al., 1996). In this matrix, each column represents an estimate of the composite population vector for the corresponding phase bins (i.e, 0–20°, 20–40°, etc.) of theta and each row is the firing of a single cell over seven theta cycles. The restriction to seven theta cycles was selected only to reduce computational requirements necessary for the analysis. Each vector of this matrix was correlated with all of the position population vectors (see position reconstruction by velocity description below). With this method, time is measured not in seconds, but in units of theta cycles (“theta time”).

Short time scale position reconstruction by velocity

If the look-ahead phenomenon is robust, then a population vector-based reconstruction should reveal the forward sweep of network activity within a single cycle. Therefore, for a window of seven theta cycles, Pearson’s correlation coefficients were calculated between all vectors of the theta time matrix, T_i, and the position vectors, P_i (P_i −65, P_i +65) from 45.5 cm behind the rat to 45.5 cm ahead of the rat based on its present location (65 bins by 0.7 cm bin size equals 45.5 cm). This window size was chosen because it was substantially larger than previous measures of place field size from this region (Maurer et al., 2006a; Maurer et al., 2005) and thus would contain the entire extent of the look-ahead (see Introduction). Correlations across all position population vectors were computationally prohibitive (i.e., correlations were not calculated on all positions of the maze, but only a spatial window of 92 cm centered on the rats exact position). The output of this analysis was a matrix with the dimensions p position by t time. See Supplemental Figure 2 for a non-sparse example of this analysis procedure. Supplemental Figure 3 is an example using empirical data.

Even with simultaneously recorded cell populations of 80 or more cells, with temporal bins of approximately 7 msec (assuming 125 msec theta cycle), there were instances of empty columns. In these circumstances, the entire column was replaced with not-a-number (NaN) place holders. Correlation matrices were calculated and stacked across all theta cycles resulting in a three dimensional matrix (n theta cycles by p positions by t temporal bins; see Supplemental Figure 4). Velocity was calculated for each single theta cycle. Then each correlation matrix was sorted by the velocity of the rat during the central theta cycle in the seven cycle window.

The correlation matrices were averaged for velocity bins ranging from 5 cm/s to 75 cm/s, in 10 cm/s intervals. Two low velocity bins, ranging from 1–3 cm/s and 3–5 cm/s were also included to examine the ‘look-ahead’ phenomenon at low velocities. With this method of binning, cellular activity at different regions of the track can contribute to the same matrix as long as they belong to the same velocity bin (comparable methods have been utilized previously for determining firing rate by velocity profiles; Maurer et al., 2005). The moving time window method was used here as opposed to a serial shift of seven cycles, in order to maximize the sample size, which results in a reduction in the variability in the resulting figures. Nonetheless, similar results were obtained with and without the moving time window employed in the construction of the theta time matrices. Moreover, similar correlation results were obtained with temporal bins between 15° and 30° and spatial bin up to 1.5 cm.

Determining the rat’s position and look-ahead

The average relative position of the rat was calculated by determining the rats’ position at the center of each 7 theta cycle sliding window and setting that position to zero (e.g., for the center timestamp of the 7 cycle theta window, the rat occupied position 65cm on the track. This was reset to zero, such that previous locations are negative and future locations to be encountered are positive). In order to quantitatively display the look-ahead, the average correlation matrices were smoothed with a Hanning window of 14 cm, which was less than half the size of dorsal place fields (Maurer et al., 2006a), and the location of maximum correlation for each temporal bin was determined. The results were plotted as black dots on top of the unsmoothed, average correlation matrices for each velocity (Figure 2). The averaged relative position of the rat by units of theta cycles for each velocity is also plotted for comparison (white line). To quantify the distance of the ‘look-ahead’, a peak-trough finding algorithm was used to find the first and last spatial locations encountered on the circular track that exhibited the maximum correlation value within a single theta cycle. In some instances, the peak-trough algorithm failed to find the maximum and minimum locations of the look ahead, typically a result of a low resolution reconstruction (see above), and these relatively rare cases (<5% of all data) were excluded from further analysis.

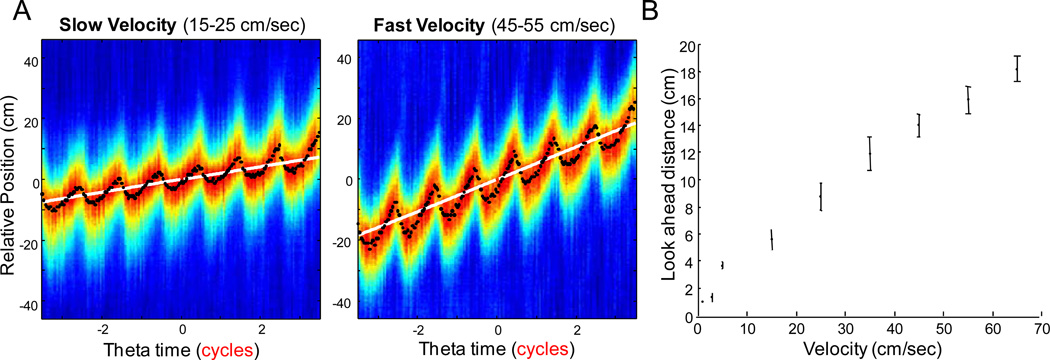
Figure 2.

(A) Average time by space correlations for two representative dorsal hippocampal CA1 datasets. The top row shows the low velocity bin of 15–25 cm/sec and the bottom row shows data from the 45–55 cm/sec velocity bin. The colors represent the average correlation values for that specific phase and relative location. The color axis is not maintained across plots, but optimized for visual inspection. The black dots are the relative spatial location of highest correlation for each theta bin, while the white line is the rats’ average relative position for each theta bin. Note that the look-ahead phenomenon is low at low velocities but is larger at higher velocities. (B) Shows the distance of the CA1 look ahead as a function of velocity. The increase in the distance of the look ahead at higher running speeds suggest that more cell assemblies are active within a theta cycle at higher velocities, that is, the phase sequence becomes larger.

Measuring the Rate of Cell Assembly Transition and Sequence Compression as a Function of Velocity

The distance between place field centers is reflected by their temporal spike lag within a single theta cycle (Diba and Buzsaki, 2008; Dragoi and Buzsaki, 2006; Geisler et al., 2007; Skaggs et al., 1996). For example, two cells with maximal place field overlap, but distinct place field centers, will fire in the sequence that their fields are visited during a single theta cycle within a relatively short temporal window. Two cells with place fields with minimal overlap (and therefore, a large amount of distance between the place field centers) will exhibit a larger temporal offset between their respective firing, although once again they will occur in the sequence that the field centers are visited. This fact can be capitalized on to calculate a cross-correlogram lag (CCG-lag; Dragoi and Buzsaki, 2006) that when plotted against distance between place field centers provides a measure of the rate of cell assembly transition. Thus, to determine the effect of velocity on the rate of cell assembly transition (defined operationally as the inverse slope of the temporal lag versus distance between place field centers), we examined the relationship between CCG-lag and the distance between the place field centers as a function of velocity. The first step of the analysis was to represent the three variables x (distance between fields [cm]), y (population cross-correlogram [degree]) and z (velocity [cm/s]) as points in a 3 dimensional space. This results in one point per spike pair within a recording session, pooled over all sessions and all animals. The density profile of distances is essentially Gaussian when projected onto the x axis, whereas the density profile of the population cross-correlogram has multiple peaks when projected onto the y axis, reflecting the theta modulation of pyramidal cells (Skaggs et al., 1996; See Supplemental Figure 4). The construction of this 3 dimensional matrix provides the means to assess the CCG-lag by distance relationship as a function of specific velocity bins.

We quantified two slopes for each z-window of the three-dimensional matrix (that is, two slopes were determined for a single CCG-lag versus distance plot): 1) a 'fast' slope, defined as an average of slopes of the main axes of the ellipsoidal density contours enclosing the three adjacent theta-peaks closest to the (0,0) point, and 2) a 'slow' slope, defined as the slope of the connecting line between the top theta-peak above the (0,0) point and the bottom peak below. The inverse of the 'fast' slope represents the velocity of the population activity bump as it 'runs-ahead' of the actual animals position at each theta cycle (the rate of cell assembly transition). The 'slow' slope represents (or is inversely proportional to) the actual running speed of the animal in real space. For all analyses of CCG-lag versus distance between place field centers, the slow slope was used to represent the rat’s velocity as opposed to the actual video tracker data for two reasons. First, it was necessary to have the velocity units in theta degrees/cm because theta frequency changes as a function of velocity (this measurement, as opposed to seconds per cm, prevents changes in theta frequency with velocity from distorting the results). Therefore, estimating the rat’s speed from the raw video tracker data is problematic. Second, if we know the distance between place field centers and how long it took the rat to travel between the two place field centers (in degrees of theta), we can let the hippocampal network tell us how fast the rat was moving.

For the quantification of the velocity dependence of these slopes, a moving velocity window was employed with a constant width of 10 cm/s (as determined by the video tracker; the data were then used to determine the rats velocity in units of cm/deg via the methods described above). The points in each velocity window were then converted into a smoothed density matrix. From the smoothed density-matrix, ten evenly spaced iso-density contours are determined and the first four highest-level contours are extracted for the three central theta peaks. These local density maxima are analogous to extracting the central segment of the “sigmoidal” shape of the relationship between theta time scale lag and the distance between place field centers as described by Diba and Buzsaki (2008). The 'fast' slopes were determined by calculating the covariance matrix from the points that define each contour. The major and minor axes of the covariance-ellipsoid at Mahalanobis distance 1 are found by calculating the eigenvectors and eigenvalues of the covariance matrix. In order to focus on the central region of interest the slopes of the 4 highest density contours centered around the 3 central peaks were averaged to obtain their mean and standard error. Similarly, for the 'slow' slope estimation, the slope of the connecting line of the centers of the covariance-ellipsoids of the top and bottom theta peak was calculated and averaged over the 4 highest density contours. The errors shown reflect the systematic uncertainties due to different choices of contour levels and outweigh the statistical errors by orders of magnitude.

Finally, sequence compression can be understood as the factor by which the population activity bump runs faster through the environment within a theta cycle than the actual position of the animal. In other words, sequence compression is the ratio of the rate of cell assembly transition (see above) to the rat’s actual velocity. Note that the rate of cell assembly transition can change while the magnitude of sequence compression may remain unaltered. Therefore, we quantified sequence compression as the ratio between the 'fast' and the 'slow' slope obtained from the CCG-lag versus distance between place field centers plots. As mentioned above, the slow slope was obtained by connecting the centers of the covariance-ellipsoids of the top and bottom theta peak. Using the slow slope to detect the rat’s velocity, as opposed to the video tracker data, tells us how long it took the rat to travel between two place field centers (in degrees of theta) relative to the distance between those centers. This method maintains equivalent units (cm/deg) between the rate of cell assembly transition and velocity. This ratio was then calculated from the ‘fast’ and the ‘slow’ slopes for each velocity bin.

Results

By correlating temporal population vectors with spatial population vectors, the hippocampal “look-ahead” could be reliably reconstructed as a function of velocity. Example reconstructions are shown in Figure 2A. Low velocities (15–25 cm/s) are shown in the left panel and high velocities (45–55 cm/s) are shown in the right panel from the same respective datasets. The colors represent the average correlation values for each phase and relative location. The color axis is normalized by the maximum correlation value for each figure. The black dots represent the relative spatial location of highest correlation for each theta bin (that is, the hippocampal look-ahead), while the white line is the rats’ average relative position in each theta bin. These data are consistent with previous results (Foster and Wilson, 2007; Itskov et al., 2008; Samsonovich and McNaughton, 1997) that have shown that the hippocampal network sweeps forward of the rat’s actual position in space. The look-ahead, that is, the phase sequence, is terminated at the end of each theta cycle, only to reemerge at the beginning of the next cycle and this process then repeats itself across theta cycles.

Applying the idea that place field size does not decrease with velocity to the Tsodyks’ schematic (see Figure 1), then the assembly composition of the phase sequence should also increase with velocity. This is qualitatively shown as an increase in the look ahead with velocity in Figure 2A and quantitatively estimated as the difference in the locations of the minimum and maximum correlations, which is shown in Figure 2B as a function of velocity. There was a significant relationship between the distance of the look ahead and velocity (R² = 0.98, p < 0.001; least-squares regression). These results suggest that the cell assembly composition of the phase sequence increases with higher running speeds.

The composition of the phase sequence can also be examined by measuring the rate of cell assembly transition (i.e. the inverse slope of the CCG-lag by the distance between place field centers) as a function of velocity. Specifically, if more cell assemblies are active within a single theta cycle (i.e., there is a greater look ahead), then the amount of time between adjacent cell assemblies (i.e., neighboring place field centers) must decrease with increasing velocity. Figure 3 illustrates an example CCG lag as a function of distance between place field centers, for relatively low velocities (A) and relatively high velocities (B). Note that the CCG lag-place field distance relationship changes from lower to higher velocities, which is shown most clearly in the supplemental movies, but also statically in the two contour plots (Figure 3A, 3B). Using a covariance ellipsoid approximation of the central contours to measure the slope (see Methods), the relationship between the CCG-lag and distance between place field centers as a function of velocity can be estimated (“fast slopes”). The “fast” slope of the CCG-lag plotted as a function of distance was nearly vertical at low velocities (resulting in slopes that approach infinity) and closer to horizontal at high velocities (resulting in slopes that approach zero), which yielded a rapid decay of slope with increasing velocity.

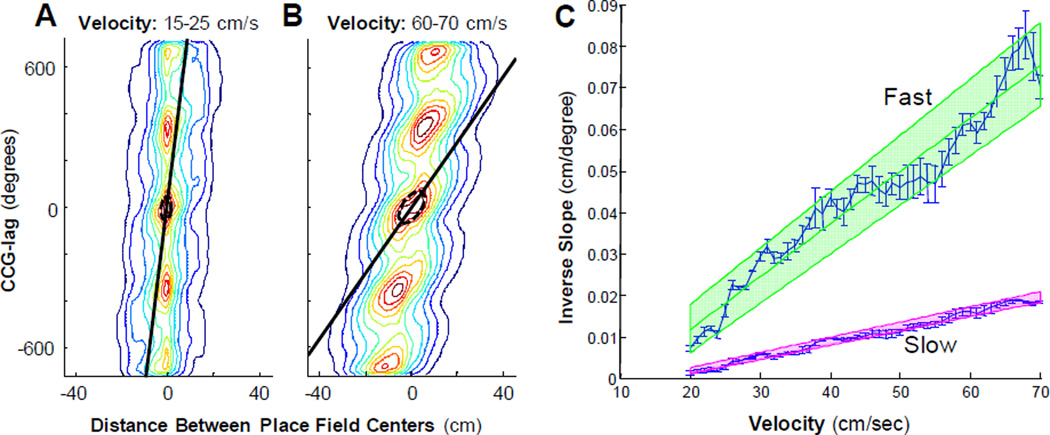
Figure 3.

The rate of cell assembly transition plotted at different velocities. The contour plots (panels A and B) show the relationship between the CCG lag versus distance between place fields (compare to Figure 2A of Dragoi and Buzsaki, 2006). The ‘fast’ slope of the CCG lag plotted as a function of the distance between field centers (black line) was determined by using a covariance ellipsoid fit of the central contours (see Methods). Note that the fast slope is nearly vertical at lower velocities (slope = 100 deg/cm; inverse slope = 0.01 cm/deg) and becomes more shallow at higher velocities (slope = 14.29 deg/cm; inverse slope = 0.07 cm/deg). Panel C shows the inverse of both the fast and ‘slow’ slope (see methods) as a function of velocity. The green line and shaded region shows the line of best fit and the 95% confidence interval for the fast slope while the pink line and shaded region shows the line of best fit and 95% confidence interval for the slow slope. There is an evident relationship between the fast slope and velocity indicating that the rate of cell assembly transition increases with higher running speeds.

Figure 3C shows the inverse of the fast slope (green shaded region) with increasing velocity for velocities greater than 20 cm/sec. The fast slope could not be estimated for velocities less than 20 cm/sec because the contour plot was circular rather than ellipsoid and an angle of rotation (see Methods) cannot be calculated from a circle. Additionally, at these lower velocities theta is often not present. It is evident from Figure 3C, however, that as the animal’s velocity increases so does the inverse of the fast slope. The error bars represent the standard error of the mean, the green line is the slope (1.27×10⁻³ ± 9×10⁻⁵⁻ sec/degree), and the shaded portion indicates the combined 95% confidence intervals of the slope and intercept. The relationship between the inverse of the fast slope and velocity was significant (R² = 0.92, p < 0.001; least-squares regression). This indicates that as the running speed of the rat increases, the amount of theta time for the activity bump to transition from one cell assembly to the next adjacent assembly decreases. The dependence of the rate of cell assembly transition on velocity could provide a mechanism that enables the rat to receive information about upcoming spatial locations for a fixed amount of time. Whether or not this increase in the ‘look ahead’ with velocity is sufficient to maintain a constant amount of sequence compression is unknown, however. If sequence compression is operationally defined as the ratio of the rate of cell assembly transition to the rat’s velocity, the effect of running speed on this parameter can be tested by measuring the ratio of the fast slope to the ‘slow slope’ of the ellipsoid contour plots (see methods).

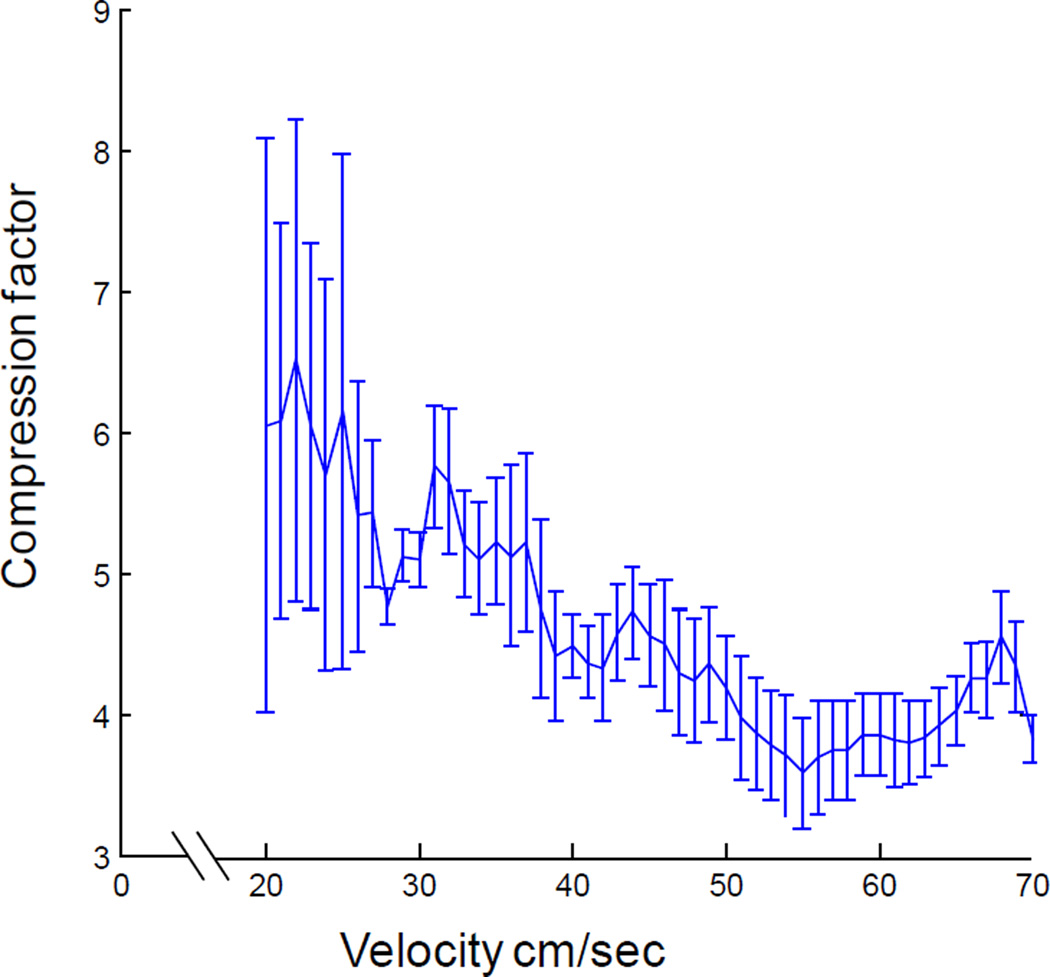
Figure 4 shows the ratio of the inverse of the fast slope to the inverse of the slow slope (rate of assembly transition/rats’ velocity) for different velocities from 20 cm/sec up to 70 cm/sec. Note that the relationship between sequence compression and velocity is asymptotic with a large compression factor near slow velocities that decreases with increasing running speed to an asymptote along the velocity axis of approximately 3.5. Figure 4 suggests that when the rat is moving slowly, the CA1 network outruns the animal, resulting in a large compression factor at lower velocities. This observation becomes intuitive when one considers that if a rat is moving at 1 cm/sec, and theta is 8 Hz, then the rat moves 0.125 cm in a single theta cycle. Under these circumstances, a look-ahead of only 3 cm would correspond to a compression factor of 24. Therefore, as long as theta is present, there will be a minimum look-ahead and slow movement will result in a large compression factor. Importantly, there is a significant relationship between velocity and sequence compression (R² = 0.66, p < 0.001; least-squares regression) such that as the rat’s running speed increases the compression factor decreases. There appears to be a minimum compression factor, however. Specifically, after 40 cm/sec sequence compression no longer decreases. In fact, at these faster velocities there is no longer a significant relationship between sequence compression and running speed (R² = 0.003, p = 0.80; least-squares regression). An overall minimum compression factor could be approximated by estimating the slope of the relationship between the fast slope and velocity (Figure 3C, green line; slope = 1.4×10⁻⁴) and dividing this by the slope of the relationship between the slow slope and velocity (Figure 3C, pink line; slope = 4.0×10⁻⁴). This calculation resulted in a compression ratio of 3.57 ± 0.13, which is nearly equivalent to the asymptote along the velocity axis in Figure 4. It is notable that when this compression factor was calculated from CCG-lags measured in msec rather than degrees of theta, the results were similar (3.75 ± 0.56). The observation that the rate of cell assembly transition increases with higher running speeds, but sequence compression does not, suggests that at higher velocities the rat catches up to the rate of cell assembly transition.

Figure 4.

Sequence compression as a function of running velocity. The compression factor decreases with increasing velocity up to ~55 cm/sec. At the faster velocities sequence compression reaches an asymptotic value of ~3.5.

Discussion

The main novel finding of the present study is that short time scale hippocampal dynamics are altered as a function of velocity. Specifically, more cell assemblies are active within a given theta cycle at higher running speeds. The measurable result of this phenomenon is an increase in the amount of space transiently represented within a theta cycle. As velocity increases, the hippocampal ‘look ahead’ increases. Moreover, because more cell assemblies are active within a given theta cycle at higher running speeds, there is an increase in the rate of cell assembly transition with velocity. This was quantified as shorter temporal offsets between pairs of neurons with neighboring place fields at high velocities. Finally, it was also observed that sequence compression decreased with increasing velocity, up to speeds of ~40 cm/sec. At faster speeds, sequence compression appeared to asymptote to a compression factor of approximately 3.5.

It is of importance to mention that theta frequency increases with running speed (e.g., Whishaw and Vanderwolf, 1973). This was controlled for in the current study by using theta phase as the measure of time. Thus, the present results were not confounded by changes in the duration of a single theta cycle. Interestingly, even though theta cycle duration decreases at higher velocities, there is still an increased look-ahead. Thus, the composition of the phase sequence includes more cell assemblies at fast compared to slow velocities regardless of a reduced time window. For example, 7 assemblies must be contained within a theta cycle that lasts only 100 msec at high velocities compared to a low velocity condition where 4 assemblies are active within a 125 msec theta cycle.

The dependence of short time scale hippocampal dynamics on velocity may serve to provide the rat with information about upcoming locations for the same amount of time when the animal’s running speed varies. The importance of this can be understood by considering the comparable situation of driving a car on the freeway. A conscientious driver knows that when tailing another car, as the speed increases the distance between their car and the automobile in front also needs to increase. This affords the driver sufficient time to react to changing conditions regardless of velocity. As in the car scenario, increasing the distance of the look ahead at higher running speeds as an animal navigates though space, may provide the rat with adequate time to change its behavior if necessary.

The change in the rate of cell assembly transition with velocity may also operate to maintain a fixed place field size. Figure 1 schematically compares the condition in which the rate of cell assembly transition changes as a function of velocity and when it does not (see Figure 1; Tsodyks et al., 1996). The spatial location of each field is aligned on the y-axis and the temporal order of firing between cells is determined from the x-axis. Figure 1A illustrates that if place field size remains the same across all velocities, then the size of the jump-back (vertical red line) is preserved by modulating the look-ahead size (represented by the diagonal alignment of dots within a single theta cycle; Figure 1A). In other words, if place field size remains the same, the look-ahead distance minus the distance covered within a single theta cycle would equal a fixed constant. To accomplish fixed place field sizes at higher velocities, more cell assemblies must become active within a single theta cycle (shown in Figure 1A with 3 assemblies active at low velocities and 6 assemblies active at higher velocities). Thus, the look-ahead at higher velocities covers a greater distance within a single theta cycle, resulting in an increase in the rate of cell assembly transition (compare assemblies active in Figure 1A). If, however, there was not a decrease in the amount of theta time between the activity of adjacent cell assemblies with velocity (as reported by Geisler et al. 2007), place field size would decrease, which has never been shown empirically and was not observed in Geisler et al. (2007).

One possible explanation for the apparent discrepancy between the present results and those of Geisler et al. (2007) may reside in the way in which the spikes were sorted in these different experiments. In Geisler et al. (2007), velocity was reduced to two values (the lowest 50% and the highest 50%), whereas in the current experiment, values were sampled continuously over the entire velocity range. Thus, the differences detected in the present study may have been a result of the greater sensitivity of the method used.

Differences in the locations of recorded CA1 neurons could also provide an explanation for the discrepant results of Geisler et al. (2007) and the current study. In the present experiment, all recorded neurons were obtained from a dorsal area of CA1 3.0mm posterior and 1.4mm lateral to bregma. In contrast, the recordings obtained in Geisler et al. (2007) included pyramidal cells that were 4.0mm posterior and 3.3mm lateral, which is from a region more ventral to the CA1 area sampled in the present study. Several factors make it plausible that changes in the composition of the phase sequence is potentially more difficult to detect in the more “ventral” region of the hippocampus sampled by Geisler et al. (2007) compared to the relatively more anterior “dorsal” region examined in the present study. First, fewer pyramidal cells are active in more ventral hippocampus compared to dorsal regions when an animal explores an environment of a specific size (Maurer et al., 2006a). Thus, there was a lower yield of cell pairs for analysis in the Geisler et al., (2007) study. A second distinguishing factor between dorsal and more ventral hippocampus is that the spacing between adjacent assemblies is relatively larger in more ventral areas of the hippocampus, and thus will yield a larger look ahead at low velocities (i.e., the distance between adjacent place field centers divided by the temporal off-set of spiking within a single theta cycle is greater in the more ventral hippocampal regions compared to the dorsal; Supplemental Figure 6). This suggests that for the ventral hippocampus the rat must travel at a much higher velocity for additional assemblies to become active compared to the dorsal hippocampus. For example, if the rat’s velocity was 5 cm per theta cycle and 6 assemblies were active within a single theta cycle (spaced 5 cm apart), then place field size would be 20 cm (look-ahead of 25 cm minus the 5 cm distance traveled = 20 cm jump-back). In order to maintain the same place field size at a velocity of 10 cm per theta cycle, an additional, 7th assembly needs to become active. The larger spacing between adjacent place field centers in more ventral areas of the hippocampus, however, requires the rat to increase its velocity a larger amount before another assembly is active. The direct consequence of this is that the rate of cell assembly transition should be less sensitive to velocity in the more ventral regions of the hippocampus relative to dorsal areas. Interestingly, firing rate in more ventral regions of the hippocampus is also less sensitive to changes in velocity (Maurer et al., 2005). Therefore, Geisler et al., (2007) may not have detected dependence of the number of active cell assemblies within a single theta cycle on velocity because, for the reasons discussed above, in the more ventral regions a much larger increase in velocity must occur before a change in this parameter can be measured.

Sequence compression is the rate at which hippocampal spatial representations change relative to the rat’s velocity. In other words, sequence compression occurs when the active place fields in CA1 transition faster than an animal’s true running speed. Because sequence compression is the ratio of two different rates (cm/sec or degrees/sec), it is a factor without units. The effect that changes in velocity have on this factor has not been empirically shown. In the current experiment this compression factor was calculated by dividing the temporal offset of cell pairs by the velocity of the rat (Dragoi and Buzsaki, 2006). When this is done for different velocities it was observed that at lower velocities the sequence compression factor is large, and this factor decreases as a function of velocity to an asymptote of a minimum compression factor of ~3.5 at 40 cm/sec. These data suggest that when the hippocampus is in a theta state, even if the rat is moving slowly, there is still a ‘look ahead’. As a rat begins to move faster, however, the velocity of the animal begins to catch up to the rate at which different spatial locations are represented in CA1. This results in a velocity-dependent decrease in sequence compression up to velocities of 40 cm/sec. At these higher velocities, the rate that the active cell assembly changes between neurons with adjacent place fields increases with velocity sufficiently to maintain a constant compression factor. An asymptotic compression factor of 3.5 indicates that, at a minimum, the CA1 activity moves through space 3.5 times faster than the rat, even at the animal’s top running speed. This may operate to ensure that a rat has some minimum amount of time to process information about upcoming locations. Although the mechanism that limits sequence compression to a factor of 3.5 is unknown, it is conceivable that the asymmetric feed-forward excitation responsible for higher compression factors at slow velocities is balanced by feed-back inhibition as the rat runs faster. Alternatively, the compression factor could be limited by mechanisms that govern intrinsic oscillations for a single neuron. Future experiments should be designed to elucidate which of these two potential mechanisms is more probable.

The finding that that sequence compression asymptotes to a minimum factor of 3.5 has interesting implications for the affect of aging on CA1 network dynamics. Although the timing of CA1 spikes relative to the theta rhythm is similar between young and old rats (Shen et al., 1997), there are several notable changes in CA1 network dynamics that occur and have been correlated with age-associated cognitive impairments (Barnes et al., 1997; for review, see Burke and Barnes, 2010; Rosenzweig and Barnes, 2003). One hypothesis that has been proposed to account for age-related cognitive deficits is that, in older animals, there is a reduction in the speed of processing that interferes with the encoding of new information (e.g., Salthouse, 1994; Salthouse and Coon, 1993). Neurobiological correlates of reduced processing speed, however, have not been reported. In fact, in CA1 conduction speed (for review, see Barnes, 1994), neuronal firing rate (e.g., Barnes et al., 1983; Mizumori et al., 1996; Shen et al., 1997), and the frequency of prominent oscillations (Gerrard et al., 2001; Smith et al., 2000) are similar between young and old animals. The reduced processing speed hypothesis of aging could remain tenable, however, if there were age-associated alterations in the short timescale dynamics of CA1 neurons. Moreover, although the firing rate by velocity relationship is identical between young and old CA1 neurons (Shen et al., 1997), aged rats run at significantly lower velocities compared to young rats. Thus, it would be interesting to examine whether the composition of the phase sequence, the rate of cell assembly transition, and sequence compression are similarly affected by velocity in young and old rats. Specifically, in animals that run at slower velocities, does the compression factor still asymptote at 55 cm/sec to a value of 3.5? Less sequence compression in aged animals would mean that these rats have less time to incorporate information about upcoming spatial locations, which would contribute to reduced processing speed.

Neurons within layer II of the medial entorhinal cortex show strong theta phase precession (Hafting et al., 2008). The primary perforant pathway input to CA1, however, arises from layer III of the medial entorhinal cortex, an area containing few neurons that precess. Thus, CA1 may inherit its phase precession indirectly from layer II of the medial entorhinal cortex via the CA3 region. This would suggest that layer II of the medial entorhinal cortex is responsible for generating theta phase precession across the entire hippocampal formation and could therefore be responsible for the origin of the observed look-ahead phenomenon (for review, see Maurer and McNaughton, 2007).

Taken together the present results suggest that the relationship between short timescale dynamics and velocity may reflect an overlooked process within the hippocampal formation (Johnson et al., 2009) involving an interaction between the ability to predict upcoming locations and velocity. Specifically, the hippocampal look-ahead may be part of a computation that is reminiscent of a Kalman filter (Eliasmith and Anderson, 2003; Finkel and Contreras, 2007; Lorincz and Buzsaki, 2000; Rao and Ballard, 1999). According to the Kalman filter analogy, by receiving information regarding current position, velocity, and heading within a single theta cycle, the hippocampal circuitry generates a prediction of where the rat will be. This predicted location may then be compared to the actual position in future theta cycles. If there is a difference detected between the population code of predicted and actual locations within a strict temporal window, the internally generated estimates and actual locations can be combined to compute “error-correction” signals, as has been plausibly modeled, for example, in computations that simulate motor control commands (Deneve et al., 2007). Based on this model the look-ahead or prediction, must increase with velocity in order for the “error correction time-window” to remain constant. But, in fact, an increase in the prediction range was observed in the present study with increasing velocity, which results in more time available time for corrections to be applied. Recent data support the idea that the hippocampus operates to make predictions that can be applied for error correction. Johnson and Redish (2007) have demonstrated that, when a rat encounters decision points on a modified t-maze, the hippocampal network is capable of sweeping ahead to positions in front of the rat. The direction of the sweep often correlated with the rat’s decision, but not always. Instances of the latter circumstance suggest that, on some trials, the outcome of a certain path was predicted, an error was calculated, and a correction was applied (Johnson and Redish, 2007). Moreover, recent human data have demonstrated a role for the hippocampus in the prediction of future events, as amnesics exhibit a deficit in imagining the future (Addis et al., 2007). Taken together, the data from the experiments reported here support the idea that hippocampal formation is capable of utilizing information from the past, presumably stored in synaptic connections, in order to construct and test future predictions.