Abstract
Arterial Spin Labeling (ASL) perfusion MRI can suffer from artifacts and quantification errors when the time delay between labeling and arrival of labeled blood in the tissue is uncertain. This transit delay is particularly uncertain in broad clinical populations, where reduced or collateral flow may occur. Measurement of transit delay by acquisition of the ASL signal at many different time delays typically extends the imaging time and degrades the sensitivity of the resulting perfusion images. Acquisition of transit delay maps at the same spatial resolution as perfusion images may not be necessary, however, because transit delay maps tend to contain little high spatial resolution information. Here, we propose the use of a reduced spatial resolution ASL prescan for the rapid measurement of transit delay. Approaches to using the derived transit delay information to optimize and quantify higher resolution continuous ASL perfusion images are described. Results in normal volunteers demonstrate heterogeneity of transit delay across different brain regions that lead to quantification errors without the transit maps and demonstrate the feasibility of this approach to perfusion and transit delay quantification.
Keywords: perfusion imaging, cerebral blood flow, arterial spin labeling, transit delay, vessel suppression
INTRODUCTION
Arterial spin labeling (ASL) is an approach to the measurement and imaging of perfusion with MRI. Due to its completely noninvasive nature, perfusion measurement using ASL has been applied increasingly to study cerebrovascular, neurologic and psychiatric diseases (1–3), both in experimental and clinical settings. However, wide clinical use has demonstrated the challenges of optimizing ASL acquisitions for subjects with very different vascular and perfusion characteristics (2,4,5).
Because the ASL signal decays with T1 after labeling, the time delay between labeling in the feeding arteries and the arrival of labeled blood in tissue can have a large effect on the measured ASL signal. If the ASL acquisition is not optimized for transit delay, quantification errors, reduced tissue signal, and bright signal in feeding arteries and arterioles may result. Strategies for minimizing such errors by control of the timing of labeling have been proposed (6–8) and used for a number of translational studies (9,10), but they require an estimate of the transit delay range. With these approaches, the greater the range of possible transit delays, the lower will be the sensitivity of the resulting perfusion image. In addition, these strategies can fail if the tissue T1 is substantially different from the T1 of blood. Eliminating the uncertainty in transit delay could help improve the quality, sensitivity, and accuracy of ASL perfusion measurements.
One simple approach to minimizing uncertainty of transit delay is to minimize the delay itself. Minimizing the distance from the labeling plane to the imaging volume can, in principle, decrease the transit delay, however this is only successful if the imaged volume is very thin. Volumetric imaging of the whole brain, for example, will still experience substantial transit delays. Labeling of arteries within the imaged volume itself using velocity selective labeling (11,12) shows promise but it is uncertain whether velocity based ASL will be successful for labeling slowly flowing blood in clinical cases with altered blood flow. Hence significant transit delays remain a challenge of volumetric ASL.
Transit delay and perfusion can be imaged simultaneously by acquiring a series of images with different timing of labeling before imaging. A model of transit delay, perfusion and potentially T1 can be fit to the dynamic signal as a function of labeling time. Dynamics of inflow can be measured by acquiring a series of separate images with different labeling preparation, acquired either sequentially (13–15), or by using Look-Locker techniques that acquire a series of images after a single preparation (16,17) or potentially by Hadamard encoding of the labeling (18,19). Multiple labeling delay imaging is an appealing method to fully characterize the inflow of labeled signal and alternative strategies for perfusion quantification that may be less sensitive to model assumptions have even been proposed based on such time series (17). However, there are two key disadvantages to multiple labeling delay imaging. One is that acquisition of so many images across an entire volume is at the limit of the capabilities of current scanners and often sequences vulnerable to artifacts or blurring are employed to achieve sufficient imaging speed. The second and most fundamental limitation, however, is that the sensitivity to perfusion per unit acquisition time of the time series is always lower than an image acquired with optimal labeling timing. Images derived from fits of multiple data points are also more readily degraded by imperfections in the source images that can decrease the diagnostic value of the derived perfusion images.
This study is based on the observation that transit delay is an inherently low spatial resolution quantity. This low resolution quality of transit delay maps arises because neighboring voxels share common arterial supply for most of the branches leading from the labeling location to the tissue. Low resolution mapping of transit delay can be performed more quickly and sensitively than high spatial resolution mapping. A quick, low resolution transit delay map can be used to guide sequence optimization for a higher resolution acquisition and/or quantification of a qualitative map containing transit and perfusion sensitivity. The focus of this work is primarily continuous ASL (CASL) but many of the concepts can be readily adapted to pulsed ASL (PASL).
THEORY
In the absence of strong magnetization transfer effects from the labeling, the relationship between the CASL signal in tissue and flow is given by (6,13,20):
| [1] |
where ΔM is the CASL difference signal, f is the perfusion rate, and T1a and T1t are the longitudinal relaxation times of blood and tissue. is the fully relaxed equilibrium magnetization of brain tissue, α is the efficiency of the labeling sequence, λ is tissue-to-blood partition coefficient of water, δ is the transit delay, τ is the labeling duration and w is the post-labeling delay. Suppression of vascular signals is assumed in this model. β has been added to the kinetic model to compensate for any static tissue signal loss caused by the vessel suppression pulses.
If the transit delay is not precisely known or measured, then ASL measurements are typically optimized to reduce transit delay dependence. As long as the T1 of tissue and blood are similar and the post-labeling delay is longer than all transit delays, ASL perfusion measurement has only weak dependence on transit delay (6). If the transit delay is unexpectedly longer than the post-labeling delay, however, reduced perfusion signal will occur. This signal reduction will be exaggerated if the labeling duration, τ, is short.
Assuming the range of transit delays in the brain is accurately known from a prescan, then the actual ASL measurement should be optimized for signal or signal-to-noise ratio (SNR). From Eq. [1], it is apparent that the maximum ASL signal will occur when the post-labeling delay is less than or equal to the shortest transit delay in the tissue of interest and the labeling duration is infinite. However, increased labeling duration also increases the time required for ASL measurement. ASL signal per unit time is a more reasonable measure for the optimization of the labeling parameters (21):
| [2] |
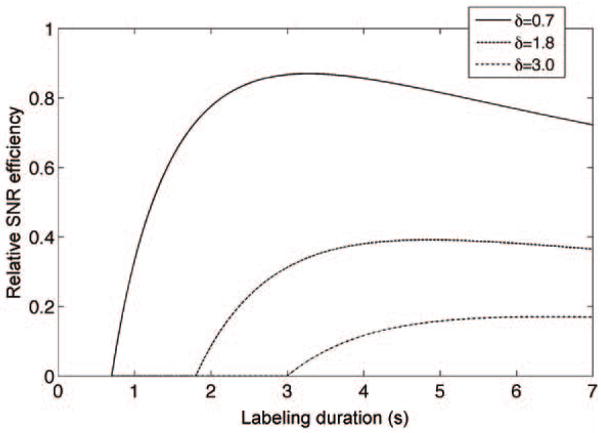
where SNReff is SNR efficiency, τ and w are defined as Eq. [1], and timage is the time for image acquisition. Theoretical curves for the SNR efficiency are plotted for three different transit delays in Fig. 1 assuming the parameters timage = 200 ms, T1b = 1.66 s (22), T1t = 1.5 s (23) and w= 0.7 s.
Figure 1.
Theoretical dependence of SNR efficiency on the labeling duration for different transit delays. A tissue T1 of 1.5 s, a blood T1 of 1.66 s and a post-labeling delay of 0.7 s were assumed.
Note that ΔM is zero if labeling duration plus post-labeling delay is less than the transit delay (from Eq. [1]), the labeling duration plus post-labeling delay need to be designed much longer than the longest transit delay (the lower limit) to be SNR efficient. As shown in Fig. 1, the theoretical SNR efficiency is at or near a maximum when the labeling duration is long compared to tissue T1. Very long labeling duration decreases SNR efficiency only slightly for very short transit delay regions, but greatly increases signal in the longest transit delay images. Hence using a post-labeling delay shorter than or equal to the shortest transit delay in tissue and a labeling duration more than twice T1 plus the post-labeling delay should be nearly optimal for a broad range of tissue transit delays.
MATERIALS AND METHODS
Overview
In this study, two separate imaging studies were performed. The first protocol was to assess the basic hypothesis that the transit delay map contains little high-resolution information by comparing the transit delay maps quantified with a series of quick, low resolution ASL scans and time-consuming high-resolution ASL scans. The second study was to evaluate the feasibility of using a series of quick, low-resolution ASL scans to measure transit delay as part of a longer, high-resolution ASL perfusion acquisition. Two possible uses of the transit delay map were considered; either to use the transit delay map to correct for the transit delay in the quantification of short post-labeling delay ASL images, or to determine the optimal post-labeling delay time prior to acquisition to assure that the delay is longer than the transit delay to any tissue in the brain. Scans were evaluated in a series of healthy volunteers.
Pulse Sequences
ASL Preparation
Pulsed-continuous arterial spin labeling (pCASL) was used for all labeling (24). This technique used repeated RF and gradient pulses to achieve truly continuous labeling but with a lower RF duty cycle compatible with the pulsed RF amplifiers used on most human scanners. In this study, an average RF amplitude of 17 mG, an average gradient of 0.07 G/cm, and a ratio of gradient during the RF to average gradient (Gmax/Gave in ref. 24) of 10 were used. A repetition time for the labeling of 1.5 ms was used. The pCASL sequence with short post-labeling delay (Fig. 2a) was repeated from 5 seconds before imaging until 700 ms before imaging, with the background suppression pulses interleaved within the sequence (25). The labeling duration and post-labeling delay of the sequence was controlled by turning off the RF and gradients during times when labeling was not desired. Whether label or control was performed was controlled by setting the amplitude and phase of the RF pulses and the amplitude of the rewinder gradient pulse (24).
Figure 2.
(a) A schematic of the long labeling sequence combined with background suppression. The selective region of the 90° saturation pulse and two 180° selective pulses are the imaging region with extension to the labeling plane. The 90° inferior saturation pulse acts on the region below the labeling plane. The control and label block are comprised of rapidly repeated gradient and RF pulses in PCASL; and (b) Vessel suppression sequence diagam. The middle two 180° pulses are adiabatic pulses, which are less sensitive to B0 and B1 inhomogeneities. 400 μs gaps were used after the gradients (shown as the dashed lines) to reduce the effect of eddy currents. A gap between the second and third segments of gradient was added to satisfy the gradient echo condition. The sequence was applied just before the spiral acquisition in (a).
Background Suppression
Background suppression (26) was achieved using spatially selective saturation and inversion pulses. Saturation of the imaged slab was performed with three selective 10-ms duration, 12.5-kHz bandwidth quadratic phase saturation pulses applied 17-ms apart with crushers along alternate directions between them. The final pulse of the three saturation pulses was applied at 5 s before imaging. Subsequently, two selective FOCI inversion pulses (27,28) and two nonselective Silver-Hoult inversion pulses were applied at 3560, 1730, 660, and 180 ms before imaging. The timing of the pulses was optimized to achieve excellent suppression across a broad range of T1’s using a least square optimization algorithm (29). The FOCI pulses were of C shape with duration 15.36 ms and bandwidth 1.08 kHz (β = 809 s−1, μ = 6.2) (30) and the selective region of the FOCI pulses were the slab centered at the center of the imaging slab and extended to the labeling plane in the inferior direction. The last two inversion pulses were hyperbolic secant (Silver-Hoult) pulses (μ = 4.5, β = 1242 s−1) of duration 10 ms and were nonselective to extend background suppression to spins below the brain. Suppression of inferior spins helps to eliminate artifacts caused by aliasing of spins just outside the volume. A selective pulse that saturates the water protons inferior to the labeling plane was applied at 320 ms before image acquisition to suppress inferior signals and avoid the inflow of unsuppressed and unlabeled blood into the imaged volume.
Because the first two background suppression pulses were applied during the labeling period, a special strategy to preserve ASL signal was required. The strategy draws from the observation that each inversion pulse reverses sign of the control minus label difference signal. Switching from label to control (or visa versa) after each inversion will continue to add to the perfusion difference image (31,32). Hence our “label” image was acquired with labeling performed between the saturation and first inversion pulse, control performed between the first and second inversion pulse, and label performed until 700 ms before imaging. The “control” image was acquired with label and control switched relative to the “label” image.
Vessel Suppression
The presence of intravascular signal in the subtraction (control minus labeled) images causes systematic errors in CASL techniques. To derive the transit delays from different post-labeling delays, it is necessary to eliminate the intravascular contamination, especially for the early delays. Bipolar gradients in echo-planar imaging have been employed to spoil the intravascular signal (33,34), however inclusion of bipolar gradients at the beginning of our repeatedly RF refocused sequence caused substantial motion related artifacts (data not shown). These artifacts likely resulted from motion induced phase shifts that violated the Carr Purcell Meiboom Gill (CPMG) phase condition (35). These artifacts were reduced with the preparation sequence. Moreover, the ability to use adiabatic pulses in the preparation increases the efficiency of vessel suppression substantially. Therefore, we implemented a preparation sequence (Fig. 2b) before the imaging sequence to eliminate the fast flowing spins in arteries. The preparation is essentially identical to a velocity selective saturation sequence used in velocity selective ASL (11). After an initial 90° pulse, two adiabatic inversion pulses are applied to achieve an echo at which time a −90° is applied to return magnetization to the longitudinal direction. Gradients are applied in the superior-to-inferior direction to provide a flow sensitive phase shift that induces a loss of signal for flowing spins. For laminar flow in a vessel, the signal from that vessel will be attenuated by a sinc function of maximum velocity. The strength of the dephasing can be characterized by the maximum vessel velocity, Vc, at which the sinc function is at its first zero. Vc is given by Eq. [4] in the reference (12).
In our implementation, the two 90° pulses were 400μs hard pulses and the two adiabatic pulses were hyperbolic tangent pulses of 3.2 ms duration (36,37). 400 μs was inserted between the gradients and RF pulses (shown as the dashed lines) to reduce artifacts from eddy currents that were observed with shorter gaps. The gradient amplitudes were 36 mT/m. Each of the four gradient pulses was of 1.488 ms duration with 360μs rise and fall ramp times. This achieved a Vc of 1 cm/s. An additional crusher gradient was applied immediately after the last 90° pulse to remove unwanted signals from transverse magnetization. The sequence of length 19.25 ms was applied just before the spiral acquisition in Fig. 2a when vessel suppression was selected.
Reference Images
In addition to the ASL difference images, two additional images were acquired for quantification. These are used to provide M0 and T1t for the perfusion quantification using Eq. [1]. These reference images were acquired with the identical imaging sequence but with a different preparation. Instead of the ASL preparation described above, a simple saturation and inversion preparation was used. For the first image, saturation at 2 s before imaging was preformed. This provided a relatively proton density weighted image. The second image was acquired with saturation at 4.3 s and a FOCI inversion pulse applied 1.65 s before imaging. The FOCI pulse was the same as the one used in the background suppression pulse. This timing produced an essentially cerebrospinal fluid (CSF) suppressed image and also provided a T1 weighted image used for T1 and M0 quantification. Because of the large, unsuppressed signal from the 3D volume, the receiver gain was automatically reduced by 30 dB relative to the perfusion acquisition to avoid receiver saturation. The reduced gain was included in the quantification of perfusion. Reference images were acquired with just one average because of their higher SNR.
Imaging Sequence
All perfusion and reference images were acquired with a 3D stack of spirals RARE imaging sequence. Spiral encoding was performed in the axial plane using gradient waveforms generated by an automatic algorithm (38). The spiral gradient waveform was constrained to 4 ms duration and the resolution was determined by the number of spiral interleaves selected. 8 interleaves produced an estimated spatial resolution of 3.07 mm while 1 interleave produced a resolution of 12.08 mm. Each preparation sequence was followed by a 90° excitation pulse and then a series of 44 spin echoes encoded with the same spiral gradient but different slice encoding phase encode gradients. 44 slices of nominally 4 mm thickness were encoded with a centric phase encode order. The echo spacing was 9.8 ms and the refocusing flip angle was 130° with the first refocusing pulse set to 155° to speed the transition to a steady-state echo amplitude. The total repetition time of the ASL preparation and imaging combination was 7 s.
In vivo Measurements
All volunteers were imaged on a 3 Tesla EXCITE HDx (GE Healthcare, Waukesha WI) using an 8 channel head coil receive array and the body transmit coil for transmission, following a protocol approved by the institutional committee on clinical investigations and after obtaining written informed consent. Two separate imaging studies were performed. Both protocols began with a 3-plane localizer to define the anatomy of interest. Based on this localizer, a 3D volume from the base of the cerebellum to the location above the top of the head was prescribed for the rest of the study. The labeling plane was automatically placed 18 mm below this volume by the pulse sequence software.
Four healthy volunteers (two males and two female, 23–40 years old 31.25 +/−8.06) were imaged in the first study to test the hypothesis whether the transit delay is inherently low-resolution quantity. After the localizer, the low-resolution transit delay measurement acquisition and 3 high-resolution transit delay measurement acquisitions were performed. The low-resolution acquisition (12.08 mm resolution) required just one interleave and one average per label-control pair, the total time for acquiring the 5 images was 84 sec. Each high-resolution acquisition (3.07 mm resolution) used 8 interleaves and one average per label-control pair, the total time for acquiring the images was 9 min 30 sec. For high-resolution measurements, this 9 min 30 sec acquisition was repeated 3 times to increase signal to noise ratio. By stepping through delays first and then repeating the acquisition for averaging, the time gap between two consecutive post-labeling delays was minimized. The three acquisitions at each delay were then averaged for subsequent analysis. Both low-resolution and high-resolution sequences sequentially acquired pCASL difference images with labeling duration of 2 s and post-labeling delays of 0.7 s, 1.3 s, 1.9 s, 2.5 s, and 3.0 s to obtain the arterial transit delay. Vessel suppression was applied in both sequences to measure the blood transit delays from the labeling plane to small capillaries, with maximum vessel velocity of 1 cm/s.
Five different subjects (four males and one female, 21–29 years old 25.20 +/−3.35) were imaged in the second study to test the feasibility of using the low-resolution ASL scans to measure transit delay as part of a longer, high resolution ASL perfusion acquisition. After the localizer, the low-resolution transit delay measurement acquisition was performed as in the first study. The reconstructed images from this sequence were quickly transferred to a workstation to perform an analysis of the optimal post-labeling delay.
After the transit delay measurement sequence, a short post-labeling delay (700 ms) and long labeling duration (4.3 s) sequence was performed with 8 interleaves and 3 averages. Vessel suppression was applied to eliminate the labeled blood in vessels that would normally occur at this delay. Vessel suppression was also applied before the reference images. Reference images were automatically acquired at the same resolution as the perfusion images.
Finally, 2 acquisitions of 8 interleaves and 3 averages were performed with labeling started 5 s before imaging and halted at the post-labeling delay suggested by the quick analysis of the transit delay measurement sequence, which we will refer to as the optimal post-labeling delay in the following. One acquisition was performed with and one without vessel suppression. Reference images were acquired both with and without vessel suppression as well.
Image Analysis
Image Reconstruction
All the image data were reconstructed by a custom IDL reconstruction routine using a standard regridding algorithm. The data were regridded into forty-four 4-mm thick slices. Each slice was regridded into a 128 × 128 matrix.
Calculation of the Transit Delay Map
In principle, arterial transit delay can be calculated by fitting the ASL signal difference as a function of the post-labeling delay (w) to Eq. [1]. However, nonlinear least square fits were found to lack robustness to imperfections in the data (may produce completely unrealistic transit delay values). Instead, we calculated the signal weighted delay:
| [4] |
where wi (i =1, …,5) is the post-labeling delay that we used in the transit delay scan, ΔM(δ, wi) is the pCASL difference signal with transit delay δ at the post-labeling delay wi. This simple first moment calculation proved to be very robust. Numerical comparison of the signal weighted delay with theoretical signal curves using Eq [1] was performed for a range of transit delays. For this comparison, the blood relaxation time, T1a, was assumed to be 1.66 s (22) and a tissue relaxation time, T1t, of 1.5s corresponding to gray matter (23) was assumed. Gray matter T1 was chosen since white matter perfusion is a small contribution to the brain CBF. The signal weighted delay, WD, was found to be a simple monotonic function of assumed delay, Fig. 3, that could be numerically inverted to calculate transit delay from WD. Calculated transit delays less than 0.7 s or larger than 3.0 s were truncated to 0.7 s and 3.0 s, respectively.
Figure 3.
Theoretical signal weighted delay as a monotonically increasing function of transit delay. A tissue T1 of 1.5 s and a blood T1 of 1.66 s were assumed.
The transit delay maps were calculated from both low-resolution and high-resolution acquisitions. High-resolution transit delay maps were calculated from the perfusion difference images averaged over three high-resolution acquisitions. In order to address whether pixel-by-pixel signals from multiple post-labeling delays have sufficient SNR to resolve the transit delays, Goodness of fits to the ASL kinetic model (ASL difference signal as a function of post-labeling delay), R square maps, were calculated for both high-resolution and low-resolution image acquisitions in the first study.
Analysis of Low-resolution and High-resolution Transit Delay Maps
For each subject in the first study, the high-resolution perfusion difference map was normalized to the a priori gray matter template of SPM2 (http://www.fil.ion.ucl.ac.uk/spm/) using SPM2 software. The warping parameters of each subject from the normalization were used to warp both low-resolution and high-resolution transit delay maps from that subject to the SPM2 template space (voxel size: 2 × 2 × 2 mm3). The transit delay maps were then smoothed, using a Gaussian kernel of 2 mm full width half maximum, in preparation for statistical analysis. The small Gaussian kernel was used in order to introduce the minimal smoothing effect to high-resolution transit-delay map but allow the estimation of local smoothness in SPM2. The smoothed high-resolution and low-resolution transit delay maps were tested for significant differences using paired t tests of SPM2 software. Corrected cluster-level analysis was performed to correct for multiple comparisons. Clusters displayed on statistical parametric maps were thresholded at a corrected cluster level of P < 0.001 by using a voxel-level threshold of p < 0.001.
Estimation of the optimal post-labeling delay
After transferring the data from the transit delay acquisition to a workstation, a semi-automated algorithm was used to determine the longest transit in the brain. This was then used to select the post-labeling delay for the subsequent acquisitions. The algorithm began by identifying the brain and dividing it into 8 regions.
First, the brain must be identified in the images. Since our multiple-delay prescan did not include anatomical images, our algorithm used the perfusion signal to define a brain mask. To avoid errors in the algorithm due to unpredictable signals near the base of the volume, the most inferior and superior slice number in which brain could be readily identified were determined by the user through visual inspection of the average of the 5 delay images. These values were then typed into the program. This was the only human intervention in the algorithm. In each slice, the maximum signal of the average perfusion difference image (across delays) was calculated. A binary mask was then generated for that slice with the value 1 for all pixels with signal greater than 20% of the maximum signal and zero for all other pixels. A clustering algorithm identified all cluster with radius less than three pixels or with connections to the edge of the image and removed them. Subsequently any holes in the remaining clusters were filled to generate a brain mask. In our study with normal volunteers, the 20% masking threshold, combined with a hole-filling algorithm reliably created a brain mask. There is a potential that this algorithm could leave out low flow lesions in some patients. Future prescan may contain a low-resolution anatomical image to help with this process.
After the brain was identified, it was automatically divided into eight regions. The middle slice number was calculated from the average of the start and end slice numbers. The center of gravity of the middle slice was selected as the center point. Three-dimensional coordinate axes with the origin at the center point divided the brain into 8 separate regions. The transit delay in each of these regions was then estimated identically to the pixel-by-pixel method described above. The optimal post-labeling delay was then defined as the value of the longest transit delay from the 8 brain regions.
Measurement of T1 Map and Proton Density Map
The signal MPD from the proton density weighted image is given by the saturation recovery equation:
| [5] |
where is the fully relaxed equilibrium magnetization of brain tissue, and tsatp is the time for the application of the saturation pulse in the proton density weighted sequence. The signal MT1 from the T1 weighted image is given by the inversion recovery equation:
| [6] |
where tsat and tinv are the times for the application of the saturation pulse and inverse pulse in the T1 weighted sequence. can be eliminated by taking the ratio of the above two equations:
| [7] |
The ratio of the T1 weighted image to proton density weighted image is a monotonically decreasing function of T1t and is therefore an invertible function of T1t. A tissue T1 map (T1t) can be obtained from the ratio of T1 weighted image to proton density weighted image. The proton density map ( ) can then be calculated from Eq. [5].
Attenuation of Static Tissue with Vessel Suppression Sequence
The vessel suppression preparation causes some attenuation of static tissue due to T2 decay during the time between 90° pulses. In our studies, the vessel suppression was also performed before the two reference images so they should have a comparable attenuation. Hence the static tissue signal loss with the vessel suppression preparation, β in Eq. [1], cancels out upon division by the reference image. Still, we are able to estimate the efficiency by comparing the reference images obtained with and without the vessel suppression preparation. Results for the efficiency in gray and white matter regions were measured.
Perfusion Quantification with Transit Delay Correction
Perfusion (f) can be calculated based on Eq. [1] from the ASL signal difference (ΔM), the transit delay map (δ), the proton density map ( ), and tissue T1 map (T1t) by assuming T1 of blood (T1b) is 1.66 s (22) and tissue-to-blood partition coefficient, λ, is 0.9 ml of blood/g of tissue (39). The labeling efficiency is reduced by the inefficiency of the background suppression inversion pulses. The background suppression efficiency was measured to be 0.75 for four adiabatic inversion pulses (36). The PCASL labeling efficiency was assumed to be 0.8 (24). All perfusion images acquired were quantified using the measured transit delay map and Eq. [1].
Perfusion Quantification with the Standard Method
Perfusion is typically quantified by assuming similar values between the T1’s of blood and brain tissue and that the post-labeling delay is longer than the transit delays in the brain. Then the ASL signal can be simplified from Eq. [1] by assuming the transit delay is the same as the optimal post-labeling delay:
| [8] |
The images acquired with the longer post-labeling delay, both with and without vessel suppression, were also quantified using this standard model and ignoring the measured transit delay map. The standard method was not used to quantify the perfusion from the images with short post-labeling delay because the assumption of a post-labeling delay longer than the transit delays will be violated.
Regional Analysis
For each subject, the non-vessel-suppressed perfusion map quantified with the standard method was normalized to the a priori gray matter template of SPM2 using SPM2 software. The warping parameters of each subject from the normalization were used to warp all quantitative perfusion maps and the transit delay map from that subject to the SPM2 template space. Standard MNI Automated Anatomical Labeling (AAL) atlas (40) was used to generate regional masks for four regions of interest: inferior frontal, superior medial frontal, occipital and basal ganglia. Each anatomical mask was projected onto the perfusion images and the transit delay map to calculate the average perfusion values and transit delays. In addition to these regions, manually drawn regions of gray matter and white matter were defined on a slice just above the third ventricle. The average perfusion values and transit delays were also calculated for the gray matter and white matter regions.
RESULTS
Analysis of Low-resolution and High-resolution Transit Delay Maps
Representative high-resolution transit delay maps are compared to the low-resolution transit delay maps, in Fig. 4a and Fig. 4b. The images are qualitatively similar but a difference image (Fig. 4c), generated by subtracting the low-resolution transit delay maps from the high-resolution transit delay maps, suggests longer transit delays in the choroid plexus of the lateral ventricles and deep white matter regions. However, map of the R square, goodness of fit calculated from the high-resolution acquisitions shows negative values in choroid plexus and white matter regions (Fig. 4d). Negative R square values mean that the fitting of multiple post-labeling delay signals to the kinetic model is even worse than for a horizontal line. This indicates that the high-resolution multiple delay images do not have sufficient SNR to estimate transit delays on the choroid plexus and white matter regions. For low-resolution images, the R square map (Fig. 4e) has positive values in all brain regions but lower values in very deep white matter regions. This higher R square reflects a combination of higher SNR and blurring in of nearby gray matter perfusion.
Figure 4.
Images obtained from high-resolution and low-resolution transit delay acquisitions: (a) transit delay map with high-resolution acquisition, in seconds; (b) transit delay map with low-resolution acquisition, in seconds; (c) subtraction images between high-resolution and low-resolution images (multiplied by 3 for better visibility), in seconds; (d) R square map from the fitting of high-resolution acquisitions; (e) R square map from the fitting of low-resolution acquisition.
Cluster-level analysis using SPM revealed that compared to low-resolution transit delay maps high-resolution transit delay maps have significant longer transit delays in part of choroid plexus of lateral ventricle and white matter regions (not shown), where high-resolution multiple delay acquisitions do not have enough SNR to obtain reliable transit delay values. This indicates that the longer transit delays measured in the high-resolution multiple delay images within the choroid plexus and the deep white matter primarily reflect a statistical bias because they do not have sufficient SNR to estimate transit delays and the low-resolution multiple delay images can more accurately estimate transit delays except, perhaps, in very deep white matter regions.
Estimation of the Optimal Post-labeling Delay
In each subject, a quick estimate of the optimal post-labeling delay was obtained to guide selection of the post-labeling delay. The average optimal post-labeling delay across the five volunteers was 1.52 ± 0.08 (from 1.41 s to 1.67 s). The transit delays estimated for the eight automatically divided regions are listed in Table 1. The mean of the pixel-by-pixel calculated transit delay values across the regions are also listed in Table 1 for comparison. The regional transit delays based on the whole region and pixel average are in excellent agreement, supporting the use of the large regions to estimate transit delay. Estimation of transit delay using large region was also supported in the literature (41). No significant transit delay differences between left and right were observed. Posterior regions had longer transit delays than anterior regions. Paired t-tests showed the significance of transit delays between anterior regions and posterior regions: p value of 0.014 for left inferior region, of 0.032 for right inferior region, of 0.003 for left superior region, and of 0.002 for right superior region. Superior regions had longer transit delays than inferior regions. Paired t-tests showed the significance of transit delays between superior regions and inferior regions: two-tailed p value of 0.003 for left anterior region, of 0.031 for left posterior region, of 0.010 for right anterior region, and of 0.034 for right posterior region.
Table 1.
Transit delays calculated from eight regions
| Regional transit delay | L Inf * Ant |
L Inf Pos |
R Inf Ant |
R Inf Pos |
L Sup Ant |
L Sup Pos |
R Sup Ant |
R Sup Pos |
|---|---|---|---|---|---|---|---|---|
| Based on whole region | 1.10 ± 0.14 | 1.30 ± 0.15 | 1.15 ± 0.12 | 1.38 ± 0.14 | 1.26 ± 0.14 | 1.44 ± 0.12 | 1.31 ± 0.09 | 1.52 ± 0.08 |
| Based on pixel average | 1.14 ± 0.14 | 1.34 ± 0.15 | 1.19 ± 0.10 | 1.41 ± 0.13 | 1.26 ± 0.15 | 1.42 ± 0.14 | 1.31 ± 0.09 | 1.53 ± 0.09 |
Inf: inferior; Sup: superior; Ant: anterior; Pos: posterior; L: left; R: right.
Transit Delay Maps
Representative multiple delay images and the corresponding calculated transit delay map are shown in Fig. 5. As expected, the basal ganglia region had shorter transit delays than other gray matter regions. Posterior regions had longer transit delays than anterior regions. The quantitative transit delays for the regions of interest (Table 2) support these basic observations. Paired t-tests showed two-tailed p-values less than 0.0015 between the basal ganglia region and the other three regions, and p-values less than 0.003 between the occipital region and the other three regions. In addition, the white matter region showed a trend towards a longer transit delay than gray matter but did not reach statistical significance.
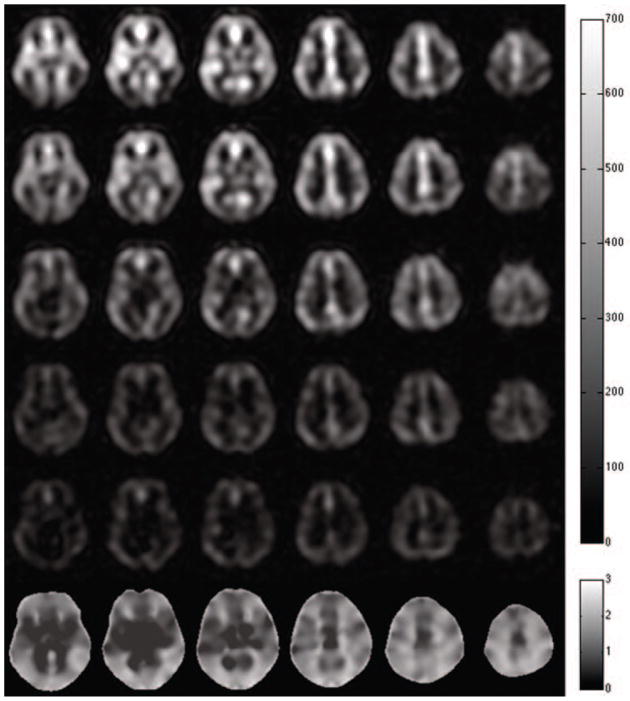
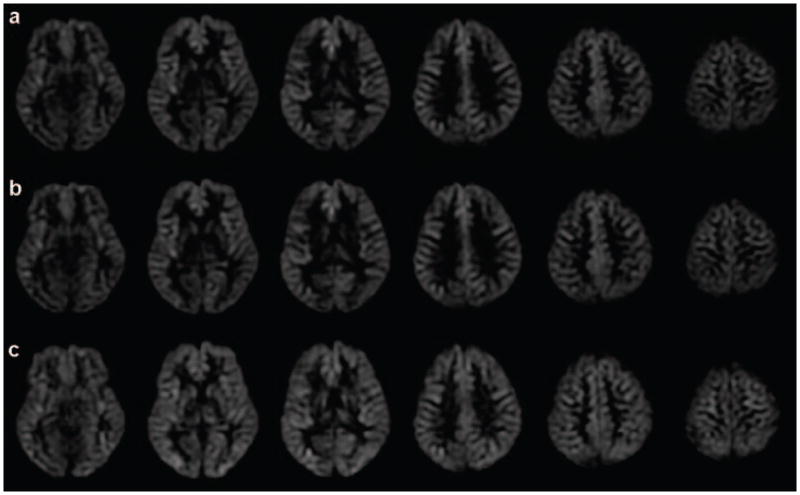
Figure 5.
The subtraction images, in arbitrary units, with constant labeling duration of 2.0 s but different delays: (a) 0.7 s, (b)1.3 s, (c) 1.9 s, (d) 2.3 s, (e) 3.0 s respectively, and (f) the transit delay map, in seconds, calculated from the subtraction images of multiple different delays.
Table 2.
Transit delays and perfusion values for the regions of interests.
| Inferior frontal | Superior medial frontal | Occipital | Basal ganglia | Gray | White | |
|---|---|---|---|---|---|---|
| Transit delay (s) | 1.16 ± 0.08 | 1.24 ± 0.17 | 1.68 ± 0.06 | 0.87 ± 0.10 | 1.41 ± 0.18 | 1.56 ± 0.09 |
| Transit corrected perf + (SD*) | 48.9 ± 2.2 | 53.3 ± 5.7 | 39.7 ± 4.8 | 40.2± 1.8 | 60.9 ± 5.6 | 21.3 ± 1.2 |
| Transit corrected perf (LD wo. VS*) | 49.8 ± 6.9 | 51.5 ± 6.6 | 54.0 ± 11.0 | 47.9 ± 5.5 | 63.5± 8.3 | 19.7 ± 0.9 |
| Transit corrected perf (LD w. VS *) | 49.1 ± 6.1 | 50.0 ± 4.1 | 45.6 ± 6.6 | 48.0 ± 4.6 | 59.7 ± 6.1 | 18.0 ± 1.2 |
| Standard perf (LD wo. VS) | 47.5 ± 6.4 | 51.1 ± 6.7 | 42.7 ± 8.2 | 40.0 ± 4.9 | 62.3 ± 8.4 | 18.1 ± 0.9 |
| Standard perf (LD w. VS) | 47.0 ± 5.6 | 49.6 ± 4.2 | 36.3 ± 4.6 | 40.1 ± 4.5 | 57.9 ± 6.2 | 16.4 ± 1.1 |
SD: Short delay acquisition. LD wo. VS: Longer delay without vessel suppression. LD w. vs: Longer delay with vessel suppression.
perf: Perfusion.
Short Delay Images
Difference images acquired with short delay and vessel suppression show clear variations in perfusion related signal intensity, Fig. 6. Bright signals are apparent in regions with short transit delays such as the basal ganglia and anterior temporal regions. After quantification using the transit delay map, perfusion in gray matter appeared much more uniform across the brain. Static tissue signal loss with the vessel suppression sequence, β in Eq. [1], although not used explicitly in the perfusion quantification, was measured for gray and white matter region: 77.53% ± 1.95% and 77.01% ± 1.87%, respectively. The percentages of tissue signal loss are consistent with the tissue T2 decay (42) and the duration of the vessel suppression sequence.
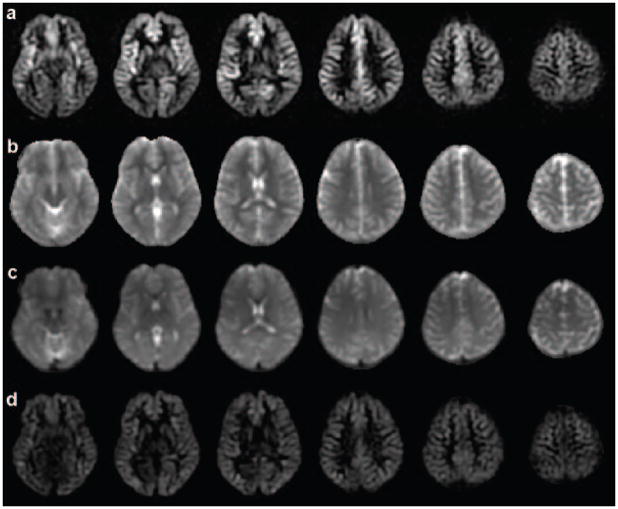
Figure 6.
The images from the short delay: (a) subtraction images from control and label pairs; (b) T1 map calculated from two reference images; (c) proton density map calculated from two reference images; (d) perfusion images with transit delay correction.
Optimal Post-Labeling Delay Images
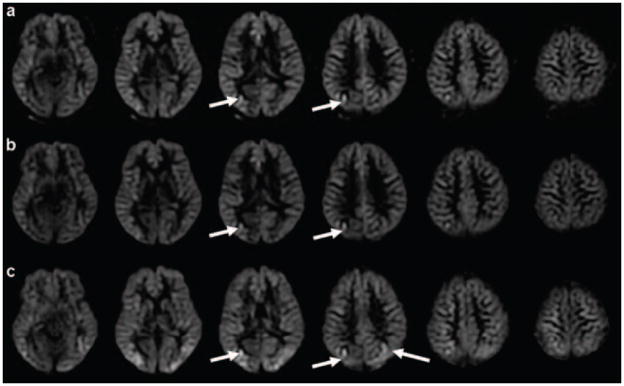
Example ASL difference images and quantitative perfusion images from the optimal post-labeling delay images are shown in Fig. 7 (without vessel suppression) and Fig. 8 (with vessel suppression). Higher signal intensity is present in the difference images without vessel suppression than those with vessel suppression. However, the quantified perfusion images do not show as clear a difference. The similar appearance of the quantified perfusion images between suppressed and unsuppressed images in the majority of the brain regions is presumably because the vessel suppression caused the same efficiency loss in the proton density reference images used for quantification. Even with the longer post-labeling delay, some portion of posterior perfusion signals appears to be contributed from smaller vessels (Vc > 1 cm/s), which can be suppressed with vessel suppression. The bright vessel signals (pointed by arrows in Fig. 7) in the posterior region of the unsuppressed images can be seen both in the difference image and the quantified perfusion images.
Figure 7.
The images without vessel suppression obtained with the optimal delay (the post-labeling delay calculated from multiple delay prescan): (a) subtraction images from control and label pairs; (b) perfusion images with the standard quantification; (c) perfusion images with transit delay correction. The bright vessel signals (pointed by arrows) can be seen both in the difference image and the quantified perfusion images.
Figure 8.
The images with vessel suppression from the optimal delay (the postlabeling delay calculated from multiple delay prescan): (a) subtraction images from control and label pairs; (b) perfusion images with the standard quantification; (c) perfusion images with transit delay correction.
Regional Analysis of Perfusion Images
The quantitative perfusion values for the anatomical regions of interest and the gray and white matter regions are listed in Table 2. Results are reported both for standard quantification and quantification with transit delay correction. The two-tailed p-values from the paired t tests between selected different perfusion quantifications are shown for the anatomical regions of interest and the gray and white matter regions in Table 3.
Table 3.
Statistical comparisons between different perfusion measures for the regions of interests
| Significance (p values) | Inferior frontal | Superior medial frontal | Occipital | Basal ganglia | Gray | White |
|---|---|---|---|---|---|---|
| Transit corrected (SD) vs. (LD w. VS) | 0.9540 | 0.3695 | 0.0319 | 0.0270 | 0.7370 | 0.0059 |
| Transit corrected vs. Standard (LD w. VS) | 0.0025 | 0.2845 | 0.0018 | 0.0004 | 0.0196 | 0.0089 |
| Transit corrected (SD) vs. Standard (LD w. VS) | 0.4262 | 0.3105 | 0.0433 | 0.9431 | 0.4488 | 0.0026 |
SD: Short delay acquisition. LD w. vs: Longer delay with vessel suppression. The p values with black fonts indicate statistically significance with threshold of 0.05.
Quantitative values derived from images acquired without vessel suppression were consistently higher than for similar images acquired without vessel suppression, but this difference did not reach significance except in the occipital region quantified with transit delay correction (p = 0.042). Since vessel suppression should reduce ASL signal, the general trend is expected. Because transit delays were measured with vessel suppression and the quantification assumes the ASL signal decays with T1 of tissue after arrival, we focus on the vessel suppressed images for the comparisons below.
Quantification of the optimal post-labeling delay images using the transit delay maps produced significantly higher perfusion values than the standard quantification approach in all regions except the superior medial frontal. The standard quantification will give underestimation both for transit delay longer than the post-labeling delay, because of incomplete arrival of the labeled blood, or shorter than the post-labeling delay, because the label decays with the shorter T1 of tissue after it arrives rather than the T1 of blood assumed by the quantification.
Comparison of quantitative values obtained using the transit delay maps applied to the short and optimal post-labeling delay images revealed relatively few differences. Perfusion was measured to be significantly lower in the basal ganglia and occipital regions and significantly higher in the white matter region when using the short delay images. These unexpected findings will be considered in the discussion.
DISCUSSION
Our quick low-resolution transit delay measurement adds little extra time to a standard ASL scan yet can obtain a quantitative transit delay map that can be used to optimize or quantify the subsequent ASL scan. Though our transit delay estimation algorithm was only semi-automatic, improved image analysis methods should make automated, real-time calculation of the transit delay possible. We compared two approaches to using transit delay information to improve ASL perfusion measurement. One used an estimate of the maximum transit delay to guide the selection of the post-labeling delay and then used the transit delay measurements to refine the already relatively transit delay insensitive standard quantification. The other employed a very short delay and relied on the transit delay measurements to correct for strong transit delay weighting in the raw ASL images. Both approaches using transit delay information provided higher perfusion values in most regions than the standard quantification approach without transit delay measurement, consistent with the incorrect assumptions of the simpler quantification.
The assumption that transit delay varies slowly with position must ultimately be tested in a range of pathologies. We can suggest two reasons, however, that the assumption is likely to hold. The first is that the local transit delay due to flow in the very small vessels is much smaller than the delay from the labeling plane. Our measured transit delays to tissue are not much larger than transit delays within the major vessel branches performed with an ASL angiography technique (43). ASL based measures of arterial blood volume, an indicator of transit delay since transit delay is blood volume divided by blood flow, suggest that 80% of the arterial blood volume vanishes when dephasing gradients that crush velocities greater than 4 cm/s are applied (44). To the extent that transit through the microvascular arterial blood volume does contribute to transit delay, the literature suggests microvascular transit delays are fairly constant across tissue types. For example, MTT measurements performed with contrast typically show similar values in gray and nearby white matter (45), as well as in tumors (46). Certainly any differences are much smaller than the 3–5 fold greater blood flow in gray matter relative to white matter. These arguments suggest that the contribution of local, small vessel effects to transit delay is both small relative to large artery effects and similar across tissue types and pathologies. Combined with the challenge of achieving sufficient SNR to accurately measure transit delay in low flow tissues like white matter, potential benefits of high-resolution transit time appear minimal.
The optimal post-labeling delay calculated from 8-region transit delay prescan may not be optimal in the pixel-by-pixel sense, because the regional average is always less than the longest pixel-wise transit delay in the region. This can be observed from the longer transit delay in the occipital region than the estimated optimal post-labeling delay. If the purpose of prescan is to guarantee the post-labeling delay longer than the transit delays in the entire brain, an empirical scale factor may be added to increase the ROI estimated regional optimal transit delay, or, alternatively, a pixel-by-pixel transit delay map may be used in the prescan calculation if further tests proved that the pixel-by-pixel based transit time calculation is sufficiently robust to guide the transit delay selection for the perfusion acquisition.
Unanticipated significant differences between the short delay and longer delay approaches were detected in the basal ganglia, occipital and white matter regions. Though further study will be required to determine the cause of the relatively small differences, several effects neglected in the theory may play a role. First, inaccuracies in transit delay measurement may be a major contributor to errors. The transit delay calculated from the signal weighted delay algorithm is somewhat sensitive to the assumed T1 of tissue, as is a more standard least-square fitting algorithm. Due to the shorter tissue T1s in basal ganglia and occipital regions (42,47), the transit delays may be underestimated in those regions (Fig. 9). The underestimation of transit delays will cause underestimation of perfusion values in both approaches but more in short delay approach, which may explain the significant differences in the basal ganglia and occipital regions. Low SNR in deep white matter biased its transit delay towards longer value, which contributes to the overestimation of the perfusion in short delay approach. Second, neglecting the spread, or dispersion, of transit delays in our theory may also contribute to errors in quantification. These effects are likely greatest in regions with long delays, such as the occipital and white matter regions. Though convenient gold standards for transit delay measurement are not available, continued refinement of methods and measurements may permit more detailed assessment of the assumptions involved in the model.
Figure 9.
The effect of tissue T1 on the calculated transit delay (using the signal weighted delay algorithm) when the tissue T1 is deviated from the assumed T1 of 1.5 s: T1t = 1.8 s (solid red) and T1t = 1.2 s (solid blue) with labeling duration of 2 s used for our multiple-delay prescan. With the same multiple delays but labeling duration of 0.6 s, calculated transit delay shows the reduced tissue T1 sensitivity for T1t = 1.8 s (dashed red) and T1t = 1.2 s (dashed blue).
Tissue T1 sensitivity is a potential source of error for transit delay measurement since T1 is not as smoothly distributed as transit delay. However, simulations suggest that this sensitivity to T1 is primarily introduced by the long, 2 s, labeling duration used for our multiple-delay prescan (Fig. 9). The labeling duration of 0.6 s with the same 5 post-labeling delays significantly reduces the sensitivity of transit delay measurement to tissue T1 (Fig. 9). Further optimization of the labeling durations and delays acquired and of the transit time quantification methods are merited to minimize T1 contributions and maximize accuracy of the measurements.
CONCLUSIONS
We have demonstrated the speed and feasibility of a low-resolution prescan approach to measuring transit delay for perfusion imaging with ASL. The transit delay map permits improved quantification and optimization of the image acquisition. Use of this approach may make ASL perfusion images and quantification more robust to the broad range of transit delays present in clinical populations.
To improve absolute perfusion quantification, our results suggest it is desirable to acquire a low-resolution transit delay map combined with a high-resolution perfusion images. We presented several potential approaches to using the low-resolution transit map for acquisition and quantification. Based on our results, choosing an intermediate post-labeling delay (1.5s) and quantifying with the transit time map seems preferable. Our short delay image showed signs of systematic error from fixed tissue T1 assumption and requires additional RF power for limited gain. Our optimal post-labeling delay strategy showed promise, but any errors in the algorithm to select the post-labeling delay could cause a poor selection of acquisition parameters that may compromise scan quality. In addition, the optimal post-labeling delay provides worse SNR than a fixed intermediate delay in regions whose transit delay is shorter than the longest transit delay. Future experience in broad populations of subjects is required before any of these approaches can be proven clearly superior.
Acknowledgments
This work was supported in part by grants CA115745, MH80729, and T32AG023480 from the National Institutes of Health.
References
- 1.Alsop DC, Detre JA, Grossman M. Assessment of cerebral blood flow in Alzheimer’s disease by spin-labeled magnetic resonance imaging. Annals of Neurology. 2000;47(1):93–100. [PubMed] [Google Scholar]
- 2.Detre JA, Alsop DC, Vives LR, Maccotta L, Teener JW, Raps EC. Noninvasive MRI evaluation of cerebral blood flow in cerebrovascular disease. Neurology. 1998;50(3):633–641. doi: 10.1212/wnl.50.3.633. [DOI] [PubMed] [Google Scholar]
- 3.Chalela JA, Alsop DC, Gonzalez-Atavales JB, Maldjian JA, Kasner SE, Detre JA. Magnetic resonance perfusion imaging in acute ischemic stroke using continuous arterial spin labeling. Stroke. 2000;31(3):680–687. doi: 10.1161/01.str.31.3.680. [DOI] [PubMed] [Google Scholar]
- 4.Calamante F, Gadian DG, Connelly A. Quantification of perfusion using bolus tracking magnetic resonance imaging in stroke: assumptions, limitations, and potential implications for clinical use. Stroke. 2002;33(4):1146–1151. doi: 10.1161/01.str.0000014208.05597.33. [DOI] [PubMed] [Google Scholar]
- 5.MacIntosh BJ, Lindsay AC, Kylintireas I, Kuker W, Gunther M, Robson MD, Kennedy J, Choudhury RP, Jezzard P. Multiple inflow pulsed arterial spin-labeling reveals delays in the arterial arrival time in minor stroke and transient ischemic attack. AJNR Am J Neuroradiol. 2010;31(10):1892–1894. doi: 10.3174/ajnr.A2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Alsop DC, Detre JA. Reduced transit-time sensitivity in noninvasive magnetic resonance imaging of Human cerebral blood flow. Journal of Cerebral Blood Flow and Metabolism. 1996;16:1236–1249. doi: 10.1097/00004647-199611000-00019. [DOI] [PubMed] [Google Scholar]
- 7.Wong EC, Buxton RB, Frank LR. Quantitative imaging of perfusion using a single subtraction (QUIPSS and QUIPSS II) Magn Reson Med. 1998;39(5):702–708. doi: 10.1002/mrm.1910390506. [DOI] [PubMed] [Google Scholar]
- 8.Luh WM, Wong EC, Bandettini PA, Hyde JS. QUIPSS II with thin-slice TI1 periodic saturation: a method for improving accuracy of quantitative perfusion imaging using pulsed arterial spin labeling. Magn Reson Med. 1999;41(6):1246–1254. doi: 10.1002/(sici)1522-2594(199906)41:6<1246::aid-mrm22>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 9.Deibler AR, Pollock JM, Kraft RA, Tan H, Burdette JH, Maldjian JA. Arterial spin-labeling in routine clinical practice, part 1: technique and artifacts. AJNR Am J Neuroradiol. 2008;29(7):1228–1234. doi: 10.3174/ajnr.A1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wang J, Licht DJ. Pediatric perfusion MR imaging using arterial spin labeling. Neuroimaging Clin N Am. 2006;16(1):149–167. ix. doi: 10.1016/j.nic.2005.10.002. [DOI] [PubMed] [Google Scholar]
- 11.Wong EC, Cronin M, Wu WC, Inglis B, Frank LR, Liu TT. Velocity-selective arterial spin labeling. Magn Reson Med. 2006;55(6):1334–1341. doi: 10.1002/mrm.20906. [DOI] [PubMed] [Google Scholar]
- 12.Duhamel G, de Bazelaire C, Alsop DC. Evaluation of systematic quantification errors in velocity-selective arterial spin labeling of the brain. Magn Reson Med. 2003;50(1):145–153. doi: 10.1002/mrm.10510. [DOI] [PubMed] [Google Scholar]
- 13.Buxton RB, Frank LR, Wong EC, Siewert B, Warach S, Edelman RR. A general kinetic model for quantitative perfusion imaging with arterial spin labeling. Magn Reson Med. 1998;40:383–396. doi: 10.1002/mrm.1910400308. [DOI] [PubMed] [Google Scholar]
- 14.Gonzalez-At JB, Alsop DC, Detre JA. Cerebral perfusion and arterial transit time changes during task activation determined with continuous arterial spin labeling. Magn Reson Med. 2000;43:739–746. doi: 10.1002/(sici)1522-2594(200005)43:5<739::aid-mrm17>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- 15.MacIntosh BJ, Filippini N, Chappell MA, Woolrich MW, Mackay CE, Jezzard P. Assessment of arterial arrival times derived from multiple inversion time pulsed arterial spin labeling MRI. Magn Reson Med. 2010;63(3):641–647. doi: 10.1002/mrm.22256. [DOI] [PubMed] [Google Scholar]
- 16.Gunther M, Bock M, Schad LR. Arterial spin labeling in combination with a look-locker sampling strategy: inflow turbo-sampling EPI-FAIR (ITS-FAIR) Magn Reson Med. 2001;46(5):974–984. doi: 10.1002/mrm.1284. [DOI] [PubMed] [Google Scholar]
- 17.Petersen ET, Lim T, Golay X. Model-free arterial spin labeling quantification approach for perfusion MRI. Magn Reson Med. 2006;55(2):219–232. doi: 10.1002/mrm.20784. [DOI] [PubMed] [Google Scholar]
- 18.Wells JA, Lythgoe MF, Gadian DG, Ordidge RJ, Thomas DL. In vivo Hadamard encoded continuous arterial spin labeling (H-CASL) Magn Reson Med. 2010;63(4):1111–1118. doi: 10.1002/mrm.22266. [DOI] [PubMed] [Google Scholar]
- 19.Gunther M. Highly efficient accelerated acquisition of perfusion inflow series by cycled arterial spin labeling. Proceedings of the 15th Annual Meeting of ISMRM; 2007. p. p380. [Google Scholar]
- 20.Wang J, Alsop DC, Li L, Listerud J, Gonzalez-At JB, Schnall MD, Detre JA. Comparison of quantitative perfusion imaging using arterial spin labeling at 1.5 and 4. 0 Tesla. Magn Reson Med. 2002;48(2):242–254. doi: 10.1002/mrm.10211. [DOI] [PubMed] [Google Scholar]
- 21.Wong EC, Buxton RB, Frank LR. A theoretical and experiemental comparison of continous and pulsed arterial spin labeling techniques for quantitative perfusion imaging. Magn Reson Med. 1998;40:348–355. doi: 10.1002/mrm.1910400303. [DOI] [PubMed] [Google Scholar]
- 22.Lu H, Clingman C, Golay X, van Zijl PC. Determining the longitudinal relaxation time (T1) of blood at 3. 0 Tesla. Magn Reson Med. 2004;52(3):679–682. doi: 10.1002/mrm.20178. [DOI] [PubMed] [Google Scholar]
- 23.Ethofer T, Mader I, Seeger U, Helms G, Erb M, Grodd W, Ludolph A, Klose U. Comparison of longitudinal metabolite relaxation times in different regions of the human brain at 1. 5 and 3 Tesla. Magn Reson Med. 2003;50(6):1296–1301. doi: 10.1002/mrm.10640. [DOI] [PubMed] [Google Scholar]
- 24.Dai W, Garcia D, de Bazelaire C, Alsop DC. Continuous flow-driven inversion for arterial spin labeling using pulsed radio frequency and gradient fields. Magn Reson Med. 2008;60(6):1488–1497. doi: 10.1002/mrm.21790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dai W, Robson PM, Shankaranarayanan A, CAD Benefits of interleaved continuous labeling and background suppression. Proceedings of Annual Meeting of 18th ISMRM; 2010. p. 1748. [Google Scholar]
- 26.Ye FQ, Frank JA, Weinberger DR, McLaughlin AC. Noise reduction in 3D perfusion imaging by attenuating the static signal in arterial spin tagging (ASSIST) Magn Reson Med. 2000;44(1):92–100. doi: 10.1002/1522-2594(200007)44:1<92::aid-mrm14>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 27.Ordidge RJ, Wylezinska M, Hugg JW, Butterworth E, Franconi F. Frequency offset corrected inversion (FOCI) pulses for use in localized spectroscopy. Magn Reson Med. 1996;36(4):562–566. doi: 10.1002/mrm.1910360410. [DOI] [PubMed] [Google Scholar]
- 28.Yongbi MN, Yang Y, Frank JA, Duyn JH. Multislice perfusion imaging in human brain using the C-FOCI inversion pulse: comparison with hyperbolic secant. Magn Reson Med. 1999;42(6):1098–1105. doi: 10.1002/(sici)1522-2594(199912)42:6<1098::aid-mrm14>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- 29.Maleki N, Dai W, Alsop DC. A systematic approach to optimizing background suppression for arterial spin labeling perfusion imaging. Proceedings of the 16th Annual Meeting of ISMRM; 2008. p. 1929. [Google Scholar]
- 30.Payne GS, Leach MO. Implementation and evaluation of frequency offset corrected inversion (FOCI) pulses on a clinical MR system. Magn Reson Med. 1997;38(5):828–833. doi: 10.1002/mrm.1910380520. [DOI] [PubMed] [Google Scholar]
- 31.Talagala SL, Ye FQ, Ledden PJ, Chesnick S. Whole-brain 3D perfusion MRI at 3. 0 T using CASL with a separate labeling coil. Magn Reson Med. 2004;52(1):131–140. doi: 10.1002/mrm.20124. [DOI] [PubMed] [Google Scholar]
- 32.Alsop DC, ADJ Background Suppressed 3D RARE Arterial Spin Labeled Perfusion MRI. Proceedings of Annual Meeting of 7th ISMRM; 1999. p. 601. [Google Scholar]
- 33.Ye FQ, Mattay VS, Jezzard P, Frank JA, Weinberger DR, McLaughlin AC. Correction for vascular artifacts in cerebral blood flow values measured by using arterial spin tagging techniques. Magn Reson Med. 1997;37(2):226–235. doi: 10.1002/mrm.1910370215. [DOI] [PubMed] [Google Scholar]
- 34.Wang J, Alsop DC, Song HK, Maldjian JA, Tang K, Salvucci AE, Detre JA. Arterial transit time imaging with flow encoding arterial spin tagging (FEAST) Magn Reson Med. 2003;50(3):599–607. doi: 10.1002/mrm.10559. [DOI] [PubMed] [Google Scholar]
- 35.Alsop DC. Phase insensitive preparation of single-shot RARE: application to diffusion imaging in humans. Magn Reson Med. 1997;38(4):527–533. doi: 10.1002/mrm.1910380404. [DOI] [PubMed] [Google Scholar]
- 36.Garcia DM, Duhamel G, Alsop DC. Efficiency of inversion pulses for background suppressed arterial spin labeling. Magn Reson Med. 2005;54(2):366–372. doi: 10.1002/mrm.20556. [DOI] [PubMed] [Google Scholar]
- 37.Hwang TL, van Zijl PC, Garwood M. Fast broadband inversion by adiabatic pulses. J Magn Reson. 1998;133(1):200–203. doi: 10.1006/jmre.1998.1441. [DOI] [PubMed] [Google Scholar]
- 38.King KF, Foo TK, Crawford CR. Optimized gradient waveforms for spiral scanning. Magn Reson Med. 1995;34(2):156–160. doi: 10.1002/mrm.1910340205. [DOI] [PubMed] [Google Scholar]
- 39.Herscovitch P, Raichle ME. What is the correct value for the brain-blood partition coefficient for water? J Cereb Blood Flow Metab. 1985;5(1):65–69. doi: 10.1038/jcbfm.1985.9. [DOI] [PubMed] [Google Scholar]
- 40.Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage. 2002;15(1):273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- 41.Figueiredo PM, Clare S, Jezzard P. Quantitative perfusion measurements using pulsed arterial spin labeling: effects of large region-of-interest analysis. J Magn Reson Imaging. 2005;21(6):676–682. doi: 10.1002/jmri.20329. [DOI] [PubMed] [Google Scholar]
- 42.Lu H, Nagae-Poetscher LM, Golay X, Lin D, Pomper M, van Zijl PC. Routine clinical brain MRI sequences for use at 3. 0 Tesla. J Magn Reson Imaging. 2005;22(1):13–22. doi: 10.1002/jmri.20356. [DOI] [PubMed] [Google Scholar]
- 43.Robson PM, Dai W, Shankaranarayanan A, Rofsky NM, Alsop DC. Time-resolved Vessel-selective Digital Subtraction MR Angiography of the Cerebral Vasculature with Arterial Spin Labeling. Radiology. 2010;257(2):507–515. doi: 10.1148/radiol.10092333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Brookes MJ, Morris PG, Gowland PA, Francis ST. Noninvasive measurement of arterial cerebral blood volume using Look-Locker EPI and arterial spin labeling. Magn Reson Med. 2007;58(1):41–54. doi: 10.1002/mrm.21199. [DOI] [PubMed] [Google Scholar]
- 45.Ibaraki M, Ito H, Shimosegawa E, Toyoshima H, Ishigame K, Takahashi K, Kanno I, Miura S. Cerebral vascular mean transit time in healthy humans: a comparative study with PET and dynamic susceptibility contrast-enhanced MRI. J Cereb Blood Flow Metab. 2007;27(2):404–413. doi: 10.1038/sj.jcbfm.9600337. [DOI] [PubMed] [Google Scholar]
- 46.Nagesh V, Chenevert TL, Tsien CI, Ross BD, Lawrence TS, Junck L, Cao Y. Quantitative characterization of hemodynamic properties and vasculature dysfunction of high-grade gliomas. NMR Biomed. 2007;20(6):566–577. doi: 10.1002/nbm.1118. [DOI] [PubMed] [Google Scholar]
- 47.Gelman N, Ewing JR, Gorell JM, Spickler EM, Solomon EG. Interregional variation of longitudinal relaxation rates in human brain at 3. 0 T: relation to estimated iron and water contents. Magn Reson Med. 2001;45(1):71–79. doi: 10.1002/1522-2594(200101)45:1<71::aid-mrm1011>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]