Evaluating bias correction in weighted proportional hazards regression

Abstract

Often in observational studies of time to an event, the study population is a biased (i.e., unrepresentative) sample of the target population. In the presence of biased samples, it is common to weight subjects by the inverse of their respective selection probabilities. Pan and Schaubel (2008) recently proposed inference procedures for an inverse selection probability weighted (ISPW) Cox model, applicable when selection probabilities are not treated as fixed but estimated empirically. The proposed weighting procedure requires auxiliary data to estimate the weights and is computationally more intense than unweighted estimation. The ignorability of sample selection process in terms of parameter estimators and predictions is often of interest, from several perspectives: e.g., to determine if weighting makes a significant difference to the analysis at hand, which would in turn address whether the collection of auxiliary data was required in future studies; to evaluate previous studies which did not correct for selection bias. In this article, we propose methods to quantify the degree of bias corrected by the weighting procedure in the partial likelihood and Breslow-Aalen estimators. Asymptotic properties of the proposed test statistics are derived. The finite-sample significance level and power are evaluated through simulation. The proposed methods are then applied to data from a national organ failure registry to evaluate the bias in a post kidney transplant survival model.

1 Introduction

In observational studies of time to an event, we often observe partial information. That is, certain information is unavailable for all subjects sampled from the target population. In applications where the model is a predictive equation instead of a causal model and will not apply to populations with different compositions (Kalton 1989), there are several possibilities for the estimation of covariate effects. One method is a complete-case analysis, which assumes that the observed subjects are a representative sample of the target population; “representative” in the sense that the relationship of interest is not systematically distorted in the sample compared to that in the target population. In survival analysis, if there exists some auxiliary factor which is correlated with the covariate of interest and affects the hazard function and selection probability, the coefficient estimates for the covariate of interest (i.e., estimated without considering the auxiliary factor) will be systematically different in the selected sample and target population. Since our goal is to estimate covariate effects in the target population, estimates obtained based on only the selected sample are biased. We hereafter refer to a factor inducing such selection bias as a biasing factor.

We consider the data structure where a potentially biased sample is selected from a representative sample of the target population. In the presence of a biased sample, an alternative to a complete-case analysis is to weight each subject by the inverse of their probability of being selected into the sample, such that the weighted sample reflects the composition of the target population. The inverse-selection-probability-weighting (ISPW) method was originally proposed by Horvitz and Thompson (1952). Binder (1992) and Lin (2000) extended the Horvitz-Thompson method to the hazard regression setting in the context of large-scale surveys or designed experiments, where selection probability for each subject is set beforehand and thus can be treated as known. However, in many practical applications, the probability of being selected is not known. If appropriate auxiliary data are available (in particular, pertaining to the biasing factors) for the representative sample, selection probability may be estimated. Pan and Schaubel (2008) proposed inference procedures for a weighted proportional hazards model with empirical weights. Specifically, selection probabilities are estimated through a logistic model fitted to the representative sample of the underlying target population, assuming the availability of auxiliary data representing the biasing factor. Parameter estimators are consistent for their corresponding underlying target population quantities. Contrary to the fixed-weight estimators in complex multistage design whose standard errors tend to be larger (Kalton 1989), the empirically weighted estimators gain efficiency relative to the unweighted estimators because the estimated weights are essentially trained by the data.

In the presence of a potentially biased sampling mechanism, it is often of interest to compare the weighted and unweighted parameter estimators, for several reasons. First, if the weighted parameter estimators are not significantly different from their unweighted counterparts, practitioners may prefer the unweighted method. Second, the comparison is useful for speculating on the presence of bias in results based on previous unweighted analyses of similar data sets. Third, in the planning of future studies, a comparison of the weighted and unweighted parameter estimators can be used to assess the value of the auxiliary data, which could be costly and/or difficult to obtain.

Here we list several scenarios where the test applies. First, one can make an informed choice between weighted and unweighted models with main effects, then carry out all the fine tuning steps (e.g., assessing functional forms, time dependence, and interactions; sub-analysis, residual diagnosis) with the selected version. Since a large number of models are fitted in model selection and modification process, the amount of computation saved could be substantial. Second, if the proposed comprehensive test is carried out with one representative sample, the conclusion can be extended to other representative samples with a similar data configuration. Taking kidney transplant waiting list data as an example, the test results from year 2000 to 2006 will be applied to year 2007 and thus be useful to policy makers in establishing future allocation policies. Third, this test also serves as a means for informally assessing bias in previous similar but unweighted analyses. Finally, consider the scenario wherein auxiliary data are unavailable to an investigator to fit a weighted model; other researchers with the required auxiliary information could carry out this test and provide the weighted estimators, if necessary, for making unbiased prediction. This final scenario corresponds to our motivating example which we will discuss in the following two paragraphs.

The proposed tests are motivated by kidney transplant data. At the time of this paper, work is well underway to restructure the kidney allocation system. Currently, deceased-donor organs are allocated primarily by waiting time. Under a newly proposed allocation system, organs would be allocated based on the difference between predicted future post-transplant and wait-list lifetime. Hence, there is great need for accurate post-transplant survival models. Note, however, that the model will be applied to wait-listed patients, not to transplanted patients. That is, the model will be used to predict the post-transplant lifetime of a wait-listed patient with a given covariate pattern; as opposed to patients with the same covariate pattern who received transplants through a possibly biased selection mechanism. Therefore, the target population consists of patients on the wait-list, not of transplant recipients.

Naturally, not all wait-listed patients will receive a transplant. If we desire to develop a model to apply to wait-listed candidates, post-transplant information is missing for candidates who were not transplanted. The goal is to estimate the effects of patient characteristics on the post-transplant hazard. Patients on the kidney waiting list are not randomly selected for transplantation. Although patients on dialysis who are not considered suitable candidates for transplantation are simply not placed on the wait list, the screening process does not end with the decision of whether or not to wait-list a patient. Certain patients are systematically bypassed on the list since they are felt to be inferior candidates for kidney transplantation, often due to the progression of concomitant illnesses which occur or further develop after the time of wait-listing. Therefore, patients transplanted with a specific covariate pattern are generally thought not to be representative of patients on the waiting list with the same covariate pattern. Hospitalization data represent a rich source of auxiliary data which could potentially account for the residual difference between patients selected to receive transplants and those left on the waiting list. At the Scientific Registry of Transplant Recipients (SRTR), it is possible to merge the wait-list/transplant data obtained from the United Network for Organ Sharing (UNOS) and the hospitalization data obtained from the Centers for Medicare and Medicaid Services (CMS). Therefore, we are able to estimate selection probabilities, treating the hospitalization information as the potential biasing factor. It is important to note that UNOS will not have real-time access to hospitalization histories, meaning that a post-transplant survival model which included covariates for hospitalization history would be of no value for deciding which patients should receive a kidney transplant under the new allocation system. Our objective is to evaluate the degree of bias in a model which is intended to apply to wait-listed patients but is fitted only to transplanted patients and has no adjustment for the potentially biased selection. We can fit the ISPW proportional hazards model of Pan and Schaubel (2008), using hospitalization history to predict transplant probabilities. The issue of whether or not the weighted model is necessary will be addressed by our proposed tests. In cases where the unweighted estimators are significantly different from the weighted ones, thus biased, a set of marginal regression coefficient estimates from the weighted model could be provided to UNOS, circumventing the need for hospitalization history to obtain unbiased predictions of post-transplant survival.

Tests for the presence of selection bias have been studied by previous authors. Pfeffermann (1993) pointed out that significant differences between the weighted and unweighted estimators essentially means that the sampling process cannot be ignored. In a fundamental paper by Rubin (1976), such conditions are “missing at random” and “observed at random”. Pfeffermann and Sverchkov (2003) studied different tests for the ignorability of the sampling design in survey studies.

The tests proposed in the current paper concern the ignorability of the selection process with respect to a subset of the regression coefficient vector; as a special case, the subset could include the entire vector. That is, under the proposed procedures, one would test whether the selection mechanism leads to a significantly different set of regression coefficients (the set including the elements of interest), excluding other covariates not of interest. In the motivating example, covariates of interest would include predictors of post-transplant survival that will be used to rank wait-listed candidates. Race would be an example of an adjustment covariate not of interest. That is, to avoid preferentially allocating to various race subgroups, race would not be present in the models used to predict survival probability. Excluding covariates not of interest from the test can potentially lead to greater power. With respect to the regression parameter, a single test is prescribed, such that only one model, either weighted or unweighted, would be chosen.

The remainder of this paper is organized as follows. In Section 2, we propose test statistics for the regression parameter and cumulative baseline hazard and describe their asymptotic properties (proved in the Web Appendix). In Section 3, the empirical significance level and power of the proposed test for the regression parameter are evaluated in simulation studies. In Section 4, each of the proposed procedures are applied to the kidney transplant data from a national organ failure registry. The proposed methods are further discussed in Section 5.

2 Proposed Inference Procedures

2.1 Set-up and notation

We start by establishing the necessary notation. First, there are N subjects in the representative sample from the target population. We let I_i (0, 1) be a sampling indicator; i.e., I_i = 1 if the ith subject is selected from the representative sample into the possibly biased study sample. In total there are $n={\sum }_{i=1}^N{I}_i$ subjects selected. For subject i with event time T_i and censoring time C_i, we define T̃_i = min(T_i, C_i), Δ_i = I(T_i ≤ C_i), Y_i(t) = I(T̃_i ≤ t), $N_i(t)=I({\stackrel{\sim }{T}}_i\le t,{\mathrm{\Delta }}_i=1)={\int }_0^t{dN}_i(s)$; with dN_i(t) = N_i(t + dt) − N_i(t), where τ is a pre-specified constant satisfying P(T̃_i > τ) > 0 and usually set to maximum follow-up time, to include all event times. The proportional hazards model applicable to the target population is as follows,

$${\lambda }_{iT}(t)={\lambda }_{0T}(t)e^{{\beta }_T^{\prime }{Z}_i(t)},$$ (1)

where λ_0T (t) is an unspecified baseline hazard and Z_i(t) is a p × 1 covariate vector. The proportional hazards model which applies to the selected sample is given by

$${\lambda }_{iS}(t)={\lambda }_{0S}(t)e^{{\beta }_S^{\prime }{Z}_i(t)},$$ (2)

where λ_0S(t) and β_S are the possibly biased version of the parameters of interest. The constants of proportionality are potentially different, as too are the baseline hazards. The hypothesis tests of interest in this report are (i) H₀: β_T = β_S vs H₁: β_T ≠ β_S and (ii) H₀: λ_0T (t) = λ_0S(t) vs H₁: λ_0T (t) ≠ λ_0S(t) for t ∈ [0, τ].

The selection probabilities are estimated through a logistic model:

$$p_i({\theta }_0)=\frac{e^{{\theta }_0^{\prime }{X}_i}}{1+e^{{\theta }_0^{\prime }{X}_i}},$$

where θ₀ is the true parameter vector and X_i is the corresponding q ×1 vector of predictors. The weight is then given by w_i(θ₀) = I_i p_i(θ₀)⁻¹. Ideally, X_i is the set of all biasing factors; that is, all factors that are predictive of selection probability and survival time and correlate with the covariates of interests. If unmeasured biasing factors exist, consistent estimators of θ₀ and hence β_T are unobtainable.

Note that proportionality is assumed for both model (1) and model (2). In most cases, proportionality won’t hold in both the target population and the selected sample. However, β_T and β_S are considered as the covariate effects averaged over time. That is, even if hazards ratio is not constant over time, which is common under practical settings, β_T and β_S are weighted averages of the hazards ratios at each time point with complicated weights. Our test can still make inference in terms of the difference between covariate effects in target population and those in the selected sample.

2.2 Estimation: Regression parameter

We assume the following regularity conditions:

1. {T_i, C_i, Z_i, I_i, X_i} are independent and identically distributed for i = 1, …, N.

2. P(T̃_i > τ) > 0.

3. ${\int }_0^{\tau }{\lambda }_{0S}(t)dt<\infty$ and ${\int }_0^{\tau }{\lambda }_{0T}(t)dt<\infty$.

4. |X_ik| < ∞; $\mid Z_{ik}(0)\mid +{\int }_0^{\tau }\mid Z_{ik}(s)\mid ds<\infty$almost surely, where the second subscript refers to vector element.

5. Positive-definiteness of the matrices, A(β₀), A^w(β₀, θ₀) and B(θ₀), where, for the quantities applicable to the possibly biased sample,

   $$\begin{array}{l}A(\beta )=E\left[{\int }_0^{\tau }{\{Z_i(t)-\overline{z}(t;\beta )\}}^{\otimes 2}{Y}_i(t){e^{{\beta }^{\prime }}}^{Z_i(t)}{\lambda }_{0S}(t)dt\right]\\ S^{(k)}(t;\beta )=n^{-1}\sum _{i=1}^N{I}_i{Y}_i(t)e^{{\beta }^{\prime }{Z}_i(t)}{Z}_i{(t)}^{\otimes k},k=0,1,2\\ \overline{Z}(t;\beta )=\frac{S^{(1)}(t;\beta )}{S^{(0)}(t;\beta )}\\ s^{(k)}(t;\beta )=\underset{N\to \infty }{lim}{S}^{(k)}(t;\beta ),k=0,1,2\\ \overline{z}(t;\beta )=\frac{s^{(1)}(t;\beta )}{s^{(0)}(t;\beta )}\end{array}$$
   and for the quantities applicable to the target population,

   $$\begin{array}{l}{A}^w(\beta ,\theta )=E\left[{\int }_0^{\tau }{\{Z_i(t)-{\overline{z}}_w(\beta ,\theta ;t)\}}^{\otimes 2}{w}_i(\theta )Y_i(t){e^{{\beta }^{\prime }}}^{Z_i(t)}{\lambda }_{0T}(t)dt\right]\\ S_w^{(k)}(t;\beta ,\theta )=N^{-1}\sum _{i=1}^N{w}_i(\theta )Y_i(t)e^{{\beta }^{\prime }{Z}_i(t)}{Z}_i{(t)}^{\otimes k},k=0,1,2\\ {\overline{Z}}_w(t;\beta ,\theta )=\frac{S_w^{(1)}(t;\beta ,\theta )}{S_w^{(0)}(t;\beta ,\theta )}\\ s_w^{(k)}(t;\beta ,\theta )=\underset{N\to \infty }{lim}{S}_w^{(k)}(t;\beta ,\theta ),k=0,1,2\\ {\overline{z}}_w(t;\beta ,\theta )=\frac{s_w^{(1)}(t;\beta ,\theta )}{s_w^{(0)}(t;\beta ,\theta )}\\ B(\theta )=E[X_i{p}_i(\theta )\{1-p_i(\theta )\}{X}_i^{\prime }]\end{array}$$

   with a^⊗0 = 1, a^⊗1 = a and a^⊗2 = aa′.

6. There exists a δ such that p_i(θ) > δ > 0 almost surely.

In addition to above regularity conditions, the ISPW method also assumes that Z_i ∪ X_i consists of all factors affecting λ_iT (t); that is, the “no-unmeasured-confounders” assumption. In addition, we assume that C_i is conditionally independent of T_i given Z_i(t) and X_i; specifically,

$$\underset{\delta \to 0}{lim}\frac{1}{\delta }P(t\le T_i<t+\delta \mid T_i\ge t,C_i\ge t,Z_i(t),X_i)=\underset{\delta \to 0}{lim}\frac{1}{\delta }P(t\le T_i<t+\delta \mid T_i\ge t,Z_i(t),X_i).$$

The regression parameter estimator for model (2), denoted by β̂_S, is the solution to the partial likelihood (Cox 1975) score equation U(β) = 0, where

$$U(\beta )=\sum _{i=1}^N{\int }_0^{\tau }{I}_i\{Z_i(t)-\overline{Z}(t;\beta )\}{dN}_i(t).$$ (3)

Andersen and Gill (1982) proved that n^1/2(β̂_S −β_S) converges asymptotically to a zero-mean Gaussian process with covariance consistently estimated by  (β̂_S)⁻¹, where

$$\widehat{A}(\beta )=-n^{-1}\frac{\partial U(\beta )}{\partial {\beta }^{\prime }}=-n^{-1}\sum _{i=1}^N{\int }_0^{\tau }{I}_i\left[\frac{S^{(2)}(t;\beta )}{S^{(0)}(t;\beta )}-\overline{Z}{(t;\beta )}^{\otimes 2}\right]{dN}_i(t).$$

In addition, the cumulative baseline hazard, ${\mathrm{\Lambda }}_{0S}(t)={\int }_0^t{\lambda }_{0S}(u)du$, can be consistently estimated by the Breslow-Aalen estimator,

$${\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S)=n^{-1}\sum _{i=1}^N{\int }_0^t{I}_i{S}^{(0)}{(s;{\widehat{\beta }}_S)}^{-1}{dN}_i(s).$$

The regression parameter estimator for the ISPW proportional hazards model is the root of the weighted score equation, U_w(β, θ̂) = 0, where

$$U_w(\beta ,\theta )=\sum _{i=1}^N{\int }_0^{\tau }{w}_i(\theta )\{Z_i(t)-{\overline{Z}}_w(t;\beta ,\theta )\}{dN}_i(t).$$ (4)

As proved in Pan and Schaubel (2008), the weighted estimator β̂_T is strongly consistent for β_T, while $N^{\frac{1}{2}}({\widehat{\beta }}_T-{\beta }_T)$ follows an asymptotic zero-mean normal distribution with a covariance matrix that can be consistently estimated by Â^w(β̂_T, θ̂)⁻¹Σ̂_w(β̂_T, θ̂)Â^w(β̂_T, θ̂)⁻¹, where

$$\begin{array}{l}{\widehat{A}}^w(\beta ,\theta )=N^{-1}\sum _{i=1}^N{\int }_0^{\tau }{\{Z_i(t)-{\overline{Z}}_w(t;\beta ,\theta )\}}^{\otimes 2}{w}_i(\theta )Y_i(t)e^{{\beta }^{\prime }{Z}_i(t)}d{\widehat{\mathrm{\Lambda }}}_0^w(t;\beta ,\theta )\\ {\widehat{\mathrm{\Lambda }}}_0^w(t;\beta ,\theta )=N^{-1}\sum _{i=1}^N{\int }_0^t{w}_i(\theta )S_w^{(0)}{(s;\beta ,\theta )}^{-1}{dN}_i(s)\\ {\widehat{\sum }}_w(\beta ,\theta )=N^{-1}\sum _{i=1}^N{\widehat{\psi }}_i^w{(\beta ,\theta )}^{\otimes 2}\\ {\widehat{\psi }}_i^w(\beta ,\theta )={\int }_0^{\tau }{w}_i(\theta )\{Z_i(t)-{\overline{Z}}_w(t;\beta ,\theta )\}{d\widehat{M}}_i(t;\beta ,\theta )-\widehat{G}(\beta ,\theta )\widehat{B}{(\theta )}^{-1}{U}_{Li}(\theta )\\ U_{Li}(\theta )=X_i\{I_i-p_i(\theta )\}\\ {d\widehat{M}}_i(t;\beta ,\theta )={dN}_i(t)-Y_i(t)e^{{\beta }^{\prime }{Z}_i}d{\widehat{\mathrm{\Lambda }}}_0^w(t;\beta ,\theta )\\ \widehat{G}(\beta ,\theta )=N^{-1}\sum _{i=1}^N{\int }_0^{\tau }\{Z_i(t)-{\overline{Z}}_w(t;\beta ,\theta )\}{X}_i^{\prime }{e}^{-{\theta }^{\prime }{X}_i}{d\widehat{M}}_i(t;\beta )\\ \widehat{B}(\theta )=-N^{-1}\frac{\partial U_L(\theta )}{\partial {\theta }^{\prime }}=N^{-1}\sum _{i=1}^N{p}_i(\theta )\{1-p_i(\theta )\}{X}_i^{\otimes 2},\end{array}$$

with a^⊗2 = aa′.

2.3 Proposed test: Regression parameter

The null hypotheses of interest are that the parameter estimators based on the potentially biased sampling design have the same limiting value as the corresponding values in the target population. These two effects will be different and hence the unweighted estimator will be biased if and only if the following conditions hold. First, there exists some biasing factor correlated with the effect of interest and not included in the proportional hazards model. Second, this factor affects the hazard function. Third, the biasing factor affects selection probability. Testing the simultaneous existence of the above three conditions is generally complicated and may in practice be quite tedious. For example, let $X_i={(X_{i1}^{\prime },X_{i2}^{\prime })}^{\prime }$, where X_i1 is captured by Z_i in the fitted Cox model and X_i2 is not. Correspondingly, we partition θ₀ as ${({\theta }_{01}^{\prime },{\theta }_{02}^{\prime })}^{\prime }$. To test each component of the biasing mechanism, one would test (i) θ₀₂ = 0, (ii) β₂ = 0 in the model ${\lambda }_i(t)={\lambda }_{0T}(t)e^{{\beta }_T^{\prime }{Z}_i+{\beta }_2^{\prime }{X}_{i2}}$ and (iii) test the hypothesis of zero pairwise association between each element of Z_i and each element of X_i2. It is possible that several of the hypotheses in (i), (ii) or (iii) could be rejected, but that the actual bias in β̂_S is negligible. Conversely, it is also possible that only a small minority of the hypotheses are rejected, but that bias in at least some elements of β̂_S is substantial. The bottom line is that explicitly testing the conditions under which bias in β̂_S can occur is cumbersome and impractical if even a moderate number of covariates are involved. Similar arguments could apply to testing H₀: Λ_0T (t) = Λ_0S(t) for t ∈ (0, τ], if testing were to proceed through first principles. Moreover, additional steps would be needed to calculate the overall significance level of the three sets of tests.

Here, we propose a single statistic to examine the degree of bias in β̂_S without appealing to first principles. The proposed statistic is based on the quantity,

$$D=C^{\prime }({\beta }_T-{\beta }_S),$$

where C is a p×h matrix of constants (typically 0’s and 1’s) defined to extract the specific contrasts of interest. Each of the h columns for C is a vector for one parameter of interests and they are tested simultaneously. For example, if we want to test the ith and jth parameter simultaneously, C = c_j||c_k, where || denotes horizontal concatenation and c_j is a p × 1 vector with the jth element equal to 1 and all other elements set to 0. The test statistic would be given by ${\widehat{D}}^{\prime }\widehat{\text{Var}}{(\widehat{D})}^{-1}\widehat{D}$, which follows a ${\chi }_h^2$ distribution under the null as n → ∞.

Theorem 1

Under conditions (a) to (f), D̂ is a consistent estimator of D; that is, $\widehat{D}\stackrel{a.s.}{\to }D$, while $n^{\frac{1}{2}}(\widehat{D}-D)$ is asymptotically zero-mean multi-normal with covariance matrix

$${\overline{p}C}^{\prime }{A}^w{({\beta }_T,{\theta }_0)}^{-1}{\mathrm{\sum }}_w({\beta }_T,{\theta }_0)A^w{({\beta }_T,{\theta }_0)}^{-1}C+C^{\prime }A{({\beta }_S)}^{-1}\mathrm{\sum }({\beta }_S)A{\left({\beta }_S\right)}^{-1}C-2{\overline{p}C}^{\prime }A{({\beta }_S)}^{-1}{\mathrm{\sum }}_{\beta }({\beta }_S,{\beta }_T,{\theta }_0)A^w{({\beta }_T,{\theta }_0)}^{-1}C,$$

where p̄≡E(n/N).

The consistency of D̂ is proved using the consistency of β̂_S (Andersen and Gill 1982) and β̂_T (Pan and Schaubel 2008) along with the continuous mapping theorem. To derive the covariance matrix of $n^{\frac{1}{2}}(\widehat{D}-D)$, the difference is decomposed into two parts,

$$n^{\frac{1}{2}}(\widehat{D}-D)={\overline{p}}^{\frac{1}{2}}{N}^{\frac{1}{2}}{C}^{\prime }({\widehat{\beta }}_T-{\beta }_T)-n^{\frac{1}{2}}{C}^{\prime }({\widehat{\beta }}_S-{\beta }_S).$$ (5)

Note that, because we assume p_i(θ) > 0 for i = 1, …, N, the average sampling probability, p̄, converges to a constant between 0 and 1, noting also that n and N go to ∞ at the same rate. The variances of $N^{\frac{1}{2}}{C}^{\prime }{\widehat{\beta }}_T$ and $n^{\frac{1}{2}}{C}^{\prime }{\widehat{\beta }}_S$ are the same as those of $N^{\frac{1}{2}}{C}^{\prime }({\widehat{\beta }}_T-{\beta }_T)$ and $n^{\frac{1}{2}}{C}^{\prime }({\widehat{\beta }}_S-{\beta }_S)$, and were derived by Pan and Schaubel (2008), along with consistent estimators. The covariance between $N^{\frac{1}{2}}{C}^{\prime }{\widehat{\beta }}_T$ and $n^{\frac{1}{2}}{C}^{\prime }{\widehat{\beta }}_S$ can be written out in terms of the covariance between $N^{-\frac{1}{2}}{C}^{\prime }{A}^w{({\beta }_T,{\theta }_0)}^{-1}{U}_w({\beta }_T,{\theta }_0)$ and $n^{-\frac{1}{2}}{C}^{\prime }A{({\beta }_S)}^{-1}U({\beta }_S)$. Specifically,

$$\text{Cov}(N^{\frac{1}{2}}{C}^{\prime }{\widehat{\beta }}_T,n^{\frac{1}{2}}{C}^{\prime }{\widehat{\beta }}_S)={\overline{p}}^{\frac{1}{2}}{C}^{\prime }A{({\beta }_S)}^{-1}{\sum }_{\beta }({\beta }_S,{\beta }_T,{\theta }_0)A^w{({\beta }_T,{\theta }_0)}^{-1}C,$$

where

$${\mathrm{\sum }}_{\beta }({\beta }_1,{\beta }_2,\theta )=E\{{\psi }_i({\beta }_1){\psi }_i^w{({\beta }_2,\theta )}^{\prime }\}.$$

with ${\psi }_i(\beta )={\int }_0^{\tau }[Z_i(t)-\overline{z}(t;\beta )]{dM}_i(t;\beta )$, where A(β_S), A^w(β_T, θ₀) and ${\psi }_i^w({\beta }_{T,}{\theta }_0)$ are defined in the calculation of the covariance matrices for β̂_S and β̂_T. They can each be estimated by replacing β_S, β_T, Λ_0S, Λ_0T and θ₀ with their sample estimates. The quantity C′Σ_β(β_S, β_T, θ₀)C equals the covariance between $N^{-\frac{1}{2}}{C}^{\prime }{U}_w({\beta }_T,{\theta }_0)$ and $n^{-\frac{1}{2}}{C}^{\prime }U({\beta }_S)$. The (j, k) element in the matrix Σ_β(β_S, β_T, θ₀) is the covariance between the jth element of $N^{-\frac{1}{2}}{U}_w({\beta }_T,{\theta }_0)$ and the kth element of $n^{-\frac{1}{2}}U({\beta }_S)$. Both the weighted (4) and unweighted score functions (3) are zero at the estimated parameter values β̂_S, β̂_T and θ̂. Furthermore, when N → ∞, each can be written as a sum of independent contributions from each subject of the selected sample. As such, an estimator of the covariance between the elements of $N^{-\frac{1}{2}}{U}_w({\beta }_T,{\theta }_0)$ and the elements of $n^{-\frac{1}{2}}U({\beta }_S)$ is the average of the outer product of the subject-specific contributions to the weighted score (4) function and unweighted score function (3). As such, the matrix Σ_β(β_S, β_T, θ₀) can hence be consistently estimated as

$${\widehat{\mathrm{\sum }}}_{\beta }({\widehat{\beta }}_S,{\widehat{\beta }}_T,\widehat{\theta })=n^{-1}\sum _{i=1}^N{I}_i{\widehat{\psi }}_i({\widehat{\beta }}_S){\widehat{\psi }}_i^w{({\widehat{\beta }}_T,\widehat{\theta })}^{\prime }.$$

The parameter estimator, both weighted and unweighted versions, can be computed using standard software; e.g., SAS’s PROC PHREG. With respect to the variance estimators, the unweighted parameter can be computed through a standard call to PHREG, while its weighted counterpart required IML. Similar comments apply to R.

2.4 Estimation: Cumulative baseline hazard

Another quantity of interest is the baseline hazard function, which is best viewed as a process over time. We use Λ_0T (t) to denote the baseline hazard function in the target population, which is consistently estimated by ${\widehat{\mathrm{\Lambda }}}_0^w(t;{\widehat{\beta }}_T,\widehat{\theta })$. A modified version of Λ_0T (t) is Λ_0S(t) with the modification resulting from the potentially biased sampling mechanism.

The unweighted version of the baseline hazard function estimator is Λ̂₀(t; β̂_S) where

$${\widehat{\mathrm{\Lambda }}}_0(t;\beta )=n^{-1}\sum _{i=1}^N{I}_i{\int }_0^t{S}^{(0)}{(s;\beta )}^{-1}{dN}_i(s).$$

In the absence of biasing factors, ${\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S)\stackrel{a.s.}{\to }{\mathrm{\Lambda }}_{0T}(t)$ uniformly in t ∈ [0, τ] (Fleming and Harrington, 1991). In the presence of biasing factors, ${\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S)\stackrel{a.s.}{\to }{\mathrm{\Lambda }}_{0S}(t)\ne {\mathrm{\Lambda }}_{0T}(t)$.

2.5 Proposed test: Cumulative baseline hazard

The quantity $\mathrm{\Delta }(t)={\mathrm{\Lambda }}_0^w(t)-{\mathrm{\Lambda }}_0(t)$ reflects the magnitude of the bias in the unweighted baseline hazard function estimator. We summarize the essential asymptotic properties of an estimator of this quantity, $\widehat{\mathrm{\Delta }}(t)={\widehat{\mathrm{\Lambda }}}_0^w(t;{\widehat{\beta }}_T,\widehat{\theta })-{\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S)$, in the following two theorems.

Theorem 2

Under conditions (a) to (f), Δ̂(t) converges uniformly to Δ(t) as n → ∞ for t ∈ [0, τ].

The consistency of Λ̂₀(t; β̂_S) to Λ_0S(t) for t ∈ (0, τ] can be demonstrated by combining the Uniform Strong Law of Large Numbers (USLLN) and the Martingale Central Limit Theorem (Fleming and Harrington 1991). The consistency of ${\widehat{\mathrm{\Lambda }}}_0^w(t;{\widehat{\beta }}_T,\widehat{\theta })$ for Λ_0T(t) is proved in Pan and Schaubel (2008) through the USLLN and various empirical process results.

Theorem 3

Under conditions (a) to (f), $n^{\frac{1}{2}}\{\widehat{\mathrm{\Delta }}(t)-\mathrm{\Delta }(t)\}$ converges weakly to a zero-mean Gaussian process with covariance function:

$$\overline{p}E\{{\phi }_i^w(s;{\beta }_T,{\theta }_0){\phi }_i^w(t;{\beta }_T,{\theta }_0)\}+E\{{\phi }_i(s;{\beta }_S){\phi }_i(t;{\beta }_S)\}-\overline{p}\text{Cov}\{N^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0^w(s;{\widehat{\beta }}_T,\widehat{\theta }),n^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S)\}-\overline{p}\text{Cov}\{N^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0^w(t;{\widehat{\beta }}_T,\widehat{\theta }),n^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0(s;{\widehat{\beta }}_S)\},$$

for (s, t) ∈ (0, τ] × (0, τ]

Since p̄ = E(n/N), it would be exchangeable if we put $N^{\frac{1}{2}}$ as the scale factor instead of $n^{\frac{1}{2}}$. The proof is similar to that of Theorem 2, in the sense that we decompose $n^{\frac{1}{2}}\{\widehat{\mathrm{\Delta }}(t)-\mathrm{\Delta }(t)\}$ into ${\overline{p}}^{\frac{1}{2}}{N}^{\frac{1}{2}}\{{\widehat{\mathrm{\Lambda }}}_0^w(t;{\widehat{\beta }}_T,\widehat{\theta })-{\mathrm{\Lambda }}_{0T}(t)\}$ and $n^{\frac{1}{2}}\{{\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S)-{\mathrm{\Lambda }}_{0S}(t)\}$. Through the Martingale Central Limit Theorem (Andersen and Gill 1982, Fleming and Harrington 1991), we obtain

$$\text{Cov}(n^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0(s;{\widehat{\beta }}_S),n^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S))=E\{{\phi }_i(s;{\beta }_S){\phi }_i(t;{\beta }_S)\},$$

where

$${\phi }_i(t;\beta )=-{\int }_0^t{\overline{z}}^{\prime }(s;\beta )d{\mathrm{\Lambda }}_{0S}(s)(t;\beta )A{(\beta )}^{-1}{\psi }_i(\beta )+{\int }_0^t\frac{{dM}_i(s;\beta ,\theta )}{s_w^{(0)}(s;\beta ,\theta )}.$$

It is proved in Pan and Schaubel (2008) that

$$\text{Cov}(N^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0^w(s;{\widehat{\beta }}_T,\widehat{\theta }),N^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0^w(t;{\widehat{\beta }}_T,\widehat{\theta }))=E\{{\phi }_i^w(s;{\beta }_T,{\theta }_0){\phi }_i^w(t;{\beta }_T,{\theta }_0)\}.$$

The covariance between $N^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0^w(s;{\widehat{\beta }}_T,\widehat{\theta })$ and $n^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S)$ results from the subject-specific contributions to each of the weighted and unweighted cumulative baseline hazard functions such that

$$\text{Cov}(N^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0^w(s;{\widehat{\beta }}_T,\widehat{\theta }),n^{\frac{1}{2}}{\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S))={\overline{p}}^{\frac{1}{2}}E\{{\phi }_i^w(s;{\beta }_T,{\theta }_0){\phi }_i(t;{\beta }_S)\}.$$

This covariance function can be consistently estimated by replacing all the unknown quantities by their empirical counterparts.

To address the question of whether or not the two baseline hazard functions are equal over the entire follow up period; i.e., H₀: Λ_0T (t) = Λ_0S(t) for t ∈ (0, τ], implying the construction of a confidence band. Lin, Fleming and Wei (1994) provide a simulation-based method to estimate a confidence band for Ŝ₀(t; β̂) = exp{−Λ̂₀(t; β̂)} based on an unweighted Cox model. We extend this general approach to our setting to generate the distribution of $\widehat{\delta }\equiv {sup}_{t\in [0,\tau ]}\mid n^{\frac{1}{2}}\{\widehat{\mathrm{\Delta }}(t)-\mathrm{\Delta }(t)\}Y(t)\mid$. We weight the δ̂ values at each time point by $Y(t)={\sum }_{i=1}^N{I}_i{Y}_i(t)$, the number of subjects at risk. Essentially, a zero-mean Gaussian process with the same covariance function as $n^{\frac{1}{2}}\widehat{\mathrm{\Delta }}(t)$ is simulated to approximate the distribution of $n^{\frac{1}{2}}\widehat{\mathrm{\Delta }}(t)$ . Specifically, we replace ${(n/N)}^{\frac{1}{2}}{N}^{-\frac{1}{2}}{\widehat{\psi }}_i^w(t;{\widehat{\beta }}_T,\theta )-n^{-\frac{1}{2}}{\widehat{\psi }}_i(t;{\widehat{\beta }}_S)$, the contribution to $n^{\frac{1}{2}}\{\widehat{\mathrm{\Delta }}(t)-\mathrm{\Delta }(t)\}$ from each subject, with $\{{(n/N)}^{\frac{1}{2}}{N}^{-\frac{1}{2}}{\widehat{\psi }}_i^w(t;{\beta }_T,\theta )-n^{-\frac{1}{2}}{\widehat{\psi }}_i(t;{\widehat{\beta }}_S)\}{H}_i$, where H_i (i = 1, …, N) are independent standard normal variables. The simulated $\{{(n/N)}^{\frac{1}{2}}{N}^{-\frac{1}{2}}{\widehat{\psi }}_i^w(t;{\widehat{\beta }}_T,\theta )-n^{-\frac{1}{2}}{\widehat{\psi }}_i(t;{\widehat{\beta }}_S)\}{H}_i$ are still asymptotically independent among all subjects. Taking the sum of all subjects at each time point, we obtain

$$n^{\frac{1}{2}}\{\stackrel{\sim }{\mathrm{\Delta }}(t)-\mathrm{\Delta }(t)\}={(n/N)}^{\frac{1}{2}}{N}^{-\frac{1}{2}}\sum _{i=1}^N{\widehat{\psi }}_i^w(t;{\widehat{\beta }}_T,\theta )H_i-n^{-\frac{1}{2}}\sum _{i=1}^N{I}_i{\widehat{\psi }}_i(t;{\widehat{\beta }}_S)H_i$$

empirically. The aggregate difference in the baseline hazard estimators, $\stackrel{\sim }{\delta }={\text{sup}}_{t\in [0,\tau ]}\mid n^{\frac{1}{2}}\{\stackrel{\sim }{\mathrm{\Delta }}(t)-\mathrm{\Delta }(t)\}Y(t)\mid$ , has the same covariance matrix as the one proposed for δ̂ on [0, τ]. The supremum is taken over all time points at which an event is observed since δ̃ doesn’t change between observed event times. The above simulation, with different sets of H_i (i = 1, …, N), is iterated a large number of times (e.g. 500). The obtained set of 500 δ̃ values, one from each iteration, form an empirical sample of δ̃’s distribution. Finally, an approximate (1 − α) confidence band for Δ(t) on [0, τ] is $\widehat{\mathrm{\Delta }}(t)\pm n^{-\frac{1}{2}}{\widehat{q}}_{\alpha }/Y(t)$, where q̂_α denotes the empirical 100(1 − α) quantile satisfying P{δ̃ > q̂ _α} = α. The applicability of this confidence band procedure in finite samples has been validated in the unweighted proportional hazards setting through numerical studies by Lin, Fleming and Wei (1994).

3 Simulation Studies

We simulated three covariates Z_i1, Z_i2 and Z_i3, where Z_i1 is distributed as Bernoulli(0.5), Z_i2 is distributed as N (0, 25) and Z_i3 is distributed as Uniform(0, 4). The event time, T_i, follows an exponential distribution with hazard ${\lambda }_i(t)={\lambda }_0(t)e^{{\beta }_0^{\prime }{Z}_i}$, where λ₀ = 0.02 and the vector of coefficients is ${\beta }_0^{\prime }=({\beta }_1,{\beta }_2,{\beta }_3)=(0.5,0.1,1.0)$. The censoring time, C_i, is uniform on (0, 40) such that the corresponding censoring percentage is approximately 20%. The representative samples (before selection) have sizes ranging from N = 100 to N = 1000, while the biased samples are created by selecting various percentages of subjects from the various Z_i1 and Z_i3 combinations. Specifically, subjects with Z_i1 = 0 are always selected; for subjects with Z_i1 = 1, the selection probabilities depend on Z_i3 level. Covariate Z_i3 has four levels [0, 1], (1, 2], (2, 3], (3, 4], and there are four corresponding selection probabilities, one for each level. Each data configuration is iterated 1, 000 times. Notice that Z_i1 and Z_i3 are independent in the representative sample before selection, but correlated in the selected sample if the selection probabilities vary across different Z_i3 levels. However, the asymptotic results in Theorem 1–3 are not restricted to independent Z_i1 and Z_i3 before selection. Thus the scenario in this simulation study is a special case of all the scenarios where the test applies.

Our goal is to estimate the regression coefficients when we fit a model with Z_i1 and Z_i2 only, such that the Cox model of interest is given by λ_iT(t) = λ_0T(t)e^{β_1TZ_i1+β_2TZ_i2}. The weights are estimated through the following logistic model, $log\{p_i({\theta }_0)/(1-p_i({\theta }_0))\}={\theta }_0^{\prime }{X}_i$, where X_i = (Z_i1, Z_i3)′. Here, Z_i3 works as a biasing factor, and the marginal effects of Z_i1 over Z_i3 in the target population and in the selected sample will be different in the presence of biasing factors. Thus, fitting an unweighted Cox model without Z_i3 could potentially introduce bias in estimating the marginal regression coefficients for Z_i13. The quantity D̂₁ is calculated by taking the difference between β̂_1T and β̂_1S from the weighted and unweighted proportional hazards models, respectively. The variance of D̂₁ is estimated using the formula derived in Theorem 1, then the proposed test statistic is computed. The hypothesis H₀: β_T1 = β_S1 is tested against H₁: β_T1 ≠ β_S1.

The performance of the D̂₁ statistic under H₀ is evaluated in Table 1. The quantity E(n) is the expected sample size after selection from the representative sample of size N. Selection probability is equal across all levels of Z_i3. That is, all subjects with Z_i1 = 0 have selection probability of 1; all subjects with Z_i1 = 1, regardless of Z_i3 values, have selection probability of 0.25 in row 1, 4 and 7; 0.5 in rows 2, 5, 8; 0.75 in rows 3, 6, 9. Although Z_i3 affects λ_i(t), it is not correlated with the factor of interest, Z_i1, nor does it predict selection probability. Therefore, the regression coefficient, β_1T, from the target population and β_1S from the selected sample are equal. For each data configuration, the unweighted and weighted β₁ estimates are obtained, with their average difference, Ê(D̂₁), listed in column 5. We also list the empirical standard deviation (ESD) of D̂ in column 6. Two sets of variance estimators are calculated. In columns 7 and 8, the variance estimator is based on Theorem 1. The ASEs using our proposed variance estimators are very close to the corresponding ESDs and the ESLs are always close to the nominal level of 5%, even when a relatively low percentage of subjects gets sampled. In columns 9 and 10, the estimated weights are inappropriately treated as fixed. Ignoring the extra variance induced by the estimation of the weights leads to incorrect asymptotic standard errors (ASE) and empirical significance levels (ESL); i.e., artificially low ASEs and, as a result, ESLs well above the nominal value.

Table 1.

Simulation Results: Performance of test for regression parameter under the null

row	N	pi(θ0)	E(n)	Ê (D̂1)	ESD	wi(θ̂) treated as estimated		wi(θ̂) treated as fixed
						ASE	ESL	ASE	ESL
1	100	0.25	62.5	−0.008	0.224	0.201	2.1%	0.112	28.4%
2		0.50	75	0.001	0.119	0.118	3.1%	0.051	38.3%
3		0.75	87.5	−0.003	0.064	0.065	3.4%	0.024	50.2%
4	500	0.25	312.5	−0.003	0.085	0.087	3.6%	0.029	55.3%
5		0.50	375	−0.001	0.047	0.046	4.0%	0.011	66.0%
6		0.75	437.5	0.000	0.026	0.026	4.8%	0.005	77.4%
7	1000	0.25	625	0.000	0.058	0.059	4.3%	0.015	63.5%
8		0.50	750	−0.001	0.032	0.033	4.4%	0.006	72.6%
9		0.75	875	−0.000	0.018	0.019	3.8%	0.002	80.0%

p_i(θ₀) = P (I_i = 1|Z_i1 = 1, Zi₃ ∈ (0, 4])

ESD = empirical standard deviation

ASE = average asymptotic standard error

ESL = empirical significance level.

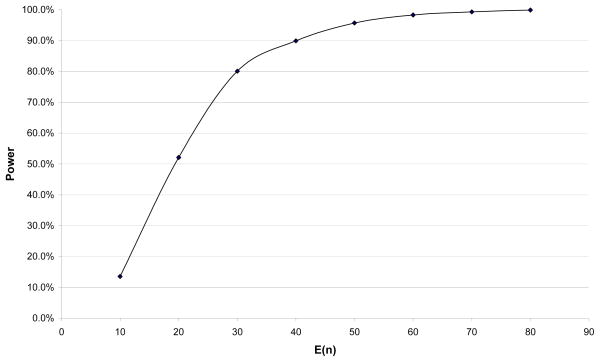
We also evaluated the power of the proposed test under various departures from H₀: β_1T = β_1S. In this case, the sampling percentages varied by Z_i3 level when Z_i1 = 1. An important factor that affects the power of our proposed test is the size of the selected sample. The power is consistently high (and near 100%) for settings with moderate size selected samples. The power is poor when the representative sample before selection is small, or when the representative sample is of moderate-size but the biased sample is small. Figure 1 shows the power when the expected sample size of the potentially biased sample increases from 10 to 90 with the same sampling scheme. With moderate sampling probabilities, the power increases from 13.5% with original sample size 100 to 95.7% when the size before sampling is 500 and plateaus close to 100% thereafter.

Figure 1.

Simulation Results: Power of proposed test of H₀: β_1T = β_1S. Note $n={\sum }_{i=1}^N{I}_i$; p_i = 1 for Z_i1 = 0; p_i = 0.4, 0.2, 0.16, 0.04 for Z_i1 = 1 and Z_i3 ∈ [0, 1], (1, 2], (2, 3], (3, 4] respectively; Ê(D̂₁) = 0.4.

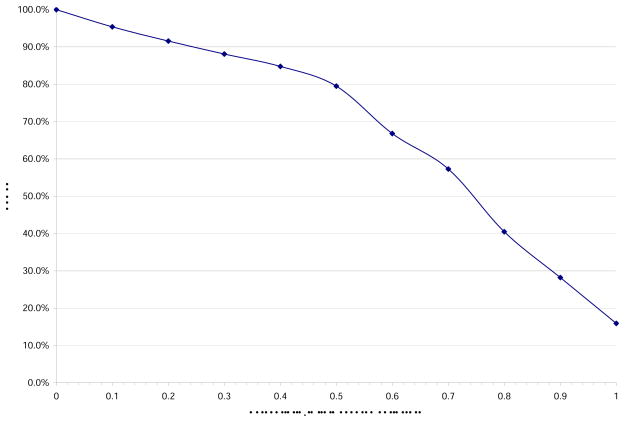
Covariate measurement error reduces the power of the proposed test to detect selection bias, as shown by our simulation results plotted in Figure 2. In the data configuration described in Section 3 with biased selection for different levels of Z_i3 when Z_i1 = 1, independent Normal (0, 3) random errors are added to Z_i3 while the resulting values remain bounded within [0, 4]. As the percentage of Z_i3 with measurement error increases, the power of our proposed test decreases from 100% to 15.9% (Figure 2).

Figure 2.

Simulation Results: Effect of measurement error on power of proposed test of H₀: β_1T = β_1S. The selection probabilities are p_i = 1 for Z_i1 = 0; p_i = 1, 0.5, 0.4, 0.1 for Z_i1 = 1 and Z_i3 ∈ [0, 1], (1, 2], (2, 3], (3, 4] respectively; Ê(D̂₁) = 0.4.

4 Application to Kidney Transplant Data

The target population consists of all patients wait-listed for primary kidney transplantation in the U.S.. Naturally, this hypothetical population is infinite. A representative sample was obtained by selecting a cross-section of all patients active on the wait-list as of January 1, 2000. In total, there were 13, 627 candidates on the waiting list that day. Candidates under age 18 were excluded. A five-year time period (01/01/2000 – 12/31/2004) was chosen over which kidney transplants among the cross-section subjects were observed. The decision for using a duration of five years can be justified by the plot of the cumulative incidence of transplantation, since the curve plateaus after approximately five years. For the purposes of estimating transplant probability, death and removal from the wait-list were treated as competing risks (Kalbfleisch and Prentice 2002). On December 31, 2004, each patient had potential observation time on wait-list of at least five years. Those who did not receive a transplant either died, or were left on the waiting list, or were removed from the waiting list due to illness or recovery of native renal function. Among the representative sample of 13, 627 patients, 6, 425 (47%) received a kidney transplant. The transplanted patients form the selected and potentially biased sample.

Demographic and clinical data on donors and recipients, dates of graft failure and death where applicable, as well as various clinical measures, were obtained from the Scientific Registry of Transplant Recipients (SRTR) and collected by the Organ Procurement and Transplant Network (OPTN). The potential biasing factors under consideration are represented in aggregate by the hospitalization history. For example, it is suspected that patients with fewer hospitalizations are preferred candidates for kidney transplantation, even after conditioning on all the covariates included in the proportional hazards model. The frequency and length of hospitalization is also correlated with many patient comorbidities, as well as the post-transplant mortality hazard.

Note that adjusting for hospitalization history through covariates in the post-transplant model is not an attractive option based on practical considerations. Specifically, hospitalization information on transplant candidates will not be available to UNOS at the time when an organ is to be allocated and hence when candidates must be ranked. The SRTR has access to both the OPTN (wait-list and transplant) and CMS (hospitalization history) databases and can link the sources by patient for those who pay for their health care expenses via Medicare. However, UNOS will not have access to updated CMS data for the purposes of ranking candidates.

We model the probability of being selected to receive a kidney transplant using a binary end point: transplanted within five years (0, 1). Implicitly, we assume that the θ̂ estimated through this approach converges to the θ₀ which governs transplant probability. In addition to hospitalization frequencies and total days hospitalized, other covariates adjusted for in the selection probability model include candidate demographics (gender, age, race), years with end stage renal dialysis (ESRD), various disease conditions (drug treated chronic obstructive pulminary disease (COPD), angina), primary diagnosis at time of listing (poly-cystic kidneys, diabetes, hypertension), functional status (from fully active daily living to severely disabled), and various interactions among these covariates. Most terms in the logistic model are significant predictors of transplant probability at the 0.05 level (Table 2). For each incidence of hospitalization, the covariate-adjusted odds of getting a transplant drops 3%, while the odds of receiving a transplant drops 1% for each additional day hospitalized holding all other factors constant (including number of hospitalizations). Of the 3, 369 patients with no previous hospitalization, 1, 974 (59%) got transplanted. In contrast, of the 10, 258 candidates with at least one hospitalization, 4, 451(43%) got transplants.

Table 2.

Analysis of SRTR Data Estimated Regression Parameters from Selection Probability Model

Covariate, Xik	θ̂k	$\widehat{SE}({\widehat{\theta }}_k)$	p	eθ̂k
Hospitalization frequency	−0.03	0.008	< 0.0001	0.97
Days hospitalized	−0.007	0.001	< 0.0001	0.99
Female	−0.30	0.05	< 0.0001	0.74
Age 18 – 24	0.63	0.13	< 0.0001	1.87
Age 25 –34	0.57	0.07	< 0.0001	1.77
Age 35 – 44	0.27	0.06	< 0.0001	1.31
Age 55 – 64	−0.26	0.05	< 0.0001	0.77
Age 65 – 70	−0.27	0.09	0.0021	0.76
Age ≥70	−0.69	0.11	< 0.0001	0.50
African American	−0.10	0.04	0.02	0.90
COPD	−0.35	0.17	0.04	0.70
Angina	−0.24	0.06	< 0.0001	0.78
Functional status: minor disability	−0.16	0.07	0.02	0.85
Polycystic kidneys	0.29	0.09	0.0008	1.34
Diabetes	−1.17	0.21	< 0.0001	0.31
Hypertension	−0.11	0.05	0.02	0.90
Years on dialysis	−0.01	0.01	0.17	0.99
Female×Hospitalization frequency	0.02	0.01	0.02	1.02
Age 65–70×Hospitalization frequency	−0.06	0.02	0.0006	0.94
Age×Diabetes	0.01	0.004	0.0092	1.01

For the 6, 425 patients who received a transplant, each recipient was followed until death, loss to follow up or the conclusion of the observation period (06/30/2006). Among the 6, 425 transplant recipients, 5, 025 were alive at the end of follow-up, while 1, 400 (22%) died.

The predicted selection probabilities from the logistic model could get very close to zero and hence lead to unrealistically large weight values. These large values are very influential on Var(β̂_T). Bounding weights at an arbitrary upper limit, u, reduces Var{β̂_T (u)} at the price of larger bias. An optimal upper bound for weights should minimize mean square error (MSE) of β̂_T(u), defined as the sum of diag[Var{β̂_T (u)}] and diag[{β̂_T (u) − β̂_T}^⊗2], where diag(A) is a vector consisting of the main diagonal of A. In our real data analysis, the weights range from 1.21 to 54.22. We observe a U-shape curve of the MSE for various upper bounds. For our application, we estimate that the minimum MSE is achieved when weights are bounded at 20.

Both weighted and unweighted proportional hazards models were fitted, adjusting for the same set of covariates: expanded criteria donor (ECD), recipients demographics (age, race, gender), years on dialysis prior to wait-listing, hepatitis C antibody (HCV) status, chronic obstructive pulmonary disease (COPD), angina, primary renal diagnosis, functional status, and stay in the intensive care unit (ICU) at the time of wait-listing. All covariates had significant effects on the post-transplant mortality hazard.

At the time of this paper, many issues regarding the proposed kidney allocation system are still under discussion by experts in all areas, especially the appropriateness of various patient characteristics as ranking criteria. For example, opinion is divided on the appropriateness of candidate age and previous time on dialysis as bases for ranking patients on the wait list. Thus, although obvious factors like race can be ruled out, we are unable to define a specific set of covariates of interest at this time. For the purposes of illustrating the proposed methods, we carry out the test for several potential ranking factors individually. Table 3 lists the difference between each of the weighted and unweighted regression coefficient estimates, as well as its corresponding standard error, Chi-square test statistic, and p value. For almost all covariates, significant differences between the weighted and unweighted covariate effects are not detected. Among all the 21 tested covariates, age 35–44 (compared to age 45–54), years on dialysis and COPD (yes vs. no) have significantly different effects in the representative sample and in the selected sample. The hazard ratio for COPD is 2.40 in the representative sample and 1.55 in the transplanted sample (p=0.008). For each additional year on dialysis, the post-transplant death hazard increases by a multiplier of 1.03 for the transplanted population and by a multiplier of 1.05 for the wait-listed population (p=0.046). The hazard for age group 35–44 is 0.79 times of that for the reference group 45–54 using the weighted estimate, while the hazard ratio decreases to 0.67 with the unweighted estimate (p=0.029).

Table 3.

Analysis of SRTR Data Tests of Differences between Regression Coefficients estimated through models fitted to Wait-Listed Candidates (β̂_T) and Transplant Recipients (β̂_S)

Covariate, Zik	β̂T	β̂S	D̂	$\widehat{SE}(\widehat{D})$	Chi-square	p
Drug-treated-COPD	0.87	0.44	0.43	0.16	6.96	0.008
Years on dialysis	0.05	0.03	0.02	0.01	3.98	0.046
Age 18 to 24	−1.10	−1.13	0.03	0.20	0.02	0.883
Age 25 to 34	−0.56	−0.73	0.16	0.20	0.63	0.426
Age 35 to 44	−0.24	−0.40	0.17	0.08	4.77	0.029
Age 55 to 64	0.51	0.49	0.02	0.05	0.12	0.730
Age 65 to 70	0.71	0.73	−0.02	0.05	0.13	0.721
Age 70 up	1.08	1.01	0.07	0.08	0.69	0.405
HCV Positive	0.25	0.28	−0.02	0.11	0.09	0.770
In ICU	1.42	1.47	−0.05	0.15	0.11	0.737
Female	−0.06	−0.07	0.01	0.04	0.06	0.800
Angina	0.37	0.30	0.07	0.06	1.33	0.249
Polycystic kidney	−0.40	−0.32	−0.08	0.07	1.49	0.222
Diabetes	0.48	0.52	−0.03	0.04	0.53	0.465
Functional status: minor disability	0.26	0.21	0.05	0.10	0.26	0.613

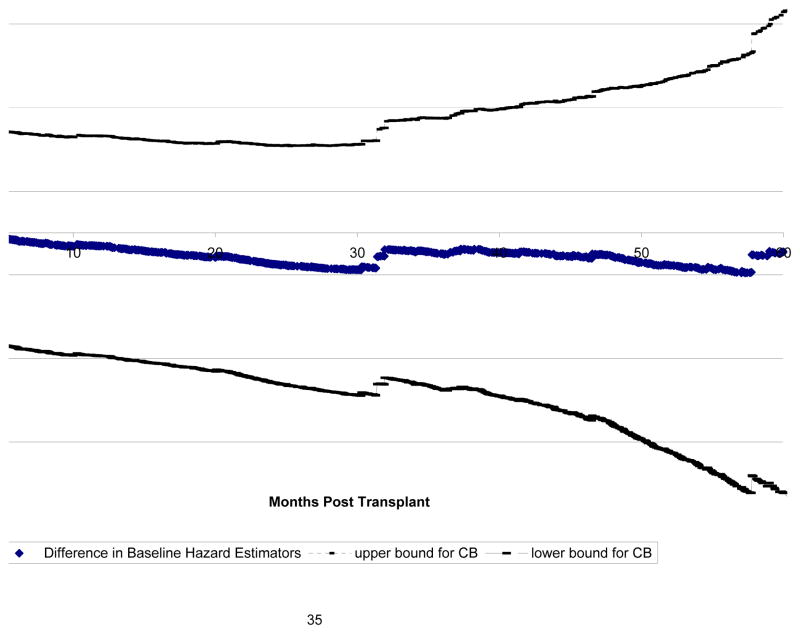
The 95% confidence bands of the difference between the baseline hazard function in the wait listed patients and that in the transplant recipients are calculated based on the results from Theorem 3 and displayed in Figure 3. It is clear from the figure that across the 5-year follow up, the two baseline functions overall do not appear to be different.

Figure 3.

Analysis of SRTR data: Test of H₀: Λ_0T (t) = Λ_0S(t).

Middle line: ${\widehat{\mathrm{\Lambda }}}_0^w(t;{\widehat{\beta }}_T,\widehat{\theta })-{\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S)$; Outer lines: 95% confidence band.

5 Discussion

Weighted proportional hazards models are an attractive option in survival analysis in the setting where only a possibly biased sample of the underlying target population is observed. Pan and Schaubel (2008) proposed an inverse selection probability weighting proportional hazards model for the setting wherein sampling probabilities are unknown. In the presence of biasing factors, the weighted proportional hazards model with estimated ISPW yields parameter estimators which are consistent and which have reduced variance relative to those which would be estimated by treating the weights as fixed. These properties come at the expense of increased complexity and computing time. To identify cases where ISPW is required for a proportional hazards model, we propose tests for estimating the bias in the unweighted regression parameter and cumulative hazard estimators. The asymptotic properties of the proposed statistics are derived. The finite sample performance of a Wald test based on the proposed statistic is examined through simulation studies with various selection probabilities and sample sizes. In the case of no biasing factors, the empirical significance level is close to 0.05. In the presence of biasing factors, the proposed test is quite powerful. In cases where the size of the selected sample is insufficient (e.g., n = 20), the power drops to very low levels (e.g., 14%). A method for evaluating the difference between the baseline cumulative hazard functions, for the target population and that for the selected sample is also proposed, with the pertinent asymptotic distributions derived.

The proposed testing procedures provide methods for making an informed choice between weighted and unweighted proportional hazards models. If no significant difference exists between the weighted and unweighted parameters, practitioners have a formal justification for choosing an unweighted model. Due to computational simplicity, the unweighted model would usually be preferred in the absence of selection bias. Currently, the alternative to the proposed tests is to eyeball differences between weighted and unweighted estimates, which is ad-hoc and subjective. The proposed tests do require computing the weighted parameter estimators. However, the information provided by the tests can still save a considerably amount of computing. That is, a carefully executed data analysis typically consists of several steps; e.g., basic main effects model, choosing functional form of covariate effects, evaluating residual diagnostics. A practical option is to evaluate selection bias using the proposed procedures on a basic main effects model, before the fine-tuning steps of the model building process. If selection bias is detected, it makes sense to carry out each of the supplementary steps using the weighted model. If selection bias is not detected, then the model can be finalized using unweighted methods. In summary, although the proposed tests require fitting a weighted model, it is not the case that the computational burden of weighting is borne even if the unweighted model is selected.

Recently there is great interest in reconstructing the organ allocation system for various organs, including kidney. A newly proposed criterion by which to rank candidates for an available donor kidney is the difference between predicted median life with a transplant and that without a transplant. It is therefore of great value to obtain an accurate post-transplant survival model applicable to the patients which require ranking; namely patients wait-listed for a kidney transplant. An ISPW proportional hazards model results in estimators applicable to all wait-listed patients, but at the expense of increased computation and complexity. Based on the proposed test, the unweighted model appears to be sufficient. Among the twenty-one covariates, only three were found to be significantly different: age 35–44, years on dialysis and presence of COPD. The majority of wait-listed patients are at least age 45 and are free of COPD. Moreover, no difference was detected with respect to the target and sample baseline cumulative hazard function.

Although our simulation studies demonstrate high power for the proposed test, we only detect three covariates with significant differences in our real example of kidney transplant analysis. There are three possible reasons leading to the low detection number. First, we examine twenty-one recipient and donor characteristics in total. If we had information on more covariates affecting the post-transplant mortality hazard, it is quite possible that we would detect more covariates with significantly different effects for the representative sample and the transplanted sample. That is, more complete covariate adjustment may result in increased precision and, hence, power. Second, although the SRTR is an invaluable source of information on U.S. kidney transplant patients, covariate measurement error is unavoidable due to inaccurate recall on the part of the patients supplying the information and/or inaccurate interpretation or recording of information. From our simulation results (Figure 2), the power of the proposed tests drops in the presence of measurement error. Further study taking measurement error into account could be an interesting and valuable extension of our current work. Finally, the representative sample is assembled by taking a cross section on a single day, other random sampling methods might be applied to achieve a larger representative sample and thus a larger selected sample. With more subjects in our models, the power of the proposed test would increase and some parameter differences with borderline p values could attain statistical significance (e.g., angina, initial diagnosis as polycystic kidney). Furthermore, if strong empirical or clinical prior knowledge exists to decide the direction of the difference between β_T and β_S, a one-sided test can be used. For example, if the effects of a given comorbidity in the wait-listed population is always larger in magnitude than that in the transplanted population (e.g., since the selection among patients with the comorbidity is more stringent), then one would employ the one-sided alternative hypothesis, H₁: D > 0.

APPENDIX

Proof of Theorem 1

The strong consistency of β̂_S was demonstrated by Andersen and Gill (1982). The consistency of the weighted parameter estimate, β̂_T, for the true parameter values applicable to the target population, β_T, is proved in Theorem 1 of Pan and Schaubel (2008). Combining these two results, as a linear combination of the difference of β̂_S and β̂_T, $\widehat{D}\stackrel{a.s.}{\to }D$ by the continuous mapping theorem.

With respect to asymptotic normality, through a Taylor expansion around β = β_S,

$$U({\widehat{\beta }}_S)-U({\beta }_S)={\frac{\partial U(\beta )}{\partial {\beta }^{\prime }}|}_{\beta ={\beta }_S^{\ast }}({\widehat{\beta }}_S-{\beta }_S),$$

where ${\beta }_S^{\ast }$ lies between β̂_S and β_S in . By the definition of Â(β),

$$n^{\frac{1}{2}}({\widehat{\beta }}_S-{\beta }_S)=\widehat{A}{\text{(}{\beta }_{\text{S}}^{\ast }\text{)}}^{-\text{1}}{n}^{-\frac{1}{2}}U({\beta }_S)$$

since U(β̂_S) = 0. Under the assumed conditions,

$$\underset{t\in [0,\tau ]}{sup}\left|\right|S^{(d)}(t;\beta )-s^{(d)}(t;\beta )\left|\right|\stackrel{a.s.}{\to }0,$$

for d = 0, 1, or 2 and any β in a compact set. Since ${\widehat{\beta }}_S\stackrel{a.s.}{\to }{\beta }_S$ and || β_* − β_S || ≤ || β̂_S − β_S ||, ${\beta }_S^{\ast }\stackrel{a.s.}{\to }{\beta }_S$. Using the continuous mapping theorem, $S^{(d)}(t;{\beta }_S^{\ast })\stackrel{a.s.}{\to }{s}^{(d)}(t;{\beta }_S)$, with s⁽⁰⁾(t; β) bounded away from zero for all β and t ∈ [0, τ]. Using the almost sure convergence of $S^{(d)}(t;{\beta }_S^{\ast })$ to s^(d)(t; β_S) and the continuous mapping theorem,

$$\frac{S^{(2)}(t;{\beta }_S^{\ast })}{S^{(0)}(t;{\beta }_S^{\ast })}-\overline{Z}{(t;{\beta }_S^{\ast })}^{\otimes 2}\stackrel{a.s.}{\to }\frac{s^{(2)}(t;{\beta }_S)}{s^{(0)}(t;{\beta }_S)}-\overline{z}{(t;{\beta }_S)}^{\otimes 2}\equiv v(t;{\beta }_S)$$

uniformly in t ∈ (0, τ]. Using the Strong Law of Large Numbers (SLLN) and the continuous mapping theorem,

$$\widehat{A}({\beta }_S^{\ast })\stackrel{a.s.}{\to }A({\beta }_S),$$

where $A(\beta )\equiv E[{\int }_0^{\tau }v(t;\beta ){dN}_i(t)]$, as defined in condition (e). Hence

$$n^{\frac{1}{2}}({\widehat{\beta }}_S-{\beta }_S)=A{({\beta }_S)}^{-1}{n}^{-\frac{1}{2}}{U}_N({\beta }_S)+o_p(1).$$ (6)

Through the definition of S^(d)(t; β) and with some basic algebra,

$$U(\beta )=\sum _{i=1}^N{\int }_0^{\tau }{I}_i[Z_i(t)-\overline{Z}(t;\beta )]{dM}_i(t;\beta ).$$

Furthermore, we can write

$$n^{-\frac{1}{2}}U({\beta }_S)=n^{-\frac{1}{2}}\sum _{i=1}^N{\int }_0^{\tau }{I}_i{\psi }_i({\beta }_S)+o_p(1),$$ (7)

where ψ_i(β) is defined in Theorem 1. Using the fact that

$$\Vert n^{-\frac{1}{2}}\sum _{i=1}^N{\int }_0^{\tau }{I}_i[{\overline{Z}}_w(t;{\beta }_S)-\overline{z}(t;{\beta }_S)]{dM}_i(t;{\beta }_S)\Vert \stackrel{P}{\to }{0}_{p\times 1}.$$

which can be demonstrated by employing various empirical process results (Pollard 1990, van der Vaart 1996, Bilias, Gu and Ying 1997, van der Vaart 2000). Combining (6) and (7),

$$n^{\frac{1}{2}}({\widehat{\beta }}_S-{\beta }_S)=A{({\beta }_S)}^{-1}{n}^{-\frac{1}{2}}\sum _{i=1}^N{\int }_0^{\tau }{I}_i{\psi }_i({\beta }_S)+o_p(1).$$ (8)

Pan and Schaubel (2008) demonstrated that

$$N^{\frac{1}{2}}({\widehat{\beta }}_T-{\beta }_T)=A^w{({\beta }_T,{\theta }_0)}^{-1}{N}^{-\frac{1}{2}}\sum _{i=1}^N{\psi }_i^w({\beta }_T,{\theta }_0)+o_p(1),$$ (9)

where

$$\begin{array}{l}{\psi }_i^w(\beta ,\theta )={\int }_0^{\tau }{w}_i(\theta )\{Z_i(t)-{\overline{z}}_w(t;\beta ,\theta )\}{dM}_i(t)-G(\beta ,\theta )B{(\theta )}^{-1}{U}_{Li}\\ G(\beta ,\theta )=E\left[{\int }_0^{\tau }\{Z_i(t)-{\overline{z}}_w(t;\beta ,\theta )\}{X}_i^{\prime }{e}^{-{\theta }^{\prime }{X}_i}{dM}_i(t;\beta )\right],\\ U_{Li}(\theta )=X_i\{I_i-p_i(\theta )\}.\end{array}$$

Combining (8) and (9),

$$n^{\frac{1}{2}}(\widehat{D}-D)={\overline{p}}^{\frac{1}{2}}{C}^{\prime }{A}^w{({\beta }_T,{\theta }_0)}^{-1}{N}^{-\frac{1}{2}}\sum _{i=1}^N{\psi }_i^w({\beta }_T,{\theta }_0)-C^{\prime }A{({\beta }_S)}^{-1}{n}^{-\frac{1}{2}}\sum _{i=1}^N{\int }_0^{\tau }{I}_i{\psi }_i({\beta }_S).$$

We now define

$$\begin{array}{l}{\widehat{F}}_1={\overline{p}}^{\frac{1}{2}}{C}^{\prime }{A}^w{({\beta }_T,{\theta }_0)}^{-1}{N}^{-\frac{1}{2}}\sum _{i=1}^N{\psi }_i^w({\beta }_T,{\theta }_0)\\ {\widehat{F}}_2=C^{\prime }A{({\beta }_S)}^{-1}{n}^{-\frac{1}{2}}\sum _{i=1}^N{\int }_0^{\tau }{I}_i{\psi }_i({\beta }_S),\end{array}$$

such that

$$\text{Var}(n^{\frac{1}{2}}(\widehat{F}-D))=\text{Var}({\widehat{F}}_1)+\text{Var}({\widehat{F}}_2)-2\text{Cov}({\widehat{F}}_1,{\widehat{F}}_2).$$ (10)

For F̂₁, ${\overline{p}}^{\frac{1}{2}}$ converges to a constant between 0 and 1, while the indicator matrix C is pre-specified and the asymptotic information matrix for the weighted Cox regression A^w(β_T, θ₀)⁻¹ is also fixed. Hence the variance of F̂₁ is the product of several constants and the variance of $N^{-\frac{1}{2}}{\sum }_{i=1}^N{\psi }_i^w({\beta }_T,{\theta }_0)$, namely ${\mathrm{\sum }}_w({\beta }_T,{\theta }_0)=E\{{\psi }_i^w{({\beta }_T,{\theta }_0)}^{\otimes 2}\}$, which was derived by Pan and Schaubel through the Multivariate Central Limit Theorem. Therefore,

$$\text{Var}({\widehat{F}}_1)={\overline{p}C}^{\prime }{A}^w{({\beta }_T,{\theta }_0)}^{-1}{\mathrm{\sum }}_w({\beta }_T,{\theta }_0)A^w{({\beta }_T,{\theta }_0)}^{-1}C.$$ (11)

Similar arguments can be applied to obtain Var(F̂₂). The matrix A(β_S) is the limiting value for Â(β̂_S) and hence can be treated as constant matrix. The variance of $n^{-\frac{1}{2}}{\sum }_{i=1}^N{\int }_0^{\tau }{I}_i{\psi }_i({\beta }_S)$ can be derived through the Martingale Central Limit Theorem (Andersen and Gill 1982). That is, Σ(β_S) = E(ψ_i(β_S)^⊗2}, such that

$$\text{Var}({\widehat{F}}_2)=C^{\prime }A{({\beta }_S)}^{-1}\mathrm{\sum }({\beta }_S)A{\left({\beta }_S\right)}^{-1}C.$$ (12)

In terms of Cov(F̂₁, F̂₂), the quantities C, A^w(β_T, θ₀)⁻¹ A(β_S) are fixed. For the covariance between $N^{-\frac{1}{2}}{\sum }_{i=1}^N{\psi }_i^w({\beta }_T,{\theta }_0)$ and $n^{-\frac{1}{2}}{\sum }_{i=1}^N{\int }_0^{\tau }{I}_i{\psi }_i({\beta }_S)$ , we consider the three possible scenarios for the combination of subject i and j. If i ≠ j, $\text{Cov}\{{\psi }_i^w({\beta }_T,{\theta }_0),I_j{\psi }_j({\beta }_S)\}=\text{Cov}({\psi }_j^w({\beta }_T,{\theta }_0),I_i{\psi }_i({\beta }_S))=0$ since subjects are all independent from each other. If i = j and I_i = 0, $\text{Cov(}{\psi }_i^w({\beta }_T,{\theta }_0),I_j{\psi }_j({\beta }_S))=\text{Cov}({\psi }_i^w({\beta }_T,{\theta }_0),0)=0$ because subject i does not contribute to the estimation of β_S. If i = j and I_i ≠ 0, $\text{Cov}\{{\psi }_i^w({\beta }_T,{\theta }_0),I_j{\psi }_j({\beta }_S)\}=E\{{\psi }_i({\beta }_S){\psi }_i^w{({\beta }_T,{\theta }_0)}^{\prime }\}$ because both ψ_i(β_S) and ${\psi }_i^w({\beta }_T,{\theta }_0)$ have expectation zero. Summing up the three types of covariances,

$$\text{Cov}\left\{N^{-\frac{1}{2}}\sum _{i=1}^N{\psi }_i^w({\beta }_T,{\theta }_0),n^{-\frac{1}{2}}\sum _{i=1}^N{\int }_0^{\tau }{I}_i{\psi }_i({\beta }_S)\right\}={(Nn)}^{-\frac{1}{2}}n{\mathrm{\sum }}_{\beta }({\beta }_S,{\beta }_T,{\theta }_0)$$

where

$${\mathrm{\sum }}_{\beta }({\beta }_1,{\beta }_2,\theta )=E\{{\psi }_i({\beta }_1){\psi }_i^w{({\beta }_2,\theta )}^{\prime }\}.$$

Combining the above results, we obtain

$$\text{Cov}({\widehat{F}}_1,{\widehat{F}}_2)={\overline{p}}^{\frac{1}{2}}{C}^{\prime }A{({\beta }_S)}^{-1}{\mathrm{\sum }}_{\beta }({\beta }_S,{\beta }_T,{\theta }_0)A^w{({\beta }_T,{\theta }_0)}^{-1}C.$$ (13)

Combining (10), (11), (12) and (13), the variance of $n^{\frac{1}{2}}(\widehat{D}-D)$ in Theorem 1 is derived.

Proof of Theorem 2

The proof of uniform consistency of of Λ̂₀(t; β̂_S) to Λ_0S(t) for t ∈ (0, τ] begins by decomposing α̂(t) = Λ̂₀(t; β̂_S)−Λ_0S(t) into two parts, α̂(t) = α̂₁(t)+ α̂₂(t) with

$$\begin{array}{l}{\widehat{\alpha }}_1(t)={\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S)-{\widehat{\mathrm{\Lambda }}}_0(t;{\beta }_S)\\ {\widehat{\alpha }}_2(t)={\widehat{\mathrm{\Lambda }}}_0(t;{\beta }_S)-{\mathrm{\Lambda }}_{0S}(t).\end{array}$$

Applying a Taylor expansion about β_S,

$$\begin{array}{l}{\widehat{\alpha }}_1(t)=N^{-1}\sum _{i=1}^N{\int }_0^t{\frac{\partial }{\partial {\beta }^{\prime }}[S^{(0)}(s;\beta )]|}_{\beta ={\beta }_{\ast }}{dN}_i(s)({\widehat{\beta }}_S-{\beta }_S)\\ =-N^{-1}\sum _{i=1}^N{\int }_0^t{\frac{S^{(1)}(s;\beta )}{S^{(0)}{(s;\beta )}^2}|}_{\beta ={\beta }_{\ast }}{dN}_i(s)({\widehat{\beta }}_S-{\beta }_S)\\ =-{\int }_0^t{\overline{Z}}^{\prime }(s;{\beta }_{\ast })d{\widehat{\mathrm{\Lambda }}}_0(s;{\beta }_{\ast })({\widehat{\beta }}_S-{\beta }_S),\end{array}$$

where β_* lies between β̂s; β_S ∈ 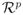. Since the quantities Z̄(s; β_*) and dΛ̂₀(s; β_*) are bounded, along with ${\widehat{\beta }}_S\stackrel{a.s.}{\to }{\beta }_S$, it follows that $\mid {\widehat{\alpha }}_1(t)\mid \stackrel{a.s.}{\to }0$.

The second component, α̂₂(t), can be rewritten as $n^{-1}{\sum }_{i=1}^N{\int }_0^t{I}_i{S}^{(0)}{(s;{\beta }_S)}^{-1}{dM}_i(s;{\beta }_S)$. By the Uniform Strong Law of Large Numbers (USLLN; Pollard 1990), $n^{-1}{\sum }_{i=1}^N{\int }_0^t{I}_i{dM}_i(s;{\beta }_S)\stackrel{a.s.}{\to }0\text{for}t\in [0,\tau ]$ for t ∈ [0, τ]. As n → ∞, $S^{(0)}(s;{\beta }_S)\stackrel{a.s.}{\to }{s}^{(0)}(s;{\beta }_S)$ which is bounded away from 0. Therefore, $\mid {\widehat{\alpha }}_2(t)\mid \stackrel{a.s.}{\to }0$.

Combining results for α̂₁(t) and α̂₂(t) and the triangle inequality,

$$\underset{t\in [0,\tau ]}{sup}\mid \widehat{\alpha }(t)\mid \le \underset{t\in [0,\tau ]}{sup}\mid {\widehat{\alpha }}_1(t)\mid +\underset{t\in [0,\tau ]}{sup}\mid {\widehat{\alpha }}_2(t)\mid ,$$

yields the required result,

$$\underset{t\in [0,\tau ]}{sup}\mid {\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S)-{\mathrm{\Lambda }}_{0S}(t)\mid \stackrel{a.s.}{\to }0.$$ (14)

Combining (14) and the convergence of ${\widehat{\mathrm{\Lambda }}}_0^w(t;{\widehat{\beta }}_T,\widehat{\theta })$ for Λ_0T (t) (Pan and Schaubel 2008), Δ̂(t; β̂_S, β̂_T, θ̂) converges uniformly to Δ(t) for t ∈ [0, τ] by continuous mapping theorem.

Proof of Theorem 3

First, we decompose

$$\begin{array}{l}{n}^{\frac{1}{2}}\{\widehat{\mathrm{\Delta }}(t;{\widehat{\beta }}_S,{\beta }_T,\widehat{\theta })-\mathrm{\Delta }(t)\}={\overline{p}}^{\frac{1}{2}}{N}^{\frac{1}{2}}\{{\widehat{\mathrm{\Lambda }}}_0^w(t;{\widehat{\beta }}_T,\widehat{\theta })-{\mathrm{\Lambda }}_{0T}(t)\}-n^{\frac{1}{2}}\{{\widehat{\mathrm{\Lambda }}}_0(t;{\widehat{\beta }}_S)-{\mathrm{\Lambda }}_{0S}(t)\}\\ ={\widehat{\xi }}_1(t)-{\widehat{\xi }}_2(t).\end{array}$$

As shown by Pan and Schaubel,

$${\widehat{\xi }}_1(t)={\overline{p}}^{\frac{1}{2}}{N}^{-\frac{1}{2}}\sum _{i=1}^N{\phi }_i^w(t;{\beta }_T,{\theta }_0)+o_p(1),$$

where

$$\begin{array}{l}b(t;\beta ,\theta )=E\{X_i{e}^{-{\theta }^{\prime }{X}_i}{Y}_i(t)e^{{\beta }^{\prime }{Z}_i(t)}\}\\ k(t;\beta ,\theta )=-E\left\{{\int }_0^t\frac{X_i{e}^{-{\theta }^{\prime }{X}_i}}{s_w^{(0)}(s;\beta ,\theta )}{dN}_i(s)+{\int }_0^t\frac{w_i(\theta )b(s;\beta ,\theta )}{s_w^{(0)}{(s;\beta ,\theta )}^2}{dN}_i(s)\right\}\\ h(t;\beta ,\theta )=-{\int }_0^t{\overline{z}}_w(s;\beta ,\theta )d{\mathrm{\Lambda }}_0(s)\\ {\phi }_i^w(t;\beta ,\theta )=k^{\prime }(t;\beta ,\theta )B{(\theta )}^{-1}{U}_{Li}+h^{\prime }(t;\beta ,\theta )A^w{(\beta ,\theta )}^{-1}{\psi }_i^w(\beta ,\theta )+{\int }_0^t\frac{w_i(\theta ){dM}_i(s;\beta ,\theta )}{s_w^{(0)}(s;\beta ,\theta )}.\end{array}$$

Through a similar derivation,

$${\widehat{\xi }}_2(t)=n^{-\frac{1}{2}}\sum _{i=1}^N{I}_i{\phi }_i(t;{\beta }_S)+o_p(1),$$

where

$${\phi }_i(t;\beta )=-{\int }_0^t{\overline{z}}^{\prime }(s;\beta )d{\mathrm{\Lambda }}_{0S}(s)(t;\beta )A{(\beta )}^{-1}{\psi }_i(\beta )+{\int }_0^t\frac{{dM}_i(s;\beta ,\theta )}{s_w^{(0)}(s;\beta ,\theta )}.$$

Asymptotic normality extends to any finite set of time points. Finally, weak convergence to a Gaussian process follows from the tightness of $n^{\frac{1}{2}}\{\widehat{\mathrm{\Delta }}(t)-\mathrm{\Delta }(t)\}$, which follows from the manageability of both ${\phi }_i^w(t;{\beta }_T,{\theta }_0)$ and φ_i(t; β_S). See Pan and Schaubel (2008) for pertinent details. For two time points (s, t) ∈ (0, τ] × (0, τ],

$$\begin{array}{l}\text{Cov}(n^{\frac{1}{2}}\{\widehat{\mathrm{\Delta }}(s;{\widehat{\beta }}_S,{\widehat{\beta }}_T,\widehat{\theta })-\mathrm{\Delta }(t)\},n^{\frac{1}{2}}\{\widehat{\mathrm{\Delta }}(t;{\widehat{\beta }}_S,{\widehat{\beta }}_T,\widehat{\theta })-\mathrm{\Delta }(t)\})\\ =\text{Cov}({\widehat{\xi }}_1(s),{\widehat{\xi }}_1(t))+\text{Cov}({\widehat{\xi }}_2(s),{\widehat{\xi }}_2(t))-\text{Cov}({\widehat{\xi }}_1(s),{\widehat{\xi }}_2(t))-\text{Cov}({\widehat{\xi }}_2(s),{\widehat{\xi }}_1(t))\end{array}$$

where

$$\begin{array}{l}\text{Cov}({\widehat{\xi }}_1(s),{\widehat{\xi }}_1(t))=\overline{p}E\{{\phi }_i^w(s;{\beta }_T,{\theta }_0){\phi }_i^w(t;{\beta }_T,{\theta }_0))\}\\ \text{Cov}({\widehat{\xi }}_2(s),{\widehat{\xi }}_2(t))=E\{{\phi }_i(s;{\beta }_S){\phi }_i(t;{\beta }_S)\}\\ \text{Cov}({\widehat{\xi }}_1(s),{\widehat{\xi }}_2(t))=\overline{p}E\{{\phi }_i^w(s;{\beta }_T,{\theta }_0){\phi }_i(t;{\beta }_S)\}\\ \text{Cov}({\widehat{\xi }}_2(s),{\widehat{\xi }}_1(t))=\overline{p}E\{{\phi }_i(s;{\beta }_S){\phi }_i^w(t;{\beta }_T,{\theta }_0)\}.\end{array}$$

through arguments similar to the derivation for Cov(F̂₁, F̂₂) and the Functional CLT (Pollard 1990).