Gap distance and Interactions in a Molecular Tunnel Junction

Abstract

The distance between electrodes in a tunnel junction cannot be determined from the external movement applied to the electrodes because of interfacial forces that distort the electrode geometry at the nanoscale. These distortions become particularly complex when molecules are present in the junction, as demonstrated here by measurements of the AC response of a molecular junction over a range of conductivities from micro Siemens to pico Siemens. Specific chemical interactions within the junction lead to distinct features in breakjunction data and these have been used to determine electrode separation in a junction functionalized with 4(5)-(2-mercaptoethyl)-1H-imidazole-2-carboxamide, a reagent developed for reading DNA sequence.

Adjustable tunnel junctions are widely used to determine the electrical properties of molecules spanning two electrodes.¹ The size of the junction is usually characterized by the measured tunnel conductance of the junction, or by the amount by which a break junction is separated by an externally applied displacement. The actual size of the nanoscale gap is not readily determined from the external measurement. When the electrodes (usually gold) are metallically bonded, and then pulled apart to form a break junction, plastic deformation of the gold leads to the formation of filaments that give rise to a constant conductance over distances that approach a nm (see Figure 3A for an example). When the filaments break, the metal surface relaxes back to a more stable configuration (i.e., they “snap back”). On approach of two metal surfaces, the electrodes can be drawn together by van der Waals interactions when they are close together, leading to instabilities in the gap. The electrodes can be repelled as contamination is trapped in the gap, leading to apparent approach distances of 100 nm or more. Examples of these events are given in the supporting information (Figs S1 and S2). It is important to be able to determine the real value of the nanoscale gap when the goal of these studies is to make devices that utilize fixed, nanofabricated tunnel junctions.

Figure 3.

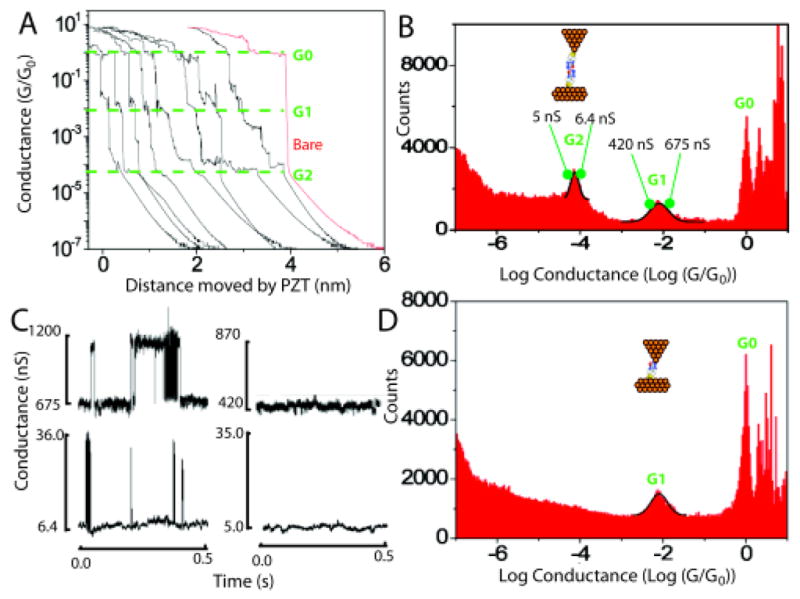
Break junction measurements of imideazole-2-carbamide functionalized tunnel junctions. A. Typical current-time plots (converted to apparent gap size using the PZT velocity). Distinct plateaus occur near G0, owing to the formation of quantum point contacts. Features near G1 and G2 are associated with molecular structures formed in the gap. The red curve is typical of data collected with unfunctionalized probes and surfaces. No plateaus are seen below G0. B. Distribution of conductances for both probe and surface functionalized. The lower conductance peak (G2) is not present when only the surface is functionalized (D) showing that this peak is associated with pairs of molecules spanning the gap, an interpretation quantitatively consistent with the values of G1 and G2. C. Telegraph noise owing to stochastic bonding of single molecules across the gap (upper left) or pairs of molecules in series (lower left). The noise vanishes when the gap conductance is adjusted to just below G1 or G2 (traces on the right).

We have proposed a read-out system for DNA sequences based on a non-covalent complex between recognition molecules tethered to fixed electrodes and the bases of a DNA molecule that is passed through the tunnel junction by electrophoresis.² Here, we report on a study of tunnel junctions based on gold electrodes functionalized with a new generation of recognition molecule, with 4(5)-(2-mercaptoethyl)-1H imideazole-2-carboxamide (hereafter imideazole-2-carbamide - Fig. 1B). The synthesis and characterization of this molecule has been described elsewhere.³ We have used ac modulation of the gap⁴ as a probe of the effective stiffness of the gap, using a logarithmic current to voltage converter to allow us to probe a range of gap conductances from close to quantum point contact ( $\text{conductance}=G_0=\frac{2e^2}{h}=77\mu \text{S}$) all the way out to the small conductances used to pass DNA bases between the electrodes (~ 6 pS). These measurements reveal the many interactions taking place in the tunnel junction, interactions that make it impossible to determine the gap from tunnel-current data alone. We determine the gap size using molecules trapped in the gap as a “molecular ruler”, molecular tunneling signals ceasing when the gap size exceeds the size of the trapped molecules.⁵ The gap size determined in this way is about 24 Å, more than large enough to pass a single-stranded DNA molecule.

Figure 1.

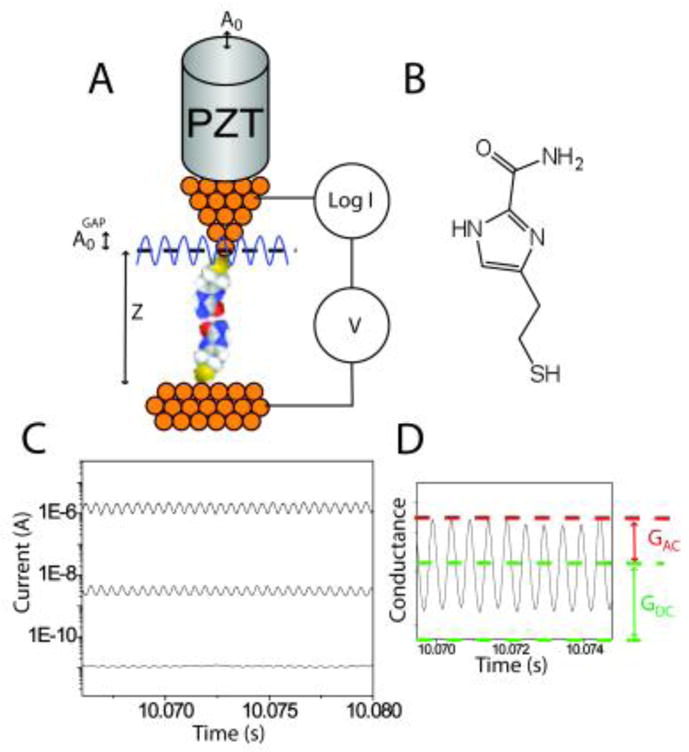
Set up for determining junction stiffness: A. An ac modulation applied to the PZT deflects it by an amount A₀. The modulation amplitude of the gap itself, A₀^GAP is different because of interaction forces in the tunnel junction. B. Imidazole-2-carboxamide. C. AC modulation of the PZT results in a corresponding modulation of the gap conductance that increases with the DC set-point current according to $G_{AC}={\beta A}_0^{\mathit{GAP}}{G}_{DC}$. D. Showing how the quantities G_AC and G_DC are extracted.

Monolayers of imideazole-2-carboxamide were formed on freshly flame-annealed Au(111) electrodes and characterized with FTIR, ellipsometry, XPS and STM (Figs. S3–S5). Importantly, ellisometry and XPS taken together suggest that the molecules stand upright on the surface with the S bonded to gold, forming a film consistent with the full 8.5 Å length of the recognition molecules. STM probes were etched from gold wire, insulated with high-density polyethylene and functionalized as described previously² (and supporting information). The functionalization of the probes was tested by comparing tunneling signals obtained on bare substrates with tunneling signals obtained from bare (i.e., unfunctionalized) probes on functionalized substrates. Tunneling measurements were recorded with an Agilent PicoSPM (Chandler AZ) interfaced to a digital storage oscilloscope and a field programmable gate array controller (PCIe-7842R, National Instruments). The entire junction was submerged in the 1 mM phosphate buffered (pH=7) aqueous electrolyte used for readout of DNA sequence.

The modulated-junction method is illustrated in Fig. 1. A small distance modulation, A₀, is applied to the gap by adding an ac signal to the voltage used to drive the PZT in the vertical direction. The PZT sensitivity was calibrated by using STM images of single atom steps on Au(111) and an amplitude, A₀, of 0.52 Å was used in the present work. This is small enough that the following expression holds for the AC modulation of the gap conductance: $G_{AC}={\beta A}_0^{\mathit{GAP}}{G}_{DC}$, where G_DC is the average gap value (supporting information) and $A_0^{\mathit{GAP}}$ is the modulation of the gap. Thus the AC signal increases in direct proportion to the DC value, as illustrated with traces of the tunneling signal in Fig. 1C. The ratio, $\frac{G_{AC}}{G_{DC}}$ (Fig. 1D) yields the quantity $\beta A_0^{\mathit{GAP}}$. The whole problem lies with the fact that $A_0^{\mathit{GAP}}\ne A_0$, the applied modulation, because of the small compliance of the STM probe.⁶ Mechanical interactions in the junction show up as rapid variations in the value of “β” derived by assuming a constant A₀. In this work, signals were acquired using a logarithmic current-to-voltage converter⁷, calibrated as described in the supporting information.

Fig. 2A shows how G_AC varies with G_DC for a bare gold probe and a bare gold substrate in a 1 mM phosphate buffer (pH=7). These data show the mean (data points) and standard deviation for 39 recordings at each G_DC, spanning a range from about 20 μS to 10 pS (at a probe bias of +0.5V). Data were fitted with six linear segments, yielding the values of the apparent decay constant, ${\beta }_{\text{app}}({\beta }_{\mathit{app}}=\frac{1}{A_0}\frac{\partial G_{AC}}{\partial G_{DC}})$. They recapitulate the data first reported for aqueous electrolyte by Vaught et al.⁸ Vaught et al. made measurements using a perchlorate electrolyte, while we used 1mM phosphate buffer – evidently, these ions do not play a significant role. At small gap conductances β_app ~ 0.9 Å⁻¹, falling as the gap conductance rises above 10⁻⁸ S. The fall is particularly marked above 10⁻⁵ S where β_app falls to almost 0.1 Å⁻¹, a consequence of strong mechanical interactions in the gap (supporting information). In the absence of such interactions, the gap could be estimated from the sum of the distances, z_nm, corresponding to each of the linear segments of constant β_nm(i.e., $z=\sum -\frac{1}{{\beta }_{nm}}ln\left(\frac{G_m}{G_n}\right)$ where G_n is the conductance at the high side of the linear segment and G_m is the conductance on the low side). Carrying this sum out yields z = 38 Å, an unrealistically large gap because it has been exaggerated by the very small value of β_app at the highest conductance.

Figure 2.

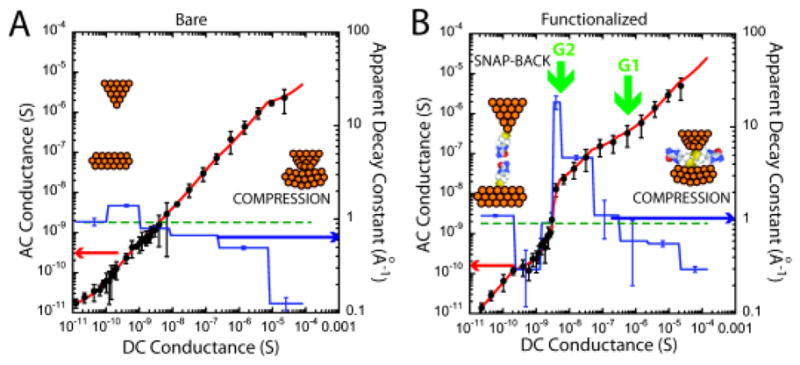
Showing how G_AC varies with G_DC for A, a bare gold probe and bare gold surface in 1 mM phosphate buffer (pH 7.0) and B, both probe and surface functionalized with imidazole-2-carboxamide in the same buffer (black dots). The red lines are linear fits to segments of the plots using the effective decay constants (i.e., the apparent β values) as shown by the blue lines (righthand axes of the plots). Rapid changes at the points labeled G1 and G2 are coincident with peaks in the conductance distributions measured by break junction methods.

When both electrodes are functionalized with imideazole-2-carboxamide (Fig. 2B) the shape of the curve changes dramatically. There is a “bump” between 10⁻⁷ S> G_DC >10⁻⁹ S where β_app reaches the extraordinary value of 18.4 Å⁻¹. Interestingly, β_app is not as much reduced at small gaps compared to the unfunctionalized system, possibly reflecting a reduced gold-gold interaction. The very large values of β_app are most readily explained by regions in which bonds between the probe and surface break, resulting in a snapping back of the electrode surfaces and a large change in current for a small motion of the probe. Jumps in the slope of this plot at ~ 10⁻⁷ S and 10⁻⁹ S are associated with molecular adhesion events as confirmed by break junction data^1a. Figure 3A shows some typical current vs. retraction-distance curves for both the probe and surface functionalized. Plateaus are evident at ~10⁻⁷ S (i.e., ~ 10⁻² G₀, labeled G1) and ~10⁻⁹ S (i.e., ~ 10⁻⁴ G₀, labeled G2). Curves taken with a bare probe (example in red) show only the plateaus near the quantum of conductance (G0). A histogram (Fig. 3B) of the current recorded from one thousand such curves shows distinct peaks at 6.2 ±2.3 × 10⁻⁷ S (i.e., ~ 10⁻² G₀ – G1) and 5.8±0.7 × 10⁻⁹ S (i.e., ~ 10⁻⁴ G₀ – G2). The likely origin of the two peaks is immediately clear when similar curves are collected and histogrammed using a bare tip and a functionalized surface (Fig. 3D). In this case, only the peak G1 appears in addition to the metallic contact peak at G0. Thus, the high current peak (at G1) is assigned to one molecule spanning the gap (via an amine-gold linkage⁹) while the low current peak (G2) is assigned to hydrogen-bonded pairs bridging the gap. Time traces of the tunnel-current noise taken at conductances above G1 and G2 (Fig. 3C) show the characteristic “telegraph” noise fluctuations owing to stochastic bond-breaking in a molecule spanning the junction.⁵ No signals are seen when the set-point is below G1 or G2 (note that signals owing to hydrogen-bonded pairs of molecules spanning the gap are too small to be seen in the traces collected near G1).

Is this assignment of G1 to one molecule and G2 to a pair in series consistent with the observation that β ~ 0.5 to 0.6 when the molecules are interacting (Fig. 2B)? $\beta =-\frac{ln\left(\frac{G_{1,2}}{G_0}\right)}{z_{1,2}}$ and using G1 = 621 nS (Fig. 3B) and z₁= 8.5 Å gives β = 0.57 Å⁻¹, while using G2 = 5.8 nS (Fig. 3B) and z₂=17 Å gives β = 0.58 Å⁻¹, consistent with one molecular length trapped in the gap at G1 and two molecular lengths trapped in the gap at G2.

The magnitude of the telegraph-noise measures how much the conductance increases when molecules bond the two electrodes together. For the single molecule, the conductance increase on bonding is 432 nS, while for the two molecules in series this value is 28 nS (supporting information). Based on distance differences alone and assuming that β is still 0.6 Å⁻¹ leads to an estimate of exp(−βL+2 βL) = exp(βL) = 164:1 for the ratio of the two conductances. This is much larger than the observed ratio (of 15:1) showing that details of the bonding play a large role in determining the size of the telegraph-noise. Note that events that cause “electronic bond fluctuations” of the electrodes are not the same as making and breaking of the chemical bonds between molecules and electrodes, as discussed in detail elsewhere.²

We are still left with the question of what the final gap is at the 6 pS conductance (G_SP) used for identifying DNA bases. Given that the gap at G2 is 17 Å, and taking the real value of β in water to be 0.92 (Fig. 2A - it appears to be less just after the bonds break in the case of the functionalized junction – Fig. 2B – because of attraction between the bonding groups) we estimate the additional distance from G1 to G_SP to be 7.5 Å for a total gap size of about 24 Å.

In summary, we have shown how the formation of molecular complexes in a tunnel junction is signaled by changes in the elastic properties of the tunnel junction, evident in the ac response of the junction, and how the structures themselves can be used as nanoscale “rulers” for determining the size of the nanojunction.