Evidence for a vertebrate catapult: elastic energy storage in the plantaris tendon during frog jumping

Abstract

Anuran jumping is one of the most powerful accelerations in vertebrate locomotion. Several species are hypothesized to use a catapult-like mechanism to store and rapidly release elastic energy, producing power outputs far beyond the capability of muscle. Most evidence for this mechanism comes from measurements of whole-body power output; the decoupling of joint motion and muscle shortening expected in a catapult-like mechanism has not been demonstrated. We used high-speed marker-based biplanar X-ray cinefluoroscopy to quantify plantaris muscle fascicle strain and ankle joint motion in frogs in order to test for two hallmarks of a catapult mechanism: (i) shortening of fascicles prior to joint movement (during tendon stretch), and (ii) rapid joint movement during the jump without rapid muscle-shortening (during tendon recoil). During all jumps, muscle fascicles shortened by an average of 7.8 per cent (54% of total strain) prior to joint movement, stretching the tendon. The subsequent period of initial joint movement and high joint angular acceleration occurred with minimal muscle fascicle length change, consistent with the recoil of the elastic tendon. These data support the plantaris longus tendon as a site of elastic energy storage during frog jumping, and demonstrate that catapult mechanisms may be employed even in sub-maximal jumps.

1. Introduction

Anuran jumping is a common model system for studying muscle-powered accelerations in vertebrates [1,2]. Skeletal muscles provide the mechanical power for the jump [1], but whole-body power output exceeds the maximum muscle power output by a factor of seven or more in some species [3,4]. These supramaximal power outputs are hypothesized to be the result of a catapult-like mechanism, which stores and subsequently releases elastic strain energy [2–5]. A catapult mechanism would require muscles to contract prior to joint motion to load energy into elastic structures, followed by joint movement owing to elastic recoil. Conclusions regarding this prediction in the literature are mixed. A study of semimembranosus function during jumping concluded that there was a tight correlation between muscle action and joint action [1]. In contrast, measurements of plantaris muscle function have observed early muscle shortening prior to significant body movement [2,6], suggesting pre-storage of elastic energy. A shortcoming of this approach is that anurans go through a complex series of postural movements early in the jump and prior to leg extension, and these motions could allow muscle shortening prior to body movement. The recoil of elastic structures in a catapult mechanism should also allow for a period of joint extension more rapid than expected from muscle contraction alone. This prediction has not been tested.

We sought to determine whether muscle and joint motion are decoupled by tendon elasticity at the ankle joint of Rana pipiens during jumping, and whether the pattern of decoupling is consistent with the hypothesized catapult mechanism. We hypothesized that shortening of the muscle would be decoupled from joint extension owing to the effect of tendon stretch and recoil. We used a new method of three-dimensional X-ray motion analysis, X-ray Reconstruction of Moving Morphology (XROMM) [7], to simultaneously track the fascicle length of the plantaris longus muscle (a large, pennate ankle extensor with a prominent tendon) and the extension of the ankle joint. If this muscle-tendon-joint system behaved like a catapult mechanism, we expected to see muscle shortening without joint movement as the tendon stretched, followed by rapid joint motion powered by tendon recoil. The null hypothesis was that joint motion would directly follow muscle shortening in the relationship determined from the muscle moment arm at the ankle joint.

2. Material and methods

(a). Animals

Four Rana pipiens (mean ± s.d.—snout-vent length: 9.2 ± 1.2 cm, mass: 93 ± 25 g) were kept in an enclosure with water and land areas and fed crickets three times per week.

(b). X-ray Reconstruction of Moving Morphology

To track the ankle joint and muscle length via XROMM, radiopaque tantalum beads (1 mm diameter with 0.3 mm hole, Bal-Tec, Los Angeles, CA, USA) were implanted into the plantaris longus muscle and affixed to the bones [7]. Frogs were anaesthetized with MS-222 and beads were implanted into the plantaris via incisions at the proximal end of the aponeurosis and as close to the origin as possible in the same fascicle plane as the prior bead, then sealed with surgical cyanoacrylate glue. Jump data showed low digitizing error for these markers (s.d. = 0.03 mm), and muscle marker distances during the pre-jump (resting) period were consistent from jump to jump, suggesting that markers were firmly fixed within the muscle tissue. Three or more non-colinear bone markers [7] were firmly implanted into each of the bones of the ankle joint (the tibiofibula and the fused tarsal bones, the tibiale and fibiale). Bone markers were constructed from a tantalum bead affixed to a 0.25 mm diameter insect pin, leaving a 1–2 mm shaft which was inserted into a hole drilled in the bone. Frogs received an intracoelomic injection of carprofen after surgery and recovered for a minimum of 5 days prior to testing.

The jumping platform was positioned between two perpendicular C-arms (OEC mobile C-arm X-ray system, 9400 series, Radiological Imaging Services, Hamburg, PA, USA) equipped with X-ray sources (20 mA, 90 kVp), image intensifiers and high-speed cameras (FASTCAM-1024PCI, Photron USA, Inc., San Diego, CA, USA) that captured video at 500 frames s⁻¹ with a 1/4000 shutter speed via a synchronized post-trigger. The system was calibrated before and after each series of jumps [7]. Six jumps over 30 cm were collected for each frog at approximately 22°C. Frogs were then euthanized with an overdose of MS-222 followed by double-pithing.

We digitized all markers in Matlab using a custom digitizing program designed for use with the XROMM system [7]. Standard deviation of the distance between same-bone markers was 0.04 mm [7]. The coordinates of each bone marker were smoothed with a 25 Hz low-pass butterworth filter in Matlab, while muscle markers were smoothed via a smoothing spline in IGOR Pro v. 6.06 (WaveMetrics, Inc., Lake Oswego, OR, USA) with a smoothing factor of 1 and an s.d. of 0.03 mm. Frogs were scanned with X-ray computed tomography with a 0.625 mm slice thickness and the relevant bone models were reconstructed using Amira V. 4.0 (Mercury Computer Systems Inc., Chelmsford, MA, USA). These bones were registered to the markers using custom scripts [7] for Maya 2009 (Autodesk, Inc., San Rafael, CA, USA). The motion of the fuzed tarsal bones relative to tibiofibula was quantified in all six degrees of freedom. Ankle extension, the primary plantaris action, was the only joint motion considered further. The three-dimensional distance between digitized markers implanted in the plantaris was used to determine muscle fascicle length. Fascicle shortening was expressed as a percentage of starting length. The start of muscle and joint movements were defined as the time at which 5 per cent of total change in length or angle occurred, respectively. The average velocity of the most distal marker over three frames immediately following toe-off was used to determine takeoff velocity. Variables are presented as mean ± 1 s.d.

(c). Tendon travel

The tendon travel method [8] was used to determine the relationship between muscle–tendon unit length and joint angle at the ankle at constant tendon length for each frog. The slope of this relationship is the muscle moment arm (electronic supplementary material, figure S1). Marked, dissected limb bones were moved through the full range of flexion and extension. Muscle–tendon unit excursion was determined from the motion of a marker on a Kevlar string that connected the tendon to a fixed load. Joint angle and muscle–tendon unit length were determined from digitized video over several cycles. The procedure was also performed for the knee and tarso–metatarsal joints.

3. Results

Observed jumps had a takeoff velocity of 161 ± 30 cm s⁻¹, which at a 45° launch angle would result in a jump distance of 52.8 ± 11.4 cm. Total fascicle shortening was 14.6 ± 5.6%, and the ankle joint was extended to 115 ± 14.8°.

Length changes in plantaris muscle fascicles were decoupled from changes in joint angle in all jumps, with a consistent sequence of events (figure 1). Fascicle-shortening began prior to the onset of joint movement (107 ± 42 ms), and approximately half of the total fascicle-shortening occurred prior to joint movement (figure 1 and table 1). Decoupling of muscle shortening and joint motion was also evident during the first half of ankle extension, during which minimal fascicle shortening (2.2 ± 1.5%) was accompanied by a large change in joint angle (53° ± 7°) and high angular acceleration (figure 1 and table 1). During this period, muscle fascicle length changes were eccentric in 75 per cent of jumps (figure 1).

Figure 1.

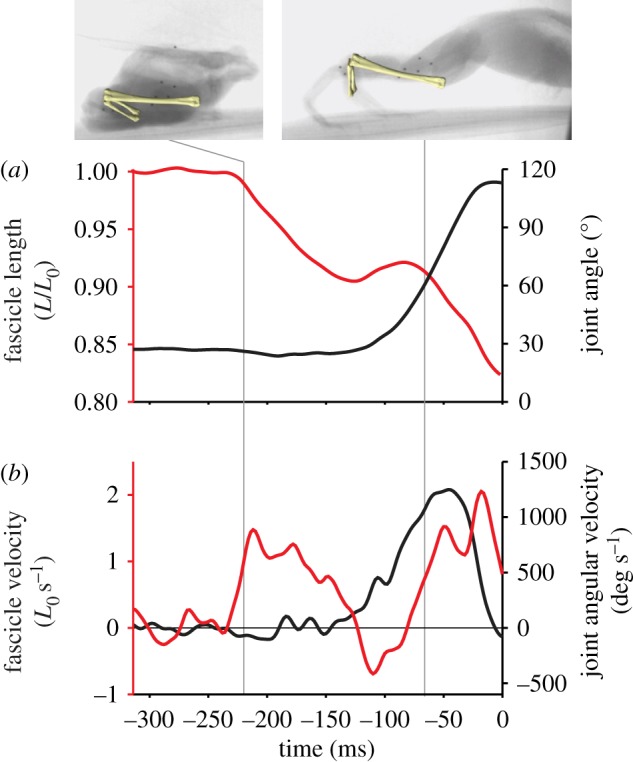
Time-course of an example jump, with cineradiography frames and superimposed bones at two points in the jump. Time 0 corresponds to toe-off. (a) Muscle fascicle length (red) and ankle joint angle (black). (b) Fascicle velocity (red) and joint angular velocity (black).

Table 1.

Summary of variables for all jumps. Pre-loading phase is from initiation of muscle shortening until the initiation of joint movement. The first 50% of ankle extension is from initiation of joint movement until 50% of maximum joint angle. The second 50% of ankle extension is from 50% of maximum joint angle until toe off.

	pre-loading	ankle extension (first 50%)	ankle extension (second 50%)
fascicle strain (%)	7.8 ± 3.3	2.2 ± 1.5	4.9 ± 2.7
fascicle shortening velocity (L s−1)	0.79 ± 0.42	0.52 ± 0.42	0.94 ± 0.60
ankle angle change (°)	5.7 ± 0.7	53 ± 7	53 ± 8
average angular velocity (deg s−1)	19 ± 51	1190 ± 494	1120 ± 393
duration (ms)	107 ± 42	49 ± 16	55 ± 17

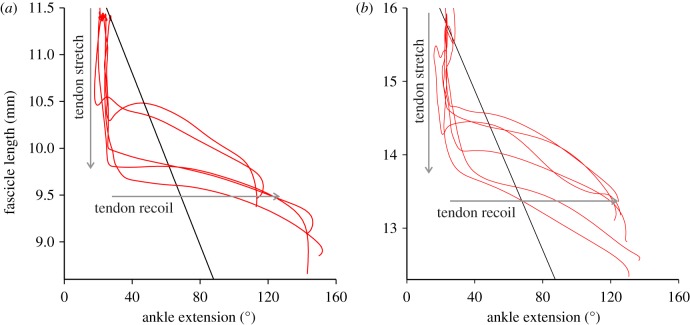
Tendon travel measurements describe the relationship between muscle length and ankle angle that would be expected in the absence of tendon elasticity (electronic supplementary material, figure S1). A comparison of these data with the muscle fascicle length–joint angle relationship observed during a jump showed noticeable decoupling (figure 2). Early in the jump, the in vivo fascicle length–joint angle relationship was vertical owing to muscle shortening without joint angle change before abruptly changing the slope as rapid joint movement occurred without corresponding muscle shortening.

Figure 2.

Muscle–joint decoupling. Regressions from tendon travel measurements (black) indicate the relationship between muscle length and ankle joint angle that would be expected in the absence of tendon elasticity. The in vivo relationship between fascicle length and joint angle (red) reflects the influence of tendon stretch and recoil. Tendon stretch occurs when muscle shortens without joint angle change, and tendon recoil occurs when joint angle changes without muscle shortening. Each panel represents a different individual.

4. Discussion

The catapult-like mechanism that has been hypothesized for frog jumping requires pre-storage of elastic energy, followed by the rapid release of this energy during the jump. The pattern of muscle length change and joint motion observed in the plantaris confirms this hypothesis. Early in the jump, the plantaris longus muscle shortened without joint movement (figures 1 and 2), showing that the tendon stretched to store work done by muscle contraction. This was followed by a period of high angular acceleration of the joint and minimal muscle shortening (table 1), indicating a substantial contribution of tendon recoil to powering ankle extension. Although we did not measure tendon length directly, the observed pattern of decoupling of muscle fascicle and joint motion would be difficult to explain by mechanisms other than tendon stretch and recoil.

The observation of fascicle lengthening during jumping was unexpected, and may reflect a constraint on the effective use of elastic power-amplifying mechanisms. This lengthening indicates energy absorption by the muscle and, because the joint was extending, the source of this energy must be tendon recoil. The only reasonable explanation of this pattern is a ‘backfire’ of the tendon on muscle, which is likely to be detrimental as it consumes some of the work done previously to stretch the tendon. Presumably, effective power amplification systems operate to maximize the stored elastic energy transferred to the joint, and thereby to the centre of mass, while minimizing the energy lost to stretching the muscle. Three of the four individuals showed jumps both with and without eccentric contractions, suggesting that, while they are anatomically equipped to prevent this loss, there was also an unknown behavioural component that varied between jumps.

Power amplification during jumping has been observed in several vertebrates based on kinematics or force-plate data [3,9,10] and muscle shortening has been observed prior to body movement [2]. Power amplification in vertebrates is typically detected by whole-body power outputs, which exceed the maximal isotonic power output multiplied by the total propulsive muscle mass. However, this study uses in vivo observations of muscle fascicle and joint decoupling to show the first evidence for power amplification in submaximal jumps [4,11]. Since elastic energy storage occurs even in frog jumps which do not show exceptional distance, takeoff velocity or power output, it is likely that elastic energy storage is far more common in accelerations than indicated by prior indirect methods of detecting it. The presence of elastic energy storage and recoil in submaximal jumps may also be informative in future investigations into the nature of the catch mechanism in anuran jumping.