Screening for prostate cancer using multivariate mixed-effects models

Abstract

Using several variables known to be related to prostate cancer, a multivariate classification method is developed to predict the onset of clinical prostate cancer. A multivariate mixed-effects model is used to describe longitudinal changes in prostate specific antigen (PSA), a free testosterone index (FTI), and body mass index (BMI) before any clinical evidence of prostate cancer. The patterns of change in these three variables are allowed to vary depending on whether the subject develops prostate cancer or not and the severity of the prostate cancer at diagnosis. An application of Bayes' theorem provides posterior probabilities that we use to predict whether an individual will develop prostate cancer and, if so, whether it is a high-risk or a low-risk cancer. The classification rule is applied sequentially one multivariate observation at a time until the subject is classified as a cancer case or until the last observation has been used. We perform the analyses using each of the three variables individually, combined together in pairs, and all three variables together in one analysis. We compare the classification results among the various analyses and a simulation study demonstrates how the sensitivity of prediction changes with respect to the number and type of variables used in the prediction process.

1. Introduction

Prostate cancer annually accounts for one of the largest number of new non-skin cancer cases reported worldwide [31] and is one of the common causes of cancer deaths in men. In the United States, for example, prostate cancer is the most common clinically diagnosed non-skin cancer with about 1 in 10 American men eventually getting a positive diagnosis. With the present shift in the age distribution toward larger numbers of old men, it is expected that there will be an even larger increase in the number of men diagnosed with prostate cancer since the chance of a diagnosis of prostate cancer increases with age [3].

Prostate specific antigen (PSA) is a glycoprotein that is produced by prostatic epithelium and can be measured in serum samples by immunoassay. Since PSA correlates with the cancer volume of the prostate, it has been found to be useful in the management of men with prostate cancer. As PSA levels increase, the extent of cancer and its chance of detection increases [4]. While PSA has been found to be a useful tumor marker for the diagnosis of men with prostate cancer, in some individual cases changes in PSA may not be predictive of cancer prognosis [2]. Also, studies have found that approximately 1 in 4 of prostate cancer patients do not attain an elevated PSA level [5, 6]. Finally, a recent study of prostate-cancer mortality in the United States and the United Kingdom [8] concluded that speculation continues to exist in the role of PSA screening and prostate cancer mortality.

Studies have found other factors in addition to PSA to be associated with prostate cancer. For example, studies have shown that testosterone is linked to prostate cancer [29, 41], while others discuss the association between body mass index (BMI) and prostate cancer [16, 19]. Giovannucci et al. [16] point out that obesity is also related to testosterone levels. It is hoped that including these two additional variables into the modeling and prediction will yield better predictions of the development of prostate cancer over PSA alone since the multivariate model that accounts for all three variables is able to account for interrelationships among the variables.

Mixed-effects models have been applied to longitudinal PSA measurements (prior to diagnosis) to obtain posterior probabilities of prostate cancer [1]. These posterior probabilities are used to predict the future development of prostate cancer. The approach first models the longitudinal PSA data using a mixed-effects model taking into account group membership so that each of the diagnostic groups has its own mean trajectory. Then, sequentially adding one observation at a time, an individual's PSA data is examined. At each time, the marginal density of the individual's data is computed for each diagnostic group and Bayes' Rule is applied to obtain the posterior probability of group membership. These posterior probabilities are then used to classify a subject as going on to develop cancer or not. This method gives an efficiency or overall classification rate of 88% and a sensitivity of 62% and specificity of 91% for classifying prostate cancer cases.

In this study we extend the work of Brant et al. [1] to a multivariate setting. That is, using longitudinal data on multivariate observations of PSA, free testosterone index (FTI), and BMI before the clinical onset of prostate cancer, we fit multivariate mixed-effects models simultaneously to all combinations of these three longitudinal variables, and use these models to predict the future development of prostate cancer and examine how the different markers related to prostate cancer contribute to the prediction process. Thus, a clinician might compare the different classification rates corresponding to the three biological markers known to be associated with prostate cancer. Using the terminology from Cook [10], we use prognostic models to assess the future risk of each of a number of disease classes. We seek models and procedures that provide good discrimination among the various disease classes [9].

In addition to Brant et al. [1], a number of papers have dealt with modeling longitudinal biomarker data to predict the development of cancer. A parametric empirical Bayes method has been described that detects when the marker level deviates from normal [23], and Inoue et al. [18] developed a fully Bayesian approach to the problem. Joint longitudinal and event process models have been developed to describe PSA trajectories and prostate cancer using latent class models [21]. Also, change-point models have been applied by a number of authors to describe the change in biomarker trajectories from a non-cancerous to cancerous stage and to predict the onset of cancer [14, 25, 27, 28, 37–40, 43]. In particular, Fieuws et al. [14] combined linear and nonlinear mixed-effects models to obtain predictions for the development of prostate cancer. In further work, Fieuws et al. [15] used a multivariate model of three variables to predict a clinical outcome. Their model combined linear, nonlinear, and generalized mixed effects models and is fit using a pairwise approach developed by Fieuws and Verbeke [13].

This paper extends the classification method of the earlier linear mixed-effects model by Brant et al. [1] to a multivariate linear mixed-effects model that classifies individuals into control, low-risk prostate cancer, and high-risk prostate cancer groups using three different repeated biological variables related to prostate cancer diagnosis. The multivariate mixed-effects model is structured such as to connect the longitudinal multivariate observations through the random effects and the error covariance matrix. This additional flexibility of the model may provide a more appropriate estimated marginal distribution of the data. This in turn leads to improved predictions in terms of men being correctly predicted to develop prostate cancer and the sensitivity of the procedure increases as additional variables are included in the model. Using the prostate cancer data along with the results of a simulation study, we show how the classification results change (sensitivity and efficiency) as the different response variables known to relate to prostate disease change in the prediction procedure. Often medical practitioners may wonder whether PSA is a sufficient diagnostic tool or whether additional information about an individual might be used in the prediction of prostate cancer.

2. Data and methods

2.1 Data

The Baltimore Longitudinal Study of Aging (BLSA) is a longitudinal study of community-dwelling volunteers that began in 1958 who return to the study center approximately once every two years for two to three days of tests [36]. New volunteers are continuously recruited into the study and since the volunteers make scheduled visits to the BLSA that it is convenient for them, the resulting data is unbalanced with participants having different numbers of visits as well as varying times between visits. All participants in the BLSA are continually monitored to obtain information regarding their health status, especially information related to prostate disease and other disease events. This monitoring continues over time regardless of the collection of prostate-related measurements and other medical examination variables. In case of hospitalization or death, information is received from the individual's family, personal physician, hospital and medical records, and the National Death Index regarding the cause of death and autopsy information is obtained when available. During the course of the BLSA, over 1580 men have been enrolled in the study. Given the volunteer nature of the study that naturally leads to unbalanced visits, the only type of missing data that can occur in the BLSA are measurements on variables that are not measured at a particular study visit. For this study, we have complete data on all the variables of interest at all considered visits.

The data used for these analyses are from 163 male BLSA participants studied between 1961 and 1997 from the BLSA with at least two repeated measurements on the variables under study and who were cancer-free at their first examination. Seventy six of these men were later diagnosed with prostate cancer during the study period. Of these 76 men with prostate cancer, 61 were classified as low-risk cancers according to the Gleason score criteria [11] and the remaining 15 were classified as high-risk cancers. Only examinations prior to the clinical diagnosis of prostate cancer were used to fit the longitudinal models and to predict the preclinical development of prostate cancer. The smaller number of BLSA participants studied in this paper is due to a number of factors. Prostate specific antigen (PSA) measurements are not available on many men prior to the PSA era. Also, for the purposes of these analyses, the men must have at least two visits with PSA, body mass index (BMI), and an index of free testosterone (FTI) measurements.

Table 1 provides descriptive statistics of our sample and first examination statistics for PSA, FTI, and BMI used to predict prostate cancer. Note that the PSA data is expressed in its original units and is also transformed to log(PSA+1) (LPSA). This transformation has been extensively used to analyze PSA data as it helps to make the data more amenable to modeling with polynomials as well as reducing the heterogeneity in the data [1, 5, 30, 44, 45]. Table 1 shows that the three groups have similar numbers of visits and lengths of follow-up. The controls tend to be younger and have lower initial PSA, while the FTI and BMI means are similar at first visit.

Table 1.

Descriptive statistics, mean (minimum and maximum), describing the BLSA sample Descriptive statistics, mean (minimum and maximum), describing the BLSA sample

	Control	Low-Risk Cancer	High-Risk Cancer	ANOVA p-value
Number of Participants	87	61	15
Visits	4.3 (2, 8)	4.5 (2, 9)	4.3 (2, 7)	0.7218
Follow-Up Time (years)	12.0 (1.9, 29.9)	13.8 (1.0, 26.1)	13.3 (1.5, 25.1)	0.3999
Descriptive Statistics at the First Visit
Age (years)	52.7 (40.1, 69.7)	57.9 (40.1, 84.1)	61.0 (42.8, 81.8)	0.0015
PSA	0.72 (0.1, 3.9)	2.45 (0.2, 16.1)	3.07 (0.1, 11.6)	< .0001
LPSA	0.50 (0.10, 1.59)	1.00 (0.18, 2.84)	1.08 (0.10, 2.53)	< .0001
FTI	7.21 (2.57, 14.19)	6.72 (1.60, 14.34)	6.18 (2.93, 11.25)	0.2833
BMI	25.9 (19.9, 36.5)	25.1 (20.7, 36.6)	24.6 (21.3, 27.1)	0.1596

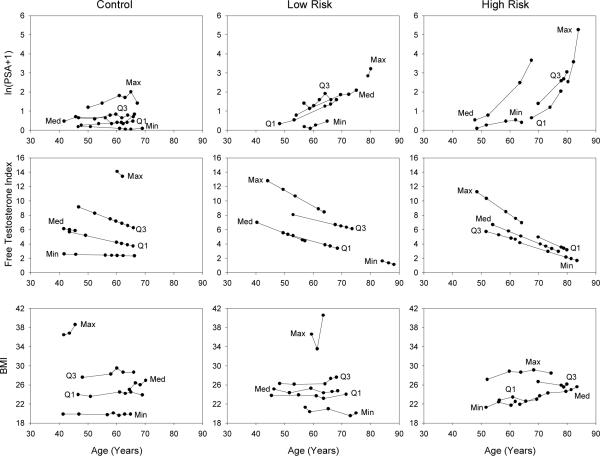
To examine longitudinal trends in the data, we compute the mean of the repeated values of each variable for each participant. For each variable and diagnostic group we select participants with the minimum, first quartile, median, third quartile, and maximum mean values. The data are presented in Figure 1. In the control group LPSA tends to start and remain low, for low-risk cancers an increasing trend is observed, and in high-risk cancers LPSA increases dramatically, especially as the data approaches the age of diagnosis. FTI exhibits linear declines with age in all diagnostic groups, while BMI appears to remain relatively constant with small linear increases with age (except possibly in some individuals with larger values) and there is a tendency for the cancer groups to have slightly lower BMI values.

Figure 1.

Longitudinal trends for participants with the minimum, first quartile, median, third quartile and maximum mean for each variable and diagnostic group

2.2 Multivariate mixed-effects model specification

The univariate linear mixed-effects model has been applied to a number of BLSA data sets [25, 26, 30]. In this paper, we apply the multivariate mixed-effects model presented by Shah, Laird, and Schoenfeld [35] to model our multivariate data consisting of LPSA, FTI, and BMI. For p response variables, let Y_i = [y_i1, y_i2, …, y_ip] be the response matrix for participant i, where y_ik is an n_i × 1 response vector for variable k, k = 1, …, p. Let y_i = Vec(Y_i), a stacked pn_i × 1 vector for all the response variables for subject i. Similarly, let E_i = [e_i1, e_i2, …, e_ip], where e_i = Vec(E_i) is the error matrix and stacked vector of error terms. Then, the multivariate mixed-effects model for participant i has the form

$${\mathit{y}}_i={\mathit{X}}_i^{\ast }\beta +{\mathit{Z}}_i^{\ast }{\mathit{b}}_i+{\mathit{e}}_i,i=1,\dots ,N$$

where ${\mathit{X}}_i^{\ast }$ and ${\mathit{Z}}_i^{\ast }$ are block diagonal matrices in which the p blocks contain the X_j and Z_j matrices of explanatory variables for each of the j = 1,…, p dependent variables. In the prostate cancer analysis that follows, the blocks of the X_j matrix contain columns corresponding to first age in the study, follow-up time, indicator variables for group membership as well as various polynomial terms and interactions among these terms. The blocks of the Z_j matrix contain columns representing the necessary random effects for intercept, follow-up time, and follow-up time². The parameter β is a q* × 1 vector of fixed-effects regression parameters and b_i is a r* × 1 vector of individual random-effects where q* is the total number of fixed effects in the model for all response variables and r* is the total number of random effects. Also, assume that b_i ~ N(0, D), where D is a r* × r* unstructured covariance matrix and e_i ~ N(0, R_i) with R_i a pn_i × pn_i covariance matrix of the error terms. The matrix D is the covariance matrix of the random effects and allows for covariance between the random effects within a given response variable as well as covariance among the random effects of different response variables. Consequently, one way in which the p different response variables are tied together is through the covariance between random effects from each response variable. The R_i covariance matrix has a specified structure to reflect the multivariate nature of the data. It is also assumed that, conditional on the random effects, the observations at the different time points are independent but that the multivariate responses at a particular time point are correlated with a p× p unstructured covariance matrix, Σ, which is the same for all time points. Consequently, Cov(e_i) = R_i = Σ ⊗ I_ni where ⊗ denotes the Kronecker product and I_ni is a n_i × n_i identity matrix.

The appropriateness of the normality assumption on the random effects can be addressed by extending the work of Verbeke and Lesafre [44]. They show that if the random effects come from a mixture of normal distributions then, as in the case of our data and from many observational longitudinal studies, if the between subject variability is large compared to the unexplained error variability, the distribution of the random effects' estimates will have the same mixture structure even when they are estimated using the usual empirical Bayes estimator of the b_i.

2.3. Model fitting and prediction

The multivariate mixed-effects model for the longitudinal data is employed to classify the participants by calculating posterior probabilities for each group (control, low-risk cancer, and high-risk cancer). Following a procedure similar to the univariate method described by Brant et al. [1] the steps are:

1. Fit the multivariate mixed-effects model to the data that include indicator variables of group membership (control, low-risk cancer, and high-risk cancer) as well as interactions of these indicator variables with other fixed-effects variables in the model.

2. The marginal distribution for diagnostic group, c, for participant i is then given by

   $${\mathit{y}}_{\mathit{ic}}~N({\mathit{X}}_{\mathit{ic}}\exists ,{\mathit{V}}_i),c=1,\dots ,g$$

   where g is the number of groups, the design matrix, X_ic, is a block diagonal matrix containing indicator variables for group c as well as age and time information for participant i, ∃ is replaced by the estimate of the fixed effects parameters, and ${\mathit{V}}_i={\mathit{Z}}_i^{\ast }\mathit{D}{{\mathit{Z}}_i^{\ast }}^T+\Sigma \otimes {\mathit{I}}_{n_i}$ is the marginal covariance matrix for participant i with model parameters replaced by their estimates. Then, given prior probabilities of the diagnostic groups, p_c, c = 1, …, g, and applying Bayes' theorem, the posterior probability that participant i with observed data, y_i, belongs to group c is given by

   $$p_{ic}=p_c{f}_{ic}({\mathit{y}}_i\mid \gamma )∕\sum _{\mathrm{j}=1}^{\mathrm{g}}{p}_j{f}_{ij}({\mathit{y}}_i\mid \gamma ),c=1,\dots ,g,$$

   where f_ij(y_i | γ) is the multivariate normal probability density function with mean X_ij∃ and covariance matrix V_i. The vector γ, contains estimates of the parameters, ∃, D, and Σ. The prior probabilities, p_j, are estimated using the observed proportions of men in each diagnostic group in the observed data. These posterior probabilities provide an absolute measure of risk for each subject at each visit.

The classification process proceeds for individual i by first calculating the posterior probabilities using the first multivariate measurement, and then sequentially repeating the process by adding one multivariate measurement at a time until the classification stopping rule is met or all the measurements have been used for individual i. The classification stopping rule is to assign individual i as developing prostate cancer if (posterior probability of low-risk + posterior probability of high-risk) ≥ 0.5 at a particular visit since the probability of having cancer exceed the probability of not having cancer (the choice of cutoff is evaluated in the application using a receiver operating characteristic (ROC) curve). If the participant is predicted to be a cancer, the larger posterior probability determines whether the participant is classified as low-risk or high-risk cancer. If the participant has not been classified as developing cancer by his final measurement, the individual is considered a control.

Though the BLSA strives to obtain clinical disease information on its participants at all times, it is, of course, possible that the participant could develop cancer after the period of observation. In this case, some participants who are currently controls (with no clinical diagnosis) and are classified as cancers by the classification process could have had correct predictions which would have made our prediction results better than are currently presented. Unfortunately, there is no way of obtaining this information beyond some date in the information collecting process. However, as mentioned above, inactive participants are monitored for disease events beyond their last visit in the longitudinal study. Among the 87 men classified as controls, 11 subsequently died of other causes. The remaining 76, are either active or have become inactive. There is an average of 5.8 years since the last examination visit where all these controls are known to be free of prostate-cancer. Consequently, in this paper we restrict our attention to cancers diagnosed during the follow-up period. We examine the sensitivity of this procedure to the cutoff value by varying the cutoff value using a ROC curve and judge the accuracy of the prediction models by computing the area under the curve (AUC) for each ROC curve.

In this study we use a cross-validation approach as applied in the earlier univariate prediction [1] in which the subject being classified is not included in the data that is used to estimate the model parameters. Note that there is the additional computational burden of repeatedly fitting multivariate mixed-effects models, especially when there are many random effects. The models are fit using SAS proc mixed (see Appendix A) which allows for missing responses at some visits even though in our study there is complete data on the multivariate responses.

2.4 Model diagnostics

Since the error variance is small compared to the between subject variance, we expect the empirical Bayes estimates to correctly reflect the true random effects distribution (see section 2,2). Consequently, to assess the model assumptions, bivariate plots are constructed of the random effects estimates. We evaluate the autocovariance in the residuals by computing the sample variogram [12]. For a stationary process, the variogram, V(k), is defined as V(k) = σ²(1 − ρ(k)), where σ² is the variance of the process and ρ(k) is the autocorrelation between variables k units apart. We estimate the variogram using the residuals from our model. If e(t) is the residual at time t, compute v_ij = ½(e(t_i) − e(t_j))² and k_ij = t_i − t_j for all distinct pairs of observations within each subject. These v_ij are plotted against the k_ij for all subjects. This plot is called the sample variogram. A plot that shows a random scatter with no trend indicates uncorrelated random deviations of the residuals. Thus, the sample variogram may be used to show that the residuals follow a white noise process.

In addition, the goodness of fit of the posterior probability of cancer to whether or not the participant had cancer is tested using the Hosmer-Lemeshow test [10]. This test compares the observed number of cancers in each of 10 deciles to the expected number computed from the posterior probabilities.

3. Results

3.1 Fitted Models

A univariate linear mixed-effects model is first fit to each of the three response variables, LPSA, FTI, and BMI. The full univariate models contain terms involving first age (FAge), longitudinal follow-up time (Time), whether or not the participant develops cancer (Cancer), a variable that indicates if the cancer is low- or high-risk (CancerType), as well as a number of polynomial and cross-product terms determined for each variable by examining the plots of the longitudinal data (Figure 1). For controls, Cancer = 0 and CancerType = 0, low-risk cancers have Cancer = 1 and CancerType = 0, and high-risk cancers have Cancer = 1 and CancerType = 1. For LPSA, FTI, and BMI, Figure 1 suggests that the trajectories of longitudinal trends appear to vary among participants. For LPSA the full model contains random effects for intercept, Time, and the square of Time (Time²). The models for FTI and BMI only contain intercept and Time random terms since these variables do not suggest any curvature in their trajectories. A backward elimination procedure is used to obtain final models in which all the highest order terms are statistically significant so that the final model is hierarchically well-formulated [26]. For FTI and BMI the CancerType variable is eliminated and so for these two variables the 15 men with high-risk cancer are included with the 61 low-risk cancer group to obtain the trajectories for the combined cancer group. However, the CancerType variable remains in the model for LPSA. Consequently, it is possible that the model for the high-risk cancers may be less precise than for the low-risk cancer group or the control group due to the smaller number of men with high-risk cancer.

Table 2 gives the estimates of the fixed effects for the univariate and multivariate models for all combinations of the three response variables. For example, from Table 2 the fitted univariate models for LPSA in the three diagnostic groups are

$$\text{Control}:\widehat{y}=2.1999-0.06296\times \text{Fage}+0.000569\times {\text{Fage}}^2-0.08336\times \text{Time}+0.000454\times {\text{Time}}^2+0.0011833\times \text{Fage}\times \text{Time},$$

$$\text{Low-Risk Cancer}:\widehat{y}=0.7876-0.03022\times \text{Fage}+0.000569\times {\text{Fage}}^2-0.08389\times \text{Time}-0.00265\times {\text{Time}}^2+0.0011833\times \text{Fage}\times \text{Time},$$

and

$$\text{High-Risk Cancer}:\widehat{y}=0.4121-0.025313\times \text{Fage}+0.000569\times {\text{Fage}}^2-0.3009\times \text{Time}-0.00265\times {\text{Time}}^2+0.006824\times \text{Fage}\times \text{Time}.$$

Table 2.

LME estimates (p-values^†) for univariate and multivariate models

Dependent Variable	Independent Variable	Univariate Models	Multivariate Models
			LPSA&FTI	LPSA&BMI	FTI&BMI	LPSA,FTI&BMI
LPSA	Intercept	2.1999 (0.0062)	2.2306 (0.0054)	2.2650 (0.0044)		2.2923 (0.0038)
	FAge	−0.06296 (0.0320)	−0.06392 (0.0285)	−0.06578 (0.0228)		−0.06663 (0.0206)
	FAge2	0.000569 (0.0344)	0.000575 (0.0313)	0.000597 (0.0239)		0.000604 (0.0220)
	Time	−0.08336 (0.0026)	−0.08259 (0.0026)	−0.08428 (0.0023)		−0.08393 (0.0022)
	Time2	0.000454 (0.4025)	0.000451 (0.4102)	0.000399 (0.4572)		0.000410 (0.4492)
	FAge × Time	0.001833 (0.0002)	0.001817 (0.0002)	0.001867 (0.0001)		0.001859 (0.0001)
	Cancer	−1.4123 (0.0004)	−1.4188 (0.0003)	−1.3841 (0.0004)		−1.3905 (0.0003)
	Cancer × FAge	0.03274 (<0.0001)	0.03285 (<0.0001)	0.03218 (<0.0001)		0.03229 (<0.0001)
	Cancer × Time	−0.00053 (0.9721)	−0.00013 (0.9931)	−0.00165 (0.9129)		−0.00116 (0.9388)
	Cancer × Time2	0.002196 (0.0046)	0.002155 (0.0057)	0.002274 (0.0029)		0.002218 (0.0040)
	CancerType	−0.3755 (0.5041)	−0.3783 (0.4999)	−0.3194 (0.5651)		−0.3211 (0.5622)
	CancerType × Fage	0.004907 (0.5924)	0.004949 (0.5883)	0.004129 (0.6486)		0.004151 (0.6461)
	CancerType × Time	−0.2162 (0.0019)	−0.2077 (0.0014)	−0.2174 (0.0017)		−0.2186 (0.0013)
	CancerType × Fage×Time	0.004991 (<0.0001)	0.005015 (<0.0001)	0.004995 (<0.0001)		0.005011 (<0.0001)
FTI	Intercept	−3.9419 (0.4993)	−3.9720 (0.4943)		−3.4059 (0.5589)	−3.0699 (0.5965)
	FAge	0.5823 (0.0091)	0.5835 (0.0086)		0.5621 (0.0116)	0.5495 (0.0131)
	FAge2	−0.00682 (0.0011)	−0.00683 (0.0010)		−0.00663 (0.0014)	−0.00652 (0.0016)
	Time	−0.1447 (<0.0001)	−0.1448 (<0.0001)		−0.1446 (<0.0001)	−0.1446 (<0.0001)
	Cancer	18.3079 (0.0072)	18.3670 (0.0067)		17.7328 (0.0090)	17.3669 (0.0101)
	Cancer × FAge	−0.7050 (0.0054)	−0.7069 (0.0050)		−0.6836 (0.0067)	−0.6698 (0.0076)
	Cancer × FAge2	0.006634 (0.0041)	0.006649 (0.0038)		0.006441 (0.0051)	0.006314 (0.0058)
BMI	Intercept	25.9245 (<0.0001)		25.9216 (<0.0001)	25.9222 (<0.0001)	25.9194 (<0.0001)
	Time	0.09069 (<0.0001)		0.09192 (<0.0001)	0.09008 (<0.0001)	0.09131 (<0.0001)
	Cancer	−0.8203 (0.0731)		−0.8226 (0.0718)	−0.8147 (0.0745)	−0.8169 (0.0734)
	Cancer × Time	−0.05288 (0.0156)		−0.05017 (0.0231)	−0.05192 (0.0171)	−0.04927 (0.0253)

^†Some non-significant fixed effects are retained in the model to ensure that the final models are hierarchically well-formulated (Morrell et al., 1997).

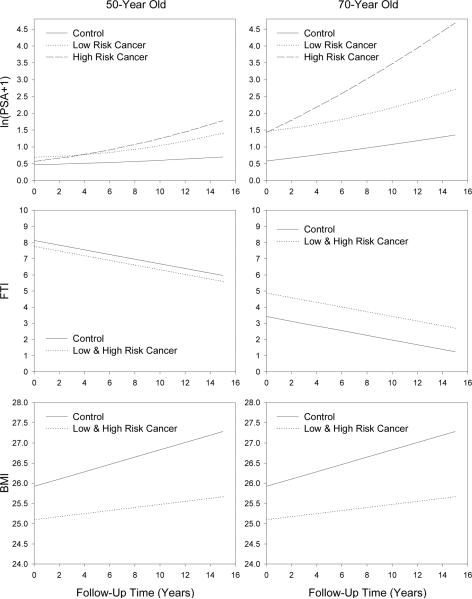
Note that Figure 2 illustrates the longitudinal fitted trends for 50 and 70-year olds for LPSA along with FTI and BMI for the three univariate models highlighting the differences in longitudinal changes between controls and those who developed low-risk or high-risk prostate cancer. The top panels indicate that high-risk cancers have a greater longitudinal change in LPSA and that the longitudinal change increases with age. In the middle panels, FTI is similar in 50-year old participants who developed cancer with those who did not develop cancer but is higher in older men who developed cancer. Finally, the lower panels illustrate that BMI is lower in participants who develop cancer and this difference appears to be constant with age. In addition, the longitudinal rate of change of BMI in men who developed cancer is less than the rate of change for those who did not develop cancer.

Figure 2.

Fitted univariate linear mixed-effects models for LPSA, FTI, and BMI for controls and those who develop low-risk or high-risk prostate cancer

Each component of the multivariate models contains the same explanatory variables as found in the corresponding final univariate models. In a similar way, the multivariate models contain the same random components as in the univariate models. In the trivariate model, this results in a 7 × 7 unstructured covariance matrix of the random effects. The covariance matrix of the random effects contains covariance terms between random effects from different variables allowing for the interrelationship among the random-effects for the trajectories among the variables.

When fitting the multivariate models we investigate whether the error covariance matrix, Σ, is unstructured or whether the errors are independent (that is Σ is a diagonal matrix). Using the AIC and BIC as a guide, we determine that it is not necessary to include correlated errors for this data set. This suggests that the relationships among the variables is accounted for by the marginal covariance matrix which contains terms that account for the random effects (including the terms that account for the relationships among random effects from different variables) and the diagonal error-covariance matrix.

Table 3 provides the estimates of the variance components from all the models. As with the fixed-effects, the estimates of these variance components do not differ substantially among the different models. Note that for each dependent variable the between-subject variability is larger than the error variability (${\widehat{\sigma }}_I^2>{\widehat{\sigma }}_{\epsilon }^2$). Consequently, the distribution of the estimated random effects is likely to closely approximate the true distribution of the random effects [44]. In addition, the multivariate models allow for correlation among random effects from different variables. Table 4 displays the estimated covariance matrices for the random-effects from the univariate and trivariate models. The blocks in the trivariate model corresponding to the individual variables are very similar to the corresponding blocks in the univariate models. Some random effects are moderately correlated between variables. For example, the correlation of the random effects for the LPSA Time² term and the BMI intercept term is −0.1815. This suggests that participants who are above average in their BMI level tend to have a lower than average quadratic term for LPSA. In addition three other LPSA and BMI random effects have similar associations: LPSA intercept, Time, and Time² with BMI Time.

Table 3.

Variances estimates among the random components

Dependent Variable	Independent Variable	Univariate Models	Multivariate Models
			LPSA&FTI	LPSA&BMI	BMI&FTI	LPSA,FTI&BMI
LPSA	Error	0.04145	0.04150	0.04145		0.04150
	Intercept	0.1006	0.1004	0.1001		0.09989
	Time	0.004929	0.005027	0.004872		0.004963
	Time2	0.000011	0.000012	0.000011		0.000011
FTI	Error	0.02560	0.02560		0.02557	0.02556
	Intercept	4.6119	4.6118		4.6177	4.6214
	Time	0.004523	0.004526		0.004538	0.004542
BMI	Error	0.5826		0.5799	0.5831	0.5805
	Intercept	8.0798		8.0693	8.0780	8.0689
	Time	0.01029		0.01072	0.01025	0.01068

Table 4.

Estimated random-effects^† covariance matrices for the univariate and trivariate mixed-effects models with correlations below the diagonals

Univariate
LPSA			FTI		BMI
PINT	PTIME	PTIME2	TINT	TTIME	BINT	BTIME
0.1006	0.009516	−0.00051	4.6119	−0.1287	8.0798	0.08509
0.4273	0.004929	−0.00021	−0.8911	0.004523	0.2951	0.01029
−0.4848	−0.9019	0.000011

Multivariate
LPSA			FTI		BMI
PINT	TIME	PTIME2	TINT	TTIME	BINT	BTIME
0.09989	0.009850	−0.00056	0.01946	−0.00057	0.1019	0.005592
0.4424	0.004963	−0.00022	−0.00312	0.000067	0.01811	0.001217
−0.5342	−0.9416	0.000011	0.000413	−6.66E–6	−0.00171	−0.00006
0.0286	−0.0206	0.0579	4.6214	−0.1292	−0.02052	−0.00870
−0.0268	0.0141	−0.0298	−0.8918	0.004542	0.007425	0.000274
0.1135	0.0905	−0.1815	−0.0034	0.0388	8.0689	0.08910
0.1712	0.1672	−0.1751	−0.0392	0.0393	0.3035	0.01068

^†PINT, PTIME, and PTIME2 are the random effects for intercept, Time and Time² for LPSA; TINT and TTIME are the random effects for intercept and Time for FTI; and BINT and BTIME are the random effects for intercept and Time for BMI.

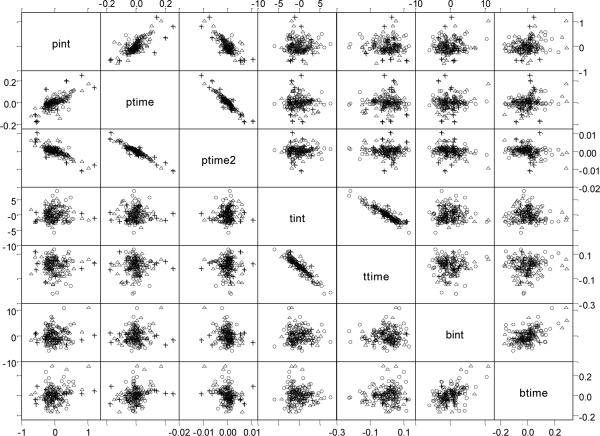
Figure 3 provides a matrix plot of the estimated random effects from the trivariate model. Most of the plots show elliptical patterns where the three diagnostic groups are interspersed among the points. However, for the LPSA random effects plots, the random effects for the high-risk group (+) appear on the outskirts of the plots. This may suggest that the dispersion for this group differs from that of the control and low-risk groups. However, with only 15 participants in the high-risk group it is probably not beneficial to fit a more general covariance structure. Thus, apart from this minor issue, it seems plausible that the pairs of random effects may come from bivariate normal distributions.

Figure 3.

Matrix plot of estimates for random effects for control (∘), low-risk cancer (△), and high-risk cancer (+) for LPSA (pint, ptime, ptime2), FTI (tint, ttime), and BMI (bint, btime)

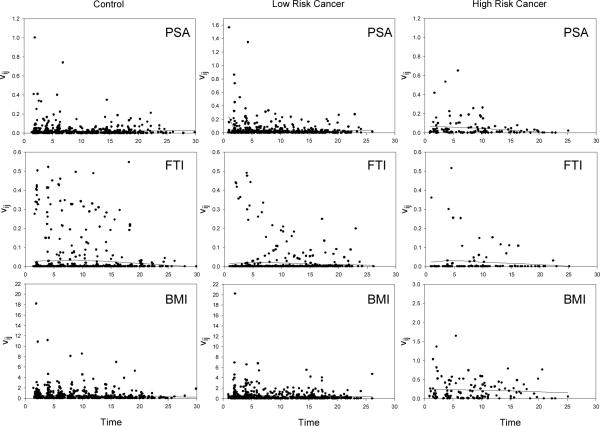
To further assess the adequacy of the model, we check for autocovariance in the residuals by computing the sample variogram. Figure 4 displays the sample variograms for each of the three variables for each diagnostic group based on residuals from the trivariate model. The sample variograms from each of the univariate models are almost identical (not shown). The loess smooth curve is overlaid on each plot. These smooth curves are either approximately flat or slightly declining over the time span indicating that the residuals are uncorrelated and hence no violation of the independence assumption is evident. We also computed residuals and plotted them against age. These residual plots (not shown) do not exhibit any systematic patterns that would give reason for concern over the model fits.

Figure 4.

Sample variograms from the trivariate mixed-effects model with the loess smoother overlaid on each plot

3.2 Predictions

A cross-validation approach is used in making predictions by omitting the individual's data being predicted and refitting the mixed-effects model. The parameters from this model are used to obtain the marginal distribution and posterior probabilities to make that individual's prediction. In this way, the subject's data does not affect his prediction.

Initially, we use the individual univariate mixed-effects models to predict the development of low-risk or high-risk prostate cancer in a similar fashion to Brant et al. [1]. Next, we use the multivariate models to predict an individual as being in the normal, low-risk, or high-risk cancer groups. First, all pairs of two dependent variables are used in the prediction process and then the model with all three dependent variables is finally used to make the predictions for each individual.

We illustrate the process using a low-risk cancer subject who had an initial visit at 51.9 years of age. Using the trivariate model, at the first visit the posterior probability the subject is a control (P(Control)) is 0.536 which provides an absolute measure of risk for the subject. Consequently the probability of being a cancer is less than 0.5 and the subject's second visit is examined. P(Control) for the second and third visits are 0.532 and 0.512. At the fourth visit, when the subject is 66.3 years of age, the P(Control) = 0.425. Consequently the probability of being a cancer is greater than 0.5 and the subject will be classified based on the probabilities of the two cancer groups. The probability of being a low-risk is 0.531 which is larger than the probability of being a high-risk cancer. Consequently the subject is correctly classified as a low-risk cancer at 66.3 years of age.

Using a cutoff of 0.5 for the posterior probabilities, Table 5 presents the sensitivity and specificity of the predictions as well as the efficiency (overall percent of correct predictions) for the various univariate and multivariate models. The bivariate model with LPSA and BMI has the highest sensitivity (89.5%), though the trivariate model that includes all three variables has a sensitivity that is only 4.0% lower. The univariate model with LPSA has the highest efficiency closely followed by the bivariate model with LPSA and FTI. Finally, the univariate model with only FTI has the highest specificity (85.1%). Using the posterior probability of cancer at the visit where the final decision is made, the Hosmer-Lemeshow goodness of fit test [10] is applied to compare the observed number of cancers in each of 10 deciles to the expected number. The p-values for all models indicate that the posterior probabilities fit the observed data well (all p-values > 0.15) with the fit generally becoming better as the number of variables in the models increase (except for the univariate BMI model which fits the data well).

Table 5.

Sensitivity and specificity for predicting prostate cancer (low-risk or high-risk) using a cutoff of 0.5

Dependent Variables	Sensitivity (%)	Specificity (%)	Efficiency (%)
Univariate Models
LPSA	86.8	75.9	81.0
FTI	51.3	85.1	69.3
BMI	64.5	49.4	56.4
Multivariate Models
LPSA&FTI	84.2	74.7	79.1
LPSA&BMI	89.5	60.9	74.2
FTI&BMI	72.4	54.0	62.6
LPSA,FTI&BMI	85.5	63.3	73.6

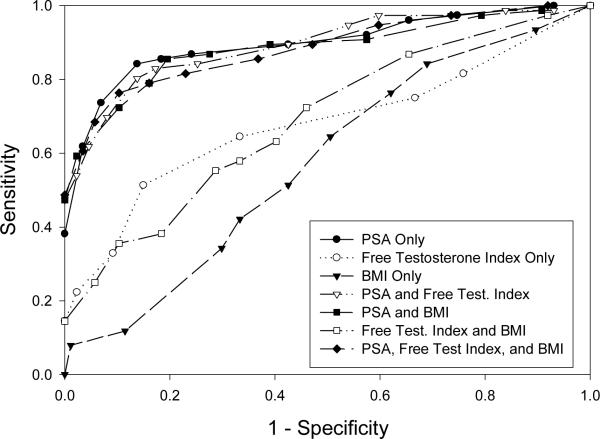
To examine the sensitivity of this procedure to the cutoff value, we vary the cutoff value and examine the resulting ROC curves [17]. We calculate the sensitivity and specificity for various cutoff values ranging from 0.1 to 0.9. Figure 5 presents the ROC curve for each of the models. The points nearest to the upper left hand corner give the best cutoff value in terms of balancing sensitivity and specificity (Table 6). When the best cutoff is chosen, the bivariate model with LPSA and BMI has the highest specificity (85.5%), the trivariate model with LPSA, FTI, and BMI has the highest sensitivity (89.7%), and the univariate model with LPSA has the highest efficiency (85.3%). In this case, there is variability in the optimal cutoff among the models but there is no systematic compelling evidence not to use a cutoff of 0.5. The ROC curves show that the four models that include LPSA have similar areas under the curve, while those that so not include LPSA have substantially lower areas under the curve and have little predictive capability. There appears to be little change in the ROC curve once PSA is included in the model. However, Cook [9, 10] points out that the ROC curve is insensitive to assessing the impact of adding new predictors.

Figure 5.

ROC curves for predicting the development of low-risk or high-risk cancer

Table 6.

Sensitivity and specificity for predicting prostate cancer with the cutoff chosen to achieve the point closest to the upper left hand corner of the ROC curve; Area under the ROC Curve; and p-value from the Hosmer-Lemeshow Test

Dependent Variables	Cutoff	Sensitivity (%)	Specificity (%)	Efficiency (%)	AUC	p-value
Univariate Models
LPSA	0.56	84.2	86.2	85.3	0.898	0.1992
FTI	0.48	64.5	66.7	65.6	0.672	0.1764
BMI	0.50	64.5	49.4	56.4	0.575	0.9237
Multivariate Models
LPSA&FTI	0.54	82.9	82.8	82.8	0.892	0.5362
LPSA&BMI	0.58	85.5	80.5	82.8	0.888	0.5257
FTI&BMI	0.55	55.3	71.3	63.8	0.694	0.6424
LPSA,FTI&BMI	0.64	76.3	89.7	83.4	0.885	0.6946

Among men correctly predicted to develop prostate cancer we compare the predictions by looking at the lead time (the time before the clinical diagnosis of cancer that the model predicted cancer). Since we have shown that LPSA is needed to obtain good predictions we compute the lead time for the univariate model with LPSA, the two bivariate models with LPSA and FTI and with LPSA and BMI, and the trivariate model with LPSA, FTI, and BMI. To achieve this, the lead times are compared for the 57 participants who were correctly predicted to develop cancer by all four models. For the univariate LPSA model the mean lead time is 10.1 years, for the bivariate LPSA and FTI model the mean lead time is 10.1 years, for the bivariate LPSA and BMI model the mean lead time is 11.7 years, and for the trivariate model the mean lead time is 12.1 years. The mean lead times differ significantly among these four variable combinations (p-value = 0.0186). Thus there are some gains in mean lead time as the number of variables used in the model increases. This would provide a greater window of opportunity to initiate preventative strategies and lifestyle modifications so as to avoid or delay the onset of prostate cancer.

4. Simulation study

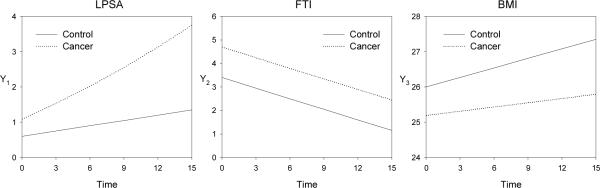
Since the data example used to illustrate the multivariate predictive method does not convincingly exhibit a clear improvement in the predictions of the multivariate procedure over the univariate procedures, a simulation study is conducted to further investigate the properties of the multivariate prediction procedure. The study mimics the prostate cancer data though we only include two groups, “controls” and “cancers” since our model did not distinguish between the two cancer groups using FTI and BMI. We select the parameters of the models in the simulation such that LPSA, FTI, and BMI trajectories are similar to the actual values for an elderly participant from the example (see Figure 2). The covariance matrices are similar to those in the prostate cancer example, but have been slightly modified to investigate a variety of options. In particular, we consider cases where the random effects are either independent across variables (so that the true random effects covariance matrix is block-diagonal) or where correlations exist among the random effects of different variables. The error covariance matrix is chosen so that the errors are either independent or have a correlation of 0.25 or 0.5 across the variables within each visit.

The data is generated with 165 subjects (90 controls and 75 cancers). Each subject has 6 repeated measurements at times 0, 3, 6, 9, 12, and 15 years. The random effects from a multivariate normal distribution for the seven random effects are generated with the specified covariance matrix. Next, the error vectors are generated from a multivariate normal distribution for the three errors with their specified covariance matrix. Finally, we compute the response variables from the chosen fixed effects, generated random effects, and errors.

The models used for each variable are:

$$\text{LPSA}:{\mathrm{y}}_{1\mathrm{i}}=(0.6+{\mathrm{b}}_{1\mathrm{i}})+(0.05+{\mathrm{b}}_{2\mathrm{i}})\times \text{time}+(0+{\mathrm{b}}_{3\mathrm{i}})\times {\text{time}}^2+0.5\times \text{cancer}+0.09\times \text{time}\times \text{cancer}+0.0025\times {\text{time}}^2\times \text{cancer}+{\mathrm{e}}_{1\mathrm{i}},$$

$$\text{FTI}:{\mathrm{y}}_{2\mathrm{i}}=(3.4+{\mathrm{b}}_{4\mathrm{i}})+({\mathrm{b}}_{5\mathrm{i}}-0.15)\times \text{time}+1.3\times \text{cancer}+{\mathrm{e}}_{2\mathrm{i}},$$

and

$$\text{BMI}:{\mathrm{y}}_{3\mathrm{i}}=(26+{\mathrm{b}}_{6\mathrm{i}})+(0.09+{\mathrm{b}}_{7\mathrm{i}})\times \text{time}-0.8\times \text{cancer}-0.05\times \text{time}\times \text{cancer}+{\mathrm{e}}_{3\mathrm{i}}.$$

Figure 6 illustrates the mean models for the 3 variables.

Figure 6.

The mean models for the three variables approximately corresponding to LPSA, FTI, and BMI in the simulation study

For each sample, seven models (three univariate models, three bivariate models, and the trivariate model) are fit and the predictions are determined using the cross-validation approach. In the simulation, the random effects are assumed to have an unstructured covariance matrix (even if the data is generated from independent random effects across variables). The within-visit covariance matrix is also assumed to have correlations among the errors (even if the data is generated with a zero correlation). The sensitivity, specificity, and efficiency are computed for each sample and model using 0.5 as the cutoff for the posterior probabilities as well as using the optimal cutoff. The AUC is also computed for each model. These values are used to compare the prediction approaches. The simulation results are compared using a randomized block design analysis with the block being the simulation replication and the variable the method of analysis (the combinations of variables in the model). Tukey's multiple comparison procedure is used to determine which of the seven methods differ significantly from each other. One hundred and fifty replications are run with the simulation programmed using SAS. Due to the computationally intensive nature of the cross-validation approach, the six simulations took an average of 96.5 hours CPU time each on a 2.80 GHz Pentium 4 with 3.71 GB RAM. Tables 7a and 7b provide the means of the sensitivity, specificity, and efficiency for each of the approaches using a cutoff of 0.5 and the optimal cutoff while Tables 8a and 8b displays the results of the comparisons among the estimation methods.

Table 7a.

Classification results from the simulation study for the different combinations of variables used in the predictions where the random effects are either independent or correlated across variables and the random errors are either independent or have a correlation of 0.25 or 0.5 within visit. The cutoff used is 0.5.

Structure of D	Error Correlation	Variables in Model†	Sensitivity*	Specificity*	Efficiency*
Independent	0	L	0.903	0.657	0.769
		F	0.773	0.543	0.648
		B	0.560	0.578	0.570
		LF	0.922	0.679	0.789
		LB	0.905	0.656	0.769
		FB	0.794	0.540	0.655
		LFB	0.924	0.682	0.792
Independent	0.25	L	0.903	0.657	0.769
		F	0.773	0.541	0.647
		B	0.562	0.580	0.572
		LF	0.922	0.675	0.788
		LB	0.905	0.658	0.770
		FB	0.794	0.544	0.658
		LFB	0.925	0.683	0.793
Independent	0.5	L	0.903	0.657	0.769
		F	0.774	0.542	0.647
		B	0.564	0.581	0.573
		LF	0.922	0.674	0.787
		LB	0.905	0.663	0.773
		FB	0.794	0.546	0.659
		LFB	0.926	0.685	0.795
Not Independent	0	L	0.903	0.657	0.769
		F	0.772	0.543	0.647
		B	0.561	0.581	0.572
		LF	0.918	0.675	0.786
		LB	0.910	0.663	0.775
		FB	0.796	0.542	0.658
		LFB	0.927	0.685	0.795
Not Independent	0.25	L	0.903	0.657	0.769
		F	0.774	0.543	0.648
		B	0.562	0.581	0.572
		LF	0.919	0.674	0.785
		LB	0.910	0.667	0.778
		FB	0.796	0.545	0.659
		LFB	0.928	0.686	0.796
Not Independent	0.5	L	0.903	0.657	0.769
		F	0.774	0.542	0.647
		B	0.565	0.579	0.572
		LF	0.919	0.673	0.785
		LB	0.909	0.672	0.779
		FB	0.797	0.547	0.661
		LFB	0.928	0.692	0.799

^†L, F, and B represent LPSA, FTI, and BMI respectively

^*The sensitivities, specificities, and efficiencies for each of the seven models fit are mean values based on 150 replications.

Table 7b.

Classification results from the simulation study for the different combinations of variables used in the predictions where the random effects are either independent or correlated across variables and the random errors are either independent or have a correlation of 0.25 or 0.5 within visit. The optimal cutoff is used.

Structure of D	Error Correlation	Variables in Model†	Sensitivity*	Specificity*	Efficiency*	AUC*
Independent	0	L	0.813	0.827	0.820	0.889
		F	0.666	0.688	0.678	0.727
		B	0.560	0.597	0.580	0.595
		LF	0.837	0.851	0.844	0.911
		LB	0.817	0.834	0.826	0.892
		FB	0.687	0.692	0.690	0.743
		LFB	0.846	0.851	0.848	0.915
Independent	0.25	L	0.813	0.827	0.820	0.889
		F	0.678	0.679	0.678	0.726
		B	0.572	0.588	0.580	0.594
		LF	0.839	0.848	0.844	0.911
		LB	0.818	0.831	0.825	0.893
		FB	0.686	0.695	0.691	0.744
		LFB	0.846	0.853	0.850	0.915
Independent	0.5	L	0.813	0.827	0.820	0.889
		F	0.675	0.679	0.677	0.727
		B	0.581	0.581	0.581	0.595
		LF	0.839	0.847	0.844	0.911
		LB	0.815	0.835	0.826	0.893
		FB	0.686	0.701	0.694	0.747
		LFB	0.845	0.856	0.851	0.915
Not Independent	0	L	0.813	0.827	0.820	0.889
		F	0.676	0.680	0.678	0.726
		B	0.574	0.584	0.580	0.593
		LF	0.830	0.852	0.842	0.909
		LB	0.823	0.839	0.832	0.898
		FB	0.697	0.687	0.692	0.744
		LFB	0.849	0.856	0.853	0.918
Not Independent	0.25	L	0.813	0.827	0.820	0.889
		F	0.674	0.681	0.678	0.726
		B	0.567	0.595	0.582	0.593
		LF	0.834	0.846	0.841	0.908
		LB	0.825	0.837	0.832	0.899
		FB	0.689	0.698	0.694	0.746
		LFB	0.847	0.858	0.853	0.917
Not Independent	0.5	L	0.813	0.827	0.820	0.889
		F	0.680	0.676	0.678	0.727
		B	0.570	0.589	0.580	0.594
		LF	0.836	0.846	0.842	0.908
		LB	0.822	0.840	0.832	0.899
		FB	0.691	0.696	0.694	0.749
		LFB	0.848	0.860	0.855	0.919

^†L, F, and B represent LPSA, FTI, and BMI respectively

^*The sensitivities, specificities, efficiencies, and AUC for each of the seven models fit are mean values based on 150 replications.

Table 8a.

Comparison of the sensitivity, specificity, and efficiency among the different variable combinations^† for the different random model structures used in the classification (means covered by the same solid line are not significantly different using the Tukey multiple comparison procedure). The cutoff used is 0.5.

^†L, F, and B represent LPSA, FTI, and BMI respectively

Table 8b.

Comparison of the sensitivity, specificity, efficiency, and AUC among the different variable combinations^† for the different random model structures used in the classification (means covered by the same solid line are not significantly different using the Tukey multiple comparison procedure). The optimal cutoff is used.

^†L, F, and B represent LPSA, FTI, and BMI respectively

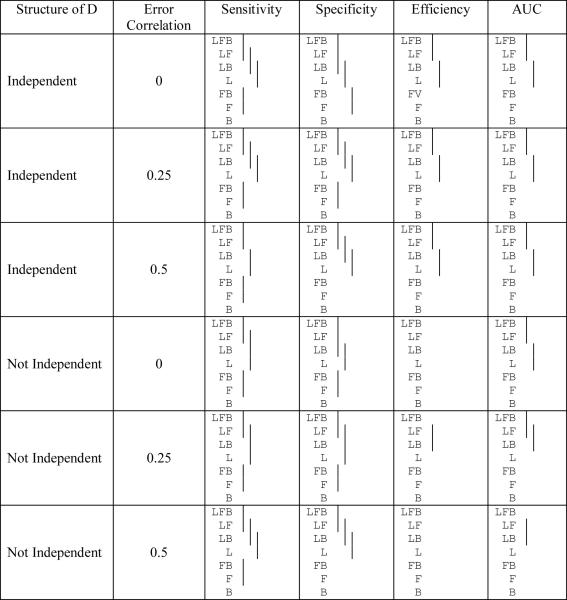
In describing the simulation results, we first address whether adding variables to the model results in improvements in sensitivity, specificity, and efficiency of the predictions (Tables 8a and 8b). The results show that the sensitivity is always ordered correctly and adding a variable almost always significantly improves sensitivity (though adding variables to the already high sensitivity of LPSA (>0.9 when the cutoff = 0.5) often does not always lead to a significant improvement). The optimal cutoff usually leads to lower specificity than the cutoff of 0.5 (average reduction of 7.7%). Even though the sensitivity improves, the specificity can change in unpredictable ways, since adding variables does not necessarily improve specificity. The specificities range from 0.54 to 0.69 using a cutoff of 0.5 and from 0.58 to 0.85 using the optimal cutoff. The optimal cutoff never provides a worse specificity than when using a cutoff of 0.5. The efficiencies always follow the correct ordering. When an additional variable is added the mean efficiency is higher, though not always significantly better. The optimal cutoff always provides a better efficiency. Finally, the results for the AUC are very similar to those for the efficiency though the AUC has more significant differences for a cutoff of 0.5 and fewer significant differences when the optimal cutoff is used. In summary, more variables generally lead to significantly improved sensitivity, efficiency, and AUC.

Next we compare the results for a constant number of variables in the model depending on the random effects and error structure of the model (Tables 9a and 9b). When there is a single variable in the model, neither the sensitivity, specificity, efficiency, nor AUC of the predictions is significantly different among the six random model structures. This is not surprising since the differences in the random structures affect the relationships among the different dependent variables. For the sensitivity, correlated random effects result in a higher sensitivity for each set of variables in the model (except for LPSA & FTI where the independent random effects have higher sensitivity) though the within-visit error correlations do not exhibit any consistent pattern. Consequently, the inter-relationships among the variables in the random effects usually leads to higher sensitivity. In contrast, the specificity is usually the highest when the within-visit errors are more highly correlated (except, again, for LPSA & FTI, and when the optimal cutoff is used there are few differences in specificity). Finally, for the efficiency, within each of the random effects structures (Correlated or Independent) the higher the correlation among the within-visit error terms, the higher the efficiency (though not all are statistically significantly different and again the efficiency for LPSA & FTI are reversed compared to the other variable combinations). The AUC again provide results that are similar to the efficiency.

Table 9a.

Comparison of the sensitivity, specificity, and efficiency among the different random model structures for the different variable combinations used in the classification (means covered by the same solid line are not significantly different using the Tukey multiple comparisons procedure). The cutoff used is 0.5.

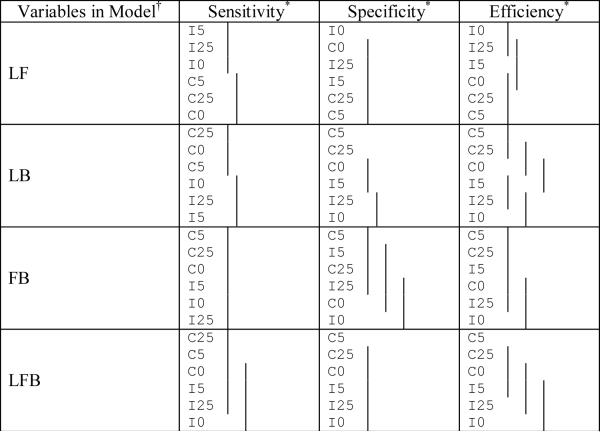^†L, F, and B represent LPSA, FTI, and BMI respectively (no significant differences exist for individual variables).

^*Notation used is I = independent random effects across variables, C = correlated random effects across variables; 0 represents the error correlation of 0, 25 represents the error correlation of 0.25, and 5 represents the error correlation of 0.5.

Table 9b.

Comparison of the sensitivity, specificity, and efficiency among the different random model structures for the different variable combinations used in the classification (means covered by the same solid line are not significantly different using the Tukey multiple comparisons procedure). The optimal cutoff is used.

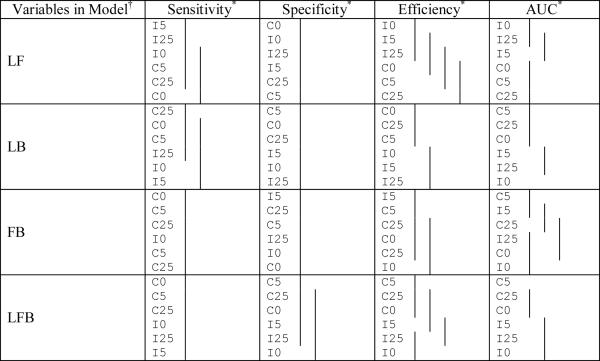^†L, F, and B represent LPSA, FTI, and BMI respectively (no significant differences exist for individual variables).

^*Notation used is I = independent random effects across variables, C = correlated random effects across variables; 0 represents the error correlation of 0, 25 represents the error correlation of 0.25, and 5 represents the error correlation of 0.5.

In summary, for the results of the simulation study the sensitivity usually increases with the number of variables in the model and is generally higher among models with correlated random effects. The specificity has no clear relationship with the number of variables but is higher when the error terms were more highly correlated. The efficiency and AUC generally increase with the number of variables and within each of the random effects structures the efficiency and AUC increase with the within-visit correlation.

5. Discussion

In this paper we present a methodology to longitudinally predict whether a subject who is prostate cancer-free at baseline will go on to develop low-risk or high-risk prostate cancer using multivariate data involving several variables known to be related to prostate cancer prior to the development of clinically diagnosed prostate cancer. We have applied a multivariate mixed-effects model to fit longitudinal profiles of LPSA, FTI, and BMI for participants who subsequently develop prostate cancer as well as for those who did not develop prostate cancer during the follow-up period. A comparison of the prediction results are made for the different univariate prediction models and the various combinations of the three variables in a multivariate model. Using Bayes' theorem to compute posterior probabilities, each of the models is used to predict whether participants will develop prostate cancer. The multivariate modeling approach which takes into account correlations among the variables at each visit, in general performs better than the univariate models according to lead time of predicting cancer before the clinical diagnosis while the sensitivity, specificity, efficiency, and AUC are similar for the different approaches. This last finding agrees with previous work of with Cook [9] who shows that once the most important variable is included, adding additional significant variables may not have a large influence on the sensitivity and specificity. However, a simulation study shows that adding variables significantly improves the sensitivity and that the overall efficiency and AUC improves as well (though not always significantly). Cook [9, 10] suggests examining at how the classifications change as variables are added to the model. For the classification to change in our approach, the posterior probabilities for the various groups must change. Comparing the posterior probability at the classification visit among the various models there is no significant change in the posterior probabilities of the control participants, while adding additional variables leads to significantly higher posterior probabilities for cancers: (i) when PSA is added to a model and (ii) for the bivariate BMI and FTI model compared to the corresponding univariate models.

The simulation study only considers subjects with equal numbers of observations. Subjects with larger numbers of repeated observations, n_i, would be expected to have a higher chance of being classified into the cancer group. This issue is not addressed in this paper but it may be an area of further research. In addition, the simulation study uses a fixed number of participants over all combinations of parameters. Investigating the effect of number of participants (and proportion of control and cancers) on the results is also worth investigating in a future study though the computational burden would be significant.

In addition to sensitivity, the lead time before diagnosis should also be considered when deciding on the number of variables to use in the prediction process. For the univariate LPSA model the mean lead time is 10.1 years, for the bivariate LPSA and FTI model the mean lead time is 10.1 years, for the bivariate LPSA and BMI model the mean lead time is 11.7 years, and for the trivariate model the mean lead time is 12.1 years. Thus, there are some gains in mean lead time as the number of variables used in the model increases. This would provide a greater window of opportunity to initiate preventative strategies and lifestyle modifications so as to avoid or delay the onset of this condition.

In addition, while missing data is not believed to be a problem for the people studied in this paper, other studies with missing data could use a multiple imputation approach using the R function, pan developed by Schafer and Yucel [34]. Maximum likelihood and Bayesian approaches to estimating the parameters of a hierarchical linear model have been described for multivariate continuous outcomes where the multivariate responses are not required to be complete [42]. An analogous approach to that described by Schafer and Yucel [34] is presented by Liu, Taylor, and Belin [22]. The model in Liu's paper appears to require that the errors are uncorrelated between the response variables whereas the models in the papers by Shah et al. [35] and Schafer and Yucel [34] allow for covariances among the errors of the different responses. A latent variable model for longitudinal multivariate data with missing covariate information was developed as well as allowing for modeling the nonignorable dropout mechanism [32, 33]. A quasi-least squares approach was applied to estimate parameters in a model for multivariate longitudinal data [7].

In conclusion, as in the case of PSA, a single variable known to be related to the development of prostate cancer, shows no effect in one quarter of all men tested. We have found that by adding additional variables to the prediction process using a multivariate procedure can increase the mean lead time before an actual clinical diagnosis with also the possibility of an increased sensitivity leading to a possible reduction in treatment for severe cases and the potential benefit of an individual's improvement in health.

Appendix A

The SAS procedure Proc Mixed is used to fit the multivariate mixed-effects models. To achieve this, the response variables are stacked, and a variable (var) is defined that identifies the response variables. The data set contains a variable, visit, that identifies the visit, and another variable id for each subject. The following repeated statement allows one to fit the desired error structure:

$$\text{repeated}\text{var}∕\text{subject}=\text{id}\ast \text{visit}\text{type}=\text{un};$$

To fit the multivariate model with independent errors (that is Σ is a diagonal matrix), the option type = un(1) is used in the repeated statement, above.