Modelling seasonal variations in the age and incidence of Kawasaki disease to explore possible infectious aetiologies

Abstract

The average age of infection is expected to vary during seasonal epidemics in a way that is predictable from the epidemiological features, such as the duration of infectiousness and the nature of population mixing. However, it is not known whether such changes can be detected and verified using routinely collected data. We examined the correlation between the weekly number and average age of cases using data on pre-vaccination measles and rotavirus. We show that age–incidence patterns can be observed and predicted for these childhood infections. Incorporating additional information about important features of the transmission dynamics improves the correspondence between model predictions and empirical data. We then explored whether knowledge of the age–incidence pattern can shed light on the epidemiological features of diseases of unknown aetiology, such as Kawasaki disease (KD). Our results indicate KD is unlikely to be triggered by a single acute immunizing infection, but is consistent with an infection of longer duration, a non-immunizing infection or co-infection with an acute agent and one with longer duration. Age–incidence patterns can lend insight into important epidemiological features of infections, providing information on transmission-relevant population mixing for known infections and clues about the aetiology of complex paediatric diseases.

1. Introduction

Interest has grown recently in the role of infectious causes for diseases of complex or unknown aetiology [1]. However, identifying and confirming the etiological agent are often difficult for diseases with multiple necessary or strongly predisposing causes, such as infection by one or more pathogens in a host with a genetic predisposition to disease [1]. Identifying a definitive link between an infectious agent and a disease of unknown aetiology can lead to improved diagnostics and treatment, including the development of vaccines or antimicrobials, rather than relying on non-specific treatments aimed at mitigating disease pathogenesis.

Epidemiological evidence that supports an infectious aetiology includes seasonality in incidence and a young age distribution indicative of the acquisition of immunity (or resistance to symptomatic disease) following infection [2,3]. The incidence and age distribution of cases may vary seasonally in a manner dependent on important epidemiological features of the infection, including the duration of infectiousness and the nature of transmission-relevant population mixing [4]. These ‘age–incidence patterns’ can be understood in terms of age-related fluctuations in the susceptible population resulting from the epidemic dynamics [4]. However, it has yet to be demonstrated whether seasonal changes in the average age of cases can be detected using routinely collected data, or that the correlation patterns between the incidence and average age of cases can predicted from models for the transmission dynamics of infection. If this approach can be validated using diseases with a well-understood infectious aetiology, then examining the age–incidence pattern for diseases with a suspected infectious aetiology may help in narrowing the search for the agent(s) involved.

Kawasaki disease (KD) is a paediatric inflammatory syndrome for which an infectious trigger is strongly suspected, but for which no causative organism(s) have been reliably identified [2,5,6]. KD is an acute systemic vasculitis of young children that is diagnosed by the presence of prolonged fever together with a constellation of clinical signs, including rash, changes to the mucous membranes and peripheries, lymphadenopathy and non-purulent conjunctival injection [7]. KD specifically and uniquely damages the coronary arteries in a minority of cases. It is the leading cause of acquired heart disease in children in asset-rich countries and may be pro-atherosclerotic [2]. Epidemiological and microbiological studies have attempted to link KD to a variety of infectious and environmental exposures, but no reliable association has been found [5,6].

The consensus is that KD is caused by a widely distributed infectious agent (or multiple agents) that evokes an abnormal immune response in genetically predisposed individuals [5,6]. There is considerable evidence to suggest a genetic component of risk. Annual incidence rates among children less than 5 years of age vary from 4 to 20 per 100 000 in the United States [8,9] to 218 per 100 000 in Japan [10] and the incidence remains as high among children of Japanese descent living in other countries [11]. Siblings of KD patients have a 6–10-fold greater incidence than the general population [12], and KD-affected children are more likely to have parents who had the condition [13]. Other aspects of the epidemiological evidence, including seasonality and spatiotemporal clustering of cases, together with the clinical features, suggest an infectious aetiology [2,5,6,14,15]. The age distribution of KD cases is similar to that of many childhood infections [2]. Most cases occur in children less than 5 years of age, but the incidence rate is relatively low in children less than six months of age, suggesting there may be protection by maternal antibodies [2,5,6]. The dramatic decline in incidence in older children implies the putative infection is widely distributed.

To determine whether examining the relationship between seasonal variation in the number and average age of cases can lend insight into the nature of the infectious trigger(s), we sought to extend and validate previous work on age–incidence patterns [4], then apply this theory to KD. We first examined observed age–incidence patterns for two acute childhood infections, measles and rotavirus, for which the aetiology is known and the transmission dynamics have been well-characterized [16–18]. We determined the extent to which the observed patterns could be predicted by mathematical models, exploring a hierarchy of models ranging from simple to more epidemiologically realistic representations of the transmission dynamics. We then examined the age–incidence pattern of KD hospitalizations in the United States and compared the observed pattern to those predicted by models consistent with hypotheses about the aetiology of this complex disease.

2. Methods

(a). Data

We examined data on measles notifications from Copenhagen, Denmark from 1905 to 1918, rotavirus hospitalizations in the United States from 1997 to 2005, and KD hospitalizations in the United States from 1989 to 2003. Measles data were obtained from weekly case reports by primary care physicians [19]. For rotavirus and KD, we analysed data from the state inpatient databases (SID) of the Healthcare Cost and Utilization Project (HCUP) (http://www.hcup-us.ahrq.gov/databases.jsp) maintained by the Agency for Healthcare Research and Quality (AHRQ), which include all hospital discharge records from community hospitals in participating states. HCUP databases bring together the data collection efforts of state data organizations, hospital associations, private data organizations and the Federal government to create a national information resource of patient-level health-care data [20].

The data had differing degrees of age resolution; see electronic supplementary material for details. To limit the influence of atypical cases in older individuals during periods of low incidence, we restricted our analysis to an age range in which greater than 90 per cent of cases occurred.

(b). Statistical analysis

Age–incidence patterns were detected by calculating the Pearson correlation coefficients between the number of cases in a given week (t) and the mean age of such cases at a lag of −26 to 26 weeks (t + l). The primary outcome variable was the lag time associated with the maximum correlation (l_max). To determine the significance of these patterns, we calculated 95% bootstrap confidence intervals by randomly permuting the average age time series 10 000 times and estimating the maximum and minimum correlation coefficients between the original case data and the permuted average age time series. We analysed the relationship looking (i) longitudinally across all years of available data, and (ii) at the cumulative data aggregated by week of the year.

(c). Model-predicted patterns

We determined the extent to which the empirical age–incidence patterns corresponded to model predictions, first using simple models to represent the transmission dynamics, then adding more complexity consistent with previously developed models (see electronic supplementary material for details). We did not explicitly fit the models to the data because of the difficulty in doing so for KD (see electronic supplementary material), but rather used the best-fit parameters for similar measles and rotavirus datasets [16,17,19]. We assumed reported cases were directly proportional to the underlying incidence (i.e. did not vary by age), and adjusted the baseline transmission rate to correspond to the average age of cases in our datasets. The simple models were intended to give a range for the expected lag times when we know only the most basic characteristics of the infection (or presumed infection, in the case of KD), while the more complex models were meant to demonstrate how well we can reproduce the observed age–incidence patterns given full knowledge of important aspects of the transmission dynamics (which is not possible at this time for KD).

3. Results

(a). Detection and validation of age–incidence patterns for measles and rotavirus

Measles epidemics occurred approximately annually from 1905 to 1918 in Copenhagen, Denmark (figure 1a) [19]. The mean number of reported measles cases (averaged by week of the year) varied between 16.9 and 139.1 cases per week, while the weekly average age of cases varied between 4.6 and 6.9 years old (figure 1b). The average age peaked just prior to the number of cases, such that a maximum correlation of 0.47 for the longitudinal analysis and 0.73 for the aggregate analysis were associated lag times of l_max = −4 weeks and −3 weeks, respectively; these correlations were highly significant (p < 0.001; figure 1c).

Figure 1.

Relationship between the average age and incidence of measles notifications in Copenhagen, Denmark. (a) The number of weekly measles notifications (blue) among children less than 15 years of age in Copenhagen from 1905 to 1918, and the average age of measles cases (red). We smoothed the data using a five week moving average. (b) Mean number and average age of measles notifications by week of the year. (c) Correlation coefficients between the number of notifications at time t and the average age of cases at time t + l for the longitudinal analysis and aggregate analysis. The dotted lines represent the range within which 95% of the maximum and minimum correlations fell when we randomly permuted the average age time series. (d) Model-predicted relationship between the number and average age of cases assuming an SEIR structure and RAS-like mixing with school-term forcing.

To model the predicted dynamics of measles, we used seasonally forced age-structured differential equation models (see electronic supplementary material; [4]). We initially explored an susceptible-exposed-infectious-recovered (SEIR) model with simple sinusoidal forcing. We used a seasonal amplitude of b = 0.15, and adjusted the baseline transmission rate such that the model predicted annual epidemics with an average age of infection between 4 and 6 years old. We explored four mixing assumptions: (i) homogeneous mixing, (ii) assortative mixing, (iii) mixing based on self-reported contact patterns [21,22], and (iv) classical ‘realistic age-structured’ (RAS) model mixing [16]. We found RAS mixing offered the closest correspondence with the observed age–incidence pattern with a predicted lag time of −11 weeks, reflecting the importance of increased rates of transmission among school-aged children in the epidemiology of measles. Other types of mixing produced lag times varying from three weeks (homogeneous mixing) to 13 weeks (self-reported mixing).

Given the importance of transmission among school-aged children in measles epidemiology, it may be more accurate to model seasonality in the transmission rate using a step function reflecting the school holiday schedule rather than a sinusoidal function. We examined the model-predicted age–incidence pattern using ‘school-term forcing’ reflecting the known holiday schedule in Copenhagen [19] and assuming that the transmission rate among school-aged children (7–14 years old) was equal to that among preschool-aged children during holiday periods and approximately nine times higher during school periods, according to the best-fit seasonal forcing parameter for England and Wales [16]. We found the lag time corresponding to the maximum correlation was now predicted to be −3 weeks, which is very close to the observed l_max of −3 to −4 weeks, although the large decrease in the average age of cases during the non-summer holidays predicted by the model was not as evident in the data (figure 1d).

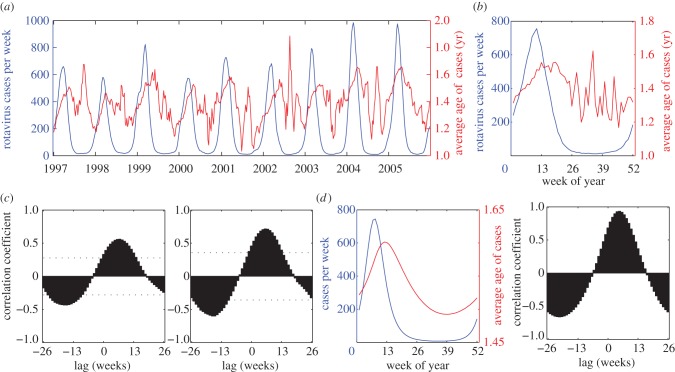
Rotavirus exhibited a different pattern from measles, with strong seasonal variation in the number of cases, ranging from a week-of-the-year average of 106–6800 cases per week, and a younger average age (1.2–1.6 years old; figure 2a,b). The mean number of rotavirus hospitalizations peaked in mid-March, while the average age of patients tended to be greatest slightly after the peak of the epidemic, such that the maximum correlation of 0.59 for the longitudinal analysis and 0.72 for the aggregate analysis both occurred at a lag of six weeks; again, these correlations were highly significant (p < 0.001; figure 2c).

Figure 2.

Relationship between the average age and incidence of rotavirus hospitalizations in the United States. (a) The number of weekly rotavirus hospitalizations (blue) among children less than 5 years of age in 16 US states from 1997 to 2005, and the average age of rotavirus patients (red). We smoothed the data using a five week moving average. (b) Mean number and average age of rotavirus cases by week of the year. (c) Correlation coefficients between the number of hospitalizations at time t and the average age of patients at time t + l for the longitudinal analysis and aggregate analysis. The dotted lines represent the range within which 95% of the maximum and minimum correlations fell when we randomly permuted the average age time series. (d) Model-predicted relationship between the number and average age of rotavirus cases assuming an SIRS-like structure for a best-fit model [17].

If we modelled the dynamics of rotavirus using a simple susceptible-infectious-recovered-susceptible (SIRS) model assuming cases represent first infection (see electronic supplementary material) and adjusted the baseline transmission rate such that the mean age of cases was approximately 1.5 years old, we found that the lag times associated with the maximum correlation varied from −8 to −5 weeks depending on the mixing assumption. However, such a model could not capture the strong seasonality in rotavirus incidence.

Epidemiological studies suggest the dynamics of rotavirus are more complex [17,23]. When we examined the age–incidence pattern predicted by a best-fitting model for rotavirus dynamics in the USA, which assumes an SIRS-like structure with reduced susceptibility to infection and disease following one to two infections and homogeneous mixing with higher rates of acquisition among infants [17], we found the lag time corresponding to the maximum correlation was predicted to be five weeks (figure 2d), which is very close to the observed l_max = 6 weeks.

In summary, it was possible to approximate the correlation pattern between seasonal variation in the incidence and mean age of infection within ±12 weeks using simple models for two diseases with different transmission dynamics and empirical age–incidence patterns. Adding detail to such models to improve their biological realism increased the accuracy of the predicted age–incidence patterns. These findings encouraged us to use simple models to assess which sorts of infections would produce the age–incidence pattern observed for KD in order to place restrictions on possible infectious aetiologies/triggers.

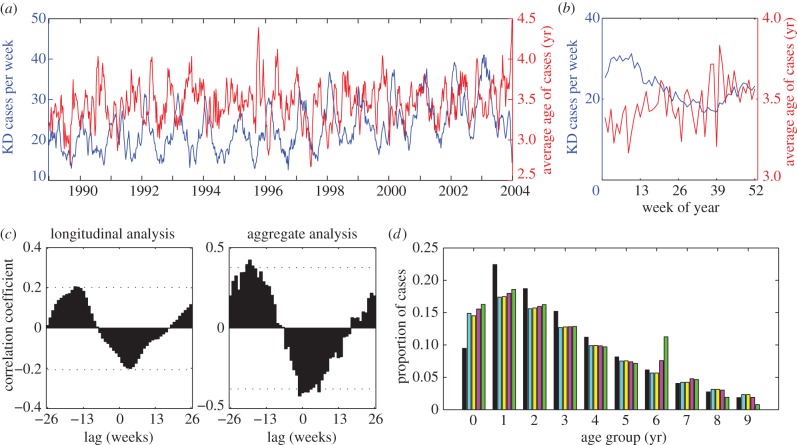
(b). Age–incidence pattern for Kawasaki disease

On average, the mean number of KD hospitalizations peaked in February–March at 31.2 hospitalizations per week and was lowest in September (16.7 hospitalizations per week); the hospitalization rate increased slightly over the 15-year period (figure 3a,b). The weekly mean age of patients ranged from 3.2 to 3.8 years old when averaged over the time series (figure 3b). Examining the data longitudinally, we found the correlation between the number and average age of KD cases varied from a maximum of 0.20 occurring at l_max = −16 weeks to a minimum of −0.20 occurring at a lag of four weeks (figure 3c). Aggregating the cases by week of the year yielded a similar result, with the maximum correlation of 0.42 occurring at l_max = −19 weeks (figure 3c). The maximum correlations were significantly greater than those expected by chance (p < 0.05).

Figure 3.

Relationship between the average age and incidence of Kawasaki disease hospitalizations in the United States. (a) The number of weekly KD hospitalizations (blue) among children less than 10 years of age in 10 US states from 1989 to 2003, and the average age of KD patients (red). We smoothed the data using a five week moving average. (b) Mean number and average age of KD cases by week of the year. (c) Correlation coefficients between the number of hospitalizations at time t and the average age of patients at time t + l for the longitudinal analysis and the aggregate analysis. The dotted lines represent the range within which 95% of the maximum and minimum correlations fell when we randomly permuted the average age time series. (d) Age distribution of KD hospitalizations among children less than 10 years of age in 10 US states compared with model-predicted age distributions under different population mixing assumptions. Black bars, KD hospitalizations; blue bars, homogeneous mixing; yellow bars, assortative mixing; pink bars, self-reported mixing; green bars, RAS mixing.

We examined a variety of models consistent with hypotheses about the aetiology of KD, including: (i) an SIR model, in which people are immediately infectious upon infection and there is life-long immunity following infection, (ii) an SEIR model, in which there is a week-long latent period following infection (during which individuals are not yet infectious) and life-long immunity, (iii) an SIRS model, in which immunity to infection wanes after 2 years, but immunity to clinical symptoms is life-long, and (iv) a model for co-infection with two agents in which each produces life-long immunity to itself but no cross-immunity (see electronic supplementary material). We varied the duration of infectiousness (D) from one week to 16 weeks, and examined four different types of population mixing, as described above. The baseline transmission rate was adjusted such that the average age of cases was between 3 and 4 years old.

In general, the patterns predicted by these models were inconsistent with the observed age–incidence pattern for KD when the duration of infectiousness was short (D = 1 week; table 1). The average age of cases was predicted to be greatest near or slightly after the peak of the epidemic, such that lag times corresponding to the maximum correlation varied from −1 to 12 weeks for the SIR, SEIR and co-infection models. Furthermore, these models often predicted strong seasonal or multi-annual epidemics when the infectious period was short, which does not reflect the seasonality of KD. The only exception was the SIRS model with self-reported mixing, for which l_max = −11 weeks. When we assumed primary school children mix with each other at much higher rates as in the RAS model, the average age of cases was also greatest prior to the peak in incidence (l_max = −12 weeks) when D = 1 week. However, under this type of mixing, a disproportionate number of cases occurred among 6 year olds (i.e. during the first year of primary school), which is not consistent with the age distribution of KD (figure 3d).

Table 1.

Predicted lag times associated with the maximum correlation (l_max; in weeks) for models- representing hypotheses regarding the aetiology of Kawasaki disease.

model	mixing	duration of infectiousness
		one week	four weeks	eight weeks	16 weeks
SIR	homogenous	−1a	−1	−1	0
	assortative	10	15	20	−24c
	self-reported	8	11	12	11
	RAS	−12bc	−12bc	−12bc	−13bc
SEIR	homogenous	−1a	1	1	1
	assortative	12	15	19	26c
	self-reported	11	13	15	15
	RAS	−12bc	−11bc	−12bc	−13bc
SIRS	homogenous	−1	−1	−1	−1
	assortative	−1	0	−4	−12c
	self-reported	−11c	−11c	−11c	−11c
	RAS	−13bc	−12bc	−11bc	−11bc
co-infection	homogenous	−2d	3a	20	−25c
	assortative	10a	15a	18	23c
	self-reported	9d	19a	16	22c
	RAS	−11bc	−13bc	−17bc	−21bc

^aEpidemics occurred biennially.

^bAge distribution of cases predicted under realistic age-structured (RAS) mixing is inconsistent with the age distribution of Kawasaki disease hospitalizations.

^cPredicted lag time within ±12 weeks of the observed lag time for Kawasaki disease.

^dEpidemics occurred triennially.

As the duration of infectiousness increased, the lag times changed little under homogeneous or RAS mixing, but tended to increase if mixing was at least somewhat assortative (table 1). When mixing was highly assortative and D = 16 weeks, the average age of cases reached a maximum during the trough of the epidemic (l_max = −24 weeks; table 1), which is more consistent with the pattern exhibited by KD hospitalizations (figure 3c,d). This was also true for the model for co-infection with an acute agent and one with a long duration under all mixing assumptions.

If we consider all model-predicted lag times within ±12 weeks of the observed −16 to −19 week range as possibly consistent with the pattern exhibited by KD hospitalizations in the USA (table 1), we are able to rule out a number of scenarios. A single acute infection is unlikely to be the triggering agent of KD unless it is imperfectly immunizing and mixing reflects self-reported contact patterns. Otherwise, the age–incidence pattern exhibited by KD is most consistent with a long duration infection or co-infection with an acute and long duration infection.

4. Discussion

The average age of infection is expected to vary during seasonal epidemics in a manner dependent on important epidemiological features, such as the duration of infectiousness and the nature of transmission-relevant mixing. Age–incidence patterns result from fluctuations in the susceptible population that vary by age combined with age-dependencies in the transmission rate, both of which influence what age group is responsible for initiating seasonal epidemics (see electronic supplementary material) [4]. We have shown here that seasonal changes in the average age of cases could be detected using routinely collected data, and were consistent with model predictions. Examining age–incidence patterns can lend insight into important epidemiological features of infections.

We found that simple models for the transmission dynamics of measles and rotavirus could predict the lag time associated with the maximum correlation with a margin of error of ±8–12 weeks. Improving the models by incorporating more information about the epidemiology of infection led to a better correspondence between models and data, such that predicted lag times were within ±1 week of those observed. The amplitude of seasonal fluctuations in the observed average age of cases was typically greater than that predicted by models, suggesting stochastic and discrete effects serve to amplify rather than obscure seasonal changes in the average age.

Since age–incidence patterns vary in a predictable manner, they may aid in the identification of unknown infections. At least one infection is thought to be involved in the aetiology of KD, but a specific agent has yet to be identified [2,5]; it is possible that a previously unidentified virus is involved [6,24]. Examining seasonal changes in the age and incidence of KD hospitalizations in the USA, we found that periods of high incidence corresponded to a low average age of cases, and vice versa. This pattern is in stark contrast to those exhibited by measles and rotavirus. By comparing the observed pattern to those predicted by a suite of models consistent with hypotheses about the aetiology of KD, we found that the age–incidence pattern of KD suggests the involvement of an imperfectly immunizing infection and/or an infectious agent that has a long duration of infectiousness.

For immunizing infections, both the SIR and SEIR models suggest that in order for the average age of cases to be highest during the summer/fall when the incidence of KD is low, the period of communicability would have to be long, i.e. on the order of four months or more, and mixing would have to be highly assortative. There has been considerable debate over whether KD results from an immunological cascade triggered by bacterial superantigens [25–27]. Immunity following such bacterial infections is typically not life-long. For such an infection, we considered an SIRS model in which immunity wanes after 2 years. In order for cases to occur primarily in childhood, we assumed that KD is the result of an abnormal immune response that occurs upon first infection in genetically predisposed individuals and subsequent infections are not associated with symptomatic illness. We cannot discard this hypothesis for an etiologic agent with any duration of infectiousness assuming transmission-relevant mixing reflects self-reported contact patterns, which is likely the case for many respiratory infections. It is also possible that infection is imperfectly immunizing, but that cases are limited to children because of age-related susceptibilities. However, in this case, the transmission rate is inestimable without a priori information on how risk varies with age.

Another hypothesis is that KD is caused by co-infection with two infectious agents, such as an acute viral infection that interacts with colonizing bacteria, leading to bacterial proliferation and toxin production [2]. Data from an animal model of KD suggest that two triggers might be responsible for KD pathogenesis [28]. Similar interactions have been hypothesized to be involved in the aetiology of invasive pneumococcal disease [29] and meningococcal disease [30,31]. We explored this using a model for co-infection with two immunizing agents, and found that the age–incidence pattern for KD is consistent with such a hypothesis provided at least one of the infections has a long period of communicability. This relationship held true for a variety of mixing assumptions, making it perhaps the most robust hypothesis. Since co-infection tends to be a rare event, the low incidence rate of KD in the USA could be consistent with co-infection among individuals with a relatively common rather than rare genetic predisposition. Knowing the prevalence of the genetic determinants of KD would help distinguish between some of the hypotheses presented here.

While there are likely age-related biases in the reporting of many diseases, including KD [32], such biases are unlikely to affect the observed age–incidence patterns unless they vary by season. Underreporting of cases, such as failure to account for cases of ‘incomplete’ KD (in which two or more of the diagnostic criteria are not met), will create bias only if the age–incidence pattern among such cases differs from that among those in our dataset. Approximately, 15 per cent of patients may not meet the full diagnostic criteria, and these cases tend to be concentrated at the extremes of the age distribution [33]. However, there is no evidence that seasonal patterns differ between incomplete and typical KD. Errors in coding of hospitalization records for KD may be constant throughout the year (rather than proportional to the true incidence) and independent of patient age. The influence of coding errors will be greater during periods of low incidence and may bias our estimates of the average age of cases. In this case, the bias is expected to vary by season, and therefore may confound our results. While this may contribute to the pattern observed for KD, by excluding all cases greater than or equal to 10 years of age (6.6%), the effect should be limited. Similarly, readmissions for KD may follow a non-seasonal pattern and be associated with an older average age, thereby generating a bias that could account for the observed pattern. However, an analysis of readmissions data from a subset of states in our dataset revealed that readmissions accounted for less than 10 per cent of all admissions, and 87 per cent of readmissions occurred within one month of the primary admission (see electronic supplementary material). Thus, this is unlikely to account entirely for the pattern we observed.

It would be interesting to test whether our findings are replicated in other populations. In Japan, where the incidence of KD is approximately 10–15 times higher than in the USA [34], nationwide surveys have been conducted every 2 years since 1970 [35]. There have been three nationwide epidemics in Japan, occurring in 1979, 1982 and 1986 [15] and more localized outbreaks have occurred regularly since then. A shift in the age distribution of KD cases towards younger individuals during these epidemics has been noted [12]. Furthermore, a bimodal seasonality has been observed over the past 20 years, with peaks in January and again in June/July [15]. It would be interesting to see if the average age of cases changes in a bimodal fashion as well. If the pattern we observe in the USA also characterizes seasonal changes in the age distribution of KD cases in other countries, it could lend further insight into the aetiology.

The models we present here were parametrized and structured to represent the transmission dynamics of measles and rotavirus or to address specific hypotheses about possible etiological agent(s) of KD, and are by no means exhaustive. Other possibilities include, but are not limited to, models for strain–variable infections with complex immunity, e.g. rhinoviruses and group A streptococci. However, we believe the method proposed here based on age–incidence patterns might be applicable to other diseases with a suspected infectious aetiology, and could be used to gain a better understanding of the transmission dynamics of known infections.