A passerine spreads its tail to facilitate a rapid recovery of its body posture during hovering

Abstract

We demonstrate experimentally that a passerine exploits tail spreading to intercept the downward flow induced by its wings to facilitate the recovery of its posture. The periodic spreading of its tail by the White-eye bird exhibits a phase correlation with both wingstroke motion and body oscillation during hovering flight. During a downstroke, a White-eye's body undergoes a remarkable pitch-down motion, with the tail undergoing an upward swing. This pitch-down motion becomes appropriately suppressed at the end of the downstroke; the bird's body posture then recovers gradually to its original status. Employing digital particle-image velocimetry, we show that the strong downward flow induced by downstroking the wings serves as an external jet flow impinging upon the tail, providing a depressing force on the tail to counteract the pitch-down motion of the bird's body. Spreading of the tail enhances a rapid recovery of the body posture because increased forces are experienced. The maximum force experienced by a spread tail is approximately 2.6 times that of a non-spread tail.

1. Introduction

The evolution and function of a bird's tail have mystified both biologists and physicists. According to some literature reports, a bird's tail increases the physiological attraction for success in mating competition; other authors suggested that a bird's tail pertains only to flight capability [1,2]. The bird literature that addresses the functions of the tail nevertheless remains sparser than for those of the wing.

Except ornamental tails that evolved to cater to sexual selection, a bird's tail is generally recognized as an air manipulator contributing to flight performance. Elongated tails of some types regarded merely as decorations have been proved aerodynamically profitable; for instance, the tail streamers improve the manoeuvrability of a swallow in flight [1,3].

The aerodynamic function of a bird's tail is relevant because flying birds frequently manipulate their tails; during flight, a bird continually alters its tail's angle of attack and extent of spread [4]. During slow flight and taking off, tails are typically spread, whereas during cruising flight tails are furled narrowly. In addition to experiments on live bird specimens, theoretical models have been established to elucidate and to predict the aerodynamic effects of bird tails. Avian tails are reported to be capable of producing lift, diminishing drag, improving manoeuvrability and controlling stability [4–11].

In most of the pertinent literature, a theoretical prediction of the tail lift is based on a slender wing model; a bird's tail is thereby regarded as a delta wing with a small aspect ratio [4,12]. Experiments on bird tails were performed to measure directly the lift force on a tail and to verify the validity of the slender wing model [5,8,13]. Given the varied approaches and the experimental manipulation in each paper, there is no consensus on the extent of lift force exactly generated by the tail, but it is agreed that the tail lift increases with the tail area and the angle of attack of the tail before aerodynamic stall occurs.

Avian tails also have a significant influence on the drag force. When extra lift forces are generated by a bird's tail, additional induced drag and profile drag, which are proportional to, respectively, the lift and the surface area, arise inevitably. The tail of some avian species plays, however, an aerodynamic role in decreasing drag by diminishing the body parasitic drag [10]. An avian tail of this kind generally serves as a splitter plate that suppresses vortex separation (or shedding), which, counterintuitively, appreciably decreases the body drag [7].

Exploiting the additional lift forces generated with tails, birds beneficially acquire locomotive stability or manoeuvrability. During slow flight, a bird's centre of lift is reported to be anterior to its centre of gravity [11]; the additional lift thereby generated by the tail might assist in stabilizing the bird's body and impeding backward tumbling. Birds likewise use their tails as rudders to facilitate a stable turn; without appropriate regulation of the tail, a turning bird might deviate from an intended route and veer outward. Furthermore, the additional lift force generated by the tail enables a bird also to turn sharply because the net force that a bird can instantaneously generate is enhanced [11].

Although evidence is accumulating that a bird's tail has solely aerodynamic benefits, authors have increasingly shifted their attention to the interaction between the tail and other parts of a bird's body. According to the literature, aerodynamic effects for only a tail might be distinct from those for a tail in the presence of a bird's body and wings [5,8,13]. Through visualization of the wake flow, avian tails have been clearly demonstrated to affect the pattern of vortex shedding, implying that avian tails interact with other air-controlling surfaces, i.e. the wings. Because of the complicated measurement and analysis of the wake, the mechanism and function of the wing–tail interaction remain generally unclear.

From a research perspective, the absence of translational speed in the hovering flight of a bird tends to simplify an analysis of the interaction between the tail and other appendages. The wake flow structures of hovering birds are more readily scrutinized experimentally than other flight modes of birds. During hovering flight, a bird generates a lift force approximately equal to its weight; the bird body is nearly stationary, i.e. the flight speed is approximately zero. Only some small bird species, such as hummingbirds, finches and passerines, are capable of executing hovering flight because it is limited by size [14,15].

Hummingbirds are capable of executing ‘symmetrical hovering’. For hovering hummingbirds, both downstroke and upstroke are reported to provide lift forces for weight support [16]. In contrast to symmetrical hovering of hummingbirds, asymmetrical hovering is typically observed in passerines and finches. During asymmetrical hovering, a bird fully extends its wings and sweeps both anteriorly and ventrally during a downstroke, whereas, during upstroke, both wings are retracted and move dorsally. The upstroke in asymmetrical hovering is generally considered aerodynamically inactive; only the downstroke provides the required lift forces [14].

On the basis of experiments, preceding authors suggested that the tail of hovering hummingbirds might be related to pitch control [17]. A hummingbird was found to deflect actively the wing-induced flow via its tail, which is speculated to induce an angular moment that contributes to pitch stability. The tail of a bird might hence act as a control surface of air that enhances the postural stability through an interaction with the flows generated by other appendages of a bird [9,17].

While investigating the flight behaviour of a passerine (Japanese White-eye, Zosterops japonicus), we found that this bird's tail continually undergoes periodic spreading during hovering flight. This phenomenon differs markedly from what has been reported for a bird's tail that is kept spread during landing or folded during steady cruising. We noticed also that a hovering White-eye undergoes a remarkable body oscillation: during downstroke, a hovering White-eye's body constantly exhibits a pitch-down motion, with the tail undergoing an upward swing. This specific phenomenon was mentioned briefly in our report addressing the stabilization of a White-eye's vision [18]. A stabilized flight posture or attitude is doubtless an imperative requisite for a flapping flyer. During downstroke, a hovering White-eye might endeavour to suppress effectively the pitch-down motion and to resume quickly its body posture. Our observations of a hovering White-eye indicate that the periodically spreading of the tail is related to a capability to retard an upward swing of the tail during the downstroke. For a hovering White-eye, there might hence exist some unknown mechanism pertaining to the spreading tail to recover body posture quickly while the tail swings up.

We found also that the timing of the tail spreading is correlated with the onset of the recovery of body posture. The spreading of the tail is speculated to be a mechanism underlying this recovery of posture. As a hovering White-eye has no forward velocity, and as there is hence no horizontal incoming flow, the spreading tail is intuitively conjectured to interact with the downwardly pointed air flows generated by the flapping wings. In the present work, we employed experimental flow visualization and numerical flow simulation to examine and to verify these speculations. We reveal the biomechanical and aerodynamic scenario according to which a White-eye tactically interacts with the wing-induced flows to facilitate quick recovery of its body posture.

2. Method and materials

2.1. Animals and experiment apparatus

We selected the Japanese White-eye (Z. japonicus), a common species of passerine in Asia, as our subject of investigation; eight individuals were used in the experiments. Detailed morphological data for the passerines are given in table 1. A White-eye's tail typically takes the shape of a shallow fork, which is more efficient aerodynamically than other shapes [11]. The flight capabilities and mechanisms of lift production of a White-eye were explored in our preceding experiments [18–20].

Table 1.

Morphological data for the Japanese White-eye (Z. japonicus). Values are reported as mean ± s.d. (n = 8).

Variable	value
body mass (g)	7.8 ± 0.5
wingspan (cm)	15.8 ± 1.2
body length (cm)	10.3 ± 0.7
wing chord (cm)	3.6 ± 0.8
single wing length (cm)	7.2 ± 0.7
tail length (cm)	3.2 ± 0.3

A transparent chamber (depth 60 cm, width 60 cm, height 120 cm) was used to conduct the experiments on the hovering White-eye. Two synchronized high-speed video cameras (X-StreamTM Vision 5, IDT) with orthogonal viewing directions were deployed to acquire images for quantitative visualization of the flow field and kinematic analysis of the spreading tail.

2.2. Image analysis

Image sequences were captured at 1000 frames s⁻¹; the corresponding temporal resolution was sufficiently large for an accurate calculation of body angles and tail areas because the average wingbeat frequency in hovering flight of a White-eye is approximately 25 Hz. During the experiments, a bird was allowed to fly freely and spontaneously, so that flight modes of several types—e.g. hovering, ascending and turning—were typically observable. Many experimental trials were conducted; only image sequences in which hovering flight was clearly observed were applied for the kinematic analysis. An image-analysis program (written with Matlab, The Mathworks, Natick, MA, USA) was developed to implement the kinematic analysis for the sequences of captured images.

In this work, we adopted the body angle to describe the extent of inclination for a bird's body posture. Body angle θ for a flying bird is defined as the angle between the longitudinal axis (roll axis) and the horizontal line (figure 1a). The longitudinal axis is defined as the line connecting the trailing tip of the tail and the midpoint between the bird's eyes.

Figure 1.

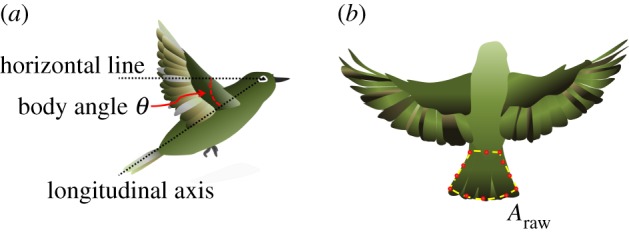
(a) Definition of body angle θ. One dotted line represents the longitudinal axis (roll axis) for the bird's body; the other one is a horizontal line. (b) The projected area of the tail (A_raw). The red dots are points lying on the outline of the tail. (Online version in colour.)

To determine the area of a bird's tail from the captured images, we first manually specified points lying on the outline of the tail (figure 1b) and computed the area with our image-analysis program. This area of the tail corresponds notably to an area projected on a vertical plane, denoted A_raw, which is inappropriate; we hence modified the projected area in terms of the geometric correlation so that the actual area of the tail is calculated as A_raw/sin(θ). The camber and flexibility of the tail were assumed unimportant at the current stage.

2.3. Quantitative flow visualization

We deployed two-dimensional digital particle-image velocimetry (PIV) to visualize quantitatively the interaction between the tail and the airflow induced by wings. We used an argon-ion laser (Stabilite 2017, Spectra Physics) as the light source, and expanded its beam into a light sheet via sheet-forming optics. Seeding particles, which were assumed to trace faithfully the flow motion, were illuminated with this light sheet. The seeding particles were water droplets (approx. 3 μm) produced with an ultrasonic fog generator. One camera (PIV camera) focused on the light sheet to record the flow field; the other camera (motion camera) recorded the locomotion of the bird simultaneously in the orthogonal direction of the PIV camera. Both cameras (resolution 1024 × 768 pixels) operated synchronally at 1000 frame s⁻¹. We computed the flow velocities with software (Insight 3G, TSI Inc.) to acquire quantitative information about the bird wake flows. The size of the interrogation window used for PIV analysis was 32 × 32 pixels, with 50 per cent overlap of the interrogation window to comply with the Nyquist criterion. Readers are referred to our prior work [19] for further technical details of the measurements of the bird flow with PIV.

To observe the natural flight behaviour of a White-eye, we imposed no physical constraint on a bird's body during the observations; the relative positions of the light sheet and the hovering bird hence varied in each trial. PIV images captured just on the frontal light sheet plane that vertically intersected the bird tail (figure 2) were selected for further flow analysis. The region of interest typically suffers from a lack of PIV data because the flapping wings might obstruct the light sheet; in this work in which we undertook numerous experiments, we analysed only those data that were nearly free of that unintended distraction.

Figure 2.

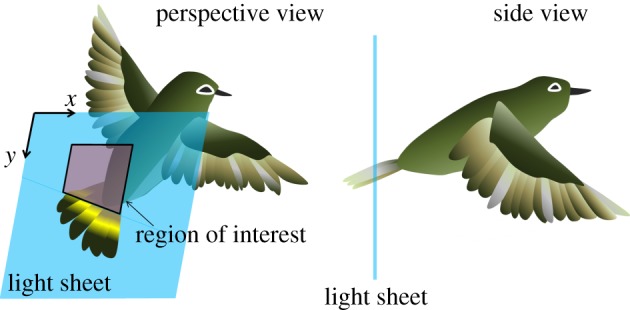
Schematic sketches to illustrate the relative positions of the light sheet and the bird. The light sheet defines a vertical plane with respect to the bird's body; this plane intersects the bird's tail. The velocity data in the region of interest (a square) were calculated to be the average speed of the flow above the tail. The length of the square (typical range from 2 to 3 cm) was chosen as the tail span that was intersected by the light sheet.

The vertical and horizontal components, respectively, denoted V_y and V_x, of the velocity of the flow situated in the region above the tail were quantified for a complete hovering cycle. V_y and V_x are defined as positive, respectively, for flow pointing downward and rightward with respect to the bird. To examine the overall trend of variation of the flow velocities above a bird's tail, we calculated the spatially averaged flow velocities v and u, which are, respectively, the mean values of V_y and V_x averaged over a square region just above the tail (figure 2). The width (usually ranges from 2 to 3 cm) of this square region was chosen as the distance between two points at which lateral edges of the tail intersected the light sheet.

2.4. Evaluation of forces

One might speculate that the aerodynamic force experienced by a spreading tail increases with the increasing area of the tail. To clarify this speculation, we evaluated computationally the aerodynamic forces experienced by the tail, which elucidates the role of tail spreading in a hovering bird. Our simulation by means of computational fluid dynamics (CFD) was conducted to predict the aerodynamic forces acting on the spread tail.

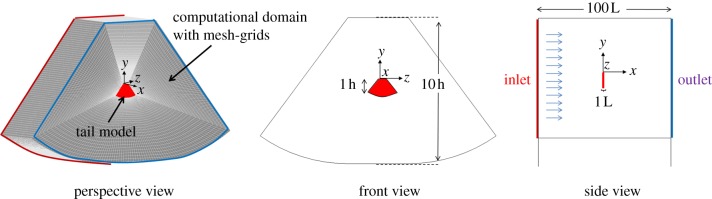
Seven extents of spreading of the tail were considered. For the fully folded (i.e. non-spread) state, the computational model of the tail was structurally simplified as a rectangular plate (length 32 mm, width 13 mm, thickness 0.1 mm). For the spread state, the computational model of the tail was considered as a geometrical combination of a rectangular plate and two circular-sector plates alongside (figure 3). Angle Φ of tail spread is defined as the central angle of the circular sector plates; Φ increases as the bird spreads its tail. Φ equals 0 and 36°, respectively, for a fully folded and a fully spread tail. We used seven values of Φ—0, 6, 12, 18, 24, 30 and 36°—for the computational model of the tail, which corresponded to seven extents of tail spreading. With commercial CFD software (CFD-RC, ESI group), these tail models were constructed based on the actual dimensions of the tails of the White-eyes.

Figure 3.

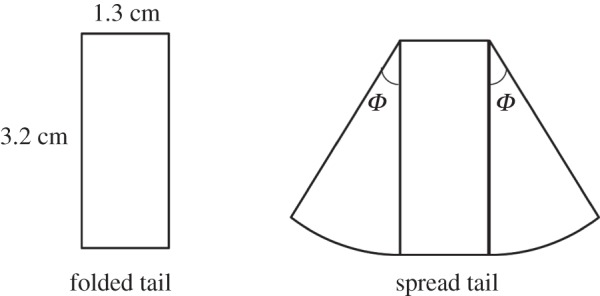
Geometries of the computational models for the folded and spread tails. A folded tail is simplified as a rectangular plate. A spread tail is considered to be constituted by a rectangular plate in combination with two circular sector plates alongside. Angle Φ of tail spread varies in a range 0–36°, corresponding to the extent of tail spreading.

The Navier–Stokes equations governing the system of three-dimensional, incompressible and steady flow are

2.1

and

2.2

in which appear velocity vector 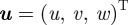, individual component u_i of the velocity vector, fluid density ρ, fluid pressure p, fluid kinematic viscosity υ and the del operator ∇. We assumed a quasi-steady flow for our simulation. The governing equations were made discrete with the finite-volume method (a second-order differencing scheme); the SIMPLEC method was used to treat the coupling between pressure and velocity.

Figure 4 shows the computational domain and the tail model in various views. For the boundary conditions, a uniform flow with constant velocity was specified at the boundary inlet, and constant pressure (standard atmospheric pressure) at the boundary outlet. A no-slip wall condition was enforced at the surface of every domain except the inlet and outlet. Tests of independence of the simulated results were conducted to ensure that the computed solutions converged satisfactorily and were independent of the grid size and dimension of the computational domain. The grids used for the simulation numbered approximately 670 000.

Figure 4.

Schematic illustrating arrangement of the physical model and the computational domain for the simulation. The inlet condition is uniform flow with its velocity acquired from PIV results; the outlet condition is constant pressure. (Online version in colour.)

Angle θ of the tail model and the flow velocity (inlet flow velocity) were chosen based on experimentally acquired data of the motion kinematics and flow fields. The pressure distributions of the front and back surfaces on the tail model were integrated, and the results were subtracted from each other to yield the normal force on the tail model.

According to a perspective of current CFD technique and general physical intuition, the cases that we simulated in this work are simple; the quantitative trend of variation of the force acting on the tail model is as expected. We compared also the computationally acquired result of the drag force (F_D) with that derived from an empirical formula indicated in a handbook of fluid dynamics [21],

2.3

which contains fluid density ρ, oncoming flow velocity V, projected area A of the objective and drag coefficient C_D. The values of the computationally obtained C_D were less than their corresponding empirical values by approximately 10 per cent; this agreement indicates that the computational results can reveal the quantitative trend of force variation for the tail spread at various values of Φ.

3. Results

During hovering, a White-eye periodically spreads its tail, as shown in figure 5. This behaviour is not arbitrary but exhibits a positive correlation with the wingstroke motions. At the beginning of a downstroke, the tail is in a fully folded state, structurally analogous to a rectangular plate. The tail gradually spreads as the downstroke proceeds. When the downstroke is nearly completed, the tail ceases to spread and immediately initiates a folding action. The tail ultimately resumes a fully folded state at the end of the upstroke. In brief, a tail-spreading cycle consists of a spreading phase and a folding phase, which approximately correspond to down- and upstrokes, respectively.

Figure 5.

Chronological sequence of images of a hovering White-eye that periodically spreads and folds its tail during a wingbeat cycle. τ denotes the time fraction (per cent) of a hovering wingbeat cycle.

A White-eye completes a hovering wingbeat cycle in 38 ± 4.23 ms (mean ± s.d.: n = 8). The period of downstroke (23 ± 1.54 ms; mean ± s.d.: n = 8) is typically greater than that of the upstroke. The duration required for a White-eye to accomplish a tail-spreading cycle is 38 ± 3.51 ms (mean ± s.d.: n = 8). To see whether there exist biological variations among the tested birds, we implemented one-way analysis of variance followed by Student–Newman–Keuls tests using software SPSS (IBM, USA). The results indicate that, in a statistical sense, there is no statistically significant difference between the period to complete a hovering wingbeat cycle and that to accomplish a tail-spreading cycle.

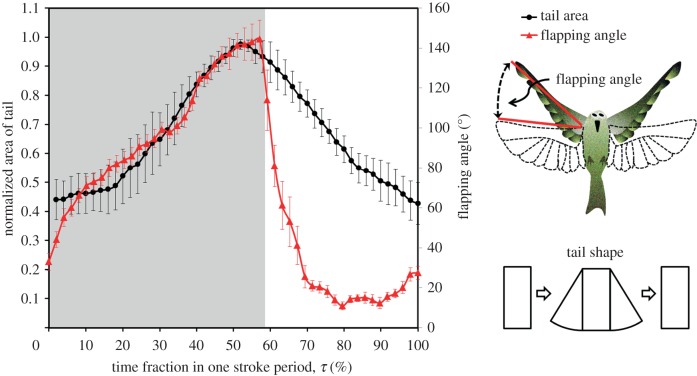
The measured area of the fully folded tail was 4.16 ± 0.75 cm² and of the fully spread tail was 10.48 ± 1.21 cm² (mean ± s.d.), although there were slight differences of tail morphology (and area) among the individual White-eyes tested. In figure 6, we show the variation of the tail area, normalized by the maximum tail area in the fully spread state, within a hovering wingbeat cycle. The normalized tail area increased from approximately 0.4 to 1 for the duration τ = 0–50% (corresponding to almost the entire downstroke stage). The maximum normalized area occurred at approximately τ = 50 per cent. For τ = 50–100%, an interval pertaining to the late downstroke stage and the entire upstroke stage, the normalized area gradually decreased to 0.4. An extra parameter, flapping angle, was introduced in figure 6 to provide a rough description of the relation between tail spreading and wing flapping. The flapping angle refers to the angle swept by a flapping wing for a frontal view. As shown in figure 6, there appears no obvious phase shift between wing kinematics and tail motions. Detailed wing kinematics of a hovering White-eye were found in our related work [19].

Figure 6.

Variation of the normalized tail area and flapping angle within one hovering wingbeat cycle. The right side presents schematic of the definition of the flapping angle and varied tail shapes. The error bars indicate s.d. (n = 8). The zone shaded grey corresponds to the period of a downstroke.

In the recorded images, we observed that a White-eye underwent an evident body oscillation during hovering, rather than just remaining in a totally motionless status. As shown in figure 7, during the earlier stage of a downstroke, a White-eye's body pitched down, with the tail being concurrently elevated. This pitch-down motion ceased at the end of the downstroke. During the succeeding upstroke period, the bird gradually resumed its body posture with a pitch-up motion.

Figure 7.

Consecutive images of a hovering White-eye undergoing body oscillation. The arrow indicates the direction towards which the tail is moving; the curve with arrow indicates the direction of rotation of the bird's body.

To dissect this unique phenomenon, we first examined the variation of body angle within a hovering cycle of the White-eye. The body angle reported in figure 8 was normalized with the maximum angle for each analysed hovering cycle. Both the initial and eventual body angle in a wingbeat cycle depended on the individual White-eye, which were approximately in a range 20–45°, but we recognized a regular trend of variation of the body angle. As shown in figure 8, the body angle decreased gradually before τ = 35 per cent, corresponding to a pitch-down motion, and increased gradually after τ = 35 per cent, corresponding to a pitch-up motion.

Figure 8.

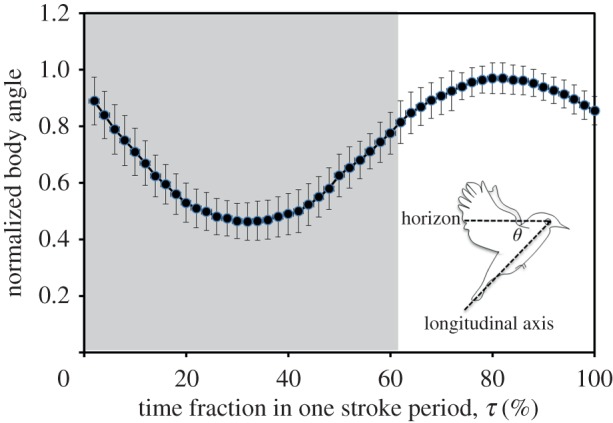
Variation of normalized body angle θ within a hovering wingbeat cycle. The inset illustrates how this angle is defined. Values are mean ± s.d. (n = 8). The zone shaded grey corresponds to the period of a downstroke. (Online version in colour.)

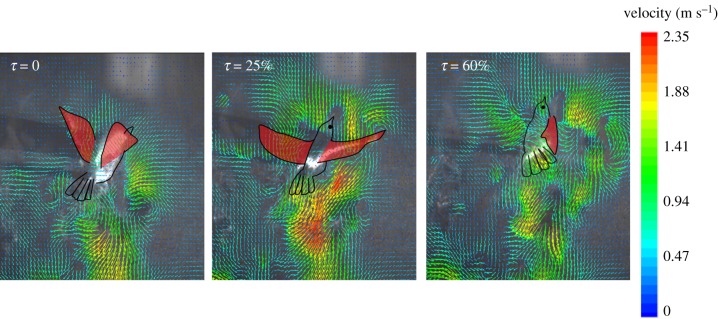
Figure 9 presents rear views of the flow fields acquired on a vertical plane intersecting the bird's tail during the downstroke period. At τ = 0, corresponding approximately to the beginning of the downstroke, no significant downward flow was observed in the region above the tail; the flow motions existing at this moment were produced predominantly by the previous wingbeat. At τ = 25 per cent, corresponding to the mid-downstroke, downward flows were produced in the region above the tail. At τ = 60 per cent, corresponding approximately to the end of the downstroke, the downward flows remained remarkably strong. This strong downward flow induced by the downstroke served mechanically as an external jet flow impinging upon the tail, providing a depressing force on the tail. As such, the pitch-down motion of the bird's body was effectively terminated.

Figure 9.

Flow fields acquired on a vertical plane intersecting the tail of a hovering White-eye during a downstroke. The instants with τ = 0, 25 and 60 per cent correspond to the beginning of a downstroke, the mid-downstroke and the end of a downstroke, respectively. The bird's body and wings are highlighted.

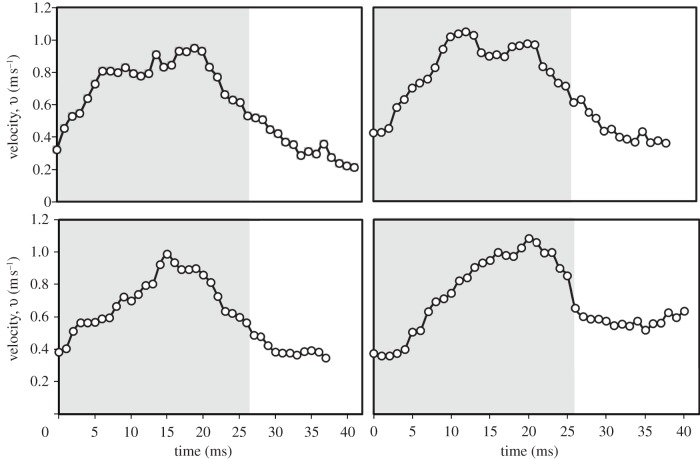
For the flow field induced in the region above the tail, its horizontal velocity component u was typically one-tenth of the vertical component v, which is a feature commonly observed in the birds tested in this work. This induced flow field was dominated by the vertical flow. Four representative results of the measured vertical velocity v for a wingbeat cycle are shown in figure 10. At the beginning of a downstroke, v was approximately 0.4 m s⁻¹; as previously mentioned, the strong downward flow observed at this moment was induced by the previous wingbeat. As the downstroke proceeded, v increased considerably. The maximum v in a wingbeat cycle was 1.12 ± 0.31 m s⁻¹ (mean ± s.d.: n = 8). Figure 10 shows that the instants at which the maximum v occurred were inconsistent, but all lay in a range approximately 10–20 ms. The observed rapid increase of velocity v of the downward flow is attributed to the powerful motion of the downstroking wings that propelled much air downward. At the end of the downstroke, which was approximately in the temporal range 15–25 ms, v ceased to increase. For the succeeding upstroke period, v gradually decreased.

Figure 10.

Four representative cases (taken from four separate individual birds) of the variation of vertical velocity v of the downward flow in the region above the tail for a wingbeat cycle. Zones shaded grey correspond to the period of a downstroke.

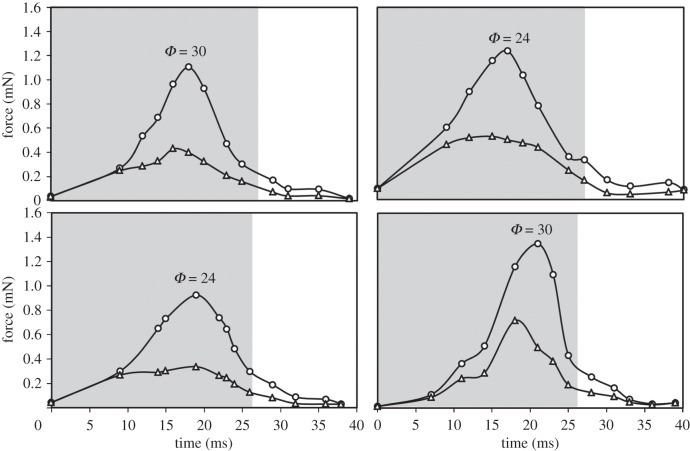
The results of numerical evaluation of the forces experienced by the bird's tail at Φ = 0, 6, 12, 18, 24, 30 and 36° are presented in figure 11, providing insight into the general trend of variation of force within a wingbeat cycle. Similarly to the variation of vertical velocity v described above, the variation of the force exhibited a common feature in that it first increased and then decreased. At the beginning of the downstroke, the depressing force on the tail was small. The force continuously increased (for time 10–20 ms) until the end of the downstroke, and then began to decrease. The maximum depressing force on the tail ranged from approximately 0.90 to 1.35 mN, and typically occurred near the mid-downstroke stage. During the upstroke, the force remained small.

Figure 11.

Four representative cases demonstrating the variation of forces experienced by spread (circle) and non-spread (triangle) tails during a wingbeat cycle. Spread angle Φ pertaining to the maximum force computed for the spread tail is noted. Zones shaded grey correspond to the period of a downstroke.

Two factors contributing to the rapidly increasing force during the downstroke are the increasing flow velocity v and the increased tail area. To examine the aerodynamic function of a spread tail and for the sake of comparison, we performed a numerical simulation on a non-spread tail that was kept folded during a wingbeat cycle, with the same flow conditions as for the spread tail. The force experienced by the spread tail surpassed the force experienced by the non-spread tail, because the area of a spread tail is greater than that of a non-spread tail. The maximum force experienced by a spread tail is approximately 2.6 times that for a non-spread tail.

4. Discussion

In this work, we demonstrate that a hovering White-eye spreads its tail to intercept the downward flow induced by the downstroking wings, which is considered capable of facilitating the recovery of the body posture of the bird. We observed directly that a White-eye typically kept its tail completely folded during rapid ascent and forward flight, but instead kept its tail completely spread during landing flight. The impressively distinctive behaviour of periodic spreading and folding of the tail of a White-eye was observed only during the hovering flight. One can thus reasonably assume that a White-eye periodically spreads and folds its tail for a purpose and might acquire some locomotive benefits in so doing.

Birds are reported to be capable of actively controlling the tail to enhance stability or manoeuvrability with the muscle at the base of the tail [22,23], but it is of biological interest that a sophisticated flyer chooses periodically to spread and to fold its tail in hovering flight, a flight mode that is considered extremely energy-consuming [15]. A clever flyer refrains from aimless motion; this distinctive tail manipulation during hovering flight should accordingly be beneficial or even crucial for a hovering White-eye.

Most prior investigations of the aerodynamic role of a bird's tail were conducted with experiments in a wind tunnel [7,8,24]. Most flight modes addressed in these experiments were gliding or forward flapping flight. It is widely accepted that, at high flying speeds, a bird tends to fold and to furl its tail to diminish drag, whereas the tail is spread to render more lifting surface to generate extra lift required for flights at small speed [11]. The lift generated by the tail contributes beneficially also to the pitch moment balance for a bird with its centre of lift anterior to the centre of mass during slow flight. A recent report also indicates that the tail of flycatchers is relatively active and might be of importance for manoeuvrability in slow flight [9]. Little research is reported on the aerodynamic functions of the tail in a hovering bird. The tail of hovering hummingbirds has been suggested to be related to pitch control; a hummingbird was found to deflect actively the wing-induced flow via its tail, which is speculated to induce an angular moment that contributes to pitch stability [17]. For a hovering White-eye, the tail is observed to spread periodically, which implies that it might interact with the flow induced by the flapping wings in the absence of incoming flow.

In our preceding work on a hovering White-eye, a substantial pitch-down (tail up) motion was observed during a downstroke [18]; this motion is attributed to an aerodynamic force that is perfectly generated posterior to the centre of mass of the bird's body to facilitate visual stabilization, but this motion must be appropriately suppressed or counteracted so that the bird's entire body posture can be quickly recovered or dynamically stabilized. To this end, a hovering White-eye periodically spreads and folds its tail, which is an efficient mechanism of posture recovery.

As shown in figure 8, body angle θ ceases to decrease and begins to increase after τ = 30 per cent; that is, the bird gradually recovers its initial posture. The increase of θ in figure 8 is strongly associated with the ‘depressed’ tail in figure 7; an external force seems to depress the rising tail to recover the bird's body posture. The flow fields measured around the bird unveil the source of this external force.

As the downstroke proceeds, much air is accelerated downward by the wings to generate lift for weight support. This downward flow propagates further downward and remains strong when it impacts the bird's tail. As manifested in figure 9, this downward flow acts as an external force to depress the rising tail.

In figure 11 we show that, under identical flow conditions, notable distinctions remain observable between the forces experienced by the spread and non-spread tails. The spread and non-spread tails exhibit a qualitatively similar trend of force variation: the force increases first and then decreases during a wingbeat cycle, which is strongly correlated with the variation of downward flow velocity in the region above the tail. The force experienced by a spread tail increases rapidly in the interval 10–20 ms. Comparisons with the case of a non-spread tail indicate that this rapidly increasing force for a spread tail stems from the increased tail area (figure 6). During the interval 10–20 ms (τ = 25–50%), the body angle ceases to decrease and begins to increase (figure 8), implying that spreading the tail increases the depressing force acting on the tail and leads to recovery of the body posture.

The maximum forces acting on the tail, typically in a range 0.90–1.35 mN, are somewhat incomparable with the body weight, but they are sufficient to cause a remarkable body rotation in a hovering White-eye. To model a White-eye with its wings kept flexed and retracted during the upstroke period, we simplified geometrically the body trunk of such a White-eye as a cylinder; for this geometry, the moment of inertia I about its central diameter axis is readily determined as [25]

4.1

in which appear mass M of the cylinder, its radius R and its length L. Substituting the body mass, radius (the largest radius of the body trunk) and the longitudinal length of the White-eye for the above parameters, we find that the moment of inertia of the White-eye has a magnitude of approximately 10⁻⁶ kg m². Given the moment of inertia and the experienced force of the tail, the angular acceleration α is determined with Newton's second law of motion in angular form,

4.2

in which appear depressing force F on the tail and moment arm r (considered to be half the longitudinal length of the bird's body). The angular acceleration α so evaluated might be insufficiently objective and inaccurate because simplification and idealization are involved. Equation (4.2) has, however, an important implication that angular acceleration α is proportional to depressing force F on the tail. Spreading of the tail hence produces a more rapid recovery of the body posture because greater forces are experienced.

According to our recognition that a spread tail can intercept increased wing-induced flow, a further intricate question emerges. Why does a White-eye not always maintain its tail fully spread during hovering flight? Monitoring, perception and reaction with immediateness are sophisticated capabilities of many creatures. A bird might continuously monitor and perceive its body movement and instantly, or simultaneously, react to it to attain an increasingly stabilized posture of flight.

We speculate that the spreading and folding of a tail are well-devised actions that regulate the flight conditions tactically and instantaneously. As the downstroke proceeds with the body swinging up (e.g. τ = 0–30% in figure 8), the White-eye gradually spreads its tail to intercept sufficient flow to depress its posterior body (τ = 20–50% in figure 6), which impedes excessive body rotation and also facilitates quick recovery of its original posture. Once the tail has intercepted sufficient flow and the body begins to swing down (τ = 40–80% in figure 8), a White-eye gradually folds its tail so that it does not intercept unnecessary and superfluous flow that could produce undesirable outcomes (τ = 50–100% in figure 6). This speculation might account for the fact that a White-eye, as a skilful and expert flyer, is observed to spread and to fold its tail periodically during hovering flight.

The unique function of periodic spreading and folding of the tail addressed in this work is evidently distinguishable from the functions of a tail in preceding reports stating that tail spreading or folding is purely to gain lift or to diminish drag for a bird. From a qualitative perspective, it is sufficient to conclude the posture recovery achieved by periodic spreading and folding of the tail from our observations and arguments above, but further quantitative effort is required to evaluate accurately the moment balance on the entire bird's body, which is impracticable at the current stage: we can scarcely obtain trustworthy values of the moment of inertia of a flying bird.

Whether the pitching rotation of the bird body mainly results from an aerodynamic effect or from another effect remains unclarified. In theory, flapping wings also contribute to body rotation through the conservation of angular momentum [26,27]. Our experimental results (figures 7 and 9) demonstrate that the tail is depressed downward during a transition from downstroke to upstroke; the bird's wings are meanwhile nearly motionless, with the bird's body concurrently undergoing a pitch-up motion. This pitch-up motion must hence have been caused by factors other than the conservation of angular momentum. Our flow-field measurements reveal that a strong downward flow is intercepted by the spread tail and consequently depresses the spread tail, accounting for the observed pitch-up motion of the bird's body.

For our computational simulation, we simplified the bird's tail as a rigid plate. This simplification might introduce an error in force evaluation because the spread tail is a surface with a slight camber and flexibility. Moreover, the flow fields around the tail were resolved numerically according to an assumption of quasi-steady flow. The spreading action of the tail is, however, both dynamic and transient; any unsteady or transient flow effects were neglected in our simulation, which would also cause errors in the evaluation of the force. Notwithstanding this simplified treatment and its errors, the computed trends of force variation are believed to be qualitatively correct, unveiling the aerodynamic and locomotive functions of a spread tail. A comparison of forces (figure 11) between the spread case (i.e. tail undergoing periodic spreading and folding) and the non-spread case (i.e. tail kept folded) indicates that a spread tail invariably encounters an increased depressing force. As made clear in our preceding work [18,19], the wake flow fields of a hovering White-eye are dominated by the strongly downwardly oriented jet flow. The flow conditions specified in our simulation are therefore realistic, and the computed results of flow velocity and forces are considered valid.

For a hovering White-eye, other mechanisms might be exploited to recover the body posture. Beyond the aerodynamic mechanism that we here propose, a hovering White-eye might employ its musculoskeletal system also to regulate its posture. A hovering bird is likely to be equipped with multiple systems to stabilize efficiently its body posture. An intriguing but complicating issue arises from an observation that a bird with its tail removed can still fly [12]. Also, insects likewise hover stably without tails. This perspective, however, is not quite objective because we are unclear about the cost to a bird or the extra mechanisms that a bird adopts in lack of a tail. We show here that a hovering White-eye exploits spreading of its tail to intercept wing-induced flow, which is a useful and beneficial mechanism to enable a quick recovery of the body posture.

5. Conclusions

A passerine exploits tail spreading to facilitate a quick recovery of its body posture during hovering flight. We employed high-speed cameras to capture the flight locomotion of White-eyes, especially the locomotion of the bird's tail and the posture of its body. We also deployed two-dimensional digital PIV to visualize quantitatively the interaction between the tail and the airflow induced by the wings, and we performed simulation by means of CFD to predict the aerodynamic forces acting on the spread tail.

During hovering, a White-eye periodically spreads its tail exhibiting a phase correlation with the wingstroke motions and the body oscillation. The normalized tail area increases from approximately 0.4 to 1 for the interval τ = 0–50% but gradually decreases to its original value thereafter. The locomotion of the tail is strongly associated with the body oscillation during hovering. The body angle decreases gradually before τ = 35 per cent but increases gradually thereafter. This decreasing angle is attributed to an aerodynamic force that is generated posterior to the centre of mass of the bird's body that causes a pitch-up body rotation. We demonstrate qualitatively and quantitatively that a passerine exploits tail spreading to intercept the downward flow induced by its wings to facilitate posture recovery.

As the downstroke proceeds, much air is accelerated downward by the wings to generate lift for weight support. This strong downward flow serves mechanically as an external jet flow impinging upon the tail, providing a depressing force on the tail. The force experienced by the spread tail surpasses the force experienced by the non-spread tail, because the area of a spread tail is greater than that for a non-spread tail. The maximum force experienced by a spread tail is approximately 2.6 times that for a non-spread tail, implying a more rapid rotation of the bird's body. This rotation caused by the depressing force imposed on the tail recovers a bird's body posture; spreading of the tail also enhances a rapid recovery of the body posture because increased forces are experienced. We speculate that a White-eye folds its tail so that it does not intercept unnecessary flow once the tail has intercepted sufficient flow and the body begins to swing down.

The unique function of periodic spreading and folding of the tail addressed in this work is distinguishable from the functions of a tail reported elsewhere, in which tail spreading or folding is contended purely to gain lift or to diminish drag for a bird. The tail of a bird might alternatively act as a control surface of air that enhances postural stability through interaction with flows generated by other appendages of a bird.