Adhesion energy can regulate vesicle fusion and stabilize partially fused states

Abstract

Release of neurotransmitters from nerve terminals occurs by fusion of synaptic vesicles with the plasma membrane, and this process is highly regulated. Although major molecular components that control docking and fusion of vesicles to the synaptic membrane have been identified, the detailed mechanics of this process is not yet understood. We have developed a mathematical model that predicts how adhesion forces imposed by docking and fusion molecular machinery would affect the fusion process. We have computed the membrane stress that is produced by adhesion-driven vesicle bending and find that it is compressive. Further, our computations of the membrane curvature predict that strong adhesion can create a metastable state with a partially opened pore that would correspond to the ‘kiss and run’ release mode. Our model predicts that the larger the vesicle size, the more likely the metastable state with a transiently opened pore. These results contribute to understanding the mechanics of the fusion process, including possible clamping of the fusion by increasing molecular adhesion, and a balance between ‘kiss and run’ and full collapse fusion modes.

1. Introduction

Neurotransmitters are packaged into synaptic vesicles that dock to the synaptic membrane, open a pore, and fuse with the synaptic membrane, thus releasing transmitters into the synaptic cleft. This process is highly regulated, and the protein machinery that controls docking and fusion has been studied extensively [1–3]. It has been established that SNARE proteins, including a vesicle protein, synaptobrevin and a membrane protein, syntaxin, form a zipper and thus bring the membrane and vesicle together, possibly overcoming the repulsive forces produced by electrostatic and hydrophilic interactions [4,5]. Opening of the pore and subsequent release of transmitter are triggered by Ca²⁺ binding to a vesicle protein, synaptotagmin, which is believed to undergo a conformational change [6,7], possibly binding to synaptic membrane and changing its curvature [8–10]. It has also been proposed that fusion is clamped by a protein, complexin [11–13], to prevent spontaneous release events, and possibly by synaptotagmin in its Ca²⁺-unbound or partially bound form [14–16].

Thus, the main components of the molecular machinery that govern the fusion process have been identified. However, little is known about the detailed mechanics of the process. A number of studies proposed that the distinct stages of the fusion include stalk formation followed by the hemifusion state and pore opening. However, it is still a matter of debate whether the intermediate state of hemifusion occurs, although a number of experimental [17–23] and computational [24,25] studies support this view. An alternative scenario has been proposed where the entire fusion process is controlled by SNARE transmembrane domains that cross both synaptic and vesicle membranes and align the pore [26,27]. Finally, a mechanism has been proposed where the stalk formation is followed directly by pore opening, bypassing the hemifusion state [28,29].

Once the pore opens, the fusion may proceed either as a full vesicle collapse or as a transient pore opening, the latter termed ‘kiss and run’ [30,31]. The kiss-and-run mechanism has been established for neurosecretory cells [32–37] but remains a matter of debate for synaptic transmission, although evidence for this fusion mode at synapses has been presented during the last decade [38–41]. It remains quite unclear how the balance between the full and transient fusion modes can be achieved and what physical forces control fusion pore expansion or resealing.

Although specific mechanisms of membrane merging, pore opening, dilation and expansion remain obscure, most of existing models agree that the membrane curvature and membrane stress are important determinants of the stalk formation and pore dilation and expansion. Several models demonstrated that the membrane tension in the contact region is a critical determinant of fusion [42–44].

In this work, we propose a coarse-grain model that attempts to link the adhesive action of the SNARE complex to the mechanics of vesicle deformation. Our analysis is based on a coarse-grain model for the deformation of lipid bilayer membranes given by Jenkins [45,46] and Steigmann [47]. The model captures the fact that lipid bilayers are fluid-like with respect to shear deformations in their plane, conserve their area (i.e. are nearly incompressible), and that the dominant contribution to changes in free energy upon deformation comes from membrane curvature. (Such models are readily combined with electrostatic forces owing to charges on the membrane surface, and they have been used widely [48–53] with considerable success to model the deformation of vesicles and cells.)

It should be noted that the model of Jenkins [46] and Steigmann [47] is broadly consistent with that of Helfrich [48,54] but differs in that it enforces local incompressibility, whereas the Helfrich model does so only in an average sense. Specifically, in the Helfrich formulation, incompressibility or area conservation is enforced by the use of a constant Lagrange multiplier, which is commonly interpreted as the average membrane tension. However, in the formulation of Jenkins [46], this multiplier is a spatially varying function and is explicitly related to the membrane tension. Hence, the membrane tension is a function of position. Seifert & Lipowsky [52,53] analysed the adhesion between a vesicle and a surface in a manner similar to that which we present, but using an energy functional that satisfies incompressibility in an average sense. They found a transition from a bound to an unbound shape at a critical value of adhesion energy, and predicted shapes of bound vesicles also similar to those we calculate. However, calculation of the membrane tension was not emphasized in their work. In addition, if one interpreted the constant Lagrange multiplier as the membrane tension, the global incompressibility formulation would lead to an unphysical prediction of a tensionless membrane. By contrast, we use the local incompressibility formulation [46], which specifically provides membrane forces and moments (including membrane tension), and our results show that the in-plane stress in the region of contact between the vesicle and plasma membrane is compressive.

We then use our membrane model to examine the partially fused state in which a small opening has appeared connecting the interior of the vesicle to the exterior of the cell around which the vesicle and plasma membranes have merged. We show that with sufficiently strong adhesion, there exists a metastable partially fused state. This provides the first mechanistic model to explain the transiently opened ‘kiss-and-run’ mode. We find that, depending on the value of a dimensionless adhesion parameter, the pore between vesicle and the exterior of the cell can open up into full collapse, or reseal, both of which type of events have been observed experimentally.

1.1. Problem statement

The two problems studied in this work are illustrated schematically in figure 1a,b below. Figure 1a shows the docking state, where the synaptic vesicle is in adhesive contact with the synaptic membrane. Before docking, the synaptic vesicle is assumed to be a spherical lipid membrane with radius R. Because both the vesicle and the cell membrane have hydrophilic groups, they naturally repel each other. This repulsion is overcome by the adhesive action of the SNARE protein complex. In our model, following Seifert & Lipowsky [52], we replace the action of the SNARE complex by an interfacial region between the vesicle and membrane, endowed with an adhesion energy per unit area. This adhesion represents the attractive forces exerted by the SNARE complex and associated molecular machinery minus membrane/vesicle repulsion caused by electrostatic and hydrophilic interaction.

Figure 1.

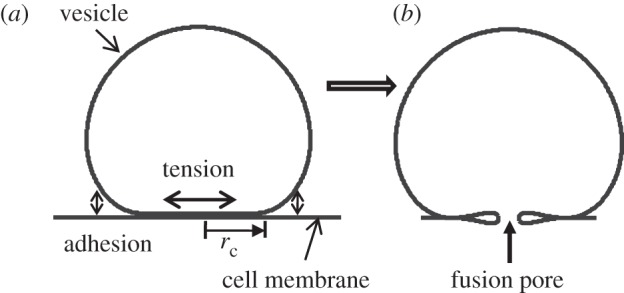
Solutions of the coarse-grain membrane model showing (a) a vesicle in adhesive contact with a membrane (docking stage), and (b) a metastable, partially opened pore (kiss-and-run mode, requires sufficiently high adhesion).

As a result of these interactions, the synaptic vesicle may deform into an unknown shape with an unknown region of contact, which is the interior of a circle of radius r_c in our axisymmetric model (figure 1a). As a result of adhesion-driven deformation, at the contact edge, the membrane is subjected to an unknown in-plane force T. Here, we examine how the adhesive energy influences the forces transmitted to the region of contact, which is where the fusion event nucleates. Our first goal, therefore, is to determine the unknown quantities, such as region of contact and forces that result from adhesive contact.

We find that our formulation is also able to capture the possibility of a metastable equilibrium shape after membrane rupture. We find that for sufficiently large adhesive strength, the state drawn in figure 1b is metastable, which corresponds to the transient fusion mode that can be followed by membrane resealing (kiss and run).

2. Equilibrium solution for the docking stage of the synaptic vesicle

To develop a model for the adhesive contact between a vesicle and a membrane, we adopt a continuum description of each membrane. This description assumes that the elastic energy density owing to deformation of the membrane is dominated by bending. The adhesive energy drives the vesicle and membrane together, while energy stored in their deformation provides resistance, and balance between the two results in equilibrium. Determining the equilibrium requires us to handle nonlinearities owing to large displacements and unknown region of contact.

2.1. Constitutive model of the lipid membrane

The constitutive behaviour of the lipid membrane has been studied by many investigators, for example starting with the work of Helfrich [54], Jenkins [45] and Steigmann [47], it has been shown that the elastic energy density of the lipid membrane can only depend on three geometric parameters:

2.1

where J is the ratio of the area of a surface element in the current configuration to that of the corresponding element in the reference configuration. H and K are the mean and Gaussian curvatures of the surface, respectively. It is well known that the lipid membrane surface is almost incompressible, which means J ≈ 1 Therefore, the elastic energy density only depends on H and K. To simplify the analysis, we adopt the often-used simple form of the elastic energy density (per unit surface area) for the membrane as follows:

2.2

where c ≈ 10–20 k_BT is the bending stiffness [48,51,55]. This equation implies that membrane bending substantially dominates over the membrane extension in storing energy. This assumption is reasonable, since in-plane bilayer elasticity, Y, is approximately 0.2 N m⁻¹, which implies that bending compliance dominates at length scales 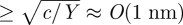. Thus, at the scale of several nanometres, lipid membranes can be considered almost inextensible, and therefore the energy density W would depend only on the membrane curvature. The bending stiffness incorporates both the intrinsic resistance of the membrane to bending and the additional stiffening owing to repulsion between charges embedded in the membrane.

2.2. Governing equations

Jenkins [46] derived the governing equations for membrane deformation of red blood cells subjected to osmotic pressure. We assume that vesicle deformation is dominated by adhesive forces so that the osmotic pressure across the non-contacting vesicle membrane can be neglected. (See Lipowsky & Seifert [52] for analyses that include the effect of pressure difference across the membrane.) The focus here is to study the deformation of the non-contact portion of the vesicle membrane. To do this, we use a flat circular membrane with radius 2L as the reference configuration for the non-contacting vesicle membrane (figure 2a). Incompressibility implies that the area of the non-contacting membrane cannot be larger than the surface area of the original vesicle, i.e. 4πR². In other words, we must have L ≤ R.

Figure 2.

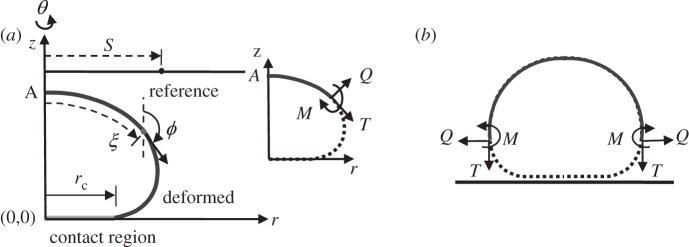
(a) Coordinate system and geometric variables used for analysis. We begin with a flat, stress-free sheet of membrane and solve for the deformed shape when its outer edge is forced to a radius of r_c. S and ξ are the arc-length of the cross-sectional curve of the reference and deformed configuration, respectively. (Note that ξ is a function of S, ξ = ξ (S).) In the deformed configuration, two distributed forces and a moment act on the membrane, as shown in the inset. (b) The free body diagram of the upper portion (π/2 ≤ ϕ ≤ π ) of the vesicle membrane. The membrane tension T is along the vertical direction and must be zero as dictated by force balance.

The derivation of the governing equations is quite involved but follows the same line of reasoning as Jenkins's [46]. Details of the derivation are given in the electronic supplementary material. Here, we state the relevant results. We use a cylindrical coordinate system (r, θ, z) to represent a continuum point in the deformed membrane, where θ is the (azimuthal) angle of revolution about the z-axis (figure 2a). We consider axisymmetric deformation, so it is sufficient to show the deformed cross section at θ = 0. Let S be the corresponding arc length in the undeformed reference configuration. The deformed membrane can be described by two coordinates, (ξ, θ), where ξ  is the arc length of the cross-sectional curve. Because of axisymmetry, ξ  is a function of S only. We also denote the angle made by the tangent of the deformed cross-section curve with the z-direction by ϕ (figure 2a).

If one makes an imaginary azimuthal cut on the deformed membrane, the relevant generalized forces (force or moment per unit length along the azimuthal direction) acting on the membrane are the transverse shear force Q, the bending moment M and the in-plane membrane force T. These generalized forces and their sign conventions are shown in the inset of figure 2a. It should be noted that the force or moment we refer to here is actually force or moment per unit length. The reason is that our problem is axisymmetric and we only focus on one cross section. We introduce the following normalized variables,

2.3a

and

2.3b

where h is the normalized mean curvature, m the normalized moment, t the normalized membrane tension and q the normalized transverse shear force. These normalized generalized forces are related to each other by (see the electronic supplementary material):

2.4a

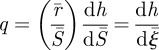2.4b

2.4c

Note that 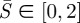. Equation (2.4a) is the relationship between moment supported at any point and the local curvature; (2.4b) shows that transverse shear balances the gradient in moment; (2.4c) relates the membrane tension to the geometrical parameters and it contains an unknown constant 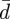which is part of the solution. In particular, equation (2.4c) states that the membrane tension is not constant unless the membrane curvature h vanishes.

It is commonly believed that the formulations of Jenkins [46], Steigmann [47] and Helfrich [48,54] are equivalent despite the fact that the former two enforce local incompressibility, whereas the latter does so in an average sense. Indeed, Steigmann et al. [56] proved that enforcing the global and local incompressibility are equivalent in that they yield the same equilibrium equations, unless the bending energy (see equation (2.2)) explicitly depends on the membrane coordinates for heterogeneous membranes [57–59]. However, it is usually not clear in the global formulation how the membrane tension is related to the constant Lagrange multiplier. A natural interpretation is that the membrane tension is equal to the constant Lagrange multiplier used to enforce area incompressibility and thus is also constant. This would predict a tensionless membrane in the fusion problem shown in figure 1a. Consider the free body diagram in figure 2b. Force equilibrium in the vertical direction of the upper portion of the membrane dictates that T = 0. Therefore, if the membrane tension is uniform, then one is forced to accept that the membrane tension T is zero everywhere. On the other hand, we discovered that, by enforcing the incompressible condition locally to ensure that the area of any material element is unchanged, the tension in the membrane is not zero and varies with location.

In the following, we use 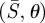as the dimensionless independent variables to describe the deformed membrane surface. Our strategy is to start with a value of L ≤ R, and to determine the forces required to bend the reference configuration comprising a flat disc into the non-contacting region. Since we do not initially know the contact radius r_c (figure 2), L is also unknown.

The normalized equilibrium equations are (see the electronic supplementary material):

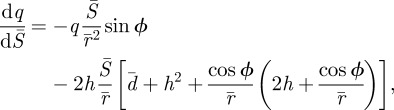2.5a

2.5b

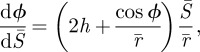2.5c

2.5d

2.5e

where 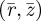are the normalized coordinates of the non-contacting vesicle membrane. These are five coupled differential equations for unknowns 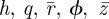. Note that 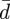is an unknown constant that is related to the membrane tension (see equation (2.4c)), which will be determined by an extra condition described below.

2.3. Boundary conditions for adhesive contact of the vesicle membrane

To derive the boundary conditions for the non-contact portion of the vesicle, we replace the cell membrane on which the vesicle adheres by a flat surface. This is motivated by the fact that the size of the vesicle is much smaller than the cell; we neglect deformations of the cell membrane. In the following, we denote the cross-sectional curve of the non-contacting vesicle membrane by Γ. Symmetry dictates that the shear force vanishes at A (figure 2a) where S = 0, i.e.,

2.6a

The slope is zero at both ends of the cross-sectional curve Γ, i.e.,

2.6b

Also, at these ends, we have

2.6c

Equations (2.6a–c) provide five boundary conditions for the five differential equations (2.5a–e). However, equation (2.5a) involves the unknown constant 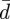(and this determines the membrane tension), which suggests that an extra boundary condition is needed to determine this constant. The physical basis for this extra condition is discussed below. (See also Seifert & Lipowsky [52].)

When the vesicle is adhering to the cell membrane, the elastic energy of the deformed non-contacting vesicle membrane tends to detach the adhering membranes, driving the contact edge inward. However, this tendency is resisted by the adhesive interactions between the vesicle and the cell membrane. We represent the adhesive protein interactions by the work of adhesion, W_ad, which is the work required to separate a unit area of surface in contact. In equilibrium, the tendency of the elastic energy to shrink the contact region is balanced by the work of adhesion. Specifically, the elastic bending energy that would be released if the contact area were shrunk by a unit amount, called the energy release rate G, must balance the work of adhesion, W_ad, i.e.,

2.7

Derivation of the first equality in equation (2.7), i.e. the relation between energy release rate and local curvature at the contact edge, is given in the electronic supplementary material. The normalized form of (2.7) is:

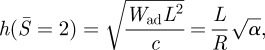2.8

where α = W_adR²/c is a dimensionless work of adhesion.

The governing equations and boundary conditions for the non-contacting vesicle membrane are normalized by the unknown length-scale L. The determination of L requires another condition, which is based on the global surface area conservation of the vesicle. Denote the radius of the contact region by r_c, which, by definition, is:

2.9

The area of the contacting membrane is therefore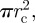 while the area of the non-contacting membrane is 4πL². The sum of these two areas must equal the original surface area of the vesicle, which is 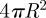. This condition implies:

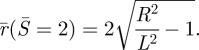2.10

Equation (2.10) is the extra condition used to determine L.

2.4. Numerical solutions

For a given value of L, the boundary value problem for the non-contacting vesicle membrane (governing equations (2.5a–e) with boundary conditions (2.6), (2.8) and (2.10)) is solved using the boundary value problem solver in Matlab. Note that there is a singularity at 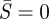(e.g. first term on the right-hand side of (2.5a)). To circumvent this numerical problem, we performed an asymptotic analysis near (see the electronic supplementary material) and solved the boundary value problem in the interval of 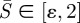with ε ≪ 1 instead of 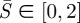. The first-order asymptotic solution provides boundary conditions at .

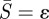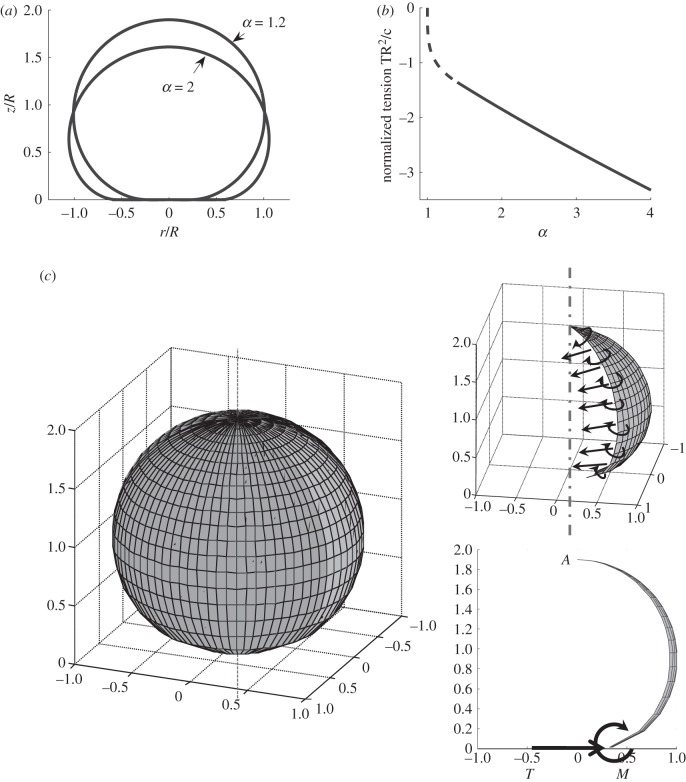
Like Seifert & Lipowsky [52], we find that a minimum value of normalized adhesion energy α = R²W_ad/c is required to obtain any finite contact, i.e. a solution of the non-contacting vesicle membrane exists for α > 1, while no solution can be found for α < 1. That is, for α > 1, the adhesive forces drive the membrane into a region of flat contact, whereas for α < 1, the adhesive forces are insufficient to flatten the vesicle. The critical value α = 1 corresponds to a sphere (point contact). The tension at the contact edge is therefore meaningful only for α > 1, and can then be determined using our numerical result and equation (2.4c). Figure 3b shows that the tension at the contact edge 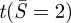is negative, meaning that the force acting on the edge of the circular disc of the contacting region is compressive. As a result, the contact region is under uniform biaxial compression. The presence of this edge compressive force is consistent with the expectation that the moment at the contact edge must be clockwise (figure 3c), that is, elastic deformation of the membrane will generate a peeling moment which is resisted by the fusion molecular machinery. Figure 3c shows a free body diagram of a meridional slice of the vesicle. In the isometric view, we show that the meriodonal slice carries moments and in-plane tension, but no shear owing to symmetry. In the view along the latitudinal direction, we show the moment and in-plane force on the contact edge. This moment is oriented along the latitudinal direction. It can be shown that the forces and moments on the meridional edge leave no net component of moment about the latitudinal direction. In other words, to maintain equilibrium, this peeling moment, M, must be balanced by the moment generated by the membrane force at the contact edge. Figure 3c shows that this moment balance is only possible if the in-plane force at the contact edge is compressive. (Recall that the force on the contact patch is equal and opposite to the force on the outer part of the membrane at the contact edge, as drawn.)

Figure 3.

(a) Cross-section shape, r versus z, for α = 1.2, 2. (b) Normalized membrane tension TR²/c at the contact edge (i.e. 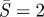) as a function of the normalized work of adhesion α. (c) Forces and moments acting on a portion of the non-contacting membrane. Moment balance about the apex point A shows that the in-plane force T at the contact edge should be compressive.

The conclusion that the contact region is under compression suggests that the principal role of adhesive forces is to bring the vesicle and membrane surfaces into close contact. The in-plane membrane compression itself does not encourage pore opening but the fact of bringing the two membranes together may provide an opportunity for nucleation of a pore, whose subsequent fate we will consider in the next section. In §4, we will return to the question of whether in-plane compression is sufficient to cause buckling of the contact region.

3. Equilibrium solution for the ‘kiss-and-run’ mode

The ‘kiss-and-run’ fusion mode requires that under some conditions, a partially fused configuration be at least mechanically metastable. Our hypothesis is that for some values of adhesion energy, the partially fused configuration (figure 1b) can indeed be metastable, thus avoiding complete collapse of the vesicle. In other words, we are interested in whether there exists an equilibrium solution for the partially fused configuration.

Consider the equilibrium solution of the docking state. Assume an infinitesimally small fusion pore is formed in the centre of the contact region (figure 4). At the edge of the fusion pore, the vesicle membrane joins the cell membrane and forms an edge, resulting in a very large curvature. The large curvature at the edge of the fusion pore results in a large bending moment, which can break the adhesive contact and separate the vesicle and cell membrane until an equilibrium configuration is reached. In equilibrium, the sharp edge relaxes to a smooth inner loop, which joins smoothly to the remaining portion of the membrane that is in contact (figure 4a). If the inner loop is so large that no equilibrium is reached before it joins with the outer loop, then we get full collapse. If equilibrium is reached before the inner loop joins the outer loop, we have a metastable equilibrium state (figure 4b).

Figure 4.

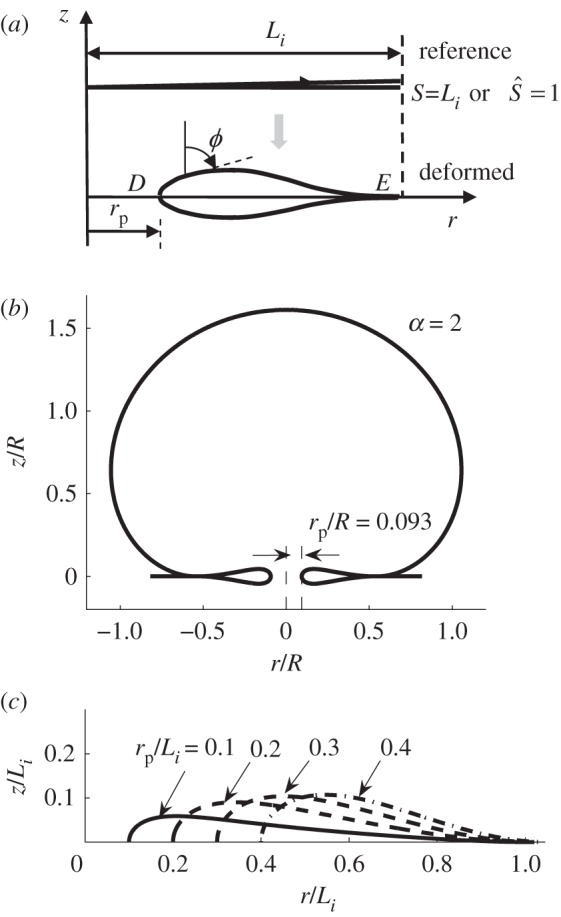
If a pore is opened by fusion of two membranes, a region with sharp curvature results. This sharp edge deforms into a smooth inner loop to avoid infinite elastic energy density. (a) Reference and deformed configuration of the inner loop. The variable S represents arc length of the cross section in the reference configuration; L_i is the total length in the reference configuration, and ϕ is the angle of the tangent in the deformed configuration with respect to the vertical axis. (b) If adhesion is sufficiently large, the size of the inner loop is smaller than the size of the outer contact region, resulting in the metastable state illustrated above. (c) Shapes of the inner loop with normalized pore radius  r_p/L_i = 0.1, 0.2, 0.3 and 0.4.

We denote the area of the inner loop by 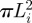. Note that L_i is an unknown quantity. Recall that previously we have modelled the cell membrane (substrate) as a rigid flat surface. When solving for the deformation of the inner loop, we relax this condition and assume that the vesicle membrane and the cell membrane are made from the same material and therefore have the same mechanical property. As a result, the equilibrium shape of the inner loop is symmetric about the r-axis (figure 4a). Furthermore, we assume the radius of the pore surrounded by the inner loop to be r_p. Note that r_p is also not known. Also, the actual opening is smaller than the value of r_p because of the finite thickness of the membrane. Specifically, r_g = r_p − t_m/2, where r_g is the gap and t_m is the membrane thickness (approx. 5 nm). An important consequence is that, since r_g > 0, r_p/R > t_m/2R; for a synaptic vesicle with R ≈ 25 nm, this implies a minimum value of r_p/R ≈ 0.1.

3.1. Equilibrium shape of the inner loop

To solve for the equilibrium configuration of the inner loop, we take advantage of the symmetry and only consider half of the inner loop (figure 4a). We normalize all the lengths by L_i and all forces by 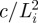, i.e.,

3.1

and

3.2

Similar to the non-contacting membrane problem in §2, we use a flat disc of radius L_i as the reference configuration. Therefore, the normalized cross-sectional arc length in the reference configuration, 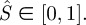We will use (S,θ) to describe the deformed surface, where θ is the azimuthal angle about z-axis.

Except for the normalization, the governing equations for the inner loop are the same as those for the outer loop (equations (2.5a–e)); however, the boundary conditions are significantly different. At point D (figure 4a), owing to the symmetry about r-axis, we should have:

3.3

3.4

3.5

At point E, we have:

3.6

and

3.7

Also, the fusion pore radius is assumed to be r_p, which implies:

3.8

Equations (3.3–3.8) provide enough boundary conditions for the governing equations (equations (2.5a–e)). Therefore, we are able to solve for shape of the inner loop using equation (2.5) and equations (3.3–3.8), given the normalized pore radius r_p/L_i. Again, we use the boundary value solver in Matlab to obtain solutions for the inner loop. Representative solutions are shown in figure 4c.

3.2. Rescaling the inner loop

It should be noted that the normalized governing equations and the boundary conditions are normalized by the unknown length L_i which is the radial extent of the inner loop. L_i is determined by the condition that at the point E, the energy release rate balances the work of adhesion, (similar to that for the non-contacting membrane, see the electronic supplementary material). This condition gives:

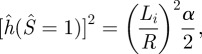3.9

where α is the normalized work of adhesion. The factor of two in equation (3.9) comes from the fact that the cell membrane contributes the same amount of energy release rate as the vesicle membrane. We use equation (3.9) to determine the length L_i after solving the governing equations subjected to the boundary conditions equations (3.3–3.8), i.e.,

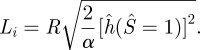3.10

Until now, we are able to solve the inner loop for any given pore radius r_p. Our numerical results show that the normalized radius of the deformed inner loop, i.e. 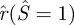, is larger than 1 for any non-zero pore radius r_p. This implies that the outer edge of the inner loop moves radially outward as the fusion pore is formed. As a result, the area of the non-contacting membrane (4πL²) will change during the formation of the fusion pore. However, the total area of the vesicle must be conserved owing to the area incompressibility of the vesicle membrane, i.e.,

3.11

The first term on the left-hand side is the area of the inner loop, the second term is the area of the non-contacting membrane, and the last two terms give the area of the flat adhering portion of the vesicle membrane. Equation (3.11) can be simplified to:

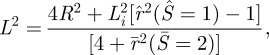3.12

which can be used to determine the non-contacting membrane area after the fusion pore is formed. With the inner loop and the non-contact portion of the membrane rescaled, we link them with a flat adhering portion along the r-axis (figure 4b). Therefore, we are able to obtain equilibrium solutions of the ‘kiss-and-run’ mode for a given normalized pore radius r_p/R and normalized adhesion energy α. For example, figure 4b shows an example of the solutions when α = 2 and r_p/R = 0.093.

To be able to assemble the inner loop and the non-contact portion of the membrane, the radial extent of the inner loop 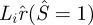, must be smaller than the radial extent of the contact region 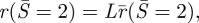that is:

3.13

Numerically, we found that, for a given r_p/R, equation (3.13) cannot be satisfied if the normalized adhesion energy α is too small, which means that no solution exists for the ‘kiss-and-run’ mode. As an example, in figure 5, we fix r_p/R = 0.1, which is the minimum pore radius needed for the ‘kiss-and-run’ mode, and plot the inner loop radius: 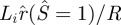and the contact radius of the outer loop: 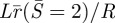or r_c/R versus α. Figure 5 shows when α > ∼2, the contact radius is larger than the radius of the inner loop at point E, i.e. the ‘kiss-and-run’ mode is metastable.

Figure 5.

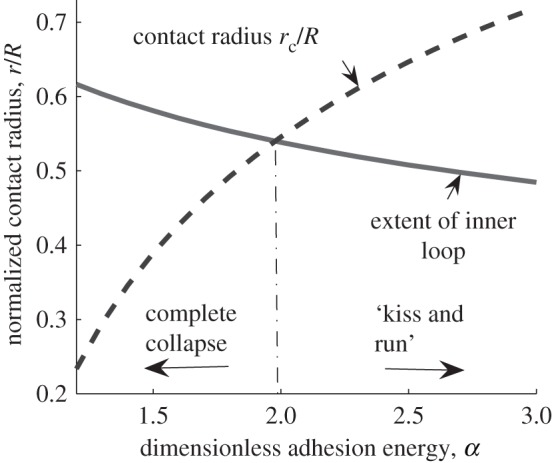
Normalized inner loop radial extent: 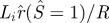(solid line) and the contact radius of the outer loop: 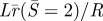(or r_c/R dashed line) versus normalized adhesion energy α. The pore radius r_p is fixed at 0.1R. The two curves intersect at a point close to α = 2.

For a given value of α, there is a maximum allowed value of pore radius r_p for which the configuration shown in figure 4b is metastable. If the pore radius exceeds this value, the outer radius of the inner region exceeds the contact radius, i.e. there is no stable solution and pore opening results immediately in full collapse. The maximum value of pore radius r_p as a function of normalized adhesion energy α is shown in figure 6a. We also plot contours of the potential energy in the region below the maximum pore radius (figure 6a). The normalized potential energy can be calculated from our numerical results using:

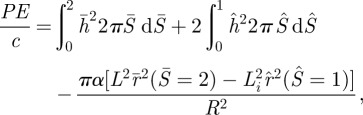3.14

where the first term and second term are the elastic energies of the non-contacting membrane and the inner loop (vesicle + cell membrane), respectively. The third term represents adhesion energy of the contacting portion.

Figure 6.

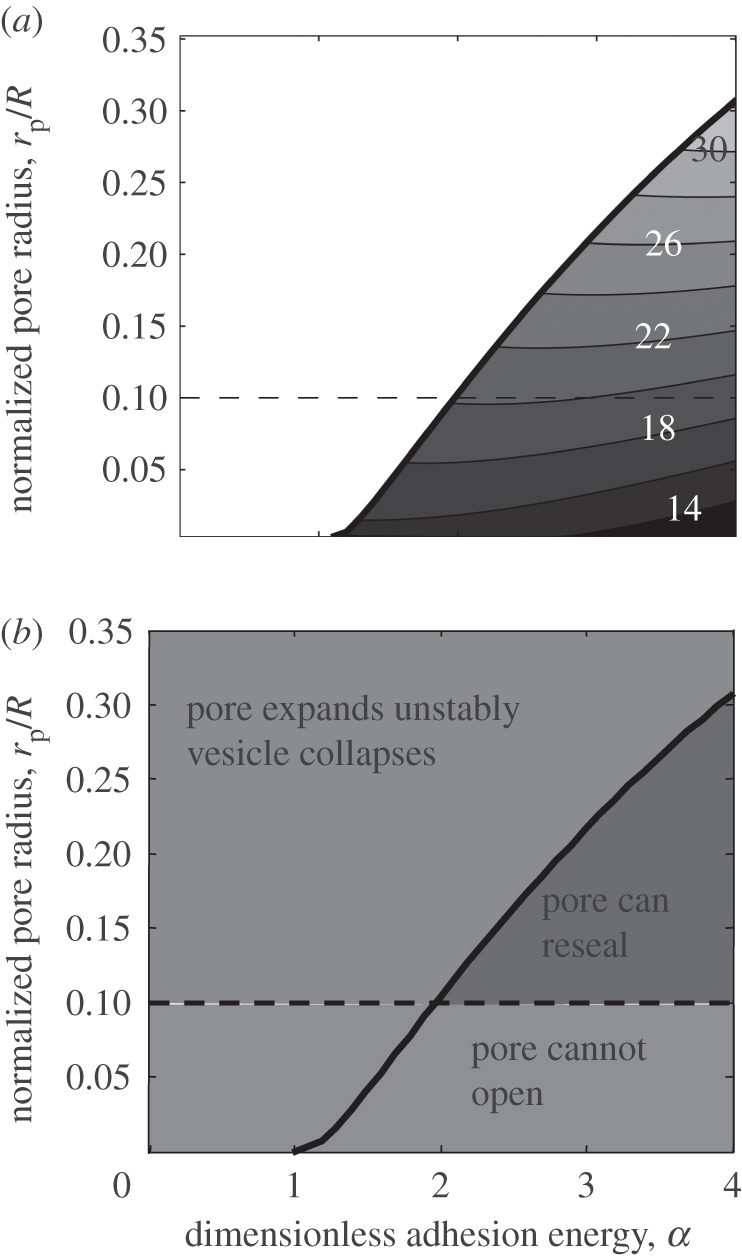
Solution map of the ‘kiss-and-run’ mode. (a) The solid line is the boundary above which no equilibrium solution can be obtained. Under the solid line, equilibrium solutions exist for a given normalized pore radius r_p/R and normalized adhesion energy α. Contour of normalized potential energy (PE/c) in the region below the maximum pore radius is shown. (b) Our solution (solid line) divides the entire area into two regions: (i) below the line, where the solution exists, and thus the pore can transiently open and then either reseal or expand; and (ii) above the line, where the solution does not exist, and thus the fusion can only occur in the full collapse mode. Also, owing to the membrane thickness, the size of pore cannot be below a certain value (the dotted line indicates this value for a typical size of a synaptic vesicle).

We note that small pore radius suffers from several limitations: first, factors such as thermal fluctuation may destabilize the fusion pore if the pore radius is too small; this is not taken into consideration in our calculations, which is based on a continuum description of the vesicle membrane; second, efficiency of the neurotransmitter release can be substantially reduced if the pore radius is too small. Therefore, the adhesion energy must be large enough to maintain the fusion pore above a certain size.

Thus, our model shows that a metastable solution potentially corresponding to the transiently opened pore, i.e. the kiss-and-run mode, exists only for certain values of the pore size and adhesion strengths (figure 6b). The larger the adhesion the greater the likelihood that an opened pore will fall within this region. Figure 6b identifies three distinct regions in the plot of adhesion and pore size. First, when the top and bottom leaflets coalesce into one, because of the finite thickness of the membrane, there is a minimum value for the pore radius. This lower limit for the pore radius must be about half the thickness of the bilayer, which is approximately 2.5 nm. For a synaptic vesicle of 50 nm in diameter, this would correspond to r_p/R = 0.1. This is shown as a horizontal line in figure 6b. The region above this line is subdivided by the solution of our equations into the area where a transiently opened pore is metastable (stronger adhesion) and the area where it does not exist and the fusion can only proceed in a full collapse mode (weaker adhesion). Thus, our model predicts that the values of molecular adhesion producing predominantly the kiss-and-run mode will be larger than those producing the full collapse mode. Furthermore, as the adhesion increases, the likelihood of the pore to reseal would increase and the clamping mechanism may take place, where any randomly opened pore would immediately reseal without releasing neurotransmitters.

4. Discussion

In this study, we have considered how the strength of adhesion between a vesicle and a plasma membrane would affect bending of the vesicle and the tension at the vesicle–membrane contact region. We have obtained a non-trivial result that strong adhesion would produce modifications in the vesicle membrane curvature resulting in compressive forces within the vesicle–membrane contact region, and this, in turn, may favour a metastable state with a transiently opened pore, that is, a ‘kiss-and-run’ fusion mode. As such, this is the first study, to our knowledge, that develops a mechanical model for the ‘kiss-and-run’ fusion mechanism.

The effects of local modifications in membrane curvature on the fusion process have been extensively studied (see Zimmerberg & Kozlov [60] for a review). In particular, it was demonstrated that Ca²⁺ binding to the Ca²⁺ fusion sensor synaptotagmin induces high positive curvature in target membranes [61], which could trigger membrane rupture and pore opening. However, the question of possible deformations of the vesicle owing to the formation of the vesicle–membrane contact region has not been explored. We show here that even very subtle deformations may produce compressions in the contact region which may affect the character of the fusion.

Our study explored the relationship between the dimensionless adhesion, α, and tensions in the vesicle–membrane contact region. In agreement with a previous study [52], we find if adhesion energy is less than a critical value, (α < 1), the SNARE complex will dock the vesicle onto the membrane with negligible change of shape. If adhesion exceeds this critical value (α > 1), we predict the formation of a distinct contact region with compressive in-plane forces in the membrane; the stronger the adhesion the stronger the compression. It is a non-trivial result that the nature of the in-plane force in the contact region is compressive, and thus it will not by itself favour pore opening or expansion. This result agrees with an experimental study [62], which used spectroscopy methods to demonstrate that tension decreases during fusion and eventually may become negative (compressive).

Furthermore, we predict that there exists a second critical value, such that if adhesion energy exceeds it, a partially fused state will be pinned and stabilized. We have obtained a family of equilibrium solutions for fixed r_p/R (figure 6), which predicts the character of the fusion process upon opening a pore. For a typical size of a synaptic vesicle (figure 6b, dotted line), if α < ∼2, an opened pore will be unstable, since there is no stable solution available to trap a partially opened pore. Thus, the kiss-and-run mode will not be possible. Let us consider now a stronger adhesion (α > ∼2). For any fixed α, we have a family of solutions for different values of r_p/R. If r_p/R is sufficiently large (top left region), the pore is unstable and the fusion proceeds in a full collapse mode. However, if r_p/R lies in the top right region, we find that the total potential energy decreases as r_p decreases. That is, the pore will tend to fluctuate in a biased way towards reducing its size. However, it may be prevented from immediately resealing by short-range hydration repulsion (not included in our model). Thus, if a pore opens for α > ∼2, we expect that it will fluctuate and eventually reseal, and may in the interim release the vesicle's contents. Larger pores may also reach the unstable boundary during these fluctuations thus being transferred to the region of collapse. The larger the value of α, the higher the probability that the pore will reseal instead of reaching the unstable boundary. Thus, increasing molecular adhesion would favour the kiss-and-run release mode.

Thus, our model suggests that the balance between kiss-and-run and full collapse fusion can be regulated by adhesion strength. This finding has important implications for understanding the fusion process. It is generally believed that stronger adhesion forces would monotonically favour fusion, and thus the fusion clamp mechanism corresponds to reducing adhesion, for example, by means of partial SNARE unzipping. Thus, models have been developed that explain the clamping of fusion by complexin via its interfering with full zippering of the SNARE complex [63]. Our results demonstrate that, in fact, fusion can be clamped by increasing the adhesion, since for sufficiently large adhesion the compressive force can prevent the pore expansion.

Our model predicts that the adhesion forces driving the full collapse fusion most efficiently will correspond to the values of α somewhere in the range between 1 and 2. It is thus of interest to estimate α for a typical synaptic vesicle. This estimate can be made based on the expression α = W_adR²/c, where the work of adhesion W_ad is the adhesive energy per unit area of the adhesive region, c is the membrane bending stiffness, and R is the vesicle size. The latter estimates are the easiest to obtain, with bending stiffness being in the range 10–20 k_BT [48,51,52], and synaptic vesicle radius being in the range 15–25 nm [64–67]. Estimating a value for W_ad, however, is far from trivial. Several studies employed atomic force microscopy (AFM) to evaluate the forces exerted by SNARE proteins on the membrane–vesicle complex [68–73]. The estimate for the SNARE zippering energy obtained by AFM is 35 k_BT [72] or possibly larger, given that an additional energy barrier has to be overcome as the distance between lipid bilayers decreases [73]. This energy serves to overcome a substantial repulsion energy of membrane bilayers which was estimated to be of the order of 40 k_BT [74,75]. Thus, although the adhesive and repulsive energies themselves are quite large, the regulation of fusion itself is expressed by the parameters W_ad and α and occurs over a delicately balanced small range of energies (just a few times higher than the thermal noise). A reasonable estimate of this energy was provided in Abdulreda and co-workers [69–71], showing that the SNARE complex would reduce the barrier for lipid merging by 1.3 k_BT. Similarly, it is hard to obtain an accurate estimate of the membrane–vesicle contact region. Electron tomography studies [76–78] sometimes show a contact of approximately 10 nm. However, this can only be taken as an upper limit for the contact region, since the spatial resolution is not sufficient to evaluate this accurately, and merging of membrane and vesicle electron density does not necessarily mean that lipids are in real contact. A more accurate estimate was obtained employing a combination of AFM and electron microscopy [79], and it gave a linear diameter of a porosome of 4–5 nm. Thus, accepting 5 nm diameter for the adhesive region, bending stiffness of 15 k_BT, the synaptic vesicle radius of 20 nm, and W_ad of 1.3 k_BT, we obtain the estimate of α = 1.8, that is within the suggested range.

It is important to note that since α is proportional to W_adR², where R is the radius of the vesicle, our model predicts that fusion of larger vesicles is more likely to involve the transient metastable pore-opened state, given that the same work of adhesion is applied. This agrees with a demonstrated transient fusion state at neurosecretory adrenal cells [32–37] with larger vesicles (approximately 200 nm diameter), as opposed to fusion of smaller synaptic vesicles (30–50 nm diameter) which mostly involves full collapse, with kiss-and-run mode being detectable only under a very narrow range of experimental conditions. Of course, one can argue that it is harder to detect kiss-and-run events at synapses. However, analysis of shapes and sizes of quantal events at adrenal chromaffin cells demonstrated that events with a pre-spike foot, those involving a transient metastable pore opening prior to full collapse, are larger than events without a foot [80]. This observation agrees with the prediction of our model that fusion of larger vesicles is more likely to involve a metastable transient state with a partially opened pore.

It has to be noted that we do not model explicitly the individual SNARE complexes. Instead, our model uses a ‘smeared’ or distributed representation of adhesion forces applied by the SNARE complexes. The advantage of this ‘smeared’-specific energy representation of the adhesive action of SNARE is that it results in a tractable axisymmetric problem formulation and clear predictions in terms of a single dimensionless parameter. This simplification is also made by necessity; although the general formulation of our model can accommodate discrete forces, how many SNARE complexes per vesicle–membrane complex mediate fusion is still a matter of debate. Recent studies of model systems suggest that two or three SNARE complexes may be sufficient to trigger fusion [81–83], and that fusion can even be activated by a single SNARE complex [84,85]. However, it is still unclear whether this occurs in vivo. Importantly, it was demonstrated that the fusion process can be dramatically accelerated when a larger number of SNARE complexes (5–10) hold the membrane–vesicle complex together [86,87]. Thus, although fusion can be potentially triggered by only a few SNARE complexes, it is likely that action potential release in vivo is mediated by a larger number of SNARE complexes per vesicle–membrane complex, that is, in the order of 5–10.

Our model represents adhesion as forces uniformly distributed over the membrane–vesicle contact region. This is a reasonable approach if we assume that a number of SNARE complexes (5–10) are distributed over the perimeter of the contact region. However, if the fusion is mediated by only 1–3 SNARE complexes, discrete adhesion points should be introduced. In this case, we expect that the two main conclusions of our model; that forces in the contact region are compressive and that large adhesion can stabilize an opened pore, will survive qualitatively though they may change quantitatively.

Since the adhesion strength will ultimately depend on the number of zippered SNARE complexes, we can hypothesize a scenario where a vesicle would be initially docked by a small number of SNARE complexes, and at that point it can either fuse spontaneously or form extra SNARE complexes strengthening adhesion forces, possibly with a participation of Ca²⁺-unbound/partially bound synaptotagmin and complexin, and thus clamp the fusion. A subsequent action potential would then trigger ‘unclamping’ and stimulate pore opening. Our model provides quantitative support for such a scenario, suggesting that increasing adhesion energy promotes fusion clamping.

Finally, we would like to discuss whether the negative (compressive) force in the contact region predicted by our model is likely to significantly perturb the membrane curvature and thus promote the stalk formation and the fusion process. More specifically, we ask whether the compression is sufficient to buckle the contact region. According to Timoshenko & Woinowsky-Krieger [88], the critical buckling force (per unit length) for a circular plate is:

4.1

where D is the bending stiffness of the plate, a is the radius of the plate and k is a numerical factor and is 3.83 for the clamped boundary condition and 2.16 for the simply supported boundary condition. In our case, the D should be interpreted as c and a is the contact radius r_c, i.e. the normalized critical compressive force is:

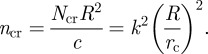4.2

As the adhesion energy increases, r_c increases and thus N_cr decreases. Since the compressive force at the contact edge increases with adhesion, buckling is more likely to occur as the adhesion increases. Using k = 3.83 (clamped condition), for α = 5, n_cr = 18.5 and 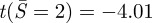; for α = 17, n_cr = 11.0 and 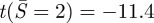. Using k = 2.16 (simply supported condition), for α = 5, n_cr = 5.9 and 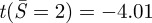; for α = 7, n_cr = 4.9 and 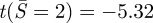. That is, even for the weaker simply supported condition, the critical value of adhesion required to buckle the contact region is greater than 5. This quantity is significantly larger than the value required for a transition from full collapse to a ‘kiss-and-run’ mode (approximately two for synaptic vesicles, as discussed above). Our model would therefore predict that in-plane compression in the contact region is insufficient to cause buckling for the smaller vesicles that undergo full collapse, but may play this role for larger neurosecretory vesicles.