Probabilistic Projections of the Total Fertility Rate for All Countries

Abstract

We describe a Bayesian projection model to produce country-specific projections of the total fertility rate (TFR) for all countries. The model decomposes the evolution of TFR into three phases: pre-transition high fertility, the fertility transition, and post-transition low fertility. The model for the fertility decline builds on the United Nations Population Division’s current deterministic projection methodology, which assumes that fertility will eventually fall below replacement level. It models the decline in TFR as the sum of two logistic functions that depend on the current TFR level, and a random term. A Bayesian hierarchical model is used to project future TFR based on both the country’s TFR history and the pattern of all countries. It is estimated from United Nations estimates of past TFR in all countries using a Markov chain Monte Carlo algorithm. The post-transition low fertility phase is modeled using an autoregressive model, in which long-term TFR projections converge toward and oscillate around replacement level. The method is evaluated using out-of-sample projections for the period since 1980 and the period since 1995, and is found to be well calibrated.

Introduction

Based on projections of fertility, mortality and migration, population forecasts predict the future size and composition of populations. These forecasts are used for many purposes, including predicting the demand for food, water, education, and medical services, as well as the future impact on labor markets, pension systems, and the environment. It is important for decision makers not only to have a point forecast that indicates the most likely scenario for a future population but also to know the uncertainty around the forecast—that is, the possible future values of an outcome and how likely each set of possible future values is.

Fertility is a key driver of the size and composition of the population. Fertility decline has been a primary determinant of population aging, and projected levels of fertility have important implications for the age structure of future populations, including the pace of population aging. The total fertility rate (TFR) is one of the key components in population projections; it is the average number of children a woman would bear if she survived through the end of the reproductive age span, experiencing at each age the age-specific fertility rates of that period.

In this article, we propose a new methodology for probabilistic projections of the TFR that could be applied to all countries of the world. The goal is to produce probabilistic projections that would ultimately be part of the population projections produced by the United Nations (UN) Population Division. Earlier versions of this methodology were described by Alkema (2008), Alkema et al. (2008a, 2009), and Raftery et al. (2009).

Until now, most operational population projections have been deterministic, produced using the standard cohort-component population projection model. Future fertility rates have typically been assigned in a deterministic way. The main organizations that have produced population projections for all or most of the world’s countries are the United Nations, the World Bank (Bos et al. 1994) and the U.S. Census Bureau (2009), all of which use the standard deterministic approach.

The UN Population Division produces projections of the TFR for 196 countries that are at various stages of the fertility transition. The TFR projections are revised every two years and published in the World Population Prospects (United Nations, Department of Economic and Social Affairs, Population Division 2009). The UN produces deterministic TFR projections. It then decomposes these projections into projected age-specific fertility rates using fertility schedules, and finally combines the age-specific projections with projections of mortality and international migration using the cohort-component projection method, to yield the medium variant of the official UN population projections. The effect of lower or higher fertility is illustrated with the low and high variants of the projections. In the high variant, half a child is added to the TFR projections in order to examine the influence of higher fertility on the population projections. Similarly, for the low variant, half a child is subtracted from the TFR projections. The high and low variants highlight the sensitivity of demographic outcomes to different assumptions about future TFR, but they do not assess the uncertainty about future fertility levels (Bongaarts and Bulatao 2000), nor do they assess the extent to which the low or high fertility variants are more likely.

Probabilistic projections of the TFR have been proposed, mostly for developed countries with low fertility. Lee (1993) and Lee and Tuljapurkar (1994) proposed a time series approach, based on the probabilistic mortality projection method of Lee and Carter (1992), for decomposing and projecting fertility in the United States. Lutz et al. (2001) developed methods based on expert judgment. The Uncertain Population of Europe project (Alders et al. 2007; Alho et al. 2006, 2008) developed probabilistic TFR projections for 18 European countries using the ex-post method based on the errors of previous projections (Keyfitz 1981; Stoto 1983). Hyndman and Booth (2008) developed a method using functional data models and applied it to Australia and France (Booth et al. 2009). These methods were developed mainly for low-fertility countries that have largely finished going through the fertility transition and for which fertility is fluctuating in a fairly stable, stationary way. They do not apply easily to countries that are still going through the fertility transition.

In this article, we develop a methodology to construct country-specific probabilistic TFR projections for all countries, using a Bayesian projection model. The next section describes the rationale for the Bayesian projection model and gives model details. The following section summarizes the results and the out-of-sample projection validation. The article concludes with a discussion of the methodology and results. Additional details of the model are given in Online Resource 1.

Data and Methods

Data

We base our projections on the five-year UN estimates of TFR for 196 countries during the period from 1950 to 2010 from the 2008 revision of the UN World Population Prospects (United Nations, Department of Economic and Social Affairs, Population Division 2009). The outcome in each five-year period (t, t + 5) is computed between July 1 of year t and July 1 of year t + 5, and centered on January 1 in year t + 3.

Three Phases

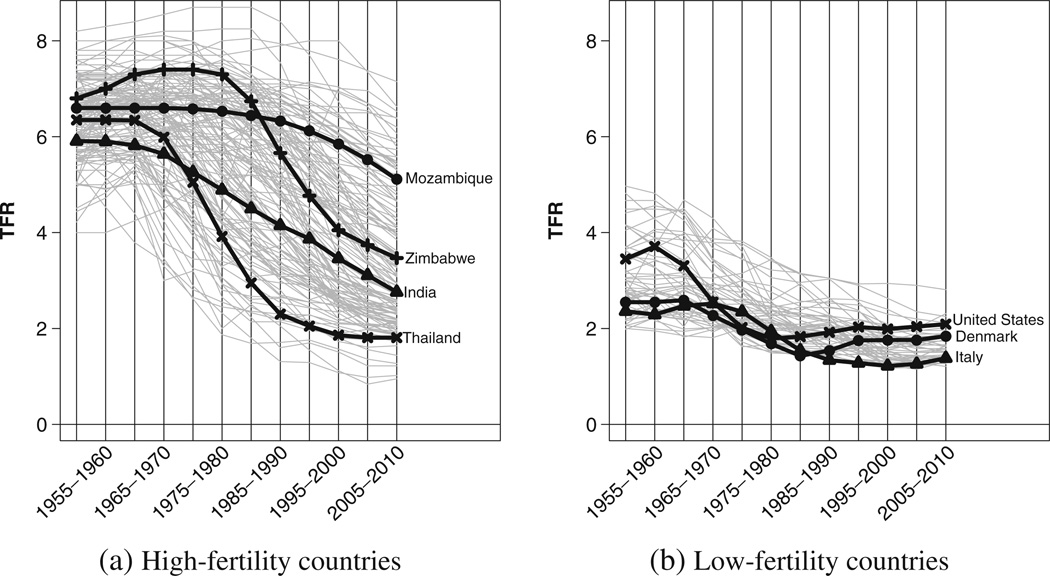
The variation between the observed trends in TFR in all countries during the observation period is illustrated in Fig. 1, with high-fertility countries (in which the maximum TFR exceeded 5 during the observation period) in the plot on the left, and the remaining medium- and low-fertility countries on the right. Some selected countries have been highlighted. In all high-fertility countries, the TFR started to decline over the past 60 years, but the countries differ with respect to the timing and start level of their fertility transition, as well as the pace of the fertility decline. The low-fertility countries are at the end of their fertility transitions or have entered a low-fertility post-transition phase.

Fig. 1.

Observed trends in TFR from 1950–1955 until 2005–2010 for (a) high-fertility countries (TFR above 5 during the observation period) and (b) low-fertility countries. Some countries, with TFR series shown in black and named, have been highlighted; the TFR series for the other countries are shown in gray

A great deal of the demographic literature over the past 60 years has been concerned with explaining trends in fertility; see the reviews by Hirschman (1994) and Mason (1997). This literature is dominated by controversy over why fertility has declined in most countries. Proposed explanations include socioeconomic and educational development, declines in child mortality, contraceptive programs, and ideational changes; see Raftery et al. (1995) for one empirical comparison of competing theories. In spite of this disagreement, the general consensus has been that, whatever the causes, the evolution of fertility includes three broad phases: a high-fertility pre-transition phase, the fertility transition itself, and a low-fertility post-transition phase.

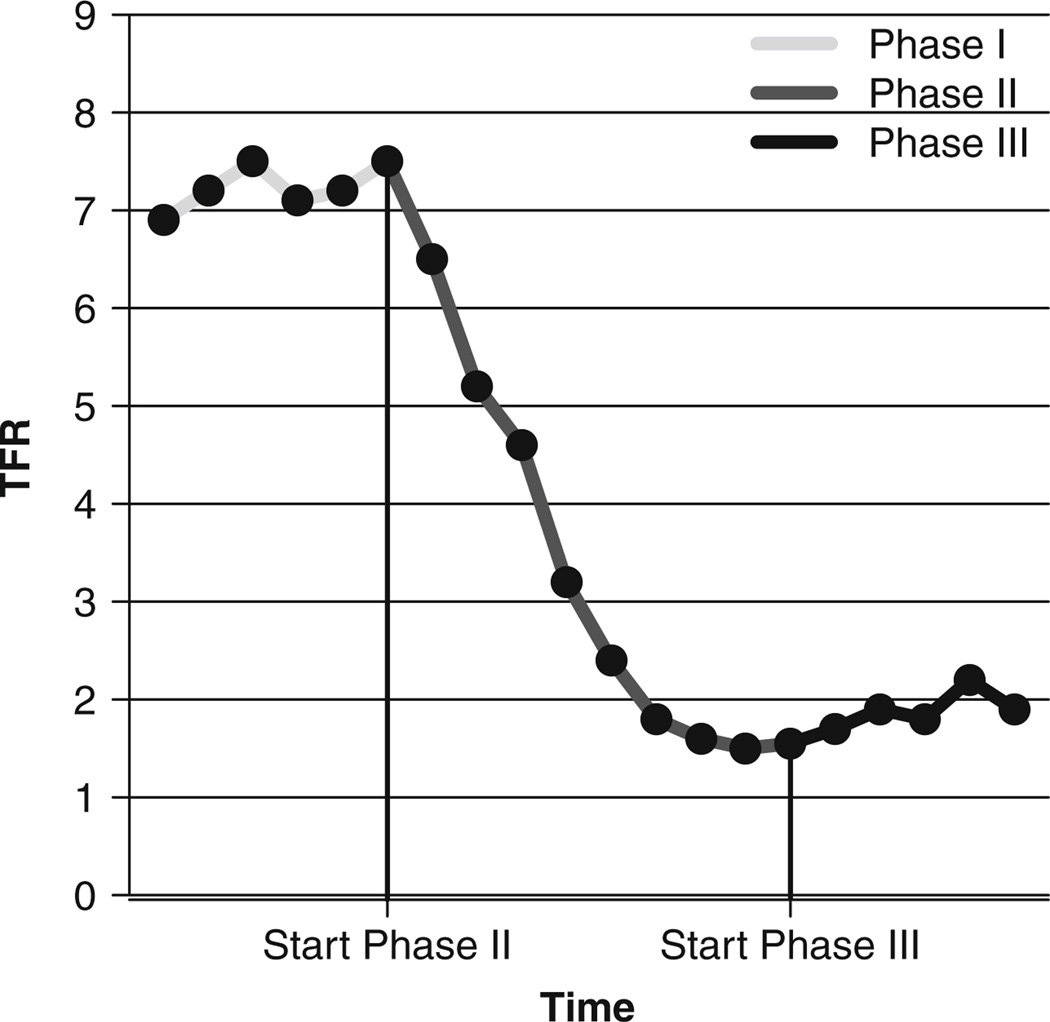
Our methodology is based on this sequence of changes. We define Phase I as the stable pre-transition high-fertility phase; the fertility transition has not started yet, and fertility fluctuates around high TFR levels (e.g., around a TFR of about 6 or 7 children). In some countries, the TFR increased before it began to decline. Phase II is the fertility transition from high fertility to replacement-level fertility or below. Phase III consists of the post-transition low fertility, which includes recovery from below-replacement fertility toward replacement fertility and oscillations around replacement-level fertility. This sequence of changes is illustrated in Fig. 2.

Fig. 2.

Illustration of the three phases of the evolution of the TFR

To construct TFR projections, we model the five-year changes in the TFR based on commonalities in past trends, as well as assumptions about the patterns underlying future TFR outcomes. Given the very different dynamics that underlie the changes in TFR in each of the three phases, a single model cannot represent these changes in the different phases. For example, the TFR might increase during Phase I at high levels, whereas the TFR is expected to decrease during Phase II. To overcome this difficulty, we capture the dynamics in each phase with a model for that phase. To classify the observation period into the different phases for each country, we developed deterministic definitions for the start and end periods of Phase II, which summarize expert opinion about the start and end of the fertility transition in a transparent manner and can be used for all countries. The observed trends in TFR in Phases II and III are used to develop a model for each phase. Phase I is not modeled because the TFR in all countries has now started to decline, so Phase I is not relevant for projections. In the next sections, we discuss the models for Phases II and III and then explain how future trajectories are constructed based on these models.

Phase II: Fertility Transition

Start and End of the Fertility Transition

Attempts have been made by others to find thresholds to identify the start of the fertility transition. Some researchers have proposed a 5%decline to detect the early stage of the fertility transition (Bongaarts 2002; Casterline 2001). We found that this threshold is too stringent for countries in which the fertility transition has started off slowly: for example, in Mozambique, the start of the fertility transition is defined to be in 1995–2000 based on this threshold, but fertility declines have been observed much before that period (see Fig. 1). We use an alternative deterministic rule to identify the onset of the fertility transition. To exclude random fluctuations during Phase I, we identify the candidate period for the start period of the fertility transition as the most recent period with a local maximum within 0.5 child of the global maximum. If this local maximum is above 5.5, the corresponding period is defined as the start period of the fertility transition, denoted by τ_c. If the local maximum is below 5.5, then higher TFR levels have most likely been observed before the start of the observation period, so we set τ_c < 1950–1955.

Similarly, we use a deterministic rule to identify the start of Phase III during the observation period for countries in which the fertility transition has ended. The countries that have entered Phase III are defined as the countries in which two subsequent five-year increases below a TFR of 2 children have been observed. By this definition, in the period 2005–2010 the start of Phase III was observed in 20 countries (Belgium, Bulgaria, Channel Islands, Czech Republic, Denmark, Estonia, Finland, France, Germany, Italy, Latvia, Luxembourg, Netherlands, Norway, Russian Federation, Singapore, Spain, Sweden, United Kingdom, and the United States). The start period of Phase III, denoted by λ_c for country c, is defined to be in the middle of the (earliest) two subsequent increments below 2. More specifically, with f_c,t the TFR in country c in period t, the start of Phase III is the earliest period t for which (1) the TFR increased from period t − 1 to period t, so that f_c,t > f_c,t−1; (2) the TFR increased again from period t to t + 1, so that f_c,t+1 > f_c,t; and (3) the TFR was below 2 in all three periods, so that f_c,p < 2 for periods p = t − 1, t, t + 1. In all, 52 post-transition outcomes (f_c,t, f_c,t+1) have been observed in Phase III.

Changes in TFR During the Fertility Transition

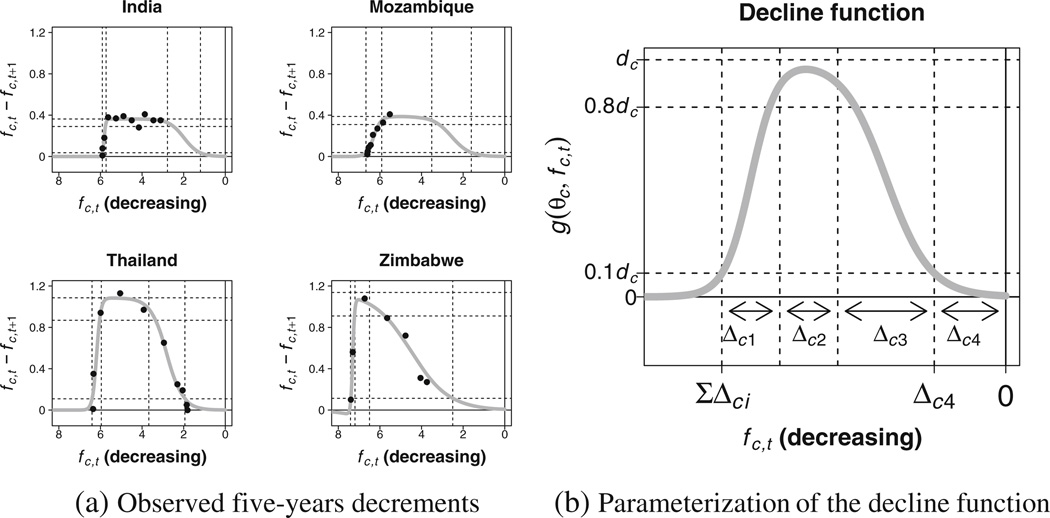
The observed decrements in TFR during the fertility transition in the four selected high-fertility countries from Fig. 1 are shown in Fig. 3a. The observed five-year decrements in TFR (decreases f_c,t − f_c,t+1) are plotted against the TFR (dots). The TFR is reversed; that is, the TFR is plotted from high to low outcomes on the horizontal axis so that when fertility is decreasing, the five-year decrements are given in chronological order when the figure is read from left to right. The plot illustrates the commonalities and differences in decrements between countries during the fertility transition. The countries differ with respect to the start level, the pace (maximum decrement), and the end level of the fertility decline. What the countries have in common is that their decrements fluctuate around a trend of accelerating rates of decline, followed by slowing rates of decline toward lower fertility, as suggested by the gray solid curve that is plotted in the same figure for each country. This phenomenon of an increasing and decreasing pace of fertility declines has been observed in many countries and is used to model the expected five-year decrements as a function of TFR, based on current UN methodology (United Nations, Department of Economic and Social Affairs, Population Division 2006).

Fig. 3.

Modeling the five-year decrements in Phase II during the fertility transition: (a) observed five-year decrements (dots) with least-squares fit of the decline function to the data points, and (b) parameterization of the decline function

Specifically, to model and project changes in TFR during the fertility transition, we decompose the five-year decrements into a systematic decline (expected decrements) with random distortion terms added to it. The outcome of the expected decrements is given by the outcome of a parametric function, which we will refer to as the decline function. This function models a trend of accelerating rates of decline, followed by slowing rates of decline toward lower fertility. The decline function, denoted by g(·, ·), is evaluated at TFR level f_c,t in period t for country c, as well as at a set of country-specific parameters θ_c = (Δ_c1, Δ_c2, Δ_c3, Δ_c4, d_c). Based on current UN methodology (United Nations, Department of Economic and Social Affairs, Population Division 2006), g(θ_c, f_c,t) is given by a double logistic function, defined as the sum of two logistic functions:

$$g({\mathbf{\theta }}_c,f_{c,t})=\frac{-d_c}{1+\text{exp }(-\frac{2\text{ ln}(9)}{{\mathrm{\Delta }}_{c1}}(f_{c,t}-{\displaystyle {\sum }_i}{\mathrm{\Delta }}_{\mathit{\text{ci}}}+0.5{\mathrm{\Delta }}_{c1}))}+\frac{d_c}{1+\text{exp }(-\frac{2\text{ ln(}9)}{{\mathrm{\Delta }}_{c3}}(f_{c,t}-{\mathrm{\Delta }}_{c4}-0.5{\mathrm{\Delta }}_{c3}))}.$$

(For additional details of the decline function, see Online Resource 1.)

The gray curves in Fig. 3a are least-squares fits of g(·, f_c,t) to the observed decrements in these countries. The fitted curves illustrate the flexibility of the double logistic function to represent various fertility declines for different outcomes of parameter vector θ_c.

The interpretation of the decline parameters is illustrated in Fig. 3b. Parameter d_c determines the maximum possible five-year decrement for country c. However, the actual maximum pace tends to be slightly smaller than d_c; it depends on the values of Δ_c1, Δ_c2, Δ_c3, and Δ_c4, which describe the TFR ranges within which the pace of the fertility decline changes. The decline starts at TFR level $U_c={\displaystyle {\sum }_{i=1}^4}{\mathrm{\Delta }}_{\mathit{\text{ci}}}$, where the decrement is between 0% and 10% of its maximum pace. Between TFR levels U_c and U_c −Δ_c1, the pace of the decline increases from around 0.1d_c to more than 0.8d_c. During the TFR range denoted by Δ_c2, the TFR declines at a higher pace than during the rest of the transition: its five-year decrements range between 0.8d_c and d_c. In Δ_c3 the pace of the fertility decline decreases further to 0.1d_c at TFR level Δ_c4. Different values of the decline parameters θ_c give rise to a broad range of fertility declines. Specifically, U_c allows for different starting levels of the decline, Δ_c4 allows for different end levels, d_c allows for a difference in the overall pace of the transition, and the ratios Δ_ci/(U_c −Δ_c4) for i = 1, 2, 3 allow for differences in the timing of acceleration and deceleration in pace.

Bayesian Hierarchical Model for Estimating the Decline Parameters

Estimating the country-specific decline parameters θ_c = (Δ_c1, Δ_c2, Δ_c3, Δ_c4, d_c) and including an uncertainty assessment of the parameter estimates for each country presents a challenge because for any one country, there are no more than 11 (and often fewer) observed five-year decrements in Phase II. We use a Bayesian hierarchical model (Gelman et al. 2004; Lindley and Smith 1972) to estimate the parameters in each country. Such a model allows us to borrow strength from the observations in all countries when we estimate the parameters for country c, and also to assess the uncertainty of the parameter estimates.

The Bayesian hierarchical model assumes that for all countries, each of their unknown decline parameters is drawn from a probability distribution that represents the range of outcomes of that decline parameter across all countries. For a specific parameter in a specific country, the probability distribution based on the world-level experience is then updated using Bayes’ theorem with the observed declines in the country, which results in the posterior distribution of the parameter of interest. The resulting estimates (draws from the posterior distribution) can be viewed as weighted averages of a “world pattern” and information from the country data.

By including only two levels of hierarchy in the Bayesian hierarchical model (country and world), the projected fertility declines for each country depend on its own past trends and the experience of all countries combined. For a country like Mozambique, its projected fertility transition is informed by its own past trends together with the experience of all other countries, including its neighboring country Zimbabwe. Additional levels of hierarchy could be added to the model on the basis of spatial proximity, for example. We did not add these additional levels of hierarchy because neighboring countries can have very different fertility declines; the start of the fertility transition in Mozambique so far has been slow, while that in the neighboring country of Zimbabwe has been fast (see Fig. 3a).

Fertility Transition Model

Based on the preceding reasoning, during the fertility transition the TFR in period t + 1 in country c is modeled as follows:

$$f_{c,t+1}=f_{c,t}-d_{c,t}+{\mathrm{\epsilon }}_{c,t},$$ (1)

where d_c,t is the expected five-year decrement and ε_c,t is a random distortion term, which models the deviation from the expected decline. This model for the TFR is called a random walk model with drift. The drift d_c,t is given by the outcome of the decline function, which is set to 0 if the TFR is below 1 based on the assumptions that the drift becomes 0 at very small TFR levels:

$$d_{c,t}=\{\begin{array}{cc}g({\mathbf{\theta }}_c,f_{c,t}),\hfill & \text{for }{f}_{c,t}>1,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$

The distributions of the random distortions in each period are given by

$${\mathrm{\epsilon }}_{c,t}~\{\begin{array}{cc}N(m_t,s_t^2),\hfill & \text{for }t={\mathrm{\tau }}_c,\hfill \\ N(0,\mathrm{\sigma }{(f_{c,t})}^2),\hfill & \text{otherwise}.\hfill \end{array}$$ (2)

Here, τ_c is the start period of the fertility transition, m_τ is the mean and s_τ is the standard deviation of the distortion in the start period, and σ(f_c,t) is the standard deviation of the distortions during the later periods. The distributions of the distortions are based on evaluation of the model fit, which showed that the distortions during the start period tend to be more positive and that the variance of the distortions in the remaining periods is highest around a TFR of 4–5, and decreases over time. Details on σ(f_c,t) are given in Online Resource 1.

The decline parameters θ_c = (Δ_c1, Δ_c2, Δ_c3, Δ_c4, d_c) are estimated with a Bayesian hierarchical model. For countries in which the fertility decline started within the observation period, the start level U_c = ∑ Δ_ci is fixed at the TFR in the start period, U_c = f_{c, τc}. Conditional on U_c, the five parameters that determine the pace of the fertility decline and the time that the transition takes in country c are Δ_c4, {Δ_ci/(U_c −Δ_c4) : i = 1, 2, 3}, and d_c. Transformations of parameters are used to restrict their outcomes to realistic values and to use common probability distributions to represent the outcomes on the world level. The maximum five-year decrement, d_c, is transformed to restrict its outcomes to between 0.25 and 2.5 child: $d_c^{*}=\text{log }\left(\frac{d_c-0.25}{2.5-d_c}\right)$. (The upper bound of 2.5 reflects the maximum pace of fertility decline observed in the past—that is, about 2 children per five-year period in China.) The world distribution of the transformed d_c’s is given by

$$d_c^{*}~N(\mathrm{\chi },{\mathrm{\psi }}^2),$$ (3)

where χ is the world mean of the $d_c^{*}’\mathrm{s}$, and ψ² is their variance. A similar approach yields world distributions of the other decline parameters. The world distribution for Δ_c4 is given by

$${\mathrm{\Delta }}_{c4}^{*}~N({\mathrm{\Delta }}_4,{\mathrm{\delta }}_4^2),$$ (4)

where ${\mathrm{\Delta }}_{c4}^{*}$ is a logit transformation of Δ_c4—namely, ${\mathrm{\Delta }}_{c4}^{*}=\text{log }\left(\frac{{\mathrm{\Delta }}_{c4}-1}{2.5-{\mathrm{\Delta }}_{c4}}\right)$—to restrict it to be between 1 and 2.5 children.

To define the world distributions of {Δ_ci/(U_c −Δ_c4) : i = 1, 2, 3}, we first define $p_{\mathit{\text{ci}}}=\frac{{\mathrm{\Delta }}_{\mathit{\text{ci}}}}{U_c-{\mathrm{\Delta }}_{c4}}$ for i = 1, 2, 3, such that ${\displaystyle {\sum }_{i=1}^3}{p}_{\mathit{\text{ci}}}=1$. For the purpose of computation, new parameters γ_ci, i = 1, 2, 3 are introduced, with the p_ci’s defined as a function of these parameters (Gelman et al. 1996): $p_{\mathit{\text{ci}}}=\frac{\text{exp}({\mathrm{\gamma }}_{\mathit{\text{ci}}})}{{\displaystyle {\sum }_j}\text{exp}({\mathrm{\gamma }}_{\mathit{\text{cj}}})}$. The hierarchical model for the γ_ci’s is given by

$${\mathrm{\gamma }}_{\mathit{\text{ci}}}~N({\mathrm{\alpha }}_i,{\mathrm{\delta }}_i^2),\text{ for }i=1,2,3,$$ (5)

where α_i is the world mean of the γ_ci’s and ${\mathrm{\delta }}_i^2$ is their variance.

Based on the Phase II model, uncertainty in future declines in Phase II arises from uncertainty in the parameters estimates of the decline functions for each country, as well as the variability of the decrements around the function.

Estimation

The parameters in the model for Phase II are estimated in a Bayesian framework. Prior distributions that are spread out are assigned to the additional model parameters (the mean and variance parameters of the distortion terms, the start level U_c for countries in which the transition started before our observation period, and the world level parameters). A Markov chain Monte Carlo (MCMC) algorithm is used to derive samples of the posterior distributions of the parameters of the fertility transition model (Gelfand and Smith 1990). For the Phase II model, the algorithm is a combination of Gibbs sampling, Metropolis–Hastings sampling, and slice sampling steps (Neal 2003). The MCMC sampling algorithm is implemented in the statistical package R. The results are based on a run of 100,000 iterations, of which the first 2,000 are discarded, yielding 98,000 samples from the posterior distributions of all model parameters. The prior distributions and additional details are given in Online Resource 1.

Estimated Decline Curves

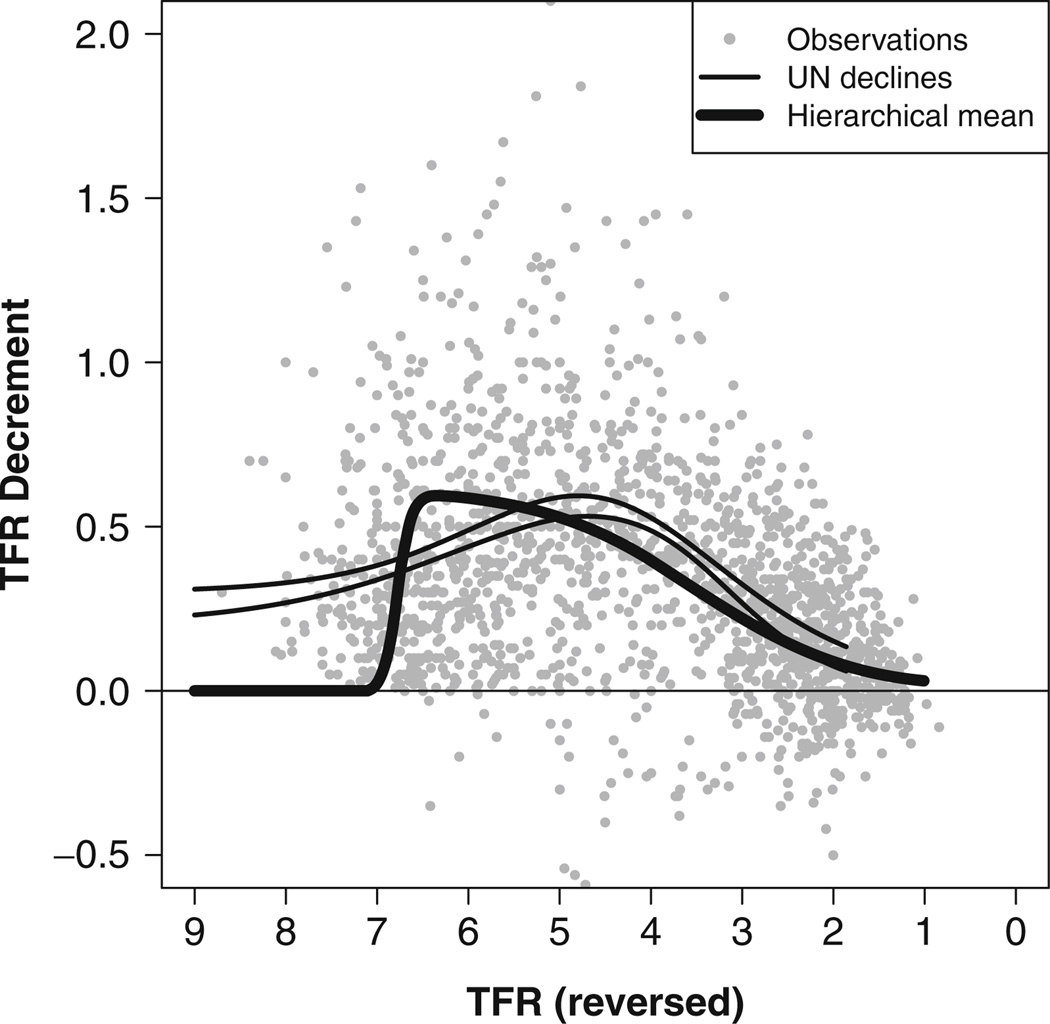
Figure 4 shows the observed five-year decrements during the fertility transition, against decreasing TFR, for all countries combined. The figure shows the world mean of the fertility transition decline curve, which is the decline curve evaluated at the posterior means of the world-level parameters.

Fig. 4.

World (hierarchical) mean of the decline curve, plotted against decreasing TFR. The five-year decrements for all countries during the fertility transition are plotted in gray. The UN fast-fast and slow-slow decline curves are shown by thin lines

For comparison, we also show the decline curves currently used by the UN. The UN uses three specific decline curves, each corresponding to one set of decline parameters. Each of these curves describes a different observed pattern of decline; they are called “slow-slow,” “fast-slow,” and “fast-fast.” For each country, the UN analyst chooses the decline curve that seems most reasonable for the future fertility decline in that country, based on what has been observed to date in that country or its region. The TFR is kept constant after it decreases to 1.85. Our method generalizes the current UN approach because we allow a wide range of parameter values for the decline curve rather than restricting it to a small number of possibilities.

The UN decline functions corresponding to the fast-fast and slow-slow declines are shown in Fig. 4. The Bayesian world decline curve differs from the UN decline curves at high TFR values, but the maximum decrements are comparable between the Bayesian and UN curves. The Bayesian world decline curve increases rapidly to its maximum outcome after the start of the decline, whereas the UN decline curves increase more slowly as TFR declines and peak at a TFR of about 5.

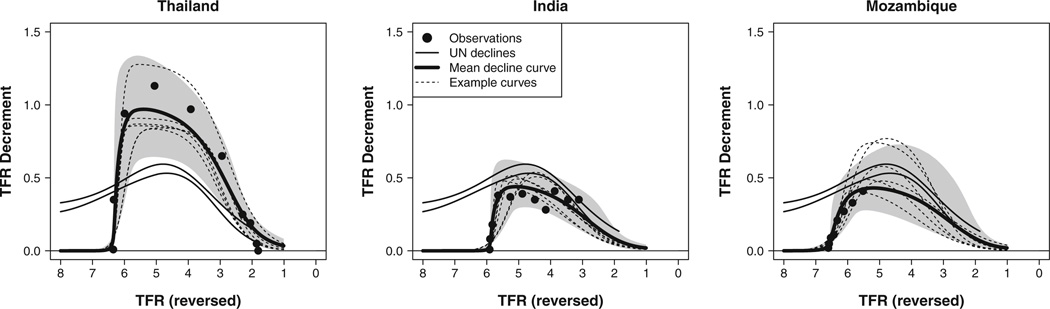
Figure 5 shows the Bayesian estimates of the decline curves for Thailand, India, and Mozambique, together with the observed decrements in those countries and the fast-fast and slow-slow UN decline curves. The shapes of the curves for Thailand and India are very different. Thailand has had a very fast fertility transition, and its mean decline curve peaked at a five-year decrement of about 1 child per five-year period. In India, the transition has been much slower, with a maximum decrement of about 0.4 children every five years. The UN decline curves do not capture the extent of the variation between these two countries. In Mozambique, the observed and projected decrements are smaller than the decrements given by the UN decline curves. Only a short part of its transition has been observed so far, which leads to great uncertainty about the pace of its future transition. The 95% projection interval (in gray) includes decline curves with a maximum decrement that ranges from about 0.3 to 0.8 children per five-year period.

Fig. 5.

Decline curves for Thailand, India, and Mozambique plotted against decreasing TFR. Examples of the decline curves simulated from the posterior distribution are shown (dashed lines), together with the mean outcomes of all curves in the posterior sample. The 95% projection intervals for the five-year decrements are represented by the gray area. The observed five-year decrements are shown by black dots, and the fast-fast and slow-slow UN decline curves are shown by thin solid lines

Phase III: Post-Transition Low Fertility

Post-Transition Model

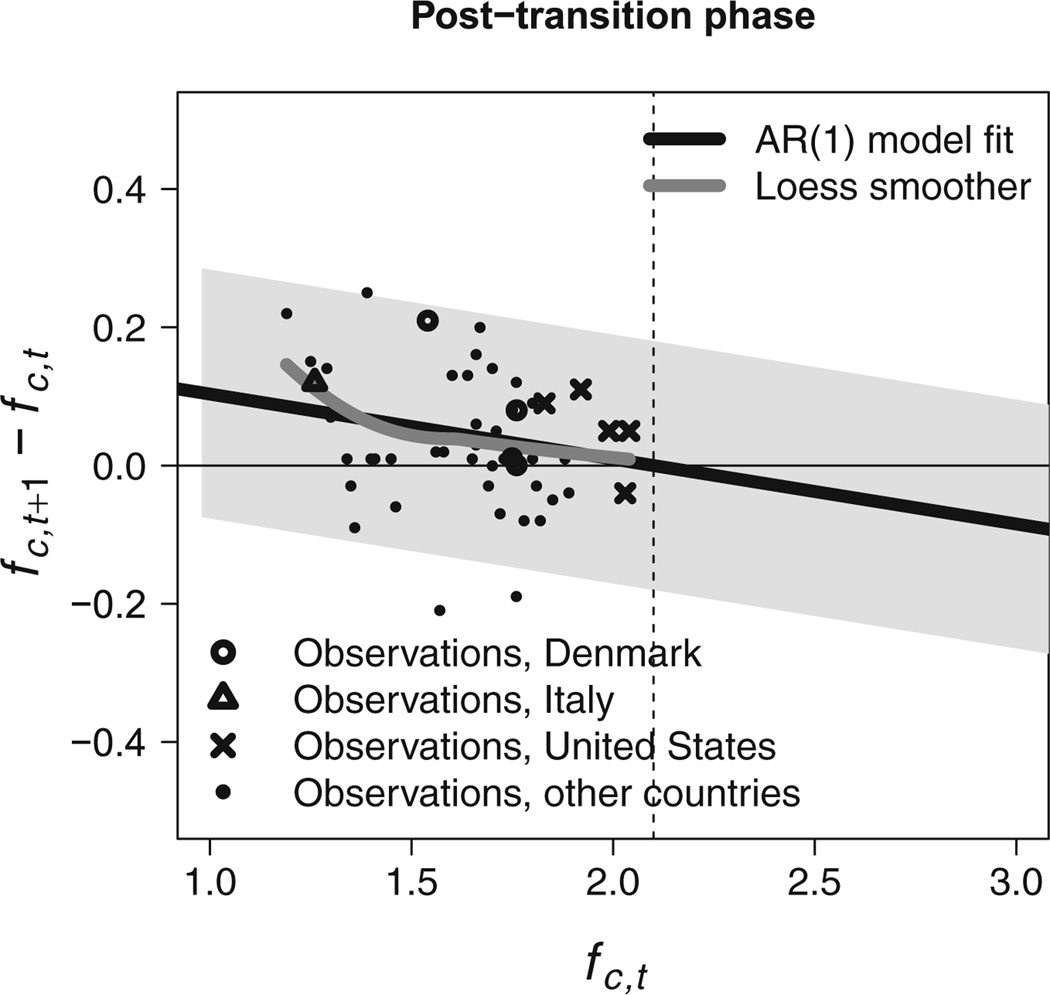
In Phase III, the TFR has decreased to around replacement-level fertility. All observed changes in the 20 countries that are currently in Phase III are shown in Fig. 6; the observed changes in Italy, Denmark, and the United States are highlighted. The dashed vertical line is drawn at the approximate replacement-level fertility, 2.1. The loess smoother (Cleveland and Devlin 1988) fitted to all data points in Phase III (the gray line) shows that the TFR tends to increase at below-replacement fertility levels; the increments tend to be larger at lower TFR levels during Phase III.

Fig. 6.

Observed changes in TFR in Phase III for Denmark, Italy, the United States, and the other countries in Phase III, together with the AR(1) model fit (black solid line with 95% projection intervals represented by the gray area) and loess smoother fitted to the data points (gray line). The dashed line is drawn at the approximate replacement-level fertility, 2.1

In long-term projections, the TFR is assumed to converge toward and fluctuate around replacement-level fertility. As proposed by Lee and Tuljapurkar (1994) and motivated by the observation of increasing increments at lower TFR levels, this process is modeled with a first-order autoregressive time series model for Phase III, an AR(1) model, with its mean fixed at the approximate replacement-level fertility, μ = 2.1:

$$f_{c,t+1}~N(\mathrm{\mu }+\mathrm{\rho }(f_{c,t}-\mu ),s^2),$$ (6)

where ρ is the autoregressive parameter with |ρ| < 1 and s is the standard deviation of the random errors. This can also be written as f_c,t+1 = f_c,t + (1 − ρ)(μ − f_c,t) + e_c,t, with errors e_c,t ~ N(0, s²). The TFR is expected to increase if it is below replacement, and it is expected to decrease if it is above replacement. The expected increase or decrease toward 2.1 is larger if the current TFR is farther from 2.1, and it depends on ρ: the smaller ρ, the more quickly the TFR will increase toward replacement-level fertility.

Bongaarts and Feeney (1998) noted that current below-replacement period TFRs may be lower than the cohort TFRs for the currently fertile cohorts, reflecting a tempo effect rather than a quantum effect. An AR(1) model for the low-fertility Phase III predicts a recovery from below-replacement period TFR, as does the Bongaarts–Feeney work, and so it may to some extent capture this phenomenon.

We considered using higher-order autoregressive models. However, many of the countries that have reached Phase III have done so only recently, and there are not enough Phase III data to inform projections from a higher-order autoregressive model. Also, we found in our validation studies that the probabilistic projections from the AR(1) model were well calibrated.

The asymptotic 100(1 − α)% projection interval based on the AR(1) model is

$$(2.1-z_{\mathrm{\alpha }}\frac{s}{\sqrt{1-{\mathrm{\rho }}^2}},2.1+z_{\mathrm{\alpha }}\frac{s}{\sqrt{1-{\mathrm{\rho }}^2}}),$$ (7)

where z_α is the $(1-\frac{\alpha }{2})$ quantile of the standard normal distribution. For example, for an 80% projection interval, z_α = 1.28; and for a 95% projection interval, z_α = 1.96. Equation 7 is the projection interval for the TFR in the distant future. Note that the autoregressive parameter ρ is not country specific, based on the assumption that the width of the asymptotic projection interval is the same for all countries.

Estimation

The AR(1) parameters ρ and s during Phase III are estimated using maximum-likelihood estimation based on the 52 data points during Phase III. The maximum-likelihood estimate for ρ is 0.906, and the estimated standard deviation of the residuals is 0.09. The fitted regression line shown in Fig. 6 fits the data well: it is very close to and overlaps with the loess smoother. The asymptotic 80% projection interval is [1.83, 2.37], and the asymptotic 95% projection interval is [1.68, 2.52]. The estimated value of ρ gives expected increases that are similar to those from the current UN methodology. The UN projects increments of 0.05 child for each five-year period until the TFR equals 1.85.

TFR Projections

TFR projections during the fertility transition are based on the Phase II model, using the sample from the posterior distribution of the model parameters. The result is a sample from the predictive distribution of future TFR trajectories for each country. For example, consider projecting f_c,t+1, the TFR in country c in period (t + 1), assuming that it is in Phase II in period t. The predictive distribution is represented by a sample $\{f_{c,t+1}^i:i=1,\dots ,I\}$. The ith member of the sample, $f_{c,t+1}^{(i)}$, is given by $f_{c,t+1}^{(i)}=f_{c,t}^{(i)}-d_{c,t}^{(i)}+{\epsilon }_{c,t,}^{(i)}\text{ where }{f}_{c,t}^{(i)}$ is the ith member of the sample of TFR outcomes in period t, $d_{c,t}^{(i)}$ is the expected decrement given by the decline function evaluated at $f_{c,t}^{(i)}\text{ and }{\mathbf{\theta }}_c^{(i)}$ (the ith sample of parameter vector θ_c), and ${\epsilon }_{c,t}^{(i)}$ is a random draw from N(0, (σ(f_c,t)²)⁽ⁱ⁾).

In each trajectory, Phase III is projected to start when the TFR has decreased to a TFR level that is around replacement-level fertility, and after the pace of the fertility decline has decreased to zero. These assumptions are incorporated into the definition of the projected start of Phase III, which is given by the earliest period t such that (1) ${\text{min}}_t\{f_{c,t}^{(i)}\}\le {\mathrm{\Delta }}_{c4}^{(i)},\text{ and }(2)f_{c,t}^{(i)}>f_{c,t-1}^{(i)}$. The TFR level ${\mathrm{\Delta }}_{c4}^{(i)}$ is the TFR outcome at which the pace of the fertility declines has decreased to 10% of the maximum five-year decrement; this TFR level is restricted to be between 1 and 2.5 children, to ensure that the fertility transition ends around replacement-level fertility. The TFR increases in period t when the sum of the expected fertility decrement (given by the decline parameters) and the random distortion term is positive. An increasing TFR in period t is more likely as the expected fertility decrements decrease and is thus more likely to occur at the end of the fertility transition. This definition of the start of Phase III means that the projected start period depends on the decline parameters as well as the random distortion terms. The start of Phase III will vary between trajectories. For projections during Phase III, the AR(1) model is used, with the parameters as described in the previous section.

In all projections, an additional prior distribution is put on future TFR outcomes, f_c,t+1 ~ U[0,U_c]. The upper bound is used to exclude TFR trajectories in which the fertility transition does not take off. The lower bound ensures positive TFR outcomes. This prior distribution is enforced by resampling any future distortion term that results in TFR outcomes outside its prior bounds.

After a large sample of TFR trajectories is constructed, the “best” TFR projection is given by the median outcome of the TFR trajectories in each period, and the bounds of the 80% projection intervals are given by the 10th and 90th percentiles.

Results

Probabilistic TFR Projections

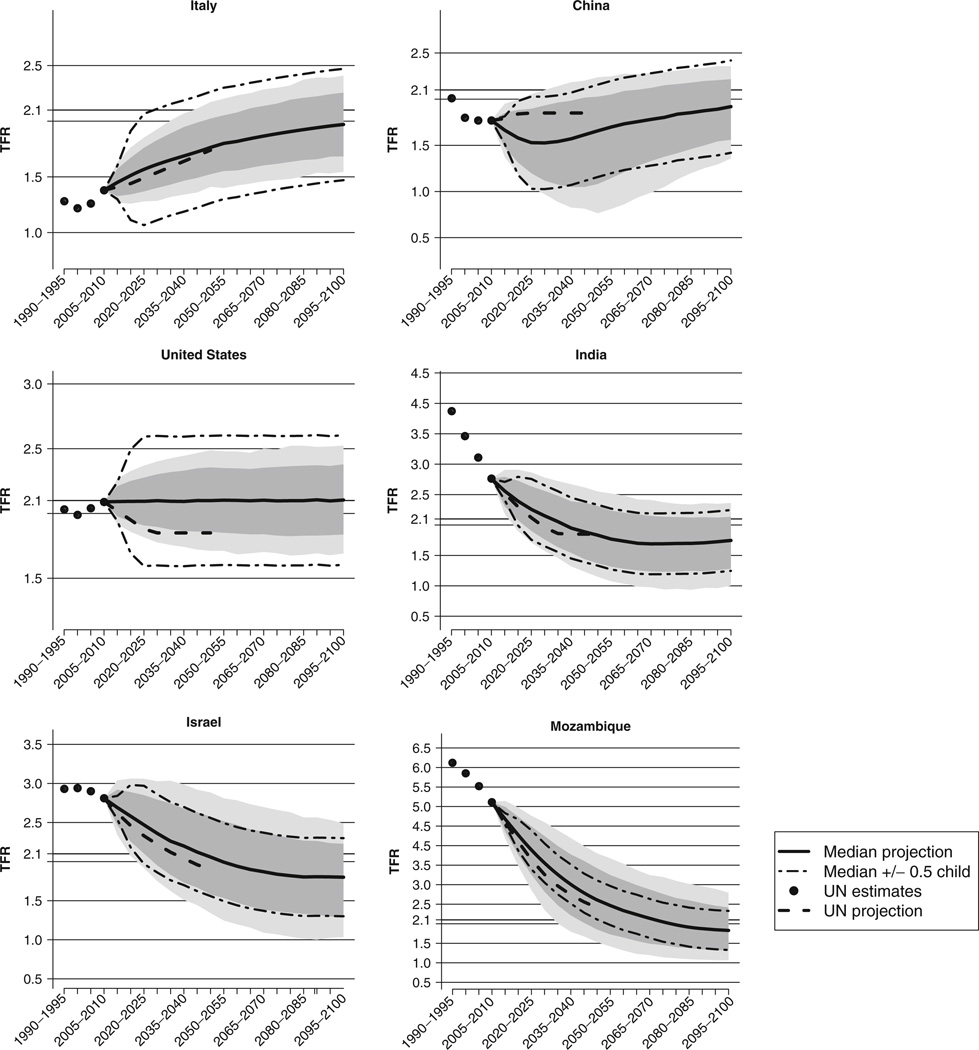
We now illustrate the results of the Bayesian projection model (BPM) for several countries. The results for all countries are given in Alkema et al. (2010). Figure 7 shows the projection intervals for future TFR in six countries with different fertility pasts and prospects—namely, Italy, China, the United States, India, Israel, and Mozambique. We also show the current UN projections and the result of adding and subtracting half a child to and from the median BPM projection, by analogy with how the UN constructs its high and low variants. The most recent UN estimates for 2005–2010 and projections for 2045–2050 and 2095–2100 for these countries are shown in Table 1.

Fig. 7.

Projection intervals for Italy, China, the United States, India, Israel, and Mozambique. The median projection, median projection plus and minus half a child, and the UN estimates and projections (2008 revision) are shown. The 80% projection intervals are represented by the dark gray area, and the 95% projection intervals indicated by the lighter gray area

Table 1.

UN estimates and projections (2008 revision), and results of Bayesian Projection Model (BPM) for 2045–2050 and 2095–2100 for selected countries, ordered by increasing TFR in 2005–2010

	UN		Bayesian Projection Model 2045–2050				Bayesian Projection Model 2095–2100
Country	2005–2010	2045–2050	Low	Median	High	Width	Low	Median	High	Width
Italy	1.38	1.74	1.52	1.76	2.02	0.50	1.68	1.97	2.26	0.57
China	1.77	1.85	1.08	1.66	2.03	0.95	1.56	1.92	2.22	0.66
United States	2.09	1.85	1.86	2.10	2.36	0.50	1.84	2.10	2.38	0.54
India	2.76	1.85	1.37	1.83	2.31	0.94	1.28	1.75	2.13	0.85
Israel	2.81	1.90	1.58	2.06	2.57	0.99	1.30	1.80	2.23	0.92
Mozambique	5.11	2.41	1.85	2.61	3.42	1.57	1.32	1.83	2.41	1.10

Note: “Low” and “High” refer to the lower and upper bounds of the 80% projection interval.

Italy

Italy is one of the countries that has had “lowest-low” fertility during the past two decades (Billari and Kohler 2004; Kohler et al. 2002; Frejka and Sobotka 2008), and various possible explanations of this have been reviewed elsewhere (Morgan and Taylor 2006). After some recovery over the past decade, Italy’s TFR is currently 1.38. Our method projects a slow recovery, with relatively tight 80% projection intervals of about plus or minus a quarter of a child. This projection is much tighter than the UN’s scenarios of plus or minus half a child. The UN projects a recovery of TFR toward 1.85, while our method projects movement toward 2.1. However, the average recovery projected by our model is so slow that the UN medium projection and the Bayesian median projection are essentially the same for 2045–2050 (1.77 and 1.76, respectively). Even by 2100, the Bayesian median projection is still below 2.1 (at 1.97), although there is a real possibility of recovery by then (the upper bound is 2.26).

Our projection of a recovery is supported by Caltabiano et al.’s (2009) more detailed analysis by region, age, and social group. Myrskyla et al. (2009) offered one possible explanation for the recovery: they postulated a recent reversal of the negative relationship between fertility and socioeconomic factors that prevailed during the fertility transition.

China

According to the UN estimates, Chinese TFR fell precipitously from the 1960s to the late 1990s but has remained constant for the past 15 years or so, at its current level of 1.77. The Bayesian median projection is that the fertility transition is not yet finished and that a further small decline will be followed by a slow recovery. The UN projection is quite different, remaining essentially constant at 1.85.

Our projection intervals for China are much wider than those for Italy, with a width of one child compared with half a child for Italy, even though fertility levels in both countries are currently below replacement. This reflects the unusual form of the Chinese data, with a steep fall followed by the abrupt end of the decline.

In fact there is controversy about whether the sudden halt to the decline over the past 15 years is real. The UN estimate of 1.77 for China’s TFR in 2005–2010 was based on official estimates. However, Gu and Cai (2009), summarizing several other studies (Cai 2008; Morgan et al. 2009; Retherford et al. 2005; Zhang and Zhao 2006), argued that the current Chinese TFR is actually lower, at about 1.5. A decline of the TFR to 1.5 over the past 15 years would also be more in line with the experience of other countries than the reported abrupt end of the decline. Reflecting this, our 80% projection intervals are also compatible with a lower current TFR value.

United States

The United States is the only country so far that has recovered to replacement level from a below-replacement turnaround (about 1.75 in the mid-1970s). Our projection is flat, with a width of about half a child. The UN projection declines fairly quickly to 1.85 and stays there. This value of 1.85 is on the edge of our 80% interval. By comparison, the U.S. Census Bureau projects a TFR of 2.0 in 2045–2049, which is higher than the UN projection and well within our interval.

Preston and Hartnett (2008) analyzed the effect of population changes on fertility. They concluded that the two most predictable changes in population composition—namely, educational attainment and ethnicity—are expected to induce relatively small changes in fertility by 2025–2029, and that these changes essentially cancel each other out. Their estimated changes in the TFR related to the tempo effect, the increasing ratio of female to male earnings, and possible restrictions on abortion access (0.15, −0.24, and 0.1, respectively) would yield TFR projections that are within our projection interval.

India

India has a TFR of 2.8 and has had a fairly rapid fertility decline. The Bayesian median projection indicates that the steady decline will continue to below-replacement level, bottoming out late in the century, and will be followed by a gradual recovery that will likely continue into the next century. As with other countries with mid-level fertility, there is considerable uncertainty about the timing of the recovery, leading to fairly wide projection intervals of slightly less than 1 child.

Israel

Israel is an unusual case because it has a technologically advanced market economy but its TFR of 2.8 is much higher than in most other such countries. Over the past 60 years its fertility has declined but has done so more slowly than in most other countries. Our projection reflects this, with a likely slow decline projected for the rest of the century. In contrast, the UN projects a faster decline.

DellaPergola (2007, 2009) and Nahmias and Stecklov (2007) analyzed proximate determinants of fertility in Israel, including fertility intentions, and concluded that future fertility decline would be slow, or perhaps non-existent. Compatible with this conclusion, we project an upper bound for 2045–2050 of 2.6, only 0.2 children below the current level. The unusual nature of the Israeli fertility transition is reflected in a relatively wide projection interval of 1 child in 2045–2049.

Mozambique

Like most other countries in sub-Saharan Africa, Mozambique has experienced a late and slow fertility decline. Reflecting this, our method projects a continued slow decline. It also reflects considerable uncertainty, with an interval width of 1.6 children in 2045–2050.

The UN projects a faster decline than our method, for Mozambique as well as for most other high-fertility countries. This is because the UN method is restricted to a small number of double logistic decline functions, none of which fits the Mozambique experience well, as shown in Fig. 5. In contrast, the double logistic curve estimated by the Bayesian method does fit the Mozambique experience well.

Mozambique has the largest difference between the UN medium projection and the Bayesian median projection for the selected countries. For 2045–2050 in Mozambique, these are 2.4 (UN) and 2.6 (Bayesian). Compared with either of these projections, the U.S. Census Bureau projection is much higher, at 3.2, anticipating an even slower decline. Guengant and May (2002) analyzed the proximate determinants of fertility, including contraceptive use, in sub-Saharan Africa and concluded that the fertility decline was likely to continue to be slow. Timaeus and Moultrie (2008) and Moultrie and Timaeus (2009) also concluded that a continued slow decline is the most likely future for sub-Saharan Africa, based on analyzing the evidence for stopping, spacing and postponing in these countries. These analyses lead to conclusions similar to those from our method.

Regional Averages

A summary of the average results by region for 2045–2050 is given in Table 2. Western, Middle, and Eastern Africa have the highest projected fertility in 2045–2050 and the widest projection intervals because of high current levels of fertility. The mean uncertainty as given by the 80% projection interval is about 1.4 children. The widths of the 80% projection intervals are about 1 child for Asia, Latin America, and the Pacific, and about 0.6 children for Europe. The 95% projection intervals are about 50% wider than the 80% projection intervals.

Table 2.

Mean projection results by region for 2045–2050: UN projection and median projection with Bayesian Projection Model (BPM), and the mean widths of the 80% and 95% projection intervals (PI)

		Projection		Mean Width
Region	UN 2005–2010	UN	BPM	95% PI	80% PI
Eastern Africa	4.6	2.3	2.6	2.1	1.4
Middle Africa	5.0	2.4	2.5	2.2	1.4
Northern Africa	2.7	1.9	1.7	1.4	1.0
Southern Africa	3.2	2.0	1.8	1.4	0.9
Western Africa	5.1	2.5	2.8	2.3	1.5
Eastern Asia	1.4	1.6	1.6	1.2	0.7
South Central Asia	2.9	2.0	1.8	1.5	1.0
South Eastern Asia	2.8	2.0	1.8	1.5	1.0
Western Asia	2.8	1.9	1.8	1.5	1.0
Eastern Europe	1.3	1.8	1.7	0.9	0.5
Northern Europe	1.7	1.8	1.9	0.9	0.6
Southern Europe	1.4	1.8	1.7	1.1	0.7
Western Europe	1.6	1.8	1.8	0.9	0.5
Caribbean	2.1	1.9	1.7	1.4	0.9
Central America	2.8	1.8	1.8	1.4	1.0
South America	2.5	1.9	1.8	1.4	0.9
Northern America	1.8	1.8	1.9	1.0	0.6
Australia/New Zealand	1.9	1.8	1.7	1.4	0.9
Melanesia	3.4	2.0	2.2	1.6	1.0
Micronesia	3.1	1.8	2.0	1.4	0.9
Polynesia	3.4	2.1	2.3	1.6	1.1

Note: Regional averages are not population-weighted, and the results are the arithmetic means of the country-specific outcomes within the region.

The probabilistic TFR projections of the Uncertain Population of Europe project (Alders et al. 2007; Alho et al. 2006, 2008) yield much wider intervals than our method for the below replacement-level European countries, with the widths of their 80% intervals averaging around 1.7 compared with our average of about 0.6. They based their intervals on past projection errors by projecting agencies, and these agencies tended to greatly underestimate the pace of decline, leading to large errors. Our projection method would have made much smaller errors in the past, leading to tighter projection intervals for the future.

Differences by 2045–2050 between the UN medium TFR projection and the BPM median TFR projection are overall small for regional averages (12% at most). The main differences between the two approaches are as follows: for regions with countries that have experienced fast fertility declines in recent decade(s), the BPM projects lower fertility by 2045–2050 than in the current UN projection (e.g., Asia and Northern and Southern Africa), whereas for other regions with high-fertility countries in 2005–2010 that have experienced slower fertility declines, the BPM projects a slower fertility decline than in the UN projection (e.g., Western, Eastern, and Middle Africa and part of Oceania).

Model Validation

We validated our projection model using out-of-sample projections. In the first set of out-of-sample projections, we used the Bayesian projection model to construct projections for 1980–2010 based on the UN estimates from 1950–1955 up to and including the five-year period 1975–1980. In the second set of out-of-sample projections, we used the BPM to construct projections for 1995–2010 based on the UN estimates from 1950–1955 up to and including the five-year period 1990–1995. The first set of projections was compared with the UN estimates for the 6 five-year periods from 1980–1985 up to 2005–2010, and the second set of projections was compared with the UN estimates for the 3 five-year periods 1995–2000, 2000–2005, and 2005–2010. In both comparisons, we excluded countries that were still in Phase I at the start of the projection period: no countries are currently in Phase I, so predictive performance for these countries is not relevant to the current projection task.

Table 3 shows the proportion of left-out UN estimates that fall outside their projection intervals. If the projection model is valid, we expect about 10% of the values, on average, to fall above the upper bound of the 80% projection interval and about 10% to fall below the lower bound. Similarly, we expect about 2.5% to fall above the upper bound of the 95% interval and about 2.5% to fall below the lower bound. The projection intervals were reasonably well calibrated in both out-of-sample projections, although the TFR was slightly over predicted in the more recent periods.

Table 3.

Model validation results: Mean squared error (MSE) and proportion of left-out UN estimates that fall above the median projected TFR and above or below their 80% and 95% projection intervals (PI) in future periods, when projecting from 1975–1980 and from 1990–1995

			Proportion of Observations
	MSE	Above Median	Above 95% PI	Below 95% PI	Above 80% PI	Below 80% PI
Data Until 1995
1980–1985	0.11	0.49	0.05	0.01	0.11	0.11
1985–1990	0.22	0.51	0.03	0.05	0.11	0.10
1990–1995	0.38	0.45	0.04	0.07	0.08	0.14
1995–2000	0.59	0.38	0.03	0.10	0.07	0.21
2000–2005	0.63	0.38	0.02	0.07	0.07	0.21
2005–2010	0.59	0.39	0.02	0.04	0.07	0.15
Data Until 1995
1995–2000	0.07	0.33	0.02	0.08	0.04	0.19
2000–2005	0.17	0.37	0.02	0.05	0.06	0.19
2005–2010	0.21	0.39	0.02	0.03	0.05	0.11

Discussion

We have proposed a new unified approach to projecting the TFR for all countries of the world. It uses a Bayesian projection model that incorporates worldwide fertility experience over the past 60 years. The method produces a full predictive distribution of future fertility trajectories. We assessed it in terms of out-of-sample predictive performance, and it yielded reasonably well-calibrated intervals.

In this article, we presented the median projections and 80% and 95% projection intervals. For policy planning purposes, the 80% projection interval may often give enough insight into future scenarios. The appealing interpretation of the 80% projection interval is that there is 1 chance in 10 of the true value being above the interval, and 1 chance in 10 of it being below the interval. The 95% projection interval is wider and can be viewed as encompassing most plausible possibilities.

The projection intervals as presented here are based on the UN estimates of past and current TFR. However, the UN estimates themselves measure the true TFR with some error, and to that extent, our projections may underestimate uncertainty about the true future TFR. Our projections can be validly viewed as probabilistic projections of future UN TFR estimates. Ideally, uncertainty about the UN estimates would be incorporated into our uncertainty assessment, but the wide variation in the availability and quality of data around the world makes this difficult. For one effort to assess uncertainty about the UN estimates of TFR, see Alkema et al. (2008b).

It is possible that the projections could be improved by including information about future trends in determinants or predictors of fertility, such as economic development. However, this would require good projections of these variables themselves far into the future, and they are arguably harder to predict than fertility itself. Projections based on determinants have been constructed for several countries at the national level (Lutz 1994; Sanderson 1998), but it would be hard to do this comparably for all countries.

In this article, we used an additive model for the positively valued TFR in Phase II and III. The additive model is appropriate during the fertility transition because the expected decrements and standard deviations of the error terms are small compared with the TFR. During Phase III, no difficulties arise either, because increases are expected at lower TFR outcomes and the standard deviations of the error terms are small compared with the TFR. If any negative outcomes would occur in the TFR projections, these outcomes would be excluded based on the zero lower bound of the prior distribution on future TFR outcomes.

The projections produced by our method could in practice provide a basis for UN projections of future TFR to be evaluated and, if necessary, revised by the UN analysts. Recent values and short-term projections of proximate determinants such as contraceptive use and fertility intentions could be especially useful for doing this. Because these data are not available uniformly for all countries, modifications of the results of our method based on these determinants could be incorporated in a more informal way by analysts, as is currently done with the UN’s deterministic projections.