Abstract
Tonic inhibition has been found experimentally in single neurons and affects the activity of neural populations. This kind of inhibition is supposed to set the background or resting level of neural activity and plays a role in the brains arousal system, e.g. during general anaesthesia. The work shows how to involve tonic inhibition in population rate-coding models by deriving a novel transfer function. The analytical and numerical study of the novel transfer function reveals the impact of tonic inhibition on the population firing rate. Finally, a first application to a recent neural field model for general anaesthesia discusses the origin of the loss of consciousness during anaesthesia.
Keywords: General anesthesia, Neural fields, Extra-synaptic receptors, GABAA, Nonlinear gain
Introduction
One of the most important questions in neuroscience is how the brain decodes and encodes external stimuli, such as visual scenes or spoken words. The corresponding neural information processing is mediated by the network of interacting neurons on different functional levels. For instance, in the early auditory system single neurons process incoming signals by decomposing the sounds into frequency bands (Sohmer and Freeman 2000), whereas later cognition or spatial source localization of sounds is processed on a neural population level (Karper and McAlpine 2004). This population activity represents the origin of macroscopically measurable activity, such as the electroencephalogram (EEG) (Niedermayer and Lopes da Silva 2005).
Interacting single neurons build up neural populations and it is reasonable to distinguish the single neuron level and the population level from a functional perspective assuming a hierarchical structure in the brain (Kaiser et al. 2010). This concept of hierarchy and the corresponding bridge between scales is essential to understand how actions on the single neuron level affects neural population activity and, more generally, has an impact on macroscopic effects. For instance, such microscopic actions are molecular actions such as the receptor bindings of neurohormons, which may control the sleep-wake cycle in humans induced by the hormon melatonin (Lieberman 1986), and anaesthetics administered during surgery which induces loss of consciousness (Antkowiak 2002). Moreover, anaesthetics are well-known to affect the EEG of mammals. Hence, molecular action on the microscopic level may tune macroscopic neural activity and has an impact on behavior. The present work shows how to bridge the two levels of single neurons and populations and how to involve molecular effects.
To bridge the scales between molecular action at neural receptors and neural population activity, let us discuss in the following the specific action of tonic inhibition. It is assumed to tune the level of excitation in neural population and may play a role in slow consciousness phenomena, such as loss of consciousness, sleep or arousal (Kopanitsa 1997). On the microscopic level, tonic inhihibition originates from specific neural receptors. Such receptors are located in the neurons membrane and respond to stimulation by opening certain ion channels. For instance, an incoming pulse at an inhibitory chemical synapse induces the transition of the neurotransmitter γ-aminobutyric acid (GABA) through the synaptic cleft and activates GABAA receptors. These, in turn, open the ion channels for Cl−-ions, induce an inward ion current and hyperpolarizes the membrane. This response may be either phasic or tonic (Yeung et al. 2003; Brickley et al. 1996; Semyanov et al. 2004), while the tonic response evolves on a larger time scale (Cavalier et al. 2005; Hamann et al. 2002). Most previous neural population models involving inhibition consider phasic inhibition only (Hutt 2011). In contrast, the present work focusses on the effect of tonic GABAA receptors on neural population activity.
GABAergic receptors may be found close to chemical synapses or more distant. Typically, the receptors close to synapses show phasic and tonic responses to stimulation, whereas more distant receptors, i.e. extra-synaptic receptors, respond by tonic inhibition only (Belelli et al. 2009; Kaneda et al. 1995). To understand the tonic inhibition, especially at receptors far from synaptic locations, it is necessary to take a closer look to the concentration of neurotransmitters around synapses. In case of large firing rates, the synapses spill out a large amount of neurotransmitters which not all may be uptaken by corresponding GABAA-receptors. The remaining neurotransmitters diffuse to more distant GABAA-receptors in extracellular space leading to an ambient concentration of neurotransmitters (Farrant and Nusser 2005; Semyanov et al. 2004; Nusser et al. 1997). This spill-over may explain the larger time scale of tonic responses found experimentally. In addition, this finding implies that already small concentrations of neurotransmitters are sufficient to generate tonic activity. However, this spill-over is just one possible mechanism besides others (Farrant and Nusser 2005).
Several previous theoretical and experimental studies (Haeusser and Clark 1997; Bernander et al. 1991; Destexhe and Paré 1999) have pointed out that increased interneuron activity may lead to a rather constant level of phasic inhibition in postsynaptic excitatory neurons which may also explain a tonic inhibitory background activity in neural populations. However, experimental studies (Semyanov et al. 2003; Brickley et al. 1996) have shown that, in fact, tonic and phasic activity are generated in different GABAA-receptors. Consequently tonic inhibition may originate either from (phasic) interneuron activity or from specific extra-synaptic receptors.
The effect of extra-synaptic receptors on the dendritic activity has not attracted much attention for many years. This may result from the relatively small number of such receptors compared to synaptic receptors (Kopanitsa 1997; Farrant and Nusser 2005). In addition, the recent development of genetic techniques in the last decade now allows to identify, classify and even localize different sub-types of GABAA receptors (Semyanov et al. 2004; Farrant and Nusser 2005). For instance, it has been shown experimentally, that δ-sub units of GABAA receptors occur exclusively at extra-synaptic sites (Belelli et al. 2009; Farrant and Nusser 2005; Nusser et al. 1998; Wei et al. 2003). This indicates a specific role of these receptors. It is interesting to note that a recent study shows that δ-sub unit receptors are not activated by spill-over (Bright et al. 2011). This finding reduces the importance of synaptic spill-over to explain tonic inhibition. Tonic inhibition induced by extra-synaptic GABAA-receptors represents a persistent increase in the cell membrane’s conductance. On the single neuron level, this diminishes the membrane time constant and, consequently, reduces the size and duration of excitatory post-synaptic potentials propagating on the dendrite. Hence tonic inhibition reduces the excitability of the membrane and increases the effective firing threshold (Farrant and Nusser 2005). Moreover, there is evidence that extra-synaptic GABAA-receptors located on axonal membranes modulate action potential conduction (Kullmann et al. 2005). On the neural population level, extra-synaptic receptors affect the excitability of interneuron-pyramidal cell networks and thus modify network oscillations (Semyanov et al. 2003). Moreover, Kopanitsa (1997) argue that the sustained spatially widespread tonic inhibition appears energetically more effective for the system to diminish neural population activity than short-lasting local phasic inhibition, since lower neurotransmitter concentrations are sufficient.
Further evidence for the importance of extra-synaptic receptors in neural information processing is their high sensitivity to modulation by various clinically relevant agents, such as anaesthetic agents (Farrant and Nusser 2005; Orser 2006). For instance, the anaesthetics midazolan and propofol enhance tonic inhibition much more than phasic inhibition in hippocampal neurons (Bai et al. 2001). Similar effects have been found in the brain stem (McDougall et al. 2008) and the thalamus (Belelli et al. 2009). Since these areas are supposed to play a role in general anaesthesia (Alkire et al. 2008), extra-synaptic receptors may mediate anaesthetic effects, such as the loss of consciousness.
The present paper aims to include the molecular effect of tonic inhibition in macroscopic structures, such as neural populations. These are not only an agglomeration of interacting single neurons, but are functional units on their own with specific properties. Although its dynamics depend on the dynamics of the underlying single neurons, the population exhibits an effective activity which is not a sum of the single neuron dynamics. In other words, neural populations are typical complex systems, which contain interacting units, which in turn are build of underlying interacting sub-units and so on. The unit on a functionally higher level results from the interaction of the underlying sub-units on a lower level, which in turn depends on the higher level units. This is called circular causality (Haken 2004). Examples for the functional units in neural populations are cortical macrocolumns in the mammalian visual cortex (Hubel and Wiesel 1963) or the barrel cortex in rodents (Petersen and Sakmann 2001). Typically, such coloumns contain several thousands of neurons. Moreover, the experimental discovery of such functional units on a higher abstract scale has triggered the development of a macroscopic theory for the dynamics of neural population activity, the so-called mean field theory (Wilson and Cowan 1973; Taylor 1999; Bressloff 2009; Faugeras et al. 2008). Successful mean-field models should take into account the most important features of single neurons and their interactions while neglecting minor features. Two of the most important features that should be taken into account are the synaptic activity on dendrites of single neurons and the threshold dynamics at the soma of the neurons. Most previous models (Bressloff and Coombes 1997; Hutt and Atay 2005; Hutt et al. 2003; Hutt and Longtin 2009) have considered an effective synaptic response function of chemical synapse and a nonlinear transfer function resulting from distributed firing thresholds on the population level. In this context, previous studies considered the membrane potential and the neural firing threshold independently (Wilson and Cowan 1972; Hutt and Atay 2005; Freeman 1979; Amit 1989). However, in fact, the firing threshold depends on the membrane potential if extra-synaptic receptors are present in the population. The present work reveals this dependence of the firing rate characteristics on the dynamics of extra-synaptic receptors.
The present work is structured as follows. The next section motivates mathematically how to include the dynamical effects of tonic inhibition on dendrites in a neural population model. This discussion yields a novel expression for the population firing rate involving effects of tonic inhibition.
Methods
Previous experimental studies have shown that extra-synaptic GABAA-receptors induce tonic inhibition in single neurons (Belelli et al. 2009). To understand better the effect of such receptors on neural population activity, the subsequent paragraphs present an approach how to incorporate extra-synaptic action in mathematical neural population models.
A prominent neural population model is the neural field which is a mean-field model that considers a rate coding mechanism. Such models allow to describe mesoscopic dynamics in neural populations such as pulse propagation in slices (Ermentrout and Kleinfeld 2001) or spatio-temporal spreading activity in the visual cortex during visual hallucinations (Bressloff et al. 2002; Ermentrout and Cowan 1979). The corresponding population firing rate P in the neural field model represents the number of spikes emitted by neurons in the population under study in a short time interval, i.e. typically few milliseconds (Hutt and Atay 2005; Wilson and Cowan 1972; Amit 1989). In this sense, P is almost instantaneous but averaged over a short time window, i.e. coarse-grained in time. Moreover, 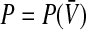 is a function of the effective averaged membrane potential
is a function of the effective averaged membrane potential 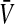 which represents an average over all neurons in the population. Here, the effective membrane potential is defined as the difference between the sum of excitatory and inhibitory potentials at the soma. If the effective membrane potential at a single neuron Vi exceeds the firing threshold Vthi of this neuron and the neuron is not in a refractory period, then this neuron fires and contributes to the population firing rate in the short time interval of the firing event.
which represents an average over all neurons in the population. Here, the effective membrane potential is defined as the difference between the sum of excitatory and inhibitory potentials at the soma. If the effective membrane potential at a single neuron Vi exceeds the firing threshold Vthi of this neuron and the neuron is not in a refractory period, then this neuron fires and contributes to the population firing rate in the short time interval of the firing event.
More mathematically, let us introduce 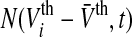 as the distribution of firing thresholds in the neural population at time t with mean firing threshold
as the distribution of firing thresholds in the neural population at time t with mean firing threshold 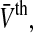 i.e. the number of non-refractory neurons with a firing threshold Vthi. Moreover one considers the probability density of effective membrane potentials
i.e. the number of non-refractory neurons with a firing threshold Vthi. Moreover one considers the probability density of effective membrane potentials 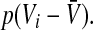 Then the number of firing neurons in the time interval
Then the number of firing neurons in the time interval 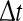 reads (Hutt and Atay 2005)
reads (Hutt and Atay 2005)
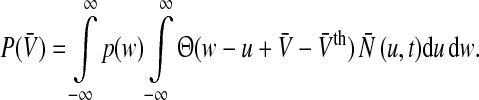 |
1 |
Here, 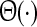 is the Heaviside function and
is the Heaviside function and 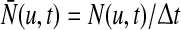 represents the population firing rate generated by a subset of non-refractory neurons. Equation 1 assumes that firing thresholds and the effective membrane potentials may take unlimited values. It has been shown previously (Hutt and Atay 2005; Amit 1989), that if the number of non-refractory neurons N is constant over time and the distribution
represents the population firing rate generated by a subset of non-refractory neurons. Equation 1 assumes that firing thresholds and the effective membrane potentials may take unlimited values. It has been shown previously (Hutt and Atay 2005; Amit 1989), that if the number of non-refractory neurons N is constant over time and the distribution 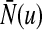 and the probability density p(w) are unimodal, then the population firing rate function
and the probability density p(w) are unimodal, then the population firing rate function 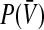 has the well-known sigmoidal shape.
has the well-known sigmoidal shape.
Although the latter considerations reflect a first good estimation on the population firing statistics, it is too simple in many aspects. For instance, it takes into account mean values of the effective membrane potentials and firing thresholds only. Recent studies have abolished these constraints (Bressloff 2009; Faugeras et al. 2008) and have shown the impact of the variance of membrane potential fluctuations on the population dynamics. Another simplification is the assumption that a single neuron emits just one spike when the effective membrane potential exceeds the firing threshold. This assumption reflects the ancient idea of McCulloch-Pitts neurons well-known from artificial neural networks (McCulloch and Pitts 1943). For these neurons the step function 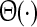 in Eq. 1 represents the corresponding transfer function. In contrast, real neurons’ firing rate, i.e. the number of spikes emitted, depend on the membrane potential. This dependence is closely related to the so-called f–I curve that gives the relation of single neuron output firing rate and an input current.
in Eq. 1 represents the corresponding transfer function. In contrast, real neurons’ firing rate, i.e. the number of spikes emitted, depend on the membrane potential. This dependence is closely related to the so-called f–I curve that gives the relation of single neuron output firing rate and an input current.
To illustrate the reasoning, let us consider stationary firing activity in the population and a time window 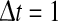 s. Then single neurons with firing rate fi emit fi spikes in the time interval
s. Then single neurons with firing rate fi emit fi spikes in the time interval 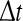 . To gain the population firing rate P, one sums up the firing rates P = ∑i fi and the firing rates may be given by the individual f–I curves fi = fi(Ii) with single input currents Ii at neuron i. We note that the membrane potential Vi may be defined as RIi with resistance of the membrane R and Vi is the voltage above the resting potential of the neuron. For shorter time intervals
. To gain the population firing rate P, one sums up the firing rates P = ∑i fi and the firing rates may be given by the individual f–I curves fi = fi(Ii) with single input currents Ii at neuron i. We note that the membrane potential Vi may be defined as RIi with resistance of the membrane R and Vi is the voltage above the resting potential of the neuron. For shorter time intervals 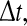 the firing rates are proportionally smaller.
the firing rates are proportionally smaller.
Hence, a more realistic population firing rate should take into account the dependence of the membrane potential and the number of spikes emitted and replace the Heaviside function 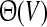 in Eq. 1 by
in Eq. 1 by 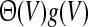 where the function g(V) reflects the dependence of the output firing rate of the membrane potential V. The function g is linearly related to the f–I curve by g(V) = [f(V/R)]/dt where the dimensionless variable dt is defined as
where the function g(V) reflects the dependence of the output firing rate of the membrane potential V. The function g is linearly related to the f–I curve by g(V) = [f(V/R)]/dt where the dimensionless variable dt is defined as 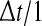 s. For instance, g(V) = 1 Hz represents a McCulloch-Pitts neurons as used in Eq. 1 whereas g(V)≠ 1 Hz reflects the new dependency.
s. For instance, g(V) = 1 Hz represents a McCulloch-Pitts neurons as used in Eq. 1 whereas g(V)≠ 1 Hz reflects the new dependency.
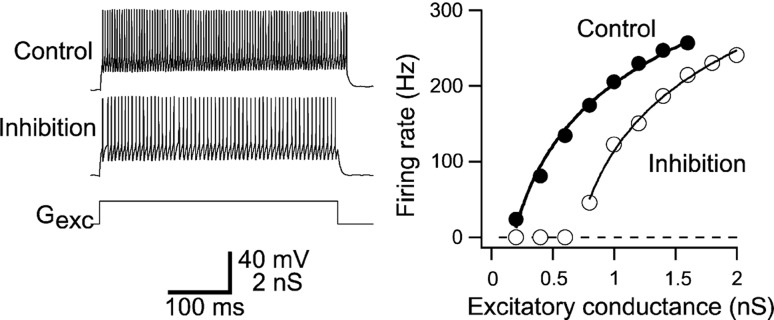
Moreover, the consideration of g(v) ≠ 1 Hz allows to include microscopic effects on single neurons, such as extra-synaptic receptor action. To illustrate the dependence of the output rate g(V) of the input activity in the presence of tonic inhibition, Fig. 1 shows such dependences of the output firing rate of a single neuron on the input conductance obtained experimentally in granule cells (Mitchell and Silver 2003). Similar effects have been observed in cortical pyramidal cells (Ulrich 2003). We observe a tonic inhibition-induced divisive effect with offset of the output rate dependent on the input magnitude. Consequently, it is necessary to consider g(V)≠ 1 Hz to take into account the effect of tonic inhibition. Previous experimental studies, e.g. (Mitchell and Silver 2003; Haeusser and Clark 1997), have shown that the tonic inhibition reduces the membrane time constant and increases the neurons’ firing threshold. Hence the subsequent part of the work investigates the effect of g(V) on the population firing rate P(V), and particularly the effect of the membrane time constant and the firing threshold.
Fig. 1.
Tonic inhibition effect on the output firing rate of neurons. Left A step-like excitatory input conductance (Gexc) generates tonic spiking activity in the absence (Control) and presence of 1nS tonic inhibition (Inhibition). Right The tonic inhibition induces an offset of the output firing rate function. Taken from Mitchell and Silver (2003)
To implement g(V)≠ 1 Hz in a neural population model, let us consider the firing rates in single neurons. In general, the output firing rate function g(V) depends nonlinearly on the input current or, equivalently, on the input potential V. This input potential may originate from synaptic responses (postsynaptic potentials) or from external stimuli.
For example, let us consider the output firing rate function in leaky integrate-and-fire models (LIF) without refraction. It reads 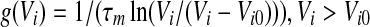 with firing threshold Vi0 of neuron i and membrane time constant τm(Gerstner and Kistler 2002). This is a model for neurons of type I, i.e. g(Vi0) = 0. For membrane potentials much larger than the firing threshold a first reasonable approximation is the linear function
with firing threshold Vi0 of neuron i and membrane time constant τm(Gerstner and Kistler 2002). This is a model for neurons of type I, i.e. g(Vi0) = 0. For membrane potentials much larger than the firing threshold a first reasonable approximation is the linear function
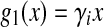 |
2 |
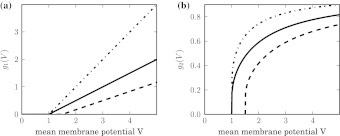
with the gain γi = 1/2τmVthi and the new firing threshold Vthi = Vi0/2 of neuron i. Here the gain depends on the membrane time constant and the firing threshold. For membrane potentials not too large, this is a good approximation since it is known that negative feedback linearizes (Ermentrout 1998) the function g(V). For simplicity, we will choose 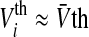 which is a good approximation for narrow firing threshold distributions. Figure 2a shows how the output firing rate model (2) changes if tonic inhibition is included. It reveals that the nonlinear gain increases for decreasing the time constant and the nonlinear gain decreases for increasing the firing threshold resembling previous experimental findings (Mitchell and Silver 2003; Haeusser and Clark 1997).
which is a good approximation for narrow firing threshold distributions. Figure 2a shows how the output firing rate model (2) changes if tonic inhibition is included. It reveals that the nonlinear gain increases for decreasing the time constant and the nonlinear gain decreases for increasing the firing threshold resembling previous experimental findings (Mitchell and Silver 2003; Haeusser and Clark 1997).
Fig. 2.
The model output firing rate functions g1(V) and g2(V). a Firing rate of a neuron without refraction corresponding to Eq. 2. b Firing rate of a neuron with refraction corresponding to Eq. 3. Parameters are τm = 1.0, Vthi = 1 (bold line), τm = 1.0, Vthi = 1.5 (dashed line) and τm = 0.5, Vthi = 1 (dashed-dotted line)
However, the firing rate in Eq. 2 grows to infinity if 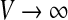 which is biophysically not reasonable . An improved model for neurons of type I may consider an absolute refractory period
which is biophysically not reasonable . An improved model for neurons of type I may consider an absolute refractory period 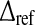 , that limits the firing rate to the maximum
, that limits the firing rate to the maximum 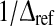 . The output firing rate of the corresponding LIF reads (Gerstner and Kistler 2002)
. The output firing rate of the corresponding LIF reads (Gerstner and Kistler 2002)
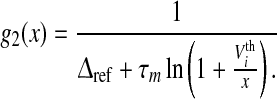 |
3 |
In the following we will choose 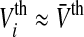 which is a good approximation for narrow firing threshold distributions
which is a good approximation for narrow firing threshold distributions 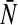 . It is important to mention that a vanishing membrane time constant τm→ 0 and
. It is important to mention that a vanishing membrane time constant τm→ 0 and 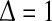 convert the type I-neuron model to the McCulloch-Pitts neuron model. Figure 2b presents the effect of shunting inhibition on the out firing rate function (3) and resembles the experimental output firing rate shown in Fig. 1.
convert the type I-neuron model to the McCulloch-Pitts neuron model. Figure 2b presents the effect of shunting inhibition on the out firing rate function (3) and resembles the experimental output firing rate shown in Fig. 1.
Our population model considers a single neural population of the general class of model neurons of type I, which may reflect properties of granular cell, cf. (Mitchell and Silver 2003) or pyramidal cells, cf. Ulrich (2003). This population may represent a certain cortical layer or a the neuronal network in a tissue slice. Moreover the population assumes identical membrane time constants for all neurons but different firing thresholds. This constraint is introduced for simplicity but may be abolished easily and does not limit the generality of the results obtained. As observed in Fig. 1, tonic inhibition may change the nonlinear gain and the offset of firing activity. Moreover, it is well-known that tonic inhibition also affects the membrane time constant (Bai et al. 2001) and the mean firing threshold distribution, called τm and 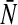 in the present model, respectively. Summarizing, the membrane time constant τm and the mean firing threshold
in the present model, respectively. Summarizing, the membrane time constant τm and the mean firing threshold 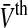 depend on the tonic inhibition level. The present work studies the dependence of the population firing rate
depend on the tonic inhibition level. The present work studies the dependence of the population firing rate 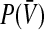 on both variables τm and
on both variables τm and 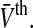
Results
To study the population firing rate 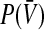 with respect to the level of tonic inhibition, at first the following paragraphs show the derivation of
with respect to the level of tonic inhibition, at first the following paragraphs show the derivation of 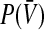 for general neuron types and discusses the corresponding nonlinear gain. Then the work focusses on type I-neurons with and without refractory period. The latter case allows an analytical study of
for general neuron types and discusses the corresponding nonlinear gain. Then the work focusses on type I-neurons with and without refractory period. The latter case allows an analytical study of 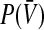 , whereas the discussion of refractory neurons is based on numerical results.
, whereas the discussion of refractory neurons is based on numerical results.
The population firing rate
To compute the population firing rate subjected to the tonic inhibition effect, let us re-formulate the population firing rate as
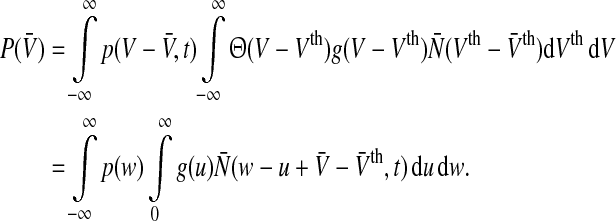 |
4 |
Here, the probability density of membrane potentials p and the firing threshold distribution 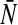 are assumed to be dependent on time. It is reasonable to assume that the probability density function p and the firing threshold distribution function per time unit
are assumed to be dependent on time. It is reasonable to assume that the probability density function p and the firing threshold distribution function per time unit 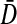 are unimodal and we choose
are unimodal and we choose
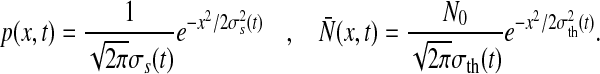 |
with N0 = n/dt and n is the number of neurons in the population under study. The terms σ2s(t) and σ2th(t) represent the time-dependent variance of the distribution of membrane potentials and firing thresholds, respectively. Then Eq. 4 reads
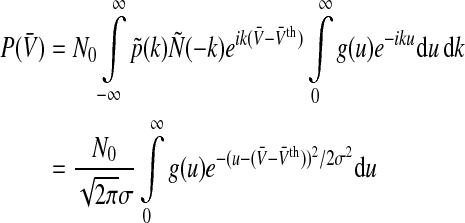 |
5 |
with the effective variance σ2 = σ2s + σ2th including the variances of the membrane potential distribution and the threshold distribution. For simplicity, here and in the following we do not note explicitely the time-dependence of the population firing rate P and the variance σ2 though it is implicit.
To learn more about the shape of the new population firing rate P(V) in Eq. 5, at first let us consider the conventional model including McCulloch-Pitts neurons with g(V) = 1 Hz. Then Eq. 5 reads
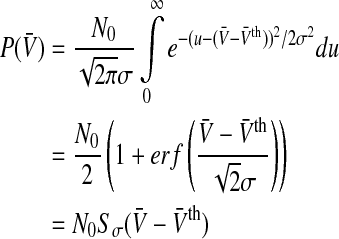 |
6 |
which is the well-established sigmoid function.
To examine the function P(V) for general g(V), let us re-write the integral in Eq. 5 as
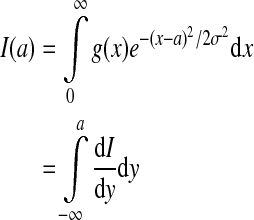 |
7 |
with 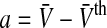 and we find
and we find
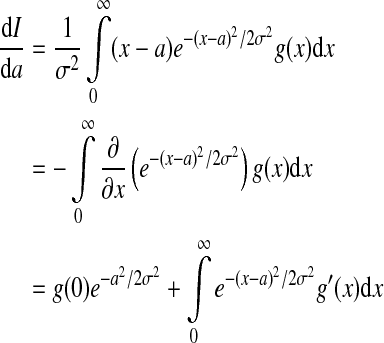 |
8 |
with 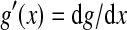 . Inserting (8) into (7) leads to
. Inserting (8) into (7) leads to
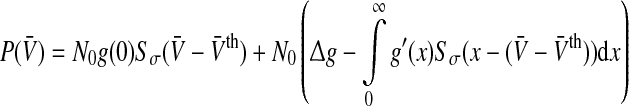 |
with 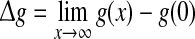 and Sσ is the sigmoid function taken from (6). The first term is proportional to the standard population firing rate (6) and the last term is the correction due to the individual dependence of the single neuron output rate on the membrane potential. In the standard case of McCulloch-Pitts neurons, i.e. g(V) = 1 Hz, the last term vanishes and P(V) is identical to the well-known conventional rate. For neurons of type I, the first term vanishes since g(0) = 0 and the last term represents the population firing rate and
and Sσ is the sigmoid function taken from (6). The first term is proportional to the standard population firing rate (6) and the last term is the correction due to the individual dependence of the single neuron output rate on the membrane potential. In the standard case of McCulloch-Pitts neurons, i.e. g(V) = 1 Hz, the last term vanishes and P(V) is identical to the well-known conventional rate. For neurons of type I, the first term vanishes since g(0) = 0 and the last term represents the population firing rate and 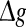 is the maximum firing rate of the single neurons leading to
is the maximum firing rate of the single neurons leading to
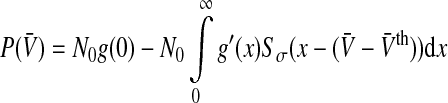 |
9 |
The first term represents the maximum population firing rate that P(V) approaches for 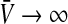 . For vanishing variance σ2→ 0, the population firing rate becomes proportional to the Heaviside function step function
. For vanishing variance σ2→ 0, the population firing rate becomes proportional to the Heaviside function step function 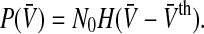
In addition, the nonlinear gain dP/dV is an important characteristic of the population firing activity since it defines the linear stability of stationary states (Hutt 2008; Atay and Hutt 2006; Owen et al. 2007). It reads
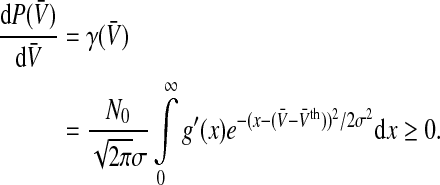 |
10 |
To get an idea about the shape of the nonlinear gain, we choose σ→ 0, i.e. the noise level is very low and the neurons in the population are almost identical, and find that the nonlinear gain of the population becomes proportional to the nonlinear gain of the single neuron as expected with
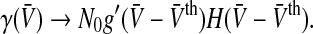 |
For g(x)≠const the nonlinear gain is non-symmetric to 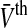 . This will be confirmed in the paragraphs below.
. This will be confirmed in the paragraphs below.
For deeper insight into the shape of the new population rate, the following paragraphs discuss the particular cases of non-refractory and refractory neurons of type I.
Neurons without refractory period
The linear output function g = g1(V) in Eq. 2 neglects refraction in the neuron and yields the population firing rate
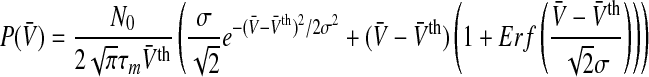 |
11 |
with the Gaussian error function 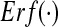 . For a vanishing variance σ2, the population firing rate reads
. For a vanishing variance σ2, the population firing rate reads
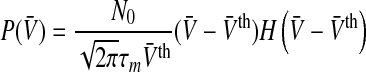 |
12 |
with the Heaviside step function 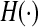 . This case reflects a single firing threshold and identical membrane potentials in all neurons.
. This case reflects a single firing threshold and identical membrane potentials in all neurons.
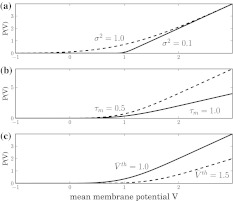
Figure 3 shows the population firing rate for various parameters. We observe in Fig. 3a that increasing the variance σ2 = σ2s + σ2th smoothes the activity threshold. This finding is reasonable since the variance σ2s reflects the level of noise in the system which is known to smoothen the population firing rate of spiking neural networks (Sutherland et al. 2009). Moreover, it is known from experiments (Mitchell and Silver 2003; Haeusser and Clark 1997) that tonic inhibition involves a decreased membrane time constant and an offset of the firing threshold to larger values. Figure 3b shows that a decrease of τm increases the slope of P(V) in accordance to experimental findings shown in Fig. 1. Figure 3c considers the increase of the mean firing threshold and reveals both an offset and a decrease in the nonlinear gain of the population firing rate. This shows good accordance to experimental findings (Mitchell and Silver 2003; Haeusser and Clark 1997).
Fig. 3.
The population firing rate P(V) for non-refractory neurons given by Eq. 12. Parameters are a τm = 1.0, 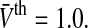 b
b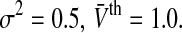 c σ2 = 0.5, τm = 1.0. Other parameters are D0 = 1.0
c σ2 = 0.5, τm = 1.0. Other parameters are D0 = 1.0
Neurons with refractory period
More realistic output firing rate models of single neurons such as in Eq. 3 with g = g2(V) take into account a refractory period leading to a maximum firing rate. Inserting Eq. 3 into Eq. 5 yields
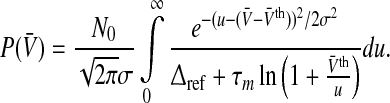 |
13 |
In the case of identical neurons and a noise-free neuronal network, all neurons share the same firing threshold and membrane potential and the variance vanishes, i.e. σ2 = 0. Mathematically, then the Gaussian function in the integrand of Eq. 13 becomes a Dirac-delta distribution and Eq. 13 recasts to the single neuron output rate g2(V) (cf. Fig. 2b) including the sharp firing threshold 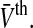
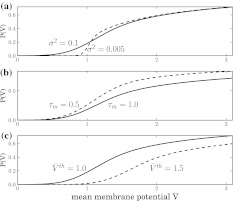
Considering non-identical firing thresholds and the presence of noise, then σ2 > 0 which smoothens the output rate but retains its principle sigmoidal shape. Figure 4a illustrates the dependence of P(V) on the variance σ2. Moreover, tonic inhibition decreases the membrane time constant and increases the firing thresholds and Fig. 4b and c show that this leads to an increase and decrease of the population firing rate, respectively.
Fig. 4.
The population firing rate P(V) for refractory neurons given by Eq. 13. Parameters are a τm = 1.0, 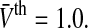 b
b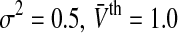 . c σ2 = 0.5, τm = 1.0. Other parameters are
. c σ2 = 0.5, τm = 1.0. Other parameters are 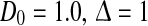
In addition to the population rate function the corresponding nonlinear gain, i.e. its derivative dP/dV, plays an important role in the stability of the neural population activity (Hutt 2008; Atay and Hutt 2006; Owen et al. 2007). The nonlinear gain reflects the level of excitation in the system.
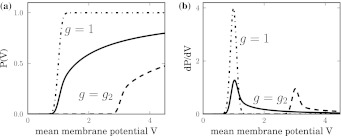
Figure 5 compares the population firing rate (a) and the nonlinear gain (b) of the conventional model (denoted as g = 1) and the new model involving neurons of type I (denoted as g = g2). We observe that, for τm > 0, the conventional rate function exhibits a much sharper first rise than the new rate while increasing V. This reflects a lower excitation of the neural population for neurons of type I. Moreover, the nonlinear gain in the conventional model is symmetric to the mean firing rate function, whereas the population of type I-neurons exhibits a long tail of the nonlinear gain.
Fig. 5.
The population firing rate P(V) and the nonlinear gain dP/dV for refractory neurons in comparison to the conventional model g = 1. The panels show the population firing rate P(V) (a) and the nonlinear gain (b) for the conventional model (g = 1, dashed-dotted line) and the new model (g = g2) according to Eq. 13. Parameters are 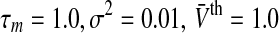 (solid line) and
(solid line) and 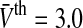 (dashed line). Other parameters are
(dashed line). Other parameters are 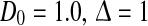
Considering tonic inhibition in the population of type I-neurons, Fig. 5 shows the offset of the population firing rate (panel a) and the nonlinear gain (panel b) for two values of the mean firing threshold. In addition, the maximum nonlinear gain dP/dV is diminished in the case of tonic inhibition. Since the maximum value of the nonlinear gain defines the stability threshold of the neural population activity about a stationary state, it appears that the tonic inhibition effect induced by a larger firing threshold renders stationary states more stable.
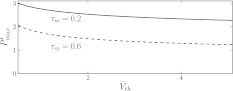
To examine this aspect in more detail, Fig. 6 shows the maximum nonlinear gain subjected to the mean firing threshold and the membrane time constants, i.e. the parameters dependent on the level of tonic inhibition. We observe that increasing the tonic inhibition level by an increased firing threshold decreases the nonlinear gain and, consequently, renders the system more stable. In contrast, a smaller membrane time constant increases the nonlinear gain. These numerical results are confirmed analytically applying Eqs. 3 and 10 leading to
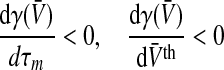 |
with 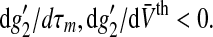
Fig. 6.
The maximum nonlinear gain 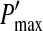 dependent on the level of tonic inhibition. Increasing
dependent on the level of tonic inhibition. Increasing 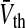 and decreasing the membrane time constant τm reflects an increased tonic inhibition level. It is defined as the global maximum of dP(V)/dV and P(V) given by Eq. 13. Parameters are
and decreasing the membrane time constant τm reflects an increased tonic inhibition level. It is defined as the global maximum of dP(V)/dV and P(V) given by Eq. 13. Parameters are 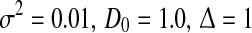
Application to general anaesthesia
In general anesthesia, the anaesthetics administered enters the brain via the blood-brain barrier and bind to neural receptors. For instance, the anaesthetic propofol binds to GABAergic synaptic and extra-synaptic receptors. Experimental studies have shown (Orser 2006) that propofol enhances tonic inhibition. To investigate the role of tonic inhibition in general anaesthesia, e.g. in the induction of the sedation and hypnosis, the subsequent paragraph considers a recent neural population model for general anaesthesia (Hutt and Longtin 2009) and studies the effect of tonic inhibition subjected to the concentration of propofol.
Propofol prolongs the decay phase of phasic synaptic GABAA receptor responses and increases the corresponding synaptic charge transfer while increasing the propofol concentration (Kitamura et al. 2002). Introducing the control parameter p ≥ 1, the decay time constant of the receptor response and the charge transfer are proportional to p in good approximation to experimental data, cf. (Hutt and Longtin 2009). Considering two populations of excitatory and inhibitory neurons and excitatory and inhibitory synapses, then the stationary state 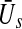 of such a network of two populations obeys (Hutt and Longtin 2009)
of such a network of two populations obeys (Hutt and Longtin 2009)
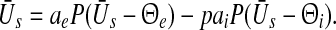 |
14 |
with the population firing rate P and the mean firing thresholds 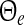 and
and 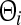 of excitatory and inhibitory neurons, respectively. The factors ae, ai represent the total synaptic strength. The stationary state
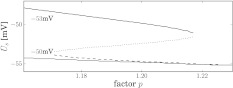
of excitatory and inhibitory neurons, respectively. The factors ae, ai represent the total synaptic strength. The stationary state 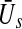 represents the difference of excitatory and inhibitory stationary membrane potentials. According to a recent hypothesis about the origin of the loss of consciousness (LOC) by Steyn-Ross et al. (Steyn-Ross and Steyn-Ross 1999; Steyn-Ross et al. 2004; Friedman et al. 2010), the LOC reflects a sudden jump from a high neural activity level (conscious state of the subject) to a low activity level (unconscious state of the subject). This jump is supposed to reflect a first-order phase transition in the neural population involving hysteresis: the jump from a high activity level to a low level emerges at a larger propofol concentration than the return from the low level activity to high level activity. Figure 7 shows the stationary states
represents the difference of excitatory and inhibitory stationary membrane potentials. According to a recent hypothesis about the origin of the loss of consciousness (LOC) by Steyn-Ross et al. (Steyn-Ross and Steyn-Ross 1999; Steyn-Ross et al. 2004; Friedman et al. 2010), the LOC reflects a sudden jump from a high neural activity level (conscious state of the subject) to a low activity level (unconscious state of the subject). This jump is supposed to reflect a first-order phase transition in the neural population involving hysteresis: the jump from a high activity level to a low level emerges at a larger propofol concentration than the return from the low level activity to high level activity. Figure 7 shows the stationary states 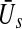 for two values of the excitatory threshold, where the larger value reflects the impact of tonic inhibition in a first approximation. For the smaller firing threshold
for two values of the excitatory threshold, where the larger value reflects the impact of tonic inhibition in a first approximation. For the smaller firing threshold 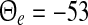 mV, it illustrates the high and low activity level, in addition to an (unstable) medium level. Increasing the mean firing threshold of excitatory neurons, i.e. considering tonic inhibition, only a single stationary state exists.
mV, it illustrates the high and low activity level, in addition to an (unstable) medium level. Increasing the mean firing threshold of excitatory neurons, i.e. considering tonic inhibition, only a single stationary state exists.
Fig. 7.
Stationary solutions in a network of excitatory and inhibitory neurons and synapses subjected to tonic inhibition. The given values −53 and −50 mV are the mean firing thresholds of excitatory neurons 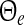 and reflect the absence (black lines) and presence (blue line) of tonic inhibition. For
and reflect the absence (black lines) and presence (blue line) of tonic inhibition. For 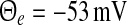 , the top branch (solid line) and bottom branch (dashed line) are linearly stable (analysis not shown), whereas the centre branch (dotted line) is unstable. Other parameters are
, the top branch (solid line) and bottom branch (dashed line) are linearly stable (analysis not shown), whereas the centre branch (dotted line) is unstable. Other parameters are 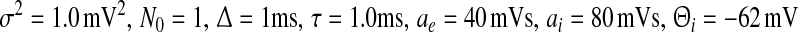 . The stationary state is given by
. The stationary state is given by 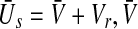 obeys Eq. 13 and Vr = − 70 mV is the neuron resting potential
obeys Eq. 13 and Vr = − 70 mV is the neuron resting potential
Discussion
The work considers a population of neurons in which the output firing rate functions of single neurons g(V) is affected by tonic inhibition. The derivation of the population firing rate function in “The population firing rate” implies that the firing rate of single neurons is stationary and depends on the membrane potential only, i.e. assumes that the f–I curve (which is proportional to the function g(V)) owns the relevant dynamical features. This is a strong assumption, but improves the conventional population firing rate model, e.g. by Wilson and Cowan (1972), that neglects the voltage-dependence of firing rates.
Relation of conventional population rate to novel rate
The new model includes the variance of the membrane potential distribution, which reflects the internal noise level, and the variance of the firing threshold distribution. If both variances are small, then the population firing rate resembles the single neuron firing rate function. This is shown for both general neuron types (“The population firing rate”) and non-refractory (“Nervous without refractory period”) and refractory (“Neurons with referactory peroid”) neurons of type I. Moreover, for a non-vanishing membrane time constants τm > 0, the population firing rate increases much slower with increasing membrane potentials for neurons of type I than in the conventional model, i.e. the nonlinear gain is smaller for a non-vanishing membrane time constant (cf. Fig. 5). In other words, the excitation in type I-neuron populations are diminished compared to the excitation in populations of McCulloch-Pitts neurons. This can also be seen in the nonlinear gain in Fig. 5, which is smaller for non-vanishing membrane time constants compared to McCulloch-Pitts neurons.
Effects of tonic inhibition on population firing rate
Tonic inhibition in single neurons increases the firing threshold and reduces the membrane time constant. Figures 5, 6 and the analytical treatment in ”Neurons with referactory peroid” show that this yields a decrease and increase of the nonlinear gain in type I-neurons. In this context, Mitchell and Silver (2003) have investigated the role of firing threshold and membrane time constant in tonic inhibition in the presence of a temporal variability of excitatory input conductances. They find that increasing the temporal variability of input conductances reduces the nonlinear gain while tonic inhibition increases the nonlinear gain. The authors conclude that the loss of nonlinear gain outweighs the gain by reduction of the membrane potential. According to this finding, one concludes that the reduction of the nonlinear gain by tonic inhibition results mainly from the increase of the firing threshold in single neurons. Considering the obvious dependence of the population firing rate and the nonlinear gain on the membrane time constant (decreased by a factor of two or three as observed in Figs. 3, 4 and 6), it is reasonable to conclude that the the membrane time constant does not change much in the presence of tonic inhibition due to its minor effect.
Effects of tonic inhibition in general anaesthesia
The general anaesthetic propofol affects the level of tonic inhibition. Consequently increasing the concentration of propofol enhances this effect. Mathematically, the model considers the increase of concentration by an increase of the control parameter p. Figure 7 shows that such an increase may lead to stable stationary states on high and low activity (for p≈ 1.2) while just a single stationary state at high activity is present in the absence of propofol (p = 1). Further increasing the concentration destroys the high-level stationary state and the system evolves on a lower activity level. The interpretation of this destruction is the loss of consciousness in subjects. Although the discussion of the stationary state in the anaesthesia model (14) reveals a first insight into the effect of tonic inhibition during anaesthesia, it is necessary to keep in mind the underlying assumptions. Most importantly, the tonic inhibition at extra-synaptic receptors implies shunting inhibition, which is known to induce nonlinear interactions between excitatory and inhibitory post-synaptic currents (Koch et al. 1983). Hence, the study of the stationary state 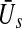 as the difference between excitatory and inhibitory post-synaptic potentials is a first approximation only. Future studies shall introduce the nonlinear interaction in
as the difference between excitatory and inhibitory post-synaptic potentials is a first approximation only. Future studies shall introduce the nonlinear interaction in 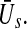 Interestingly, including tonic inhibition removes the two stable states and retains a single stationary state at a low activity level. This result points out that tonic inhibition inhibits the neural population activity. Moreover, it raises the question on the importance of the two stable states in general anaesthesia and the LOC. It appears that tonic inhibition may facilitate a single stationary state during anaesthesia and the importance of a phase transition to lower levels for LOC is doubtful.
Interestingly, including tonic inhibition removes the two stable states and retains a single stationary state at a low activity level. This result points out that tonic inhibition inhibits the neural population activity. Moreover, it raises the question on the importance of the two stable states in general anaesthesia and the LOC. It appears that tonic inhibition may facilitate a single stationary state during anaesthesia and the importance of a phase transition to lower levels for LOC is doubtful.
Perspectives
The present work represents the first consideration of tonic inhibition in population models and considers the most obvious inhibition effects, such as the shift of the firing threshold. Future work will focus on more subtle effects of tonic inhibition, such as the shift of the f–I curve dependent on the input frequency (Mitchell and Silver 2003) and the consideration of synaptic excitation and inhibition currents that add non-linearly at the soma due to the involved shunting inhibition.
Acknowledgments
The research resuting to presented work has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013) / ERC grant agreement n 257253.
References
- Alkire M, Hudetz A, Tononi G. Consciousness and anesthesia. Science. 2008;322:876–880. doi: 10.1126/science.1149213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amit DJ. Modeling brain function: the world of attactor neural networks. Cambridge: Cambridge University Press; 1989. [Google Scholar]
- Antkowiak B. In vitro networks: cortical mechanisms of anaesthetic action. Brit J Anaesth. 2002;89(1):102–111. doi: 10.1093/bja/aef154. [DOI] [PubMed] [Google Scholar]
- Atay FM, Hutt A. Neural fields with distributed transmission speeds and constant feedback delays. SIAM J Appl Dyn Syst. 2006;5(4):670–698. doi: 10.1137/050629367. [DOI] [Google Scholar]
- Bai D, Zhu G, Pennefather P, Jackson MF, MacDonald JF, Orser B. Distinct functional and pharmacological properties of tonic and quantal inhibitory postsynaptic currents mediated by γ-aminobutyric acid a receptors in hippocampal neurons. Molec Pharmacol. 2001;59:814–824. doi: 10.1124/mol.59.4.814. [DOI] [PubMed] [Google Scholar]
- Belelli D, Harrison NL, Maguire J, Macdonald RL, Walker MC, Cope DW. Extra-synaptic GABAA receptors: form, pharmacology, and function. J Neurosc. 2009;29(41):12757–12763. doi: 10.1523/JNEUROSCI.3340-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernander O, Douglas RJ, Martin KAC, Koch C. Synaptic background activity influences spatio-temporal integration in single pyramidal cells. Proceed Nat Acad Sci USA. 1991;88:11569–11573. doi: 10.1073/pnas.88.24.11569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressloff PC. Stochastic neural field theory and the system size expansion. SIAM J Appl Math. 2009;70:1488–1521. doi: 10.1137/090756971. [DOI] [Google Scholar]
- Bressloff PC, Coombes S. Physics of the extended neuron. Int J Mod Phys B. 1997;11(20):2343–2392. doi: 10.1142/S0217979297001209. [DOI] [Google Scholar]
- Bressloff PC, Cowan JD, Golubitsky M, Thomas PJ, Wiener MC. Geometric visual hallucinations, euclidean symmetry and the functional architecture of striate cortex. Philos Trans R Soc B. 2002;356:299–330. doi: 10.1098/rstb.2000.0769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brickley SG, Cull-Candy SG, Farrant M. Development of a tonic form of synaotic inhibition in rat cerebellar granule cells resulting from persistent activation of GABAA receptors. J Physiol. 1996;497(3):753–759. doi: 10.1113/jphysiol.1996.sp021806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bright DP, Renzi M, Bartram J, McGee TP, MacKenzie G, Hosie AM, Farrant M, Brickley SG. Profound desensitization by ambient gaba limits activation of delta-containing GABAA receptors during spillover. J Neurosci. 2011;31(2):753–763. doi: 10.1523/JNEUROSCI.2996-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavalier P, Hamann M, Rossi D, Mobbs P, Attwell D. Tonic excitation and inhibition of neurons: ambient transmitter sources and computational consequences. Prog Biophys Mol Biol. 2005;87:3–16. doi: 10.1016/j.pbiomolbio.2004.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Paré D. Impact of network activity on the integrative properties of neocortical pyramidal neurons in vivo. J Neurophysiol. 1999;81:1531–1547. doi: 10.1152/jn.1999.81.4.1531. [DOI] [PubMed] [Google Scholar]
- Ermentrout G. Linearization of f–i curves by adaptation. Neur Comp. 1998;10:1721–1729. doi: 10.1162/089976698300017106. [DOI] [PubMed] [Google Scholar]
- Ermentrout G, Cowan J. A mathematical theory of visual hallucination patterns. Biol Cybern. 1979;34:137–150. doi: 10.1007/BF00336965. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB, Kleinfeld D. Traveling electrical waves in cortex: insights from phase dynamics and speculation on a computational role. Neuron. 2001;29:33–44. doi: 10.1016/S0896-6273(01)00178-7. [DOI] [PubMed] [Google Scholar]
- Farrant M, Nusser Z. Variations on an inhibitory theme: phasic and tonic activation of GABAA receptors. Nature Rev Neurosci. 2005;6:215–229. doi: 10.1038/nrn1625. [DOI] [PubMed] [Google Scholar]
- Faugeras OD, Touboul JD, Cessac B. A constructive mean-field analysis of multi population neural networks with random synaptic weights and stochastic inputs. Front Comput Neurosci. 2008;3:1. doi: 10.3389/neuro.10.001.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman W. Nonlinear gain mediating cortical stimulus-response relations. Biol Cybern. 1979;33:237–247. doi: 10.1007/BF00337412. [DOI] [PubMed] [Google Scholar]
- Friedman EB, Sun Y, Moore JT, Hung H-T, Meng QC, Perera P, Joiner WJ, Thomas SA, Eckenhoff RG, Sehgal A, Kelz MB. A conserved behavioral state barrier impedes transitions between anesthetic-induced unconsciousness and wakefulness: evidence for neural inertia. PLoS ONE. 2010;5(7):e11903. doi: 10.1371/journal.pone.0011903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstner W, Kistler W. Spiking neuron models. Cambridge: Cambridge University Press; 2002. [Google Scholar]
- Haeusser M, Clark BA. Tonic synaptic inhibition modulates neuronal output pattern and spatiotemporal synaptic integration. Neuron. 1997;19:665–678. doi: 10.1016/S0896-6273(00)80379-7. [DOI] [PubMed] [Google Scholar]
- Haken H. Synergetics. Berlin: Springer; 2004. [Google Scholar]
- Hamann M, Rossi D, Attwell D. Tonic and spillover inhibition of granule cells control information flow through cerebellar cortex. Neuron. 2002;33:625–633. doi: 10.1016/S0896-6273(02)00593-7. [DOI] [PubMed] [Google Scholar]
- Hubel D, Wiesel T. Receptive fields of cells in striate cortex of very young, visually unexperienced kittens. J Physiol. 1963;26:994. doi: 10.1152/jn.1963.26.6.994. [DOI] [PubMed] [Google Scholar]
- Hutt A. Local excitation-lateral inhibition interaction yields oscillatory instabilities in nonlocally interacting systems involving finite propagation delay. Phys Lett A. 2008;372:541–546. doi: 10.1016/j.physleta.2007.08.018. [DOI] [Google Scholar]
- Hutt A, editor. Sleep and anesthesia: neural correlates in theory and experiment. Number 15 in Springer series in computational neuroscience. New York: Springer; 2011. [Google Scholar]
- Hutt A, Atay F. Analysis of nonlocal neural fields for both general and gamma-distributed connectivities. Physica D. 2005;203:30–54. doi: 10.1016/j.physd.2005.03.002. [DOI] [Google Scholar]
- Hutt A, Longtin A. Effects of the anesthetic agent propofol on neural populations. Cogn Neurodyn. 2009;4(1):37–59. doi: 10.1007/s11571-009-9092-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutt A, Bestehorn M, Wennekers T. Pattern formation in intracortical neuronal fields. Network Comput Neural Syst. 2003;14:351–368. doi: 10.1088/0954-898X/14/2/310. [DOI] [PubMed] [Google Scholar]
- Kaiser M, Hilgetag CC, Kötter R. Hierarchy and dynamics of neural networks. Front Neuroinf. 2010;4:112. doi: 10.3389/fninf.2010.00112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaneda M, Farrant M, Cull-Candy SG. Whole-cell and single-channel currents activated by gaba and glycine in granule cells of the rat cerebellum. J Physiol. 1995;485(2):419–435. doi: 10.1113/jphysiol.1995.sp020739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karper NS, McAlpine S. Optimal neural population coding of an auditory spatial cue. Nature. 2004;430:682–686. doi: 10.1038/nature02768. [DOI] [PubMed] [Google Scholar]
- Kitamura A, Marszalec W, Yeh J, Narahashi T. Effects of halothane and propofol on excitatory and inhibitory synaptic transmission in rat cortical neurons. J Pharmacol. 2002;304(1):162–171. doi: 10.1124/jpet.102.043273. [DOI] [PubMed] [Google Scholar]
- Koch C, Poggio T, Torre V. Nonlinear interactions in a dendritic tree: Localization, timing, and role in information processing. Proc Nati Acad Sci USA. 1983;80:2799–2802. doi: 10.1073/pnas.80.9.2799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopanitsa MV. Extrasynaptic receptors of neurotransmitters: distribution, mechanisms of activation, and physiological role. Neurophysiology. 1997;29(6):448–458. doi: 10.1007/BF02463356. [DOI] [Google Scholar]
- Kullmann DM, Ruiz A, Rusakov DM, Scott R, Semyanov A, Walker MC. Presynaptic, extrasynaptic and axonal GABAA receptors in the cns: where and why? Prog Biophys Mol Biol. 2005;87:33–46. doi: 10.1016/j.pbiomolbio.2004.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman HR. Behavior, sleep and melatonin. J Neural Transm Suppl. 1986;21:233–241. [PubMed] [Google Scholar]
- McCulloch W, Pitts W. A logical calculus of the ideas immanent in nervous activity. Bull Math Biol. 1943;5:115–133. [PubMed] [Google Scholar]
- McDougall SJ, Bailey TW, Mendelowitz D, Andresen MC. Propofol enhances both tonic and phasic inhibitory currents in second-order neurons of the solitary tract nucleus (nts) Neuropharmacol. 2008;54:552–563. doi: 10.1016/j.neuropharm.2007.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell SJ, Silver RA. Shunting inhibition modulates neuronal gain during synaptic excitation. Neuron. 2003;38:433–445. doi: 10.1016/S0896-6273(03)00200-9. [DOI] [PubMed] [Google Scholar]
- Niedermayer E, Lopes da Silva F, editors. Electroencephalography: basic principles, clinical applications, and related fields. Philadelphia: Lippincott, Williams and Williams; 2005. [Google Scholar]
- Nusser Z, Cull-Candy S, Farrant M. Differences in synaptic GABAA receptor number underlie variation in gaba mini amplitude. Neuron. 1997;19:697–709. doi: 10.1016/S0896-6273(00)80382-7. [DOI] [PubMed] [Google Scholar]
- Nusser Z, Sieghart W, Somogyi P. Segregation of different GABAA receptors to synaptic and extrasynaptic membranes of cerebellar granule cells. J Neurosc. 1998;18:1693–1703. doi: 10.1523/JNEUROSCI.18-05-01693.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orser B. Extrasynaptic GABAA receptors are critical targets for sedative-hypnotic drugs. J Clin Sleep Med. 2006;2:S12–8. [PubMed] [Google Scholar]
- Owen MR, Laing CR, Coombes S. Bumps and rings in a two-dimensional neural field: splitting and rotational instabilities. New J Phys. 2007;9:378. doi: 10.1088/1367-2630/9/10/378. [DOI] [Google Scholar]
- Petersen CC, Sakmann B. Functionally independent columns of rat somatosensory barrel cortex revealed with voltage-sensitive dye imaging. J Neurosci. 2001;21(21):8435–46. doi: 10.1523/JNEUROSCI.21-21-08435.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semyanov A, Walker MC, Kullmann DM. Gaba uptake regulates cortical excitability via cell-type specific tonic inhibition. Nat Neurosci. 2003;6:484–490. doi: 10.1038/nn1043. [DOI] [PubMed] [Google Scholar]
- Semyanov A, Walker MC, Kullmann DM, Silver RA. Tonically active GABAA receptors: modulating gain and maintaining the tone. Trends Neurosc. 2004;27(5):262–269. doi: 10.1016/j.tins.2004.03.005. [DOI] [PubMed] [Google Scholar]
- Sohmer H, Freeman S. Basic and clinical physiology of the inner ear receptors and their neural pathways in the brain. J Basic Clin Physiol Pharmacol. 2000;11(4):367–374. doi: 10.1515/JBCPP.2000.11.4.367. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross M, Steyn-Ross D. Theoretical electroencephalogram stationary spectrum for a white-noise-driven cortex: evidence for a general anesthetic-induced phase transition. Phys Rev E. 1999;60(6):7299–7311. doi: 10.1103/PhysRevE.60.7299. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross M, Steyn-Ross D, Sleigh J. Modelling general anaesthesia as a first-order phase transition in the cortex. Prog Biophys Molecul Biol. 2004;85(2-3):369–385. doi: 10.1016/j.pbiomolbio.2004.02.001. [DOI] [PubMed] [Google Scholar]
- Sutherland C, Doiron B, Longtin A. Feedback-induced gain control in stochastic spiking networks. Biol Cybern. 2009;100:475–489. doi: 10.1007/s00422-009-0298-5. [DOI] [PubMed] [Google Scholar]
- Taylor JG. Neural bubble dynamics in two dimensions: foundations. Biol Cybern. 1999;80:5167–5174. doi: 10.1007/s004220050534. [DOI] [Google Scholar]
- Ulrich D. Differential arithmetic of shunting inhibition for voltage and spike rate in neocortical pyramidal cells. Eur J Neurosci. 2003;18(8):2159–65. doi: 10.1046/j.1460-9568.2003.02942.x. [DOI] [PubMed] [Google Scholar]
- Wei W, Zhang N, Peng Z, Houser CR, Mody I. Perisynaptic localization of subunit-containing GABAA receptors and their activation by gaba spillover in the mouse dentate gyrus. J Neurosci. 2003;23:10650–10661. doi: 10.1523/JNEUROSCI.23-33-10650.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson H, Cowan J. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. 1972;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson H, Cowan J. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik. 1973;13:55–80. doi: 10.1007/BF00288786. [DOI] [PubMed] [Google Scholar]
- Yeung JYT, Canning KJ, Zhu G, Pennefather P, Macdonald JF, Orser BA. Tonically activated GABAA receptors in hippocampal neurons are high-affinity, low-conductance sensors for extracellular gaba. Molec Pharmacol. 2003;63(1):2–8. doi: 10.1124/mol.63.1.2. [DOI] [PubMed] [Google Scholar]