Abstract
The receptive fields of cells in the lateral geniculate nucleus (LGN) are shaped by their diverse set of impinging inputs: feedforward synaptic inputs stemming from retina, and feedback inputs stemming from the visual cortex and the thalamic reticular nucleus. To probe the possible roles of these feedforward and feedback inputs in shaping the temporal receptive-field structure of LGN relay cells, we here present and investigate a minimal mechanistic firing-rate model tailored to elucidate their disparate features. The model for LGN relay ON cells includes feedforward excitation and inhibition (via interneurons) from retinal ON cells and excitatory and inhibitory (via thalamic reticular nucleus cells and interneurons) feedback from cortical ON and OFF cells. From a general firing-rate model formulated in terms of Volterra integral equations, we derive a single delay differential equation with absolute delay governing the dynamics of the system. A freely available and easy-to-use GUI-based MATLAB version of this minimal mechanistic LGN circuit model is provided. We particularly investigate the LGN relay-cell impulse response and find through thorough explorations of the model’s parameter space that both purely feedforward models and feedback models with feedforward excitation only, can account quantitatively for previously reported experimental results. We find, however, that the purely feedforward model predicts two impulse response measures, the time to first peak and the biphasic index (measuring the relative weight of the rebound phase) to be anticorrelated. In contrast, the models with feedback predict different correlations between these two measures. This suggests an experimental test assessing the relative importance of feedforward and feedback connections in shaping the impulse response of LGN relay cells.
Keywords: LGN, Mechanistic, Rate model, Thalamocortical, Corticothalamic, Feedback, Feedforward, Impulse response
Introduction
Relay cells in the lateral geniculate nucleus (LGN) in the early visual system receive synaptic inputs from a variety of sources (Sherman and Guillery 2001): direct feedforward excitation from retinal ganglion cells, indirect feedforward inhibition via intrageniculate interneurons in turn excited by retinal ganglion cells, feedback inhibition from the thalamic reticular nucleus (TRN) and feedback excitation from primary visual cortex. Both intrageniculate interneurons and TRN cells also receive excitatory feedback from cortex opening up for feedback inhibition involving the entire thalamocortical loop, acting on the LGN relay cells.
LGN relay cells typically inherit their most salient receptive-field structure features from the retinal ganglion cells providing the dominant feedforward inputs (Mastronarde 1987a,b; Usrey et al. 1999; Ruksenas et al. 2000). The role of the prominent cortical feedback to LGN is more unclear, however (Briggs and Usrey 2008, 2011). This cortical feedback has been shown to be able to switch LGN relay cells from burst to tonic firing modes (McCormick and von Krosigk 1992; Godwin et al. 1996) and to modify the response properties of LGN cells to visual stimuli both in cat (Geisert et al. 1981; Vidyasagar and Urbas 1982; Murphy and Sillito 1987; Sillito et al. 1993, 1994; Cudeiro and Sillito 1996; Wörgötter et al. 1998; Andolina et al. 2007) and monkey (Marrocco et al. 1982; McClurkin and Marrocco 1984; McClurkin et al. 1994; Marrocco et al. 1996). For example, cortical feedback has been shown to affect the length tuning of relay-cell responses (Murphy and Sillito 1987), the response to patch-grating stimuli (Sillito et al. 1993; Cudeiro and Sillito 1996; Sillito and Jones 2002) and the temporal response precision to drifting gratings (Andolina et al. 2007). However, experiments with selective blocking of cortical feedback are notoriously difficult to do, and studies have reported both enhanced and reduced responses of LGN neurons from cortical feedback. The identification of a particular role of this feedback has thus been difficult.
Mathematical models in neuroscience can be categorized into three types: descriptive, mechanistic, and interpretive (Dayan and Abbott 2001). Descriptive models are used to summarize experimental data compactly (see, e.g., Jing et al. 2010), while mechanistic models aim to account for the observed neural properties on the basis of known neural physiology and anatomy (see, e.g., Wang and Zhang 2007; Saglam et al. 2009; and Liang et al. 2010). The third category, interpretive models, aims instead to model the functional roles of neural systems, for example, relating neuronal responses to the task of processing useful information for the animal (see, e.g., Satoh and Usui 2009).
Following the introduction of the difference-of-Gaussians (DOG) model for the spatial receptive-field of retinal ganglion cells by Rodieck (1965), most modeling of the response properties of cells in retina, LGN and visual cortex have been descriptive. Numerous spatiotemporal receptive-field functions have been suggested (see, e.g., Ch.2 in Dayan and Abbott 2001), essentially identifying filter functions accounting for the signal processing done by the underlying neural networks (Cruse 1997). In contrast, mechanistic models have aimed to find out how these filtering properties arise from the underlying neural circuitry in the visual system (Einevoll and Heggelund 2000; Einevoll and Plesser 2002, 2011).
A few mechanistic mathematical models have been investigated to elucidate effects of cortical feedback on LGN neurons. They have focused on cortical feedback effects on visual latency (Köhn and Wörgötter 1996), thalamocortical oscillations (Destexhe et al. 1998; Destexhe 2000; Mayer et al. 2007; Bhattacharya et al. 2011), temporal structure of spike trains (Wörgötter et al. 1998), synchronization of LGN cells (Kirkland and Gerstein 1998; Kirkland et al. 2000), object segmentation based on motion cues (Hillenbrand and van Hemmen 2000), LGN relay-cell responses to bipartite drifting grating stimuli (Hayot and Tranchina 2001), and cortical feedback effects on recorded relay-cell impulse responses (Yousif and Denham 2007). In these models, each of the different populations in the early visual pathway (retinal, LGN, TRN, and cortical cells) have typically been represented by spatially structured grids of neurons, and comprehensive numerical simulations have been necessary for model analysis. Importantly, the large number of parameters in the models have generally precluded thorough analysis of the properties of the model across the parameter space.
In the present paper, we develop a minimal mechanistic mathematical model aimed at highlighting salient feedforward and feedback effects on LGN relay cells following visual stimulation. A particular focus is the investigation of how the detailed shape of the LGN impulse response is formed by the interplay between feedforward and feedback actions (Cai et al. 1997; Usrey et al. 1999; Yousif and Denham 2007).
Our mechanistic model is framed in terms of firing rates (Einevoll and Plesser 2002) and focuses solely on the temporal aspects of the signal processing; the lateral spatial dimension is thus omitted. For simplicity, we do not model the intrageniculate interneurons or TRN cells explicitly. Instead we incorporate their effects in a more general way by allowing for both feedforward inhibition via interneurons and inhibitory cortical feedback effects via TRN cells or interneurons. The LGN cells divide into two types, ON and OFF. The first responds preferably to light spots on a dark background, the latter preferably to dark spots on a light background. Here we assume the feedforward parts of the ON and OFF pathways to be separate, but we allow for ON/OFF cross-connections in the cortical feedback (Wang et al. 2006). The model is formulated in terms of coupled integral equations (Ermentrout 1998; Nordbø et al. 2007), but a crucial feature is that it can be mapped onto a much simpler differential form. The final model is represented by a single delay differential equation with absolute delay (MacDonald 1979) which is readily solved by standard mathematical software. To further facilitate its use we have made a freely available MATLAB version of the model, LGNcircuit, with a simple graphical user interface (GUI).
Mathematical model
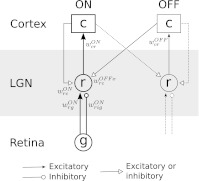
The overall structure of our firing-rate model is illustrated in Fig. 1. The focus of attention is the firing rate of an LGN relay cell with ON symmetry. It receives both direct feedforward excitation and indirect feedforward inhibition (via intrageniculate interneurons not explicitly represented in the model) from an ON ganglion cell in retina. It further receives cortical feedback both from cortical ON cells and cortical OFF cells. The cortical feedback can be both excitatory (direct) and inhibitory (indirect via TRN cells or intrageniculate interneurons). The cortical ON and OFF cells are in turn assumed to be driven by the LGN ON and OFF relay cells, respectively.
Fig. 1.
Schematic overview of the present minimal mechanistic thalamocortical circuit model. Cell types are: retinal ganglion cells (g), LGN relay cells (r), and cortical cells (c). OFF pathway is included in an indirect way with the OFF LGN relay cell modeled as a ‘shadow cell’ of the corresponding ON LGN relay cell. Synaptic connections explicitly included in the model are represented by solid lines; connections included implicitly are shown with dotted lines. Feedforward connections in the ON pathway are shown with thick lines
General firing-rate model on integral form
Below we present the model for the firing rate of an ON LGN relay cell, but a completely analogous derivation can be done for OFF LGN relay cells. The time-dependent firing rate 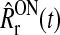 for such an ON cell is assumed to be given by (Dayan and Abbott 2001)
for such an ON cell is assumed to be given by (Dayan and Abbott 2001)
 |
1 |
where 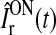 denotes the time-dependent input to the ON LGN cell, and FONr(x) is a firing-rate function converting the input into an output firing rate. For convenience we choose the input
denotes the time-dependent input to the ON LGN cell, and FONr(x) is a firing-rate function converting the input into an output firing rate. For convenience we choose the input  to have the same dimension as firing rates.
to have the same dimension as firing rates.
It is further convenient to separate the time-dependent from the background activities, and we thus use the notation
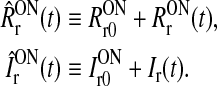 |
2 |
Here RONr0 and RONr(t) are set to denote the background firing rate (assumed to be stationary) and the stimulus-evoked change of the firing rate, respectively. Further, IONr0 denotes the background input to the ON LGN cell, while Ir(t) denotes the stimulus-evoked change in this input. With this notation the firing rate of the LGN ON cell is given by
 |
3 |
A common choice of firing rate functions Fr(x) for LGN neurons has been the half-wave rectification function (F(x) = [x]+; [x < 0]+ = 0, [x ≥ 0]+ = x) (Gazères et al. 1998; Troyer et al. 1998, 2002; Einevoll and Heggelund 2000), but sigmoidal functions have also been used (Hayot and Tranchina 2001; Yousif and Denham 2007). For now we leave FONr(x), as well as the other firing-rate functions introduced below, unspecified.
In our model the ON and OFF pathways are coupled via the cortical feedback (Wang et al. 2006; Yousif and Denham 2007), and we consequently also need a model for OFF LGN relay cells. Here we model OFF LGN relay cells as ‘shadow’ cells of the ON cells, i.e., they are assumed to receive the same time-dependent input with opposite phase, i.e., opposite sign (Troyer et al. 2002). The firing rate of an OFF cell is thus in analogy with (3) given by
 |
4 |
where IOFFr0 is the background input to the OFF LGN cell.
The total input to the ON LGN relay cell is obtained by summing the excitatory and inhibitory feedforward contributions stemming from retina and the feedback contributions from cortex, i.e.,
 |
5 |
Here wONrg is the weight of the direct feedforward excitatory connection from retina onto the ON LGN cell, and wONrig the weight of the corresponding indirect feedforward inhibitory connection via intrageniculate interneurons. The parameter wONrc represents the weight of the feedback connection from the ON cortical cells, while the parameter wOFFxrc represents the weight of the feedback cross-connection from the OFF cortical cell to the ON LGN cell. Further, hONrg(t), hONrig(t), hONcr(t), and hOFFcr(t) are temporal coupling kernels, and (h * r)(t) is a temporal convolution between the kernel h(t) and the firing rate r(t) defined by
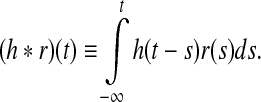 |
6 |
The coupling kernel hONrg(t), for example, represents the contribution to the present input to the ON relay cell due to firing that has occurred in the ON retinal ganglion cell a time t in the past. The kernels must thus be causal, i.e., h(t < 0) = 0, and presently we assume that all coupling kernels are normalized, i.e.,  .
.
As seen from (5) the cortical feedback to the LGN relay cells is assumed to be provided by cortical cells of both symmetries, i.e., ON and OFF (cf. Fig. 1). For simplicity we neglect that cortical cells exhibit different orientation tuning, and we thus include only one ON and one OFF cell type. We further make the assumption that the cortical cells are driven by relay cells of the same symmetry only (Hubel and Wiesel 1962; Jin et al. 2008). The firing rates of these cortical ON and OFF cells are mathematically represented by (Ermentrout 1998; Nordbø et al. 2007)
 |
7 |
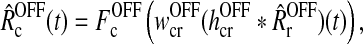 |
8 |
where wONcr and wOFFcr are feedforward connection weights from LGN to cortex, and hONcr(t) and hOFFcr(t) the corresponding temporal coupling kernels.
If we now, in analogy to (2), separate the firing rates of the ON retinal ganglion cells and the cortical cells into background and stimulus-evoked contributions, i.e.,
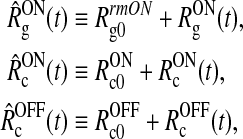 |
9 |
Eq. (5) can be split up into two separate equations determining the net background and stimulus-evoked inputs:
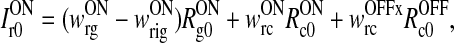 |
10 |
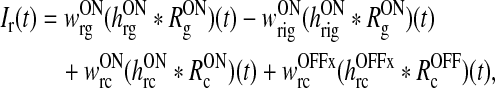 |
11 |
where we have used that the coupling kernels h(t) are normalized. Provided we now specify (1) the firing-rate functions (FONr, FOFFr, FONc, FOFFc), (2) the coupling kernels h(t), (3) the firing rate of the retinal ganglion cell  providing the feedforward input to LGN ON cells, and (4) the background firing rate of the LGN OFF cell IOFFr0, the Eqs. (3)–(11) constitute a complete mathematical model in terms of integral equations. This integral equation set can in principle be solved numerically for any choice of coupling kernels and firing-rate functions, but this approach will not be pursued here.
providing the feedforward input to LGN ON cells, and (4) the background firing rate of the LGN OFF cell IOFFr0, the Eqs. (3)–(11) constitute a complete mathematical model in terms of integral equations. This integral equation set can in principle be solved numerically for any choice of coupling kernels and firing-rate functions, but this approach will not be pursued here.
Model on differential form
To obtain a simpler model which also can be mapped to a differential form more amenable to numerical evaluation, we now choose the following normalized temporal kernels for the thalamocortical feedback loop:
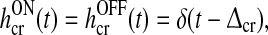 |
12 |
 |
13 |
where δ(t) is the Dirac δ-function, and  is the Heaviside unit step function. The feedforward kernels hONcr(t) and hOFFcr(t) represent simple delays in the feedforward connections between LGN and cortex. The kernel hONrc(t), which represents the feedback coupling between the cortical ON cell and the LGN ON cell, is modeled as a delayed decaying exponential, i.e., a delayed (RC) low-pass filter (Einevoll and Plesser 2002). The same kernel is assumed for the feedback cross-connection hOFFxrc(t) from the cortical OFF cell to the LGN ON cell. The choice of imposing a low-pass filter in the feedback connections, and not in the feedforward connections, was made to allow for a straightforward mapping of the model from integral to a differential form (see below). We nevertheless expect the combined use of a simple delay and a low-pass filter kernel to represent salient features of how relay cell responses are affected by the thalamocortical loop.
is the Heaviside unit step function. The feedforward kernels hONcr(t) and hOFFcr(t) represent simple delays in the feedforward connections between LGN and cortex. The kernel hONrc(t), which represents the feedback coupling between the cortical ON cell and the LGN ON cell, is modeled as a delayed decaying exponential, i.e., a delayed (RC) low-pass filter (Einevoll and Plesser 2002). The same kernel is assumed for the feedback cross-connection hOFFxrc(t) from the cortical OFF cell to the LGN ON cell. The choice of imposing a low-pass filter in the feedback connections, and not in the feedforward connections, was made to allow for a straightforward mapping of the model from integral to a differential form (see below). We nevertheless expect the combined use of a simple delay and a low-pass filter kernel to represent salient features of how relay cell responses are affected by the thalamocortical loop.
For the retinal ganglion cell driving the ON LGN relay cell we define the normalized firing rate rONg(t) as
 |
14 |
where Ag is the maximum deviation of the ganglion-cell firing rate from the background firing rate RONg0. |rONg(t)| will thus always be between 0 and 1.
Finally we require that model parameters and firing-rate functions are such that the model predicts the background firing rates of the cortical neurons providing the feedback to be zero (Heeger 1991), i.e., that there is no cortical feedback effects onto the relay cells in the background state. This means that
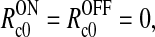 |
15 |
so that  and
and  .
.
We then introduce the auxiliary dynamical variable z(t) as
 |
16 |
This new dynamical variable essentially corresponds to the filtered feedback onto the ON LGN relay cell. Note that z = 0 when no visual stimulus is present.
As described in detail in Appendix 1 the system described by (3)–(11) can be transformed into the following differential delay equation with absolute delay (MacDonald 1979) in terms of the auxiliary variable z(t):
 |
17 |
where we have introduced the auxiliary variable 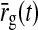 , corresponding to the stimulus-evoked retinal firing rate filtered through the feedforward kernel, i.e.,
, corresponding to the stimulus-evoked retinal firing rate filtered through the feedforward kernel, i.e.,
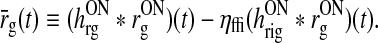 |
18 |
Here we have defined ηffi as the ratio of the feedforward inhibitory and excitatory weights, i.e.,
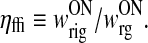 |
19 |
In addition the total feedback delay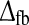 has been introduced as
has been introduced as
 |
20 |
and we also have introduced the dimensionless quantities
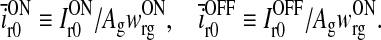 |
21 |
With the introduction of 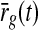 in (18) and z(t) in (16), Ir(t) in (11) can be compactly written as
in (18) and z(t) in (16), Ir(t) in (11) can be compactly written as
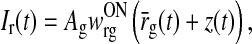 |
22 |
and we now have the following relationships between the firing rates and our new variables,
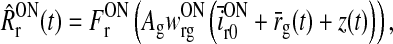 |
23 |
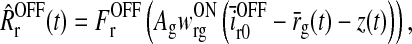 |
24 |
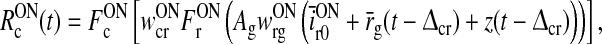 |
25 |
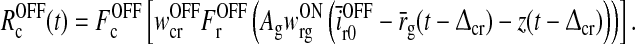 |
26 |
Given (1) the firing-rate functions (FONr, FOFFr, FONc, FOFFc), (2) the retinogeniculate coupling kernels hONrg and hONrig, and (3) the retinal ganglion-cell firing rate rONg(t) providing the feedforward input, the above equations provide a straightforward numerical recipe for calculating the response of the LGN and cortical neurons. The central equation is the differential delay equation with absolute delay (17) describing the dynamics of the auxiliary variable z(t), while (23)–(26) simply translate the result for z(t) into the desired firing rates.
Model with threshold firing-rate functions
We now assume the firing-rate functions of both the LGN and cortical cells to be half-wave rectifying functions (Gazères et al. 1998; Troyer et al. 1998, 2002; Einevoll and Heggelund 2000; Dayan and Abbott 2001), i.e.,
 |
27 |
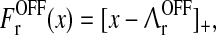 |
28 |
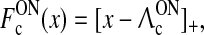 |
29 |
 |
30 |
where  ,
,  ,
,  and
and  are threshold values. With the additional prior assumption (15) that the background firing rates of the cortical neurons providing the feedback are zero, the delay differential Eq. (17) for z(t) simplifies substantially. As described in Appendix 2 we find
are threshold values. With the additional prior assumption (15) that the background firing rates of the cortical neurons providing the feedback are zero, the delay differential Eq. (17) for z(t) simplifies substantially. As described in Appendix 2 we find
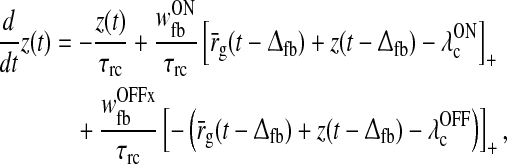 |
31 |
where the total weights of the thalamocortical feedback loop are given by
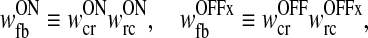 |
32 |
and we have introduced new effective firing thresholds for the cortical cells as
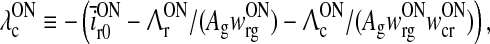 |
33 |
 |
34 |
The formulas relating the dynamical variable z(t) to the firing rates (23)–(26) are also substantially simplified,
 |
35 |
 |
36 |
 |
37 |
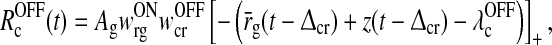 |
38 |
where we further have introduced new effective firing thresholds for the relay cells as
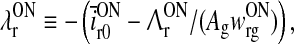 |
39 |
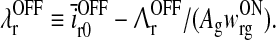 |
40 |
In the absence of visual stimuli both  and z(t) are zero. From (37) and (38) we thus see that in order to fulfill the requirement (15) of zero background firing rates of the cortical cells feeding back to the LGN, λONc must be non-negative and λOFFc must be non-positive.
and z(t) are zero. From (37) and (38) we thus see that in order to fulfill the requirement (15) of zero background firing rates of the cortical cells feeding back to the LGN, λONc must be non-negative and λOFFc must be non-positive.
A notable feature of the differential delay equation for z(t) in (31), is that the relay-cell threshold values  and
and  only enter indirectly via λONc and λOFFc, cf. (33) and (34). These threshold values thus mainly affect the translation of the dynamical variables
only enter indirectly via λONc and λOFFc, cf. (33) and (34). These threshold values thus mainly affect the translation of the dynamical variables  and z(t) into predictions for the relay-cell firing rates as described by (35) and (36). From the expressions (31)–(38) we further see that the product AgwONrg essentially is a trivial scaling factor that only affects the overall magnitude of resulting firing rates.
and z(t) into predictions for the relay-cell firing rates as described by (35) and (36). From the expressions (31)–(38) we further see that the product AgwONrg essentially is a trivial scaling factor that only affects the overall magnitude of resulting firing rates.
Throughout the rest of the paper we will focus on the model with threshold firing-rate functions specified by (31)–(40) as well as previous definitions. To facilitate an easier communication of our model, we present, in accordance with ‘good model description practice’ (Nordlie et al. 2009a), an overview of our model in Tables 1 and 2. We also illustrate some salient elements of the model in Fig. 2.
Table 1.
Tabular description of the model, part 1
| Model summary | |||
|---|---|---|---|
| Neural elements | Retina (ON), lateral geniculate nucleus (ON/OFF), cortex (ON/OFF) | ||
| Neurons | Neurons modeled as firing rate units | ||
| Stimulus | Drifting sinusoidal gratings, light impulses | ||
| Neural elements | |||
|---|---|---|---|
| Name | Elements | Size | |
| g | Retina (retinal ganglion cell) | 1 | |
| r | Lateral geniculate nucleus (geniculate relay cell) | 2 | |
| c | Cortex (cortical cell) | 2 | |
| Connectivity | |||
|---|---|---|---|
| Syn. weight | Source | Target | Temporal kernel |
| wONrg | g | r |  |
| wONrig | g | r | 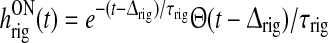 |
| w{ON,OFF}cr | r | c |  |
| w{ON,OFFx}rc | c | r | 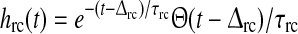 |
| General firing-rate model | |||
|---|---|---|---|
| Firing rate ganglion cell (ON) | 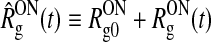 |
||
| Firing rate relay cells | 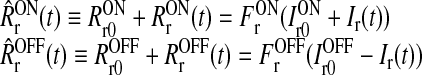 |
||
| Firing rate cortical cells | 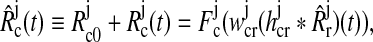 |
||
| where Rjk0 (k = g, r, c; j = ON, OFF) is background firing rate, Rjk(t) is stimulus-evoked change in firing rate. Background input: | |||
| IONr0 = (wONrg −wONrig) RONg0 + wONrcRONc0 + wOFFxrcROFFc0 | |||
| Stimulus-evoked input: | |||
 |
|||
F is the firing rate function, 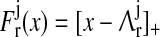 and and 
|
|||
| Stimulus | Drifting sinusoidal gratings: 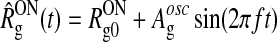
|
||
Light impulses:  , with , with |
|||
 |
|||
Table 2.
Tabular description of the model, part 2
| Final numerical model | |
|---|---|
| Dynamical system | Auxiliary variable |
 | |
| Delay differential equation | |
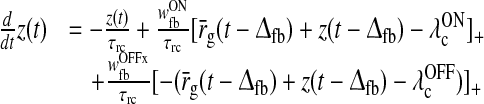 | |
| where | |
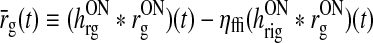 | |
| Firing rate relay cells |  |
| Firing rate cortical cells | 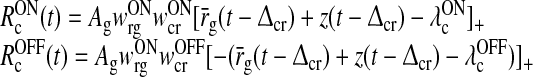 |
Fig. 2.
Illustration of salient features of the LGN circuit model described by (31)–(40). a shows an example trace of the ON LGN relay-cell firing rate  (in units of AgwONrg) where λONr is so small that the relay-cell firing-rate function in (35) always is in the linear regime. In b the stimulus-evoked (i.e., time-dependent) part RONr(t) of this relay-cell firing rate is shown. c Shows the corresponding firing rate in the cortical ON cell for two cases: without thalamocortical feedforward delay (
(in units of AgwONrg) where λONr is so small that the relay-cell firing-rate function in (35) always is in the linear regime. In b the stimulus-evoked (i.e., time-dependent) part RONr(t) of this relay-cell firing rate is shown. c Shows the corresponding firing rate in the cortical ON cell for two cases: without thalamocortical feedforward delay (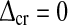 , solid line) and with a feedforward delay
, solid line) and with a feedforward delay  (dashed line). The half-wave rectification function implies that there is only non-zero cortical firing at times when
(dashed line). The half-wave rectification function implies that there is only non-zero cortical firing at times when 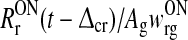 is larger than λONc, cf. b. The corresponding firing rate of the cortical OFF cell is shown in d. Here a response is only elicited when
is larger than λONc, cf. b. The corresponding firing rate of the cortical OFF cell is shown in d. Here a response is only elicited when  is less than λOFFc, cf. b. In the example we have set wONcr = wOFFcr = 1, and cortical feedback to LGN is absent, i.e., wONrc = wOFFxrc = 0
is less than λOFFc, cf. b. In the example we have set wONcr = wOFFcr = 1, and cortical feedback to LGN is absent, i.e., wONrc = wOFFxrc = 0
Linear model for balanced ON/OFF feedback
The differential Eq. (31) for the filtered feedback effect z(t) is non-linear due to the presence of the half-wave rectification functions. However, for the special case when (1) the ON and OFF feedback weights are opposite with the same magnitude, i.e., wONfb = −wOFFxfb ≡ wfb, and (2) the thresholds of the ON and OFF cortical cells both are zero, i.e., λONc = λOFFc = 0, the combined effect of the feedback from the cortical ON and OFF cells turns out to be linear. In this case the two half-wave rectifying functions on the right hand side of (31) add up to a linear function, i.e., [x]+ − [−x]+ = x, and the differential delay equation for z(t) simplifies to
 |
41 |
If in addition the relay-cell threshold λONr is sufficiently low so that 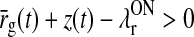 , the half-wave rectification function [x]+ can be replaced with x in (35), and we then have a completely linear model for the stimulus-evoked relay-cell response (Einevoll and Plesser 2002, 2011).
, the half-wave rectification function [x]+ can be replaced with x in (35), and we then have a completely linear model for the stimulus-evoked relay-cell response (Einevoll and Plesser 2002, 2011).
Feedforward temporal coupling kernels
While the particular choice of thalamocortical and corticothalamic temporal coupling kernels in (12) and (13), respectively, is required to map the system on integral form onto a single first-order differential system, no particular requirements are imposed on the feedforward excitatory and inhibitory temporal kernels hONrg(t) and hONrig(t). For simplicity, we here assume that they both are decaying exponentials (Einevoll and Plesser 2002) where the onset of the inhibitory effect, which is disynaptic since it is mediated by the intrageniculate interneuron, is delayed by a time  compared to the onset of the excitatory effect, i.e.,
compared to the onset of the excitatory effect, i.e.,
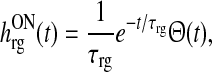 |
42 |
 |
43 |
Here τrg and τrig are the time constants of the two feedforward pathways.
Linear systems analysis
Linear systems such as (41) with a linear relay-cell firing rate function are most transparently described in frequency space. For linear systems the response to a sinusoidal input is a (phase-shifted) sinusoidal output, and the transfer function, i.e., the ratio between the output and input sinusoidal signals, completely specifies the system (Oppenheim and Willsky 1996; Einevoll and Plesser 2002). But also for non-linear neural systems, this measure has been used to characterize input/output relationships (e.g., Blomquist et al. 2009).
For our geniculate model circuit the transfer function  is defined via (Einevoll and Plesser 2002)
is defined via (Einevoll and Plesser 2002)
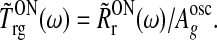 |
44 |
Here ω is the so called angular temporal frequency related to the more traditional temporal frequency f via ω = 2π f. Further, Aoscg is the amplitude of the sinusoidally oscillating input firing rate RONg(t), while 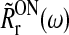 is a complex representation of the first harmonic Fourier amplitude, as well as phase-shift, of the evoked relay-cell firing-rate RONr(t) (Einevoll and Plesser 2002).
is a complex representation of the first harmonic Fourier amplitude, as well as phase-shift, of the evoked relay-cell firing-rate RONr(t) (Einevoll and Plesser 2002).
This firing-rate transfer function  from retina to LGN can in the general case be evaluated numerically by solving our model (31) with sinusoidal retinal input imposed, and then perform a numerical Fourier transform of the resulting relay-cell firing rate (see "Appendix 3" for details). However, for our linear system (41), with feedforward coupling kernels described by (42)–(43), we can find a closed-form solution. Following the approach in Einevoll and Plesser (2002) we find
from retina to LGN can in the general case be evaluated numerically by solving our model (31) with sinusoidal retinal input imposed, and then perform a numerical Fourier transform of the resulting relay-cell firing rate (see "Appendix 3" for details). However, for our linear system (41), with feedforward coupling kernels described by (42)–(43), we can find a closed-form solution. Following the approach in Einevoll and Plesser (2002) we find
 |
45 |
Here 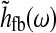 is the Fourier transform of the total kernel for the thalamocortical loop, i.e.,
is the Fourier transform of the total kernel for the thalamocortical loop, i.e.,
 |
46 |
With the convention
 |
47 |
we find with the use of (12) and (13) that
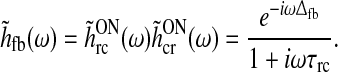 |
48 |
The Fourier transform of the feedforward kernels in (42) and (43) are
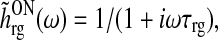 |
49 |
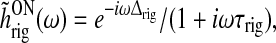 |
50 |
and the resulting transfer function becomes (Einevoll and Plesser 2002)
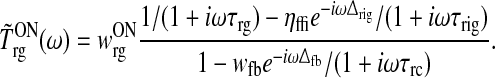 |
51 |
A core feature of such a linear-system transfer function is that it is independent of retinal processing. This implies that the analysis of results from experiments with drifting-grating stimuli, where the input firing-rate from retinal ganglion cells will be sinusoidally modulated, in principle is more straightforward than for other choices of visual stimuli (e.g., flashing spots and white-noise).
Results
Our model can in principle predict responses of LGN relay cells to any kind of visual stimuli, i.e., any kind of incoming firing-rate patterns from retinal ganglion cells. Many types of visual stimuli have been used, e.g., flashing spots, drifting gratings or white-noise stimuli to extract impulse responses. The main emphasis in this paper is on how the feedforward and feedback elements of the thalamocortical circuit modify the impulse responses of LGN relay cells compared to the impulse response of the retinal ganglion cells driving the circuit (Cai et al. 1997; Usrey et al. 1999; Yousif and Denham 2007). First, however, we will briefly investigate the model response to sinusoidal gratings.
Drifting sinusoidal gratings
The use of sinusoidal drifting gratings as visual stimuli has a long history in visual neuroscience (Enroth-Cugell and Robson 1966; Shapley and Lennie 1985). A main advantage of such stimuli is that for linear systems each frequency component can be probed individually. Drifting sinusoidal stimuli have also been used to probe the temporal signal processing properties of LGN relay neurons (Derrington and Fuchs 1979; Kaplan et al. 1987, 1993; Mukherjee and Kaplan 1995; Marrocco et al. 1996). Typically the temporal frequency tuning curves have exhibited maxima between 6 and 10 Hz, but the measured tuning curves have been quite variable (Derrington and Fuchs 1979; Kaplan et al. 1979, 1987), and have further been found to depend on the level of arousal (Kaplan et al. 1993; Mukherjee and Kaplan 1995). Further, the retinogeniculate transfer ratio, i.e., the amplitude of the transfer function (44), has correspondingly been found to exhibit a band-pass property where the peak also occurs for temporal frequencies f around 6–10 Hz (Kaplan et al. 1987, 1993; Mukherjee and Kaplan 1995). Attempts have also been made to unravel cortical feedback effects by investigating changes in the tuning curves when feedback effects are altered by cortical inactivation. However, such experiments have proved very difficult to do, and the reported results have been inconclusive (Marrocco et al. 1996; Casti et al. 2004).
In the modeling of drifting-grating response the retinal firing rate providing the feedforward input is assumed to be linear, i.e.,
 |
52 |
In the general case the relay-cell firing rate must first be evaluated numerically for each input frequency separately by solving the differential Eq. (31) to get the auxiliary variable z(t), followed by use of (35) to obtain the relay-cell firing rate 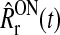 . Then in the second step, the amplitude of the first Fourier component
. Then in the second step, the amplitude of the first Fourier component  of this relay-cell firing rate must be calculated to get the (complex-valued) transfer function; see "Appendix 3" for details. This extracted amplitude divided by the amplitude Aoscg of the oscillating retinal input gives the transfer ratio.
of this relay-cell firing rate must be calculated to get the (complex-valued) transfer function; see "Appendix 3" for details. This extracted amplitude divided by the amplitude Aoscg of the oscillating retinal input gives the transfer ratio.
For the cases where the cortical feedback is absent, i.e., wONfb = wOFFxfb = 0, or the ON/OFF feedback is ’balanced’ so that (41) applies, and the amplitude of the resulting sinusoidal variation of the relay-cell firing rate is so small that the argument of the half-wave rectification in (35) is always positive, the system will be linear. In these situations we already have the transfer function: it is given by the closed-form expression in (51).
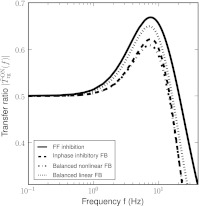
In Fig. 3 we show the transfer ratio, i.e., the magnitude  of the transfer function, for four example cases: (1) only feedforward excitation and inhibition, i.e., no cortical feedback, (2) feedforward excitation and inphase inhibition, i.e., inhibitory feedback driven by cortical ON cells (ηffi = 0, wONfb < 0, wOFFxfb = 0), (3) feedforward excitation plus a balanced combination of inphase inhibition (driven by cortical ON cells) and antiphase excitation (driven by cortical OFF cell), i.e., ηffi = 0, wONfb < 0, wOFFxfb > 0, and (4) feedforward excitation and balanced, effectively linear, feedback from cortical ON and OFF cells. For cases (2)–(3) the results are found using the numerical scheme briefly outlined above. For cases (1) and (4) the transfer ratio is found directly from the analytical formula (51). The different transfer-ratio tuning curves for our four example models are seen to be quite similar and also in qualitative accordance with previous experimental observations (Kaplan et al. 1987; Mukherjee and Kaplan 1995).
of the transfer function, for four example cases: (1) only feedforward excitation and inhibition, i.e., no cortical feedback, (2) feedforward excitation and inphase inhibition, i.e., inhibitory feedback driven by cortical ON cells (ηffi = 0, wONfb < 0, wOFFxfb = 0), (3) feedforward excitation plus a balanced combination of inphase inhibition (driven by cortical ON cells) and antiphase excitation (driven by cortical OFF cell), i.e., ηffi = 0, wONfb < 0, wOFFxfb > 0, and (4) feedforward excitation and balanced, effectively linear, feedback from cortical ON and OFF cells. For cases (2)–(3) the results are found using the numerical scheme briefly outlined above. For cases (1) and (4) the transfer ratio is found directly from the analytical formula (51). The different transfer-ratio tuning curves for our four example models are seen to be quite similar and also in qualitative accordance with previous experimental observations (Kaplan et al. 1987; Mukherjee and Kaplan 1995).
Fig. 3.
Example retinogeniculate transfer ratios  for various combinations of feedforward and feedback LGN circuit connections. Solid line Linear model with feedforward excitation and inhibition only, so that (51) is applicable. Parameters: ηffi = 0.5, τrg = 10 ms, τrig = 30 ms,
for various combinations of feedforward and feedback LGN circuit connections. Solid line Linear model with feedforward excitation and inhibition only, so that (51) is applicable. Parameters: ηffi = 0.5, τrg = 10 ms, τrig = 30 ms,  (wONfb = wOFFxfb = 0). Dashed line Non-linear model with feedforward excitation and inphase inhibition. Parameters: τrg = 26 ms, wONfb = −1, wOFFxfb = 0, τrc = 39 ms,
(wONfb = wOFFxfb = 0). Dashed line Non-linear model with feedforward excitation and inphase inhibition. Parameters: τrg = 26 ms, wONfb = −1, wOFFxfb = 0, τrc = 39 ms, 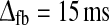 and λONc = 0.2 (ηffi = 0). Dash-dotted line Balanced non-linear model with feedforward excitation and a combination of inphase inhibitory and antiphase excitatory feedback. Parameters: τrg = 26 ms, wONfb = −wOFFxfb = −1, τrc = 39 ms,
and λONc = 0.2 (ηffi = 0). Dash-dotted line Balanced non-linear model with feedforward excitation and a combination of inphase inhibitory and antiphase excitatory feedback. Parameters: τrg = 26 ms, wONfb = −wOFFxfb = −1, τrc = 39 ms, 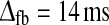 , λONc = 0.2, λOFFc = −0.2 (ηffi = 0). Dotted line Linear model with feedforward excitation and balanced linear feedback so that (51) is applicable. Parameters: τrg = 21 ms, wfb = −1, τrc = 42 ms,
, λONc = 0.2, λOFFc = −0.2 (ηffi = 0). Dotted line Linear model with feedforward excitation and balanced linear feedback so that (51) is applicable. Parameters: τrg = 21 ms, wfb = −1, τrc = 42 ms, 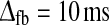 . The relay-cell threshold λONr is in all cases set to be negative (λONr = −1), and the amplitude Aoscg of the sinusoidal driving input from retina set to be so small (Aoscg = 0.7) in the numerical simulations so that the firing-rate function for the relay ON cell always is in the linear regime
. The relay-cell threshold λONr is in all cases set to be negative (λONr = −1), and the amplitude Aoscg of the sinusoidal driving input from retina set to be so small (Aoscg = 0.7) in the numerical simulations so that the firing-rate function for the relay ON cell always is in the linear regime
Our results for drifting-grating stimuli indicate that it might be difficult to disambiguate feedforward and feedback effects from transfer function frequency tuning curves. We thus turn to another type of visual stimulus.
Impulse response
For neurons in the visual system the impulse response corresponds to the change in firing rate following a very brief light stimulation by a point-like light source. White-noise analysis of LGN neurons, as well as their retinal input, has revealed characteristic biphasic temporal structures of this impulse response (DeAngelis et al. 1995; Cai et al. 1997; Usrey et al. 1999). For ON neurons, for example, a brief point-like increased illumination in the receptive field center typically gives a positive impulse-response phase lasting for about 50 ms or so, followed by a negative rebound phase lasting for about the same time or longer (Cai et al. 1997; Usrey et al. 1999). Usrey et al. (1999) did a comprehensive study of impulse responses of LGN neurons and their dominant retinal input, and their investigations revealed characteristic differences between the input and output impulse responses: (1) the peak of the maximum impulse response of the LGN neuron was delayed compared to its retinal input, (2) the amplitude of the negative rebound phase for the LGN neurons was typically larger in relative terms than for their retinal input.
Here we explore within the context of our model how the detailed form of the impulse response of LGN neurons is affected by feedforward and feedback circuit effects. The relatively simple model structure, and thus modest number of crucial model parameters, allow for a comprehensive investigation of the model parameter space.
Following Yousif and Denham (2007) we model the (normalized) biphasic impulse response of the retinal input as follows:
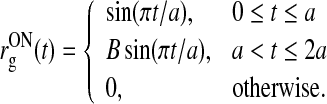 |
53 |
Here B is a positive number smaller than one, and a is the duration of each phase of the signal. The form of this retinal impulse response function with B = 0.38 and a = 42.5 ms is shown in Fig. 4. These parameter values give the time 21.2 ms for the maximum of the impulse reponse and a relative amplitude value of 0.38 for the negative rebound phase compared to the amplitude of the first positive phase. These numbers correspond to the mean of the range of values reported by Usrey et al. (1999).
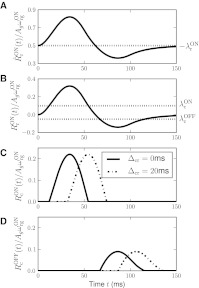
Fig. 4.
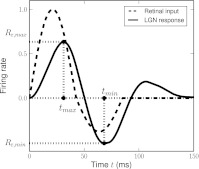
Impulse response. Biphasic normalized impulse response for a retinal ganglion cell (dashed line) and the corresponding impulse response of an LGN relay cell driven by the ganglion cell (solid line). The depicted normalized retinal-input impulse response is used throughout this paper and is described by the formula in (53) with parameter values B = 0.38 and a = 42.5 ms. Rr,max the maximal value of the relay-cell response in the first phase (occurring at tmax), and Rr,min the magnitude at the minimum of for the second phase (occurring at tmin). The biphasic indexIBP is defined as the ratio of these two quantities, i.e., IBP ≡ Rr,min/Rr,max
In the present model application we assume for simplicity that the relay-cell threshold value and the magnitude of the retinal input pulse are such that the half-wave rectification non-linearity [x]+ in the firing-rate function for the relay ON cell in (35) never comes into play, and can be replaced by x, i.e., that the firing-rate function always operates in the linear regime, cf., top panel in Fig. 2. Beyond the requirement of assuring a linear impulse response, the choice of relay-cell threshold value λONr will thus not affect the calculated impulse response.
In Fig. 4 we also show an illustration of an LGN impulse response driven by the retinal-input impulse response depicted in the same figure (see caption for model parameters). Compared to the input impulse response, the example LGN impulse response exhibits both of the characteristic features observed by Usrey et al. (1999): delayed maximum response in the first phase and a larger negative rebound, both in absolute and relative terms, in the second phase. The example LGN response in the figure is triphasic, i.e., it has a second positive rebound phase after the negative rebound phase. While Cai et al. (1997) reported most of the measured LGN impulse responses to be biphasic, some cells were also found to have mono- or triphasic responses.
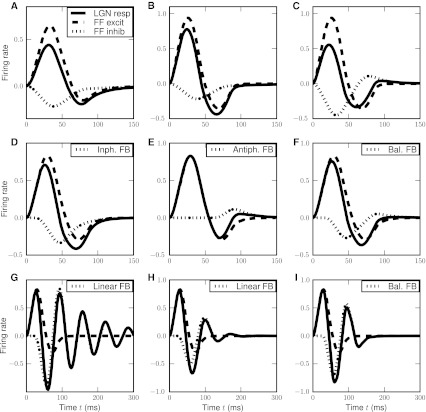
In Fig. 5 we illustrate the formation of the ON LGN impulse response RONr(t) by feedforward and feedback contributions in a variety of situations. In all cases the normalized retinal impulse response rONg(t) is the same as in Fig. 4. In the top row we focus on feedforward contributions only, i.e., cortical feedback effects are assumed to be absent, wONfb = wOFFxfb = 0, and the relative weight of the feedforward inhibition compared to the feedforward excitation is fixed at ηffi = 0.7. In panel a we show results for a feedforward model with time constants τrg = 20 ms and τrig = 65 ms. The total impulse response, given by a sum of a biphasic excitatory (positive) response and a monophasic inhibitory (negative) response, is biphasic and long-lasting. With a reduction of the excitatory time constant to τrg = 5 ms as for panel b, the excitatory part of the LGN impulse response is shifted to shorter times and increases in amplitude both for the initial positive phase and for the negative rebound phase. As a consequence the total impulse response becomes stronger than in a. Panel c shows an example of a situation where a triphasic impulse response arises. Here the same small value τrg = 5 ms for the excitatory time constant is combined with the choice τrig = 20 ms for the inhibitory time constant giving a biphasic inhibitory contribution as well. Since τrig is larger than τrg, the duration of the inhibitory contribution will be longer than the excitatory contribution. As seen in panel c the second phase of the inhibitory component will thus give rise to a third phase of the total impulse response RONr(t).
Fig. 5.
Example LGN impulse responses illustrating various effects of feedforward and feedback connections in the LGN circuit. Solid lines Example impulse responses for relay ON cells RONr(t) calculated from Eqs. (18), (31), and (35) for the situation when λONr is such that there are no rectification effects on the response, 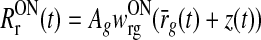 . Dashed lines Contribution from feedforward excitation alone, i.e., AgwONrg (hONrg*RONg)(t). Dotted lines Contribution from feedforward inhibition. i.e., −AgwONrg ηffi (hONrig*RONg)(t), or feedback, i.e., AgwONrgz(t), alone, see specification for each panel. All quantities are shown in units of AgwONrg. a–c Feedforward excitation and inhibition only with ηffi = 0.7. A: τrg = 20 ms, τrig = 65 ms. b τrg = 5 ms, τrig = 65 ms. c τrg = 5 ms, τrig = 20 ms. d Feedforward excitation and inphase inhibitory feedback: τrg = 10 ms, wONfb = −0.75, wOFFxfb = 0, τrc = 20 ms,
. Dashed lines Contribution from feedforward excitation alone, i.e., AgwONrg (hONrg*RONg)(t). Dotted lines Contribution from feedforward inhibition. i.e., −AgwONrg ηffi (hONrig*RONg)(t), or feedback, i.e., AgwONrgz(t), alone, see specification for each panel. All quantities are shown in units of AgwONrg. a–c Feedforward excitation and inhibition only with ηffi = 0.7. A: τrg = 20 ms, τrig = 65 ms. b τrg = 5 ms, τrig = 65 ms. c τrg = 5 ms, τrig = 20 ms. d Feedforward excitation and inphase inhibitory feedback: τrg = 10 ms, wONfb = −0.75, wOFFxfb = 0, τrc = 20 ms, 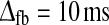 , λONc = 0. E: Feedforward excitation and antiphase excitatory feedback. Parameters as in d except wONfb = 0, wOFFxfb = 0.75, λOFFc = 0. f Feedforward excitation and balanced non-linear feedback. Parameters as in d except wONfb = −0.75, wOFFxfb = 0.75, λONc = 0.15, λOFFc = −0.15. g Feedforward excitation and balanced linear feedback: τrg = 10 ms, wfb = wONfb = −wOFFxfb = −1.8, τrc = 20 ms,
, λONc = 0. E: Feedforward excitation and antiphase excitatory feedback. Parameters as in d except wONfb = 0, wOFFxfb = 0.75, λOFFc = 0. f Feedforward excitation and balanced non-linear feedback. Parameters as in d except wONfb = −0.75, wOFFxfb = 0.75, λONc = 0.15, λOFFc = −0.15. g Feedforward excitation and balanced linear feedback: τrg = 10 ms, wfb = wONfb = −wOFFxfb = −1.8, τrc = 20 ms,  , λONc = λOFFc = 0. h Same as G with wfb = wONfb = −wOFFxfb = −1.0. I Same as G with λONc = 0.15, λOFFc = −0.15. Note different time axes in g–i
, λONc = λOFFc = 0. h Same as G with wfb = wONfb = −wOFFxfb = −1.0. I Same as G with λONc = 0.15, λOFFc = −0.15. Note different time axes in g–i
In the second row of Fig. 5 we correspondingly illustrate the formation of the LGN impulse response RONr(t) by feedback contributions. Here the feedforward inhibition is set to zero, i.e., ηffi = 0, and the feedforward excitatory time constant is fixed to τrg = 10 ms. In panel d we show results for RONr(t) for a model with inphase cortical inhibitory feedback, i.e., inhibitory feedback from ON cortical cells only. For the choice of feedback model parameters used in panel d with (1) substantial feedback (wONfb = −0.75), (2) low firing threshold for the cortical ON cell (λONc = 0), and (3) significant time delays in the thalamocortical loop (τfb = 20 ms, 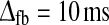 ) a sizable monophasic inhibitory feedback contribution to the impulse response is observed. The total impulse response, i.e., the sum of the feedforward excitatory and feedback inhibitory contribution, thus adds up to a biphasic response qualitatively similar to the purely feedforward impulse responses seen in panels a–c.
) a sizable monophasic inhibitory feedback contribution to the impulse response is observed. The total impulse response, i.e., the sum of the feedforward excitatory and feedback inhibitory contribution, thus adds up to a biphasic response qualitatively similar to the purely feedforward impulse responses seen in panels a–c.
Panel e shows the corresponding results for a model with antiphase cortical excitatory feedback only, i.e., excitatory feedback from OFF cortical cells. Even with a similarly strong feedback as in the previous inphase case (wOFFxfb = 0.75), as well as the same temporal parameters for the cortical loop, a much weaker feedback effect on the relay ON cells is observed. This is because the cortical OFF cells providing this feedback will only be activated during the second phase of the excitatory feedforward contribution to the ON LGN-cell impulse response. Only during this negative phase for the ON relay cells will the OFF relay cells be activated and thus drive the cortical OFF cells responsible for the antiphase feedback. As seen in panel e this weak feedback effect nevertheless gives rise to a small third phase, i.e., a triphasic impulse response.
In panel f in Fig. 5 we show an example where the inphase inhibitory and antiphase excitatory feedback illustrated in panels d and e, respectively, are combined. The same temporal parameters are used, but we have raised the threshold for firing for the cortical cells by imposing non-zero threshold values, i.e., λONc = 0.15, λOFFc = −0.15. For this particular non-linear balanced-feedback case we find a total impulse response very similar to what is obtained by assuming inphase inhibitory feedback alone, cf. panel d.
For the special case when (1) the ON and OFF feedback weights are opposite with the same magnitude, i.e., wONfb = −wOFFxfb ≡ wfb, and (2) the threshold values of the ON and OFF cortical cells both are zero, i.e., λONc = λOFFc = 0, the model becomes fully linear, cf. (41). For this situation the simulated LGN impulse response often shows characteristic oscillations. An example is given in panel g in the lower row of Fig. 5 where we used wfb = −1.8, i.e., a strong feedback weight, and altogether nine phases can be seen. In panel h wfb has been reduced to −1.0, and the oscillatory behavior is less prominent.
The oscillatory characteristics of the impulse response function seen in panels g and h can be understood on the basis of the expression for the linear transfer function in (51). For the model parameters employed in these two panels, this transfer function formula predicts resonance peaks in the transfer ratio for frequencies corresponding to periods of about 65–70 ms, in accordance with the characteristic oscillation times observed in panels g and h. The transfer function formula (51) further predicts lower resonance peaks in panel h than in panel g due to the reduced weight of the cortical feedback, wfb = −1 versus wfb = −1.8. This is again in accordance with the less prominent oscillations seen in panel h compared to panel g.
In panel i we see that the introduction of thresholding non-linearities, i.e., λONc = 0.15 and λOFFc = −0.15, in the neurons providing the cortical feedback also has the effect of reducing the oscillations in the impulse response.
Feedforward versus feedback effects on impulse response
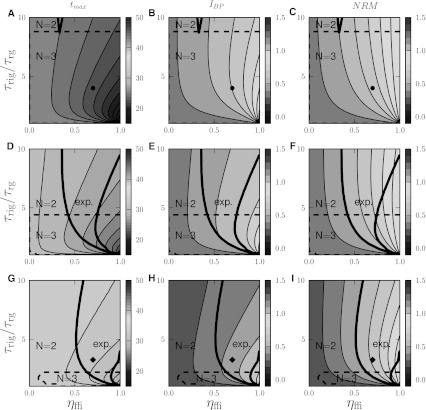
The various examples in Fig. 5 illustrate the large variety of LGN impulse responses that can be produced by our model. In this section we do a more systematic exploration of the model with the aim of identifying regions of the model parameter space for which the predicted impulse responses are compatible with what has been observed in previous experiments (Cai et al. 1997; Usrey et al. 1999). We thus need specific measures characterizing salient features of the LGN impulse response. In accordance with these previous experimental studies we focus on three measures: (1) the time of the first maximum of the response tmax, (2) the biphasic index (IBP) (Cai et al. 1997), and (3) the normalized rebound magnitude (NRM) (Usrey et al. 1999). IBP corresponds to the ratio between the peak magnitude of the (negative) rebound phase and the peak magnitude of the first (positive) phase, cf. Fig. 4. NRM is defined as the magnitude of the integral over the impulse response from the start of the second phase to the end of the impulse response, divided by the integral over the first phase of the impulse response. We only calculate NRM for the cases where the impulse response has three or fewer dominant phases, see "Appendix 3".
In Figs. 6, 7, 8 we show the three measures (tmax, IBP, NRM) for different combinations of model parameters. The retinal impulse response depicted in Fig. 4, which has a time to first maximum and biphasic index corresponding to the average of the experimental results reported by Usrey et al. (1999), provides in all cases the input. These three measures have been recorded experimentally by Cai et al. (1997) and Usrey et al. (1999) for LGN neurons, and as an aid in the interpretation of the ’phase diagrams’ of our model, we have marked the parameter regions where the model results are within previously obtained experimental bounds. From Cai et al. (1997) we extracted (for adult cats) rough lower and upper bounds for tmax to be 25 and 40 ms, respectively. Further, their data suggested that corresponding bounds for IBP could be set to 0.2 and 0.6. Rough lower and upper bounds for NRM were found in Usrey et al. (1999) to be 0.5 and 0.95, respectively.
Fig. 6.
Dependence of LGN impulse-response measures on relative weight (ηffi) and time constant (τrig/τrg) of feedforward inhibition. Parameter dependence of the three impulse-response measures tmax(left column ), biphasic index (IBP; middle column), and normalized rebound magnitude (NRM; right column) for models with feedforward excitation and inhibition, only. The retinal impulse response providing the input is depicted in Fig. 4. In all cases 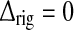 . Top row τrg = 5 ms; middle row τrg = 10 ms; bottom row τrg = 20 ms. The regions confined by thick black lines and marked ‘exp.’ correspond to parameter values which give impulse-response model predictions in agreement with the experimental bounds described in the text. The experimental bounds are
. Top row τrg = 5 ms; middle row τrg = 10 ms; bottom row τrg = 20 ms. The regions confined by thick black lines and marked ‘exp.’ correspond to parameter values which give impulse-response model predictions in agreement with the experimental bounds described in the text. The experimental bounds are 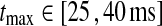 ,
, 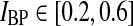 , NRM
, NRM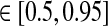 . The dashed lines represent separatrices between regions with biphasic (N = 2) and triphasic (N = 3) impulse responses. The circles in the top row panels and the diamonds in the bottom row correspond to the examples in c and a in Fig. 5, respectively
. The dashed lines represent separatrices between regions with biphasic (N = 2) and triphasic (N = 3) impulse responses. The circles in the top row panels and the diamonds in the bottom row correspond to the examples in c and a in Fig. 5, respectively
Fig. 7.
Dependence of LGN impulse-response measures on weight (wfb) and time delay  of cortical feedback via thalamocortical loop. Parameter dependence of the three impulse-response measures tmax (left column), biphasic index (IBP; middle column), and normalized rebound magnitude (NRM; right column) for models with feedforward excitation and various types of cortical feedback. The retinal impulse response providing the input is depicted in Fig. 4. In all cases τrg = 10 ms, τrc = 20 ms. Top row inphase inhibitory feedback only: λONc = 0, wOFFxfb = 0. Middle row balanced linear feedback: wONfb = −wOFFxfb ≡ wfb, λONc = λOFFc = 0. Bottom row balanced non-linear feedback: wONfb = −w\rm OFFxfb ≡ wfb, λONc = 0.15, λOFFc = −0.15. The regions confined by thick black lines and marked ‘exp.’ in top and bottom row panels, correspond to parameter values which give impulse-response model predictions in agreement with the experimental bounds, see text. The experimental bounds are
of cortical feedback via thalamocortical loop. Parameter dependence of the three impulse-response measures tmax (left column), biphasic index (IBP; middle column), and normalized rebound magnitude (NRM; right column) for models with feedforward excitation and various types of cortical feedback. The retinal impulse response providing the input is depicted in Fig. 4. In all cases τrg = 10 ms, τrc = 20 ms. Top row inphase inhibitory feedback only: λONc = 0, wOFFxfb = 0. Middle row balanced linear feedback: wONfb = −wOFFxfb ≡ wfb, λONc = λOFFc = 0. Bottom row balanced non-linear feedback: wONfb = −w\rm OFFxfb ≡ wfb, λONc = 0.15, λOFFc = −0.15. The regions confined by thick black lines and marked ‘exp.’ in top and bottom row panels, correspond to parameter values which give impulse-response model predictions in agreement with the experimental bounds, see text. The experimental bounds are 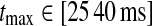 ,
,  , NRM
, NRM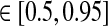 . In the middle row only two tiny regions compatible with these bounds were found. The dashed lines in the panels in the bottom row represent separatrices between regions with biphasic (N = 2), triphasic (N = 3), and multiphasic (N > 3) impulse responses. For the models in the top row, only biphasic (N = 2) responses are found, and all models in the middle row have three or more phases (for wfb < 0). The circles in the top row panels correspond to the example in Fig. 5d. The diamonds and triangles in the middle row correspondingly point out the examples in Fig. 5g and h, respectively. Likewise, the square and triangle in the bottom row show the examples in Fig. 5f and i. In the middle and last rows NRM cannot be evaluated for all parameter combinations according to our criteria (cf. Appendix 3), and this region of phase space is shown in white
. In the middle row only two tiny regions compatible with these bounds were found. The dashed lines in the panels in the bottom row represent separatrices between regions with biphasic (N = 2), triphasic (N = 3), and multiphasic (N > 3) impulse responses. For the models in the top row, only biphasic (N = 2) responses are found, and all models in the middle row have three or more phases (for wfb < 0). The circles in the top row panels correspond to the example in Fig. 5d. The diamonds and triangles in the middle row correspondingly point out the examples in Fig. 5g and h, respectively. Likewise, the square and triangle in the bottom row show the examples in Fig. 5f and i. In the middle and last rows NRM cannot be evaluated for all parameter combinations according to our criteria (cf. Appendix 3), and this region of phase space is shown in white
Fig. 8.
Dependence of LGN impulse-response measures on relative weight of feedforward inhibition (ηffi) and weight of cortical feedback via thalamocortical loop (wfb) for models with feedforward excitation and inhibition and balanced linear cortical feedback. Parameter dependence of the three impulse-response measures tmax (left column), biphasic index (IBP; middle column), and normalized rebound magnitude (NRM; right column) for linear models with feedforward excitation, feedforward inhibition and balanced linear feedback (wONfb = −wOFFxfb ≡ wfb, λONc = λOFFc = 0). The retinal impulse response providing the input is depicted in Fig. 4. In all cases τrg = 10 ms, τrc = 20 ms. Top row τrig = 20 ms, 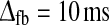 . Middle row τrig = 20 ms,
. Middle row τrig = 20 ms, 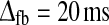 . Bottom row: τrig = 40 ms,
. Bottom row: τrig = 40 ms, 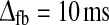 . The regions confined by thick black lines and marked ‘exp.’ correspond to parameter values which give impulse-response model predictions in agreement with the experimental bounds described in the text, i.e.,
. The regions confined by thick black lines and marked ‘exp.’ correspond to parameter values which give impulse-response model predictions in agreement with the experimental bounds described in the text, i.e., 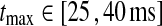 ,
, 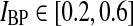 , and NRM
, and NRM . The dashed lines represent separatrices between regions with biphasic (N = 2), triphasic or multiphasic (N ≥ 3) impulse responses. In the middle rowNRM cannot be evaluated for all parameter combinations according to our criteria (cf. Appendix 3), and this region of phase space is shown in white
. The dashed lines represent separatrices between regions with biphasic (N = 2), triphasic or multiphasic (N ≥ 3) impulse responses. In the middle rowNRM cannot be evaluated for all parameter combinations according to our criteria (cf. Appendix 3), and this region of phase space is shown in white
In Fig. 6 we show the three measures tmax, IBP, and NRM for the case with only feedforward connections as a function of two quantities: the relative strength of the feedforward inhibition ηffi (19) and the ratio of the feedforward time constants τrig/τrg. The three rows show the same plots for three choices of the feedforward excitatory time constants: τrg = 5 ms, τrg = 10 ms, and τrg = 20 ms. A sizable fraction of the model parameters considered in Fig. 6 is seen to give impulse-response predictions in accordance with the rough experimental bounds found from Cai et al. (1997) and Usrey et al. (1999).
The peak time tmax (first column) generally decreases with increasing weight ηffi of the feedforward inhibition. This can be qualitatively understood by inspection of panels a–c in Fig. 5. With a longer inhibitory than excitatory time constant, i.e., τrig > τrg, the first peak of the excitatory contribution will occur earlier than the corresponding negative peak for the inhibitory contribution. This implies that the peak of the total impulse response will occur earlier than for the excitatory contribution alone. With larger inhibitory weights this effect will be even more prominent, resulting in the observed ’anti-correlation’ of tmax and ηffi. For the two other measures IBP and NRM we observe the opposite trend in Fig. 6. Both IBP and NRM increase with increasing inhibition ηffi. This correlation is as expected as both quantities essentially measure the depth of the rebound phase which naturally is expected to increase with increased feedforward inhibition.
The different dependency of the experimental measures on ηffi suggests an anti-correlation between tmax and the two rebound depth measures IBP and NRM. This is indeed confirmed by direct evaluation of the correlation coefficient ρ, i.e.,
 |
54 |
when x = tmax and y = IBP. In (54) N is the number of data points considered, and 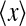 and std(x) represent the mean and standard deviation, respectively, of the quantity x evaluated over the same data points. The marked regions in Fig. 6 found to have model predictions within the experimental bounds for tmax, IBP and NRM, might serve as a tentative indicator for the spread in biologically appropriate model parameters that can be expected in impulse-response experiments. The correlation coefficient ρ(tmax, IBP) evaluated over these marked regions may thus be a model prediction that can be compared with experimental data. When evaluated over these marked parameter regions, the models in Fig. 6 give ρ(tmax,IBP) = −0.93, ρ(tmax,IBP) = −0.76 and ρ(tmax,IBP) = −0.95 for τrg = 5, 10, and 20, respectively.
and std(x) represent the mean and standard deviation, respectively, of the quantity x evaluated over the same data points. The marked regions in Fig. 6 found to have model predictions within the experimental bounds for tmax, IBP and NRM, might serve as a tentative indicator for the spread in biologically appropriate model parameters that can be expected in impulse-response experiments. The correlation coefficient ρ(tmax, IBP) evaluated over these marked regions may thus be a model prediction that can be compared with experimental data. When evaluated over these marked parameter regions, the models in Fig. 6 give ρ(tmax,IBP) = −0.93, ρ(tmax,IBP) = −0.76 and ρ(tmax,IBP) = −0.95 for τrg = 5, 10, and 20, respectively.
While these results assume undelayed onset of feedforward inhibition compared to excitation, i.e.,  , they do not change much when non-zero onset delays are assumed. The observed anticorrelation remained for
, they do not change much when non-zero onset delays are assumed. The observed anticorrelation remained for  , i.e., ρ(tmax, IBP) was found to always be more negative than −0.7 for the models considered in Fig. 6 (results not shown).
, i.e., ρ(tmax, IBP) was found to always be more negative than −0.7 for the models considered in Fig. 6 (results not shown).
In Fig. 6 we also show the number of phases the impulse response has for the various parameter choices. For these purely feedforward models the response is either biphasic (N = 2) or triphasic (N = 3), and the results indicate that an increase in excitatory time constant τrg tends to increase the likelihood for observing biphasic impulse responses.
In Fig. 7 we turn to models with cortical feedback and no feedforward inhibition and show the three same measures tmax, IBP, and NRM as functions of the strength of the cortical feedback (wONfb and/or wOFFxfb) and the total feedback delay 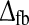 (20). We mainly focus on the models for which the net effect of the cortical feedback is to increase the size of the negative rebound compared to the retinal input, and in the top row of Fig. 7 we show results for the case where the only cortical feedback effect is inphase and inhibitory, i.e., wONfb < 0, wOFFxfb = 0 (and λONc = 0). As for the feedforward models considered in Fig. 6, the peak time tmax decreases with increasing magnitude of the inhibitory weight. This effect will necessarily always be present due to the unavoidable delay imposed on the inhibitory action by the round trip in the thalamocortical loop. As for the feedforward-inhibition case, the rebound measures IBP and NRM also increase with increased inhibition, i.e., increased |wONfb|, for the inphase feedback case, cf. panels b and c in Fig. 7. However, unlike for the feedforward-inhibition case, Fig. 7 shows a less clear pattern of covariation between tmax and IBP or NRM when the model parameters wONfb and
(20). We mainly focus on the models for which the net effect of the cortical feedback is to increase the size of the negative rebound compared to the retinal input, and in the top row of Fig. 7 we show results for the case where the only cortical feedback effect is inphase and inhibitory, i.e., wONfb < 0, wOFFxfb = 0 (and λONc = 0). As for the feedforward models considered in Fig. 6, the peak time tmax decreases with increasing magnitude of the inhibitory weight. This effect will necessarily always be present due to the unavoidable delay imposed on the inhibitory action by the round trip in the thalamocortical loop. As for the feedforward-inhibition case, the rebound measures IBP and NRM also increase with increased inhibition, i.e., increased |wONfb|, for the inphase feedback case, cf. panels b and c in Fig. 7. However, unlike for the feedforward-inhibition case, Fig. 7 shows a less clear pattern of covariation between tmax and IBP or NRM when the model parameters wONfb and 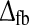 are varied. This is confirmed by evaluation of the correlation coefficient ρ(tmax, IBP) in (54). For the inphase inhibitory-feedback model in the top row only a modest negative correlation coefficient, ρ(tmax,IBP) = −0.30, was obtained when evaluating (54) over the region found to be compatible with the experimental bounds.
are varied. This is confirmed by evaluation of the correlation coefficient ρ(tmax, IBP) in (54). For the inphase inhibitory-feedback model in the top row only a modest negative correlation coefficient, ρ(tmax,IBP) = −0.30, was obtained when evaluating (54) over the region found to be compatible with the experimental bounds.
Another difference from the feedforward-inhibition models is that there can only be two phases in the impulse response. This is a consequence of our assumption of absence of cortical feedback effects when only the background inputs are present, i.e., the effective threshold λONc in (31) must be non-negative. The requirement λONc ≥ 0 implies for the case with inphase feedback alone, that only the positive phase of the feedforward excitatory contribution to the impulse response can drive the cortical ON population. Consequently, the cortical response will be monophasic, and the resulting relay-cell response biphasic. Thus all models in the top row of Fig. 7 corresponds to N = 2.
In the middle row of Fig. 7 we show results for tmax, IBP, and NRM when the inphase inhibitory feedback is supplemented by an antiphase excitatory feedback of the same magnitude, i.e., wfb ≡ wONfb = −wOFFxfb. It is further assumed that λOFFc = λONc = 0, making the model fully linear (41). The addition of the antiphase excitation makes the impulse response prone to oscillations. In fact, for all combinations of wfb and 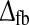 considered in the middle row panels the number of phases N is three or more (for wfb < 0), and for the white-colored part of the plot of NRM in panel f the oscillations persisted so long that the NRM measure could not be calculated. An example of this situation is given by the impulse-response plot depicted in panel g of Fig. 5. For this linear feedback model only a small set of combinations of wfb and
considered in the middle row panels the number of phases N is three or more (for wfb < 0), and for the white-colored part of the plot of NRM in panel f the oscillations persisted so long that the NRM measure could not be calculated. An example of this situation is given by the impulse-response plot depicted in panel g of Fig. 5. For this linear feedback model only a small set of combinations of wfb and 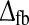 give impulse-response functions in accordance with all three aforementioned experimental bounds.
give impulse-response functions in accordance with all three aforementioned experimental bounds.
The example impulse response function in panel i of Fig. 5 suggests that the introduction of thresholding non-linearities in the cortical cells providing the cortical feedback will counteract the tendency for models with balanced inphase and antiphase feedback to have oscillatory impulse responses. This is confirmed by the plots in the bottom row of Fig. 7. Here the cortical thresholds are set to λONc = 0.15 and λOFFc = −0.15, respectively. While tmax is little affected by the introduction of the thresholds compared to the linear case in the middle row, the tendency to oscillate for large feedback weights is strongly reduced, as manifested by lower values of IBP, and NRM. In fact, a sizable region of the (wfb, 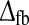 ) phase space now gives impulse-response functions in accordance with the experimental bounds.
) phase space now gives impulse-response functions in accordance with the experimental bounds.
For the purely feedforward models in Fig. 6, tmax and IBP were strongly anticorrelated, and ρ(tmax, IBP) was between −0.76 and −0.95. A much weaker correlation between tmax and IBP is found for the feedback models in Fig. 7. As mentioned above the value found for the inphase inhibitory-feedback model in the top row was ρ(tmax,IBP) = −0.30. For the balanced linear feedback models in the middle row, a small positive correlation coefficient ρ(tmax,IBP) = 0.29 was found for the small regions of parameter space satisfying all criteria. For the balanced non-linear feedback model in the bottom row of Fig. 7, a larger positive correlation coefficient ρ(tmax,IBP) = 0.64 was found.
Only a limited number of the models in Fig. 7d–f with balanced linear feedback alone give predictions in accordance with the experimental bounds for tmax, IBP, and NRM simultaneously. However, this can be remedied by inclusion of feedforward inhibition. In such combined linear models with both feedforward and feedback interaction, large values of IBP and NRM (in accordance with experimental observation) can be obtained without the generation of oscillations typically accompanying strong cortical feedback. In Fig. 8 we show results for such combined models with feedforward inhibition added to the balanced linear cortical feedback. In the top row we show results for τrg = 10 ms, τrig = 20 ms, τfb = 20 ms, and 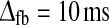 . For these parameters a sizable number of combinations of wfb and ηffi give predictions within the experimental bounds. The required amount of feedforward inhibition ηffi needed in order to obtain the large values of IBP and NRM seen in experiments, is reduced with the present addition of cortical feedback with inhibitory inphase action, i.e., wfb < 0. For the part of parameter space compatible with the experimental bounds, tmax and IBP are only weakly anticorrelated, ρ(tmax,IBP) = −0.30.
. For these parameters a sizable number of combinations of wfb and ηffi give predictions within the experimental bounds. The required amount of feedforward inhibition ηffi needed in order to obtain the large values of IBP and NRM seen in experiments, is reduced with the present addition of cortical feedback with inhibitory inphase action, i.e., wfb < 0. For the part of parameter space compatible with the experimental bounds, tmax and IBP are only weakly anticorrelated, ρ(tmax,IBP) = −0.30.
When the delay parameter 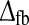 is increased from 10 to 20 ms as shown in the middle row of Fig. 8, the cortical feedback inhibition arrives closer to the minimum provided by the feedforward contributions to the impulse-response function. Consequently, the total impulse response gets more prone to oscillations, and this leads to a shrinking of the size of the region in the (wfb, ηffi) parameter space where the impulse-response predictions are within the experimental bounds. In this region tmax and IBP is found to have a weak positive correlation, ρ(tmax,IBP) = 0.32.
is increased from 10 to 20 ms as shown in the middle row of Fig. 8, the cortical feedback inhibition arrives closer to the minimum provided by the feedforward contributions to the impulse-response function. Consequently, the total impulse response gets more prone to oscillations, and this leads to a shrinking of the size of the region in the (wfb, ηffi) parameter space where the impulse-response predictions are within the experimental bounds. In this region tmax and IBP is found to have a weak positive correlation, ρ(tmax,IBP) = 0.32.
In the bottom row of Fig. 8 we have instead modified the situation in the top row by increasing the inhibitory time constant τrig to 40 ms This gives an even larger region of the parameter space where model predictions are in accordance with the experimental observations. Here tmax and IBP are moderately anticorrelated, ρ(tmax,IBP) = −0.46.
Scheme for comparison with experiments
In Fig. 6, 7, 8 we calculated the experimental measures (tmax, IBP, NRM) for different combinations of LGN circuit model parameters, but only the single retinal impulse response depicted in Fig. 4 was considered as input. This retinal impulse response was chosen to have time to first maximum tretmax and biphasic index IretBP corresponding to average values of the experimental results reported in Usrey et al. (1999). We found the correlation coefficient ρ(tmax, IBP) to vary significantly between different variations of the LGN circuit. This suggests an experimental test for assessing the relative importance of feedforward and feedback effects in shaping the LGN relay cells according to predictions from our model.
The response latency of relay cells and their retinal input may vary over tens of milliseconds (Guido and Sherman 1998; Wolfe and Palmer 1998). However, this large variability appears to be mainly due to the variability of the latency of the retinal input: Usrey et al. (1999), for example, found the latency difference between the relay-cell firing and the retinal input for cat X cells to vary with less than 1 ms around the mean value of about 4 ms. One approach for comparison with experiments would thus be to (1) consider subsets of experimental data of the type reported in Usrey et al. (1999) comprising, say, (nonlagged) X cell pairs with similar shapes of retinal impulse responses, (2) temporally align the different experimental traces according to the values of tretmax of the retinal input, (3) calculate correlation coefficients of the type in Eq. (54), and (4) compare with model predictions.
This approach limits the number of cell pairs that can be used in the evaluation of the correlation coefficients. A better approach may be to search for other experimental measures with characteristic correlations also in data including variations in the retinal impulse response. For example, one may consider the correlations between relative differences in time to first maximum and biphasic index, i.e., between
 |
55 |
The study of Usrey et al. (1999) provides an estimate for the typical spread in the shape of the retinal impulse response, and we extracted the following intervals of the measures involved: 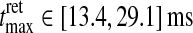 ,
,  . The retinal impulse response used in Figs. 4, 5, 6, 8 corresponds to the median value, i.e., tretmax = 21.2 ms and IretBP = 0.38. When only a single retinal impulse response is used, the correlation coefficient
. The retinal impulse response used in Figs. 4, 5, 6, 8 corresponds to the median value, i.e., tretmax = 21.2 ms and IretBP = 0.38. When only a single retinal impulse response is used, the correlation coefficient  will be identical to the previously calculated correlation coefficient ρ(tmax, IBP). When the ensemble of models included in the calculation of
will be identical to the previously calculated correlation coefficient ρ(tmax, IBP). When the ensemble of models included in the calculation of  incorporates spread in the form of the retinal impulse response function, however, this will no longer be so. In Fig. 9 we show the variation of
incorporates spread in the form of the retinal impulse response function, however, this will no longer be so. In Fig. 9 we show the variation of  as a function of the size of the ensemble of retinal impulse responses, i.e., from including only a single retinal impulse response (corresponding to the average value) to including the full intervals measured by Usrey et al. (1999). Panel a in the figure shows the results for
as a function of the size of the ensemble of retinal impulse responses, i.e., from including only a single retinal impulse response (corresponding to the average value) to including the full intervals measured by Usrey et al. (1999). Panel a in the figure shows the results for  for the pure feedforward model in the middle row of Fig. 6 (τrg = 10 ms) as well as the three feedback models considered in Fig. 7. While the correlation coefficients are seen to vary somewhat when including more variation in the retinal impulse responses, clear separations between the various model types are largely maintained. The corresponding results for τrg = 20 ms are shown in panel b, where the pure feedforward model corresponds to the model in the bottom row of Fig. 6 while the feedback models have no direct counterparts in the presented phase plots. Here the various model types exhibit even clearer differences in their correlation coefficients. This suggests that evaluation of
for the pure feedforward model in the middle row of Fig. 6 (τrg = 10 ms) as well as the three feedback models considered in Fig. 7. While the correlation coefficients are seen to vary somewhat when including more variation in the retinal impulse responses, clear separations between the various model types are largely maintained. The corresponding results for τrg = 20 ms are shown in panel b, where the pure feedforward model corresponds to the model in the bottom row of Fig. 6 while the feedback models have no direct counterparts in the presented phase plots. Here the various model types exhibit even clearer differences in their correlation coefficients. This suggests that evaluation of 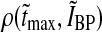 over an ensemble of measurements including different retinal impulse responses may be used to distinguish between different candidate LGN circuit models.
over an ensemble of measurements including different retinal impulse responses may be used to distinguish between different candidate LGN circuit models.
Fig. 9.
Correlation coefficients between 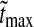 and
and 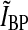 for various ensembles of retinal impulse responses providing input. The correlation coefficient (54) for the quantities
for various ensembles of retinal impulse responses providing input. The correlation coefficient (54) for the quantities 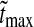 and
and 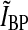 defined in (55) is calculated for various ensembles of retinal inputs, i.e., various fractions of the interval of time to first max and biphasic index of retinal impulse responses observed in Usrey et al. (1999):
defined in (55) is calculated for various ensembles of retinal inputs, i.e., various fractions of the interval of time to first max and biphasic index of retinal impulse responses observed in Usrey et al. (1999):  ,
,  . The fraction zero corresponds to a single retinal impulse response modeled by (53) corresponding to the median value, i.e., tretmax = 21.2 ms and IretBP = 0.38, the fraction one corresponds to the entire interval, the fraction 1/2 to the intervals
. The fraction zero corresponds to a single retinal impulse response modeled by (53) corresponding to the median value, i.e., tretmax = 21.2 ms and IretBP = 0.38, the fraction one corresponds to the entire interval, the fraction 1/2 to the intervals 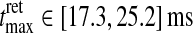 ,
, 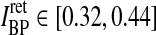 , etc.. For each value of the fraction a total about 2,000 simulations are done with (1) retinal input parameters tretmax (a/2 in (53)) and IretBP (B in (53)) randomly drawn from uniform distributions on the relevant intervals, and (2) LGN circuit model parameters drawn from uniform distributions over the two depicted parameters in the relevant ’phase plots’ in Figs. 6 and 7. Only the parameter choices that give models producing LGN impulse responses within the experimental bounds
, etc.. For each value of the fraction a total about 2,000 simulations are done with (1) retinal input parameters tretmax (a/2 in (53)) and IretBP (B in (53)) randomly drawn from uniform distributions on the relevant intervals, and (2) LGN circuit model parameters drawn from uniform distributions over the two depicted parameters in the relevant ’phase plots’ in Figs. 6 and 7. Only the parameter choices that give models producing LGN impulse responses within the experimental bounds 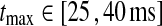 ,
,  , and NRM
, and NRM are included in the evaluation of the correlation coefficients. Result for the pure feedforward model in Fig. 6(d–f) (’FF only’) and all three feedback models in Fig. 7 (top row ’Inph FB’, middle row ’Linear FB’, bottom row ’Bal. FB’) are shown. a τrg = 10 ms. b τrg = 20 ms. In B, no LGN impulse responses within the experimental bounds were obtained for the linear feedback model for small fractions of the parameter intervals, hence the absent line for fractions <0.6
are included in the evaluation of the correlation coefficients. Result for the pure feedforward model in Fig. 6(d–f) (’FF only’) and all three feedback models in Fig. 7 (top row ’Inph FB’, middle row ’Linear FB’, bottom row ’Bal. FB’) are shown. a τrg = 10 ms. b τrg = 20 ms. In B, no LGN impulse responses within the experimental bounds were obtained for the linear feedback model for small fractions of the parameter intervals, hence the absent line for fractions <0.6
MATLAB GUI-version of model
To further facilitate the use of our new LGN circuit model we have made a freely available MATLAB version of it LGNcircuit, with a simple graphical user interface (GUI). In this program the retinal input is read in as a simple data file. In addition to investigating the response of LGN cells to a retinal impulse response, the program also readily handles retinal inputs characteristic for stimulation with flashing spots or drifting sinusoidal gratings. This freely available program can be downloaded from the model repository ModelDB.
Discussion
We have presented and investigated a conceptually simple ’minimal mechanistic’ model describing temporal processing of visual stimuli in the lateral geniculate nucleus (LGN). The model has been tailored to highlight salient feedforward and feedback effects on LGN relay cells while keeping a modest model complexity and thus a modest number of model parameters. The final model (31) is mathematically represented by a delay differential equation with absolute delay, readily amenable for numerical analysis. To further facilitate use of the model we have made a MATLAB version of it, LGNcircuit, with a simple graphical user interface (GUI).
In terms of model applications the main focus in the present paper has been on impulse responses, i.e., the firing-rate response to a very brief stimulation of a small test spot placed in the receptive-field center of the LGN neuron in question. Unlike previous modeling efforts aimed to investigate cortical feedback effects on LGN cells, the modest model complexity has allowed us to do comprehensive investigations of the model parameter space. In particular we have investigated in Figs. 6, 7, 8 how characteristic experimental measures of this impulse response, such as the time to first peak, the biphasic index, and the normalized rebound magnitude (Cai et al. 1997; Usrey et al. 1999), vary with model parameters. We find here that both purely feedforward models (Fig. 6) as well as models with feedforward excitation combined with cortical feedback (Fig. 7) can account for the experimental results reported so far for the LGN impulse responses (Cai et al. 1997; Usrey et al. 1999). Thus it appears that we cannot based on such observations alone make any statement of whether feedforward or feedback effects dominate in determining the detailed shape of the impulse responses.
However, our study suggests that the measures of time to first peak and the biphasic index over a population of LGN neurons receiving similar retinal input will be differently correlated depending on whether feedforward or feedback effects dominate. For the feedforward models considered in Fig. 6 we found (for the collection of models compatible with present experiments) that the time to first peak and the biphasic index were strongly anticorrelated. In contrast, weak or positive correlations between these measures were found for the experimentally relevant feedback models in Fig. 7. As illustrated by Fig. 9 this qualitative difference remains also when a variety of retinal impulse responses are considered and a generalized correlation measure is used. This points to a specific suggestion for how to probe the relative importance of the feedforward and feedback contributions in shaping the temporal part of LGN impulse responses.
It should be noted, however, that our model, like all previous models we are aware of that address the role of corticothalamic feedback on relay-cell firing (Köhn and Wörgötter 1996; Lumer et al. 1997; Wörgötter et al. 1998; Kirkland and Gerstein 1998; Kirkland et al. 2000; Hillenbrand and van Hemmen 2000; Yousif and Denham 2007), assume the cortical cells providing the feedback to be driven by the relay cells in the model. It could instead be that some of the corticothalamic feedback to a relay cell is driven by cortical cells that are activated by other relay cells with a shorter latency. If so, all models including ours is inaccurate on this point. Since the corticothalamic feedback loops can be quite fast (Sillito and Jones 2004; Briggs and Usrey 2005, 2007, 2011), the first feedback onto a particular relay cell may arrive simultaneously with or even before the retinal input. If so, the above model prediction cannot be trusted, as a main factor affecting the differences in the correlation coefficients for the different circuit models likely is the differences in timing between the feedforward and feedback inputs. Such early cortical feedback will in our model be similar to adding a term to the expression for the feedforward input in Eq. (18). While this is not pursued here, one would expect that such ’early-feedback’ models generally would give correlation coefficients more similar to values for the present feedforward models, so that the presently described test will not be applicable.
A recent study by Wang et al. (2006) found a characteristic pattern in the feedback connections to LGN cells: the functional effect of the feedback cross-connections (i.e., from cortical ON to LGN OFF cells, or from cortical OFF to LGN ON cells) is phase-reversed from the effect of the inphase connections (i.e., from cortical ON to LGN ON cells, or from cortical OFF to LGN OFF cells). Partially motivated by this observation, we have in the present paper focused on two situations in terms of the cortical-feedback organization: (1) inphase inhibitory feedback alone, and (2) inphase inhibition combined with antiphase excitation (from the cross connection). Under the latter point, we have specifically investigated the situation where the magnitude of the inphase and antiphase feedback weights are the same. With such balanced feedback, and perfect half-wave rectifying cortical firing-rate functions with zero firing thresholds, the net effect of the feedback becomes effectively linear (41). Provided the background relay-cell firing rate is so large that no rectification effects occur at the relay-cell level, the whole relay-cell model then becomes linear, allowing for straightforward analysis of its properties (Einevoll and Plesser 2002), and even an analytical formula for the transfer function (45). In this linear-feedback regime the impulse response typically becomes more prone to oscillations due to thalamocortical loop effects, but whether this regime has its experimental counterpart is not known.
Most parameters in our firing-rate model are a priori unknown as they are difficult to measure directly in experiments, particularly in an in vivo setting. Also, the appropriate numbers for time constants to use in the coupling kernels in a firing-rate model is not necessarily directly given by corresponding time constants of the EPSPs and IPSPs connecting individual neurons (Gerstner 2000). Recently, our group has undertaken a systematic and comprehensive numerical investigation of the response of leaky integrate-and-firing spiking neurons to strong synaptic inputs, characteristic for the retinogeniculate connection (Nordlie et al. 2010). The results of the study is that the time constant of a rate model might in many situations be well approximated by the time constant of the synaptic connection. However, this finding should be tested further using a similar numerical approach one available spike-based models made particulary for the retinogeniculate transmission (Carandini et al. 2007; Casti et al. 2008). Rate-model time constants extracted from such a study would reduce the number of unknown parameters in our model and thus make the predictions better constrained.
Experiments with cortical inactivation have proven very difficult to do, and the reports from such have been inconclusive in the sense that both excitatory and inhibitory effects have been reported, see Introduction for references. If future experiments are able to constrain the parameters describing the thalamocortical feedback loop, our MATLAB GUI-based model is so numerically undemanding and easy to use that the calculations reported here can easily be redone to make new and more precise predictions.
In our model only a single time constant is used to account for the excitatory and inhibitory synaptic connections. In reality these synaptic actions will be mediated by several receptor types with different characteristic time constants (e.g., AMPA and NMDA for the excitatory connection, and GABAA and GABAB for the inhibitory connections). The best choice of time constants in the synaptic coupling kernels in our model will likely reflect the underlying mixture of these different receptors. The model formalism can, however, be straightforwardly extended to include several time constants in the coupling kernels: for the feedforward connections term it would amount to add more terms to the expression describing the filtered retinal input (18), for the feedback connections it would increase the number of differential equations to be solved in the final numerical model (cf. ’linear chain trick’ as described in Appendix 1). As the strategy behind the present paper is to limit the number of (unknown) model parameters and instead do a comprehensive evaluation of the parameter space of a more restricted number of salient model parameters, we have not pursued such an extension here. Further, we do not expect that the qualitative conclusions regarding the differences in correlation coefficients between tmax and IBP for the different model types would change even with such a model extension. These differences rely mainly on the reduced firing of LGN relay cells being driven from the retina in the feedforward case and from the LGN relay cells themselves in the case of feedback through the thalamocortical loop, and will likely be relatively little affected by changes in the detailed form of the temporal coupling kernels.
Acknowledgments
We thank Tom Tetzlaff and Hans E. Plesser for careful reading of the manuscript. This work was supported by the Research Council of Norway under the eScience programme (grant no. 178892).
Appendix 1: Derivation of model on differential form
In the present appendix we derive the differential Eq. (17) for the dynamical variable z(t) defined in (16) when the coupling kernels hON/OFFcr and hON/OFFxrc in (12) and (13) are assumed.
Insertion of (12) into (7) gives, by means of (6),
 |
56 |
where we also have used the definition for 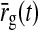 in (18) and
in (18) and 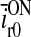 in (21). (Note that the notation
in (21). (Note that the notation  in (7) has been replaced by RONc(t) in (56) since the background firing rates of the cortical cells have been assumed zero.) Correspondingly, we find that
in (7) has been replaced by RONc(t) in (56) since the background firing rates of the cortical cells have been assumed zero.) Correspondingly, we find that
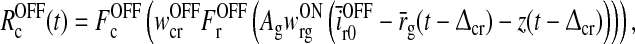 |
57 |
and we have arrived at (25) and (26), respectively.
Differentiation of the expression for the differential delay equation with absolute delay z in (16) with respect to t gives
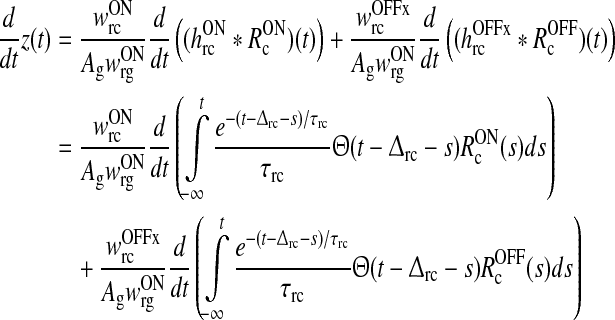 |
58 |
where we have used (13). Since 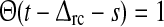 only for
only for  , the integrals in (58) can be rewritten as
, the integrals in (58) can be rewritten as
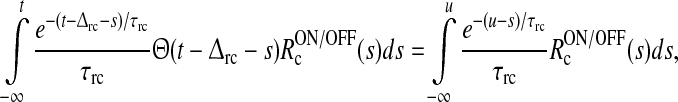 |
59 |
where we have introduced 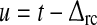 . By means of the general differentiation rule
. By means of the general differentiation rule
 |
60 |
we now find for the first integral in (58),
 |
61 |
For the OFF integral in (58) we correspondingly find
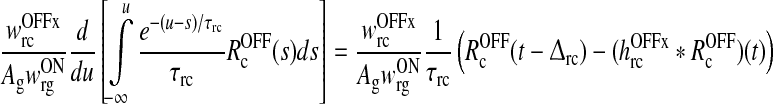 |
62 |
With the use of the definition for z(t) in (16) we thus find that the differential equation for z(t) in (58) simplifies to
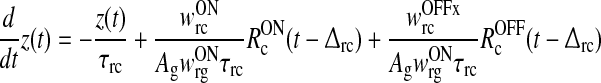 |
63 |
Use of the expressions for RONc(t) and ROFFc(t) in (56) and (57), respectively, and the definition  in (20), then gives the delay differential equation with absolute delay (17) for z(t) in the main text.
in (20), then gives the delay differential equation with absolute delay (17) for z(t) in the main text.
Appendix 2 : Threshold firing-rate functions
Use of threshold firing-rate functions as described in (27)–(30) in the expression for RONc(t) in (25) gives
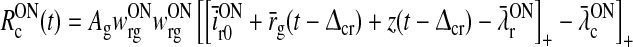 |
64 |
where we have introduced  and
and 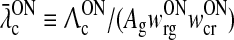 . The requirement of zero background firing rate for the cortical ON cells translates to the constraint
. The requirement of zero background firing rate for the cortical ON cells translates to the constraint
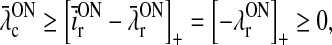 |
65 |
where we have used the definition of λONr in (39).
Since we enforce that 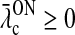 , the innermost half-wave rectification in (64) can be removed. (For the cases where
, the innermost half-wave rectification in (64) can be removed. (For the cases where  , the function (64) will be zero also with the innermost half-wave rectification function replaced by the linear function). The expression (64) thus simplifies to
, the function (64) will be zero also with the innermost half-wave rectification function replaced by the linear function). The expression (64) thus simplifies to
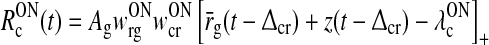 |
66 |
corresponding to (37) in the main text. Here the definition of λONc0 in (33) has been used. A corresponding argument for ROFFc(t) gives
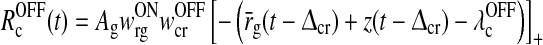 |
67 |
corresponding to (38) in the main text. Insertion of these new expression for RONc(t) and ROFFc(t) into
 |
68 |
then gives (31) in the main text.
Appendix 3: Numerical methods
General: In the numerical investigations we needed to solve the delay differential equation in (31). This was done in MATLAB using the routine
dde23
(and in the case of zero delay the routine
ode45
). The auxiliary variable z(t) was set to be zero for all times prior to stimulus onset.
Simulation of drifting-grating responses: In numerical evaluations of the responses to drifting gratings, the transient part of the response following stimulus onset was omitted. The MATLAB routine
fft
implementing the fast Fourier transform was then used to extract the first harmonic component from the steady-state part of the response.
Simulations of impulse response: We first simulated the first 250 ms of impulse response after onset of the retinal input, cf. Fig. 4 to obtain tmax and IBP. If four or more phases were present in these first 250 ms, we evaluated the impulse-response for 250 ms more. The normalized rebound magnitude (NRM) was then found by evaluating the integrals over the first and all subsequent phases, respectively, using the MATLAB routine
quadl
. However, if the area of the fourth phase was found to be larger than one hundredth of the area of the first phase, NRM was not calculated, cf. white regions in the phase plots in Figs. 7 and 8.
References
- Andolina IM, Jones HE, Wang W, Sillito AM. Corticothalamic feedback enhances stimulus response precision in the visual system. Proc Natl Acad Sci. 2007;104:1685–1690. doi: 10.1073/pnas.0609318104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhattacharya BM, Coyle D, Maguire LP. A thalamo-cortico-thalamic neural mass model to study alpha rhythms in Alzheimer’s disease. Neural Netw. 2011;24:631–645. doi: 10.1016/j.neunet.2011.02.009. [DOI] [PubMed] [Google Scholar]
- Blomquist P, Devor A, Indahl UG, Einevoll GT, Dale AM. Estimation of thalamocortical and intracortical network models from joint thalamic single-electrode and cortical laminar-electrode recordings in the rat barrel system. PLoS Comput Biol. 2009;5:e1000328. doi: 10.1371/journal.pcbi.1000328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggs F, Usrey WM. Temporal properties of feedforward and feedback pathways between the thalamus and visual cortex in ferret. Thalamus Relat Syst. 2005;3:133–139. doi: 10.1017/S1472928807000131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggs F, Usrey WM. A fast, reciprocal pathway between the lateral geniculate nucleus and visual cortex in the macaque monkey. J Neurosci. 2007;27:5431–5436. doi: 10.1523/JNEUROSCI.1035-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggs F, Usrey WM. Emerging views of corticothalamic function. Curr Opin Neurobiol. 2008;18:403–407. doi: 10.1016/j.conb.2008.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggs F, Usrey WM. Corticogeniculate feedback and visual processing in the primate. J Physiol. 2011;589(1):33–40. doi: 10.1113/jphysiol.2010.193599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai D, Deangelis G, Freeman R. Spatiotemporal receptive field organization in the lateral geniculate nucleus of cats and kittens. J Neurophysiol. 1997;78:1045–1061. doi: 10.1152/jn.1997.78.2.1045. [DOI] [PubMed] [Google Scholar]
- Carandini M, Horton JC, Sincich LC. Thalamic filtering of retinal spike trains by postsynpatic summation. J Vision. 2007;7:1–11. doi: 10.1167/7.14.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casti A, Xiao Y, Kaplan E (2004) Effects of cortical feedback on LGN dynamics. Soc Neurosci Abstracts 409(7)
- Casti A, Hayot F, Xiao Y, Kaplan E. A simple model of retina-LGN transmission. J Comp Neurosci. 2008;24:235–252. doi: 10.1007/s10827-007-0053-7. [DOI] [PubMed] [Google Scholar]
- Cruse H. Neural networks as cynernetic systems. Stuttgart: Thieme Verlag; 1997. [Google Scholar]
- Cudeiro J, Sillito AM. Spatial frequency tuning of orientation-discontinuity-sensitive corticofugal feedback to the cat lateral geniculate nucleus. J Physiol. 1996;490:481–492. doi: 10.1113/jphysiol.1996.sp021159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P, Abbott L. Theoretical neuroscience. Cambridge, MA: The MIT Press; 2001. [Google Scholar]
- DeAngelis GC, Ohzawa I, Freeman RD. Receptive-field dynamics in the central visual pathways. Trends Neurosci. 1995;18:451–458. doi: 10.1016/0166-2236(95)94496-R. [DOI] [PubMed] [Google Scholar]
- Derrington AM, Fuchs AF. Spatial and temporal properties of x and y cells in the cat lateral geniculate nucleus. J Physiol. 1979;293:347–364. doi: 10.1113/jphysiol.1979.sp012893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Contreras D, Steriade M. Mechanisms underlying the synchronizing action of corticothalamic feedback through inhibition of thalamic relay cells. J Neurophysiol. 1998;79:999–1016. doi: 10.1152/jn.1998.79.2.999. [DOI] [PubMed] [Google Scholar]
- Destexhe A. Modelling corticothalamic feedback and the gating of the thalamus by the cerebral cortex. J Physiol (Paris) 2000;94:391–410. doi: 10.1016/S0928-4257(00)01093-7. [DOI] [PubMed] [Google Scholar]
- Einevoll G, Heggelund P. Mathematical models for the spatial receptive-field organization of nonlagged X cells in dorsal lateral geniculate nucleus of cat. Vis Neurosci. 2000;17:871–885. doi: 10.1017/S0952523800176060. [DOI] [PubMed] [Google Scholar]
- Einevoll GT, Plesser HE. Linear mechanistic models for the dorsal lateral geniculate nucleus of cat probed using drifting grating stimuli. Netw Comp Neural. 2002;13:503–530. doi: 10.1088/0954-898X/13/4/305. [DOI] [PubMed] [Google Scholar]
- Einevoll GT, Plesser HE (2011) Extended difference-of-Gaussians model incorporating cortical feedback for relay cells in the lateral geniculate nucleus of cat. Cogn Neurodyn. doi:10.1007/s11571-011-9183-8 [DOI] [PMC free article] [PubMed]
- Enroth-Cugell C, Robson J. The constrast sensitivity of retinal ganglion cells of the cat. J Physiol. 1966;181:517–552. doi: 10.1113/jphysiol.1966.sp008107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout B. Neural networks as spatio-temporal pattern-forming systems. Rep Prog Phys. 1998;61:353–430. doi: 10.1088/0034-4885/61/4/002. [DOI] [Google Scholar]
- Gazères N, Borg-Graham LJ, Frégnac Y. A phenomenological model of visually evoked spike trains in cat geniculate nonlagged x-cells. Vis Neurosci. 1998;15:1157–1174. doi: 10.1017/S0952523898156158. [DOI] [PubMed] [Google Scholar]
- Geisert EE, Langsetmo A, Spear PD. Influence of the cortico-geniculate pathway on response properties of cat lateral geniculate neurons. Brain Res. 1981;208(2):409–415. doi: 10.1016/0006-8993(81)90568-0. [DOI] [PubMed] [Google Scholar]
- Gerstner W. Population dynamics of spiking neurons: fast transients, asynchronous states, and locking. Neural Comp. 2000;12:43–89. doi: 10.1162/089976600300015899. [DOI] [PubMed] [Google Scholar]
- Godwin DW, Vaughan JW, Sherman SM. Metabotropic glutamate receptors switch visual response mode of lateral geniculate nucleus cells from burst to tonic. J Neurophysiol. 1996;76(3):1800–1816. doi: 10.1152/jn.1996.76.3.1800. [DOI] [PubMed] [Google Scholar]
- Guido W, Sherman SM. Response latencies of cells in the cat’s lateral geniculate nucleus are less variable during burst than tonic firing. Vis Neurosci. 1998;15:231–237. doi: 10.1017/S0952523898152033. [DOI] [PubMed] [Google Scholar]
- Hayot F, Tranchina D. Modeling corticofugal feedback and the sensitivity of lateral geniculate neurons to orientation discontinuity. Vis Neurosci. 2001;18:865–877. [PubMed] [Google Scholar]
- Heeger D. Nonlinear model of neural responses in cat visual cortex. In: MS Landy, JA Movshon., editors. Computational models of visual processing. Cambridge, MA: MIT Press; 1991. pp. 119–133. [Google Scholar]
- Hillenbrand U, Hemmen LJ. Spatiotemporal adaptation through corticothalamic loops: a hypothesis. Vis Neurosci. 2000;17:107–118. doi: 10.1017/S0952523800171111. [DOI] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol. 1962;160:106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J, Weng C, Yeh CI, Gordon JA, Ruthazer ES, Stryker MP, Swadlow HA, Alonso JM. On- and off-domains of geniculate afferents in cat primary visual cortex. Nat Neurosci. 2008;11:88–94. doi: 10.1038/nn2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jing W, Liu W-Z, Gong X-W, Gong H-Q, Liang P-J. Visual pattern recognition based on spatio-temporal patterns of retinal ganglion cells’ activities. Cogn Neurodyn. 2010;3:179–188. doi: 10.1007/s11571-010-9119-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaplan E, Marcus S, So YT. Effects of dark adaptation on spatial and temporal properties of receptive fields in cat lateral geniculate nucleus. J Physiol. 1979;294:561–580. doi: 10.1113/jphysiol.1979.sp012946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaplan E, Mukherjee P, Shapley R. Information filtering in the lateral geniculate nucleus. In: Shapley R, Lam DM-K, editors. Contrast sensitivity. Cambridge, MA: MIT Press; 1993. pp. 183–200. [Google Scholar]
- Kaplan E, Purpura K, Shapley RM. Contrast affects the transmission of visual information through the mammalian lateral geniculate nucleus. J Physiol. 1987;391:267–288. doi: 10.1113/jphysiol.1987.sp016737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkland KL, Gerstein GL. A model of cortically induced synchronization in the lateral geniculate nucleus of the cat: a role for low-threshold calcium channels. Vision Res. 1998;38:2007–2022. doi: 10.1016/S0042-6989(97)00385-4. [DOI] [PubMed] [Google Scholar]
- Kirkland KL, Sillito AM, Jones HE, West DC, Gerstein GL. Oscillations and long-lasting correlations in a model of the lateral geniculate nucleus and visual cortex. J Neurophysiol. 2000;84:1863–1868. doi: 10.1152/jn.2000.84.4.1863. [DOI] [PubMed] [Google Scholar]
- Köhn J, Wörgötter F. Corticofugal feedback can reduce the visual latency of responses to antagonistic stimuli. Biol Cybern. 1996;75(3):199–209. doi: 10.1007/s004220050287. [DOI] [PubMed] [Google Scholar]
- Liang L, Wang R, Zhang Z. The modeling and simulation of visuospatial working memory. Cogn Neurodyn. 2010;4:359–366. doi: 10.1007/s11571-010-9129-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lumer ED, Edelman GM, Tononi G. Neural Dynamics in a model of the thalamocortical System. I Layers, loops and the emergence of fast synchronous rhythms. Cereb Cortex. 1997;7:207–227. doi: 10.1093/cercor/7.3.207. [DOI] [PubMed] [Google Scholar]
- MacDonald M (1979) Time lags in biological models (Lecture Notes in Biomathematics). Springer, Berlin
- Marrocco RT, McClurkin JW, Alkire MT. The influence of the visual cortex on the spatiotemporal response properties of lateral geniculate nucleus cells. Brain Res. 1996;737(1–2):110–118. doi: 10.1016/0006-8993(96)00660-9. [DOI] [PubMed] [Google Scholar]
- Marrocco RT, McClurkin JW, Young RA. Modulation of lateral geniculate nucleus cell responsiveness by visual activation of the corticogeniculate pathway. J Neurosci. 1982;2(2):256–263. doi: 10.1523/JNEUROSCI.02-02-00256.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mastronarde DN. Two classes of single-input x-cells in cat lateral geniculate nucleus. i. receptive-field properties and classification of cells. J Neurophysiol. 1987;57(2):357–380. doi: 10.1152/jn.1987.57.2.357. [DOI] [PubMed] [Google Scholar]
- Mastronarde DN. Two classes of single-input x-cells in cat lateral geniculate nucleus. ii. retinal inputs and the generation of receptive-field properties. J Neurophysiol. 1987;57(2):381–413. doi: 10.1152/jn.1987.57.2.381. [DOI] [PubMed] [Google Scholar]
- Mayer J, Schuster HG, Claussen JC, Mölle M. Corticothalamic projections control synchronization in locally coupled bistable thalamic oscillators. Phys Rev Lett. 2007;99:068102. doi: 10.1103/PhysRevLett.99.068102. [DOI] [PubMed] [Google Scholar]
- McClurkin JW, Marrocco RT. Visual cortical input alters spatial tuning in monkey lateral geniculate nucleus cells. J Physiol. 1984;348:135–152. doi: 10.1113/jphysiol.1984.sp015103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClurkin JW, Optican LM, Richmond BJ. Cortical feedback increases visual information transmitted by monkey parvocellular lateral geniculate nucleus neurons. Vis Neurosci. 1994;11(3):601–617. doi: 10.1017/S0952523800002492. [DOI] [PubMed] [Google Scholar]
- McCormick DA, Krosigk M. Corticothalamic activation modulates thalamic firing through glutamate “metabotropic” receptors. Proc Natl Acad Sci USA. 1992;89:2774–2778. doi: 10.1073/pnas.89.7.2774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee P, Kaplan E. Dynamics of neurons in the cat lateral geniculate nucleus: in vivo electrophysiology and computational modeling. J Neurophysiol. 1995;74:1222–1243. doi: 10.1152/jn.1995.74.3.1222. [DOI] [PubMed] [Google Scholar]
- Murphy PC, Sillito AM. Corticofugal feedback influences the generation of length tuning in the visual pathway. Nature. 1987;329(6141):727–729. doi: 10.1038/329727a0. [DOI] [PubMed] [Google Scholar]
- Nordbø O, Wyller J, Einevoll GT. Neural network firing-rate models on integral form: effects of temporal coupling kernels on equilibrium-state stability. Biol Cybern. 2007;97(3):195–209. doi: 10.1007/s00422-007-0167-z. [DOI] [PubMed] [Google Scholar]
- Nordlie E, Gewaltig M-O, Plesser HE. Towards reproducible descriptions of neuronal network models. PLoS Comput Biol. 2009;5(8):e1000456. doi: 10.1371/journal.pcbi.1000456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordlie E, Tetzlaff T, Einevoll GT. Firing-rate response properties of spiking neurons: beyond the diffusion limit. Front Comput Neurosci. 2010;4:459. doi: 10.3389/fncom.2010.00149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oppenheim A, Willsky A. Signals and systems, 2nd ed. Upper Saddle River, NJ: Prentice Hall; 1996. [Google Scholar]
- Rodieck R. Quantitative analysis of cat retinal ganglion cell response to visual stimuli. Vis Res. 1965;5:583–601. doi: 10.1016/0042-6989(65)90033-7. [DOI] [PubMed] [Google Scholar]
- Ruksenas O, Fjeld IT, Heggelund P. Spatial summation and center-surround antagonism in the receptive field of single units in the dorsal lateral geniculate nucleus of cat: comparison with retinal input. Vis Neurosci. 2000;17:855–870. doi: 10.1017/S0952523800176059. [DOI] [PubMed] [Google Scholar]
- Saglam M, Hayashida Y, Murayama N. A retinal circuit model accounting for wide-field amacrine cells. Cogn Neurodyn. 2009;1:25–32. doi: 10.1007/s11571-008-9059-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satoh S, Usui S. Engineering-approach accelerates computational understanding of V1–V2 neural properties. Cogn Neurodyn. 2009;3:1–8. doi: 10.1007/s11571-008-9065-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapley R, Lennie P. Spatial frequency analysis in the visual system. Annu Rev Neurosci. 1985;8:547–583. doi: 10.1146/annurev.ne.08.030185.002555. [DOI] [PubMed] [Google Scholar]
- Sherman S, Guillery R. Exploring the thalamus. New York: Academic Press; 2001. [Google Scholar]
- Sillito AM, Cudeiro J, Murphy PC. Orientation sensitive elements in the corticofugal influence on centre-surround interactions in the dorsal lateral geniculate nucleus. Exp Brain Res. 1993;93(1):6–16. doi: 10.1007/BF00227775. [DOI] [PubMed] [Google Scholar]
- Sillito AM, Jones HE. Corticothalamic interactions in the transfer of visual information. Philos Trans R Soc Lond B Biol Sci. 2002;357(1428):1739–1752. doi: 10.1098/rstb.2002.1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sillito AM, Jones HE. Feedback systems in visual processing. In: Chalupa LM, Wernes JS, editors. The visual neurosciences, Vol 1. Cambridge, MA: MIT Press; 2004. pp. 609–624. [Google Scholar]
- Sillito AM, Jones HE, Gerstein GL, West DC. Feature-linked synchronization of thalamic relay cell firing induced by feedback from visual cortex. Nature. 1994;369:479–482. doi: 10.1038/369479a0. [DOI] [PubMed] [Google Scholar]
- Troyer TW, Krukowski AE, Priebe NJ, Miller KD. Contrast-invariant orientation tuning in cat visual cortex: thalamocortical input tuning and correlation-based intracortical connectivity. J Neurosci. 1998;18:5908–5927. doi: 10.1523/JNEUROSCI.18-15-05908.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Troyer TW, Krukowski AE, Miller KD. LGN input to simple cells and contrast-invariant orientation tuning: an analysis. J Neurophysiol. 2002;87:2741–2752. doi: 10.1152/jn.2002.87.6.2741. [DOI] [PubMed] [Google Scholar]
- Usrey WM, Reppas JB, Reid RC. Specificity and strength of retinogeniculate connections. J Neurophysiol. 1999;82(6):3527–3540. doi: 10.1152/jn.1999.82.6.3527. [DOI] [PubMed] [Google Scholar]
- Vidyasagar TR, Urbas JV. Orientation sensitivity of cat lgn neurones with and without inputs from visual cortical areas 17 and 18. Exp Brain Res. 1982;46(2):157–169. doi: 10.1007/BF00237172. [DOI] [PubMed] [Google Scholar]
- Wang W, Jones HE, Andolina IM, Sillito AM. Functional alignment of feedback effects from visual cortex to thalamus. Nat Neurosci. 2006;9:1330–1336. doi: 10.1038/nn1768. [DOI] [PubMed] [Google Scholar]
- Wang R, Zhang Z. Energy coding in biological neural networks. Cogn Neurodyn. 2007;3:203–212. doi: 10.1007/s11571-007-9015-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe J, Palmer LA. Temporal diversity in the lateral geniculate nucleus of cat. Vis Neurosci. 1998;15:653–675. doi: 10.1017/S0952523898154068. [DOI] [PubMed] [Google Scholar]
- Wörgötter F, Nelle E, Li B, Funke K. The influence of corticofugal feedback on the temporal structure of visual responses of cat thalamic relay cells. J Physiol. 1998;509(Pt 3):797–815. doi: 10.1111/j.1469-7793.1998.797bm.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yousif N, Denham M. The role of cortical feedback in the generation of the temporal receptive field responses of lateral geniculate nucleus neurons: a computational modelling study. Biol Cybern. 2007;97(4):269–277. doi: 10.1007/s00422-007-0171-3. [DOI] [PubMed] [Google Scholar]