Abstract
During slow-wave sleep, general anesthesia, and generalized seizures, there is an absence of consciousness. These states are characterized by low-frequency large-amplitude traveling waves in scalp electroencephalogram. Therefore the oscillatory state might be an indication of failure to form coherent neuronal assemblies necessary for consciousness. A generalized seizure event is a pathological brain state that is the clearest manifestation of waves of synchronized neuronal activity. Since gap junctions provide a direct electrical connection between adjoining neurons, thus enhancing synchronous behavior, reducing gap-junction conductance should suppress seizures; however there is no clear experimental evidence for this. Here we report theoretical predictions for a physiologically-based cortical model that describes the general anesthetic phase transition from consciousness to coma, and includes both chemical synaptic and direct electrotonic synapses. The model dynamics exhibits both Hopf (temporal) and Turing (spatial) instabilities; the Hopf instability corresponds to the slow (≲8 Hz) oscillatory states similar to those seen in slow-wave sleep, general anesthesia, and seizures. We argue that a delicately balanced interplay between Hopf and Turing modes provides a canonical mechanism for the default non-cognitive rest state of the brain. We show that the Turing mode, set by gap-junction diffusion, is generally protective against entering oscillatory modes; and that weakening the Turing mode by reducing gap conduction can release an uncontrolled Hopf oscillation and hence an increased propensity for seizure and simultaneously an increased sensitivity to GABAergic anesthesia.
Keywords: Seizure, Gap junctions, Mean-field cortical model, Hopf oscillations, Turing patterns, Nonlinear interactions, Phase coherence
Introduction
It is widely believed that direct electrotonic (gap junction) synapses between cortical neurons could play a crucial role in determining cortical stability (Carlen et al. 2000; Perez Velazquez and Carlen 2000). Intuitively, the presence of gap junctions would be expected to enhance synchronous behavior between adjoined neurons. We might expect that pathological (seizure) and physiological (slow-wave sleep) synchronous states could be controlled or suppressed by applying a pharmacological agent that modulates gap-junction conductance.
However, there is growing debate in the literature about the potential therapeutic benefit of opening versus closing neuronal gap junctions. This debate arises from the apparently contradictory experimental results reported by different research groups. It has been observed that modafinil induces wakefulness by opening gap junctions (Beck et al. 2008), and that increased physiological GABA activity—such as occurs in slow-wave sleep—as well as general anesthetic drugs, close gap junctions (Shinohara et al. 2000; Wentlandt et al. 2006). Many report that gap-junction blocking agents suppress seizure activity in both in vivo (Gajda et al. 2003, 2005; Nilsen et al. 2006) and in vitro animal models (Jahromi et al. 2002; Pais et al. 2003), yet others provide evidence that these drugs may enhance seizure activity (Yang and Ling 2007; Voss et al. 2009; Jacobson et al. 2010). The excitation and suppression effects may be dependent on concentration (Gajda et al. 2005; Voss et al. 2009). For example, one of the actions of quinine is to reversibly block connexin-36 (Cx36) (Juszczak and Swiergiel 2009), the dominant gap-junction type found in GABAergic cortical interneurons (Bennett and Zukin 2004). In one report (Gajda et al. 2005), the effect of quinine on 4-aminopyridine-induced seizures in the anesthetized adult rat was characterized as suppressive because the duration and amplitude of ictal events was reduced—despite the fact that quinine actually increased seizure frequency and was unable to prevent the induction of seizures.
The evidence from Cx36 knockout mice is less confusing: compared with their wild-type peers, mice lacking the connexin-36 gene are much more prone to ictal burst discharges in vitro (kainate-induced seizure-like events in hippocampal slices) (Pais et al. 2003) and generalized tonic-clonic seizures in vivo (pentylenetetrazol) (Jacobson et al. 2010). Thus the knockout experiments, together with a subset of the pharmacological experiments, suggest that interneuronal gap junctions may be protective against seizure, and that their ablation can enhance pathological excitability. There are also data that suggest that Cx36 knockout mice are more sensitive to the hypnotic effects of anesthetic drugs (Jacobson et al. 2011).
The puzzling discrepancies in the pharmacological and genetic experiments demonstrate that our understanding of gap-junction blockers, off-target impacts, and possible gene-knockout compensations, is very incomplete. But more fundamentally, we have little idea of the biological significance of electrotonic coupling, its modulation, and the role it plays in the maintenance of normal versus pathological brain rhythms.
To help address this deficit, we present a physiologically-motivated mathematical model of the cortex that shows how coupling via inhibitory electrical synapses can generate spatially organized patterns of brain activity known as Turing structures. These structures are modulated in time by a low-frequency (1–4 Hz) Hopf instability whose emergence is determined by the strength of the postsynaptic response to firing activity from the population of inhibitory cells. Our model focuses on the behavior of the cortex in the vicinity of a general anesthetic phase transition where the equilibrium manifold displays multiple steady states: an activated “up state”, and a quiescent “down state”, these being separated by an unstable intermediate “mid state”. In our previous anesthesia modeling we have identified the upper activated state with consciousness, and the quiescent bottom state with drug-induced unconsciousness. The presence of the unstable mid-state separatrix implies an abrupt, first-order jump between the conscious (up) and unconscious (down) states brought about by increasing the level of inhibitory drive (Steyn-Ross et al. 1999, 2001a, b, 2003, 2004).
In the up state, nonlinear interactions between the Hopf and Turing instabilities can result in frequency splitting of the Hopf oscillation (Steyn-Ross et al. 2010), generating in an ultra-low frequency (∼0.1 Hz) “beating” pattern that resembles the slow waxing and waning of BOLD activity during noncognitive rest (Raichle et al. 2001; Fox et al. 2005). Unlike other models which explicitly include realistic brain connections (Honey et al. 2007; Ghosh et al. 2008; Deco et al. 2009), our resting-state model is devoid of anatomical structure. The lack of biological fidelity may be justified on the grounds that, at the time-scale of seconds, functional connectivity is largely independent of anatomical connectivity (Honey et al. 2007; Mantini et al. 2007) with significant correlation between function and anatomy only emerging at longer times (∼minutes).
Exploration of the chemical–electrical Hopf–Turing interactions uncovers some counterintuitive and unexpected cortical behaviors. We find that closing gap junctions (i.e., weakening Turing structures) in an idling cortex tends to unbalance the temporal–spatial competition in favor of the temporal mode, allowing a synchronous whole-of-cortex seizure oscillation to develop. Seizure onset is marked by a pronounced reduction in spatial coherence corresponding to the emergence of a chaotic spatiotemporal precursor to full seizure. However, in a small area of parameter space close to the edge of the multistability region, the Hopf (dynamic) instability is replaced by a saddle (static) instability. In this case, gap-junction closure can precipitate the cortex from a chaotic precursor state into a low-firing inactivated state, and seizure is suppressed.
In this paper we report our numerical investigations of the stability properties of a homogeneous (i.e., structure-free) cortex that has access to multiple steady states. We make stepped changes in interneuron-to-interneuron diffusive coupling, and observe the resulting spatiotemporal response to alterations in the relative balance between Turing (spatial) and Hopf (temporal) destabilizations of the homogeneous steady state. For an up-state idling cortex, decreasing gap-junction conductance can allow the Hopf instability to grow, evolving via a chaotic phase into a gross-scale synchronized oscillation resembling grand mal seizure.
Theoretical methodology
Model overview
Our model is a mean-field (i.e., spatially-averaged) continuum description of a sheet of cortical tissue containing excitatory and inhibitory neural populations that communicate along nonmyelinated (local) and myelinated (distant) connections at chemical synapses (Steyn-Ross et al. 2009, 2010). Additionally, interneurons are assumed to be coupled in a nearest-neighbor fashion via a dense network of dendritic gap junctions to form a two-dimensional syncytium (Fukuda et al. 2006); excitatory-to-excitatory gap junctions are also included (Traub et al. 2001) but with much lower coupling strength since their occurrence seems to be rare (Bennett and Zukin 2004; Dudek 2002).
Soma potentials and firing rates
The population-average excitatory (e) and inhibitory (i) soma potentials Ve,i determine the local firing rates Qe,i via a sigmoidal mapping 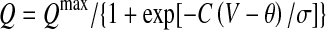 with firing threshold θ and standard deviation
with firing threshold θ and standard deviation 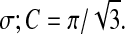 The firing rates act as outgoing sources of local and long-range spike fluxes.
The firing rates act as outgoing sources of local and long-range spike fluxes.
Chemical synapses
Incoming spike fluxes 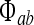 (where a and b are labels each standing for either e or i) induce excitatory and inhibitory postsynaptic potentials (PSPs) that are integrated at the soma to perturb the soma potential away from its resting value Vreste,i,
(where a and b are labels each standing for either e or i) induce excitatory and inhibitory postsynaptic potentials (PSPs) that are integrated at the soma to perturb the soma potential away from its resting value Vreste,i,
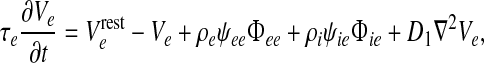 |
1 |
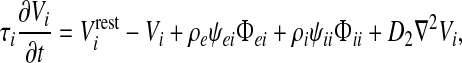 |
2 |
where τe,i are the soma time-constants; ρa are signed synaptic strengths (ρe > 0, ρi < 0); and ψab are dimensionless reversal-potential weights: ψab = (Vreva − Vb)/(Vreva − Vrestb). (See Table 1 for values and symbol definitions).
Table 1.
Standard values for the cortical model. Subscript label b means destination cell can be either of type e (excitatory) or i (inhibitory)
| Symbol | Description | Value | Unit |
|---|---|---|---|
| τe,i | Soma time constant | 0.040, 0.040 | s |
| Vreve,i | Cell reversal potential | 0, −70 | mV |
| Vreste,i | Cell resting potential | −64, −64 | mV |
| ρe,i | Synaptic gain at resting voltage | (1.00, −1.05) × 10−3 | mV s |
| γe,i | Rate-constant for chemical synaptic input | 170, 50/λi | s−1 |
| D2 |
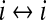 gap-junction diffusive coupling strength gap-junction diffusive coupling strength |
0.1–0.7 | cm2 |
| D1 |
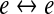 gap-junction diffusive coupling strength gap-junction diffusive coupling strength |
D2/100 | cm2 |
| Nαeb | Long-range e→ b axonal connectivity | 2,000 | – |
| Nβeb,ib | Local e→ b, i→ b axonal connectivity | 800, 600 | – |
| ϕsceb | e→ b incoming flux intensity from subcortex | 300 | s−1 |
| v | Axonal conduction speed | 140 | cm s−1 |
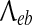 |
Inverse-length scale for e→ b axonal connections | 4 | cm−1 |
| Qmaxe,i | Maximum firing rate | 30, 60 | s−1 |
| θe,i | Sigmoid threshold voltage | −58.5, −58.5 | mV |
| σe,i | Standard deviation for threshold | 3, 5 | mV |
Gap-junction synapses
The final terms on the right of (1, 2) are the electro-synaptic voltage inputs arising from diffusive gap-junction currents; the D1,2 coefficients are the excitatory and inhibitory diffusive-coupling strengths. In earlier work (Steyn-Ross et al. 2007), we estimated the size of the diffusive coupling strength arising from gap-junction connections between inhibitory neurons as having an upper limit of D2 ≈ 0.6 cm2, and here we explore the consequences of allowing D2 to vary over the range 0.7 ≥ D2/cm2 ≥ 0.1. Taking the soma relaxation time τi = 40 ms as our time-scale, the ratio D2/τi defines a diffusion coefficient for voltage change in the inhibitory neural population: in time t, a voltage perturbation can be expected to diffuse across a two-dimensional sheet of cortical tissue through an rms distance 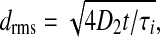 thus the speed of propagation for gap-junction-mediated voltage change will scale as
thus the speed of propagation for gap-junction-mediated voltage change will scale as 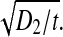 In contrast to the relative abundance of inhibitory-to-inhibitory gap junctions in cortex (Fukuda et al. 2006), evidence for networks of excitatory-to-excitatory gap junctions is very sparse (Bennett and Zukin 2004), so in our modeling we have arbitrarily set the excitatory coupling strength at a small fraction of the inhibitory value, D1 = D2/100, implying that inhibitory diffusive changes will propagate ten times faster than excitatory changes; this inhibitory dominance is a prerequisite for spontaneous emergence of Turing patterns (Turing 1952) that form localized islands and peninsulas of elevated cortical activity.
In contrast to the relative abundance of inhibitory-to-inhibitory gap junctions in cortex (Fukuda et al. 2006), evidence for networks of excitatory-to-excitatory gap junctions is very sparse (Bennett and Zukin 2004), so in our modeling we have arbitrarily set the excitatory coupling strength at a small fraction of the inhibitory value, D1 = D2/100, implying that inhibitory diffusive changes will propagate ten times faster than excitatory changes; this inhibitory dominance is a prerequisite for spontaneous emergence of Turing patterns (Turing 1952) that form localized islands and peninsulas of elevated cortical activity.
Postsynaptic potentials
The 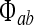 incoming fluxes in (1, 2) obey second-order differential equations,
incoming fluxes in (1, 2) obey second-order differential equations,
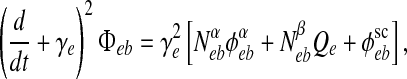 |
3 |
 |
4 |
where γe,i is the rate-constant (inverse time-to-peak) for the PSP response function; Nα,βab is the number of incoming long-range (α), short-range (β) synaptic connections; and ϕsceb is the fixed intensity of incoming subcortical flux corresponding to a small level of background stimulation. (Usually in our numerical simulations we add to ϕsceb a small amount of spatiotemporal white noise to allow the cortex to explore its nearby statespace.)
Long-range cortico-cortical inputs
The ϕαeb long-range excitatory fluxes in (3) are described by a damped wave equation (Robinson et al. 1997),
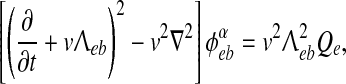 |
5 |
where v is the average axonal conduction speed, and 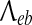 is an inverse-length scale for the long-range connections.
is an inverse-length scale for the long-range connections.
Analytical overview
Our analysis proceeds by mapping out the equilibrium states of the homogeneous cortex over a two-dimensional domain of excitatory and inhibitory driving influences. We focus attention on the small region of multistability that is close to the fold marking the separation between multiple and singleton equilibrium points since this boundary locates the domain subspace where the cortex is maximally sensitive to perturbations and therefore most likely to develop instabilities. We vary gap-junction diffusion, and obtain linearized predictions for onset, offset, and interactions between Turing (spatial) and Hopf (temporal) instabilities. For details, see Results.
Numerical simulations
We test the linear predictions with a series of numerical simulations of the full nonlinear equations, and demonstrate that, depending on the relative balance of excitatory and inhibitory drives, reductions in the Turing mode can either unleash an unconstrained Hopf oscillation (seizure), or suppress the oscillation altogether.
All numerical simulations use a grid resolution of Nx × Ny = 60 × 60 to represent a square cortex of size 25 cm × 25 cm, giving a lattice spacing of δx = δy = 4.1667 mm. The integration time-step is δt = 0.4 ms, corresponding to an effective sampling rate of 2,500 s−1 at each grid point. In order to create the Qe(x, t) space–time strip-charts displayed below in Fig. 2c, 10 s of simulation data are recorded from each of the 60 rows down the middle of the grid (i.e., at column Ny/2 = 30) to give a 60 × 25,000 array of space–time points from which the 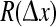 phase coherence graphs of Fig. 2e are computed.
phase coherence graphs of Fig. 2e are computed.
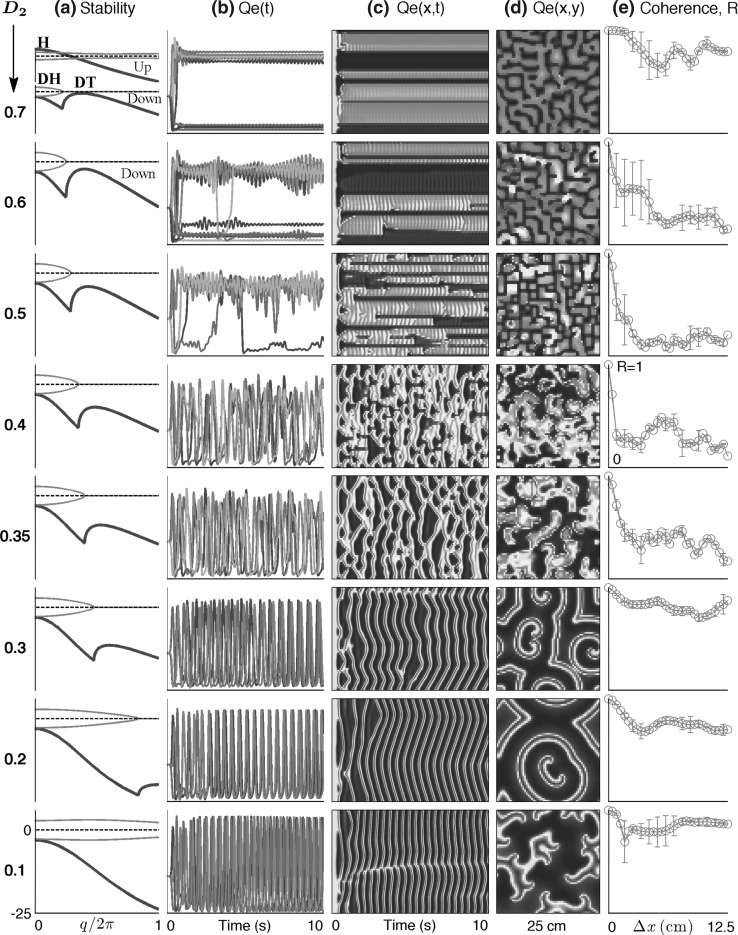
Fig. 2.
Cortical stability and spatiotemporal dynamics for stepped reductions in inhibitory diffusion D2. a Dispersion curves showing real (blue) and imaginary (red) components of the dominant eigenvalue as a function of wavenumber q for top-branch (“up”) and bottom-branch (“down”) equilibria marked in Fig. 1. For D2 = 0.7 cm2, maximum instability in the up-state occurs at q = 0, predicting a whole-of-cortex Hopf (H) oscillation at a frequency of ∼3 Hz, while for the down-state a damped Hopf (DH) and a weakly damped Turing (DT) instability at q/2π ≈ 0.4 waves/cm are expected. For stepped reductions in diffusion D2, the DH Turing peak diminishes in strength. Columns b–e show results of 10-s numerical simulations of the model equations for a 25 cm × 25 cm square cortex initialized at the unstable mid-branch equilibrium. bQe(t): time-series of excitatory firing rate for a regularly-spaced subset of grid points (identified with differently colored lines) aligned parallel to the x-axis; cQe(x, t): space–time view of cortical activity (red = high, blue = low firing-rate); dQe(x, y): bird’s-eye view of activity after 10s; e phase coherence for pairs of pixels separated by distance 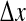 across the grid. Simulation details: grid resolution = 60 × 60; time-step = 0.4 ms. (Color figure online)
across the grid. Simulation details: grid resolution = 60 × 60; time-step = 0.4 ms. (Color figure online)
Phase coherence
Our calculation of phase coherence R is a straightforward generalization of Eq. [8] of Mormann et al. (2000); see the Appendix for further details and sample computer code. In brief, for each simulation run, we quantify fluctuation coherence by computing the instantaneous phase ϕ(x) at nominated grid points relative to the phase ϕ(x0) at a central reference pixel x0; the absolute time-averaged phase differences then give a spatial distribution of coherence values
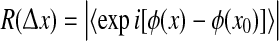 |
6 |
where 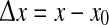 varies over the range 0–12.5 cm (i.e., up to half the width of the cortical grid). A coherence value of R = 1 indicates perfect phase locking, while R = 0 means there is no consistent phase relationship.
varies over the range 0–12.5 cm (i.e., up to half the width of the cortical grid). A coherence value of R = 1 indicates perfect phase locking, while R = 0 means there is no consistent phase relationship.
Results
At equilibrium, cortex can access multiple steady states
For normal, healthy brain function, we assume that the cerebral cortex remains close to a stable steady state, and that the electrical activity detected by a scalp EEG electrode consists of small voltage fluctuations about this steady state. Precisely which steady state the cortex is in will be determined by a dynamic balance between excitatory and inhibitory drives arising from both external and internal sources.
For modeling purposes, we represent “inhibitory drive” as a dimensionless scale-factor λ which increases the effectiveness of each incoming inhibitory action-potential spike. We scale the area ρi of the resulting inhibitory postsynaptic potential (IPSP) without changing its amplitude. This constant-height area scaling of the IPSP is a reasonable model for the cellular effect of some common anesthetics such as propofol (Steyn-Ross et al. 1999; Kitamura et al. 2002; Bojak and Liley 2005; Hutt and Longtin 2010).
For our “excitatory drive” parameter, we have chosen 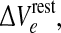 a small positive offset imposed on the resting voltage Vreste of the population of excitatory neurons.1 The range of cortical states is thus projected onto a two-dimensional
a small positive offset imposed on the resting voltage Vreste of the population of excitatory neurons.1 The range of cortical states is thus projected onto a two-dimensional 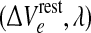 domain whose axes represent intrinsic neuronal excitability, and inhibitory synaptic gain respectively (see Fig. 1).
domain whose axes represent intrinsic neuronal excitability, and inhibitory synaptic gain respectively (see Fig. 1).
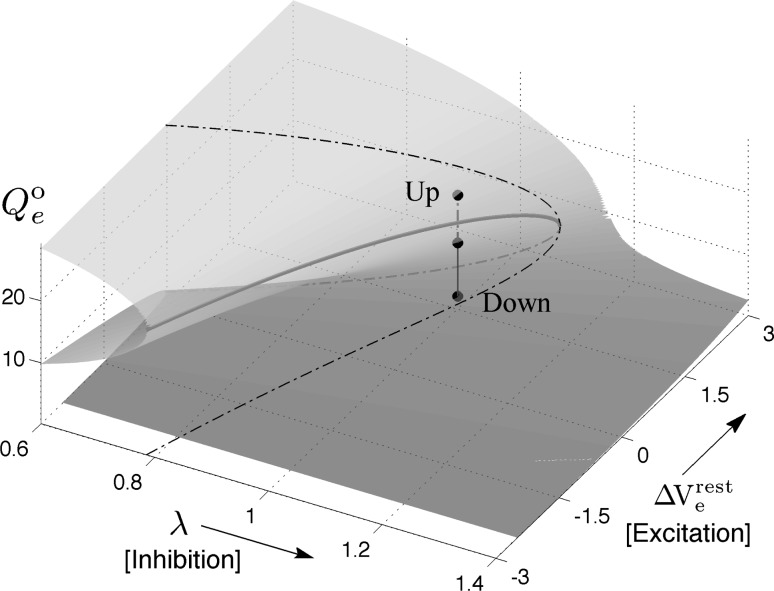
Fig. 1.
Manifold of equilibrium states for the mean-field cortical model. Surface shows how the steady-state firing rate Qoe (vertical axis; spikes/s) is distributed across a two-dimensional domain defined by excitatory drive 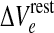 (mV) and inhibitory drive λ. Dashed-black curve encloses the region of multiple steady states; red curve marks the infinite-slope cusp where the surface folds back on itself. We select a reference point at domain coordinate
(mV) and inhibitory drive λ. Dashed-black curve encloses the region of multiple steady states; red curve marks the infinite-slope cusp where the surface folds back on itself. We select a reference point at domain coordinate 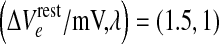 where the cortex has access to three steady-state firing rates (gray-shaded beads): from top to bottom, these firing rates are Qoe = 18.47, 10.77, 2.15 s−1. (Color figure online)
where the cortex has access to three steady-state firing rates (gray-shaded beads): from top to bottom, these firing rates are Qoe = 18.47, 10.77, 2.15 s−1. (Color figure online)
To locate the manifold of equilibrium states, we set all time- and space-derivatives in the differential equations to zero, then solve the resulting nonlinear algebraic equations numerically to compute the steady-state firing rates (Qoe, Qoi) and soma voltages (Voe, Voi) of the excitatory and inhibitory neural populations. A typical equilibrium manifold is shown in Fig. 1. Interestingly, for certain combinations of excitatory and inhibitory drive, the model predicts that the cortex has up to three equilibrium states available to it: an active high-firing upper branch (“up-state”); an inactive low-firing branch (“down-state”); and a reentrant middle branch which is always unstable with respect to small perturbations. The upper and lower branches are generally stable, but can be destabilized in time and space by alterations to the IPSP rate-constant (γi) and the interneuronal gap-junction coupling strength (D2) respectively (Steyn-Ross et al. 2007). In the present work, we investigate the stability changes brought about by stepped reductions in the D2-conductance at the domain coordinate 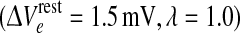 shown in Fig. 1; these reductions in inhibitory diffusion represent pharamacological blockade of dendritic gap-junction connections between interneurons.
shown in Fig. 1; these reductions in inhibitory diffusion represent pharamacological blockade of dendritic gap-junction connections between interneurons.
Resting state of the cortex arises from balanced interaction between Turing and Hopf instabilities
The cortical model can exhibit both Hopf (temporal) and Turing (spatial) instabilities. If the D2 gap-junction connectivity between interneurons is set too high, a “frozen” Turing pattern can result (Steyn-Ross et al. 2007) in which different regions of the cortex precipitate into either high-firing or low-firing modes of activity, and remain there. On the other hand, without gap-junction connections, a sufficiently small value of the γi inhibitory rate-constant can lead to an unrestrained Hopf instability that manifests as synchronized global oscillations in firing that we and others have identified as seizure (Robinson et al. 2002; Kramer et al. 2005; Liley and Bojak 2005; Wilson et al. 2006). Either extreme state is pathological.
Instead of allowing one or other instability to dominate, it is natural to contemplate a balanced interaction between modes that allows the Hopf temporal dynamics to modulate the Turing pattern-forming tendencies (and vice versa). Such a balanced interaction—as illustrated by the Qe(t) time-series (b) and Qe(x, t) space–time strip-chart (c) in the top row of Fig. 2—might represent cortical activity during the default non-cognitive resting state of the brain when driven by low-level subcortical stimulation (Steyn-Ross et al. 2009). Here, the moderately high value for gap-junction coupling (D2 = 0.7 cm2) has allowed a Turing pattern of separated regions of high- (up-state) and low-firing (down-state) activity to emerge, but the activity patterns are not frozen in time because the Hopf instability interacts with the Turing to produce a low-amplitude ∼3-Hz oscillation that is largely coherent across the cortex.
The stability graphs in column (a) of Fig. 2 provide some predictive guidance about which instability modes will be significant. The blue traces in (a) show the real part of the dominant eigenvalue, 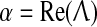 (in s−1), as a function of (scaled) wavenumber q/2π, for the up-state equilibrium (upper graph), and for the down-state equilibrium (lower graph); the red traces show the predicted oscillation frequency extracted from the imaginary part,
(in s−1), as a function of (scaled) wavenumber q/2π, for the up-state equilibrium (upper graph), and for the down-state equilibrium (lower graph); the red traces show the predicted oscillation frequency extracted from the imaginary part, 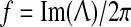 (in Hz). The homogeneous equilibrium is expected to become unstable if α > 0 (blue curve crosses dashed zero-axis and goes positive), with maximum instability growth at the spatial frequency that maximizes α. Thus for D2 = 0.7 cm2, the up-state is predicted to destabilize in favor of a whole-of-cortex Hopf (H) oscillation (peak instability occurs at q = 0), while the down-state shows a damped Hopf (DH at q = 0) plus a weakly damped Turing (DT) that peaks at spatial frequency q/2π ≈ 0.4 waves/cm (i.e., wavelength ∼2.5 cm), consistent with the structured cortical activity seen in the bird’s-eye view of (d). Thus modal interplay between the top-branch H and bottom-branch DT instabilities is responsible for the emergent temporal and spatial patterns captured in columns (b–d).
(in Hz). The homogeneous equilibrium is expected to become unstable if α > 0 (blue curve crosses dashed zero-axis and goes positive), with maximum instability growth at the spatial frequency that maximizes α. Thus for D2 = 0.7 cm2, the up-state is predicted to destabilize in favor of a whole-of-cortex Hopf (H) oscillation (peak instability occurs at q = 0), while the down-state shows a damped Hopf (DH at q = 0) plus a weakly damped Turing (DT) that peaks at spatial frequency q/2π ≈ 0.4 waves/cm (i.e., wavelength ∼2.5 cm), consistent with the structured cortical activity seen in the bird’s-eye view of (d). Thus modal interplay between the top-branch H and bottom-branch DT instabilities is responsible for the emergent temporal and spatial patterns captured in columns (b–d).
In activated rest state, blocking gap junctions can both promote and suppress seizures
The second and subsequent rows of Fig. 2 show the effect of stepped reductions in gap-junction conductance. While the up-state stability curves, with their dominant Hopf instability (marked H in the topmost D2 = 0.7 cm2 graph), are little changed by reductions in D2 (so are not shown), the down-state Turing instability (marked DT) becomes substantially weakened. This suppression of Turing influence has a profound and unexpected impact on cortical dynamics: the coherent, small oscillations about the up and down states (top row: D2 = 0.7 cm2) are replaced by coherent giant fluctuations (bottom three rows: D2 = 0.3, 0.2, 0.1 cm2) that generate synchronized waves of cortical activity; we interpret this dynamics as a fully-developed seizure state resulting from an unrestrained Hopf instability. Thus blockade of gap junctions has taken the cortex from a state of non-cognitive rest to full-blown seizure.
Column (e) of Fig. 2 plots phase coherence R as a function of grid-point separation 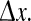 The top row (D2 = 0.7 cm2: activated rest) and the bottom three rows (D2 = 0.3, 0.2, 0.1 cm2: seizure) are all characterized by large coherence values that do not decay significantly with distance, i.e., the fluctuations have a large coherence length. However, in the transition zone (D2 = 0.6, 0.5, 0.4, 0.35 cm2) the coherence length decreases markedly, achieving a minimum coherence at the point D2 = 0.4 cm2 where the fluctuations appear to be maximally turbulent and chaotic. These modeling results show that seizure onset might be heralded by a low-coherence chaotic EEG precursor. This prediction is supported by clinical observations of EEG phase decoherence in the period leading up to seizure (Chávez et al. 2003; Mormann et al. 2003; Amor et al. 2009).
The top row (D2 = 0.7 cm2: activated rest) and the bottom three rows (D2 = 0.3, 0.2, 0.1 cm2: seizure) are all characterized by large coherence values that do not decay significantly with distance, i.e., the fluctuations have a large coherence length. However, in the transition zone (D2 = 0.6, 0.5, 0.4, 0.35 cm2) the coherence length decreases markedly, achieving a minimum coherence at the point D2 = 0.4 cm2 where the fluctuations appear to be maximally turbulent and chaotic. These modeling results show that seizure onset might be heralded by a low-coherence chaotic EEG precursor. This prediction is supported by clinical observations of EEG phase decoherence in the period leading up to seizure (Chávez et al. 2003; Mormann et al. 2003; Amor et al. 2009).
Figure 2 demonstrates that blockade of gap-junction diffusion provides a possible route to seizure. This invites the provocative conclusion that diffusion-mediated Turing structures are protective against “runaway” Hopf instability, and that application of gap-junction blockers may in fact precipitate seizure by weakening Turing mediation. If this is true, then gap-junction blockers are antithetical to seizure suppression or prevention.
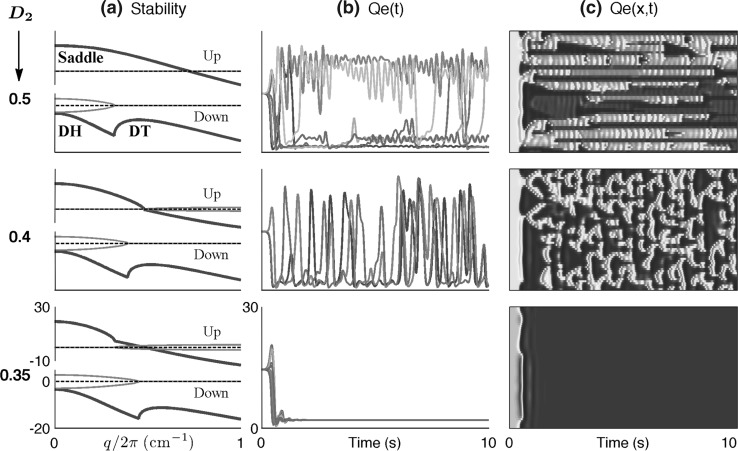
However, Fig. 3 contradicts this simple determination. For this second series of experiments we have displaced the cortex reference coordinate from the Fig. 1 value of 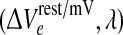 = (1.5, 1.0) to (1.5, 1.016); this represents a tiny increase in inhibitory drive that moves the up-state very close to the loss-of-consciousness cusp on the manifold surface. This subtle change in coordinate causes the up-state stability graph to transform from the 3-Hz Hopf oscillation of Fig. 2a to a zero-frequency instability (Fig. 3a) that we label as “saddle” (in analogy to zero-frequency saddle–node bifurcations in two-variable dynamical systems (Steyn-Ross et al. 2006)). Commencing from a balanced Hopf–Turing default state (not shown), step reductions in D2 interneuronal gap-junction coupling take the cortex through a chaotic phase (D2 = 0.5, 0.4 cm2), but further reductions in diffusive coupling cause the cortex to collapse into a low-firing coma-like state (D2 = 0.35 cm2). In this case, weakened Turing mediation cannot unleash an unconstrained Hopf oscillation because the only surviving Hopf instability is the heavily damped DH mode on the bottom branch.
= (1.5, 1.0) to (1.5, 1.016); this represents a tiny increase in inhibitory drive that moves the up-state very close to the loss-of-consciousness cusp on the manifold surface. This subtle change in coordinate causes the up-state stability graph to transform from the 3-Hz Hopf oscillation of Fig. 2a to a zero-frequency instability (Fig. 3a) that we label as “saddle” (in analogy to zero-frequency saddle–node bifurcations in two-variable dynamical systems (Steyn-Ross et al. 2006)). Commencing from a balanced Hopf–Turing default state (not shown), step reductions in D2 interneuronal gap-junction coupling take the cortex through a chaotic phase (D2 = 0.5, 0.4 cm2), but further reductions in diffusive coupling cause the cortex to collapse into a low-firing coma-like state (D2 = 0.35 cm2). In this case, weakened Turing mediation cannot unleash an unconstrained Hopf oscillation because the only surviving Hopf instability is the heavily damped DH mode on the bottom branch.
Fig. 3.
Model sensitivity to a very small increase in cortical inhibition to λi = 1.016 (previously 1.0 in Fig. 2). Gap-junction diffusion (in cm2) is decreased from D2 = 0.5 (top row) to 0.4 (middle row) to 0.35 (bottom row). a Predicted linear stability for up- and down-states as a function of wavenumber q. The 3-Hz Hopf instability in the up-state has become a saddle instability, while the down-state dispersion curves are little changed. b and c show 10-s numerical simulations for a cortex initialized at the unstable mid-branch equilibrium values: bQe(t) time-series for excitatory firing activity at selected pixels distributed at equal intervals along a line parallel to the grid x-axis; cQe(x, t) space–time view of cortical activity. As for Fig. 2, initial decrease in inhibitory diffusion (D2 = 0.5, 0.4 cm2) leads to chaotic precursor to seizure, but further blockade now suppresses seizure-like activity completely Graph scales: a Blue = real part of dominant eigenvalue (in s−1); red = (imaginary part)/2π (Hz); horizontal axis is scaled wavenumber q/2π (waves/cm). b Vertical scale for Qe runs from zero to 30 spikes/s; time axis runs from 0 to 10 s. c Space–time plot with vertical scale showing 25-cm x-axis extent of cortical grid, horizontal axis showing time; color scale: red = high activity, blue = low activity. (Color figure online)
Overview of gap-junction effect on seizure
We now summarize the impact of gap-junction modulation on cortical behavior. For the multi-root region of Fig. 1, the final state of the cortex depends on the relative stabilities of the homogeneous, Hopf, and Turing states of the awake (activated) and comatose (quiescent) phases. We can obtain guidance as to which mode will dominate by examining the dispersion diagrams of Figs. 2 and 3.
For the “awake” state at small diffusion (D2 = 0.1cm2, bottom row of Fig. 2), the bottom-branch homogeneous stability is swamped by the top-branch Hopf instability, resulting in whole-of-cortex large-amplitude oscillations (seizure). Increasing D2 causes the full-blown seizure to weaken as the bottom-branch Turing instability becomes steadily less damped, allowing it to compete with, and eventually dominate, the Hopf mode (see top row: D2 = 0.7cm2). We now see a state of oscillating Turing patterns that we identify as the “default–wake” state. For intermediate values of D2, neither instability dominates, and a Turing–Hopf turbulent phase with chaotic spatiotemporal patterns emerges. We identify this turbulent phase as the incoherent prelude to seizure.
Moving the cortex towards a state of anesthesia has a pronounced effect on the upper-branch dispersion graphs. Comparing Figs. 2a and 3a, we see that a homogeneous (“saddle”) instability has replaced the upper-branch Hopf instability. For D2 = 0.35cm2 (bottom row of Fig. 3), the lower branch is a fixed-point attractor with damped Hopf and Turing modes, so the cortex settles into a homogenous low-firing quiescent state. Thus, for the anesthetized cortex, closing gap junctions does not promote seizure activity. As D2 increases, the Turing and Hopf modes, although still damped, interact to destabilize the homogeneous state, resulting in the mixed-mode chaotic state. A further increase in D2 produces the small-amplitude oscillations of the Turing-dominated “default” state.
Our theoretical model may explain the conflicting experimental results reported in the literature. Comparing Figs. 2 and 3, we conclude that the dynamic impact of closing gap junctions is complex, and depends sensitively on how close the cortical operating point is to the fold in the cortical domain. Closing gap junctions may suppress seizure by inducing coma, but equally, gap-junction closure could allow emergence of an uncontrolled Hopf instability. Nevertheless, at the opposite extreme, fully open gap junctions should provide Turing mediation and protection against giant temporal oscillations.
Discussion
In this paper we have argued that the presence of a continuous network of gap-junction connections between cortical interneurons could play a crucial role in maintaining cortical stability. The relative abundance of inhibitory-to-inhibitory gap junctions (Fukuda et al. 2006; Bennett and Zukin 2004) provides the strong inhibitory diffusion required for the spontaneous emergence of Turing patterns of “up” (elevated) and “down” (suppressed) states of cortical activity. This pattern-forming tendency competes with, and modulates, the temporal rhythms arising from a Hopf instability. We suggest that a balanced competition between both types of instability is essential for a healthy functioning brain, and that loss of Turing control can lead to the unrestrained growth of the Hopf mode, leading to gross scale, synchronized waves of seizure activity.
In this paper we have not differentiated between physiological and pathological oscillations. We picture the distinction between the slow oscillations of slow-wave sleep and those found in seizures as being primarily one of degree rather than kind. During seizures, there are as yet unknown processes that result in uncontrolled neuronal recruitment, manifest as larger, steeper waves.
How might inhibitory diffusive coupling strength be varied in a real brain? In addition to direct manipulation via exogenous application to cortical tissue of gap junction blockers (e.g., quinine, mefloquin, carbenoxolone) and openers (trimethylamine), there is a wide range of naturally occurring endogenous conditions—both physiological and pathological—that are associated with transient gap-junction closing (e.g., intracellular acidosis, hypercalcemia, and cyclic AMP-dependent protein kinase activation) and opening (alkalosis, hypocalcemia) (Connors and Long 2004). Rapid transmission of inhibition may also be facilitated via other neurobiological mechanisms such as ephaptic coupling, and glial-modulated chemical diffusion through the extracellular space (Bullock et al. 2005). Conversely, seizure propensity may be exacerbated if the rapid transmission of diffusive inhibition is impaired by, for example, interneuronal pathology or tissue scarring.
Healthy brain activity relies on transient, fluctuating, coherent interplay between segregated neuronal populations. We suggest that a dynamically maintained Turing–Hopf balance ensures that the brain remains delicately responsive to changes in stimulus: the Turing mode creates spontaneous spatial aggregates, while the Hopf oscillation synchronizes small-amplitude temporal fluctuations both within and across aggregates. But if the Hopf mode is allowed to dominate, the fluctuations can grow into large-amplitude whole-of-cortex oscillations that manifest as coherent traveling waves that we identify as seizure. If our model is correct, then the transition—from the healthy coherent state of balanced cortical idling (top row of Fig. 2) to the unhealthy hypercoherent seizure state of Hopf dominance (bottom three rows of Fig. 2)—will be marked by a turbulent intermediate regime that is characterized by profoundly reduced spatial coherence (fourth row). This prediction, that the coherent seizure state should be preceded by an incoherent precursor, is broadly consistent with recent phase coherence analyses of MEG and EEG recordings from epileptic patients (Chávez et al. 2003; Mormann et al. 2003; Amor et al. 2009). The conformance with experiment suggests that the model may provide some insight into why blockade of gap junctions is not necessarily therapeutically useful for the treatment and prevention of seizure events in the brain.
Although our cortical model is deliberately incomplete (e.g., it lacks anatomical structure and a thalamus), it exhibits a surprisingly diverse range of dynamic spatiotemporal behaviors, some of which may be physiologically relevant. (We note that some form of seizure activity is found in the nervous systems of all species of animals, thus seizure propensity cannot depend on precise neuroanatomical detail.) This diversity arises naturally if we assume, as a general principle, that the brain is able to organize itself so that it can harness and make useful any incipient instabilities available to it, such as Turing patterning and Hopf oscillations. It is then plausible that a failure in the balancing of the unstable modes could lead to pathological states such as seizure.
Acknowledgments
This work was supported by the Royal Society of New Zealand Marsden Fund, contract 07-UOW-037.
Glossary
- BOLD
Blood oxygen level-dependent signal
- EEG
Electroencephalogram
- E(I)PSP
Excitatory (inhibitory) postsynaptic potential
- MEG
Magnetoencephalogram
Appendix
Phase coherence calculations for Figs. 2 and 3
Consider a (real) time-series X(t). Its Hilbert transform is a complex time-series known as the analytic signal; by computing the four-quadrant arctangent of the ratio of its imaginary and real parts we obtain a time-series for ϕ(t), the instantaneous phase angle. The phase similarity between two time-series X(t) and Y(t) can be determined by examining the time-series of their phase differences 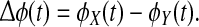 If X and Y are tightly phase-coupled, then plotting
If X and Y are tightly phase-coupled, then plotting 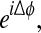 the difference signal mapped to the unit circle, will give a tightly clustered angular distribution of phasors, whereas if X and Y have a relative phase relation that is incoherent, the difference phasors will be randomly distributed around the complex circle.
the difference signal mapped to the unit circle, will give a tightly clustered angular distribution of phasors, whereas if X and Y have a relative phase relation that is incoherent, the difference phasors will be randomly distributed around the complex circle.
We define the mean phase coherenceR of the X and Y time-series as the length of the time-averaged phasor for the angular distribution of phase differences, 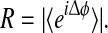 If X and Y are tightly phase coupled, then R ≈ 1, and if they are uncoupled, R ≈ 0.
If X and Y are tightly phase coupled, then R ≈ 1, and if they are uncoupled, R ≈ 0.
A Matlab implementation of the phase coherence algorithm reads as follows: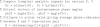
Let X ≡ Qe(x0, t) and Y ≡ Qe(xk, t) be a pair of cortical firing-rate time-series belonging respectively to rows 0 and k of a given Fig. 2c strip-chart. The x-axis separation between these two rows is 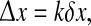 and the mean phase coherence,
and the mean phase coherence, 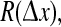 of their time-series gives a measure of the degree to which cortical activity is correlated for an electrode pair separated by distance
of their time-series gives a measure of the degree to which cortical activity is correlated for an electrode pair separated by distance 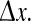 We fix the x0 reference position to be close to the center of the grid, and vary the position of the second electrode xk with k = 0, ±1, ±2, … corresponding to stepped increases in electrode separation ranging from
We fix the x0 reference position to be close to the center of the grid, and vary the position of the second electrode xk with k = 0, ±1, ±2, … corresponding to stepped increases in electrode separation ranging from 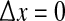 to 12.5 cm. In this way we are able to construct the Fig. 2e graphs showing the variation of phase coherence with distance.
to 12.5 cm. In this way we are able to construct the Fig. 2e graphs showing the variation of phase coherence with distance.
In these calculations, we took care to skip over first 1 s of recording to allow time for the initial transients to settle out. We used a 5-s recording window with 1-s overlap, and followed Mormann et al. (2000) in applying a Hanning window, retaining only the middle 80% of each segment to minimize edge distortions from the Hilbert transform. Because we expect phase symmetry for rows ±k symmetrically displaced either side of the x0 reference position, we used the standard deviation in their phase coherence values to estimate the error bars at separation 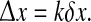
Footnotes
We could equally well have chosen to increase the level of subcortical drive entering the cortex, or we could have scaled ρe, the strength of the excitatory postsynaptic potential (EPSP); however, neither of these alternatives substantially alters the qualitative model predictions reported here.
Contributor Information
Moira L. Steyn-Ross, Phone: +64-7-8384585, FAX: +64-7-8384835, Email: msr@waikato.ac.nz
D. Alistair Steyn-Ross, Email: asr@waikato.ac.nz.
Jamie W. Sleigh, Email: Jamie.Sleigh@waikatodhb.health.nz
References
- Amor F, Baillet S, Navarro V, Adam C, Martinerie J, Quyen MLV. Cortical local and long-range synchronization interplay in human absence seizure initiation. NeuroImage. 2009;45(3):950–962. doi: 10.1016/j.neuroimage.2008.12.011. [DOI] [PubMed] [Google Scholar]
- Beck P, Odle A, Wallace-Huitt T, Skinner RD, Garcia-Rill E. Modafinil increases arousal determined by P13 potential amplitude: an effect blocked by gap junction antagonists. Sleep. 2008;31(12):1647–1654. doi: 10.1093/sleep/31.12.1647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett MV, Zukin RS. Electrical coupling and neuronal synchronization in the mammalian brain. Neuron. 2004;41:495–511. doi: 10.1016/S0896-6273(04)00043-1. [DOI] [PubMed] [Google Scholar]
- Bojak I, Liley DTJ. Modeling the effects of anesthesia on the electroencephalogram. Phys Rev E. 2005;71:041902. doi: 10.1103/PhysRevE.71.041902. [DOI] [PubMed] [Google Scholar]
- Bullock TH, Bennett MVL, Johnston D, Josephson R, Marder E, Fields RD. Neuroscience. The neuron doctrine, redux. Science. 2005;310(5749):791–793. doi: 10.1126/science.1114394. [DOI] [PubMed] [Google Scholar]
- Carlen PL, Skinner F, Zhang L, Naus C, Kushnir M, Perez Velazquez JL. The role of gap junctions in seizures. Brain Res Rev. 2000;32(1):235–241. doi: 10.1016/S0165-0173(99)00084-3. [DOI] [PubMed] [Google Scholar]
- Chávez M, LeVan Quyen M, Navarro V, Baulac M, Martinerie J. Spatio-temporal dynamics prior to neocortical seizures: amplitude versus phase couplings. IEEE Trans Biomed Eng. 2003;50(5):571–583. doi: 10.1109/TBME.2003.810696. [DOI] [PubMed] [Google Scholar]
- Connors BW, Long MA. Electrical synapses in the mammalian brain. Annu Rev Neurosci. 2004;27:393–418. doi: 10.1146/annurev.neuro.26.041002.131128. [DOI] [PubMed] [Google Scholar]
- Deco G, Jirsa V, McIntosh AR, Sporns O, Kötter R. Key role of coupling, delay, and noise in resting brain fluctuations. Proc Natl Acad Sci USA. 2009;106(25):10302–10307. doi: 10.1073/pnas.0901831106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudek FE. Gap junctions and fast oscillations: a role in seizures and epileptogenesis? Epilepsy Curr. 2002;2(4):133–136. doi: 10.1046/j.1535-7597.2002.t01-1-00051.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci USA. 2005;102(27):9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda T, Kosaka T, Singer W, Galuske RAW. Gap junctions among dendrites of cortical GABAergic neurons establish a dense and widespread intercolumnar network. J Neurosci. 2006;26:3434–3443. doi: 10.1523/JNEUROSCI.4076-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gajda Z, Gyengesi E, Hermesz E, Ali KS, Szente M. Involvement of gap junctions in the manifestation and control of the duration of seizures in rats in vivo. Epilepsia. 2003;44(12):1596–1600. doi: 10.1111/j.0013-9580.2003.25803.x. [DOI] [PubMed] [Google Scholar]
- Gajda Z, Szupera Z, Blazso G, Szente M. Quinine, a blocker of neuronal Cx36 channels, suppresses seizure activity in the rat neocortex in vivo. Epilepsia. 2005;56:1581–1591. doi: 10.1111/j.1528-1167.2005.00254.x. [DOI] [PubMed] [Google Scholar]
- Ghosh A, Rho Y, McIntosh AR, Kötter R, Jirsa VK. Noise during rest enables the exploration of the brain’s dynamic repertoire. PLoS Comput Biol. 2008;4(10):e1000196. doi: 10.1371/journal.pcbi.1000196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey CJ, Kötter R, Breakspear M, Sporns O. Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc Natl Acad Sci USA. 2007;104(24):10240–10245. doi: 10.1073/pnas.0701519104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutt A, Longtin A. Effects of the anesthetic agent propofol on neural populations. Cogn Neurodyn. 2010;4(1):37–59. doi: 10.1007/s11571-009-9092-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobson GM, Voss LJ, Melin SM, Mason JP, Cursons RT, Steyn-Ross DA, et al. Connexin36 knockout mice display increased sensitivity to pentylenetetrazol-induced seizure-like behaviors. Brain Res. 2010;1360:198–204. doi: 10.1016/j.brainres.2010.09.006. [DOI] [PubMed] [Google Scholar]
- Jacobson GM, Voss LJ, Melin SM, Cursons RTM, Sleigh JW. The role of connexin36 gap junctions in modulating the hypnotic effects of isoflurane and propofol in mice. Anaesthesia. 2011;66(5):361–367. doi: 10.1111/j.1365-2044.2011.06658.x. [DOI] [PubMed] [Google Scholar]
- Jahromi SS, Wentlandt K, Piran S, Carlen PL. Anticonvulsant actions of gap junctional blockers in an in vitro seizure model. J Neurophysiol. 2002;88(4):1893–1902. doi: 10.1152/jn.2002.88.4.1893. [DOI] [PubMed] [Google Scholar]
- Juszczak GR, Swiergiel AH. Properties of gap junction blockers and their behavioural, cognitive and electrophysiological effects: animal and human studies. Prog Neuropsychopharmacol Biol Psychiatry. 2009;33:181–198. doi: 10.1016/j.pnpbp.2008.12.014. [DOI] [PubMed] [Google Scholar]
- Kitamura A, Marszalec W, Yeh JZ, Narahashi T. Effects of halothane and propofol on excitatory and inhibitory synaptic transmission in rat cortical neurons. J Pharmacol. 2002;304(1):162–171. doi: 10.1124/jpet.102.043273. [DOI] [PubMed] [Google Scholar]
- Kramer MA, Kirsch HE, Szeri AJ. Pathological pattern formation and cortical propagation of epileptic seizures. J R Soc Lond Interface. 2005;2:113–207. doi: 10.1098/rsif.2004.0028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liley DTJ, Bojak I. Understanding the transition to seizure by modeling the epileptiform activity of general anesthetic agents. Clin Neurophysiol. 2005;22(5):300–313. [PubMed] [Google Scholar]
- Mantini D, Perrucci MG, Del Gratta C, Romani GL, Corbetta M. Electrophysiological signatures of resting state networks in the human brain. Proc Natl Acad Sci USA. 2007;104(32):13170–13175. doi: 10.1073/pnas.0700668104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mormann F, Lehnertz K, David P, Elger CE. Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients. Physica D. 2000;144:358–369. doi: 10.1016/S0167-2789(00)00087-7. [DOI] [Google Scholar]
- Mormann F, Kreuz T, Andrzejak RG, David P, Lehnertz K, Elger CE. Epileptic seizures are preceded by a decrease in synchronization. Epilepsy Res. 2003;53(3):173–185. doi: 10.1016/S0920-1211(03)00002-0. [DOI] [PubMed] [Google Scholar]
- Nilsen KE, Kelso AR, Cock HR. Antiepileptic effect of gap-junction blockers in a rat model of refractory focal cortical epilepsy. Epilepsia. 2006;47(7):1169–1175. doi: 10.1111/j.1528-1167.2006.00540.x. [DOI] [PubMed] [Google Scholar]
- Pais I, Hormuzdi SG, Monyer H, Traub RD, Wood IC, Buhl EH, et al. Sharp wave-like activity in the hippocampus in vitro in mice lacking the gap junction protein connexin 36. J Neurophysiol. 2003;89:2046–2054. doi: 10.1152/jn.00549.2002. [DOI] [PubMed] [Google Scholar]
- Perez Velazquez JL, Carlen PL. Gap junctions, synchrony and seizures. Trends Neurosci. 2000;23(2):68–74. doi: 10.1016/S0166-2236(99)01497-6. [DOI] [PubMed] [Google Scholar]
- Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proc Natl Acad Sci USA. 2001;98:676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson PA, Rennie CJ, Wright JJ. Propagation and stability of waves of electrical activity in the cerebral cortex. Phys Rev E. 1997;56:826–840. doi: 10.1103/PhysRevE.56.826. [DOI] [Google Scholar]
- Robinson PA, Rennie CJ, Rowe DL. Dynamics of large-scale brain activity in normal arousal states and epileptic seizures. Phys Rev E. 2002;65(4):041924. doi: 10.1103/PhysRevE.65.041924. [DOI] [PubMed] [Google Scholar]
- Shinohara K, Hiruma H, Funabashi T, Kimura F. Gabaergic modulation of gap junction communication in slice cultures of the rat suprachiasmatic nucleus. Neurosci. 2000;96(3):591–596. doi: 10.1016/S0306-4522(99)00556-4. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross ML, Steyn-Ross DA, Sleigh JW, Liley DTJ. Theoretical electroencephalogram stationary spectrum for a white-noise-driven cortex: evidence for a general anesthetic-induced phase transition. Phys Rev E. 1999;60:7299–7311. doi: 10.1103/PhysRevE.60.7299. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross DA, Steyn-Ross ML, Wilcocks LC, Sleigh JW. Toward a theory of the general anesthetic-induced phase transition of the cerebral cortex: II. Stochastic numerical simulations, spectral entropy, and correlations. Phys Rev E. 2001;64:011918. doi: 10.1103/PhysRevE.64.011918. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross ML, Steyn-Ross DA, Sleigh JW, Wilcocks LC. Toward a theory of the general anesthetic-induced phase transition of the cerebral cortex: I. A statistical mechanics analogy. Phys Rev E. 2001;64:011917. doi: 10.1103/PhysRevE.64.011917. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross ML, Steyn-Ross DA, Sleigh JW, Whiting DR. Theoretical predictions for spatial covariance of the EEG signal during the anesthetic-induced phase transition: Increased correlation length and emergence of self-organization. Phys Rev E. 2003;68:021902. doi: 10.1103/PhysRevE.68.021902. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross ML, Steyn-Ross DA, Sleigh JW. Modelling general anaesthesia as a first-order phase transition in the cortex. Prog Biophys Mol Biol. 2004;85:369–385. doi: 10.1016/j.pbiomolbio.2004.02.001. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross DA, Steyn-Ross ML, Wilson MT, Sleigh JW. White-noise susceptibility and critical slowing in neurons near spiking threshold. Phys Rev E. 2006;74:051920. doi: 10.1103/PhysRevE.74.051920. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross ML, Steyn-Ross DA, Wilson MT, Sleigh JW. Gap junctions mediate large-scale Turing structures in a mean-field cortex driven by subcortical noise. Phys Rev E. 2007;76:011916. doi: 10.1103/PhysRevE.76.011916. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross ML, Steyn-Ross DA, Wilson MT, Sleigh JW. Modeling brain activation patterns for the default and cognitive states. NeuroImage. 2009;45:298–311. doi: 10.1016/j.neuroimage.2008.11.036. [DOI] [PubMed] [Google Scholar]
- Steyn-Ross ML, Steyn-Ross DA, Sleigh JW, Wilson MT. A mechanism for ultra-slow oscillations in the cortical default network. Bull Math Biol. 2010;73(2):398–416. doi: 10.1007/s11538-010-9565-9. [DOI] [PubMed] [Google Scholar]
- Traub RD, Whittington MA, Buhl EH, LeBeau FE, Bibbig A, Boyd S, et al. A possible role for gap junctions in generation of very fast EEG oscillations preceding the onset of, and perhaps initiating, seizures. Epilepsia. 2001;42(2):153–170. doi: 10.1046/j.1528-1157.2001.26900.x. [DOI] [PubMed] [Google Scholar]
- Turing AM. The chemical basis of morphogenesis. Philos Trans R Soc London. 1952;237:37–72. doi: 10.1098/rstb.1952.0012. [DOI] [Google Scholar]
- Voss LJ, Jacobson G, Sleigh JW, Steyn-Ross DA, Steyn-Ross ML. Excitatory effects of gap junction blockers on cerebral cortex seizure-like activity in rats and mice. Epilepsia. 2009;50(8):1971–1978. doi: 10.1111/j.1528-1167.2009.02087.x. [DOI] [PubMed] [Google Scholar]
- Wentlandt K, Samoilova M, Carlen PL, El Beheiry H. General anesthetics inhibit gap junction communication in cultured organotypic hippocampal slices. Anaesth Analg. 2006;102(6):1692–1698. doi: 10.1213/01.ane.0000202472.41103.78. [DOI] [PubMed] [Google Scholar]
- Wilson MT, Sleigh JW, Steyn-Ross DA, Steyn-Ross ML. General anesthetic-induced seizures can be explained by a mean-field model of cortical dynamics. Anesthesiology. 2006;104:588–593. doi: 10.1097/00000542-200603000-00026. [DOI] [PubMed] [Google Scholar]
- Yang L, Ling DSF. Carbenoxolone modifies spontaneous inhibitory and excitatory synaptic transmission in rat somatosensory cortex. Neurosci Lett. 2007;416:221–226. doi: 10.1016/j.neulet.2007.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]