Abstract
Latent state-trait (LST) analysis is frequently applied in psychological research to determine the degree to which observed scores reflect stable person-specific effects, effects of situations and/or person-situation interactions, and random measurement error. Most LST applications use multiple repeatedly measured observed variables as indicators of latent trait and latent state residual factors. In practice, such indicators often show shared indicator-specific (or methods) variance over time. In this article, the authors compare four approaches to account for such method effects in LST models and discuss the strengths and weaknesses of each approach based on theoretical considerations, simulations, and applications to actual data sets. The simulation study revealed that the LST model with indicator-specific traits (Eid, 1996) and the LST model with M − 1 correlated method factors (Eid, Schneider, & Schwenkmezger, 1999) performed well, whereas the model with M orthogonal method factors used in the early work of Steyer, Ferring, and Schmitt (1992) and the correlated uniqueness approach (Kenny, 1976) showed limitations under conditions of either low or high method-specificity. Recommendations for the choice of an appropriate model are provided.
Keywords: Latent state-trait analysis, method effects, indicator-specific effects, correlated uniqueness, longitudinal modeling, confirmatory factor analysis
Many theories in psychology are concerned with the distinction of temporally stable versus variable (occasion-specific) components of behavior. As Hertzog and Nesselroade (1987) pointed out, “Generally it is certainly the case that most psychological attributes will neither be, strictly speaking, traits or states. That is, attributes can have both trait and state components” (p. 95). In the late 1980s and early ‘90s, the first attempts were made to use latent variable techniques such as structural equation modeling (SEM) to analyze the degree to which psychological measurements reflect stable attributes, occasion-specific fluctuations, and random measurement error (e.g., Hertzog & Nesselroade, 1987; Ormel & Schaufeli, 1991).
Latent state-trait (LST) theory (Steyer, Majcen, Schwenkmezger, & Buchner, 1989; Steyer & Schmitt, 1990; Steyer, Ferring, & Schmitt, 1992; Steyer, Schmitt, & Eid, 1999) provides a powerful theoretical framework for defining latent trait, latent state residual, and measurement error variables. In contrast to traditional factor analytic approaches, LST theory explicitly defines these latent variables as conditional expectations of observed variables given persons and situations or as functions of such conditional expectations (for details see Appendix A as well as Steyer & Schmitt, 1990; Steyer et al., 1992, 1999). As a consequence, LST theory provides well-defined latent variables that have a clear and unambiguous interpretation, making this a very strong psychometric theory for analyzing stable, occasion-specific, and random error components of psychological measurements.
Since the early theoretical work by Steyer and colleagues, there has been an ever growing interest in LST theory and models. Models of LST theory are widely applied in various fields of psychology, including research in personality (e.g., Deinzer et al., 1995; Schmitt, Gollwitzer, Maes, & Arbach, 2005; Moskowitz & Zuroff, 2004; Vautier, 2004), emotion (e.g., Windle & Dumenci, 1998), subjective well-being (e.g., Eid & Diener, 2004), job satisfaction (Dormann, Fay, Zapf, & Frese, 2006), marketing (Baumgartner & Steenkamp, 2006), psychoneuroendocrinology (Kirschbaum, Steyer, Eid, Patalla, Schwenkmezger, & Hellhammer, 1990), psychophysiology (e.g., Hagemann, Hewig, Seifert, Naumann, & Bartussek, 2005), and psychopathology (King, Molina, & Chassin, 2008). Furthermore, the past 20 years have witnessed a dramatic increase in the development, testing, and extension of LST models in such varying contexts as multiconstruct modeling (Dumenci & Windle, 1998; Eid, Notz, Steyer, & Schwenkmezger, 1994; Steyer, Schwenkmezger, & Auer, 1990), categorical data analysis (Eid, 1995; 1996; Eid & Hoffmann, 1998), latent class analysis (Eid, 2007; Eid & Langeheine, 1999), hierarchical LST models (Schermelleh-Engel, Keith, Moosbrugger, & Hodapp, 2004), mixture distribution analysis (Courvoisier, Eid, & Nussbeck, 2007), autoregressive models (Cole, Martin, & Steiger, 2005; Ciesla, Cole, & Steiger, 2007; Kenny & Zautra, 1995; Steyer & Schmitt, 1994), latent change models (Eid & Hoffmann, 1998), latent growth curve analysis (Tisak & Tisak, 2000), person-level LST analysis (Hamaker, Nesselroade, & Molenaar, 2007), and multimethod measurement (Courvoisier, 2006; Courvoisier, Nussbeck, Eid, Geiser, & Cole, 2008).
In the present article, our focus is on modeling method effects in LST models. Schmitt (2006) defined a psychological assessment method as “a set containing a variety of instruments and procedures that uncover psychological attributes of objects and transform these attributes into symbols that can be processed” (p. 17). Method effects may arise due to the use of, for example, different items, tests, raters, or even different situations or occasions of measurement that contain specific components not shared with other indicators of the same construct (see Podsakoff, MacKenzie, Lee, & Podsakoff [2003] for a detailed overview of sources of method variance in the behavioral sciences).
The present study extends on the work by LaGrange and Cole (2008) who recently compared different approaches to modeling method effects in LST models. As in LaGrange and Cole’s (2008) study, our focus here is on multiple indicator LST models (Steyer et al., 1992; 1999). In contrast to single indicator LST models (Kenny & Zautra, 1995, 2001), multiple indicator LST models make use of multiple repeatedly administered scales or items to measure latent trait, latent state residual, and measurement error variables. Method effects are typically present in multiple indicator applications due to the repeated administration of the same indicators over time (Cole & Maxwell, 2003). The purpose of this article is to (1) provide a theoretical review of different approaches for handling method effects in LST analyses, (2) examine the performance of these approaches based on a simulation study and applications to real data, and (3) discuss advantages and limitations based on the theoretical considerations and empirical findings of this study.
In contrast to Courvoisier et al. (Courvoisier, 2006; Courvoisier et al., 2008) who considered the case of multiple methods (e.g., raters) each of which provide multiple indicators at each time point, our main focus here is on the more common situation in which one either studies (1) multiple indicators pertaining to just a single method or rater over time (e.g., multiple repeatedly administered self-report items), or (2) different methods (e.g., different raters) provide just a single indicator at each time point. Such a design is used in the vast majority of applications of LST models. (Later on, we will return to the advantages of using multiple indicators for each method based on an application.) As we explain in detail below, even in LST designs that use just a single method, method effects occur routinely due to having multiple repeatedly measured indicators.
The LST Model With No Method Factors
The starting point for a multiple indicator LST analysis is a set of repeatedly administered observed indicator variables Yit (i = indicator, i = 1,…, m; t = time point, t = 1, …, n) that pertain to the same construct (e.g., anxiety, subjective well-being, extraversion etc.)1. Indicators for a construct in an LST model could, for example, be different items, scale scores, or physiological measures, but also scores obtained from different raters.2 In the most simple LST model, each observed variable measures an (occasion-unspecific) latent trait factor T and an (occasion-specific) latent state residual factor SRt (e.g., Eid & Diener, 2004):
| (1) |
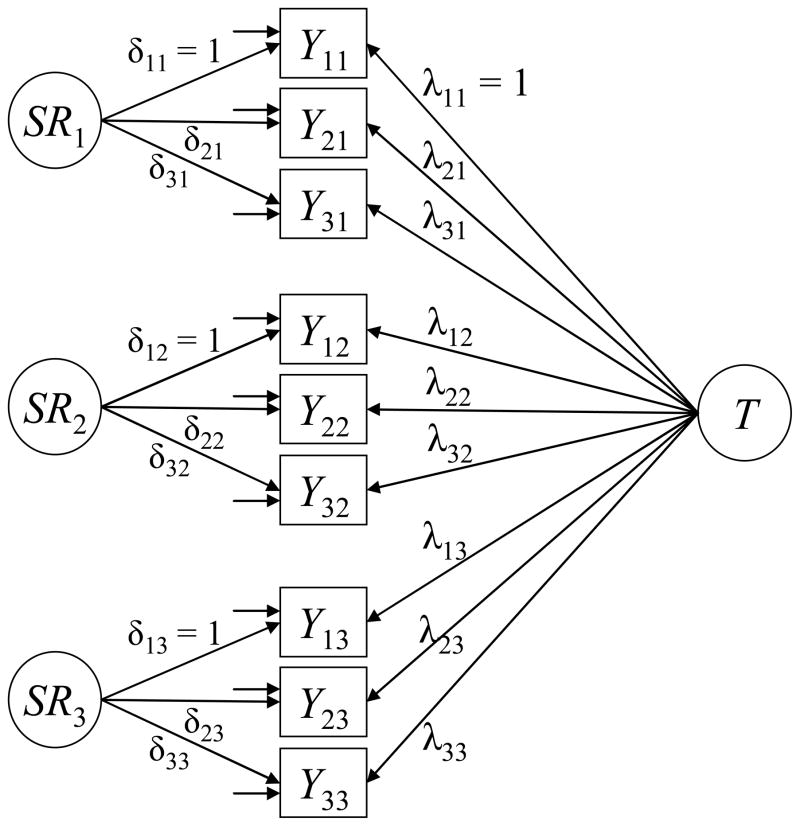
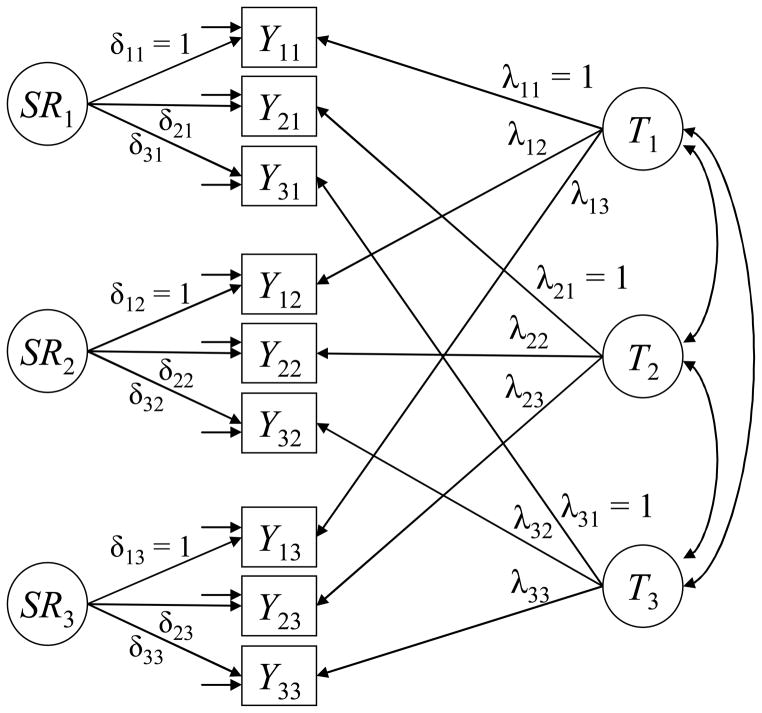
where λit represents a trait factor loading, δit represents a state residual factor loading, εit is an error variable, and all variables are in deviation form (i.e., mean-centered). The latent trait factor T represents the time-unspecific (stable) component and is by definition uncorrelated with the latent state residual factors SRt.3 The factors SRt reflect the effects of the situation as well as person × situation interactions (Steyer et al., 1992, 1999). The error variable εit is by definition uncorrelated with T and all SRt (Steyer et al., 1992). In line with Steyer et al. (1999) we additionally make the assumption that (1) all latent state residual factors SRt are uncorrelated with each other4 and (2) all error variables are uncorrelated with each other. There are no method factors in this model. Hence, we refer to this model as the “no method factor” (NM) model. Figure 1 shows a path diagram of the NM model for three observed variables measured on three time points.
Figure 1.
LST model with no method factors (NM). Yit denotes the ith observed variable (indicator) measured at time t. T: latent trait factor. SRt: latent state residual factor. λit: trait factor loading. δit: state residual factor loading.
Given the uncorrelatedness of trait, state residual, and error variables, the following variance decomposition holds for the observed variables:
| (2) |
This additive variance decomposition allows defining three coefficients of determination that are of key interest to virtually all LST applications: the consistency (CO), occasion-specificity (OSpe), and reliability (Rel) coefficients (Steyer et al., 1999). CO indicates to which degree individual differences are determined by stable person-specific effects:
| (3) |
The OSpe coefficient indicates to which degree individual differences are determined by the situation and/or person × situation interactions:
| (4) |
The reliability coefficient indicates the degree to which observed individual differences are due to reliable sources of variances (rather than measurement error) and therefore equals the sum of consistency and occasion-specificity coefficient:
| (5) |
The consistency, occasion-specificity, and (1 – reliability) coefficients sum up to 1, that is, CO(Yit) + OSpe(Yit) + [1 − Rel(Yit)] = 1.
Substantively, the coefficients of consistency and occasion-specificity are useful to study the degree of stability versus situation-dependence of psychological measurements. For example, Windle and Dumenci (1998) examined trait and state residual components of depressed mood among mothers and their adolescent children and found that depressed mood was both stable and situation-dependent for both reporters. After removing variance due to occasion-specificity, the authors demonstrated a clearer link between maternal and adolescent depression than had previously been established. In sum, the estimation of these variance components is the main focus of most studies that employ LST models, and these coefficients are also of key interest to the present study on method effects. In particular, we are interested in how reliably these coefficients are estimated in different approaches for modeling method effects.
Method Effects in LST Models
The NM model assumes that the variances and covariances of the observed variables (indicators) are fully explained by the latent trait factors, state residual factors, and error variables. Error variables are assumed to be uncorrelated. This implies that indicators may not share idiosyncratic components with themselves over time. However, in practice, most indicators contain a unique (method-specific) component that may not be shared with the remaining indicators (Steyer et al., 1992; Cole et al., 2005). As a consequence, identical indicators may be more highly correlated with themselves over time than with other indicators (Cole & Maxwell, 2003).
In LST analyses, method effects may be present for at least two reasons. First, if questionnaire items serve as indicators, these items may, for example, differ in wording (e.g., some items may be positively, others negatively worded) or content. Slight differences in item content are usually desired features of a scale in order to achieve greater construct validity of that measure (Cronbach, 1990). Second, even stronger indicator-specific effects must be expected if different indicators of the same construct were obtained from distinct methods or raters (e.g., self- vs. other ratings; Geiser, Eid, Nussbeck, Courvoisier, & Cole, 2010). The use of multiple, possibly very different methods to measure the constructs of interest has been strongly advocated since Campbell and Fiske’s (1959) seminal article on the multitrait-multimethod (MTMM) matrix (Eid & Diener, 2006). As Cole and colleagues (2007) note, “In an ideal world, all researchers would use at least three (and preferably more) completely orthogonal methods to measure all constructs in every study” (p. 382). When different methods are used as indicators, the convergent validity of such methods will often be rather low (e.g., Fiske & Campbell, 1992), and, as shown below, this must be taken into account when conducting an LST analysis in order to avoid bias in parameter estimation.
In sum, method effects are a ubiquitous phenomenon in longitudinal research, whether different indicators represent different items, raters, or other types of methods. The issue of method effects has been extensively discussed in the general literature in the context of longitudinal structural equation models (e.g., Cole & Maxwell, 2003; Jöreskog, 1979a, b; Marsh & Grayson, 1995; Raffalovich & Bohrnstedt, 1987; Sörbom, 1975; Tisak & Tisak, 2000). Although LST models with method factors were presented early in the history of LST theory (Steyer et al., 1992), the problem of method effects has not received much explicit attention in the context of LST analyses. Most LST studies have treated such effects as a nuisance or “side-effect”, and various authors have addressed this problem in very different ways (see Appendix B for an overview of applications of LST models and the type of approaches used in these studies to deal with method effects). The only paper we know of that has explicitly studied the performance of different approaches to modeling method effects in the context of LST analysis is a recent study by LaGrange and Cole (2008). Before we summarize LaGrange and Cole’s findings, we discuss different approaches to modeling method effects in LST analyses.
Approaches for Addressing Method Effects in LST Models
The Correlated Uniqueness Approach
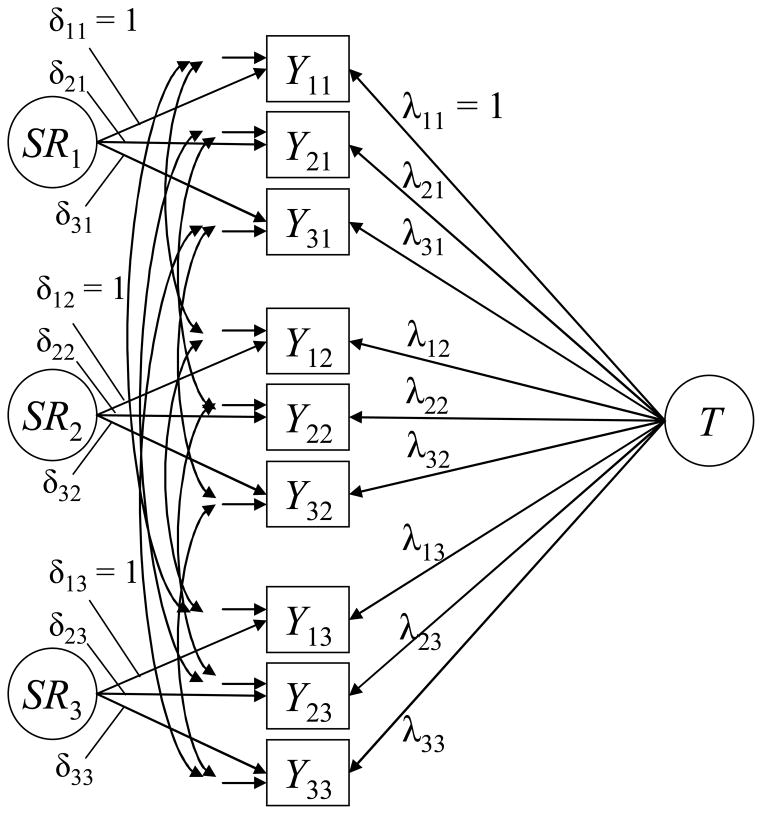
A frequently used way to account for shared method variance in longitudinal models is to allow the error variables of the same indicator to correlate over time (so-called auto-correlated errors or correlated uniquenesses [CU]; see Figure 2). This approach has been proposed early in the literature on longitudinal structural equation models (e.g., Jöreskog, 1979a, b; Sörbom, 1975) and is known as CU approach in the context of multitrait-multimethod (MTMM) analysis (Kenny, 1976; Marsh & Grayson, 1995). Correlated error variables of the same indicators account for the higher correlations of identical indicators over time when shared indicator-specific variance is present. This approach to modeling method effects has been applied to LST analyses, for example, by Steyer et al. (1990) as well as Yasuda, Lawrenz, van Whitlock, Lubin, and Lei (2004).
Figure 2.
LST model with orthogonal method factors (OM). Mi indicates the method factor for indicator i. γit: method factor loading.
Although straightforward, the CU approach has a number of theoretical and practical limitations. One theoretical limitation is that, as pointed out by a reviewer of this paper, an LST model with added correlations between the error variables can no longer be considered an LST model according to Steyer et al.’s theoretical LST framework. In the presence of correlated residuals, the initially well-defined latent variables in LST models lose their clear meaning, because person-specific method effects become confounded with random measurement error. As explained in more detail in Appendix A, this is at odds with the fundamental theoretical concepts of LST theory (Steyer et al., 1992, 1999). A practical consequence is that CU models typically lead to an underestimation of the reliabilities of the indicators when method effects are present (e.g., Eid, Lischetzke, Nussbeck, & Trierweiler, 2003), because they do not consider method effects as part of the true score (systematic) variance of a variable, but confound reliable person-specific method effects with random measurement error. In addition, method variance cannot be expressed as a separate variance component.
As pointed out by Lance, Noble, and Scullen (2001), another problem is that CU models become less and less parsimonious as the number of indicators increases because more and more error correlations have to be estimated. Finally, an important limitation of the CU approach is that it assumes method effects to be orthogonal. This assumption is violated if two indicators share method effects over and above one or more other indicators. This will often be the case when structurally different methods will be used as indicators (e.g., other ratings may be more similar to each other than to self-ratings). Conway et al. (2004) showed that application of the CU approach can result in biased estimates of convergent and discriminant validity in MTMM models when methods are actually correlated.
In sum, the CU approach treats method effects as a mere nuisance and part of the “error”. From a psychometric point of view, however, it seems to be desirable to separate all reliable sources of variance from random measurement error, rather than treating method effects as part of the error variable. In addition, in many applications, the assumption of orthogonal method effects may not be appropriate theoretically. Most importantly, an LST model with correlated residuals is, strictly speaking, not a “true” LST model from a theoretical perspective. Despite these limitations, the CU approach continues to be widely used in longitudinal studies (Cole et al., 2007; Conway et al., 2004) and recent methodological work has advocated its use in longitudinal research (Cole & Maxwell, 2003), including LST modeling (LaGrange & Cole, 2008).
The Orthogonal Method Factor Approach
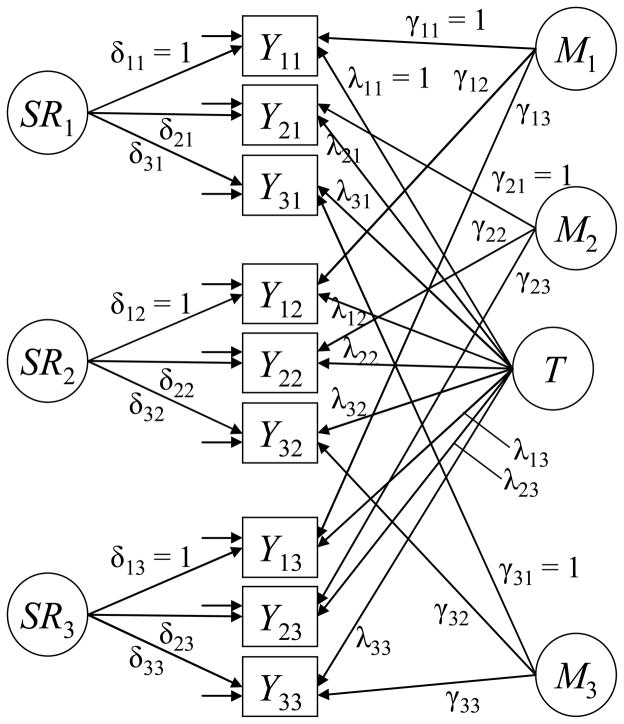
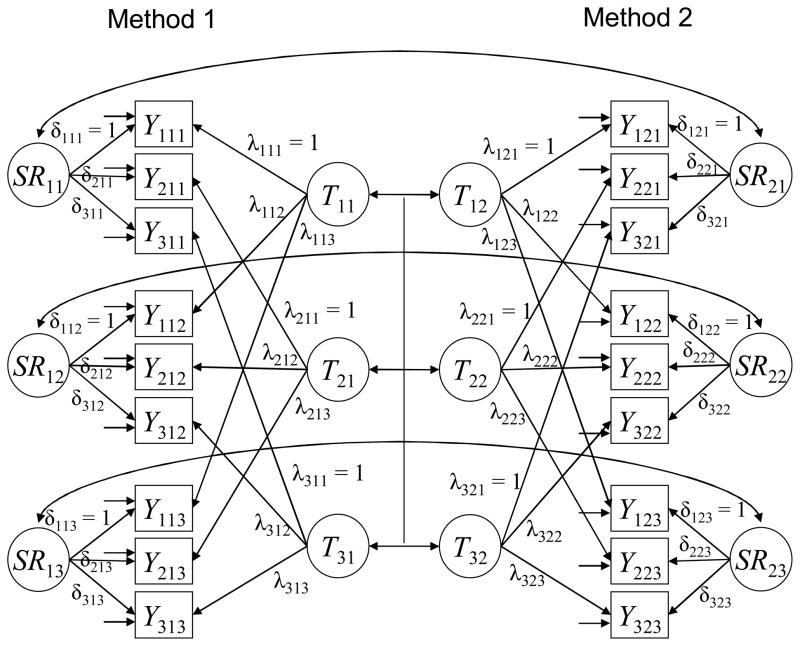
Steyer et al. (1992) had originally suggested accounting for method effects in LST models by specifying as many method factors as there are different indicators (a method factor for each indicator; see Figure 3), thereby extending the basic LST measurement equation as follows:
| (8) |
where Mi is a method factor common to all indicators with the same index i and γit is the method factor loading. The method factors are assumed to be uncorrelated (“orthogonal methods”, OM) with each other and with all other latent and error variables in the model. The factors Mi have also been interpreted as “specific traits”, as they represent the stable part of a specific indicator that is unique to that indicator and not shared with the remaining indicators (Steyer et al., 1992).
Figure 3.
LST model with correlated error variables for the same indicators over time (CU model).
In contrast to the CU approach, the model in Equation 8 separates stable indicator-specific (methods) effects from random error. It is more restrictive (and therefore more parsimonious) than the CU model for I > 3. The OM model does not, however, solve the problem of potentially correlated method effects, as it also assumes method effects to be orthogonal5.
More importantly, the OM model suffers from similar theoretical limitations as the CU model. Although the model had originally been presented by Steyer et al. (1992), strictly speaking, it cannot be considered a “true” LST model according to Steyer et al.’s (1992) LST framework6. The reason is that this framework requires all latent variables to be explicitly defined in terms of conditional expectations or well-defined functions of conditional expectations of observed variables (see Appendix A). The method factors Mi, however, cannot be defined based on the conditional expectations considered in LST theory (for details see Appendix A as well as Eid, 1996). As a first consequence, the meaning of these factors is not entirely clear (i.e., are they residuals with regard to the general trait factor? Do they represent method effects or specific traits?) and their presence in an LST model also renders the meaning of the remaining, formerly well-defined latent variables ambiguous.
A second consequence is that there is no solid theoretical basis for assuming the method factors Mi to be uncorrelated with each other and with the remaining factors in the model. This assumption is made merely for convenience and to enhance the identification status of the model, but there are no clear psychometric reasons why the factors should be uncorrelated. In addition to these conceptual problems, the OM model often leads to an overfactorization in practical applications (i.e., at least one of the method factors often has no significant loadings or variance; e.g., Eid, 2000; Steyer & Schmitt, 1994). This issue may be related to the weak psychometric foundation of these factors. We consider this model here despite these limitations given that, to date, it is the most frequently used approach to deal with method effects in LST analyses (29.09 % of applications that we found in which method effects were explicitly modeled used this approach).
The M − 1 Approach
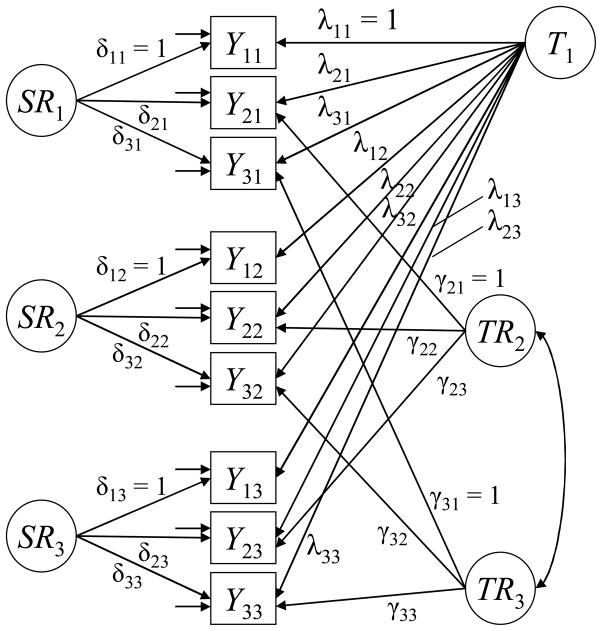
Given the theoretical and empirical issues with the OM approach, Eid, Schneider, and Schwenkmezger (1999; Eid, 2000) developed an approach that selects a “gold standard” or reference indicator. The latent trait factor pertaining to the reference indicator is chosen as comparison standard, so that for this indicator, no method factor is included. Hence, the model specifies one method factor less than methods/indicators used in the study and will therefore be referred to as M − 1 approach (see Figure 4). Stable method effects in the remaining indicators are examined relative to the reference indicator. Therefore, all non-reference indicators load onto (1) the reference trait factor and (2) a residual method factor. All method factors can be correlated, but method factors are by definition uncorrelated with the reference trait factor. Let r denote the reference indicator. Then the M − 1 model can be written as follows:
| (9) |
where I (i ≠ r) denotes an indicator variable, which has the value 1 if i ≠ r and the zero if i = r. We indicate the reference trait factor as Tr to make clear that this factor is not a common trait factor in this approach, but is specific to the reference indicator. TRi indicates the method factor for a non-reference indicator i, i ≠ r. TRi here stands for “trait residual for indicator i”, as the method factors in this model are defined as regression residuals with regard to the reference trait factor Tr (see Appendix A as well as Eid et al. [1999] for the exact mathematical definitions). We chose the label TRi (rather than Mi) to make the meaning of this method factor as a trait residual clearer and to emphasize that these method factors differ from the method factors Mi in the OM approach.
Figure 4.
LST model with M − 1 correlated method factors (M − 1). TRi indicates the trait-residual method factor for indicator i. γit: method factor loading. In this example, there is no method factor for the first indicator (reference indicator Y1t). Consequently, the latent trait factor is specific to the reference indicator. The method factors reflect the stable part in the non-reference indicators (Y2t and Y3t) that is not shared with the reference indicator.
Eid et al.’s (1999) approach has the advantage that all factors in this approach are well-defined latent variables that are in line with the core framework of LST theory: The method factors are defined as linear regression residuals with respect to a reference latent trait variable and therefore have a clear theoretical status and interpretation: They represent that part of the trait variance in the non-reference indicators that is not shared with the trait variance in the reference indicator. Further, due to the consideration of just M − 1 method factors, an overfactorization is avoided. In addition, this approach addresses the issue of potentially correlated method effects as it allows method factors to be correlated.
A limitation of the M − 1 approach is that it requires the selection of a reference indicator that serves as the comparison standard (the first indicator in Figure 4). The selection of a reference or gold-standard indicator may not always be easy, particularly when all items or scales are conceived of as equivalent (or interchangeable). Furthermore, the specification with a reference indicator implies that the latent trait factor in the model becomes specific to the first indicator. That is, the latent trait factor is now identical to the latent trait component pertaining to the first indicator and no longer reflects a common latent trait factor (see Appendix A). This implies that the trait factor is “method-specific”, that is, it contains the stable method variance pertaining to the reference variable (Geiser et al., 2008). The “method effects” (or “specific trait effects”) are defined relative to a reference trait variable. We return to these issues in the discussion where we provide detailed guidelines as to the choice of a reference indicator/method when using this approach in LST analyses.
The Indicator-Specific Trait Factor Approach
The indicator-specific trait (IT) factor approach (see Figure 5) takes the stable idiosyncratic effects of each variable into account by allowing each variable to load onto its own (indicator-specific) trait factor Ti (Eid, 1996; Marsh & Grayson, 1994; Steyer et al., 1999; for applications see Bonnefon et al., 2007; Eid & Diener, 2004):
| (10) |
Figure 5.
LST model with indicator-specific trait factors (IT). Ti indicates the trait factor for indicator i.
The additional index i in Ti makes clear that the trait variable is no longer a general trait factor, but is specific to indicator i in this model. All Ti factors can be correlated. The IT model has several advantages. First, as in the M − 1 approach, all latent variables in the IT model can be constructively defined based on the fundamental concepts of LST theory (see Appendix A). Second, neither correlated errors nor additional method factors need to be specified. The degree of method-specificity is reflected in the magnitude of the correlations among the IT factors. In the case of perfect unidimensionality of traits (no stable method effects), the population correlations of the IT factors would be equal to 1 and the model would reduce to the NM model (the LST model with a general trait factor and no method factors, Figure 1). Low correlations among the IT factors indicate strong method effects (i.e., the stable components of each indicator are only to a small degree shared with the other indicators). As in the M − 1 approach, the trait factors are indicator-specific and therefore contain the method-specific effects of their respective indicators7.
The model with IT factors most directly reflects the idea that different indicators may represent different traits rather than the exact same trait. This makes this model attractive especially in cases where a researcher would a priori assume that indicators represent distinct traits or facets of a broadly defined construct or when different indicators represent different methods or raters each of which may capture different aspects of a construct. Although allowing for IT factors, the model still assumes that different indicators measured at the same measurement occasion share the same occasion-specific influences, an assumption that may or may not be reasonable in practice—as is demonstrated in one of the empirical applications below.
Differences in the Definition of CO: Common, Unique, and Total Consistency
An important difference between the four models concerns differences in the types of consistency coefficients available in each model. Estimates of consistency are among the key parameters of interest in an LST analysis, as they inform us about the degree to which indicators measure stable aspects of behavior (as opposed to occasion-specific influences). Hence, it is useful for researchers to know which types of consistency coefficients are available in which approach and how these are correctly interpreted.
For LST analyses in general—and for the purpose of the present study in particular—it is useful to consider three different types of consistency coefficients: common consistency, unique consistency, and total consistency8. Following Steyer et al. (1992), we define common consistency (CCO) as that part of the variance of an indicator that is stable over time and shared across indicators. We define unique consistency (UCO) as that part of the variance of an indicator that is stable over time, but not shared with other indicators9 or a reference indicator. Finally, we define total consistency (TCO) as the sum of CCO and UCO. Hence, TCO represents the total stable part of the variance of an indicator.
One aspect in the comparison of different approaches is to which extent (and in which way) they allow defining and estimating CCO, UCO, and TCO. This comparison is of interest because it (1) sheds more light on conceptual differences between the four approaches in general and (2) shows that the models differ in the composition and meaning of these coefficients as explained below.
The bottom portion of Table 1 shows the properties of these three coefficients for each model. In the NM model, only CCO can be defined, as the model assumes that indicators are homogeneous and that there are no stable method effects over time. Hence, there are no method factors, and CCO = TCO in this model. Note that both coefficients might be biased in the NM model in practice if stable indicator-specific method effects are actually present, because the NM model does not account for these effects.
Table 1.
Overview of Different Approaches To Modeling Method Effects in LST Models
| CU | OM | M − 1 | IT | ||||
|---|---|---|---|---|---|---|---|
| Representation of method effects | Correlated error variables for the same indicator over time | Method factors | Method factors | Indicator-specific trait factors and their correlations | |||
| Correlated method effects? | No | No | Yes | Yes | |||
| Separation of method effects and measurement error? | No | Yes | Yes | Yes | |||
| Method effects as separate variance component? | No (confounded with error) | Yes (unique consistency coefficient) | Yes (unique consistency coefficient), except for the reference indicator | No (confounded with trait) | |||
| Common consistency | -- | ||||||
| Unique consistency | -- | -- | |||||
| Total consistency | -- |
Note. CU = correlated uniqueness approach; OM = M orthogonal method factor approach; M − 1 = M − 1 correlated method factor approach; IT = indicator specific trait factor approach. The index r denotes the reference indicator. I (i ≠ r) is an indicator variable that has the value 1 if i ≠ r and the value zero if i = r .
The CU approach allows defining CCO, but not UCO (and consequently not TCO). The reason is that in this model, stable method effects are reflected in error correlations and are not represented by latent method factors. Hence, no variance component for unique consistency can be defined and the total consistency of an indicator cannot be estimated. Another consequence is that the reliability of an indicator will be underestimated in the CU model whenever stable method effects are present, because UCO as a reliable source of variance is not separated from error. The underestimation of the reliability will increase as the amount of stable method variance increases, because more and more reliable variance is treated as part of the error.
The OM approach allows calculating all three types of consistency coefficients:
| (11) |
| (12) |
| (13) |
Eid et al.’s (1999)M − 1 approach also allows defining all three types of consistency coefficients. However, these are defined differently and two of them have a different meaning than the corresponding coefficients in the OM approach. We therefore indicate these coefficients with an asterisk (*) to make clear that they differ conceptually from the coefficients in Equations 11–13:
| (14) |
| (15) |
| (16) |
CCO* indicates the proportion of variance of an indicator that is explained by the reference trait factor Tr (rather than by a common trait factor as in the OM approach). For reference indicators, this coefficient equals the total consistency (see Equation 16), because there is no method factor for these indicators. UCO* indicates that part of the stable variance of an indicator that is not shared with the stable variance of the reference indicators. This coefficient is only defined for non-reference indicators. The total consistency, TCO*, has the same meaning as (and is thus comparable to) TCO in the OM approach: it represents the total proportion of stable indicator variance.
In the IT model, CCO and UCO cannot be defined, as this model neither contains common trait factors nor method factors. Hence, only TCO can be estimated, which, in this model, is given by:
| (17) |
The definition of OSpe does not differ between the approaches. Table 1 summarizes key properties of the four approaches.
Importance of Comparing Different Approaches
It is well-known from the literature on MTMM analysis (e.g., Kenny & Kashy, 1992; Marsh, 1989; Widaman, 1985) that there are theoretical differences between different approaches to modeling method effects (Cole et al., 2007; Geiser, Eid, & Nussbeck, 2008; Geiser, Eid, West, Lischetzke, & Nussbeck, 2010; Pohl, Steyer, & Kraus, 2008). Not all models lead to meaningful and interpretable results in all applications (Marsh, 1989). Therefore, it is critical that theoretical differences between models be taken into account when selecting a model (Eid et al., 2008). In addition, research on the performance of confirmatory factor models for MTMM data has shown that models with method factors may show serious problems in convergence, estimation, and interpretation (Marsh, 1989; Marsh & Bailey, 1991). LST models as such are complex latent variable models in which each observed variable loads onto two factors. Adding additional components (e.g., method factors) to the model makes the model even more complex and may lead to additional complications in estimation and interpretation. Furthermore, different approaches may perform differently under different conditions (e.g., small versus large sample sizes; high vs. low method-specificity). Knowledge about such differences can increase the odds that an approach will perform well in a particular application and can therefore help researchers to successfully analyze their data. This is especially true given that many LST applications use relatively small sample sizes (see Appendix B). Finally, to our knowledge, it has not yet been studied to which extent different approaches for dealing with method effects properly recover the key parameters of interest in an LST analysis, namely the consistency, occasion-specificity, and reliability coefficients.
LaGrange and Cole (2008) recently studied the performance of four different multimethod approaches in the so-called trait-state occasion (TSO) model (Cole et al., 2005). The TSO model is an extension of the basic LST model that allows for autoregressive components among the latent state residual factors. In their simulation study, LaGrange and Cole considered four different approaches using a design with four time points and a sample size of N = 500, respectively. Based on their results, they recommended the CU and OM approaches.
Limitations of LaGrange and Cole’s study are that they (1) did not systematically vary the level of method-specificity so that it remains unclear whether their recommendations generalize across different levels of method variance, (2) considered only one sample size condition (N = 500), and (3) did not study the performance of the IT model. A literature review of applications of LST models (see Appendix B) revealed that sample sizes used in LST studies vary widely (range N = 38 through N = 37,041). Not all LST models may perform well, for example, at small sample sizes. Furthermore, it can also be assumed that the amount of method variance varies across studies. The amount of method variance is an important factor in LST studies as some models can theoretically be expected to show fewer problems at different levels of method specificity than others as explained in detail below. Further, the IT model appears to be a promising alternative to other approaches as it deals with indicator-specificity in a straightforward way and is in line with LST theory.
Study 1: Simulation Study
The goal of the simulation study was to extend and increase the generalizability of previous simulation work (LaGrange & Cole, 2008) by systematically varying (1) the amount of method variance (unique consistency) and (2) the sample size. We deemed these conditions of primary relevance for the following reasons. We expected the amount of method variance to have a substantial impact on model performance in some of the models. In particular, we expected to see more problems at lower levels of method variance in models that include method factors (the OM and M − 1 models). The reason is that the estimation of model parameters related to method factors likely becomes more unstable when method-specificity is low because method factor loadings and method factor variances will be estimated to values that are relatively close to zero in these cases. This may cause method factors to collapse, causing convergence problems, improper solutions and/or parameter bias. These problems were expected to be more frequent at lower sample sizes that involve more sampling fluctuations than larger samples.
An interesting question in this regard was whether the OM or the M − 1 model would show a better relative performance under conditions of low method-specificity. We expected the M − 1 model to perform better relative to the OM model because (1) the M − 1 model uses fewer method factors and (2) the method factors in the M − 1 model are clearly defined as trait residuals and are in line with LST theory, whereas the theoretical status of the OM method factors is less clear (see Appendix A). Problems related to conditions of low method variance were expected to be less severe for the NM, CU, and IT models, because these models do not include method factors that could become unstable or collapse under conditions of low method variance.
Furthermore, we expected conditions of high method variance (and low common consistency) to cause instability and estimation problems primarily in the OM and CU models, because (in contrast to the M − 1 and IT models), these models assume common trait factors. These common trait factors were expected to become increasingly unstable as common consistency decreases and method variance increases. Problems under conditions of high method-specificity were also expected for the NM model, as this model (1) also includes common trait factors and (2) does not account for method effects at all and thus becomes increasingly misspecified as the amount of method variance increases.
Finally, we expected the IT model to be least problematic overall, because it (1) contains only well-defined latent variables and (2) captures method variance in terms of correlations between indicator-specific trait variables. This model should work well whether method effects are high or low, because the trait factors in this model are indicator-specific and will thus show substantial loadings whether different indicators show low convergent validity (high method variance) or high convergent validity (low method variance).
We also studied different sample size conditions in order to further increase the generalizability of our simulation findings. Important questions in this regard where, (1) What is the minimum required sample size for the reliable application of different LST models? and (2) Which model performs well under which sample size condition?
Method
Simulation design
We generated data based on the OM model (Figure 3). The OM model was used because (1) to date it represents the most frequently used approach to deal with method effects and (2) it easily allowed us to systematically vary the amount of method variance. We specified six different conditions in which the indicators contained different amounts of indicator-specific method variance (from low to very high method-specificity): 5 %, 10 %, 20 %, 25 %, 35 %, and 40 %. Common trait variance was varied accordingly with values of 45 %, 40 %, 30 %, 25 %, 15 %, and 10 %, so that methods and trait variance would always make up 50 % of the total indicator variance. Hence, 50 % of the indicator-variance was considered to be stable over time in each population model. The amount of occasion-specific variance as well as error variance of the indicators was held constant at 30 % and 20 % in all conditions, respectively, so that indicator reliability would equal .8. We studied ten different sample size conditions (N = 50, 100, 200, 235, 300, 400, 500, 700, 1000, and 2000). These sample size conditions represent the range of sample sizes in the LST literature10 of the sample sizes found in empirical LST studies (see Appendix B). For each of the 6 (method variance) × 10 (sample size) conditions, we generated 1,000 data sets, assuming multivariate normality. Simulated data for all five models (NM, CU, OM, M − 1, and IT) were generated and fit using the external Monte Carlo function in Mplus (Muthén & Muthén, 1998–2010); subsequent analyses of model parameters were performed in SAS.
Outcome variables
We studied the proportion of non-converged and improper cases as well as parameter estimate bias for all conditions. We counted a replication as non-converged if a solution could not be reached by Mplus after 1000 iterations. All converged solutions that produced warning messages about non-positive definite residual or latent variable covariance matrices were classified as improper cases.11 Parameter estimate bias was examined for the consistency, occasion-specificity, and reliability coefficients as defined above. Bias was calculated as
and averaged across indicators.
Results
Model convergence
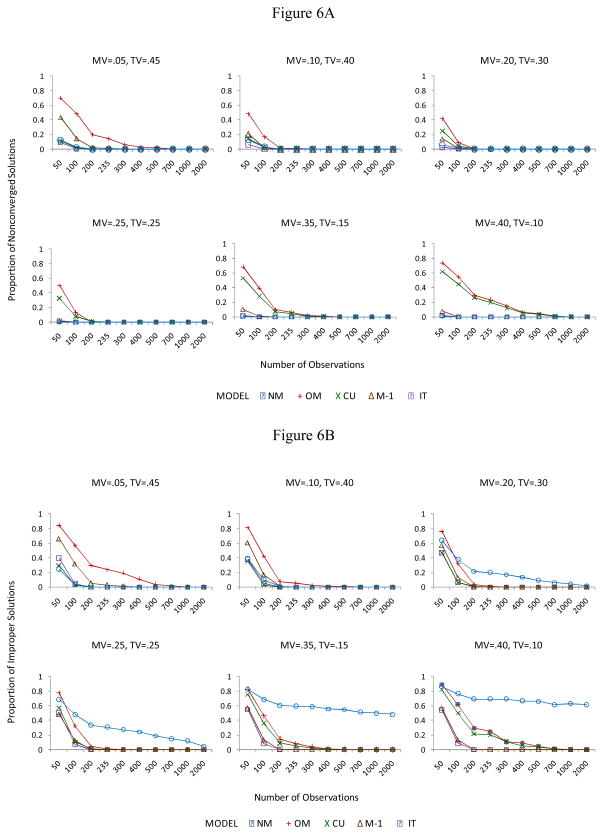
Figure 6A shows the proportion of non-converged solutions across all conditions. Overall, convergence problems were mainly an issue at sample sizes below N = 300. The model with the highest overall frequency of convergence problems was the OM model. Convergence problems were largest for this model in the two most extreme conditions (lowest and highest amount of method variance). The CU model showed a relatively high frequency of convergence problems when method variance was large or moderate, but was well-behaved when method variance was small. The M − 1 model showed some convergence problems when method effects were small, whereas it showed few problems at conditions of moderate to high method variance. The IT and NM models were least problematic in terms of model convergence.
Figure 6.
Non-convergence and improper solutions in the simulation study. A: Proportion of non-converged replications. B: Proportion of improper solutions among converged replications. MV = method variance; TV = trait variance.
Improper solutions
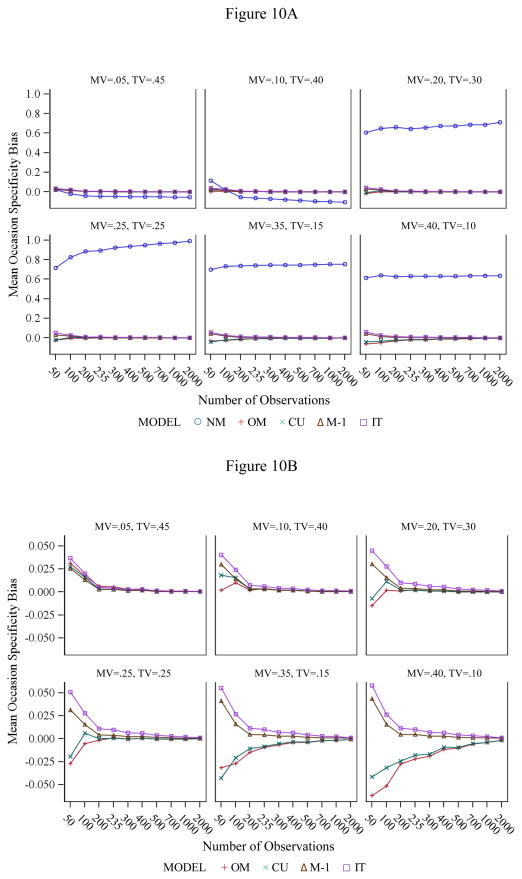
The vast majority of improper solutions represented solutions with non-positive definite residual covariance matrices (i.e., negative residual variance estimates). Non-positive definite latent variable covariance matrices only occurred for the IT model. Further, they only occurred under conditions of low method specificity (5 or 10 %) and small sample size (N ≤ 100). This can be explained by the fact that for low method specificity, IT factors are more homogenous and become strongly correlated. In small samples, sampling fluctuations can cause some of the IT correlations to be estimated to values close to (or even above) 1.0. In addition, linear dependencies may arise due to high correlations, which can also result in non-positive definite latent variable covariance matrices.
Figure 6B presents the proportion of improper solutions for all models across conditions. All models showed severe problems at the lowest sample size of N = 50. For the higher sample size conditions, there were differences between models as well as between conditions. The highest proportion of improper solutions occurred for the NM model at conditions of moderate to high method specificity, whereas this model was well-behaved when method effects were small. For the remaining models, improper solutions were common only at the lower sample size conditions. The OM model generally produced a high number of replications with improper parameter estimates, in particular when either trait or method variance were small. The CU model tended to show more improper estimates when method variance was large relative to trait variance, and was well-behaved otherwise. In contrast, the M − 1 model showed more problems when method variance was small (5 %), and was unproblematic in the remaining conditions. The IT model showed the lowest frequency of improper solutions of all models, and it tended to show no improper solutions at all for N ≥ 200.
Parameter estimate bias
Average parameter estimate bias was studied for the coefficients of consistency (as far as applicable), occasion-specificity, and reliability. The bias averages are presented for proper solutions only (the corresponding values for all converged cases including improper solutions can be found in the online supplemental material). In general, trends where similar for all versus proper-only solutions, albeit bias was generally more pronounced if improper cases where included.
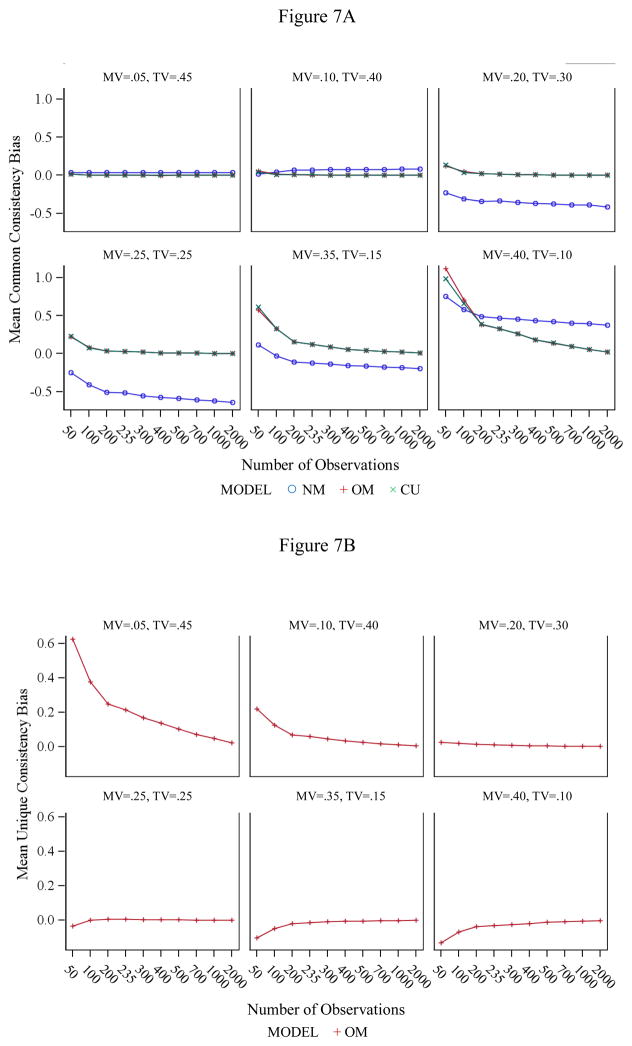
Common consistency bias (see Figure 7A) was examined for the NM, OM, and CU models only, because CCO is not defined in the IT model and is defined relative to a comparison indicator in the M − 1 model and thus not directly comparable. CCO tended to be strongly overestimated in the OM and CU models at lower sample sizes when method variance was large (≥ 35 %). In the NM model, strong bias occurred except when method variance was small (5 or 10 %). The direction of bias in the NM model was inconsistent (the model sometimes over- and sometimes underestimated TCO), so that we examined the distribution of parameter estimates in detail for this model for different conditions.
Figure 7.
Mean consistency bias in the simulation study. A: common consistency bias. B: unique consistency bias. MV = method variance; TV = trait variance.
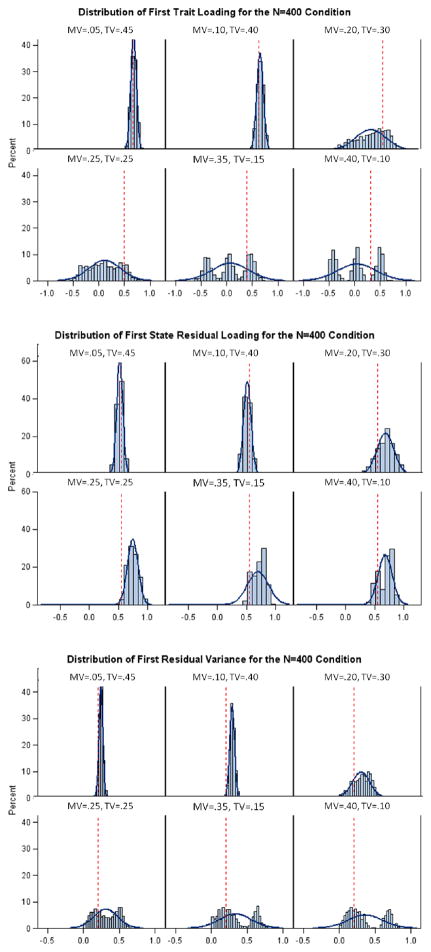
Figure 8 shows the distributions of the trait loading, state residual loading, and residual variance for the first indicator in the N = 400 condition (results were very similar across indicators and sample sizes so that this example can be seen as representative). It can be seen that as method specificity increased, parameter estimates in the NM model became increasingly dispersed and for the conditions with high method variance followed bi- or trimodal distributions, showing that parameter estimates were completely unreliable for this model when method variance was moderate to high.12 Given these extreme parameter distributions, average bias estimates are not really meaningful for this model at moderate to large method variance and explain the inconsistency in the direction of average bias.
Figure 8.
Distribution of the trait loading, state residual loading, and residual variance of the first indicator in the NM model for the N = 400 condition. The red line indicates the true population value. MV = method variance; TV = trait variance.
Unique consistency bias (see Figure 7B) was examined for the OM model only, because UCO is not defined (or defined differently) in the other models. UCO bias occurred mainly under conditions of low method variance (5 and 10 %), where UCO tended to be overestimated, particularly in the 5 % method variance condition.
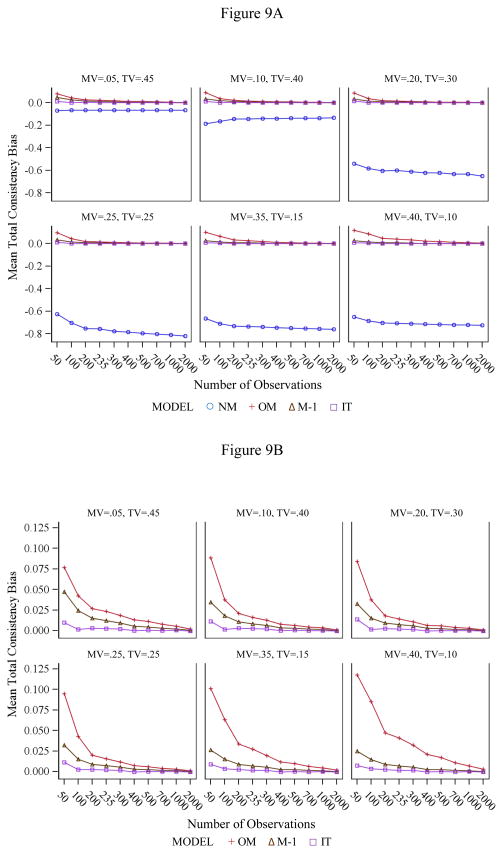
Total consistency bias was studied for the NM, OM, M − 1, and IT models (see Figure 9A). The NM model showed strong bias for moderate to high method variance, whereas bias in the OM, M − 1, and IT models was relatively small (mostly below 10 %). We therefore also include a figure without the NM model to allow for a more detailed comparison of the remaining models (Figure 9B). There was a consistent tendency across conditions for the OM model to show a larger positive bias than the M − 1 and IT models. Besides the NM model, the OM model was the only model that showed a bias above 10 % for some of the conditions. Bias in the OM model was especially pronounced in the conditions with high method (and low trait) variance.
Figure 9.
Mean total consistency bias in the simulation study. A: all models. B: without the NM model. MV = method variance; TV = trait variance.
Occasion-specificity bias (see Figure 10A for all models and 10B without NM) was examined for all models and was below 10 % for all conditions and all models except the NM model. The NM model showed large bias in all conditions except when method variance was as low as 5 or 10 %. However, average bias and direction of bias in the NM model has to be interpreted with caution given the bimodal parameter distributions in the high method specificity conditions (see Figure 8).
Figure 10.
Mean occasion specificity bias in the simulation study. A: all models. B: without the NM model. MV = method variance; TV = trait variance.
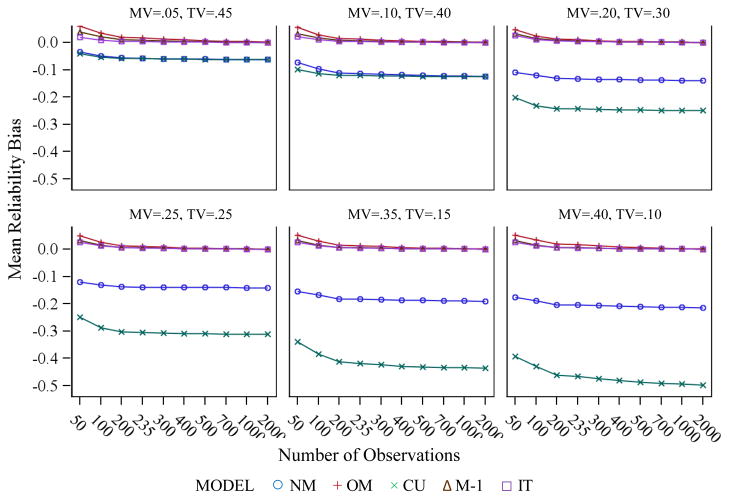
Reliability bias (see Figure 11) was also studied for all models. It can be seen that reliability was properly estimated by all models under all conditions except the NM and CU models, both of which consistently underestimated reliability. Underestimation in the CU model increased systematically as method variance increased, with the strongest bias of −50 % found for the highest (40 %) method variance condition. Again, given the bimodal distribution of the residual variance estimates in the NM model for moderate to high levels of method variance (see Figure 8), the average bias estimates are not really meaningful for this model.
Figure 11.
Mean reliability bias in the simulation study. MV = method variance; TV = trait variance.
Discussion
The results of the simulation study where well in line with our theoretical expectations. The overall best performing model was the IT model, with the least problems in terms of convergence, improper solutions, and parameter bias. The second best model was the M − 1 model, which, as expected, only showed some problems at low samples sizes when method effects where very small. The CU model performed reasonably well in general, but showed problems when method effects where strong (and trait effects weak). Furthermore, as theoretically expected, the CU model systematically underestimated the reliabilities of the indicators across all conditions. The OM model consistently performed worse than all other models (except for the NM model), which may be surprising, because it represents the data generating model. As predicted, it showed the most problems when method variance was either very low or very high. We suspect that these conditions cause instability in the model that lead to various kinds of problems. The NM model, which ignores method effects and thus becomes increasingly misspecified as the amount of method variance increases, performed worst in terms of improper solutions and bias. This model produced completely unreliable parameter estimates when method effects where moderate to large.
As shown by our literature review (see Appendix B), small sample sizes are quite common in LST research. It is therefore of interest which sample size can be seen as “large enough” to use the models discussed here. Our simulation suggests that samples sizes as small as N = 50 may not be appropriate for LST analyses in general, at least not under the conditions studied here, as most models showed severe estimation problems under this condition. On the other hand, there were many situations in which models tended to perform well at a sample size as small as N = 100. This was particularly true for the IT model. For most other models that account for method effects, problems tended to vanish or were at least significantly reduced when sample sizes where moderate to large, say N ≥ 300.
Study 2: Applied Examples
We present real data applications to two method types: items and raters. The first data set uses multiple, supposedly homogeneous items as indicators. For this case, we expect relatively minor, yet non-negligible method effects. The second data example uses ratings from multiple sources. Given that multiple reporters often show rather low convergent validity even when they provide responses on the same measure (e.g., Geiser et al., 2010), we expected method effects to be rather strong in this example. Both studies can be seen as typical examples of LST applications in terms of sample size, number of waves, and number of indicators. These applications are of interest for three reasons: they (1) allow us to examine the models’ behavior in practice under two different but common (and natural) conditions (homogeneous vs. heterogeneous indicators), (2) illustrate the practical use and meaning of different types of consistency coefficients in different models and (3) demonstrate the need for more complex models in cases were it may not be reasonable to assume homogeneity of occasion-specific effects across indicators (Data Example #2).
Method
Data Example 1: Multiple items
In our first example, we analyzed data from N = 360 firefighters taken from a larger health promotion study (Moe et al., 2002). Data for this study were collected annually for 6 years; we use the first three waves of data in our example. For our analyses, we selected three items of the General Health subscale of the SF-36 (Ware, Snow, Kosinski, & Gandek, 1993).13 Item 1 asked respondents to give a broad assessment of their current states of health (“In general, would you say your health is”) on a scale of 1 (‘Excellent’) to 5 (‘Poor’). Item 2 (“I am as healthy as anybody I know”) and Item 3 (“My health is excellent”) were slightly more specific and were scored on a scale of 1 (‘Definitely True’) to 5 (‘Definitely False’). We chose these three items for two reasons. First, they were each positively worded and were rather homogeneous in terms of content. Hence, these items allowed us to demonstrate that even in this case, method effects may be non-negligible. Second, despite the apparent homogeneity of the items, Item 1 can be seen as a marker variable for measuring general health. Furthermore, Item 1 is measured on a different response scale than the two other items. This made it easy for us to select this item as a reference indicator in the application of the M − 1 approach to these data. Substantively, these data are interesting for an LST analysis because these analyses allow us to find out to which degree the rating of perceived general health depends on momentary (occasion-specific) influences versus a stable person-specific level.
Data Example 2: Multiple raters
Data for this example come from the first three waves of the Adult and Family Development Project (Chassin, Rogosch, & Barrerra, 1991), a longitudinal study of the intergenerational effects of familial alcoholism. 454 children (mean age = 12.7), along with each of their mothers and fathers, provided annual, in-person reports of the target children’s externalizing symptomatology using the Child Behavior Checklist (CBCL; for details of scoring, see Achenbach & Edelbrock, 1981, or Chassin et al., 1991). The current analyses are based on N = 294 complete cases for which self-, mother-, and father reports on the same 22 items were available. An interesting substantive question that can be answered by LST analysis is whether externalizing problem behavior is best conceived of as a stable trait or whether it is more situation-dependent.
Results
Goodness of fit
We fit all five models to each data set. Table 2 shows the goodness of fit statistics for all models. It can be seen that in both applications, all models that take method effects into account fit the data well. In contrast, the NM model showed a very bad fit in Application 1. In Application 2, the NM model did not even converge to a solution after 1,000 iterations14. Although we consider only two applications here, these findings demonstrate once again that method effects are an important issue in LST models, even when indicators are supposedly unidimensional items (as in Application 1). Inspection of the descriptive model comparison indices (the AIC and BIC coefficients) revealed that although these indices are close for all models, the IT model showed the best relative fit in both applications. This result is interesting, given that this model also showed the best performance in our simulation study.
Table 2.
Goodness of Fit Indices for Different LST Models Applied to Real Data
| General Health (N = 360)
|
Child Externalizing Problems (N = 294)
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| χ2 (df) | p(χ2) | RMSEA | SRMR | TLI | AIC | BIC | χ2 (df) | p(χ2) | RMSEA | SRMR | TLI | AIC | BIC | |
| NM | 102.77 (18) | < .001 | .11 | .04 | .90 | 6656 | 6796 | —a | —a | —a | —a | —a | —a | —a |
| CU | 5.62 (9) | .78 | .00 | .01 | 1.01 | 6577 | 6752 | 14.37 (9) | .11 | .05 | .02 | .98 | −259 | −93 |
| OM | 5.62 (9) | .78 | .00 | .01 | 1.01 | 6577 | 6752 | 14.37 (9) | .11 | .05 | .02 | .98 | −259 | −93 |
| M − 1 | 13.15 (11) | .28 | .02 | .02 | 1.00 | 6581 | 6748 | 16.76 (11) | .12 | .04 | .02 | .99 | −261 | −102 |
| IT | 16.94 (15) | .32 | .02 | .02 | 1.00 | 6577 | 6728 | 20.01 (15) | .17 | .03 | .02 | .99 | −265 | −122 |
Note. NM = model with no method factors; CU = correlated uniqueness approach; OM = M orthogonal method factor approach; M − 1 = M − 1 correlated method factor approach; IT = indicator specific trait factor approach. RMSEA = root mean square error of approximation; SRMR = standardized root mean square residual; TLI = Tucker-Lewis index. Models 2 and 3 are equivalent models for a 3 indicators × 3 time points design and therefore show an identical fit in these applications.
No convergence after 1,000 iterations.
Variance components
Table 3 provides the estimated consistency, occasion-specificity, and reliability coefficients in each model. As can be seen, non-negligible method effects occurred in both studies, although as expected, method effects were stronger in the multirater data example. This can be seen most easily from the higher UCO coefficients in the OM and M − 1 models in the second application. In the CU model, the higher method-specificity is reflected in higher error correlations in the multirater example (.47 ≤ r ≤ .69) compared to the multi-item application (.03 ≤ r ≤ .39; none of the error correlations for Item 3 were significant at an alpha level of .05). The IT model depicts method effects in terms of correlations between the indicator-specific traits. In the multirater example, these were lower (.37 ≤ r ≤ .51) than in the multi-item application (.73 ≤ r ≤ .89), showing once again that method-specificity was stronger in the multirater case.
Table 3.
Estimated Variance Components for Different LST Models Applied to the Health Data (N = 360)
| CCO | UCO | TCO | OSpe | Rel | |
|---|---|---|---|---|---|
| NM | |||||
| Item 1, time 1 | .56 | — | .56 | .03 a | .60 |
| Item 2, time 1 | .27 | — | .27 | .17 a | .44 |
| Item 3, time 1 | .47 | — | .47 | .40 a | .88 |
| Item 1, time 2 | .74 | — | .74 | .02 a | .76 |
| Item 2, time 2 | .27 | — | .27 | .12 a | .39 |
| Item 3, time 2 | .52 | — | .52 | .34 a | .86 |
| Item 1, time 3 | .61 | — | .61 | .05 | .66 |
| Item 2, time 3 | .19 | — | .19 | .20 | .39 |
| Item 3, time 3 | .38 | — | .38 | .26 | .64 |
| CU | |||||
| Item 1, time 1 | .44 | — | — | .08 | .52 |
| Item 2, time 1 | .28 | — | — | .18 | .46 |
| Item 3, time 1 | .52 | — | — | .30 | .82 |
| Item 1, time 2 | .67 | — | — | .03 a | .69 |
| Item 2, time 2 | .30 | — | — | .10 a | .40 |
| Item 3, time 2 | .60 | — | — | .23 a | .83 |
| Item 1, time 3 | .46 | — | — | .11 | .57 |
| Item 2, time 3 | .19 | — | — | .18 | .37 |
| Item 3, time 3 | .40 | — | — | .26 | .66 |
| OM | |||||
| Item 1, time 1 | .44 | .16 | .59 | .08 | .68 |
| Item 2, time 1 | .28 | .15 | .43 | .18 | .61 |
| Item 3, time 1 | .52 | .04 b | .55 | .30 | .86 |
| Item 1, time 2 | .67 | .07 | .74 | .03 a | .77 |
| Item 2, time 2 | .30 | .12 | .42 | .10 a | .52 |
| Item 3, time 2 | .60 | .00 b | .60 | .23 a | .83 |
| Item 1, time 3 | .46 | .20 | .66 | .11 | .77 |
| Item 2, time 3 | .19 | .14 | .34 | .18 | .52 |
| Item 3, time 3 | .40 | .04 b | .44 | .26 | .70 |
| M − 1 c | |||||
| Item 1, time 1 | .58 | — | .58 | .08 | .66 |
| Item 2, time 1 | .23 d | .25 d | .48 | .16 | .64 |
| Item 3, time 1 | .42 d | .17 d | .59 | .26 | .86 |
| Item 1, time 2 | .74 | — | .74 | .05 a | .79 |
| Item 2, time 2 | .24 d | .16 d | .39 | .13 a | .52 |
| Item 3, time 2 | .47 d | .07 d | .54 | .28 a | .82 |
| Item 1, time 3 | .63 | — | .63 | .09 | .72 |
| Item 2, time 3 | .16 d | .17 d | .33 | .17 | .5 |
| Item 3, time 3 | .33 d | .13 d | .45 | .24 | .69 |
| IT | |||||
| Item 1, time 1 | — | — | .58 | .07 | .65 |
| Item 2, time 1 | — | — | .45 | .17 | .62 |
| Item 3, time 1 | — | — | .56 | .28 | .83 |
| Item 1, time 2 | — | — | .73 | .06 | .79 |
| Item 2, time 2 | — | — | .42 | .12 | .54 |
| Item 3, time 2 | — | — | .56 | .27 | .83 |
| Item 1, time 3 | — | — | .63 | .08 | .72 |
| Item 2, time 3 | — | — | .32 | .18 | .50 |
| Item 3, time 3 | — | — | .44 | .23 | .68 |
Note. NM = model with no method factors; CU = correlated uniqueness approach; OM = M orthogonal method factor approach; M − 1 = M − 1 correlated method factor approach; IT = indicator specific trait factor approach. CCO = common consistency; UCO = unique consistency; TCO = total consistency; OSpe = occasion-specificity. The items were taken from the SF-36 scale (Ware, Snow, Kosinski, & Gandek, 1993). Item 1: “In general, would you say your health is… (1 = excellent, 2 = very good, 3 = good, 4 = fair, 5 = poor)”; Item 2: “I am as healthy as anybody I know”; Item 3: “My health is excellent”. Items 2 and 3 were scored on the following 5-point scale: 1 = definitely true, 2 = mostly true, 3 = don’t know, 4 = mostly false, 5 = definitely false.
the variance of the corresponding state residual factor was non-significant (p ≥ .08).
the variance of the corresponding method factor was non-significant (p > .82).
Item 1 served as reference method in this model.
to be interpreted relative to the reference method. Dashes indicate that a coefficient is not applicable. TCO and OSpe do not always add up to the reliability coefficient due to rounding errors.
Note that the estimates of common and unique consistency in the OM model differ from the corresponding estimates in the M − 1 model. This is expected given that these coefficients are defined relative to a reference indicator in the M − 1 approach and consequently also have a different interpretation: CCO* represents the amount of stable variance shared with the reference indicator, whereas UCO* represents the amount of stable variance not shared with the reference indicator. Consequently, these estimates cannot be directly compared (although TCO, OSpe, and Rel can).
Discussion
Two specific issues that occurred in the application of the OM model are particularly noteworthy. In the first application, the method factor for the third item (“My health is excellent”) had no significant variance and none of the loadings on this factor was statistically significant. Hence, in this application, one method factor seemed to be redundant. As mentioned above, this problem is not uncommon in practical applications of this model. In the application to the multirater data, all method factors were significant in the OM model. However, the residual variance of the father report score at time 1 was estimated to be zero and consequently, the reliability was estimated to be 1.00 for this indicator. This can be seen as a close-to-improper solution, as it seems unrealistic to assume perfect reliability of father reports of externalizing problem behavior.
The CU model, which in this application is statistically equivalent to the OM model, showed a similar issue in the first application: Neither one of the error correlations related to Item 3 were statistically significantly different from zero. Furthermore, the CU model consistently provided unrealistically low reliability estimates compared to the remaining models, especially in the multirater case.
Occasion-specific effects were estimated to be low by all models in both applications. In the multi-item application, only the third item showed a substantial amount of occasion-specific variance (Ospe ≥ .23 in all models at all time points), whereas especially Item 1 did not seem to be prone to occasion-specific influences (Ospe ≤ .11). This makes sense theoretically as the first two items (especially Item 1) refer more to the general health status (and thus should be less influenced by occasion-specific deviations from the general health status of a person), whereas for Item 3 it is less clear whether it refers to a momentary or general evaluation of perceived health.
Method-specific occasion-specificity
An interesting result that requires our specific attention is that in the multirater application, all models indicated that occasion-specific effects were small (mean Ospe = .08, range: .01 ≤ Ospe ≤ .23) and even statistically non-significant for a number of indicators. Furthermore, none of the occasion-specific factors had a significant variance estimate. This result is surprising as one would theoretically expect that self- and parent reports of externalizing problem behaviors show a non-trivial amount of occasion-specific variance. Given that all models fit the data well, one might be tempted to conclude that this expectation is disconfirmed and that occasion-specific effects are indeed negligible—suggesting that the self- and parent report measures of externalizing problem behavior are for the most part trait-measures. However, this would be an erroneous conclusion. Conventional LST models assume that occasion-specific effects are unidimensional across all indicators measured at the same time point. In our example, this implies that the situation and its impact on the measurements of externalizing behavior are identical for self-, mother, and father reports.
The assumption of homogenous occasion-specific effects is reasonable in many cases when indicators are homogeneous (e.g., tau-equivalent scales or items obtained from a single rater). It is likely violated, however, when indicators represent distinct methods (e.g., different raters as in our second application). Different raters are likely in different (inner or outer) situations even if their ratings are collected at exactly the same time point. Consequently, standard LST models confound method-specific occasion-specific influences with measurement error. Thus, they may strongly underestimate the amount of occasion-specific variance when the scores of multiple raters are used as indicators of latent trait and latent state residual variables. An additional consequence is that the reliabilities of the indicators are likely underestimated, as rater-specific occasion-specific influences become part of the error variable (when in fact they should be considered part of the true variance of the indicators).
The IT model for modeling method-specific occasion-specificity
To illustrate the issue of method-specific occasion-specificity, we fit an additional, extended IT model to the externalizing problem behavior data (illustrated for just two methods in Figure 10). In contrast to the conventional IT model, this LST model used multiple indicators per rater (i.e., three indicators for child ratings, three indicators for mothers, and three indicators for fathers at each time point). Although the ratings of children, mothers, and fathers were still modeled simultaneously, a separate IT structure was assumed for each type of rater. The advantage of this model is that occasion-specific effects can be modeled as being rater-specific, thereby avoiding an underestimation of the true amount of occasion-specific variance. The rater-specific occasion-specific residual factors measured at the same measurement occasion can be correlated across raters. These correlations indicate to which degree occasion-specific effects generalize across different raters. Only if these correlations equal one could we assume occasion-specific effects to be homogeneous across raters—as is done in the conventional LST model with just a single indicator per rater. 15
In our example, we actually used an extended variant of the model shown in Figure 10 that included three (instead of just two) methods to model child, mother, and father ratings simultaneously. Hence, there were separate trait and separate occasion-specific residual factors for each type of rater. To fit this model to the externalizing problem behavior data set, we constructed three item parcels (instead of just one single score) for each rater. This was done by randomly assigning the 22 items to three sets and then calculating the mean of the items in each item set, respectively. Parcels consisted of identical items across raters and time points.
The extended IT model with multiple indicators for each type of rater also fit the data well, χ2(252) = 341.44, p < .01, CFI = .98, RMSEA = .04, SRMR = .04. In line with theoretical predictions, it turned out that, regardless of the type of rater, all occasion-specific factors had highly significant variances. Furthermore, most indicators did show a substantial amount of occasion-specific variance (mean Ospe = .2, range: .03 ≤ Ospe≤ .44). These values are substantially higher than the occasion-specificities estimated in each of the conventional LST models. This is even more impressive if one takes into account that this model used parcels (i.e., “test thirds” of the initial scale) so that each indicator represented only one third of the full scale. Furthermore, reliability estimates (mean Rel = .78, range: .6 ≤ Rel≤ .95) also were higher in this model than reliabilities in the conventional IT model (mean Rel = .72, range: .56 ≤ Rel≤ .89), although each indicator represented only a third of the full scale. The occasion-specificities and reliabilities of the full scales are thus strongly underestimated by the conventional LST analysis with single indicators per rater.
In addition, the latent correlations between occasion-specific factors pertaining to different methods were only of small to moderate size (.11≤ r≤ .43), and two of them were not statistically significant (p≥ .22). These findings clearly demonstrate that unidimensionality of occasion-specific effects is not a reasonable assumption in this example, as all of the correlations between occasion-specific factors were far below 1.00. Only the more complex model with multiple indicators per each rater could thus adequately reflect the degree of occasion-specificity and reliability of these data.
Overall Discussion
Our review of the diverse literature of LST applications revealed that nearly 80 % of applications used one or more of the four approaches discussed in this paper to account for method effects. 16 The largest proportion of LST applications (29.09 %) to date have used the OM approach originally proposed by Steyer et al. (1992) and recently advocated by LaGrange and Cole (2008). Our simulation study and applications showed, however, that this approach may not always be the best choice. In particular, this model performed rather poorly in our simulation study under conditions where method effects accounted for either a small (5–10 %) or a large (35–40 %) portion of the total indicator variance, and estimates based on this model also raised concerns as to the adequacy of this model in our applications to actual psychological data. In summary, the model appeared to be rather unstable at conditions of high or low method-specificity, at least at small to moderate sample sizes (up to about N = 500 for some conditions). The apparent instability of the OM model under conditions of low method variance and low trait variance is likely caused by method and trait factors becoming weakly identified and thus unstable in those situations.
This finding has practical implications, given that many (if not most) empirical applications have to deal with only a small amount of method-specific variance. This is because users oftentimes construct their measures (e.g., test halves) in such a way as to maximize their homogeneity. Of course, homogeneity of indicators definitely is a desirable feature, and we encourage authors to select unidimensional measures. Nonetheless, our literature review suggests that even when test halves were designed to be perfectly homogeneous, method effects still occurred and had to be accounted for in the majority of cases. In addition, rather weak method effects are also expected in designs with long lags between the measurements occasions. The OM approach seems to be prone to estimation problems in these cases and may not return reliable parameter estimates.
In addition, it is frequently observed in empirical applications (and was again observed in one of the applications reported in this paper) that one of the method factors in the OM model “collapses” and returns no significant variance or loadings (e.g., Schermelleh-Engel et al., 2004; Steyer & Schmitt, 1994). We may speculate that this result is more likely to occur in cases where method effects are modest, as this condition may lead to lower stability in the methods related estimates in this model and may even cause problems of empirical underidentification. Such empirical underidentification problems may be the cause of the high rate of non-converged solutions we identified for this model in our simulation study—despite the fact that the model was used to generate the data.
An important practical question is: Should researchers interpret the results if one of the method factors in the OM model vanishes empirically, and if so, how? Should one assume that the corresponding indicators are free of method-specific influences? Should those indicators be seen as gold-standard indicators as in the M − 1 approach? We doubt that this would be a sensible interpretation, given that the lack of a method factor for a particular set of indicators is empirically driven rather than theoretically well-founded and might just represent a chance finding. In addition, this result changes the interpretation of the model parameters in a significant way: If one method factor “disappears”, then the trait factor in the model is no longer interpretable as a “general trait” that is common to all indicators, but it actually becomes specific to the set of indicators that have no significant method factor as in the M − 1 approach. Hence, researchers need to be cautious in their interpretation of the parameters of this model in these cases, as the interpretation will be different from their original expectation.
In summary, we cannot unanimously recommend the OM model for LST applications. One reason for the frequent “successful” use of this approach in the literature may be that many applications used only two measurement occasions. For such models to be identified, all loadings on the method factors must be fixed, which may increase the model’s stability.
Another popular approach studied in this paper is the CU model that allows for correlated errors of the same indicators over time. This approach has generally been found to perform well in the context of MTMM research (e.g., Marsh & Bailey, 1991) and is widely used in longitudinal studies. LaGrange and Cole (2008) also recommended this approach in the context of LST modeling. The results of our study are somewhat mixed for this model. Although overall, the CU approach performed better than the OM approach, the CU model did not perform well under conditions with rather large method effects, at least for small to moderate sample sizes.
In addition, the CU approach is plagued by a number of theoretical and conceptual problems, some of which are well-known (e.g., Lance et al., 2002). The CU approach confounds stable indicator-specific variance (i.e., unique consistency) with random measurement error. In the present study, this was shown by downward-biased estimates of indicator reliabilities in all simulation conditions as well as both real data applications. As theoretically expected, the underestimation of the reliabilities systematically increased with increasing method variance. Hence, the CU model does not allow properly estimating indicator reliabilities, and it also does not allow estimating the total consistency of an indicator, given that the unique consistency is represented by error covariances (rather than a latent variable). This is troublesome, given that researchers are often interested in proper estimates of the reliabilities and total consistencies of their indicators. These conceptual issues make the CU model a less attractive option for LST analyses from a psychometric and practical point of view.
In addition to these issues, we note that the CU approach appears to be prone to similar interpretation problems as the OM approach when method effects are weak. With small method effects, the error correlations associated with one set of indicators may be close to zero and non-significant—as was the case in our first empirical application. As has been shown by Cole, Ciesla, and Steiger (2007), failure to include all relevant error correlations in a model leads to a change in the interpretation of the factor that is supposed to be an underlying general factor across all items. With regard to the CU model, this again means that the trait factor becomes specific to those indicators with no significant error correlations—which is very likely not in line with what the researcher had intended.
Finally, and probably most importantly, both the OM and CU models should be used with caution because they do not belong to the family of “true” LST models in the sense that the latent variables in these models cannot be derived based on the core LST framework provided by Steyer et al. (1992, 1999). Only in the NM, M − 1, and IT models are the latent variables well-defined on the basis of the fundamental latent variables of LST theory.
In summary, we recommend that the CU model be used only when the M − 1 approach or the IT model to be discussed next do not fit the data. This may be the case, for example, when method effects do not follow a unidimensional structure across time. The CU model might help as a last resort in these cases, as it does not require method effects to be unidimensional. On the other hand, the CU model makes the assumption that method effects are orthogonal, which may also be violated in practice. Hence, researchers need to carefully consider whether this approach is appropriate for their data.
Our findings suggest that the M − 1 and the IT approach are more theoretically sound, less prone to empirical problems and may be more broadly applicable than the OM and CU approaches. Both models performed well across most conditions studied in our simulation as well as in both real data applications, although the M − 1 model showed some problems at small sample sizes when the amount of method variance was small. From a theoretical point of view, the M − 1 approach seems to be most useful when a researcher can identify one indicator as clearly outstanding relative to the remaining indicators. This could, for instance, be a scale that researchers in the field agree upon as a gold standard measure, an item that is theoretically most appropriate for measuring the construct, or a marker variable that has proven to be a particularly good indicator in prior studies. For example, in our application to the firefighter data, there were clear substantive reasons for choosing the general statement of health as a reference indicator because it was structurally different from the two more specific indicators and could be seen as best representing the construct “perceived general health”. In the multi-rater data example, there were also clear arguments as to why the child report of externalizing symptomatology was chosen as reference indicator; the child is differentiated from both parents by developmental stage and thus represents a unique method source.
If no indicator or method is particularly outstanding or special, the choice of a reference indicator may be more difficult. For example, items may be randomly sampled from an item pool, and consequently, none of the items may be particularly outstanding. A promising approach for applications with no clear reference indicator seems to be the model with IT factors that does not require the selection of a reference method. Although the IT approach performed very well in general, theoretically, it seems to be a particularly good choice when method effects are expected to be rather strong. Strong method effects may imply that different indicators reflect distinct facets of a construct (or even distinct constructs) and therefore should be modeled as separate traits (see Fiske & Campbell, 1992, for a related discussion). Under these conditions, however, researchers should carefully examine whether the assumption of unidimensionality of occasion-specific effects across indicators made by all conventional LST models is still reasonable. As shown by our application to multirater-data, one complication in this regard is that violations of this assumption may not be detectable based on model fit; all models that accounted for method effects fit the data well and were virtually indistinguishable based on fit indices (this was also found in the simulation study). Therefore, researchers need to refer to substantive theory to check whether the obtained estimates of occasion-specificity and reliability are reasonably large. If this does not seem to be the case, multiple indicator LST models that do not require the assumption of homogenous occasion-specific effects across all indicators may be more appropriate.
With small amounts of method variance, the IT factors will be highly correlated, signaling rather high homogeneity of indicators (e.g., in our application of firefighters’ health). This is not a problem per se if model convergence is achieved and all estimates are proper. However, it could be an undesirable feature when trait factors are used as independent variables in extended analyses with covariates. Here, issues of multicollinearity may arise that may complicate the analysis and interpretation of the results (Eid et al., 1999). One approach to the problem of collinearity is the specification of a higher order trait factor on which the correlated first order IT factors load (for an example, see Schmuckle & Egloff, 2005). This second order “common trait” could then be used as a single predictor in an extended analysis. However, as has been shown by Eid (1996), such a factor cannot be constructively defined based on the fundamental latent variables considered in LST theory. As a consequence, although we can attach an “intuitive meaning” to this factor (“it is what the first order trait factors share in common”), this factor does not have a clear meaning (in terms of a conditional expectation or function of a conditional expectation of an observed variable; see Appendix A for details). This does not mean that such an approach should not be used. However, it means that researchers should be aware that with such a model they leave the ground of well-defined latent variables as provided in classical LST theory and have to be more careful with the interpretation of such a factor (Eid, 1996).
Another option would be to define a common trait as an average of the first order trait factors. Such an approach has recently been presented by Pohl and Steyer (2010) in the context of cross-sectional MTMM models. The advantage of this approach is that the “higher order trait” does have a clear meaning as the average of the (psychometrically well-defined) first order latent trait variables. The question would of course be whether it is meaningful to look at this average. This question needs to be carefully addressed based on substantive theory in each individual application.
Finally, if indicators are very homogeneous, and consequently, collinearity is an issue, one may opt for the M − 1 approach and define a single specific trait factor based on a reference indicator. Given that indicators are close to unidimensional, from a substantive point of view, it may not really matter which indicator is chosen as reference indicator to represent the trait.
Limitations
One critique of our recommendation of the M − 1 and IT approaches may be that neither of these approaches allows defining “pure”, “method-free” trait factors, as the trait factors in both approaches contain method-specific variance. Consequently, common and unique consistency coefficients either cannot be defined (IT model) or are defined relative to a reference indicator (M − 1 model). This may be seen as a limitation by researchers who are interested in modeling a single common trait factor and/or in separating common and unique consistency for all indicators.
Another limitation is that in our simulation study, we only considered two factors: method variance and sample size. Other parameters likely also influence model performance. For example, it would be interesting to study whether a larger number of measurement occasions and/or an increased number of high quality indicators could reduce some of the estimation problems observed at small sample sizes. Future research should also examine how the inclusion of an autoregressive component as in LaGrange and Cole’s (2008) study interacts with different sample sizes and levels of method variance.
Conclusion
We fully agree with LaGrange and Cole (2008) that a model should mainly be selected based on theoretical (rather than empirical) considerations. In line with Eid (1996), we believe that there is good reason to select an LST model variant in which all latent variables are explicitly defined as conditional expectations of observed variables. Such models are in line with the fundamental concepts of LST theory (Steyer & Schmitt, 1990), and they provide well-defined and clearly interpretable latent variables. This is the case for both the M − 1 and IT models. Interestingly, these two models also showed the best performance in our simulation study. Based on our theoretical and empirical results, we recommend that readers use one of the two approaches depending on their particular research problem to account for method effects in LST analyses.
Supplementary Material
Figure 12.
IT model for m = 2 methods. This model includes multiple indicators Yimt, indicator-specific trait factors Tim, and state residual factors SRmt separately for each method. This accounts for the fact that occasion-specific effects may not generalize perfectly across different methods. All trait factors can be correlated. Occasion-specific factors pertaining to different methods at the same measurement occasion can also be correlated, indicating the generalizability of occasion-specific effects across different methods.
Table 4.
Estimated Variance Components for Different LST Models Applied to the Externalizing Problem Behavior Data (N = 294)
| CCO | UCO | TCO | OSpe | Rel | |
|---|---|---|---|---|---|
| CU | |||||
| Child report time 1 | .21 | — | — | .02 a | .23 |
| Mother report time 1 | .32 | — | — | .02 a | .34 |
| Father report time 1 | .34 | — | — | .23 a | .57 |
| Child report Time 2 | .18 | — | — | .17 a | .35 |
| Mother report time 2 | .36 | — | — | .03 a | .39 |
| Father report time 2 | .38 | — | — | .03 a | .41 |
| Child report Time 3 | .12 | — | — | .04 a | .16 |
| Mother report time 3 | .34 | — | — | .13 a | .48 |
| Father report time 3 | .39 | — | — | .03 a | .42 |
| OM | |||||
| Child report time 1 | .21 | .36 | .56 | .02 a | .58 |
| Mother report time 1 | .32 | .34 | .66 | .02 a | .68 |
| Father report time 1 | .34 b | .43 b | .77 b | .23 b | 1.00 b |
| Child report Time 2 | .18 | .52 | .70 | .17 a | .87 |
| Mother report time 2 | .36 | .38 | .74 | .03 a | .77 |
| Father report time 2 | .38 | .27 | .65 | .03 a | .68 |
| Child report Time 3 | .12 | .41 | .53 | .04 a | .57 |
| Mother report time 3 | .34 | .29 | .64 | .13 a | .77 |
| Father report time 3 | .39 | .28 | .67 | .03 a | .70 |
| M − 1 c | |||||
| Child report time 1 | .56 | — | .56 | .02 a | .58 |
| Mother report time 1 | .11 d | .56 d | .67 | .01 a | .68 |
| Father report time 1 | .09 d | .65 d | .74 | .23 a | .97 |
| Child report Time 2 | .70 d | — | .70 | .13 a | .83 |
| Mother report time 2 | .10 d | .64 d | .74 | .03 a | .77 |
| Father report time 2 | .10 d | .56 d | .66 | .03 a | .69 |
| Child report Time 3 | .52 | — | .52 | .03 a | .55 |
| Mother report time 3 | .07 d | .57 d | .64 | .22 a | .87 |
| Father report time 3 | .12 d | .55 d | .67 | .02 a | .70 |
| IT | |||||
| Child report time 1 | — | — | .57 | .03 a | .60 |
| Mother report time 1 | — | — | .67 | .02 a | .68 |
| Father report time 1 | — | — | .73 | .16 a | .89 |
| Child report Time 2 | — | — | .70 | .13 a | .83 |
| Mother report time 2 | — | — | .74 | .03 a | .78 |
| Father report time 2 | — | — | .66 | .03 a | .69 |
| Child report Time 3 | — | — | .52 | .03 a | .56 |
| Mother report time 3 | — | — | .64 | .15 a | .79 |
| Father report time 3 | — | — | .68 | .03 a | .71 |
Note. NM = model with no method factors; CU = correlated uniqueness approach; OM = M orthogonal method factor approach; M − 1 = M − 1 correlated method factor approach; IT = indicator specific trait factor approach. CCO = common consistency; UCO = unique consistency; TCO = total consistency; OSpe = occasion-specificity; Rel = reliability. Sum scores of the Externalizing Problem Behavior Scale of the Child Behavior Checklist (CBCL; Achenbach & Edelbrock, 1983) served as indicators. The model without method factors did not converge for these data.
the variances of all state residual factors were non-significant (p ≥ .28).
In this model, the residual variance of the father report indicator at time 1 was estimated to be zero.
Child report served as reference method in this model.
to be interpreted relative to the reference method (child report). Dashes indicate that a coefficient is not applicable. TCO and OSpe do not always add up to the reliability coefficient due to rounding errors.
Acknowledgments
The data used in this study were collected under grants funded by the National Institute on Alcohol Abuse and Alcoholism (R01AA016213, PI: Laurie Chassin), and the National Institute on Arthritis and Musculoskeletal and Skin Diseases (R01 45901, PI: Diane Elliot).
The authors wish to thank Laurie Chassin and Diane Elliot for supplying datasets and providing helpful comments on earlier drafts, and Brian Keller for his assistance.
Appendix A Fundamental Concepts of LST Theory and Constructive Definition of Latent Variables
In this appendix, we summarize the fundamental concepts of LST theory (e.g., Steyer et al., 1992) and show that all latent variables in LST theory are defined as conditional expectations of observed variables or well-defined functions of these conditional expectations. Further, we show that the NM, IT and M − 1 models can be formulated directly on the basis of these well-defined latent variables. As a consequence, all latent factors in these models are also well-defined in the sense that they are conditional expectations of observed variables or well-defined functions of these conditional expectations. In addition, we explain why the latent variables in the CU and OM models cannot be derived on the basis of the fundamental concepts of LST theory, so that, in a strict sense, these models cannot be considered “true” LST models.
Random Experiment
The starting point for introducing the fundamental concepts of LST theory is the definition of the underlying random experiment (RE). This RE characterizes the empirical phenomenon of interest in LST research (i.e., the measurement of persons in situations) and provides the formal theoretical background based on which (1) the relevant latent variables and (2) appropriate statistical measurement models can be defined. This RE differs from classical experiments in that it does not involve an experimental manipulation of independent variables. Instead, this experiment refers to measuring an attribute of the same person across different situations using multiple measurements (e.g., multiple indicators, raters, observations, or methods) at each time point. Formally, the RE in LST theory consists of the following set Ω of possible outcomes (e.g., Eid, 1996; Steyer et al., 1992):
| (A1) |
where ΩU is the set of observational units u (persons), ΩSitt is the set of situations at time t, t = 1, …, n, ΩMeat is the set comprising all measurements at time t, and × is the Cartesian product operator. Because we assume multiple measurements per person at each time point, each set ΩMeat itself consists of the Cartesian product of subsets ΩMeait:
| (A2) |
where the subsets ΩMeait contain the values on the observed indicators i (e.g., item or scale scores), i = 1, …, m at time t.
As an example, consider the case of m = 2 indicators (i = 1, 2), each of which is measured on n = 2 time points (t = 1, 2). For this example, Ω can be written as:
| (A3) |
Further, an element of Ω can be written as ω = (u, sit1, mea11, mea21, sit2, mea12, mea22), where u indicates the specific person drawn from the set of persons ΩU, sit1 indicates the specific situation drawn from the set of situations ΩSit1 on the first time point, mea11 indicates the specific score observed for the first indicator (e.g., test or questionnaire) on the first time point, mea21 indicates the specific score observed for the second indicator on the first time point, sit2 indicates the specific situation drawn from the set of situations ΩSit2 on the second time point, mea12 indicates the specific score observed for the first indicator on the second time point, and mea22 indicates the specific score observed for the second indicator on the second time point. It is important to note that (1) the term “situation” refers to both inner and outer influences and (2) the situations do not have to be known. Moreover, they need not be the same for all persons (Steyer, 1988).
The values of the random variable Yit are the observed scores obtained for indicator i at time t. The values of the mapping pu: Ω → ΩU are the persons u. The values of the mapping pSitt: Ω → ΩSitt are the situations in which the persons are measured at a particular measurement occasion t. The values of (pu, pSitt) are the persons in situations at time t.
Definition of Basic Latent Variables
The latent state variables Sit are defined as:
| (A4) |
In Equation A4, E (Yit | pu, pSitt) denotes the conditional expectation (regression) of an observed variable Yit given the person and the situation. The measurement error variables εit are defined as:
| (A5) |
Equation A5 shows that εit is defined as a residual with regard to the regressor E (Yit | pu, pSitt). Taken together, Equations A4 and A5 imply the following basic decomposition of observed variables in LST theory:
| (A6) |
where εit by definition has an expected value of zero and is uncorrelated with the regressor Sit (Steyer, 1989; Zimmerman, 1975). The following simple manipulation of E (Yit | pu, pSitt) allows defining latent trait and latent state residual variables:
| (A7) |
The latent trait variables are defined as the conditional expectation of an observed variable given the person:
| (A8) |
The latent state residual variables are defined as the conditional expectation given the person and the situation minus the conditional expectation of an observed variable given the person:
| (A9) |
Equation A9 shows that individual values on the variable SRit represent the differences between latent state and a latent trait scores. Consequently, Sit = Tit + SRit. Combining this equation with Equation A6 yields the basic decomposition of observed variables in LST theory:
| (A10) |
Up to this point, no restrictive assumptions have been made. We have just defined the basic concepts of LST theory. All latent variables defined above are indicator-specific, that is, each observed variable is decomposed into its own latent trait, latent state residual, and error variable. Consequently, no testable assumptions are implied so far. More importantly, at this point, the variances of the latent variables cannot be estimated without further assumptions due to underidentification. The next section describes how—based on the concepts above—restrictive assumptions can be introduced to obtain three identified LST measurement models, the NM, IT, and M − 1 models. For simplicity, we assume that all observed and latent variables are in deviation form (i.e., mean centered), so that there are no additive constants.
Definition of the NM Model
The NM model is defined by the following assumptions:
-
Congenerity of latent trait variables across all m indicators and all n time points:
(A11) where i, i′ ∈ I ≡ {1,…, m}, t, t′ ∈ K ≡ {1,…, n} and λii′tt′ is a real constant.
-
Occasion-specific congenerity of latent state residual variables:
(A12) where δii′t is a real constant.
Equation A11 and A12 can be understood as homogeneity assumptions. Equation A11 states that all indicator-specific latent trait variables differ only by a multiplicative constant. Likewise, Equation A12 states that all indicator-specific state residual variables measured on the same occasion of measurement differ only by a multiplicative constant. It can be shown that these two assumptions imply the existence of a common (indicator- and occasion-unspecific) latent trait factor T for all indicators and common (occasion-specific) latent state residual factors SRt for all indicators measured at the same occasion of measurement (e.g., Steyer, 1988). In addition, the following mean and covariance restrictions apply in this model:17
E(εit) = E(SRt) = Cov(T, SRt) = Cov(T, εit) = Cov(εit, SRt′) = 0, Cov(SRt, SRt′) = 0 for t ≠ t′, and Cov(εit, εi′t′) = 0 for (i, t) ≠ (i′, t′).
Definition of the IT Model
In the IT model, each indicator loads onto its own latent trait factor, that is, trait factors are assumed to be indicator-specific. Consequently, the first assumption differs from the first assumption made in the NM model.
-
Indicator-specific congenerity of latent trait variables:
(A14) where i ∈ I ≡ {1,…, m}, t, t′ ∈ K ≡ {1, …, n}. In contrast to Equation A11, Equation A14 postulates homogeneity of trait variables Tit and Tit′ only for indicators with the same index i, implying the existence of common (but indicator-specific) trait factors Ti. Hence, this assumption is less restrictive than the assumption in Equation A11. Common occasion-specific factors are defined in the same way as for the NM model (see Equation A12). In addition, the following mean and covariance restrictions apply in this model: E(εit) = E(SRt) = Cov (Ti, SRt) = Cov(Ti, εit), = Cov(εit, SRt′) = 0, Cov(SRt, SRt′) = 0 for t ≠ t′, and, Cov(εit, εi′t′) = 0 for (i, t) ≠ (i′, t′).
Definition of the M − 1 Model
In the M − 1 model, a reference indicator Yrt with corresponding reference trait variable Trt is selected (Eid et al., 1999). Indicator-specific congenerity of the reference trait variables Trt is assumed:
-
Congenerity of reference trait variables:
(A15) where r ∈ I ≡ {1, …, m}, t, t′ ∈ K ≡ {1, …, n}. This homogeneity assumption implies the existence of a common trait factor Tr for the reference indicators. Further, the non-reference trait variables are linearly regressed on the reference trait factor Tr:
- Linear regression of the non-reference trait variables on the reference trait factor Tr:
(A16) - Definition of method variables TRit as residuals of this regression analysis:
(A17) -
Assumption of congenerity of trait residual variables:
(A18) where γitt′ is a real constant. Equation A18 postulates homogeneity of method variables TRit and TRit′ pertaining to the same indicator i, implying the existence of common trait residual factors TRi. In addition, the following mean and covariance restrictions apply in this model: E(εit) = E(SRt) = E(TRi) = Cov(Tr, SRt) = Cov(Tr, TRi) = Cov(Tr εit) = Cov(TRi SRt) = Cov(TRi, εi′t) = Cov(εit SRt′) = 0, Cov (SRt, SRt′) = 0 for t ≠ t′, and Cov(εit, εi′t′) = 0 for (i, t) ≠ (i′, t′).
The CU Model
The CU model is defined by the same assumptions as the NM model, but relaxes the assumption of uncorrelated errors such that error variables with the same index i can be correlated:
| (A19) |
Equation A19 shows that, in contrast to the IT and M − 1 models, the CU model does not define person-specific method effects as a well-defined function of the conditional expectation E(Yit | pu) (i.e., as a function of the latent trait variables Tit), but instead views person-specific method effects as part of the error variables εit. This view, however, is not in line with the definition of the error variable in LST theory (see Equation A5). According to Equation A5, the error variable is defined as that part of an observed variable that is not due to systematic person or situation effects (i.e., that part of Yik that is not determined by the regressors pu and pSitt). However, logically, a person-specific method effect must be related to the conditional expectation given the person E(Yit | pu), because a person-specific method effect reflects one part of Yik that is systematic and stable over time. Consequently, the implicit assumption made in the CU model, according to which method effects are part of the error variable is at odds with the basic definition of the error variable in Steyer et al.’s (1992) LST theory. Therefore, the CU model cannot be considered an LST model in a strict sense.
The OM Model
As has been shown by Eid (1996), the common method factors Mi specified in the OM model cannot be defined as well-defined functions of the conditional expectation E(Yit | pu) (i.e., as functions of the latent trait variables Tit). Consequently, the theoretical status of the method factors Mi is unclear, at least according to Steyer et al.’s (1992) classical LST framework. Moreover, the theoretical status of the remaining latent variables in this model also becomes dubious when the factors Mi are included, because the Mi factors reflect part of the stability of the indicators, albeit not in a well-defined way. Consequently, like the CU model, the OM model cannot be considered an LST model in a strict sense (Eid, 1996).
Appendix B Summary of Empirical Studies That Have Used Multiple Indicator LST Models
| Article | N | W | I | Model | Construct |
|---|---|---|---|---|---|
| Steyer, Majcen, Schwenkmezger, Buchner, 1989 | 64 | 2 | 2 | NM | anxiety |
| Steyer, Schwenkmezger & Auer, 1990 | 179 | 2 | 2 | CU | anxiety |
| Steyer & Schmitt, 1990 | 152 | 3 | 4 | CU, IT | attitudes toward guest workers |
| Kirschbaum et al., 1990 | 48 | 2 | 2 | NM | salivary cortisol |
| 54 | 3 | 2 | NM | salivary cortisol | |
| Ormel & Schaufeli, 1991a | 226 | 3 | 2 | M − 1 | psychological distress, locus of control, & self-esteem |
| 389 | 5 | 2 | NM | psychological distress, locus of control, & self-esteem | |
| Schmitt & Steyer, 1993 | 380 | 2 | 2 | OM | social desirability |
| 215 | 3 | 2 | OM | social desirability | |
| Steyer & Schmitt, 1994 | 502 | 4 | 2 | M − 1 | well being |
| Eid, Notz, Steyer, Schwenkmezger, 1994 | 496 | 4 | 2 | OM | mood level & mood reactivity |
| Deinzer et al., 1995 | 502 | 4 | 2 | OM | 12 personality dimensions |
| Preville et al, 1996 | 46 | 3 | 5 | NM | cortisol reactivity |
| Dumenci & Windle, 1996 | 805 | 4 | 4 | OM | depressive symptoms |
| Dumenci & Windle, 1998 | 1061 | 4 | 3 | OM | depressed mood |
| Windle & Dumenci, 1998 | 536 | 4 | 4 | OM | depressed mood |
| Eid & Hoffmann, 1998 | 370 | 4 | 2 | IT | interest in topic of radioactivity |
| Eid, Schneider & Schwenkmezger, 1999 | 176 | 3 | 2 | M − 1 | self-perceived mood deviation |
| Steyer, Schmitt & Eid, 1999 | 503 | 2 | 2 | IT | awakeness vs. sleepiness mood state |
| Eid & Diener, 1999 | 180 | 3 | 2 | IT | affect |
| Schmitt & Maes, 2000 | 1065 | 2 | 2 | OM | depressive symptoms |
| Schmitt, 2000 | 206 | 3 | 2 | OM | mother-daughter attachment & family cohesion |
| J. Tisak & M.S. Tisak, 2000 | 116 | 3 | 4 | OM | affective commitment |
| 117 | 3 | 4 | OM | continuance commitment | |
| Schmukle, Egloff, & Burns, 2002 | 292 | 3 | 2 | IT | positive affect & negative affect |
| Mohiyeddini, Hautzinger, & Bauer, 2002 | 188 | 2 | 2 | OM | depression |
| Hagemann et al., 2002 | 59 | 4 | 2 | NM | resting EEG asymmetry |
| Blickle, 2003 | 209 | 2 | 4 | IT | intraorganizational influence attempts |
| Moskowitz & Zuroff, 2004 | 119 | 3 | 2 | IT | flux, pulse, & spin |
| Davey et al., 2004 | 737 | 5 | 3 | CU, M − 1 | depressive symptoms |
| Schermelleh-Engel et al., 2004 | 395 | 3 | 3 | M − 1 | test anxiety |
| Yasuda et al, 2004 | 235 | 3 | 5 | CU | affect |
| Eid & Diener, 2004 | 249 | 3 | 2 | IT | subjective well-being |
| Schmitt, Gollwitzer, Maes, & Arbach, 2005 | 1258 | 2 | 2 | M − 1 | justice sensitivity |
| Hagemann et al., 2005 | 59 | 3 | 2 | NM | resting EEG asymmetry |
| Schmukle & Egloff, 2005 | 65 | 2 | 2 | IT | implicit & explicit |
| Khoo et al., 2006 | 188 | 3 | 4 | OM | conscientiousness |
| Baumgartner & Steenkamp, 2006 | 1991 | 3 | 9 | modified OM | brand loyalty & deal proneness |
| Dormann et al., 2006 | 157 | 4 | 2 | CU | job satisfaction |
| Hellhammer et al., 2007 | 239 | 6 | 2 | NM | cortisol rise after wakening |
| Bonnefon, Vautier, & Eid, 2007 | 484 | 2 | 6 | IT | contrapositive reasoning |
| Courvoisier et al., 2007a | 501 | 4 | 2 | M − 1 | mood |
| Booth, Granger, & Shirtcliff, 2008 | 724 | 4 | 2 | NM | cortisol levels |
| Hermes et al., 2009 | 38 | 2 | 2 | NM | cerebral blood flow |
| Olatunji & Cole, 2009a | 787 | 8 | 2 | TSO | anxiety |
| Ziegler, Ehrlenspiel, & Brand, 2009 | 156 | 2 | 4 | CU | competitive anxiety |
| Boll et al., 2010 | 709 | 2 | 2 | OM | differential parental treatment |
| Courvoisier et al., 2010a | 307 | 6 | 2 | IT | mood |
| Danner et al., 2010 | 173 | 2 | 2 | OM | intelligence, decision making, learning |
| Weijters et al., 2010 | 1506 | 2 | 3 | CU | response style |
| Courvoisier et al., 2011a | 15,282 | 4 | 2 | IT | psychosocial health |
| Kertes & van Dulmen, 2011 | 164 | 3 | 2 | NM | cortisol |
| Lorber & O’Leary, 2011a | 396 | 4 | 2 | OM, IT b | aggression |
| Luhmann, Schimmack, & Eid, 2011a | 37,041 | 16 | 2 | M − 1 | affective well-being |
| Ploubidis & Frangou, 2011 | 3445 | 2 | 30 | NM | psychological distress |
| Stalder et al., 2011 | 64 | 3 | 2 | CM | hair cortisol |
| Eid, Courvoisier, & Lischetzke, in pressa | 305 | 6 | 2 | IT | mood |
| Median | 249 | 3 | 2 |
| Mean | 1349.298c | 3.474 | 3.140 |
| Mode | -- | 3 | 2 |
| Minimum | 38 | 2 | 2 |
| Maximum | 37,041 | 16 | 30 |
| SD | 5227.155 | 2.097 | 3.847 |
Note. W = number of waves; I = number of indicators per wave; CU = correlated uniqueness approach; OM = M orthogonal method factor approach; M − 1 = M − 1 correlated method factor approach; IT = indicator-specific trait factor approach; TSO = trait state occasion model without method factors; CM = M correlated method factor approach.
Denotes studies which tested LST models with an autoregressive component.
Not explicitly interpreted as an IT model by the authors of this paper.
The mean sample size without including the Courvoisier et al. (2011) and Luhmann et al. (2011) study is N = 447.
References in Appendix
- Baumgartner H, Steenkamp JBEM. An extended paradigm for measurement analysis of marketing constructs applicable to panel data. Journal of Marketing Research. 2006;43:431–442. [Google Scholar]
- Blickle G. Convergence of agents’ and targets’ reports on intraorganizational influence attempts. European Journal of Psychological Assessment. 2003;19:40–53. [Google Scholar]
- Boll T, Michels T, Ferring D, Filipp SH. Trait and state components of perceived parental differential treatment in middle adulthood. Journal of Individual Differences. 2010;31:158–165. [Google Scholar]
- Bonnefon JF, Vautier S, Eid M. Modeling individual differences in contrapositive reasoning with continuous latent state and trait variables. Personality and Individual Differences. 2007;42:1403–1413. [Google Scholar]
- Booth A, Granger DA, Shirtcliff EA. Gender- and age-related differences in the association between social relationship quality and trait levels of salivary cortisol. Journal of Research on Adolescence. 2008;18:239–260. [Google Scholar]
- Courvoisier DS, Eid M, Lischetzke T, Schreibner WH. Psychometric properties of a computerized mobile phone method for assessing mood in daily life. Emotion. 2010;1:115–124. doi: 10.1037/a0017813. [DOI] [PubMed] [Google Scholar]
- Courvoisier DS, Agoritsas T, Glauser J, Michaud K, Wolfe F, Contoni E, Perneger TV, Finckh A. Pain is the most important predictor of psychosocial health in patients with rheumatoid arthritis. Arthritis care and Research. 2011 doi: 10.1002/acr.20652. [DOI] [PubMed] [Google Scholar]
- Danner D, Hagemann D, Schankin A, Hager M, Funke J. Beyond IQ: A latent state-trait analysis of general intelligence, dynamic decision making, and implicit learning. Intelligence. 2011;39:323–334. [Google Scholar]
- Davey A, Halverson CF, Jr, Zonderman AB, Costa PT., Jr Change in depressive symptoms in the Baltimore Longitudinal Study of Aging. Journal of Gerontology. 2004;59B:270–277. doi: 10.1093/geronb/59.6.p270. [DOI] [PubMed] [Google Scholar]
- Deinzer R, Steyer R, Eid M, Notz P, Schwenkmezger P, Ostendorf F. Situational effects in trait assessment: The FPI, NEOFFI, and EPI questionnaires. 1995. [Google Scholar]
- Dormann C, Fay D, Zapf D, Frese M. A state-trait analysis of job satisfaction: On the effect of core self-evaluations. Applied Psychology: An International Review. 2006;55:27–51. [Google Scholar]
- Dumenci L, Windle M. A latent trait-state model of adolescent depression using the Center for Epidemiologic Studies-Depression Scale. Multivariate Behavioral Research. 1996;31:313–330. doi: 10.1207/s15327906mbr3103_3. [DOI] [PubMed] [Google Scholar]
- Dumenci L, Windle M. A multitrait-multioccasion generalization of the latent trait-state model: Description and application. Structural Equation Modeling. 1998;5:391–410. [Google Scholar]
- Eid M, Courvoisier DS, Lischetzke T. Structural equation modeling of ambulatory assessment data. In: Mehl MR, Conner TS, editors. Handbook of research methods for studying daily life. (in press) [Google Scholar]
- Eid M, Diener E. Intraindividuality variability in affect: Reliability, validity, and personality correlates. Journal of Personality and Social Psychology. 1999;4:662–676. [Google Scholar]
- Eid M, Diener E. Global judgments of subjective well-being: Situational variability and long-term stability. Social Indicators Research. 2004;65:245–277. [Google Scholar]
- Eid M, Hoffmann L. Meauring variability and change with an item response model for polytomous variables. Journal of Educational and Behavioral Statistics. 1998;23:193–215. [Google Scholar]
- Eid M, Notz P, Steyer R, Schwenkmezger P. Validating scales for the assessment of mood level and variability by latent state-trait analyses. Personality and Individual Differences. 1993;16:63–76. [Google Scholar]
- Eid M, Schneider C, Schwenkmezger P. Do you feel better or worse? The validity of perceived deviations of mood states from mood traits. European Journal of Personality. 1999;13:283–306. [Google Scholar]
- Hagemann D, Hewig J, Seifert J, Naumann E, Bartussek D. The latent state-trait structure of resting EEG asymmetry: Replication and extension. Psychophysiology. 2005;42:740–752. doi: 10.1111/j.1469-8986.2005.00367.x. [DOI] [PubMed] [Google Scholar]
- Hagemann D, Naumann E, Thayer JF, Bartussek D. Does resting electroencephalograph asymmetry reflect a trait? An application of latent state-trait theory. Journal of Personality and Social Psychology. 2002;82:619–641. [PubMed] [Google Scholar]
- Hellhammer J, Fries E, Schweisthal OW, Schlotz W, Stone AA, Hagemann D. Several daily measurements are necessary to reliably asess the cortisol rise after awakening: State- and trait components. Psychoneuroendocrinology. 2007;32:80–86. doi: 10.1016/j.psyneuen.2006.10.005. [DOI] [PubMed] [Google Scholar]
- Hermes M, Hagemann D, Britz P, Lieser S, Bertsch K, Naumann E, Walter C. Latent state-trait structure of cerebral blood flow in a resting state. Biological Psychology. 2009;80:196–202. doi: 10.1016/j.biopsycho.2008.09.003. [DOI] [PubMed] [Google Scholar]
- Kertes DA, van Dulmen M. Latent state trait modeling of children’s cortisol at two points of the diurnal cycle. Psychoneuroendocrinology. 2011 doi: 10.1016/j.psyneuen.2011.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khoo S-T, West SG, Wu W, Kwok O-M. Longitudinal methods. In: Eid M, Diener E, editors. Handbook of multimethod measurement in psychology. Washington: APA; 2006. pp. 301–317. [Google Scholar]
- Kirschbaum C, Steyer R, Eid M, Patalla U, Schwenkmezger P, Hellhammer DH. Cortisol and behavior: Application of a latent state-trait model to salivary cortisol. Psychoneuroendocrinology. 1990;15:297–307. doi: 10.1016/0306-4530(90)90080-s. [DOI] [PubMed] [Google Scholar]
- Lorber MF, O’Leary KD. Stability, change, and informan variance in newlyweds’ physical aggression: Individual and dyadic processes. Aggressive Behavior. 2011;37:1–15. doi: 10.1002/ab.20414. [DOI] [PubMed] [Google Scholar]
- Luhmann M, Schimmack U, Eid M. Stability and variability in the relationship between subjective well-being and income. Journal of Research in Personality. 2011;45:186–197. [Google Scholar]
- Mohiyeddini C, Hautzinger M, Bauer S. Eine Latent-State-Trait Analyse zur Bestimmung der dispositionellen und zustandsbedingten Anteile dreier Instrumente zur Erfassung von Depressionen: ADS, BDI, und SDS [A latent state-trait analysis to determine the dispositional and state-dependent aspects of three instruments to measure depression: The ADS, BDI, and SDS] Diagnostica. 2002;48:12–18. [Google Scholar]
- Moskowitz DS, Zuroff DC. Flux, pulse, and spin: Dynamic additions to the personality lexicon. Journal of Personality and Social Psychology. 2004;86:880–893. doi: 10.1037/0022-3514.86.6.880. [DOI] [PubMed] [Google Scholar]
- Olatunji BO, Cole DA. The longidutinal structure of general and specific anxiety dimensions in children: Testing a latent trait-state-occasion model. Psychological Assessment. 2009;21:412–424. doi: 10.1037/a0016206. [DOI] [PubMed] [Google Scholar]
- Ormel J, Schaufeli WB. Stability and change in psychological distress and their relationship with self-esteem and locus of control: A dynamic equilibrium model. Journal of Personality and Social Psychology. 1991;60:288–299. doi: 10.1037//0022-3514.60.2.288. [DOI] [PubMed] [Google Scholar]
- Ploubidis GB, Frangou S. Neuroticism and psychological distress: To what extent is their association due to person-environment correlation? European Psychiatry. 2011;26:1–5. doi: 10.1016/j.eurpsy.2009.11.003. [DOI] [PubMed] [Google Scholar]
- Preville M, Susman E, Zarit SH, Symer M, Bosworth HB, Reid JD. A measurement model of cortisol reactivity of healthy older adults. Journal of Gerontology. 1996;51B:64–69. doi: 10.1093/geronb/51b.2.p64. [DOI] [PubMed] [Google Scholar]
- Schermelleh-Engel K, Keith N, Moosbrugger H, Hodapp H. Decomposing person and occasion-specific effects: An extension of latent state-trait (LST) theory to hierarchical LST models. Psychological Methods. 2004;9:198–219. doi: 10.1037/1082-989X.9.2.198. [DOI] [PubMed] [Google Scholar]
- Schmitt M, Gollwitzer M, Maes J, Arbach D. Justice sensitivity: Assessment and location in the personality space. European Journal of Psychological Assessment. 2005;21:202–211. [Google Scholar]
- Schmitt M, Maes J. Simplification of the Beck-Depression-Inventory (BDI) Diagnostica. 2000;46:38–46. [Google Scholar]
- Schmitt MJ, Steyer R. A latent state-trait model (not only) for social desirability. Personality and Individual Differences. 1993;14:519–529. [Google Scholar]
- Schmuckle SC, Egloff B, Burns LR. The relationship between positive and negative affect in the Positive and Negative Affect Scale. Journal of Research in Personality. 2002;36:463–475. [Google Scholar]
- Schmuckle SC, Egloff B. A latent state-trait analysis of implicit and explicit personality measures. European Journal of Psychological Assessment. 2005;21:100–107. [Google Scholar]
- Stalder T, Steudte S, Miller R, Skoluda N, Dettenborn L, Kirschbaum C. Intraindividual stability of hair cortisol concentrations. Psychoneuroendocrinology. 2011 doi: 10.1016/j.psyneuen.2011.08.007. [DOI] [PubMed] [Google Scholar]
- Steyer R, Majcen AM, Schwenkmezger P, Buchner A. A latent state-trait anxiety model and its application to determine consistency and specificity coefficients. Anxiety Research. 1989;1:281–299. [Google Scholar]
- Steyer R, Schmitt MJ. Latent state-trait models in attitude research. Quality and Quantity. 1990;24:427–445. [Google Scholar]
- Steyer R, Schmitt M. The theory of confounding and its application in causal modeling with latent variables. In: von Eye A, Clogg CC, editors. Latent variables analysis. Thousand Oaks, CA: Sage; 1994. [Google Scholar]
- Steyer R, Schmitt M, Eid M. Latent state-trait theory and research in personality and individual differences. European Journal of Personality. 1999;13:389–408. [Google Scholar]
- Steyer R, Schwenkmezger P, Auer A. The emotional and cognitive components of trait anxiety: A latent state-trait model. Personality and Individual Differences. 1990;11:125–134. [Google Scholar]
- Tisak J, Tisak MS. Permanency and ephemerality of psychological measures with application to organizational commitment. Psychological Methods. 2000;5:175–198. doi: 10.1037/1082-989x.5.2.175. [DOI] [PubMed] [Google Scholar]
- Weijters B, Geuens M, Schillewaert N. The stability of individual response styles. Psychological Methods. 2010;15:96–110. doi: 10.1037/a0018721. [DOI] [PubMed] [Google Scholar]
- Windle M, Dumenci L. An investigation of maternal and adolescent depressed mood using a latent trait-state model. Journal of Research on Adolescence. 1998;8:461–484. [Google Scholar]
- Yasuda T, Lawrenz C, Van Whitlock R, Lubin B, Lei PW. Assessment of intraindividual variability in positive and negative affect using latent state-trait model analyses. Educational and Psychological Measurement. 2004;64:514–530. [Google Scholar]
- Ziegler M, Ehrlenspiel F, Brand R. Latent state-trait theory: An application in sport psychology. Psychology of Sport and Exercise. 2009;10:344–349. [Google Scholar]
Footnotes
Details on the exact definition of the latent variables in LST theory are provided in Appendix A.
In the classical LST model, the observed variables are assumed to be continuous (e.g., test or questionnaire scores, physiological measurements on a continuous scale etc.), although Eid (1995, 1996; Eid & Hoffmann, 1998) has shown how to define LST models for ordered categorical indicators. For the sake of simplicity, we will assume continuous indicators throughout this article.
The uncorrelatedness of T and SRt follows from the definition of the SRt factors as residuals with respect to T. See Appendix A as well as Steyer & Schmitt (1990) for details.
Note that the assumption of uncorrelated SRt factors can be relaxed. Steyer and Schmitt (1994) as well as Cole et al. (2005) discuss LST models with autoregressive components that do not make the assumption of uncorrelated state residual variables.
We do not consider a model with I correlated method factors here given that such models have been shown to suffer from severe conceptual problems, as well as difficulties in identification, estimation, and interpretation in the context of MTMM and LST analyses (see, e.g., Conway et al., 2004; Grayson & Marsh, 1994; Kenny & Kashy, 1992; LaGrange & Cole, 2008; Marsh, 1989; Marsh & Bailey, 1991).
The OM aproach is no longer supported by Steyer and colleagues. Instead, these authors now favor models in which method effects are constructively defined as latent difference variables (Pohl et al., 2008; Pohl & Steyer, 2010).
One might be tempted to extend the model to separate “common” trait effects from “method-specific” effects by specifying a second order factor on the basis of the indicator-specific trait factors. Such a model has been discussed by Marsh and Grayson (1994) and applied by Schmukle and Egloff (2005). However, Eid (1996) has shown that this extended model cannot be formulated on the basis of the random experiment considered in LST theory. As a consequence, the second order factor as well as the first order residual factors in this model are not well-defined latent variables and have no clear psychometric meaning. We therefore do not consider such a model here. A more well-defined approach could for example define a common trait factor as the average of the indicator-specific latent trait variables. A related approach has been discussed by Pohl and Steyer (2010) in the context of MTMM analyses. However, this is not the central focus of the present paper and we therefore do not consider this extension here.
It should be noted that, as a consequence of the fact that only the NM, M − 1, and IT models are LST models according Steyer et al.’s (1992) framework, in a strict sense, the different types of consistency coefficients presented here have a clear meaning only in these models, but not in the CU and OM models.
The UCO coefficient has also been referred to as method-specificity coefficient in the LST literature (e.g., Steyer et al., 1992; Eid et al., 1999). We prefer the term unique consistency coefficient because (1) this label makes clear that this variance component reflects part of the stable variance of an indicator and (2) occasion-specific (i.e., non-stable) method effects are not captured by this coefficient.
The condition with N = 235 was included because this represented the median sample size found in our original literature review prior to conducting the simulation study. After acceptance of this article, we updated our literature review. The median sample size changed slightly to N = 249.
This criterion leads to a rather conservative estimate of improper solutions, because not all cases with non-positive definite matrices are actually associated with offending (i.e., out-of-range) parameter estimates (e.g., negative variances). Sometimes, these messages are caused by linear dependencies that do not lead to inadmissible parameter estimates. We decided to use this strict criterion because researchers typically refuse to interpret a solution that yields these types of warning messages.
We suspect that the mixture distributions of the parameter estimates seen at high levels of method variance indicate that the estimation routine attempts to compensate for the extreme misspecification in different ways across replications, sometimes over- and sometimes underestimating consistency.
Item level analyses should in general take the ordinal scale level of the measures into account. For the sake of simplicity and to save space, we treated the indicators as continuous in the present application. Nonetheless, we urge researchers to use appropriate estimation methods for ordinal variables in actual substantive applications at the item level (see Eid, 1996, as well as Eid & Hoffmann, 1998, for a detailed description of LST models for ordinal variables).
The non-convergence of this model is likely due to strong method effects in this application due to the use of multiple reporters.
Courvoisier (2006) as well as Courvoisier et al. (2008) also proposed a multiple indicator LST approach. Courvoisier et al.’s approach differs from the approach presented here in that their approach contrasts different methods against a reference method. The purpose of the model presented here is simply to illustrate that conventional LST models may be inappropriate for modeling occasion-specific effects if different indicators represent different methods that do not share the exact same occasion-specific effects.
Interestingly, it appears from our review that almost all applications that did not account for method effects used physiological measures such as cortisol level etc. as indicators for which method effects did not seem to play a role.
Some of the mean and covariance restrictions in this model (and other models discussed here) directly follow from the definition of the latent variables in Equations A4, A5, A8, and A9 (i.e., they do not require additional assumptions), whereas others do require the additional assumption of conditional regressive independence (Steyer & Schmitt, 1990; Steyer et al., 1992). For simplicity and clarity, we do not distinguish between those restrictions that follow from the basic definitions and those that require additional assumptions. Interested readers may consult Steyer (1988) or Steyer and Schmitt (1990) for more details.
Publisher's Disclaimer: The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at www.apa.org/pubs/journals/met
References
- Achenbach TM, Edelbrock CS. Behavioral problems and competencies reported by parents of normal and disturbed children aged four through sixteen. Monographs for the Society for Research in Child Development. 1981;46(1) serial no. 188. [PubMed] [Google Scholar]
- Baumgartner H, Steenkamp JBEM. An extended paradigm for measurement analysis of marketing constructs applicable to panel data. Journal of Marketing Research. 2006;43:431–442. [Google Scholar]
- Bonnefon JF, Vautier S, Eid M. Modeling individual differences in contrapositive reasoning with continuous latent state and trait variables. Personality and Individual Differences. 2007;42:1403–1413. [Google Scholar]
- Campbell DT, Fiske DW. Convergent and discriminant validation by the multitrait-multimethod matrix. Psychological Bulletin. 1959;56:81–105. [PubMed] [Google Scholar]
- Chassin L, Rogosch F, Barrera M. Substance use and symptomatology among adolescent children of alcoholics. Journal of Abnormal Psychology. 1991;100:449–463. doi: 10.1037/0021-843X.100.4.449. [DOI] [PubMed] [Google Scholar]
- Ciesla JA, Cole DA, Steiger JH. Extending the trait-state-occasion model: How important is within-wave measurement equivalence? Structural Equation Modeling. 2007;14:77–97. [Google Scholar]
- Cole DA, Ciesla JA, Steiger JH. The insidious effects of failing to include design-driven correlated residuals in latent-variable covariance structure analysis. Psychological Methods. 2007;12:381–398. doi: 10.1037/1082-989X.12.4.381. [DOI] [PubMed] [Google Scholar]
- Cole DA, Martin NM, Steiger JH. Empirical and conceptual problems with longitudinal trait-state models: Introducing a trait-state-occasion model. Psychological Methods. 2005;10:3–20. doi: 10.1037/1082-989X.10.1.3. [DOI] [PubMed] [Google Scholar]
- Cole DA, Maxwell SE. Testing mediational models with longitudinal data: Questions and tips in the use of structural equation modeling. Journal of Abnormal Psychology. 2003;112:558–577. doi: 10.1037/0021-843X.112.4.558. [DOI] [PubMed] [Google Scholar]
- Conway JM, Lievens F, Scullen SE, Lance CE. Bias in the correlated uniqueness model for MTMM data. Structural Equation Modeling. 2004;11:535–559. [Google Scholar]
- Courvoisier DS. Unpublished doctoral dissertation. University of Geneva; Switzerland: 2006. Unfolding the constituents of psychological scores: Development and application of mixture and multitrait-multimethod LST models. [Google Scholar]
- Courvoisier DS, Eid M, Nussbeck FW. Mixture Distribution State-Trait-Models: Basic ideas and applications. Psychological Methods. 2007;12:80–104. doi: 10.1037/1082-989X.12.1.80. [DOI] [PubMed] [Google Scholar]
- Courvoisier DS, Nussbeck FW, Eid M, Geiser C, Cole DA. Analyzing the convergent validity of states and traits: Development and application of multimethod latent state-trait models. Psychological Assessment. 2008;20:270–280. doi: 10.1037/a0012812. [DOI] [PubMed] [Google Scholar]
- Cronbach LJ. Essentials of psychological testing. New York: Harper & Row; 1990. [Google Scholar]
- Deinzer R, Steyer R, Eid M, Notz P, Schwenkmezger P, Ostendorf F, Neubauer A. Situational effects in trait assessment: The FPI, NEOFFI and EPI questionnaires. European Journal of Personality. 1995;9:1–23. [Google Scholar]
- Dormann C, Fay D, Zapf D, Frese M. A state-trait analysis of job satisfaction: On the effect of core self-evaluations. Applied Psychology: An International Review. 2006;55:27–51. [Google Scholar]
- Dumenci L, Windle M. A multitrait-multioccasion generalization of the latent trait-state model: Description and application. Structural Equation Modeling. 1998;5:391–410. [Google Scholar]
- Eid M. Modelle der Messung von Personen in Situationen [Models for measuring persons in situations] Weinheim, Germany: Psychologie Verlags Union; 1995. [Google Scholar]
- Eid M. Longitudinal confirmatory factor analysis for polytomous item responses: Model definition and model selection on the basis of stochastic measurement theory. Methods of Psychological Research - online. 1996;1:65–85. [Google Scholar]
- Eid M. A multitrait-multimethod model with minimal assumptions. Psychometrika. 2000;65:241–261. [Google Scholar]
- Eid M. Latent class models for analyzing variability and change. In: Ong A, van Dulmen M, editors. Handbook of Methods in Positive Psychology. Oxford: Oxford University Press; 2007. pp. 591–607. [Google Scholar]
- Eid M, Diener E. Global judgments of subjective well-being: Situational variability and long-term stability. Social Indicators Research. 2004;65:245–277. [Google Scholar]
- Eid M, Diener E. Handbook of multimethod measurement in psychology. Washington, DC: American Psychological Association; 2006. [Google Scholar]
- Eid M, Hoffmann L. Measuring variability and change with an item response model for polytomous variables. Journal of Educational and Behavioral Statistics. 1998;23:193–215. [Google Scholar]
- Eid M, Langeheine R. Measuring consistency and occasion specificity with latent class models: A new model and its application to the measurement of affect. Psychological Methods. 1999;4:100–116. [Google Scholar]
- Eid M, Lischetzke T, Nussbeck FW, Trierweiler LI. Separating trait effects from trait-specific method effects in multitrait-multimethod models: A multiple indicator CT-C(M−1) model. Psychological Methods. 2003;8:38–60. doi: 10.1037/1082-989x.8.1.38. [DOI] [PubMed] [Google Scholar]
- Eid M, Notz P, Steyer R, Schwenkmezger P. Validating scales for the assessment of mood level and variability by latent state-trait analyses. Personality and Individual Differences. 1994;16:63–76. [Google Scholar]
- Eid M, Nussbeck FW, Geiser C, Cole DA, Gollwitzer M, Lischetzke T. Structural equation modeling of multitrait-multimethod data: Different models for different types of methods. Psychological Methods. 2008;13:230–253. doi: 10.1037/a0013219. [DOI] [PubMed] [Google Scholar]
- Eid M, Schneider C, Schwenkmezger P. Do you feel better or worse? The validity of perceived deviations of mood states from mood traits. European Journal of Personality. 1999;13:283–306. [Google Scholar]
- Fiske DW, Campbell DT. Citations do not solve problems. Psychological Bulletin. 1992;112:393–395. [Google Scholar]
- Geiser C, Eid M, Nussbeck FW. On the meaning of the latent variables in the CT-C(M−1) model: A comment on Maydeu-Olivares and Coffman (2006) Psychological Methods. 2008;13:49–57. doi: 10.1037/1082-989X.13.1.49. [DOI] [PubMed] [Google Scholar]
- Geiser C, Eid M, Nussbeck FW, Courvoisier DS, Cole DA. Analyzing true change in longitudinal multitrait-multimethod studies: Application of a multimethod change model to depression and anxiety in children. Developmental Psychology. 2010;46:29–45. doi: 10.1037/a0017888. [DOI] [PubMed] [Google Scholar]
- Geiser C, Eid M, West SG, Lischetzke T, Nussbeck FW. A comparison of method effects in two confirmatory factor models for structurally different methods. Structural Equation Modeling (in press) [Google Scholar]
- Hagemann D, Hewig J, Seifert J, Naumann E, Bartussek D. The latent state-trait structure of resting EEG asymmetry: Replication and extension. Psychophysiology. 2005;42:740–752. doi: 10.1111/j.1469-8986.2005.00367.x. [DOI] [PubMed] [Google Scholar]
- Hamaker EL, Nesselroade JR, Molenaar PCM. The integrated trait-state model. Journal of Research in Personality. 2007;41:295–315. [Google Scholar]
- Hertzog C, Nesselroade JR. Beyond autoregressive models: Some implications of the trait-state distinction for the structural modeling of developmental change. Child Development. 1987;58:93–109. [PubMed] [Google Scholar]
- Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling. 1999;6:1–55. [Google Scholar]
- Jöreskog KG. Statistical models and methods for analysis of longitudinal data. In: Jöreskog KG, Sörbom D, editors. Advances in factor analysis and structural equation models. Cambridge, MA: Abt; 1979a. pp. 129–169. [Google Scholar]
- Jöreskog KG. Statistical estimation of structural models in longitudinal-developmental investigations. In: Nesselroade JR, Baltes PB, editors. Longitudinal research in the study of behavior and development. New York: Academic Press; 1979b. pp. 303–351. [Google Scholar]
- Kenny DA. An empirical application of confirmatory factor analysis to the multitrait–multimethod matrix. Journal of Experimental Social Psychology. 1976;12:247–252. [Google Scholar]
- Kenny DA. Trait-state models for longitudinal data. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, D.C: American Psychological Association; 2001. pp. 243–263. [Google Scholar]
- Kenny DA, Kashy DA. The analysis of the multitrait-multimethod matrix by confirmatory factor analysis. Psychological Bulletin. 1992;112:165–172. [Google Scholar]
- Kenny DA, Zautra A. The trait-state-error model for multiwave data. Journal of Consulting and Clinical Psychology. 1995;63:52–59. doi: 10.1037//0022-006x.63.1.52. [DOI] [PubMed] [Google Scholar]
- King KM, Molina BSG, Chassin L. A state-trait model of negative life event occurence in adolescence: Predictors of stability in the occurrence of stressors. Journal of Clinical Child and Adolescent Psychology. 2008;37:848–859. doi: 10.1080/15374410802359643. [DOI] [PubMed] [Google Scholar]
- Kirschbaum C, Steyer R, Eid M, Patalla U, Schwenkmezger P, Hellhammer DH. Cortisol and behavior: 2. Application of a latent state-trait model to salivary cortisol. Psychoneuroendocrinology. 1990;15:297–307. doi: 10.1016/0306-4530(90)90080-s. [DOI] [PubMed] [Google Scholar]
- LaGrange B, Cole DA. An expansion of the trait-state-occasion model: Accounting for shared method variance. Structural Equation Modeling. 2008;15:241–271. [Google Scholar]
- Lance CE, Noble CL, Scullen SE. A critique of the correlated trait correlated method and correlated uniqueness models for multitrait–multimethod data. Psychological Methods. 2002;7:228–244. doi: 10.1037/1082-989x.7.2.228. [DOI] [PubMed] [Google Scholar]
- Marsh HW. Confirmatory factor analysis of multitrait-multimethod data: Many problems and a few solutions. Applied Psychological Measurement. 1989;13:335–361. [Google Scholar]
- Marsh HW, Bailey M. Confirmatory factor analysis of multitrait-multimethod data: A comparison of alternative models. Applied Psychological Measurement. 1991;15:47–70. [Google Scholar]
- Marsh HW, Grayson D. Longitudinal confirmatory factor analysis: Common, time-specific, item-specific, and residual-error components of variance. Structural equation modeling. 1994;1:116–145. [Google Scholar]
- Marsh HW, Grayson DA. Latent variable models of multitrait-multimethod data. In: Hoyle RH, editor. Structural equation modeling. Concepts, issues, and applications. Thousands Oaks, CA: Sage; 1995. pp. 177–198. [Google Scholar]
- Moe EL, Elliot DL, Goldberg L, Kuehl KS, Stevens VJ, Breger RKR, DeFrancesco CL, Ernst D, Duncan T, Dlacki K, Dolen S. Promoting Healthy Lifestyles: Alternative Models’ Effects (PHLAME) Health Education and Research. 2002;17:586–596. doi: 10.1093/her/17.5.586. [DOI] [PubMed] [Google Scholar]
- Moskowitz DS, Zuroff DC. Flux, pulse, and spin: Dynamic additions to the personality lexicon. Personality Processes and Individual Differences. 2004;86:880–893. doi: 10.1037/0022-3514.86.6.880. [DOI] [PubMed] [Google Scholar]
- Muthén LK, Muthén BO. Mplus User’s Guide. 4. Los Angeles, CA: Muthén & Muthén; 1998–2006. [Google Scholar]
- Ormel J, Schaufeli WB. Stability and change in psychological distress and their relationship with self-esteem and locus of control: A dynamic equilibrium model. Journal of Personality and Social Psychology. 1991;60:288–299. doi: 10.1037//0022-3514.60.2.288. [DOI] [PubMed] [Google Scholar]
- Pohl S, Steyer R. Modeling common traits and method effects in multitrait-multimethod analysis. Multivariate Behavioral Research. 2010;45:1–28. doi: 10.1080/00273170903504729. [DOI] [PubMed] [Google Scholar]
- Pohl S, Steyer R, Kraus K. Modelling method effects as individual causal effects. Journal of the Royal Statistical Society Series A. 2008;171:41–63. [Google Scholar]
- Podsakoff PM, MacKenzie SM, Lee J, Podsakoff NP. Common method variance in behavioral research: A critical review and suggested remedies. Journal of Applied Psychology. 2003;88:879–903. doi: 10.1037/0021-9010.88.5.879. [DOI] [PubMed] [Google Scholar]
- Raffalovich LE, Bohrnstedt GW. Common, specific, and error variance components of factor models: Estimation with longitudinal data. Sociological Methods & Research. 1987;15:385–405. [Google Scholar]
- Schermelleh-Engel K, Keith N, Moosbrugger H, Hodapp V. Decomposing person and occasion-specific effects: An extension of latent state-trait theory to hierarchical LST models. Psychological Methods. 2004;9:198–219. doi: 10.1037/1082-989X.9.2.198. [DOI] [PubMed] [Google Scholar]
- Schmitt M. Conceptual, theoretical, and historical foundations of multimethod assessment. In: Eid M, Diener E, editors. Handbook of multimethod measurement in psychology. Washington, DC: APA; 2006. pp. 9–25. [Google Scholar]
- Schmitt M, Gollwitzer M, Maes J, Arbach D. Justice Sensitivity: Assessment and location in the personality space. European Journal of Psychological Assessment. 2005;21:202–211. [Google Scholar]
- Schmukle SC, Egloff B. A latent state-trait analysis of implicit and explicit personality measures. European Journal of Psychological Assessment. 2005;21:100–107. [Google Scholar]
- Sörbom D. Detection of correlated errors in longitudinal data. British Journal of Mathematical and Statistical Psychology. 1975;28:138–151. [Google Scholar]
- Steyer R. Unpublished habilitation thesis. University of Trier; Trier, Germany: 1988. Experiment, Regression und Kausalität. Die logische Struktur kausaler Regressionsmodelle [Experiment, regression, and causality. The logical structure of causal regression models] [Google Scholar]
- Steyer R. Models of classical psychometric test theory as stochastic measurement models: Representation, uniqueness, meaningfulness, identifiability, and testability. Methodika. 1989;3:25–60. [Google Scholar]
- Steyer R, Ferring D, Schmitt MJ. States and traits in psychological assessment. European Journal of Psychological Assessment. 1992;8:79–98. [Google Scholar]
- Steyer R, Majcen AM, Schwenkmezger P, Buchner A. A latent state-trait anxiety model and its application to determine consistency and specificity coefficients. Anxiety Research. 1989;1:281–299. [Google Scholar]
- Steyer R, Schmitt M. The effects of aggregation across and within occasions on consistency, specificity, and reliability. Methodika. 1990;4:58–94. [Google Scholar]
- Steyer R, Schmitt T. The theory of confounding and its application in causal modeling with latent variables. In: von Eye A, Clogg CC, editors. Latent variables analysis. Applications for developmental research. Newbury Park, CA: Sage; 1994. pp. 36–67. [Google Scholar]
- Steyer R, Schmitt M, Eid M. Latent state-trait theory and research in personality and individual differences. European Journal of Personality. 1999;13:389–408. [Google Scholar]
- Steyer R, Schwenkmezger P, Auer A. The emotional and cognitive components of trait anxiety: A latent state-trait model. Personality and Individual Differences. 1990;11:125–134. [Google Scholar]
- Suppes P, Zinnes JL. Basic measurement theory. In: Luce RD, Bush RR, Galanter E, editors. Handbook of mathematical psychology. New York: Wiley; 1963. [Google Scholar]
- Tisak J, Tisak MS. Permanency and ephemerality of psychological measures with application to organizational commitment. Psychological Methods. 2000;5:175–198. doi: 10.1037/1082-989x.5.2.175. [DOI] [PubMed] [Google Scholar]
- Vautier S. A longitudinal SEM approach to STAI data: Two comprehensive multitrait-multistate models. Journal of Personality Assessment. 2004;83:167–179. doi: 10.1207/s15327752jpa8302_11. [DOI] [PubMed] [Google Scholar]
- Ware J, Snow K, Kosinski M, Gandek B. Manual and interpretation guide. Boston: The Health Institute, New England Medical Center; 1993. SF-36 health survey. [Google Scholar]
- Widaman KF. Hierarchically nested covariance structure models for multitrait-multimethod data. Applied Psychological Measurement. 1985;9:1–26. [Google Scholar]
- Windle M, Dumenci L. An investigation of maternal and adolescent depressed mood using a latent trait-state model. Journal of Research on Adolescence. 1998;8:461–484. [Google Scholar]
- Yasuda T, Lawrenz C, Van Whitlock R, Lubin B, Lei PW. Assessment of intraindividual variability in positive and negative affect using latent state-trait model analyses. Educational and Psychological Measurement. 2004;64:514–530. [Google Scholar]
- Zimmerman DW. Probability spaces, Hilbert spaces, and the axioms of test theory. Psychometrika. 1975;40:395–41. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.