Self-Complementarity within Proteins: Bridging the Gap between Binding and Folding

Abstract

Complementarity, in terms of both shape and electrostatic potential, has been quantitatively estimated at protein-protein interfaces and used extensively to predict the specific geometry of association between interacting proteins. In this work, we attempted to place both binding and folding on a common conceptual platform based on complementarity. To that end, we estimated (for the first time to our knowledge) electrostatic complementarity (E_m) for residues buried within proteins. E_m measures the correlation of surface electrostatic potential at protein interiors. The results show fairly uniform and significant values for all amino acids. Interestingly, hydrophobic side chains also attain appreciable complementarity primarily due to the trajectory of the main chain. Previous work from our laboratory characterized the surface (or shape) complementarity (S_m) of interior residues, and both of these measures have now been combined to derive two scoring functions to identify the native fold amid a set of decoys. These scoring functions are somewhat similar to functions that discriminate among multiple solutions in a protein-protein docking exercise. The performances of both of these functions on state-of-the-art databases were comparable if not better than most currently available scoring functions. Thus, analogously to interfacial residues of protein chains associated (docked) with specific geometry, amino acids found in the native interior have to satisfy fairly stringent constraints in terms of both S_m and E_m. The functions were also found to be useful for correctly identifying the same fold for two sequences with low sequence identity. Finally, inspired by the Ramachandran plot, we developed a plot of S_m versus E_m (referred to as the complementarity plot) that identifies residues with suboptimal packing and electrostatics which appear to be correlated to coordinate errors.

Introduction

All forms of biomolecular recognition are said to involve interaction between complementary molecular surfaces. This specific match between two interacting surfaces is primarily supposed to have a dual aspect: 1) surface (or shape) complementarity (1) arising out of the steric fit of closely packed interface atoms in van der Waals contact; and 2), electrostatic complementarity (2) mediated by long-range electric fields due to charged or partially charged atoms. For small-molecule ligands or cofactors binding to proteins, the above point of view appears to be only partially true. Not only can one ligand adopt a wide range of conformations upon binding to different proteins, the binding pocket also exhibits more variability in shape and physicochemical characteristics than can be accounted for by the multiple conformations adopted by the ligand (3–5). For protein-protein interfaces, however, the concept appears to have greater plausibility and wider appeal. Due to the relatively larger size of protein-protein interfaces (∼1600 Å² on average) (6), the surfaces have to be carefully tailored so that extended areas buried upon association can move into close contact. A variety of shape correlation and electrostatic complementarity measures incorporated into docking algorithms have been shown to be effective in predicting the interfaces between interacting proteins (7,8). Electrostatic complementarity based on optimized charge distribution has also been used to match two halves of the same molecule (myoglobin) from a repertoire of homologous structures (9). On the other hand, surface complementarity has found application in determining native side-chain torsions within proteins (10,11) and has also served to rationalize the variability in the quaternary arrangements of legume lectins (12). Lawrence and Colman (1) and McCoy et al. (2) formulated and estimated shape correlation (S_c) and electrostatic complementarity (EC) measures for a wide range of proteins in quaternary association, protein-inhibitor, and antigen-antibody complexes. It thus appears reasonable that threshold values of geometric and electrostatic complementarities will have to be satisfied for the stereospecific association between two polypeptide chains. Within proteins, surface complementarity (S_m) has been used to enumerate specific modes of packing between amino acid side chains (13) and, somewhat analogously to protein interfaces, all residues upon burial achieve uniformly high measures of surface fit (14).

Although the notion of complementarity lends itself naturally to the characterization of interprotein association, it has been suggested that both binding and folding should be approached from a common conceptual platform (15,16). The native conformation adopted by the polypeptide chain leads to the stereospecific packing of its buried side chains and optimal electrostatic interactions due to the strategic three-dimensional placement of charges. Thus, folding can possibly be described as the self-recognition of the polypeptide chain as it collapses onto itself. However, one inherent problem in equating binding with folding lies in the different characteristics of protein interiors compared with interfaces. Barring dimers, interfaces resemble protein surfaces rather than interiors, both in their composition and in the spatial distribution of amino acid residues (17). Unlike hydrophobic clusters found within proteins, nonpolar residues are found in isolation at protein-protein interfaces, surrounded by polar or charged amino acids. However, despite these differences, the fact remains that both interfacial (1) and interior atoms (13,14) have to satisfy fairly stringent packing requirements, and, at least for the interfaces, significant values of electrostatic complementarity have been found (2,8). To explore the similarities or equivalence between binding and folding (in terms of complementarity), we first estimated the electrostatic complementarity (E_m) of residues buried within proteins from a representative database of crystal structures. Second, in similarity to protein-protein docking (7), we used scoring functions based on S_m and E_m for protein fold recognition, validated in state-of-the-art databases. Lastly, to detect local regions of suboptimal packing and/or electrostatics in a native fold, we developed a plot based on S_m and E_m (in analogy to the famous Ramachandran plot (18)) to identify such residues, which appear to be correlated to coordinate errors.

Materials and Methods

Two representative databases of high-resolution protein crystal structures (resolution ≤ 2.0 Å, R-factor ≤ 20%, sequence identity ≤ 30%) were used in the calculations. The first database (DB1), consisting of 719 polypeptide chains, is described in detail elsewhere (13). This database was used in the computation of all relevant statistics involving S_m. We assembled a subset of this larger database consisting of 400 polypeptide chains (DB2) by removing proteins with deeply embedded prosthetic groups (e.g., cytochromes) and any missing atoms (data set S1 in the Supporting Material). DB2 (composed of 65 all α, 70 all β, 106 α|β, 124 α+β, and 35 multidomain proteins) was used in the calculation of E_m of amino acid residues and their related statistics. Sixty-two of these proteins were found to contain metal ions as an integral part of their structure. Hydrogen atoms were geometrically fixed to all structures by means of the program REDUCE (19).

Before calculating the electrostatic potential, we assigned partial charges and atomic radii for all protein atoms from the AMBER94 all-atom molecular-mechanics force field (20). Asp, Glu, Lys, Arg, doubly-protonated histidine (Hip), and both the carboxy and amino terminal groups were considered to be ionized. Crystallographic water molecules and surface-bound ligands were excluded from the calculations and thus modeled as bulk solvent. Ionic radii were assigned to the bound metal ions according to their charges (21).

The van der Waals surfaces of the polypeptide chains were sampled at 10 dots/Ų. The details of the surface generation were discussed in a previous report (14). We estimated the exposure of individual atoms to solvent by rolling a probe sphere of radius 1.4 Å over the protein atoms (22), and estimated the burial (Bur) of individual residues by the ratio of solvent-accessible surface areas of the amino acid X in the polypeptide chain to that of an identical residue located in a Gly-X-Gly peptide fragment with a fully extended conformation.

The finite-difference Poisson-Boltzmann method as implemented in Delphi (version 4) (23,24) was used to compute the electrostatic potential of the molecular surface along the polypeptide chain. The protein interior was considered to be a low dielectric medium (dielectric constant of 2) and the surrounding solvent was considered a high dielectric medium (dielectric constant of 80). Ionic strength was set to zero because adoption of physiological strength has been found to have little effect on the final electrostatic solution (25,26), and calculations were performed at 298 K. The dielectric boundary and the partial charges were mapped onto a cubic grid either 151× 151 × 151 or 201 × 201 × 201 grid points/side in size (the latter for proteins that exhibited pronounced asymmetry in their physical dimensions). The percentage grid fill was set to 80% with a scale of 1.2 grid points/Å. Boundary potentials were approximated by the Debye-Hückel potential of the dipole equivalent to the molecular charge distribution. A probe radius of 1.4 Å was used to delineate the dielectric boundary. The linearized Poisson-Boltzmann equation (LPBE) was then solved iteratively until convergence. The number of cycles to convergence was automatically determined by the program (with the convergence threshold based on the maximum change in potential set to 0.0001 kT/e), and was monitored by examining a plot of convergence in the output log file.

Delphi requires a set of surface points on which the electrostatic potentials are to be computed along with a set of atoms that contribute to the potential. After generating the van der Waals surface of the entire polypeptide chain, we identified the dot surface points of the individual amino acids (targets) and fed them to the program along with the selected set of (charged) atoms. The electrostatic potential for each residue surface was then calculated twice: first, due to the atoms of the particular target residue, and second, from the rest of the protein excluding the selected amino acid. In either case, atoms that did not contribute to the potential (dummy atoms) were only assigned their radii with zero charge, to maintain the scaling and orientation of the molecule on the grid. Thus, each dot surface point of the (selected) residue was tagged with two values of electrostatic potential. Adapted from the function EC originally proposed by McCoy et al. (2) (for protein-protein interfaces), the E_m of an amino acid residue (within protein) was then defined as the negative of the correlation coefficient (Pearson's) between these two sets of potential values:

$$E_m=-\left(\frac{\sum _{i=1}^N\left(\phi \left(i\right)-\overline{\phi }\right)\left({\phi }^{\prime }\left(i\right)-{\overline{\phi }}^{\prime }\right)}{{\left(\sum _{i=1}^N{\left(\phi \left(i\right)-\overline{\phi }\right)}^2\sum _{i=1}^N{\left({\phi }^{\prime }\left(i\right)-{\overline{\phi }}^{\prime }\right)}^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right),$$ (1)

where for a given residue consisting of a total of N dot surface points, $\phi \left(i\right)$ is the potential on its i^th point realized due to its own atoms and ${\phi }^{\prime }\left(i\right)$, due to the rest of the protein atoms, and $\overline{\phi }$ and ${\overline{\phi }}^{\prime }$ are the mean potentials of $\phi \left(i\right)$, i = 1…N and ${\phi }^{\prime }\left(i\right)$, i = 1…N respectively.

After calculating the electrostatic potentials, we divided the values corresponding to N dot surface points into two distinct sets based on whether the dot point was obtained from main-chain or side-chain atoms of the target residue, and calculated E_m separately for each set. Thus for a given residue, E_m was estimated for the entire residue ($E_m^{all}$, as described above), the side-chain surface points $\left(E_m^{sc}\right)$, and the main-chain surface points $\left(E_m^{mc}\right)$.

The calculation of S_m has been discussed extensively in previous studies (13,14). Briefly, S_m can be calculated between the side-chain surface points of a target residue and all other dot points in its immediate neighborhood (within a distance of 3.5 Å), contributed by the rest of the protein. Any dot surface point (which is essentially an area element) is characterized by its coordinates (x, y, z) and the direction cosines of its normal (dl, dm, dn). S_m is then defined (following Lawrence and Colman (1)) to be the median of the distribution {S(a,b)}, S(a,b), calculated by the following equation:

$$S\left(a,b\right)={\mathbf{n}}_a·{\mathbf{n}}_b.\exp \left(-w.d_{ab}^2\right),$$ (2)

where ${\mathbf{n}}_a$ and ${\mathbf{n}}_b$ are two unit normal vectors corresponding to the dot surface point a (located on the side-chain surface of the target residue) and b (the dot point nearest to a, within 3.5 Å), respectively, with d_ab the distance between them and w, a scaling constant set to 0.5. After identifying nearest neighbors, we could also partition the side-chain surface points of the specified residue into two sets by virtue of their neighbors coming from either side-chain or main-chain atoms, and calculate S_m separately for each set. Thus, every target residue (side chain) has three measures of S_m based on the choice of its nearest neighbors (surface points), whether obtained from side-chain $\left(S_m^{sc}\right)$, main-chain $\left(S_m^{mc}\right)$ atoms alone, or all atoms $\left(S_m^{all}\right)$. Because glycines lack any nonhydrogen side-chain atom, they were excluded as targets from all calculations.

Two scoring functions (based on the amino acid identity (Res), burial (Bur), $E_m^{sc}$, and $S_m^{sc}$) were formulated to identify the native fold amid a set of decoys. Only residues that were completely (0.00 ≤ Bur ≤ 0.05) or partially (0.05 < Bur ≤ 0.3) buried were considered. Initially, the average and standard deviation (SD) for both $S_m^{sc}$ ($\overline{S_m^{sc}}$, ${\sigma }_S$) and $E_m^{sc}$ ($\overline{E_m^{sc}}$, ${\sigma }_E$) were estimated (over their respective databases, DB1 and DB2) separately for different amino acid residues (Ala, Val, etc.) distributed into three bins based on their burial (bin 1: 0.0 ≤ Bur ≤ 0.05; bin 2: 0.05 < Bur ≤ 0.15; bin 3: 0.15 < Bur ≤ 0.30). The center (mode:$E_0^{sc}$) and the halfwidth at half-maximum height (${\gamma }_E$) were also computed for individual residues (in different burial bins) from the normalized frequency distributions in $E_m^{sc}$ by numerical curve fitting. For the first measure, we computed $S_m^{sc}\left(i\right)$, $E_m^{sc}\left(i\right)$ for all buried residues (i = 1….N; Bur ≤ 0.30) of a given polypeptide chain, and calculated the following expression:

$$C{S}_{gl}=\frac{1}{N}\sum _{i=1,Bur\le 0.3}^N\left(\frac{1}{\sqrt{2\pi }{\sigma }_S}\exp \left(-\frac{1}{2}{\left(\frac{S_m^{sc}\left(i\right)-\overline{S_m^{sc}}}{{\sigma }_S}\right)}^2\right)\right)\left(\frac{1}{\pi }\left(\frac{{\gamma }_E}{{\left(E_m^{sc}\left(i\right)-E_0^{sc}\right)}^2+{\gamma }_E^2}\right)\right)=\frac{1}{N}\sum _{i=1,Bur\le 0.3}^N\text{Gaussian}\left(S_m^{sc}\left(i\right)\right)·\text{Lorentzian}\left(E_m^{sc}\left(i\right)\right)$$ (3)

The second scoring function was based on the conditional probability distributions of $E_m^{sc}$ and $S_m^{sc}$ for each residue type within a particular burial bin. As in the previous case, three burial bins were considered. Distributions of $E_m^{sc}$ and $S_m^{sc}$ for a given residue type in a particular burial bin were then divided into intervals of 0.05. The conditional probability distributions of $E_m^{sc}$ and $S_m^{sc}$ were then defined as

$$P\left(C_m^{sc}\left(i\right)|\left\{\text{Res}\left(\text{i}\right),Bur\left(i\right)\right\}\right)=\frac{N\left(C_m^{sc}\left(i\right)\cap \text{Res}\left(\text{i}\right)\cap Bur\left(i\right)\right)}{N\left(\text{Res}\left(\text{i}\right)\cap Bur\left(i\right)\right)}.$$ (4)

for the i^th residue along the polypeptide chain, where $C_m^{sc}$ stands for either $E_m^{sc}$ or $S_m^{sc}$, and N denotes the count of residues in the specified sets.

Thus, for example,

$$P\left(S_m^{sc}:0.45-0.5|\left\{Valine,Bur:0.0-0.05\right\}\right)=\frac{N\left(Valine\cap \left(0.0\le Bur\le 0.05\right)\cap \left(0.45<S_m^{sc}\le 0.5\right)\right)}{N\left(Valine\cap \left(0.0\le Bur\le 0.05\right)\right)}.$$

For any given polypeptide chain, the products of the conditional probabilities in $S_m^{sc}$ and $E_m^{sc}$ for each (i^th) residue (i = 1…N, Bur ≤ 0.30) were then summed and divided by the total number of buried residues (N), giving rise to the following measure:

$$C{S}_{cp}=\frac{1}{N}\sum _{i=1,Bur\le 0.3}^N(P\left(S_m^{sc}\left(i\right)|\left\{\text{Res}\left(i\right),\text{Bur}\left(\text{i}\right)\right\}\right))(P\left(E_m^{sc}\left(i\right)|\left\{\text{Res}\left(i\right),\text{Bur}\left(\text{i}\right)\right\}\right))$$ (5)

Z-scores corresponding to the native structure (along with its rank) for the complementarity scores (CS_gl, CS_cp) were calculated in a multiple decoy set by the following equation:

$$Z_{CS}=\frac{C{S}_{native}-\overline{CS}}{\sigma },$$ (6)

where $C{S}_{native}$ is the score obtained for the parameter CS_gl or CS_cp from the native structure, and $\overline{CS}$ and σ are the mean and SD for the scores in the decoy set. Average $Z_{CS}$ (〈Z〉) was calculated for the successful hits (native at rank 1) in a decoy set.

Results

E_m within proteins

The electrostatic potential within proteins was computed by means of the LPBE as implemented in Delphi (23,24), and estimation of E_m was adapted (see Eq. 1) from a method proposed by McCoy et al. (2) for protein-protein interfaces. Nonlinear PBE at nonzero ionic strengths is preferred for highly charged molecules such as DNA (24), microtubules, and ribosomal subunits (27). Globular proteins, however, have appreciably low net charge densities, and LPBE has been used extensively to compute electrostatic potentials at protein-protein interfaces and solvent-exposed residue surfaces (25,28,29). Electrostatic potentials estimated by nonlinear PBE (in a trial calculation involving 150 polypeptide chains) under physiological counterionic strength (0.15 M NaCl, ion exclusion radii: 2.0 Å) were virtually identical to those calculated by LBPE (Fig. S1).

E_m was estimated for all residues at the protein interior (burial ≤ 0.30; see Materials and Methods) from a database of 400 polypeptide chains (DB2). To test the sensitivity of E_m with respect to the internal dielectric of the continuum (ε_p), we repeated all calculations three times, setting ε_p to 2, 4, and 10, respectively. The root mean-square deviations (RMSDs) among these three sets of E_m values for different residues were negligible, indicating the invariance of E_m at least in the commonly used ranges of ε_p (Fig. S2). Identical calculations performed with higher internal dielectric (ε_p = 20 and 40) also preserved the overall trends in the results (Table S1). It should be noted that E_m estimates the correlation between potentials generated by the two sets of atoms (over a collection of surface points) regardless of their magnitude.

Before the statistical analysis was performed, all completely/partially buried (target) residues were distributed in three burial bins (burial: 0.0–0.05, 0.05–0.15, 0.15–0.30; see Materials and Methods). Enumeration of the average E_m values in each burial bin for different amino acids (targets), calculated over the entire residue surface $\left(\overline{E_m^{all}}\right)$, revealed a fairly uniform distribution among the different residues, within the range of ∼0.5–0.7 (Table 1). The high positive values of $E_m^{all}$ throughout the protein interior suggest that individual residues buried within proteins have anticorrelated (complementary) surface electrostatic potentials (Fig. S3) similar to those of protein-protein interfaces (2). In fact, $\overline{E_m^{all}}$ values for hydrophobic residues were comparable to those for polar and charged amino acids. From these observations, we thought that the main-chain surface points could be contributing predominantly to $E_m^{all}$, especially for hydrophobic residues. To test this hypothesis, we segregated the surface points by virtue of their residence on main-chain/side-chain atoms, and calculated E_m separately for each set, i.e., $E_m^{sc}$ and $E_m^{mc}$ for side- and main-chain surface points, respectively. As expected, $\overline{E_m^{mc}}$ values were again uniform for all the amino acids and comparable in magnitude to $\overline{E_m^{all}}$. Interestingly, even for hydrophobic residues, $\overline{E_m^{sc}}$ was also found to exhibit fairly significant values. However, differences were observed in $\overline{E_m^{sc}}$ between hydrophobic (Val: 0.48, Leu: 0.46, Ile: 0.48, Phe: 0.41) and charged/polar (Asn: 0.67, Gln: 0.64, Asp: 0.61, Glu: 0.63, Lys: 0.62, Arg: 0.56) residues, albeit within 1 SD (∼0.1–0.25; Table 1). Somewhat reduced values were obtained for sulfur-containing amino acids (Cys: 0.34, Met: 0.32) and proline (0.34). A similar pattern was observed in all three burial bins, indicating that within the protein interior, the distribution in E_m appears to be independent of the exposure of a residue to solvent.

Table 1.

Native electrostatic complementarities of completely buried residues

Residue	$\overline{E_m^{all}}$	$\overline{E_m^{sc}}$	$\overline{E_m^{mc}}$
ALA	0.68 (0.17)	0.48 (0.25)	0.72 (0.17)
VAL	0.62 (0.16)	0.48 (0.18)	0.72 (0.16)
LEU	0.61 (0.16)	0.46 (0.19)	0.73 (0.16)
ILE	0.61 (0.16)	0.48 (0.17)	0.72 (0.16)
PHE	0.56 (0.15)	0.41 (0.16)	0.70 (0.17)
TYR	0.58 (0.15)	0.50 (0.19)	0.69 (0.18)
TRP	0.57 (0.15)	0.50 (0.17)	0.68 (0.20)
SER	0.64 (0.18)	0.59 (0.27)	0.67 (0.18)
THR	0.62 (0.16)	0.55 (0.23)	0.68 (0.18)
CYS	0.51 (0.18)	0.34 (0.22)	0.66 (0.21)
MET	0.45 (0.13)	0.32 (0.16)	0.72 (0.16)
ASP	0.63 (0.22)	0.61 (0.26)	0.62 (0.17)
GLU	0.64 (0.25)	0.63 (0.28)	0.66 (0.19)
ASN	0.68 (0.17)	0.67 (0.22)	0.68 (0.17)
GLN	0.66 (0.17)	0.64 (0.21)	0.70 (0.18)
LYS	0.72 (0.17)	0.62 (0.22)	0.75 (0.15)
ARG	0.68 (0.16)	0.56 (0.19)	0.75 (0.15)
PRO	0.53 (0.20)	0.34 (0.23)	0.65 (0.19)
HIS	0.54 (0.26)	0.50 (0.28)	0.65 (0.21)

Average E_m values and their SDs (in parentheses) for different residues in the first burial bin (0.0 ≤ Bur ≤ 0.05) were calculated from all atoms on the entire residue surface $\left(\overline{E_m^{all}}\right)$, the side-chain surface $\left(\overline{E_m^{sc}}\right)$, and the main-chain surface $\left(\overline{E_m^{mc}}\right)$.

To assess the relative contribution of side- or main-chain atoms to E_m, we performed four more sets of calculations based on the choice of residue surface (target: side chain/main chain) on which to calculate the electrostatic potentials and the atoms (side chain/main chain) contributing to the potential:

• Set 1: Main-chain surface, main-chain atoms.

• Set 2: Side-chain surface, main-chain atoms.

• Set 3: Side-chain surface, side-chain atoms.

• Set 4: Side-chain surface, side-chain atoms of the target, and all atoms from the rest of the polypeptide chain.

Except for the choice of surfaces and atoms, the method used to calculate E_m was identical to that outlined above. As expected, set 1 gave a uniform distribution in $\overline{E_m}$ with elevated values for all residues (Table S2). For set 2, fairly significant values of $\overline{E_m}$ were still retained for hydrophobic residues (Ala: 0.43, Val: 0.44, Leu: 0.42, Ile: 0.43, Phe: 0.36, Met: 0.38), which is a reflection of the long-range electric fields generated by the main-chain atoms overwhelmingly contributing to the complementarity attained on hydrophobic side-chain surfaces. This was confirmed by the comparison of $\overline{E_m}$ in set 2 and $\overline{E_m^{sc}}$: both sets of values were almost identical for hydrophobic residues (Table 1 and Table S2), whereas polar/charged residues exhibited a marked reduction in set 2 compared with $\overline{E_m^{sc}}$, because the contribution of side-chain atoms carrying high partial charges was disregarded in set 2. For both set 3 and set 4, $\overline{E_m}$ for hydrophobic residues were practically negligible (Table S2); however, polar/charged residues gave consistently high values for set 4 but were distinctly reduced for set 3. The substantial increase in $\overline{E_m}$ for set 4 relative to set 3 (except for alanine) was indicative of the considerable role played by the main-chain atoms (contributed by the rest of the polypeptide chain) in the overall determination of $\overline{E_m}$. This holds true even for hydrophilic amino acids, where the main-chain atoms contribute appreciably to the neutralization of the electric fields generated by polar/charged side-chain atoms.

It is thus evident that the long-range electric fields generated by main-chain atoms cast their shadow over the side-chain surface in such a manner that all residues, regardless of their hydrophobicity and burial, attain a fairly uniform level of overall complementarity. Polar/charged (side-chain) atoms of hydrophilic residues additionally contribute to the elevated complementarity attained on their side-chain surfaces.

Application of S_m and E_m in fold recognition and structure validation

The second part of the work has to do with the application of S_m and E_m in the area of protein fold recognition and structure validation. Two such scoring functions were designed based on the combined use of the complementarity measures obtained for different residues distributed in the aforementioned burial bins.

Plots of the normalized frequency distributions in $S_m^{sc}$, $E_m^{sc}$ for the individual residues in each burial bin (i.e., $P\left(S_m^{sc}|\left\{\text{Res},\text{Bur}\right\}\right)$, $P\left(E_m^{sc}|\left\{\text{Res},\text{Bur}\right\}\right)$) gave characteristic curves (symmetric for $S_m^{sc}$ and negatively skewed for $E_m^{sc}$), which fitted best to Gaussian and Lorentzian functions for $S_m^{sc}$ and $E_m^{sc}$, respectively (goodness of fit, R² ≥ 0.85 for all cases; Fig. 1). From these observations, the first scoring function (CS_gl) was designed based on Gaussian for $S_m^{sc}$ and Lorentzian for $E_m^{sc}$ (see Eq. 3.). The second function (CS_cp) directly multiplies the conditional probabilities $P\left(S_m^{sc}|\left\{\text{Res},\text{Bur}\right\}\right)$ and $P\left(E_m^{sc}|\left\{\text{Res},\text{Bur}\right\}\right)$ for each residue along the polypeptide chain to obtain the joint probability of their co-occurrence. These individual probabilities were averaged over all buried residues (Bur ≤ 0.3) in the polypeptide chain to give the final score (see Eq. 5.). The conditional probabilities were estimated previously (see Materials and Methods).

Figure 1.

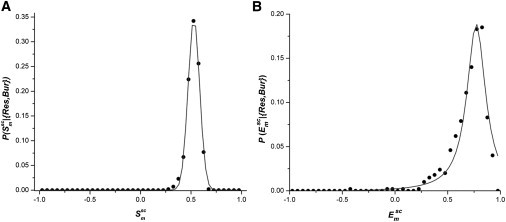
Normalized frequency distributions of $S_m^{sc}$ and $E_m^{sc}$ give characteristic curves that fit best to Gaussian and Lorentzian functions, respectively. These normalized frequencies for a given burial bin (Bur) and residue type (Res) can also be interpreted as conditional probabilities $P\left(S_m^{sc}|\left\{\text{Res},\text{Bur}\right\}\right)$ and $P\left(E_m^{sc}|\left\{\text{Res},\text{Bur}\right\}\right)$. (A) Distribution in $S_m^{sc}$ for leucine (0.0 ≤ Bur ≤ 0.05) fitted to a Gaussian function (R² = 0.997). (B) Distribution in $E_m^{sc}$ for asparagine (same burial) fitted to a Lorentzian function (R² = 0.948). Similar curves were obtained for all completely/partially buried amino acids for all three burial bins.

It is to be noted that both CS_gl and CS_cp are averages of individual scores given by all the completely/partially buried residues in a protein and thus are independent of the polypeptide chain length. Thus, for any given native structure, one would expect their values to cluster around optimal numbers characteristic of native folds. The distributions of CS_gl and CS_cp computed for the native folds (in DB2) had a very good linear correlation between each other (R² = 0.94; Fig. S4) and gave mean values of 3.7 (± 0.437) and 0.015 (± 0.0017), respectively. Thus for the native folds, these functions exhibit a reduced scatter about the mean, whereas for decoys, reduced scores for both functions are to be expected. The decoy sets used to benchmark and validate the scoring functions included both single and multiple decoys, with Z-scores calculated for the latter (see Eq. 6.). Because both of the knowledge-based scoring functions were parameterized on crystal structures alone, NMR structures were excluded in their validation.

Identification of the native crystal structure from decoys

One of the single decoy sets tested, Misfold (30), consists of 26 pairs of structures. In each pair, the native sequence is threaded onto an unrelated fold to generate the decoy. Twenty-five pairs were considered in the calculation (with the exception of 1CBH, which is an NMR structure). The Pdberr decoy set (31) consists of three correctly solved x-ray crystal structures along with their erroneous decoy counterparts, whereas sgpa (32) contains the experimental structure of Streptomyces griseus Protease A (2SGA) and its two corresponding decoys, generated by molecular-dynamics simulations. For the three data sets, both functions successfully identified the native structure from the corresponding decoys for all cases (Table S3). A comparison with other knowledge-based scoring functions (Table S4) shows that the performance of the complementarity scores in single decoy sets is as efficient as or better than the other functions.

The four-state reduced decoy set (33) consists of seven sequences (chain length ranging from 54–75 residues), each with nearly 600–700 decoys that include structures with RMSD (C^α atoms) ranging from 0.8 to 9.4 Å from the native. Out of the seven sequences, six native structures were correctly identified (rank 1) by CS_gl and CS_cp with significant Z-scores (Table S5 A). In the case of 4RXN (all-β class), the native structure was found to be at ranks 10 and 15, respectively, for CS_gl and CS_cp. Further investigation revealed that 4RXN has negligible side-chain packing between its secondary structural elements. The decoy set, Fisa (34), contains four small (43–76 residues) all-α proteins, with 500 decoys for each set. Major failures were encountered for this decoy set, where both CS_gl and CS_cp were successful in detecting the native at the top rank in two out of the four proteins (Table S5 B). 1HDD-C was detected at ranks 4 (CS_gl) and 5 (CS_cp); however, for 1FC2, both of the functions failed entirely, leading to insignificant or negative Z-scores. This was due to minimal packing between the helices for these low-resolution structures (2.8 Å). It is notable (Table S6) that for 1HDD-C, 1FC2, and 4RXN, failure is quite common even for the other functions.

Hg_structal is a decoy set composed of 29 globins (35). Each globin was built by comparative modeling using 29 other globins as templates, with C^α RMSDs ranging from 1.96 to 8.57 Å. Thus, for each native globin chain there are 29 decoys. In 23 out of 29 globins, both CS_gl and CS_cp were able to correctly detect the native at the top rank (〈Z〉: 3.23 and 3.24, respectively; Table S7 A). For similar decoy sets, ig_structal CS_gl and CS_cp were successful in 48 and 50 cases (〈Z〉: 3.89, 3.91) out of 61 immunoglobulins, whereas for ig_structal_hires (subset of 20 high-resolution structures), 100% success was achieved for both (Table S7, B and C).

The ROSETTA all-atom decoy sets are built for small, single-domain proteins by the fragment insertion-simulated annealing strategy. The latest ROSETTA decoy set (36) contains >75,000 decoys for 41 proteins (25 of which are x-ray structures, and with the number of decoys in each set ranging from 1610 to 1934), sampling a wide variety of topological folds and polypeptide chain lengths ranging from 35 to 85 amino acids. CS_gl, CS_cp were able to rank the native in 23 and 24 instances, respectively (out of 25). The high average Z-scores (7.24 and 6.98) also demonstrate the discriminatory ability of both scoring functions (Table S8). The only major failure was encountered for 1CC5 (detected at ranks 36 and 58), which is a cytochrome C molecule with an embedded Fe⁺²-containing protoporphyrin IX ring. Because only protein atoms were considered, a false picture of interior atomic packing was available to the scoring functions.

CASP9 (37) is probably the most challenging test, because the decoys are the best-predicted near-native models submitted by different groups that participated in the CASP experiment. CASP9 (conducted in July–August, 2010) consisted of 111 valid targets with 90 x-ray crystal structures. T0543 (2XRQ) and T0605 (3NMD) were not considered in the calculation, the former because of its excessively huge chain length (887 residues) and the latter because it is a single standalone helix. For the remaining 88 targets (with a total of 9197 models, chain length ranging from 83 to 611 residues) CS_gl and CS_cp detected the native at the top rank in 70, 72 and 85, 86 within rank 5 (<Z>: 3.65, 3.95), respectively (Table S9).

Discrimination between good and bad RMSD models

To test the sensitivity of the functions with respect to deviations from the experimentally determined coordinates of the side-chain atoms, we selected 10 native (top ranked) targets from CASP9 along with their corresponding models. After superposing the models onto the native structure by Dali server (38), we calculated the RMSD of the side-chain atoms at a one-to-one atomic correspondence with respect to the native. Local deviations (in C^α) > 10 Å were considered to be so large as to lose all structural relationship with the corresponding region of the native, as well as models that were nonsuperposable (by Dali), and these were thus not included in the calculation. CS_gl and CS_cp of the native structure and ∼60 models per target were then plotted (Fig. 2 and Fig. S5) as a function of their RMSDs (ranging from ∼1.5 to 10 Å). Although the scores generally fell with an increase in RMSD, especially in the range of 1.5–5 Å, there was substantial scatter among the points that belied the expectation of obtaining a functional relationship between the two variables. However, because these RMSDs contain contributions from both main- and side-chain deviations, we performed a second calculation (with 10 structures; Fig. 2) in which the backbone coordinates were held fixed and errors were incorporated into the side-chain conformations using three distinct methods: 1), randomizing the side-chain χ-angles (50 erroneous models) (13); 2), subjecting the same 50 models as in method 1 to an energy minimization protocol (using CHARMM (39)) as described previously (13); and 3), obtaining a unique solution as determined by SCWRL4.0 (11) upon threading. Two distinct clusters were obtained for methods 1 and 2, and energy minimization significantly improved scores in method 2 relative to method 1. The models derived from SCWRL4.0 (method 3) generally gave values closest to the native (Fig. 2 and Fig. S6), and rarely a few structures from method 2 gave similar/slightly better scores than method 3 (Fig. S6). Thus, the scores indeed reflect errors in side-chain coordinates as estimated by RMSD (with respect to native) and generally drop with an increase in error.

Figure 2.

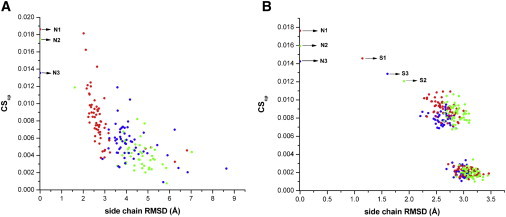
Complementarity scores drop with increased errors in side-chain coordinates. (A) CS_cp values as a function of side-chain RMSDs for three CASP9 targets (native and models). N1, N2, and N3 correspond to the native crystal structures of T0522 (3NRD), T0623 (3NKH), and T0586 (3NEU), respectively, and their corresponding models plotted in red, green, and blue. (B) CS_cp values as a function of side-chain RMSDs for three globular proteins and their models (see text). N1, N2, N3 and S1, S2, S3 correspond to the native structures and the unique solutions generated by SCWRL4.0 for 2OEB (red), 3COU (green), and 2HAQ (blue), respectively. The two distinct clusters are for structures produced by randomization of the side-chain conformers (with lower values) and energy minimization of the same set of randomized conformers (higher values). Similar patterns were obtained for CS_gl. Except for 2HAQ, all structures are from DB2.

Fold recognition by cross-threading

The scoring functions were also tested for protein pairs that belonged to the same fold but had low sequence identity upon alignment. We selected 100 such pairs (sequence identities ranging from 6% to 30%) sampling diverse folds from the PREFAB4.0 database (40). The sequence identities upon structural alignment for each pair were determined by Dali Server (38) and their folds assigned according to the SCOP database (41) (data set S2). For every pair, we aligned the two native sequences using CLUSTAL W (42). Insertions in the sequence to be threaded onto the main chain (of its partner) were excised, whereas deletions were padded with glycine to maintain the correct position of the threaded residues consistent with the alignment. For the cross-threaded sequences, padded polyglycine stretches at the N- and C-termini were also excised before the calculations were performed. When the fold was part of a larger polypeptide chain (domain), two possibilities were considered. If the fold was found to be completely separated from the other domains in the chain, it was considered in isolation for all subsequent calculations, whereas if the fold was found to be integrally embedded in the composite structure, the entire chain was used to calculate $S_m^{sc}$ and $E_m^{sc}$, and the relevant residues in the domain were then used to compute CS_gl and CS_cp. For all pairs, the native structures gave characteristic similar scores (Table S10) for both CS_gl and CS_cp. The two sequences were then cross-threaded onto the backbone of each other, with their side-chain torsions being set to values determined by SCWRL4.0 (11). For each such pair, 100 random sequences (≤15% identity between any two sequences in a set) were threaded onto each of the two corresponding templates according to the same protocol. Hydrogen atoms were geometrically fixed by REDUCE (19) in all models. In a large majority of the cases, the average score of the two cross-threaded structures was found to be markedly lower than that of their native counterparts but noticeably higher (Z ≥ 2 for 86, 87 pairs) than those obtained from the random decoys (〈Z〉: 3.43, 3.33 for CS_gl, CS_cp, respectively). However, below 15% sequence identity, there was a drop in the Z-scores (<1.5 for 5 out of 21 such pairs) primarily due to large mismatches in structural (Dali server) and sequence (CLUSTL W) alignments. In general, large variations were observed in the Z-scores (ranging from 0.4 to 8.0; Table S10) for different folds.

Complementarity plot

In contrast to evaluating the overall quality of an atomic model in terms of packing and electrostatics, $S_m^{sc}$ and $E_m^{sc}$ can also be used to identify local packing defects and regions of suboptimal electrostatics in a crystal structure. To that end, we plotted the individual ($S_m^{sc}$, $E_m^{sc}$) values of completely/partially buried residues in a complementarity plot (CP) spanning −1.0 to 1.0 in both the X $\left(S_m^{sc}\right)$ and Y $\left(E_m^{sc}\right)$ axes. Given the fact that for residues in correctly folded proteins both $S_m^{sc}$ and $E_m^{sc}$ are largely constrained to a limited range of values (as a function of their burial), regions in CP encompassing points corresponding to such amino acids could be clearly delineated. From DB2, we plotted $S_m^{sc}$ and $E_m^{sc}$ of all (target) residues irrespective of the amino acid type separately based on their burial bins, accounting for 23,850, 10,624, and 13,255 residues in bins 1, 2, and 3, respectively (see Materials and Methods). Thus, in all, three plots (CP1, CP2, and CP3) were obtained (Fig. S7, Fig. S8, and Fig. S9). Each two-dimensional plot was then divided into square grids (0.05 × 0.05 wide) and the probability of finding any residue (P_grid) in a particular grid was estimated by the ratio of the number of points in that grid to the total number of points in the plot. The plots were then contoured based on their probability values P_grid ≥ 0.005 for the first contour level and ≥ 0.002 for the second. The cumulative probability of locating a point within the second (outer) contour for the three plots was 91%, 90%, and 88%, respectively, whereas for the first (inner) contour, the probability gradually dropped with increasing solvent exposure to 82%, 76%, and 71%, respectively. Inspired by the Ramachandran plot (18), we termed the region within the first contour “probable”, that between the first and second contours “less probable”, and that outside the second contour “improbable”. In such a plot, residues with low $S_m^{sc}$ and $E_m^{sc}$ (<0.2 for both) are easily identified. However, in general, residues with suboptimal packing (as a function of their burial) and electrostatics could lie in sections partially spanning all three regions of the plots.

To test whether these suboptimal points (in CPs) were correlated with coordinate errors, we obtained 20 pairs of crystal structures consisting of an upgraded structure and its superseded partner from the PDB (Table S11). Subsequent to superposition by Dali server, residues from each pair were selected whose RMSD between side-chain atoms exceeded 1.5 Å for the first burial bin (with respect to native) and 2.0 Å for the second and third bins (method 1) (43). These residues were considered to be erroneous in the superseded PDB file. In addition, the calculation was repeated for residue pairs whose deviation in the side-chain (χ₁) torsion was >40° (method 2) (43). Of note, the same residue could have different burials in the two files (superseded and upgraded).

The distribution of points for the upgraded and superseded structures was markedly different in the plots. Based on DB2, 82.1%, 9.2%, and 8.7% of the total points were found to be located in the probable, less-probable, and improbable regions, respectively, for the first burial bin (for the other bins, see Table S12). In sharp contrast, the distribution (method 1) was respectively 41.4%, 14.6%, 44.0% for the superseded structures, and 80.2%, 9.6%, and 10.2% for the upgraded structures. Deviation from the expected distribution (DB2) was estimated by χ² in each plot (CP1, CP2, and CP3) for both the superseded and upgraded sets. χ² (df = 3–1: probable, less probable, improbable; ${\chi }_{0.05}^2$ = 5.991) for burial bins 1, 2, 3 were found to be 1.1, 10.2, 15.7 and 503.9, 275.3, 187.8 for the upgraded and superseded sets, respectively. A similar pattern was also obtained for method 2 (Table S13). Thus, residues with positional errors have a heightened tendency to lie in the less-probable and improbable regions of the plot (Fig. 3, Fig. S10, and Fig. S11) associated with low complementarities. However, because CPs are essentially probabilistic in nature, there is a significant likelihood to encounter false positives (in the probable regions), specifically with regard to coordinate errors.

Figure 3.

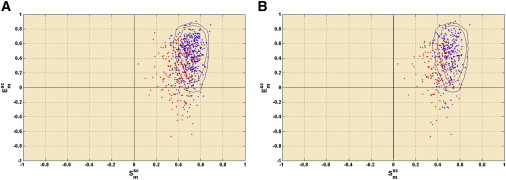
Distribution of points in CP1. Distribution of points from superseded (erroneous: red) and upgraded structures (blue) in the CP for burial bin 1 (0.0 ≤ Bur ≤ 0.05). Errors were estimated by (A) side-chain RMSD and (B) deviation in χ₁ torsion angles (see text).

Discussion

In the case of specific association, at least among proteins, some correspondence is to be expected between the geometrical features of their associating surfaces and their electrostatic potentials at the interface. Likewise, for a correctly folded globular protein, all buried residues should achieve optimal packing within the interior of the molecule and meticulously balance the electric fields that arise from different parts of the folded chain so as to neutralize all destabilizing electrostatic effects. Several calculations have confirmed that for correctly folded proteins, all residues upon burial exhibit fairly high levels of S_m for their side-chain atoms, enabling dense packing (13,14). To our knowledge, this is the first time that E_m has been calculated within proteins to extend the analogy between folding and binding. The results show that one of the universal characteristics of correctly folded proteins is the almost uniformly elevated values in $S_m^{sc}$ and $E_m^{sc}$ attained by all deeply buried residues (Fig. S12). However, the constraints in $S_m^{sc}$ appear to be more stringent relative to $E_m^{sc}$, given its reduced SD, compared with the latter. The nature of short- and long-range forces that determine the values of $S_m^{sc}$ and $E_m^{sc}$ also gives rise to their contrasting features. $S_m^{sc}$ is a function of burial, whereas $E_m^{sc}$ is not (Table S14). Furthermore, the primary determinants of $S_m^{sc}$ and $E_m^{sc}$ are side-chain atoms (for all residues) and main-chain atoms (for hydrophobic residues), respectively, whereas both side-chain and main-chain atoms contribute equally to the $E_m^{sc}$ of hydrophilic residues.

The fact that both folding and binding require a narrow window of S_m and E_m values was used to predict the native fold of a sequence. Both functions (CS_gl and CS_cp) based on the probability distributions in $S_m^{sc}$ and $E_m^{sc}$ performed successfully in state-of-the-art decoy sets. This could be considered analogous to protein-protein docking, wherein both surface and electrostatic complementarities rise to their optimum values upon the interlocking of interacting protein molecules in the correct stereospecific geometry of association. That is to say, folding can be envisaged as the docking of interior residues to their respective native environments consistent with short- and long-range forces. The fact that the performance of both functions was comparable to or better than the best scoring functions currently available in the literature demonstrates the practical application of complementarity in the area of protein folding and structure prediction. The functions were also found to be useful for correctly identifying the same fold for two sequences with low sequence identity. Lastly, individual residues with suboptimal packing and electrostatics are easily identified in the CPs, which are highly correlated with coordinate errors. In contrast to the Ramachandran plot, which detects errors in backbone atoms due to local steric overlap, CPs detect side-chain conformations that are in disharmony with short- and long-range forces sustaining the native fold.