The Effect of Ionic Strength, Temperature, and Pressure on the Interaction Potential of Dense Protein Solutions: From Nonlinear Pressure Response to Protein Crystallization

Abstract

Understanding the intermolecular interaction potential, V(r), of proteins under the influence of temperature, pressure, and salt concentration is essential for understanding protein aggregation, crystallization, and protein phase behavior in general. Here, we report small-angle x-ray scattering studies on dense lysozyme solutions of high ionic strength as a function of temperature and pressure. We show that the interaction potential changes in a nonlinear fashion over a wide range of temperatures, salt, and protein concentrations. Neither temperature nor protein and salt concentration lead to marked changes in the pressure dependence of V(r), indicating that changes of the water structure dominate the pressure dependence of the intermolecular forces. Furthermore, by analysis of the temperature, pressure, and ionic strength dependence of the normalized second virial coefficient, b₂, we show that the interaction can be fine-tuned by pressure, which can be used to optimize b₂ values for controlled protein crystallization.

Introduction

Investigating the physics and chemistry that govern the interaction and phase behavior of proteins in concentrated salt solutions is essential for understanding and controlling protein aggregation and crystallization processes (1–3). Even today, the search for optimal crystallization conditions is usually carried out by a trial-and-error routine, i.e., empirical screening through a large field of parameter sets until suitable crystals are obtained (4,5). Here, a more complete knowledge of the interaction between proteins in solution can help us to predetermine nucleation and crystallization conditions more precisely, which is even more important when only small amounts of protein are available (6).

The use of salt (e.g., NaCl, Na₂SO₄) as a precipitation agent is largely due to electrostatic screening effects, which decreases the effective repulsive electrostatic interaction of charged proteins (7–9). However, in addition to the amount and type of salt added (10), other parameters can be chosen to direct protein crystallization, such as cosolvents, temperature, and hydrostatic pressure. The latter parameter was explored in a series of studies on various proteins, such as subtilisin (11,12), glucose isomerase (13–15), thaumatin (16,17), and lysozyme (17–26). These studies investigated the solubility, nucleation, and growth rates of protein crystals under pressure, yielding diverse results for different proteins, however. Less attention has been directed toward the resulting protein crystal structure and quality (17,22,27) as well as toward the intermolecular interaction potential controlling protein crystallization and phase behavior (28,29).

The various experimental parameters impose different effects on the repulsive and attractive part of the interaction potential of proteins. In fact, an exact interplay of attractive and repulsive intermolecular forces is crucial for obtaining high quality protein crystals. The second virial coefficient, B₂, was found to be a useful measure for the overall interaction of proteins in solution (30). Interaction potentials that tend to be merely attractive with low (negative) second virial coefficients result in poorly ordered protein aggregates. On the other hand, high positive B₂ values correspond to solution conditions where the repulsive interactions dominate and no precipitation of the protein is observed. A crystallization window with a second virial coefficient in a narrow range of slightly negative values presents optimal crystallization conditions (31,32).

The influence of salt ions on the local water structure is a reason for many specific ion effects like their varying ability to precipitate proteins from solution (10). The classification of anions and cations in this context is generally given by the classical Hofmeister series (10,33–35). Their ability to influence the local water structure is also often discussed in terms of their water-structure-making (cosmotropic) or water-structure-breaking (chaotropic) propensities (35).

The application of pressure has been shown to affect the intermolecular interactions of proteins in solution in a nonlinear way, which seems to be connected to the stability of the second hydration shell of water against hydrostatic pressure, i.e., to pressure-induced changes of the water structure in the multi-kbar range (36). Recently, it has also been shown that the addition of particular cosolvents, such as trimethylamine-n-oxide (TMAO) that is known to alter the local water structure, can markedly counteract this effect (37). In the pressure-range discussed here, the protein remains always in its natively folded state (37). Different from the monomeric lysozyme, oligomeric proteins tend to dissociate already in the low kbar-range (29).

In this work, we studied the combined effects of temperature, pressure, and ionic strength (NaCl concentration) on the protein-protein interaction potential of dense lysozyme solutions. Moreover, the use of pressure to modulate B₂ and finally modulate protein crystallization in situ is explored. The protein lysozyme was used as a well-characterized model protein, as it is known to be stable at all solution conditions studied here. The interactions were probed by small-angle x-ray scattering (SAXS) in combination with a liquid-state theoretical approach, applying the mean spherical approximation in combination with a modified Derjaguin-Landau-Verwey-Overbeck interaction potential (36,37).

Experimental Section

Materials

Lysozyme from hen egg white (14.3 kDa, pI = 11) was purchased from Roche, Mannheim, Germany. A 25 mM Bis-Tris (Fluka BioChemistry, purity = 99.0%; Sigma-Aldrich, St. Louis, MO) buffer solution at pH = 7 was used to keep the pH value of the solvent constant at all pressure conditions studied. The protein concentrations were varied between 0.5 and 20 wt % with salt concentrations ranging from 0 up to 500 mM NaCl. Sodium chloride was purchased from Merck, Darmstadt, Germany.

Experimental setup

Small-angle x-ray scattering experiments were carried out at beamline BL9 (38), DELTA, Dortmund, and at beamline BW4 (39,40), HASYLAB, Hamburg, Germany, at wavelengths of the incident beam of λ = 1.2395 Å (BL9) and λ = 1.381 Å (BW4), respectively. The high-pressure sample environment was generated by a custom-built high pressure cell employing two flat diamond windows of 1-mm thickness (41). With this setup, a pressure range from 1 bar up to 4 kbar can be reached. For the measurements at atmospheric pressure, a capillary holder sample cell was used. With both sample cells, a temperature range from 8 to 45°C was accessible.

The two-dimensional scattering patterns were recorded using an image-plate detector, and azimuthally averaged with the Fit2D software package (42). The resulting scattering curves were corrected for solvent and background scattering by subtracting the scattering curve measured with a solvent-filled sample cell.

Data analysis

The scattering intensity from diluted protein solution can be described by the form factor P(q) with q = (4π/λ)sin (θ/2) being the wave vector transfer, and θ is the scattering angle. For lysozyme in solution, the form factor can be described by that of an ellipsoid of revolution as

$$P\left(q\right)=\underset{0}{\overset{1}{\int }}\frac{j_1{\left(q\sqrt{a^2+x^2\left(b^2-a^2\right)}\right)}^2}{{\left(q\sqrt{a^2+x^2\left(b^2-a^2\right)}\right)}^4}\text{d}x,$$ (1)

with the semiaxes a and b (43,44). Lysozyme is approximately an ellipsoid with volume (π/6) × 4.5 × 3.0 × 3.0 nm³ (see (46)).

For solutions of higher protein concentration, an additional scattering contribution has to be taken into account, which originates from the intermolecular interaction of the particles. The resulting SAXS signal can be described within the decoupling approximation as a product of the form factor P(q) and an effective structure factor

$$S_{\text{eff}}\left(q\right)=1+\frac{{\langle F\left(q\right)\rangle }_{\Omega }^2}{P\left(q\right)}\left(S\left(q\right)-1\right).$$ (2)

Here, 〈F(q)〉_Ω is the spherical average of the Fourier transform of the protein electron density, and S(q) is the intermolecular structure factor. By measuring the scattering pattern at both dense and highly diluted concentrations, the structure factor S(q) can be determined.

The intermolecular structure factor can also be calculated theoretically in the mean spherical approximation, using a modified Derjaguin-Landau-Verwey-Overbeck potential V(r) to model the interaction of the proteins (36,44,45). The potential V(r) is given by the sum over a hard-sphere potential, V_HS(r), a repulsive screened-Coulomb potential, V_SC(r), and an attractive part, modeled as a Yukawa potential, V_Y(r). The single contributions can be calculated as

$$\begin{array}{l}{V}_{\text{HS}}\left(r\right)=\{\begin{array}{cc}\mathrm{\infty }& ,r\le \sigma \\ 0& ,r>\sigma ,\end{array}\hfill \\ V_{\text{SC}}\left(r\right)=\{\begin{array}{cc}0& ,r\le \sigma \\ \frac{Z^2{e}^2}{4\pi {\epsilon }_0{\epsilon }_r{\left(1+0.5\kappa \sigma \right)}^2}\frac{e^{-\kappa (r-\sigma )}}{r}& ,r>\sigma ,\end{array}\hfill \\ V_{\text{Y}}\left(r\right)=\{\begin{array}{cc}0& ,r\le \sigma \\ -J\sigma \frac{e^{-\left(r-\sigma \right)/d}}{r}& ,r>\sigma .\end{array}\hfill \end{array}$$ (3)

Here, e is the elementary charge, ε₀ the vacuum dielectric constant, ε_r the dielectric permittivity of the solution, and κ the reciprocal Debye-Hückel screening length (κ⁻¹ = 0.306 nm (c_s/M)^−1/2, at room temperature, where c_s is the molar salt concentration (46)). The pressure and temperature dependence of the dielectric permittivity of the solution, ε_r, was taken into account as well, following Floriano and Nascimento (47). The dielectric permittivity shows a minor monotonic increase with pressure and a decrease with temperature. At pH 7, the effective protein charge in the model was kept constant at a value of Z = 8 (48). Additionally, an effective protein hard-sphere diameter of σ = 2.99 nm and a d value (width of the attractive part of V_Y(r)) of d = 0.3 nm was used. With this, only the strength J of the attractive potential is unknown, which can now be determined from fits to the experimental data. The overall scattering intensity, which was refined to the experimental data, is calculated as

$$I\left(q\right)=P\left(q\right)·S_{\text{eff}}\left(q\right)+c.$$ (4)

Here c is a constant background added, thus allowing us to determine the intermolecular interaction potential V(r) of lysozyme in solution. From this, also the second virial coefficient, B₂, can be calculated as

$$B_2=2\pi \underset{0}{\overset{\mathrm{\infty }}{\int }}\left(1-e^{-V\left(r\right)/k_{\text{B}}T}\right)r^2\text{d}r$$ (5)

for particles interacting with pair potential V(r) when their centers are separated by the distance r. B₂ is an integral characteristics value for the two-body intermolecular interaction, revealing—by its sign—attractive or repulsive interactions of the particles. To compare the values for proteins of different sizes, the dimensionless normalized second virial coefficient is calculated by factoring out the hard sphere part, B₂^HS, of the integral (49):

$$b_2=\frac{B_2}{B_2^{\text{HS}}}=1+\frac{3}{8{\left(R+\delta /2\right)}^3}\underset{2R+\delta }{\overset{\mathrm{\infty }}{\int }}\left(1-e^{-\left[V_{\text{SC}}\left(r\right)+V_{\text{Y}}\left(r\right)\right]/k_{\text{B}}T}\right)r^2\text{d}r.$$ (6)

Here, R = σ/2, and the parameter δ prevents the divergence of the integral at r = 2R. In accordance with the literature, the value for δ was taken as δ = 0.1437 nm (46,49). By definition, positive b₂ values generally correspond to repulsive interactions whereas negative values correspond to dominating attractive forces.

Results and Discussion

The interaction of lysozyme molecules in salt solution

In a first step, we used our approach to measure the SAXS intensities at various lysozyme and NaCl concentrations at atmospheric pressure and compared the results with existing data for lysozyme in salt-free solution (36). The influence of an increasing ionic strength on the SAXS data is shown in Fig. 1 a together with the fits of the data. As shown, the model used can also be successfully applied for solutions of high ionic strength, giving refinements with reasonable quality.

Figure 1.

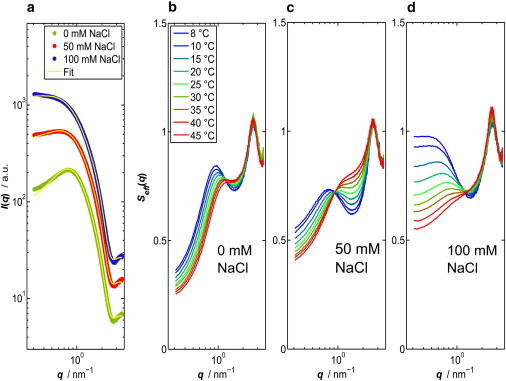
(a) SAXS intensities of a 10 wt % lysozyme solution at 25°C for NaCl concentrations of 0, 50, and 100 mM (bottom to top). The SAXS curves were shifted vertically for reasons of clarity. The refinement of the data is also shown. (b–d) Corresponding effective structure factors, S_eff(q), at various salt concentrations and temperatures.

The effective structure factor, S_eff(q), of 10 wt % lysozyme upon addition of 0, 50, and 100 mM NaCl in solution is presented in Fig. 1, b–d. Here, the scattering curve of the dense protein solution was divided by the form factor of lysozyme, calculated by fitting the scattering data of the 0.5 wt % lysozyme solution with the program GNOM (50). Clearly, a drastic increase of the attractive interaction of the proteins is seen with increasing ionic strength, indicated by a marked increase of the scattering intensity at small q values. Furthermore, as expected, an increasing attractivity is observed upon a decrease of temperature from 45 to 8°C.

The interaction potential, V(r), and the strength of the attractive interaction, J, is calculated by fitting the model described above to the experimental data. Fig. 2 depicts the temperature dependence of J at various NaCl concentrations. As can be seen, a marked temperature dependence of the attractive interaction is observed for all salt concentrations. The attractive interaction is independent of the protein concentration under salt-free conditions only. With increasing ionic strength of the solution, an increase of the protein concentration reduces the attractive interaction parameter, J (i.e., leads to an increase of repulsive interaction). With increasing protein concentration, intermolecular distances decrease, thus leading to a more pronounced effect of charge screening on V(r) and hence J.

Figure 2.

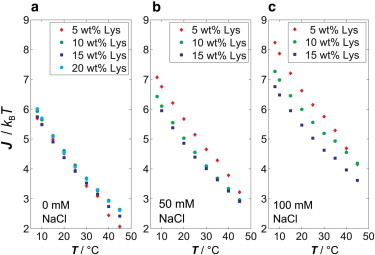
Temperature dependence of the strength of the interprotein attractive interaction, J, as a function of NaCl and protein concentration (p = 1 bar).

The effect of pressure on the interaction potential in concentrated salt solutions

The application of pressure has recently been shown to affect the interaction potential of dense protein solution in a nonlinear way (36). The strength of the attractive interaction, J, is decreasing as a function of pressure up to pressures of ∼2 kbar. Upon a further pressure increase, this behavior changes and the attractive interaction increases again. This effect is probably governed by the collapse of the second hydration shell of water starting at pressures at ∼2 kbar, and can be altered by water-structure influencing cosolvents such as TMAO (37). The influence of TMAO on the water structure results in a shift of the minimum of J(p) to smaller pressures, which can be explained by a counteracting effect of TMAO and pressure on the water structure.

The addition of salt to a protein solution is known to screen the repulsive interactions of the proteins. In addition, water structure weakening or breaking effects connected to specific ion effects may be present (33,34). The effective structure factors for a 10 wt % lysozyme 100 mM NaCl solution at pressures from 1 bar up to 3 kbar are depicted in Fig. 3 a. The nonlinear behavior of the structure factor with increasing pressure is still visible in salt solution. The minimum in J(p) is shifted to smaller J values, but also to slightly lower pressures with increasing protein concentration (Fig. 3 b). The results for J(p) of the 10 wt % lysozyme solution are shown in Fig. 3, c and d, for various temperatures and NaCl concentrations. The minimum in J(p) at ∼1.5 kbar remains up to 400 mM NaCl, and the J value increases with increasing NaCl concentration, i.e., increased screening of the positively charged lysozyme (Fig. 3 d). As shown in Fig. 3 c, the location of the minimum in J(p) is also independent of temperature, and J values decrease by ∼30% upon an increase of temperature from 10 to 40°C.

Figure 3.

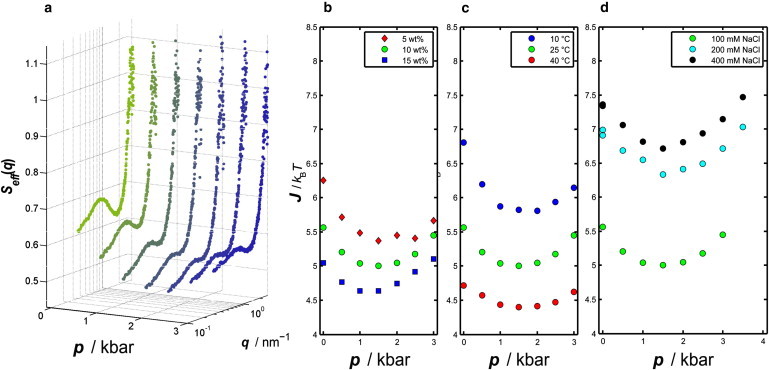
(a) Effective structure factor, S_eff(q), of a 10 wt % lysozyme solution with 100 mM NaCl at 25°C as a function of pressure. (b and c) Results of the refinement for J(p) as a function protein concentration (25°C, 100 mM NaCl) and temperature (10 wt % Lys, 100 mM NaCl). (d) Strength of the attractive interaction, J, for different NaCl concentrations ranging from 100 mM (bottom) to 400 mM (top) NaCl (10 wt % Lys, 25°C).

Pressure dependence of the second virial coefficient

To reveal optimal crystallization conditions under the influence of all thermodynamic potentials, the pressure dependence of the second virial coefficient in salty protein solution should be implemented as well. We calculated the pressure dependence of the normalized second virial coefficient from the measured interaction potentials. A suitable crystallization slot is generally found for b₂ values only lying in a narrow range (30). This slot appears for b₂ values typically between ∼−0.85 and −3.2 (46). In Fig. 4, the measured values for b₂ are shown as a function of temperature and pressure for a salt concentration of 100 mM NaCl. As can be seen, b₂ increases with increasing temperature, and it displays a maximum at a pressure of ∼2 kbar. As expected, the nonlinear pressure dependence of V(r) is also reflected in b₂(p): At pressures up to 2 kbar, an increase of pressure results in an increase of b₂. For pressures higher than ∼2 kbar, b₂ decreases again. The increase of b₂ with increasing pressure is much steeper at low temperatures, resulting in a more pronounced maximum of b₂(p) compared to temperatures as high as 40°C, where a broad maximum is observed.

Figure 4.

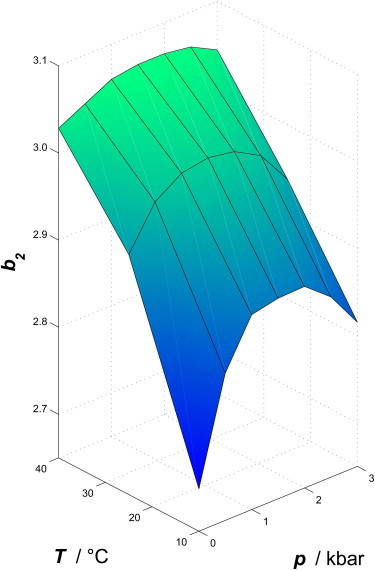
Normalized second virial coefficient, b₂, for 10 wt % lysozyme in 100 mM NaCl solution as a function of temperature and pressure.

Favorable crystallization conditions, corresponding to b₂ values lower than ∼−0.85, are reached for higher NaCl concentrations. For example, a salt concentration of 500 mM NaCl shifts b₂ to values ∼−1 at ambient pressure (49). The increase in pressure has a nonlinear effect on the interprotein potential even under high salt concentrations (Fig. 3). The observed pressure dependence of the second virial coefficient is in good agreement with recent observations by Crisman and Randolph (27). They studied the crystallization behavior of recombinant human growth hormone at elevated pressure and found an increase of the virial coefficient with increasing pressure from 1 to 2500 bar. They observed crystal growth under high pressure at solution conditions that formed amorphous precipitates at atmospheric pressure only, and detected no crystal growth under high pressure at solution conditions that produced crystals at 1 bar. In this study, the crystallization agent poly(ethylene glycol) was employed.

The formation of crystals under pressure

Fig. 5 depicts the SAXS data of lysozyme in 500 mM NaCl solution at different pressures. Several Bragg reflections are detectable in the low-angle region between 1.0 and 2.2 nm⁻¹, which indicate formation of lysozyme crystals at high pressures. The limited q-range accessible to SAXS means that only the first reflections can be recorded. Upon crystal formation, in the fluid/crystal coexistence region, unambiguous extraction of S_eff(q) and J is no longer feasible. Fig. 5 a shows the scattering intensity, where the diffuse SAXS scattering contribution in this q-regime, approximated by I(q) = Ae^αq+β, was subtracted from the scattering signal. The comparison with literature data reveals that tetragonal lysozyme is formed under these conditions (51–53). Indexing of the first Bragg reflections allows us to calculate the lattice constants a = b and c as well as the volume of the tetragonal unit cell. Here we also show the positions of the first reflections of tetragonal lysozyme crystals that were grown at ambient pressure and measured at 0.51 kbar (depicted by vertical lines, single crystal data, taken by Fourme et al. (51)). The corresponding unit cell parameters a = b and c, calculated from the Bragg reflections by using the program CELREF (54), are shown in Fig. 6 b together with the values taken from Fourme et al. (51) (dashed lines).

Figure 5.

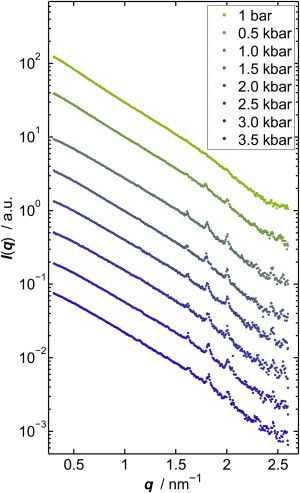
SAXS intensities of a 10 wt % lysozyme solution with 500 mM NaCl at 25°C and different pressures. The SAXS curves were shifted vertically for reasons of clarity.

Figure 6.

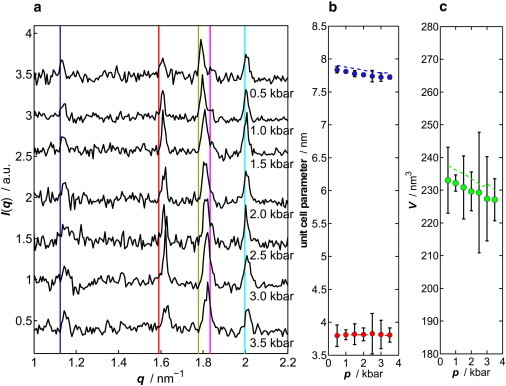
(a) Pressure-induced Bragg reflections of a 10 wt % lysozyme solution in 500 mM NaCl at 25°C (scattering signal after background subtraction). The scattering signals were shifted vertically for reasons of clarity. (Vertical lines) Reflection positions calculated from unit cell parameters of tetragonal lysozyme under 0.51 kbar pressure, reported by Fourme et al. (51). (b) Corresponding unit cell parameters a = b (top) and c (bottom), and (c) the volume of the unit cell as a function of pressure. (Dashed lines) Data from Fourme et al. (51).

At ambient pressure, a ≈ 7.8 nm and c ≈ 3.8 nm. Small differences observed with respect to the literature data may be due to different solution (e.g., 0.5 M vs. 1.7 M NaCl in Fourme et al. (51)) and pH conditions. Please note that in our study, polycrystalline crystal formation was observed in situ under high-pressure conditions, whereas pressure effects on protein crystals have been reported so far on ambient-pressure pregrown crystals only. The application of pressure results in anisotropic compression of lysozyme crystals, i.e., a compression of the a axis, whereas the c-axis length stays approximately constant. Linear refinement of the data shows that the unit-cell volume (Fig. 6 c) contracts by 2.07 nm³ kbar⁻¹, which is slightly less than the 1.1% per kbar reported by Kundrot et al. (55) and 2.50 nm³ kbar⁻¹ for this pressure range reported by Fourme et al. (51). By extrapolating the measured unit cell parameter to 1 bar, one obtains a unit cell volume of 234.04 nm³, which is 1.3–1.9% smaller than those reported (51,55,56). The slightly smaller compressibility of the c axis and the smaller unit cell volume might be due to the fact that in the latter cases crystals were pregrown at atmospheric pressure.

Conclusions

In this work, we report SAXS studies on concentrated lysozyme solutions of high ionic strength as a function of temperature and pressure. The conditions reported here concern the native protein that has not undergone any significant conformational changes. Deciphering the intermolecular interaction potential of proteins under the influence of temperature, pressure, protein, and salt concentration is essential for understanding protein aggregation and fibrillation, protein crystallization, and protein phase behavior in general. We could show that the interaction potential changes in a nonlinear fashion with pressure at all temperatures (10–40°C), salt, and protein concentrations studied.

Notably, neither temperature nor protein and salt concentration lead to marked changes in the pressure dependence of V(r), indicating that changes of the water structure by pressure, i.e., the collapse of the second hydration shell in the multi-kbar pressure range, probably dominates the pressure dependence of V(r). Generally, more than one route is available to crystallize proteins. The application of pressure leads to increasing values of the normalized second virial coefficient for pressures in the lower pressure region (below ∼2 kbar), which can be used to decrease a too-strongly attractive interaction leading to a b₂-value region more suitable for controlled protein crystallization. More systematic studies will be carried out in the near future to explore this effect in more detail and to reveal the crystal quality under the various pressure, temperature, and salt conditions employed.