Abstract
Bubble formation in the conduits of woody plants sets a challenge for uninterrupted water transportation from the soil up to the canopy. Freezing and thawing of stems has been shown to increase the number of air-filled (embolized) conduits, especially in trees with large conduit diameters. Despite numerous experimental studies, the mechanisms leading to bubble formation during freezing have not been addressed theoretically. We used classical nucleation theory and fluid mechanics to show which mechanisms are most likely to be responsible for bubble formation during freezing and what parameters determine the likelihood of the process. Our results confirm the common assumption that bubble formation during freezing is most likely due to gas segregation by ice. If xylem conduit walls are not permeable to the salts expelled by ice during the freezing process, osmotic pressures high enough for air seeding could be created. The build-up rate of segregated solutes in front of the ice-water interface depends equally on conduit diameter and freezing velocity. Therefore, bubble formation probability depends on these variables. The dependence of bubble formation probability on freezing velocity means that the experimental results obtained for cavitation threshold conduit diameters during freeze/thaw cycles depend on the experimental setup; namely sample size and cooling rate. The velocity dependence also suggests that to avoid bubble formation during freezing trees should have narrow conduits where freezing is likely to be fast (e.g., branches or outermost layer of the xylem). Avoidance of bubble formation during freezing could thus be one piece of the explanation why xylem conduit size of temperate and boreal zone trees varies quite systematically.
Keywords: air seeding, cavitation, gas segregation, nucleation, xylem
Introduction
Formation of bubbles (cavitation) in xylem conduits is one of the major challenges for the cohesion-tension theory of the ascent of sap. Reduction of conductivity or bubble formation has been observed in various species when xylem tension is high (e.g., Sperry, 1995; Hacke and Sauter, 1996a) and mechanisms of refilling embolized conduits are the focus of numerous studies (see, e.g., Holbrook and Zwieniecki, 1999; Tyree et al., 1999; Cochard et al., 2001; Hacke and Sperry, 2003; Stiller et al., 2005; Lee and Kim, 2008; Salleo et al., 2008; Secchi and Zwieniecki, 2011).
Winter sets a new challenge to the water conducting system. Freezing and thawing has been shown to induce xylem embolization, leading to almost 100% loss in conductivity in some species (e.g., Sperry et al., 1988; Hacke and Sauter, 1996b; Langan et al., 1997; Davis et al., 1999; Feild and Brodribb, 2001). The extent of the loss of conductivity has been shown to depend on the mean conduit diameter such that large conduits embolize easier than small (LoGullo and Salleo, 1993; Davis et al., 1999). Globally, mean conduit diameter also decreases with increasing probability of freezing temperatures (see Sperry, 1995) and therefore, the vulnerability to freezing/thaw-induced embolization has been related to species distribution (Pockman and Sperry, 1997; Cavender-Bares and Holbrook, 2001; Stuart et al., 2007). High xylem water tension increases the vulnerability to freeze/thaw – induced embolization (Langan et al., 1997; Lemoine et al., 1999; Pittermann and Sperry, 2006; Stuart et al., 2007), and therefore plants growing in dry habitats can be affected by wintertime embolization more than species in well-hydrated habitats.
Although widely studied (additional to those sited above, e.g., Sucoff, 1969; Sperry et al., 1988; Just and Sauter, 1991; Cordero and Nilsen, 2002) freeze/thaw-induced cavitation in plants has not been addressed theoretically, and therefore our knowledge on the mechanisms leading to bubble formation in this specific situation is inadequate. Based on the common occurrence of dissolved gases in xylem sap and the insolubility of gases in ice, many studies make the assumption that loss of conductivity is due to bubbles formed by gas segregation during the freezing process (e.g., Lybeck, 1959; Sucoff, 1969; Martinez-Vilalta and Pockman, 2002). However, similarly to dissolved gases freezing segregates other solutes and may increase the xylem water tension by increasing the osmotic pressure in the unfrozen water at the freezing domain (see, e.g., Wolfe and Bryant, 1999). Therefore, it is reasonable to assume that, like in drought-induced cavitation, bubbles could also form via homogenous nucleation (vaporization of water), heterogeneous nucleation (vaporization of water that initiates on the hydrophilic surfaces of cell walls), or “air seeding” (air captured in cell walls or adjacent embolized conduits is pulled through the pit membrane pores to fill the cavitating conduit; see, e.g., Sperry et al., 1988; Cochard et al., 1992; Hölttä et al., 2002; Pittermann and Sperry, 2003).
The mechanism of bubble formation determines how xylem structure affects the likelihood of embolism formation due to freezing. In gas segregation, the bubbles should form most easily where the gas concentration is highest, whereas in the other mechanisms the solute concentration in the freezing conduit could lead to bubble formation in the still unfrozen conduits. Therefore, in the first case the size of the freezing conduit may be the key factor (see Pittermann and Sperry, 2006), but in the second case the size and structure of the conduits close to the freezing zone could be more important.
In this study we use calculations based on fluid mechanics and classical nucleation theory to lay the basis for understanding the loss of conductivity during freezing/thaw events. Our objectives were (1) to show which mechanisms are most likely to be involved in bubble formation during freezing, (2) to determine the key parameters affecting bubble formation probability during freezing, and (3) to compare calculated results with existing experimental studies.
To meet these objectives we present the equations governing the nucleation processes and develop equations for calculating the solute concentration at the leading edge of an advancing ice front. These calculations relate to all the mechanisms as both bubble formation via vaporization of water and segregation of gases rely on nucleation of a new phase. In addition, the amount of segregated solutes determines the maximum xylem tension that could be produced during freezing. This tension affects both vaporization of water and air seeding.
To complete the calculations we had to make assumptions about the homogeneity of ice formation and xylem structure as well as the symmetry of the temperature field. These assumptions may not describe the actual process of ice crystal formation in the xylem properly, but we developed the equations in non-dimensional form and as such they can be used for describing solute segregation in front of any phase interface as long as treatment in one dimension is sufficient to describe the problem. Furthermore, the insights into the mechanisms involved in bubble formation during freezing and the variables that control the dynamics revealed by these calculations are independent of these assumptions.
Materials and Methods
Nucleation theory and bubble formation probability
Xylem water tensions range from very slight (0.1 MPa) to more than 10 MPa (see, e.g., Taiz and Zeiger, 2002). At these pressures water is in a metastable state, but the degree of metastability is low (Δμ/Δμspin ≪ 1, where Δμ is the chemical potential difference of current and equilibrium state, Δμspin is the chemical potential difference at the spinodal and saturation states; see, e.g., Shen and Debenedetti, 2001), and the phase transition between liquid and gas phase occurs via nucleation. Thermodynamically, the probability of nucleation of a new phase within a system depends on the balance between the tendency of the system to find the state of minimum free energy in a given environment (stable state as opposed to metastable) and the energy needed for forming an interface between the old and the emerging phase. Balancing these forces leads to a minimum size required for a stable cluster of the new phase. Smaller clusters than the critical size dissolve back to the previous phase; while larger clusters grow spontaneously to form the new stable state. According to classical nucleation theory, the formation rate of critical size clusters (# per time and volume) can be written as
| (1) |
where A is a kinetic frequency factor, kB the Boltzmann’s constant, T temperature and W the free energy barrier (or the reversible work) of formation of a critical size cluster (see, e.g., Debenedetti, 1996).
Far away from the spinodal decomposition limit, bubble nucleation in the xylem can be treated by means of classical nucleation theory. Following the approach of Blander and Katz (1975) and assuming spherical bubbles, the free energy barrier W for homogenous nucleation (water free from impurities and all the surrounding surfaces totally wettable) is then given by the expression
| (2) |
where γ is the interfacial tension and rc is the radius of the critical size cluster given by
| (3) |
where Δp is the pressure difference between the interior of the critical cluster and the bulk metastable mother phase.
The kinetic frequency factor A describes the rate of molecular exchange through the bubble surface per unit area and can be written as
| (4) |
where N is the number density and m the molecular mass of the mother substance, and B describes the type of equilibrium assumed between the critical size cluster and the bulk phase. In the case of bubble formation we can require thermodynamic equilibrium (opposed to mechanical) and in that case B = 1 (Debenedetti, 1996). Typically, the size of a critical cluster is of the order of magnitude 1 nm and it is very unlikely to obtain a bubble of diameter 1 μm unless there is time for the bubble to grow (see, e.g., Kulmala et al., 2007).
For homogenous nucleation in a pure liquid the pressure difference between the bubble and the mother phase (Δp in Eq. 3) can be approximated by
| (5) |
where pe is the saturation vapor pressure of the mother phase, ρ indicates the density of a substance and subscripts V and L stand for vapor (bubble) and liquid (water) respectively (Blander and Katz, 1975).
If the liquid is a dilute solution of solvent and dissolved gases, Δp can be written as
| (6) |
where Cg/Cgsat is the supersaturation ratio of the gas in the liquid, pLsat is the saturation vapor pressure of the pure liquid and
| (7) |
where V0 is the molecular volume (volume/molecule) of the liquid (Tucker and Ward, 1975; Wilt, 1985). Because Δp depends on the supersaturation ratio of the dissolved gases, we have to calculate the evolution of gas concentration in a freezing conduit to calculate the bubble formation probability by segregation of gases.
In the presence of non-wettable surfaces, bubble nucleation is more likely to initiate heterogeneously on the surface than in the bulk liquid and the lowering effect of the surface to the nucleation energy barrier can be written as
| (8) |
where F (value < 1) can take different forms depending on the assumptions of the surface structure (e.g., Debenedetti, 1996). However, ice surfaces can be assumed totally wettable (Wettlaufer, 1998) and thus freezing of cell walls lowers the heterogeneous nucleation rate. Heterogeneous nucleation can also occur if small particles of non-soluble materials act as nucleation sites. When present they, similarly to non-wettable surfaces, would make bubble formation more likely by decreasing the energy barrier of bubble formation.
Nucleation is a purely stochastic process. Individual nucleation events (i.e., successful formation of a critical size cluster) are independent of each other and do not depend on the number of trials. The probability of a single molecule to act as an initiator of nucleation at a certain moment of time is very small. Thus the probability of finding a bubble with a diameter equal to or larger than the critical radius in a conduit can be calculated from Poisson distribution and becomes
| (9) |
where V is the volume of the conduit and t is time (e.g., Koop et al., 1996). Whether the conduit will embolize still depends on whether the bubble (1) grows fast enough to fill the whole conduit before being enclosed by ice during freezing, or (2) whether it dissolves or grows during thawing. This depends on the size of the bubbles trapped in the ice and the xylem water tension during thawing (see Mayr and Sperry, 2010). In this study we do not consider bubble growth, and discuss embolization during thawing only briefly. Our focus is on bubble formation probability during freezing, which makes embolization upon thawing possible.
Solute concentration in advance of a moving ice front
Xylem sap naturally contains dissolved gases and solutes (e.g., Sucoff, 1969; Canny, 1995). Because the solubility of these substances in ice is much lower than that in water, as the xylem freezes, they are expelled from the ice and solute concentration in the remaining water increases. This may increase the likelihood of bubble formation in two ways: (1) either via increasing the likelihood of formation of a gas bubble in the freezing conduit (see Eqs 1–7), or (2) via increasing the osmotic concentration in the freezing conduits, which leads to increasing xylem water tension and higher probability of bubble formation in the unfrozen conduits. Based on the conservation of mass, the change in solute concentration C in the liquid in front of a solidification front moving with velocity v(t) can be written as
| (10) |
where D is the binary diffusion coefficient of the solute in the liquid (assumed to be constant at a given temperature) and the velocity of the moving solid front (see, e.g., Bianchi and Viskanta, 1997). The term on the right represents the net flux of solutes diffusing away from the vicinity of the interface and the second term on the left accounts for the solutes expelled by the moving ice front. The build-up of the solute concentration is thus a competition between two processes: freezing increases the concentration close to the ice front, but the concentration gradient produced that way decreases naturally by diffusion. The total concentration at the ice-water boundary therefore depends on the freezing velocity relative to the diffusion rate.
In a cylindrical stem that freezes homogenously from the outer surface inward in radial direction, the solidification front inside one conduit can be approximated by a planar surface (i.e., the conduits are not freezing radially from the cell wall toward the center, but from the outer cell wall to the inner). As long as the radius of the stem is more than four times larger than that of the conduit (r/R < 0.25) the error resulting from the curvature of the ice surface compared to a plane is less than 1%. Xylem conduit diameters are typically of the order of magnitude 10–100 μm and stem diameter 1–100 cm and we can thus use the planar surface approximation and a one-dimensional Cartesian form of Eq. 10 to represent our situation. Writing Eq. 10 in dimensionless form gives
| (11) |
where the non-dimensional concentration C* is taken relative to the initial solute concentration, the non-dimensional time τ relative to the freezing time of the conduit or the freezing domain, x represents the dimensionless spatial coordinate relative to the conduit diameter or the characteristic distance of the freezing domain (d) and Pe is the dimensionless Péclet number (see e.g., Bird et al., 2002) that describes the ratio of mass transport resulting from advection (ice front expelling the gas) and diffusion.
| (12) |
If Pe is constant (v is constant), Eq. 11 can be solved analytically.
Using the conservation of mass
| (13) |
both at the liquid–solid boundary x = 0 and at the conduit wall x = 1 we get
| (14) |
where Cs is the ratio of the solubility of the solute in the solid and the liquid, K is a constant of integration and F(τ) is a function of the dimensionless time. Throughout the freezing process the solution has to fulfill Eq. 11. Substituting (Eq. 14) back to (Eq. 11) and solving for F(τ) with initial condition
| (15) |
we get
| (16) |
for the gas concentration in the liquid as a function of time and space. Although developed for a conduit freezing along the stem radius (note, not conduit radius), Eq. 16 is applicable for the solute concentration in front of any advancing ice front as long as the geometry allows for one-dimensional treatment. Solute concentration in front of ice moving along conduit elements, e.g., from branches downward (see e.g., Zweifel and Häsler, 2000 and references therein) or the solute concentration between two ice crystals growing in one dimension would follow Eq. 16 with the characteristic distance d in Eq. 12 replaced by the length of the conduit or the distance between the crystal surfaces. However, when choosing the boundary conditions, we assumed that the cell wall or the boundary at the other end does not form a barrier for water movement or solute diffusion. Therefore, Eq. 16 applies accurately only when far away from such a boundary.
Calculations
We used Matlab 7.0 to calculate solute concentrations, nucleation rates and bubble formation probabilities based on Eqs 1–16. In all the calculations for bubble formation via gas segregation we assumed the interfacial surface tension to be that of a planar surface. This is justified by the macroscopic size of xylem conduits (∼10–100 μm) compared to the size of the forming bubbles (∼1 nm). All the nucleation rates were calculated per conduit and when not stated otherwise, we used a cylindrical conduit with diameter 50 μm and length 20 mm. That size is typical of temperate deciduous trees experiencing frequent freezing and freeze-thaw cycles (Hacke and Sauter, 1996a). Our assumptions that xylem freezes homogenously and that the cell walls do not form a barrier for solute diffusion out of the cells means that our calculations represent a conservative estimate for the solute concentrations in freezing conduits and consequently are conservative also for bubble formation probability. If the freezing was not homogenous and ice inside conduits formed in a curved rather than in a planar fashion, or the cell walls reflected solutes, the solute concentration would increase faster in the unfrozen part of the conduit and make osmotic concentration higher and/or bubble formation more likely than presented here. On the other hand, for bubble formation via gas segregation we set the initial gas concentration in the conduit to the saturation concentration, which may be an overestimation in wintertime (see e.g., Levy et al., 1999; Spicer and Holbrook, 2005). For the ratio of the solubility of solutes in ice and water we use CS = 1/1000 which is in the low end of the range reported for ions smaller in size than O2, N2, or CO2 (see e.g., Killawee et al., 1998). This makes our estimates conservative for the increase in gas concentration, but possibly slightly optimistic for the increase in osmotic pressure.
Results
Solute concentration in freezing conduits
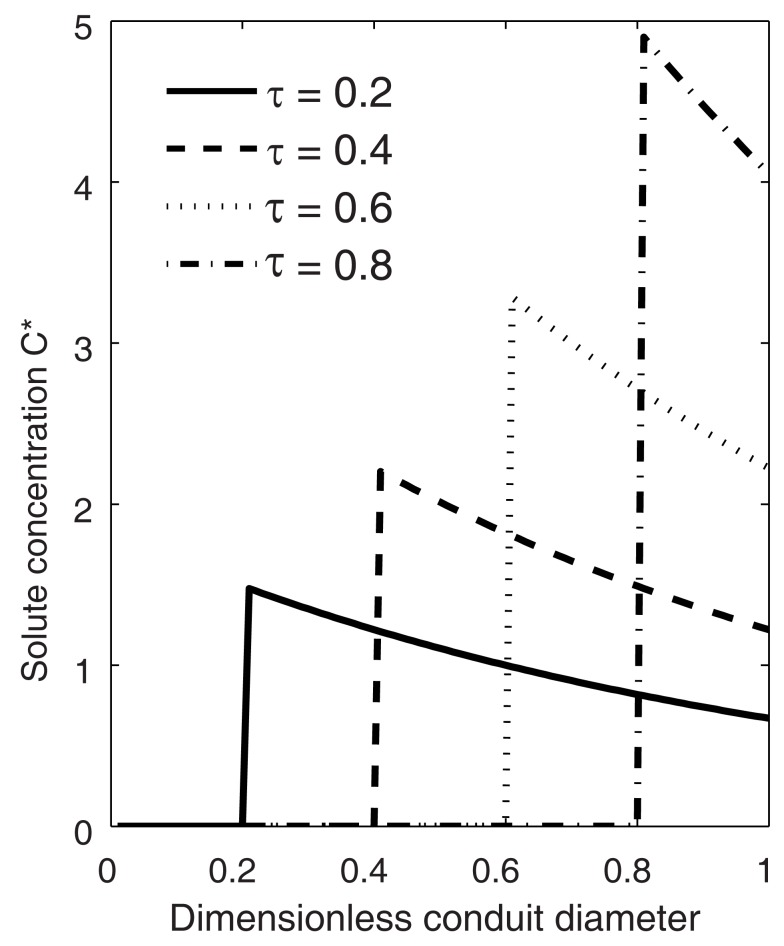
In front of a moving solid-liquid interface, at any instant (τ), the highest concentration is obtained right at the interface, and the solute concentration in the liquid decreases with increasing distance from the interface (Eq. 16; Figure 1). The Peclét number Pe (i.e., the balance between advection and diffusion) determines both the rate of increase of the concentration at the interface and the rate of decrease with increasing distance from the ice front. When Pe reaches 0 (no freezing), Eq. 16 approaches the initial concentration (i.e., C* = 1), and a constant concentration is maintained. For each solute, Pe depends on conduit diameter and freezing velocity (Eq. 12), so that the larger the conduit or freezing domain and the larger the freezing velocity the higher concentrations are obtained.
Figure 1.
Solute concentration (C*) in a conduit during freezing presented in a stationary coordinate system (coordinate system immobilization transformation where the location of the origin of Eq. 16 is at vτ, and v fulfills x/τ = 1). At time τ = 0.2 the ice-water interface is at the location 0.2, and at time τ = 1 the whole conduit is frozen. The concentrations were calculated using Eq. 16. The Peclet number Pe = 1 (Eq. 12) and solute solubility in ice/solubility in water, CS = 0.001.
The concentration at the interface increases in time as the ice front moves toward the boundary of the domain. The ultimate maximum concentration obtained in a freezing domain, , is found at the ice-water interface (x = 0) when τ = 1. From Eq. 16 we obtain
| (17) |
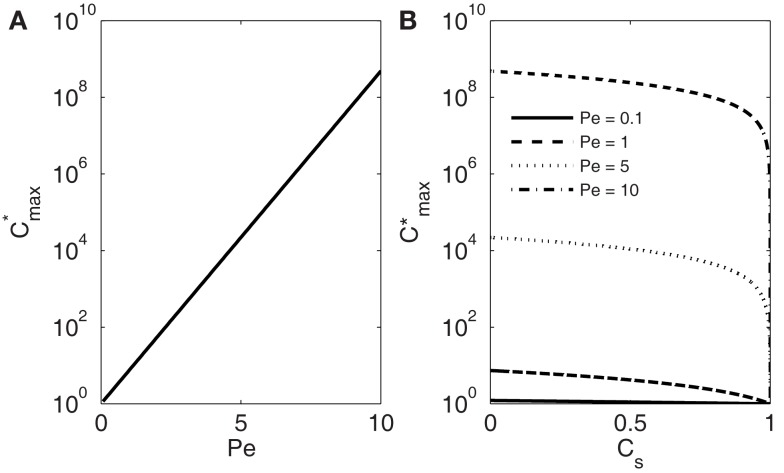
The maximum concentration thus strongly depends on Pe increasing exponentially with increasing conduit diameter and freezing velocity (Figure 2A).
Figure 2.
Dependence of the maximum solute concentration obtained during freezing (; Eq. 17) on Pe (A) and CS (B). In (A) the solute solubility in ice/solubility in water CS is 0.001. The maximum concentrations are always obtained at the ice-water interface (see Figure 1). If the solubility in ice is less than half of the solubility in water (CS < 0.5) the maximum concentration depends only slightly on CS. Because of the molecular size, CS for solutes present in xylem sap is well below that.
With any Pe, the maximum concentration decreases with increasing solute solubility in ice, and when CS reaches 1, also rapidly approaches 1 (the dimensionless initial concentration; Figure 2B). The value of CS depends on the structure of ice and the molecular size of the dissolved solutes (see e.g., Top et al., 1985). Typically for gases and salts CS is ≪0.1 (see e.g., Killawee et al., 1998), which means that in natural conditions inside tree stems Pe affects much more strongly than CS. If Pe was large (large conduit diameter, high freezing velocity, or low diffusivity), solute concentrations could grow several orders of magnitude above the initial solute concentration in xylem sap (Figure 2A).
Bubble formation mechanisms during freezing
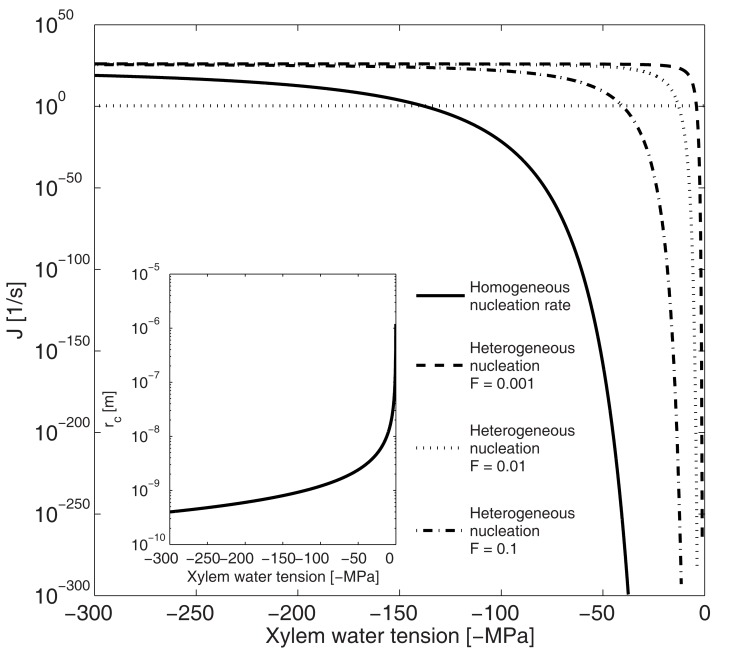
Based on our calculations (Eqs 1–5) and supported by previous studies (see e.g., Tyree and Sperry, 1989; Hölttä et al., 2002), homogenous bubble nucleation in the xylem by vaporization of water is unlikely. The tension in the xylem has to exceed 100 MPa, for homogenous nucleation rate to reach 1/s, which is the nucleation rate at which bubble formation becomes likely in typical xylem conduits (Eq. 9; Figure 3). This is an order of magnitude larger than any reported xylem tensions. The nucleation rate increases as the critical radius of the formed bubble decreases (Figure 3 insert), and therefore, in general, where nucleation is fast lots of small bubbles will form. At a nucleation rate of 1/s the critical radius of a nucleus is ∼1 nm (Figure 3 insert), which is a typical size for the critical cluster initiation in phase transition processes (e.g., Kulmala et al., 2007).
Figure 3.
Dependence of nucleation rate (J) and critical radius (rc insert) on xylem water tension for homogenous and heterogeneous vaporization of water in a conduit 50 μm in diameter and 20 mm in length. Homogenous nucleation rate at xylem tensions < 100 MPa is so low, and the critical radius so large, that bubble formation is unlikely. The energy barrier for nucleation (Eq. 2) has to decrease by a factor (F; Eq. 8) of 10 for heterogeneous vaporization of water to become likely at xylem water tensions below −50 MPa. The horizontal line shows the nucleation rate at which bubble formation becomes likely in conduits of this size (Eq. 9).
To create a 100-MPa tension by segregation of solutes from xylem sap would require solute concentrations of the order of magnitude 104 mol m−3 (if the reflection coefficient of cell walls was 1). In principle such high concentrations could be obtained during freezing provided that Pe was large enough (Figure 2). If the initial salt concentration in the xylem was at the upper end of the reported range (10−3–1 mol m−3; see e.g., Epstein, 1972; Jeffrey, 1987), Pe of values from 4 to 8 eight would lead to that concentration (Figure 2A). In a typical conduit (diameter ∼50 μm), this would mean a freezing velocity of 16–80 μm s−1 [diffusivity of salts in water typically 10−9 m2 s−1 (Table 1)]. Robson and Petty (1987), Robson et al., 1988) report freezing velocities of 1.75–25 μm s−1 in stem segments freezing radially, and in the veins of leaves freezing longitudinally ice propagation velocities of the order of magnitude 100–1000 μm s−1 have been observed (Hacker and Neuner, 2007). Therefore, obtaining a Pe of this magnitude in the freezing xylem does not seem completely impossible. However, the required concentration exceeds the solubility of the most common salts by an order of magnitude (Table 1; see also Luo and Roux, 2010), and therefore the required osmotic pressure would not be achieved. Furthermore, the xylem cell walls are permeable to at least some part of the solutes (see Canny, 1990, 1995), and will thus not create osmotic pressures similar to semipermeable membranes.
Table 1.
Diffusivities (D) and solubilities (S) of typical solutes in xylem sap.
| D × 10−10 m2 s−1 | S mol m−3 | |
|---|---|---|
| CO2 | 2.2 | 75 |
| N2 | 5.5 | 0.9 |
| O2 | 3.7 | 2.2 |
| KCl | 20 | 3757 |
| NaCl | 15 | 6138 |
The diffusivities for gases at 0°C were calculated according to Wilke–Chang model (see Bird et al., 2002) and the Partington rule was applied to calculate the liquid molar volumes (see e.g., Maloka, 2005). Diffusivities of salts were obtained from Chang and Myerson (1985), and were measured at 25°C. Solubilities at 0°C for gases were calculated using Henry’s law constants (Sanders, 1999), and for salts obtained from Haynes (2012).
In heterogeneous nucleation the energy barrier for bubble formation is lower than in homogenous nucleation (Eq. 8), and therefore the xylem tension required for bubble formation is also reduced. To make heterogeneous nucleation likely at the saturation concentrations of the most common salts (∼−30 MPa osmotic pressure; see Luo and Roux, 2010), the energy barrier should decrease by a factor of 10 (Figure 3). This could happen if the nucleation surfaces (hydrophobic surfaces on the cell walls or small solid particles in the sap) were more than 10 times larger than the critical radius of the stable new phase cluster and the contact angle between water and the surfaces was larger than 120° (Liu, 1999). The contact angle between water and xylem conduit walls has been measured to be 40°–55° (Zwieniecki and Holbrook, 2000). Therefore, similarly to homogeneous nucleation, heterogeneous nucleation can be considered quite unlikely during freezing.
In air seeding, the xylem water tension that would lead to bubble expansion to a previously water filled conduit depends on the surface tension of water and the diameter of the pores in the cell wall through which the bubble would expand (e.g., Sperry et al., 1988; Hölttä et al., 2002). Surface tension increases with decreasing temperature, which means that the lower the temperature the higher the xylem water tension required for air seeding. The increase, however, is only 5% from 25 to 0°C (Haynes, 2012), and would have a negligible effect on the experimental values reported for threshold xylem water tensions for air seeding; 0.5–10 MPa (see e.g., Sperry et al., 1988; Choat et al., 2005; Christman et al., 2009). These tensions would require salt concentrations from a few hundred to a few thousand mol m−3, and could easily be obtained by segregation of salts during freezing (Figure 2A). Whether these concentrations would lead to the required osmotic pressures depends on whether xylem conduit walls reflect the salts, and are thus capable of producing osmotic pressures (see Canny, 1995). All in all, if bubble formation during freezing was due to an increase in xylem water tension resulting from salt segregation, air seeding would be the most likely mechanism (see Just and Sauter, 1991 or Pittermann and Sperry, 2003 for experimental evidence).
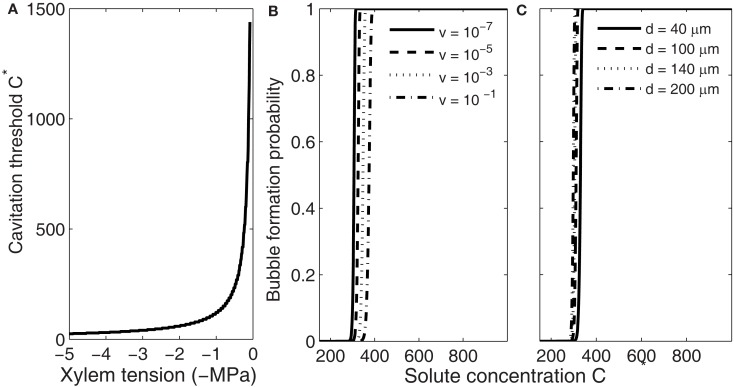
Bubble formation via segregation of gases differs from the other three mechanisms in that this mechanism does not require high xylem water tensions. The nucleation rate depends on the gas concentration in the freezing conduit (Eqs 1–3, 6, and 7); the higher the concentration the more likely bubbles are to form. Therefore, bubbles are most likely to form right at the water–ice interface inside the freezing conduit (Figure 1). The concentration at which bubble formation becomes likely depends on xylem water tension (Figure 4A) but is much lower than the solute concentration required for producing high enough xylem water tensions for homogenous and heterogeneous nucleation. At xylem water tension 0.1 MPa it is of the order of magnitude 1000 times the saturation concentration, but drops quickly with increasing xylem water tension, and at 5 MPa tension only 20 times the saturation concentration is required. For each xylem water tension, the supersaturation at which bubble formation becomes likely depends slightly on the freezing velocity and conduit diameter (Figures 4B,C). The slight sensitivity to these parameters stems from the time dependence of the bubble formation probability (Eq. 9), and is similar to the effect conduit size has on nucleation events in general; the larger the conduit or the slower the freezing velocity, the more there is time for a successful bubble formation event to occur. But whether the required gas concentration is obtained during freezing depends strongly on both conduit diameter and freezing velocity (Figures 1 and 2). Note that the dependence of nucleation on freezing velocity (Figure 4B) is opposite to the dependence of the increase in the concentration of segregated gas on freezing velocity. In the case of segregated gases the higher the freezing velocity is the higher the concentration and the more likely bubble formation occurs.
Figure 4.
Dependence of the threshold solute concentration for bubble formation via gas segregation on xylem water tension (A), freezing velocity (B), and conduit diameter (C). Xylem water tension determines the concentration at which bubble formation becomes likely, but whether that concentration is obtained during freezing depends on freezing velocity and conduit size (Pe; see Figure 2). (B,C) Show that slightly higher concentrations are needed for bubble formation become likely in small than in large conduits (Eq. 9) and if the time allowed for nucleation to take place is short (high freezing velocity, see Eq. 18). Here the initial gas concentration was set to saturation and C* values presented concentrations above saturation.
Based on our calculations supersaturations required for bubble formation via gas segregation could be easily obtained during freezing (Figure 2). There is evidence that concentrations of dissolved gases in xylem sap are higher than concentrations of other solutes. CO2 concentrations ranging from 1 to 22 mol m−3 (1–30% of saturation at 0°C; Table 1) have been measured (Levy et al., 1999). Nitrogen and oxygen are much less soluble in water than CO2 (Table 1), and even if the reported concentrations are low, 0.77–1.34 mol m−3 (Gansert, 2003; Spicer and Holbrook, 2005), these could lead to super saturation and bubble formation during freezing (Figure 2; Table 1). Xylem water tensions tend also to be low during freezing because of low transpiration. This together with the ease of producing high enough gas concentrations in the freezing conduits suggests that bubble formation via segregation of gases is the most likely mechanism during freezing.
Bubble formation probability, conduit size, and freezing velocity
The probability of bubble formation depends on the nucleation rate, conduit volume, and time allowed for nucleation (Eq. 9). In the case of gas segregation the time allowed for the nucleation to take place in a conduit is the time required for freezing the entire conduit. Assuming a cylindrical conduit freezing along the radius of the stem, inserting t = d/v for the freezing time (constant velocity approximation) into Eq. 9 we get
| (18) |
for the probability of finding at least one bubble larger than the critical size in a conduit of volume after the entire freezing time. Here h is the length of the conduit. Strictly speaking, because ice partially fills the conduit during freezing, the diameter used in the calculation of the volume should not be the conduit diameter but an effective average diameter representing the unfrozen volume. This, however, has a negligible effect on the probability because the concentration increase affecting the nucleation rate overrules the volume dependence.
From Eq. 18 it is evident that, if the conduit does not freeze longitudinally, conduit diameter, d, has a stronger effect on the probability than conduit length, h. If freezing is longitudinal the freezing time should be written as t = h/v, which leads to equal importance of conduit length and diameter. For bubble formation via gas segregation, however, the dependence on conduit diameter becomes stronger and the dependence on freezing velocity is reversed because the nucleation rate depends exponentially on the gas concentration, which depends exponentially and equally on the conduit diameter and the freezing velocity (Eqs 6, 12, and 16). The increase in gas concentration in front of the moving ice front does not depend on conduit volume or any other dimensions than the length of the domain along which freezing occurs. Therefore, conduit volume affects bubble formation probability only weakly. If ice formation started from several directions inside a conduit and proceeded in three dimensions, volume would affect the concentration obtained more strongly. In air seeding, bubble formation probability should not depend on conduit volume at all unless conduit size or diameter correlates with the pore size through which bubbles can extend (see Christman et al., 2009, 2012). Therefore, the dependence of bubble formation on conduit dimensions can tell which mechanism was involved and how freezing proceeded.
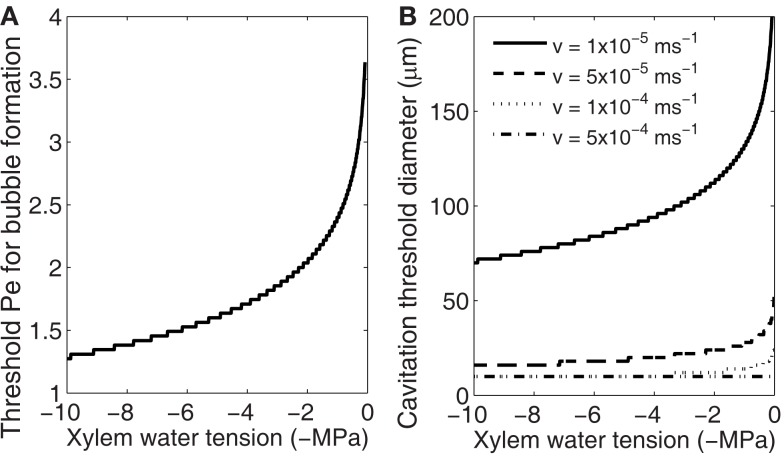
Because the bubble formation probability depends on accumulation of gases and the concentration at which bubble formation becomes likely depends on xylem water tension (Figure 4A), for each xylem water tension there is a threshold Pe at which cavitation starts to occur (Figure 5A). The threshold Pe decreases with increasing tension meaning that the diameter of the conduits likely to cavitate (cavitation threshold diameter) and/or the freezing velocity at which cavitation begins decreases with increasing tension. Also, several cavitation threshold diameters exist at the same xylem tension, and they depend on the freezing velocity; the higher the freezing velocity the smaller the threshold diameter (Figure 5B). This means that for the same sample, one can obtain a higher loss of conductivity when freezing the sample fast than if it freezes slowly. The freezing velocity will depend on the size and structure of the sample (heat capacity, thermal conductivity) as well as the temperature difference between the sample and outside air (or other cooling fluid). Inside the xylem, the freezing velocity of conduits of different size may also vary because of these reasons. Therefore, even if large conduits are theoretically more susceptible to bubble formation during freezing, some variation is this pattern may occur (see e.g., Mayr and Sperry, 2010 and references therein).
Figure 5.
Dependence of Pe (A) and conduit diameter (B) at which bubble formation becomes likely on xylem water tension. The larger the xylem water tension the smaller Pe is required (A). Pe depends on freezing velocity, conduit diameter, and diffusivity of solutes (Eq. 12) and therefore at the same xylem water tension a different threshold conduit diameters are obtained at different freezing velocities (B).
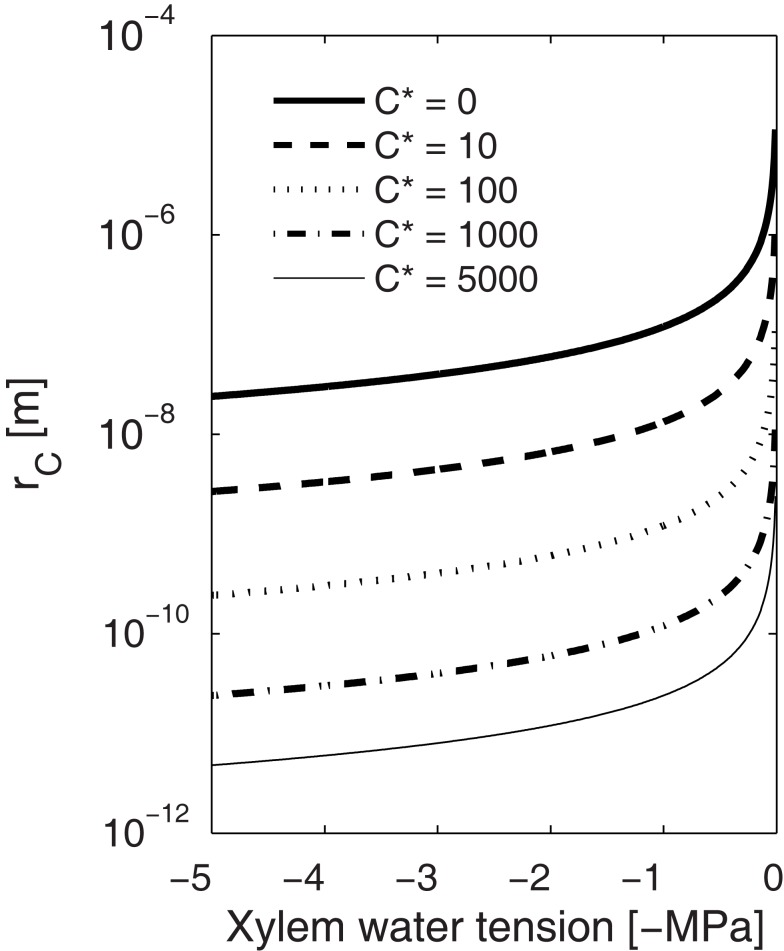
High freezing velocity also results in smaller but more numerous bubbles because the higher the gas concentration, the lower the energy barrier for nucleation (Eqs 2, 3, 6, and 7), the smaller the critical size bubble, and the higher the nucleation rate. Also, during fast freezing there will be less time for bubbles to grow before enclosed in ice. Therefore, one could expect smaller but more numerous bubbles trapped in conduits freezing rapidly than in conduits freezing slowly. Narrow conduits observed containing more and smaller bubbles than wide conduits (see Ewers, 1985) may thus be due to differences in the freezing velocity. Similarly, the size of the bubbles formed decreases with increasing xylem water tension as presented by Pittermann and Sperry (2006). These small bubbles, even if numerous, are more likely to redissolve to the liquid during thawing. Dissolving bubbles to the liquid is a reverse process to bubble formation, and therefore the ease with which bubbles dissolve depends also on xylem water tension (see also Mayr and Sperry, 2010). From Eq. 3 we can calculate the pressure dependence of the minimum size of bubbles that will not dissolve to the liquid. If there are no dissolved gases in the liquid (C* = 0; Figure 6), all bubbles smaller than 0.1 μm will dissolve under tensions of 0–1 MPa, and only slightly positive pressures would be needed to force bubbles, filling even the largest conduits (d ∼ 10−4 m), to redissolve. On the other hand, if xylem tension is high or there are already dissolved gasses present in the liquid, dissolving becomes increasingly difficult and avoiding bubbles altogether consequently more important. It is worth noting that if freezing is fast enough and the bubbles have little time to grow, these minuscule bubbles, either trapped in the ice or in the eutectic domains between the crystals, would be invisible even with a scanning electron microscope (SEM), but during thawing, if the xylem tension was high enough, capable of causing embolization (Figure 6).
Figure 6.
Dependence of the critical radius (rc) of a gas bubble on xylem water tension at different solute concentrations (C*). Bubbles larger than rc at a certain tension will grow spontaneously and smaller will redissolve to the solution. Similarly, during thawing, smaller bubbles than rc are more likely to redissolve, and the higher the xylem water tension or gas concentration the smaller the bubble has to be to redissolve. This means that while bubble formation is more likely at high freezing velocities (high Pe leads to high C*), the small bubbles are more likely to redissolve during thawing than bubbles that may form during slow freezing.
Discussion
Loss of xylem conductivity after freeze/thaw cycles is a phenomenon that potentially affects large areas of vegetation in temperate and boreal zones as well as at high altitudes even in the tropics. The susceptibility of plants to freezing-induced loss of conductivity is therefore an interesting topic from the point of view of both plant survival (e.g., Pockman and Sperry, 1997) and ecological adaptations (see e.g., Améglio et al., 2002; Pittermann and Sperry, 2003; Sperry, 2003; Choat et al., 2011). Bubble formation during freezing sets the stage for loss of conductivity during thawing (see e.g., Pittermann and Sperry, 2006; Mayr and Sperry, 2010), and the mechanism behind bubble formation during freezing determines how environmental conditions and xylem characteristics affect the likelihood of loss of conductivity. Our calculations confirm the common assumption that the most likely mechanism of bubble formation during freezing is segregation of dissolved gases, although air seeding could also happen if segregation of solutes created osmotic pressures in the xylem (see e.g. Mayr et al., 2007). In freezing conditions bubble formation via vaporization of water (homogenous or heterogeneous nucleation), although possible, is highly unlikely and would require very large xylem tensions to occur (Figure 3).
In gas segregation, the gas concentration and thus also the bubble formation probability is highest right at the water-ice interface (Figure 1). Therefore, bubbles formed via this mechanism will become trapped in the ice. In air seeding, the bubbles should rather form in unfrozen conduits and completely gas filled conduits could be expected. Bubble formation via gas segregation in one conduit could lead to air seeding in an adjacent conduit if the xylem tension and pore size are large enough. This combination of mechanisms could explain the occurrence of empty conduits in frozen samples next to ice filled conduits containing bubbles (see Mayr and Sperry, 2010 and references therein). Our calculations do not predict bubbles forming necessarily in the middle of the conduit. The location where bubbles will be found depends on the build-up of the gas concentration (Figure 1), which depends on the initial amount of solutes, the conduit diameter (or the characteristic length of the freezing domain) and freezing velocity. Supporting this, ice-trapped bubbles in different locations in a conduit can be seen in pictures of some studies (e.g., Utsumi et al., 1999), and Ball et al. (2006) showed that such bubbles can form when gas becomes trapped during freeze-induced filling of embolized conduits with ice. But the link between the location, conduit size, and freezing velocity remains unconfirmed.
Our calculations show that for a plant with certain conduit diameter distribution, freezing velocity is the main variable determining whether bubbles form during freezing (Figure 5). Only few studies address the possible dependence of loss of xylem conductivity on freezing velocity (see Robson and Petty, 1987; Sperry and Sullivan, 1992). Bubble size and shape has been shown to depend on freezing velocity in conifer stem segments (Robson et al., 1988), but based on these studies it is unclear how much freezing velocity contributed to the number of bubbles found, to the size of conduits where they were found and to the distribution of the bubbles trapped in the ice. Therefore, our results remain to be experimentally verified. Slow thawing, on the other hand, has been shown to decrease loss of conductivity (Langan et al., 1997), which is consistent with the probabilistic nature of bubble formation and redissolving processes (Eq. 9), as suggested by Langan et al. (1997).
In experimental set-ups freezing velocity depends on the sample size, the thermal conductivity of the sample and heat exchange rate between the sample and the cooling system. With equal heat flux, large specimens tend to freeze slower than small because of their larger heat capacity. Several studies have reported different threshold conduit diameters for freezing-induced cavitation. Davis et al. (1999) and Pittermann and Sperry (2003), for example, report a sigmoidal relationship between mean conduit diameter and percentage loss of conductivity (similar to Figure 4). Using cooling rates of 0.25 and 0.2°C/min for samples ranging from 2 to 16 mm in diameter and not less than 20 cm in length they found a threshold diameter of 30–40 μm. Based on our calculations at 0.5 MPa xylem water tension these threshold diameters would have required freezing at a velocity of ∼50 μm s−1 (Eq. 12; Table 1), which is well in the range of reported freezing velocities (see above). On the other hand, Feild and Brodribb (2001) used a cooling rate of 0.1°C/min and found a linear correlation with mean conduit diameter and percentage loss of conductivity for the 12 species they studied. If we assume that they used samples of similar size and thermal conductivity their freezing velocity would be half of that of Davis et al. (1999) and Pittermann and Sperry (2003) resulting in a threshold diameter of 60 μm. The largest mean diameter of their samples was about 30 μm and in that case the linearity would result from the conduit diameter distribution, although their high loss of conductivity (up to 80% with mean diameter 30 μm) suggests that their samples might have been smaller than those of Davis et al. (1999) and Pittermann and Sperry (2003). Calculating the freezing velocity inside a sample from the cooling rate of the surrounding fluid is a complex task (see e.g., Brower et al., 1984; Bird et al., 2002) and beyond the scope of this study. We also know little about how freezing inside tree stems proceeds (see Discussion below). However, together with these examples our calculations demonstrate that these apparently conflicting results may be due to the different experimental set-ups. Also, if the species in these studies differed in susceptibility to air seeding or properties affecting the build-up of osmotic concentration in the xylem, different threshold diameters, and relationships between conduit diameter and loss of conductivity would be expected.
Interestingly, it has also been observed that the likelihood of embolization during thawing of frozen vessels depends on the minimum temperature to which they were exposed. Low minimum temperatures seem to increase likelihood of embolization (Pockman and Sperry, 1997; Ball et al., 2006). According to our calculations, the only significant dependence of bubble formation via gas segregation on temperature (heat flux) results from the effect of temperature on freezing velocity. A minimum temperature obtained with a constant cooling rate should not influence freezing velocity unless the sample cools slower than the surroundings or it is does not freeze homogenously. In the first case the temperature gradient between the sample and the surroundings or inside the sample would increase until the minimum temperature was reached, and this increase would increase the freezing velocity. If the temperature was then kept constant at the minimum, freezing velocity would decrease with the decreasing gradient as the ice front moves further away from the surface and the gas concentration would stop increasing (see Bianchi and Viskanta, 1997). In the second, differences in thermal conductivity of materials (water, ice, cell walls) would lead to spatial and temporal variations in the local heat flux. Thermal conductivity of water, for example is only about 25% of that of ice (Haynes, 2012), and the thermal conductivity of the fibers in the cell walls is less than 10% of that of ice (Simpson and TenWolde, 1999). Therefore, as freezing progresses freezing velocity should increase with increasing amount of ice, whereas cell walls should decrease the freezing velocity. Crystal formation and freezing velocity can also depend on the micro-scale geometry of the freezing surfaces (Richards, 1989). Therefore, in reality it is quite likely that freezing velocity in plant conduits would vary locally even with a constant cooling rate, and factors not accounted for in this study could lead to freezing velocity and bubble formation probability depending on the minimum temperature. The temperature of a frozen sample is also inversely proportional to the amount of water remaining liquid between ice crystals (Wettlaufer, 1998) and the solute concentration in that water increases as the volume of the liquid phase decreases. This could lead to increased bubble formation as a function of minimum temperature as the domains between the crystals at −6 and −11°C might still be large enough to contain bubbles that would grow under thawing. However, despite the complexity of the freezing process inside plants relative to the simplicity of our model, the relationship between solute segregation, freezing velocity, and conduit size of Eq. 11 holds, and our calculations describe the dynamics of bubble formation during freezing in general terms (see Calculations).
According to our study, plants have two options to avoid bubble formation during freezing. If the freezing domains are large, they should try to make them freeze slowly, or if freezing is fast, they should try to freeze along small domains. In general, small specimens freeze more rapidly than large and therefore, if freezing occurs perpendicular to the conduits, having narrower conduits in the branches than in the stem may be important in this respect. Also, building narrow-conduit late wood closest to the surface and/or increasing the bark thickness where the conduits are largest will protect the large conduits against rapid freezing. Generally, earlywood/latewood formation with distinct boundaries is not found in the tropics where frequent freeze/thaw cycles are unlikely (e.g., Verheyden et al., 2005). All of the structural traits that can prevent bubble formation during freezing in xylem conduits are similar to those important to drought tolerance in general. Therefore, there may be other functional reasons for the lack or existence of early/late wood or conduit size distribution. But latewood formation would certainly protect the large earlywood conduits against fast freezing, especially since the thermal conductivity of the stem also decreases with increasing cell wall thickness (Simpson and TenWolde, 1999). Freezing could therefore be one component acting in favor of this kind of a growth pattern.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful for support from the Andrew W. Mellon Foundation and the Materials Research Science and Engineering Center at Harvard University. We also thank the Australian Research Council for support (DP110105380).
References
- Améglio T., Bodet C., Lacointe A., Cochard H. (2002). Winter embolism, mechanisms of xylem hydraulic conductivity recovery and springtime growth patterns in walnut and peach trees. Tree Physiol. 22, 1211–1220 10.1093/treephys/22.17.1211 [DOI] [PubMed] [Google Scholar]
- Ball M. C., Canny M. J., Huang C. X., Egerton J. J. G., Wolfe J. (2006). Freeze/thaw-induced embolism depends on nadir temperature: the heterogeneous hydration hypothesis. Plant Cell Environ. 29, 729–745 10.1111/j.1365-3040.2005.01426.x [DOI] [PubMed] [Google Scholar]
- Bianchi M. V., Viskanta R. (1997). Gas segregation during solidification processes. Int. J. Heat Mass Transf. 40, 2035–2043 10.1016/S0017-9310(96)00283-9 [DOI] [Google Scholar]
- Bird R. B., Stewart W. E., Lightfoot E. N. (2002). Transport Phenomena. New York: John Wiley & Sons [Google Scholar]
- Blander M., Katz J. L. (1975). Bubble nucleation in liquids. AIChE J. 21, 833–848 10.1002/aic.690210502 [DOI] [Google Scholar]
- Brower R. C., Kessler D. A., Koplik J., Lenive H. (1984). Geometrical models of interface evolution. Phys. Rev. A 29, 1335–1342 10.1103/PhysRevA.29.1335 [DOI] [PubMed] [Google Scholar]
- Canny M. J. (1990). Rates of apoplastic diffusion in wheat leaves. New Phytol. 116, 263–268 10.1111/j.1469-8137.1990.tb04713.x [DOI] [Google Scholar]
- Canny M. J. (1995). Apoplastic water and solute movement: new rules for an old space. Annu. Rev. Plant Physiol. Plant Mol. Biol. 46, 215–236 10.1146/annurev.pp.46.060195.001243 [DOI] [Google Scholar]
- Cavender-Bares J., Holbrook N. M. (2001). Hydraulic properties and freezing-induced cavitation in sympatric evergreen and deciduous oaks with contrasting habitats. Plant Cell Environ. 24, 1243–1256 10.1046/j.1365-3040.2001.00797.x [DOI] [Google Scholar]
- Chang Y. C., Myerson A. S. (1985). The diffusivity of potassium chloride and sodium chloride in concentrated, saturated and supersaturated aqueous solutions. AIChE J. 31, 890–894 10.1002/aic.690310118 [DOI] [Google Scholar]
- Choat B., Lahr E. C., Melcher P. J., Zwieniecki M. A., Holbrook N. M. (2005). The spatial pattern of air seeding thresholds in mature sugar maple trees. Plant Cell Environ. 28, 1082–1089 10.1111/j.1365-3040.2005.01336.x [DOI] [Google Scholar]
- Choat B., Medek D. E., Stuart S. A., Pasquet-Kok J., Egerton J. J. G., Salari H., Sack L., Ball M. C. (2011). Xylem traits mediate a trade-off between resistance to freeze–thaw-induced embolism and photosynthetic capacity in overwintering evergreens. New Phytol. 191, 996–1005 10.1111/j.1469-8137.2011.03772.x [DOI] [PubMed] [Google Scholar]
- Christman M. A., Sperry J. S., Adler F. R. (2009). Testing the ‘rare pit’ hypothesis for xylem cavitation resistance in three species of Acer. New Phytol. 182, 664–674 10.1111/j.1469-8137.2009.02776.x [DOI] [PubMed] [Google Scholar]
- Christman M. A., Sperry J. S., Smith D. D. (2012). Rare pits, large vessels and extreme vulnerability to cavitation in a ring-porous tree species. New Phytol. 193, 713–720 10.1111/j.1469-8137.2011.03984.x [DOI] [PubMed] [Google Scholar]
- Cochard H., Cruiziat P., Tyree M. T. (1992). Use of positive pressure to establish vulnerability curves: further support for the air-seeding hypothesis and implications for pressure-volume analysis. Plant Physiol. 10, 205–209 10.1104/pp.100.1.205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cochard H., Lemoine D., Ameglio T., Granier A. (2001). Mechanisms of xylem recovery from winter embolism in Fagus sylvatica. Tree Physiol. 21, 27–33 10.1093/treephys/21.1.27 [DOI] [PubMed] [Google Scholar]
- Cordero R. A., Nilsen E. T. (2002). Effects of summer drought and winter freezing on stem hydraulic conductivity of Rhododendron species from contrasting climates. Tree Physiol. 22, 919–928 10.1093/treephys/22.13.919 [DOI] [PubMed] [Google Scholar]
- Davis D. D., Sperry J. S., Hacke U. G. (1999). The relationship between xylem conduit diameter and cavitation caused by freezing. Am. J. Bot. 86, 1367–1372 10.2307/2656919 [DOI] [PubMed] [Google Scholar]
- Debenedetti P. G. (1996). Metastable Liquids. Princeton, NJ: Princeton University Press [Google Scholar]
- Epstein E. (1972). Mineral Nutrition of Plants, Principles and Perspectives. New York: Wiley & Sons [Google Scholar]
- Ewers F. W. (1985). Xylem structure and water conduction in conifer trees, dicot trees, and lianas. Int. Assoc. Wood Anat. Bull. 6, 309–317 [Google Scholar]
- Feild T. S., Brodribb T. (2001). Stem water transport and freeze-thaw xylem embolism in conifers and angiosperms in a Tasmanian treeline heath. Oecologia 127, 314–320 10.1007/s004420000603 [DOI] [PubMed] [Google Scholar]
- Gansert D. (2003). Xylem sap flow as a major pathway for oxygen supply to the sapwood of birch (Betula pubescens Ehr.). Plant Cell Environ. 26, 1803–1814 10.1046/j.1365-3040.2003.01097.x [DOI] [Google Scholar]
- Hacker J., Neuner G. (2007). Ice propagation in plants visualized at the tissue level by infrared differential thermal analysis (IDTA). Tree Physiol. 27, 1661–1670 10.1093/treephys/27.12.1661 [DOI] [PubMed] [Google Scholar]
- Hacke U. G., Sauter J. J. (1996a). Drought-induced xylem dysfunction in petioles, branches and roots of Populus balsamifera L. and Alnus glutinosa (L.) Gaertn. Plant Physiol. 111, 413–417 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hacke U. G., Sauter J. J. (1996b). Xylem dysfunction during winter and recovery of hydraulic conductivity in diffuse-porous and ring-porous trees. Oecologia 105, 435–439 10.1007/BF00330005 [DOI] [PubMed] [Google Scholar]
- Hacke U. G., Sperry J. S. (2003). Limits of xylem refilling under negative pressure in Laurus nobilis and Acer negundo. Plant Cell Environ. 26, 303–311 10.1046/j.1365-3040.2003.00962.x [DOI] [Google Scholar]
- Haynes W. M. (ed.). (2012). CRC Handbook of Chemistry and Physics, 92nd Edn Boca Raton, FL: CRC Press/Taylor and Francis [Google Scholar]
- Holbrook N. M., Zwieniecki M. A. (1999). Embolism repair and xylem tension. Do we need a miracle? Plant Physiol. 120, 7–10 10.1104/pp.120.1.7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hölttä T., Vesala T., Perämäki M., Nikinmaa E. (2002). Relationships between embolism, stem water tension and diameter change. J. Theor. Biol. 215, 23–38 10.1006/jtbi.2001.2485 [DOI] [PubMed] [Google Scholar]
- Jeffrey D. W. (1987). Soil-Plant Relationships, An Ecological Approach. Portland, OR: Timber Press [Google Scholar]
- Just J., Sauter J. J. (1991). Changes in hydraulic conductivity upon freezing of the xylem of Populus x canadensis Moench “robusta.” Trees 5, 117–121 10.1007/BF00227494 [DOI] [Google Scholar]
- Killawee J. A., Fairchild I. J., Tison J.-L., Jansen L., Lorrain R. (1998). Segregation of solutes and gases in experimental freezing of dilute solutions: implications for natural glacial systems. Geochim. Cosmochim. Acta 62, 3637–3655 10.1016/S0016-7037(98)00268-3 [DOI] [Google Scholar]
- Koop T., Luo B. P., Biermann U. M., Peter T. (1996). “Freezing of binary and ternary solutions of H2SO4, HNO3 and H2O under stratospheric conditions: nucleation statistics and experiments,” in Nucleation and Atmosphere Aerosols, eds Kulmala M., Wagner P. E. (Tarrytown, NY: Pergamon; ), 318–321 [Google Scholar]
- Kulmala M., Riipinen I., Sipilä M., Manninen H. E., Petäjä T., Junninen H., Dal Maso M., Mordas G., Mirme A., Vana M., Hirsikko A., Laakso L., Harrison R. M., Hanson I., Leung C., Lehtinen K. E. J., Kerminen V. M. (2007). Toward direct measurement of atmospheric nucleation. Science 318, 89–92 10.1126/science.1144124 [DOI] [PubMed] [Google Scholar]
- Langan S. J., Ewers F. W., Davis S. D. (1997). Xylem dysfunction caused by water stress and freezing in two species of co-occurring chaparral shrubs. Plant Cell Environ. 20, 425–437 10.1046/j.1365-3040.1997.d01-94.x [DOI] [Google Scholar]
- Lee S.-J., Kim Y. (2008). In vivo visualization of the water-refilling process in xylem vessels using x-ray micro-imaging. Ann. Bot. 101, 595–602 10.1093/aob/mcm312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemoine D., Granier A., Cochard H. (1999). Mechanism of freeze-induced embolism in Fagus sylvatica L. Trees 13, 206–210 10.1007/PL00009751 [DOI] [Google Scholar]
- Levy P. E., Meir P., Allen S. J., Jarvis P. G. (1999). The effect of aqueous transport of CO2 in xylem sap on gas exchange in woody plants. Tree Physiol. 19, 53–58 10.1093/treephys/19.1.53 [DOI] [PubMed] [Google Scholar]
- Liu X. Y. (1999). A new kinematic model for three-dimensional heterogeneous nucleation. J. Chem. Phys. 111, 1628–1635 10.1063/1.479391 [DOI] [Google Scholar]
- LoGullo M. A., Salleo S. (1993). Different vulnerabilities of Quercus ilex L. to freeze- and summer drought-induced xylem embolism: an ecological interpretation. Plant Cell Environ. 16, 511–519 10.1111/j.1365-3040.1993.tb00898.x [DOI] [Google Scholar]
- Luo Y., Roux B. (2010). Simulation of osmotic pressure in concentrated aqueous salt solutions. J. Phys. Chem. Lett. 1, 183–189 10.1021/jz900079w [DOI] [Google Scholar]
- Lybeck B. R. (1959). Winter freezing in relation to the rise of sap in tall trees. Plant Physiol. 34, 482–486 10.1104/pp.34.4.482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maloka I. E. (2005). Generalized liquid molar volume at the normal boiling point correlation. Pet. Sci. Technol. 23, 133–136 10.1081/LFT-200028046 [DOI] [Google Scholar]
- Martinez-Vilalta J., Pockman W. T. (2002). The vulnerability to freezing-induced xylem cavitation of Larrea tridentata (Zygophyllaceae) in the Chihuahuan desert. Am. J. Bot. 89, 1916–1924 10.3732/ajb.89.12.1916 [DOI] [PubMed] [Google Scholar]
- Mayr S., Cochard H., Ameglio T., Kikuta S. B. (2007). Embolism formation during freezing in the wood of Picea abies. Plant Physiol. 143, 60–67 10.1104/pp.106.085704 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayr S., Sperry J. S. (2010). Freeze-thaw-induced embolism in Pinus contorta: centrifuge experiments validate the “thaw-expansion hypothesis” but conflict with ultrasonic emission data. New Phytol. 185, 1016–1024 10.1111/j.1469-8137.2009.03133.x [DOI] [PubMed] [Google Scholar]
- Pittermann J., Sperry J. S. (2003). Tracheid diameter is the key trait determining the extent of freezing-induced embolism in conifers. Tree Physiol. 23, 907–914 10.1093/treephys/23.13.907 [DOI] [PubMed] [Google Scholar]
- Pittermann J., Sperry J. S. (2006). Analysis of freeze-thaw embolism in conifers. The interaction between cavitation pressure and tracheid size. Plant Physiol. 140, 374–382 10.1104/pp.105.067900 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pockman W. T., Sperry J. S. (1997). Freezing-induced xylem cavitation and the northern limit of Larrea tridentata. Oecologia 109, 19–27 10.1007/s004420050053 [DOI] [PubMed] [Google Scholar]
- Richards P. M. (1989). Effect of surface roughening on liquid-solid interface velocity. J. Mater. Res. 4, 607–611 10.1557/JMR.1989.0607 [DOI] [Google Scholar]
- Robson D. J., McHardy W. J., Petty J. A. (1988). Freezing in conifer xylem II. Pit aspiration and bubble formation. J. Exp. Bot. 39, 1617–1621 10.1093/jxb/39.11.1617 [DOI] [Google Scholar]
- Robson D. J., Petty J. A. (1987). Freezing in conifer xylem I. Pressure changes and growth velocity of ice. J. Exp. Bot. 38, 1901–1908 10.1093/jxb/38.11.1901 [DOI] [Google Scholar]
- Salleo S., Trifilo P., LoGullo M. A. (2008). Vessel wall vibrations: trigger for embolism repair? Funct. Plant Biol. 35, 289–297 10.1071/FP07239 [DOI] [PubMed] [Google Scholar]
- Sanders R. (1999). Henry’s Law Constants. Available at: http://www.mpchmainz.mpg.de/sander/res/henry.html
- Secchi F., Zwieniecki M. A. (2011). Sensing embolism in xylem vessels: the role of sucrose as a trigger for refilling. Plant Cell Environ. 34, 514–524 10.1111/j.1365-3040.2010.02259.x [DOI] [PubMed] [Google Scholar]
- Shen V. K., Debenedetti P. G. (2001). Density-functional study of homogenous bubble nucleation in the stretched Lennard-Jones fluid. J. Chem. Phys. 114, 4149–4159 10.1063/1.1344604 [DOI] [Google Scholar]
- Simpson W., TenWolde A. (1999). “Physical properties and moisture relations of wood,” in Wood Handbook, Chap. 3 (Madison, WI: United States Department of Agriculture; ), 3–25 [Google Scholar]
- Sperry J. S. (1995). “Limitations on stem water transport and their consequences,” in Plant Stems Physiology and Functional Morphology, ed. Gartner B. L. (San Diego, CA: Academic Press; ), 105–120 [Google Scholar]
- Sperry J. S. (2003). Evolution of water transport and xylem structure. Int. J. Plant Sci. 164, S115–S127 10.1086/368398 [DOI] [Google Scholar]
- Sperry J. S., Donnelly J. R., Tyree M. T. (1988). Seasonal occurrence of xylem embolism in sugar maple (Acer saccharum). Am. J. Bot. 75, 1212–1218 10.2307/2444104 [DOI] [Google Scholar]
- Sperry J. S., Sullivan J. E. M. (1992). Xylem embolism in response to freeze-thaw cycles and water stress in ring-porous, diffuse-porous and conifer species. Plant Physiol. 100, 605–613 10.1104/pp.100.2.605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spicer R., Holbrook N. M. (2005). Within-stem oxygen concentration and sap flow in four temperate tree species: does long-lived xylem parenchyma experience hypoxia? Plant Cell Environ. 28, 192–201 10.1111/j.1365-3040.2004.01262.x [DOI] [Google Scholar]
- Stiller V., Sperry J. S., Lafitte R. (2005). Embolized conduits of rice (Oryza sativa Poaceae) refill despite negative xylem pressure. Am. J. Bot. 92, 1970–1974 10.3732/ajb.92.12.1970 [DOI] [PubMed] [Google Scholar]
- Stuart S. A., Choat B., Martin K. C., Holbrook N. M., Ball M. C. (2007). The role of freezing in setting the latitudinal limits of mangrove forests. New Phytol. 173, 576–583 10.1111/j.1469-8137.2006.01938.x [DOI] [PubMed] [Google Scholar]
- Sucoff E. (1969). Freezing of conifer xylem and the cohesion-tension theory. Physiol. Plant 22, 424–431 10.1111/j.1399-3054.1969.tb07394.x [DOI] [Google Scholar]
- Taiz L., Zeiger E. (2002). Plant Physiology, 3rd Edn Sunderland, MA: Sinauer Associates Inc [Google Scholar]
- Top Z., Martin S., Becker P. (1985). On the dissolved surface oxygen supersaturation in the Arctic. Geophys. Res. Lett. 12, 821–823 10.1029/GL012i012p00821 [DOI] [Google Scholar]
- Tucker A. S., Ward C. A. (1975). Critical state of bubbles in liquid-gas solutions. J. Appl. Phys. 46, 4801–4808 10.1063/1.321506 [DOI] [Google Scholar]
- Tyree M. T., Salleo S., Nardini A., LoGullo M. A., Mosca R. (1999). Refilling of embolized vessels in young stems of Laurel. Do we need a new paradigm? Plant Physiol. 120, 11–21 10.1104/pp.120.1.11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyree M. T., Sperry J. S. (1989). Vulnerability of xylem to cavitation and embolism. Annu. Rev. Plant Physiol. Plant Mol. Biol. 40, 19–38 10.1146/annurev.pp.40.060189.000315 [DOI] [Google Scholar]
- Utsumi Y., Sano Y., Funada R., Fujikawa S., Ohtani J. (1999). The progression of cavitation in earlywood vessels of Fraxinus mandshurica var japonica during freezing and thawing. Plant Physiol. 121, 897–904 10.1104/pp.121.3.897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verheyden A., De Ridder F., Schmitz N., Beeckman H., Koedam N. (2005). High-resolution time series of vessel density in Kenyan mangrove trees reveal a link with climate. New Phytol. 167, 425–435 10.1111/j.1469-8137.2005.01415.x [DOI] [PubMed] [Google Scholar]
- Wettlaufer J. S. (1998). “Introduction to crystallization phenomena in sea ice,” in Advanced Study Institute: Physics of Ice-Covered Seas, ed. Leppäranta M. (Helsinki: Helsinki University Press; ), 105–194 [Google Scholar]
- Wilt P. M. (1985). Nucleation rates and bubble stability in water-carbon dioxide solutions. J. Colloid Interface Sci. 112, 530–538 10.1016/0021-9797(86)90122-0 [DOI] [Google Scholar]
- Wolfe J., Bryant G. (1999). Freezing, drying and/or vitrification of membrane-solute-water systems. Cryobiology 39, 103–129 10.1006/cryo.1999.2195 [DOI] [PubMed] [Google Scholar]
- Zweifel R., Häsler R. (2000). Frost-induced reversible shrinkage of bark of mature subalpine conifers. Agr. Forest Meteorol. 102, 213–222 10.1016/S0168-1923(00)00135-0 [DOI] [Google Scholar]
- Zwieniecki M. A., Holbrook N. M. (2000). Bordered pit structure and vessel wall surface properties. Implications for embolism repair. Plant Physiol. 123, 1015–1020 10.1104/pp.123.3.1015 [DOI] [PMC free article] [PubMed] [Google Scholar]