Abstract
We present a full-field reflection phase microscope that combines low-coherence interferometry and off-axis digital holographic microscopy (DHM). The reflection-based DHM provides highly sensitive and a single-shot imaging of cellular dynamics while the use of low coherence source provides a depth-selective measurement. The setup uniquely uses a diffraction grating in the reference arm to generate an interference image of uniform contrast over the entire field-of-view albeit low-coherence light source. We have measured the path-length sensitivity of our instrument to be approximately that makes it suitable for nanometer-scale full-field measurement of membrane dynamics in live cells.
OCIS codes: (120.3890) Medical optics instrumentation, (170.4500) Optical coherence tomography, (170.1530) Cell analysis
1. Introduction
Bio-microrheology is the quantitative study of mechanical properties of live cells [1]. Variations in mechanical properties are intrinsic indicators of ongoing cellular processes such as increase in elasticity of certain cancer cells [2], change of membrane stiffness in malaria-infected red blood cells [3], changes in cellular adhesion [4], and so forth. The measurement of rheological properties of cell membranes is advantageous since it may also indirectly provide information on the internal structures of cell [1]. A number of different techniques exist to assess membrane rheological properties of live cells. These include atomic force microscopy (AFM) [5], optical and magnetic tweezers [6, 7], pipette aspiration [8–10], electric field deformation [11], and full-field transmission phase microscopy [12]. Many of these methods are invasive and use large deformations that may lead to cell damage or cell’s response to mechanical strain rather than its intrinsic response. For point-measurement techniques such as AFM, the time scales to probe large surface areas of cell membrane are in minutes, preventing the study of high-speed cell membrane dynamics over a wider surface area. Full-field transmission phase microscopy has been successfully utilized to measure membrane flcutuations in red blood cells over a broad range of temporal and spatial frequencies [12]. Furthermore, the measured membrane fluctuations can be used in appropriate mathematical models to calculate rheological properties of red blood cells [13, 14]. However, for most type of cells, which have complicated 3-D internal cellular structures, transmission-type optical techniques will not be suitable as they will probe a combination of membrane as well as bulk properties of cells that are difficult to decouple. In this context, properly designed reflection-based phase microscopy with depth-sectioning capability can play vital role to exclusively access the membrane dynamics of nucleated cells. Moreover, transmission mode techniques measure relative phase shift induced by the sample with respect to that by the medium. Thus, the measured phase shift is proportional to the refractive index difference, Δn, between the sample and the medium. In contrast, reflection phase microscopy techniques yield phase measurement proportional to the index of refraction, n, of the medium rather than the relative index, Δn. Thus, reflection-based optical methods promise a 2n/Δn advantage in measurement sensitivity over the transmission-based optical techniques.
Low-coherence interferometry is necessary to exclusively sample the reflection signal from the depth of interest. In the past, both spectral domain as well as time domain optical coherence tomography (OCT) based implementations of reflection phase microscopy have been reported [15–19]. Joo et al. and Choma et al. have independently developed similar setups using self phase-referenced spectral domain phase microscopy setups using point illumination [15, 16]. Ellerbee et al. used the phase sensitive OCT based configuration in [15] to visualize the motion of intracellular structures [20]. In recent past, we have designed and developed a quantitative phase microscope based on spectral domain OCT and line-field illumination [19]. The line-field reflection phase microscope exploited low-coherent illumination and confocal gating to successfully obtain the surface profile of cell membrane with sub-nanometer axial resolution. Using the line-field approach, we demonstrated 1 kHz frame rate with more than hundred data points along the line illumination. The first full-field phase sensitive OCT was reported using swept-source OCT configuration, which required 1024 wavelength encoded images to generate a volume phase image [17]. Moreover, the acquisition rate (25 ms integration time per wavelength) was not sufficient to observe cellular dynamics. In order to observe intrinsic membrane motion of living cells, Yamauchi et al. developed a full-field time-domain reflection phase microscope based on phase shifting interferometry and captured sectional surface profile of living cells. But the time resolution was limited to 1.25 sec due to the need for taking multiple images [18]. There was an attempt to use an off-axis digital holography with low-coherence source to take a full-field phase image in a single shot [21]. But the tilting of reference mirror caused uneven interference contrast and thereby impeded full-field imaging.
In this paper, we present the first single-shot full-field reflection phase microscope based on low-coherence interferometry and off-axis interferometry. Its unique design provides the wavefront tilt in the reference beam such that it interferes with the sample beam across the whole field-of-view. The single-shot interferograms are processed to determine the optical phase of the beam reflected back from the sample under investigation, providing its surface profile without the need for raster or 1-D scanning. Since single-shot interferograms are required to retrieve sample phase, the amount of light returning from the cell and camera frame rate will define the speed of the surface imaging. We have demonstrated 1 kHz full-field imaging (2400 times faster than the work reported in Ref [18].) to observe the membrane motion related to the thermal fluctuations in HeLa cells. The measured membrane fluctuations, which are typically on the order of a nanometer or less, can in turn be used to estimate mechanical properties of plasma membrane in nucleated cells using methods similar to that for erythrocytes [13].
2. Full-field reflection phase microscope
2.1 Experimental setup
Figure 1 shows the schematic of our single-shot full-field reflection phase microscope (FF-RPM). Light from a mode-locked Ti:Sapphire laser (center wavelength, λc = 800 nm) is coupled into a single-mode fiber for delivery as well as for spectrum broadening. The full-width-half-maximum spectral width, Δλ, at the fiber output measures 50 nm, which yields a round trip coherence length of 4 μm in a typical culture medium with refractive index, n, equal to 1.33. The sample beam that travels through lenses L2, L3, L4, and a water immersion objective lens L5 (Olympus UPlanSApo 60×/1.2 W), reflects off the sample surface and makes an image of the sample on a high-speed complementary metal oxide semiconductor (CMOS) camera (Photron 1024PCI) via L6 and L15. The reference beam, which passes through L7, L8, L9 and L10, is diverted on its way back using a beam splitter BS2. Portion of the reference beam that goes back through BS2 is blocked using a spatial filter S1. On the other hand, the deflected beam passes through L11-L14 and combines with the returning sample beam at the 3rd beam splitter BS3. For off-axis interferometry, a diffraction grating G is introduced in one of the conjugate planes. Out of multiple diffracted orders, we choose only the +1st order by placing a spatial filter S2 in the Fourier plane of lens L12. As a result, the diffracted reference beam interferes with the sample beam in the image plane at an angle. We note that the period of the diffraction grating and the magnification between the grating and the camera provide the desired angular shift to the reference beam for off-axis interferometry. Since the grating and the camera suffice the imaging condition, the optical path length measured from any point on the grating to the corresponding pixel on the camera is constant. As a result, we achieve homogeneous fringe visibility across the whole field-of-view unlike the setup in [21] that simply used reference mirror tilt for off-axis interferometry. We note that the proposed setup is capable of taking quantitative phase images in double-pass transmission mode [22] as well as reflection mode, which is achieved by placing the coherence gate on the glass slide or the cell membrane, respectively.
Fig. 1.
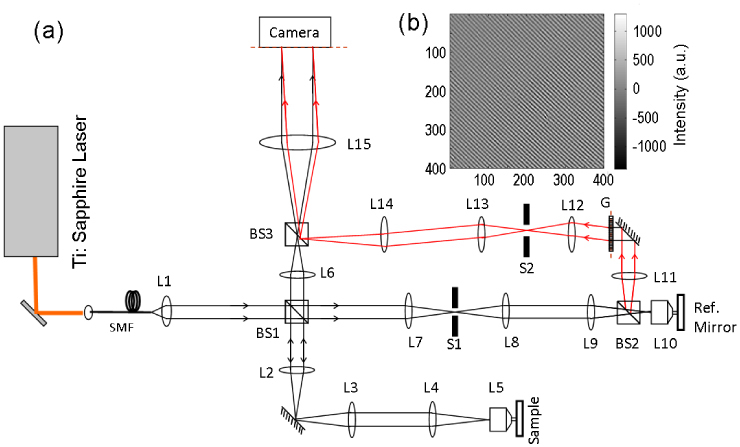
(a) Schematic of full-field single-shot reflection phase microscope. SMF: single mode fiber, Li: ith spherical lens, BSi: ith beam splitter, G: diffraction grating, Si: ith spatial filter. (b) Typical interferogram with a flat surface as the sample after subtracting the no fringe image representing the DC signal.
2.2 Signal processing
Figure 1(b) shows a measured interferogram with a flat surface as the sample. As expected, the spatial fringes are straight as well as equally spaced when the sample is flat. The total measured intensity at the CMOS camera can be written as
| (1) |
where and are the reference and sample beam intensity distributions, respectively. u and v represent the frequency of spatial fringes along the x- and y- axes, and is the spatially varying phase associated with the sample under study. We also acquire a no-fringe image that represents the DC component in Eq. (1) by shifting the coherence gate out of the sample. By subtracting the no-fringe image from the original interferogram, we get only the interference term.
Figure 2 (a) shows interference portion of the 2-D interferogram recorded by our full-field reflection phase microscope, using a 40 microns microsphere immersed in water as a sample. The fringes, which are straight and equally-spaced for a flat sample, are changed by the modified wavefront of the sample beam reflected off the microsphere. In order to extract the profile of the sample under investigation, we take Hilbert transform of the interference portion of the 2-D interferogram, which yields both amplitude and phase of the returning sample beam. In the past, this approach has been used to retrieve sample amplitude and phase information in a transmission type quantitative phase microscope [12, 23]. Figure 2 (b) shows the amplitude of the 2-D Fourier transform of the interferogram in Fig. 2 (a). More specifically, the 1st and −1st order components are shown in the first and third quadrants, respectively. We crop the 1st order component in the Fourier image, shift it to the center of the Fourier plane (see Fig. 2 (c)), and then take the inverse Fourier transform. The phase of the inverse Fourier transformed image (Fig. 2 (d)) provides the optical phase of the sample beam wavefront. By applying 2-D spatial phase unwrapping, the surface profile of the sample without 2π phase ambiguity is obtained as shown in the Fig. 2 (e). The high measured phase profile of the bead can be explained by the fact that in reflection phase setup the change in phase is linearly related to the change in the axial position Δl as
| (2) |
where nm is the refractive index of the medium (nm = 1.33 for pure water).
Fig. 2.
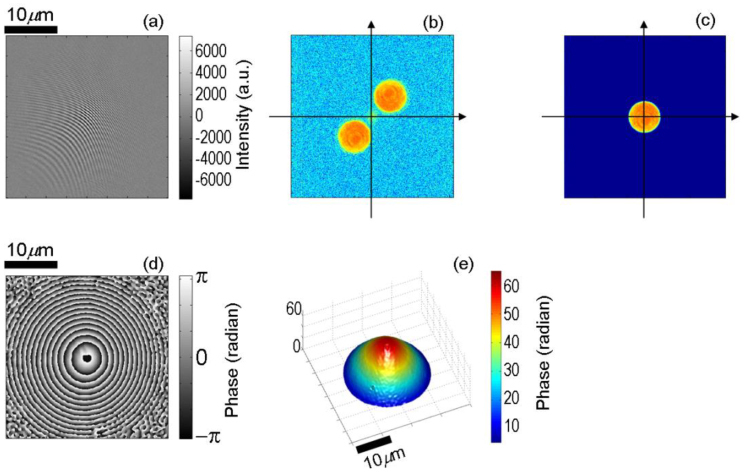
Surface profile of a 40 microns diameter polystyrene microsphere measured using our single-shot full-field reflection phase microscope. (a) Interferogram after subtracting the no fringe image representing the DC signal, (b) amplitude component of the 2-dimensional Fourier transform of (a), (c) spatially filtered image of (b), (d) phase component of the inverse Fourier transform of (c), and (e) unwrapped phase image derived from (d).
3. Results and discussion
3.1 Common mode noise rejection and measurement sensitivity
Intrinsic membrane fluctuations in living cells are typically on the order of a nanometer or less; the measurement of these small membrane fluctuations requires the development of quantitative phase microscopes with high signal-to-noise ratio (SNR). In this section, we show the measurement sensitivity of our full-field RPM in terms of the least detectable axial motion; the configuration to measure the measurement sensitivity is shown in Fig. 3(a) . The full-field illumination shines on both the surfaces; mirror M1 mounted on a translation stage and mirror M2 attached to a Lead Zirconate Titanate (PZT) actuator.
Fig. 3.
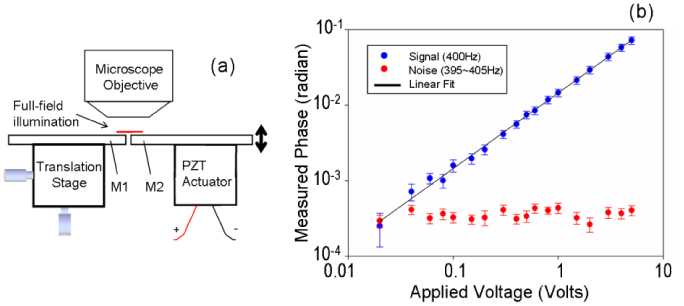
(a) Configuration to determine the sensitivity of FF-RPM. and (b) Measured phase fluctuation (radian) as a function of applied voltage. Mi: ith mirror, PZT: Lead Zirconate Titanate.
In order to suppress the common mode noise due to independent mechanical or thermal fluctuations of the reference beam path with respect to the sample beam path, we utilize a self-phase referencing method which is previously described in Ref [19]. Since the phase of all the points in the full-field illumination is acquired at the same time, every point in the field of view shares the same interferometric noise as any other point. We take the phase measured from a portion of the beam illuminating the reflector M1 as the reference phase, representing the common-mode noise. By subtracting this reference phase from the phase of the subsequent points on M2, we remove the common-mode noise to obtain actual fluctuation of the surface M2.
To demonstrate common-mode phase noise rejection, the PZT actuator was driven at the frequency of 400 Hz whereas the amplitude of the PZT driving voltage was varied from 0.02 - 5 Volts. Single-shot phase images of the M1 and M2 were acquired simultaneously for duration of 1 second at 1 millisecond intervals. The temporal power spectral density (PSD) was calculated from the temporal fluctuation of the phase measured from M2, and the square-root of the PSD at 400 Hz was selected to determine the axial motion signal. Figure 3(b) shows the measured axial motion at 400 Hz versus PZT driving voltage; the plot is well fit by the line 14.5 mrad/Volt. Figure 3(b) also shows the noise floor estimated by taking the average of the square-root of the PSD from 395 - 405 Hz excluding the 400 Hz frequency. The maximum noise was only 0.44 . This corresponds to 21 , since, in a reflection-mode phase-sensitive setup, the change in phase is linearly related to the change in the axial position Δl as illustrated in Eq. (2).
3.2 Quantitative phase imaging of live cells
To demonstrate high-speed quantitative imaging of live cells, we sub-cultured HeLa cells on glass slides 2 days before the measurement and immersed in standard culture medium (Dulbecco's Modified Eagle Medium). As mentioned earlier, our setup is capable of taking transmission phase images as well as reflection phase images. Figures 4(a) and 4(b) show the location of the coherence gate for double-pass transmission phase imaging [22] and the full-field reflection phase imaging, respectively. In double-pass transmission phase imaging, the illumination light passes through the cell, reflects off the glass surface and then passes through the cell again [22]. The measured transmission phase difference is related to the sample height as
| (3) |
where is the mean of the refractive index difference between culture medium and cytoplasm and h is the height of the cell. Figure 4(c) shows the corresponding transmission phase image of a live HeLa cell. The height of the cell was roughly estimated to be 8.5 by substituting = 0.03 [24] and = 4 in Eq. (2).
Fig. 4.
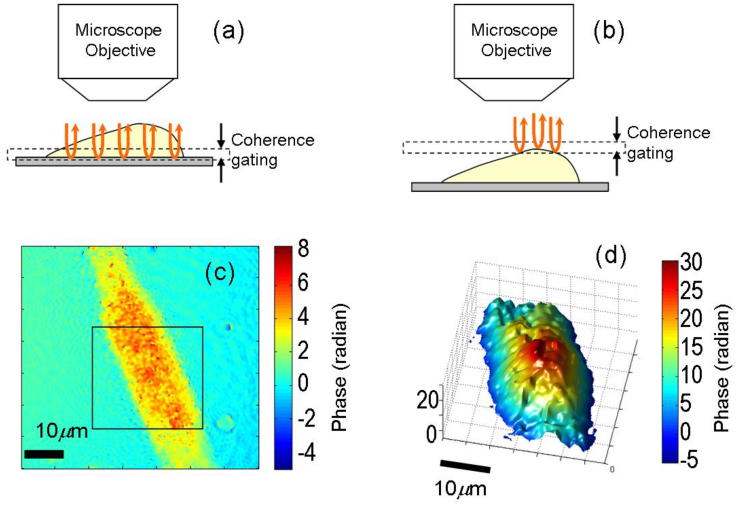
(a,b) Location of coherence gate for double-pass transmission and reflection phase imaging, respectively. (c) Double-pass transmission phase image of a HeLa cell, and (d) Single-shot reflection phase image of the region inside square box in (c).
For full-field reflection phase imaging, the focal plane as well as the coherence gate are placed on the cell surface. Since the backscattered light from out-of-coherence gate region does not contribute to the interference, we gather the full-field phase information [see Fig. 4(d)] of cell surface within the coherence gate as depicted in Fig. 4(b). To get maximum contribution from cell plasma membrane, we adjust the reference arm mirror so that the coherence gate is centered at the surface. This indicates that, at the most, only half the coherence gate (2 µm) is inside the cell. Moreover, due to the Gaussian nature of the coherence gate, most of the signal contribution would be from regions neighboring the center of the coherence gate. In this case, the reflection phase difference is directly related to the height difference as
| (4) |
where is the refractive index of the culture medium (typically = 1.335). Substituting ΔφR = 25 radians in Eq. (4), the differential height of the cell sampled by the coherence gating is estimated to be 1.2 µm. This illustrates that since our method employs coherence gating [see Fig. 4 (b)], the acquired reflection phase image is a partial shape of the cell surface. We note that the features (or roughness) of the phase image in Fig. 4(d) may be attributed to the speckle phase noise due to high spatial coherence of the source. Using an optical source with lower spatial and temporal coherence will help reduce the speckle phase noise as well as further suppress contributions from the internal organelles that are rather close to the cell plasma membrane.
The advantage of the reflection-mode imaging is also evident when comparing Eqs. (3) and (4) in the context of SNR. In other words, assuming that the phase sensitivity of the transmission and reflection-mode measurements is same, the height resolution (or measurement sensitivity) of the reflection phase imaging is 40 times better than that of transmission measurement. Moreover, the reflection phase image will reveal the shape of the cell surface independent of the distribution of intracellular refractive index since it depends only on the refractive index of the medium which can be accurately measured by a conventional refractometer.
3.3 Measurement of cell membrane fluctuation
As discussed in section 1, membrane fluctuations are intrinsic indicator of overall cellular condition and have been used in the past to successfully estimate membrane mechanical properties in relation to different stages of malaria infection in human red blood cells [3]. But for eukaryotic cells having complex internal structures, our full-field reflection phase microscope is well-suited to selectively measure membrane fluctuations by effectively choosing to reject contributions from the internal cellular structures.
To demonstrate our system’s capabilities, we have studied the membrane fluctuations in HeLa cells under different cell conditions. More specifically, we prepared (i) a sample of living normal HeLa cells, (ii) a fixed HeLa cell sample after treatment with 2% paraformaldehyde and (iii) a sample of HeLa cells treated with 8 nM Cytochalasin-D which inhibits actin polymerization [25]. The frame rate of the image acquisition was set to 1 kHz and the data was recorded for duration of 1 sec for each cell. As shown in Fig. 5(a) , the sample under test was tilted to simultaneously acquire membrane fluctuations as well as background phase from the coverslip. By subtracting the background phase change observed on the coverslip, the common-mode mechanical noise was eliminated. We measured the temporal fluctuations on the cell surface and calculated the PSD of membrane motion for each cell. Figure 5(b) shows the mean PSD for each cell population. The number of normal, fixed, and Cytochalasin-D treated cells used in this study were N = 22, 20, and 33, respectively. As expected, the PSD of the fixed cells was measured smaller and flatter than the normal ones implying that the cell membrane became stiffer after chemical fixation. On the other hand, the PSD of the Cytochalasin-D treated cells was measured larger than the normal ones implying that the cell membrane became softer due to the inhibition of actin polymerization.
Fig. 5.
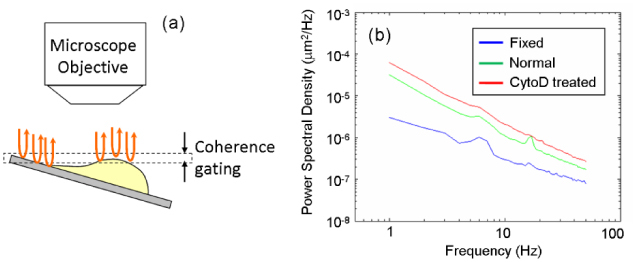
Setup and results of the cell membrane fluctuation measurement. (a) Location of coherence gate; the sample is tilted to simultaneously acquire membrane fluctuations as well as background phase from the coverslip. (b) Power spectral density of membrane fluctuations as a function of frequency for three different populations: blue, formalin fixed; green, normal; and red, Cytochalasin-D treated HeLa cells.
4. Conclusion
We have proposed and demonstrated, for the first time, a quantitative reflection phase microscope based on en-face optical coherence tomography and off-axis digital holography. The setup utilizes a diffraction grating in the reference arm to provide the desired angular tilt to the reference beam for off-axis interferometry. The full-field illumination allows single-shot phase measurement of multiple points on the surface of interest and enables the use of self phase-referencing method to reject common-mode noise inherent in interferometric setups using a separate reference arm. In our full-field reflection phase microscope, the self-phase referencing suppressed phase detection noise down to as low as 21 . With such high phase sensitivity, we were able to resolve thermal motion of the cell surface in the field of view, which was on the order of 100 picometers to 150 nanometers. A potential application of the full-field reflection phase microscope is to use the membrane fluctuations to estimate the mechanical properties of cell membrane; these variations in cell membrane mechanical properties can serve as non-invasive biomarker to study pathophysiology of general cell types [13]. Another future direction includes full-field and multi-cell imaging of cellular electromotility, including cell membrane motion driven by the action potential in single mammalian cells [26].
Acknowledgements
This work was funded by the National Center for Research Resources of the National Institutes of Health ( P41-RR02594-25), the National Science Foundation ( DBI-0754339), and Hamamatsu Photonics.
References and links
- 1.Weihs D., Mason T. G., Teitell M. A., “Bio-microrheology: a frontier in microrheology,” Biophys. J. 91(11), 4296–4305 (2006). 10.1529/biophysj.106.081109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Beil M., Micoulet A., von Wichert G., Paschke S., Walther P., Omary M. B., Van Veldhoven P. P., Gern U., Wolff-Hieber E., Eggermann J., Waltenberger J., Adler G., Spatz J., Seufferlein T., “Sphingosylphosphorylcholine regulates keratin network architecture and visco-elastic properties of human cancer cells,” Nat. Cell Biol. 5(9), 803–811 (2003). 10.1038/ncb1037 [DOI] [PubMed] [Google Scholar]
- 3.Park Y. K., Diez-Silva M., Popescu G., Lykotrafitis G., Choi W. S., Feld M. S., Suresh S., “Refractive index maps and membrane dynamics of human red blood cells parasitized by Plasmodium falciparum,” Proc. Natl. Acad. Sci. U.S.A. 105(37), 13730–13735 (2008). 10.1073/pnas.0806100105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Almqvist N., Bhatia R., Primbs G., Desai N., Banerjee S., Lal R., “Elasticity and adhesion force mapping reveals real-time clustering of growth factor receptors and associated changes in local cellular rheological properties,” Biophys. J. 86(3), 1753–1762 (2004). 10.1016/S0006-3495(04)74243-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Alcaraz J., Buscemi L., Grabulosa M., Trepat X., Fabry B., Farre R., Navajas D., “Microrheology of human lung epithelial cells measured by atomic force microscopy,” Biophys. J. 84(3), 2071–2079 (2003). 10.1016/S0006-3495(03)75014-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Puig-de-Morales-Marinkovic M., Turner K. T., Butler J. P., Fredberg J. J., Suresh S., “Viscoelasticity of the human red blood cell,” Am. J. Physiol. Cell Physiol. 293(2), C597–C605 (2007). 10.1152/ajpcell.00562.2006 [DOI] [PubMed] [Google Scholar]
- 7.Svoboda K., Block S. M., “Biological applications of optical forces,” Annu. Rev. Biophys. Biomol. Struct. 23(1), 247–285 (1994). 10.1146/annurev.bb.23.060194.001335 [DOI] [PubMed] [Google Scholar]
- 8.Evans E., Leung A., “Adhesivity and rigidity of erythrocyte membrane in relation to wheat germ agglutinin binding,” J. Cell Biol. 98(4), 1201–1208 (1984). 10.1083/jcb.98.4.1201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hebbel R. P., Leung A., Mohandas N., “Oxidation-induced changes in microrheologic properties of the red blood cell membrane,” Blood 76(5), 1015–1020 (1990). [PubMed] [Google Scholar]
- 10.Engstrom K. G., Moller B., Meiselman H. J., “Optical Evaluation of Red Blood Cell Geometry Using Micropipette aspiration,” Blood Cells 18(2), 241–257, discussion 258–265 (1992). [PubMed] [Google Scholar]
- 11.Engelhardt H., Gaub H., Sackmann E., “Viscoelastic properties of Erythrocyte Membranes in High-Frequency Electric Fields,” Nature 307(5949), 378–380 (1984). 10.1038/307378a0 [DOI] [PubMed] [Google Scholar]
- 12.Popescu G., Ikeda T., Dasari R. R., Feld M. S., “Diffraction phase microscopy for quantifying cell structure and dynamics,” Opt. Lett. 31(6), 775–777 (2006). 10.1364/OL.31.000775 [DOI] [PubMed] [Google Scholar]
- 13.Park Y., Best C. A., Badizadegan K., Dasari R. R., Feld M. S., Kuriabova T., Henle M. L., Levine A. J., Popescu G., “Measurement of red blood cell mechanics during morphological changes,” Proc. Natl. Acad. Sci. U.S.A. 107(15), 6731–6736 (2010). 10.1073/pnas.0909533107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang R., Ding H., Mir M., Tangella K., Popescu G., “Effective 3D viscoelasticity of red blood cells measured by diffraction phase microscopy,” Biomed. Opt. Express 2(3), 485–490 (2011). 10.1364/BOE.2.000485 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Choma M. A., Ellerbee A. K., Yang C., Creazzo T. L., Izatt J. A., “Spectral-domain phase microscopy,” Opt. Lett. 30(10), 1162–1164 (2005). 10.1364/OL.30.001162 [DOI] [PubMed] [Google Scholar]
- 16.Joo C., Akkin T., Cense B., Park B. H., de Boer J. F., “Spectral-domain optical coherence phase microscopy for quantitative phase-contrast imaging,” Opt. Lett. 30(16), 2131–2133 (2005). 10.1364/OL.30.002131 [DOI] [PubMed] [Google Scholar]
- 17.Sarunic M. V., Weinberg S., Izatt J. A., “Full-field swept-source phase microscopy,” Opt. Lett. 31(10), 1462–1464 (2006). 10.1364/OL.31.001462 [DOI] [PubMed] [Google Scholar]
- 18.Yamauchi T., Iwai H., Miwa M., Yamashita Y., “Low-coherent quantitative phase microscope for nanometer-scale measurement of living cells morphology,” Opt. Express 16(16), 12227–12238 (2008). 10.1364/OE.16.012227 [DOI] [PubMed] [Google Scholar]
- 19.Yaqoob Z., Choi W., Oh S., Lue N., Park Y., Fang-Yen C., Dasari R. R., Badizadegan K., Feld M. S., “Improved phase sensitivity in spectral domain phase microscopy using line-field illumination and self phase-referencing,” Opt. Express 17(13), 10681–10687 (2009). 10.1364/OE.17.010681 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ellerbee A. K., Creazzo T. L., Izatt J. A., “Investigating nanoscale cellular dynamics with cross-sectional spectral domain phase microscopy,” Opt. Express 15(13), 8115–8124 (2007). 10.1364/OE.15.008115 [DOI] [PubMed] [Google Scholar]
- 21.Massatsch P., Charriere F., Cuche E., Marquet P., Depeursinge C. D., “Time-domain optical coherence tomography with digital holographic microscopy,” Appl. Opt. 44(10), 1806–1812 (2005). 10.1364/AO.44.001806 [DOI] [PubMed] [Google Scholar]
- 22.Iwai H., Fang-Yen C., Popescu G., Wax A., Badizadegan K., Dasari R. R., Feld M. S., “Quantitative phase imaging using actively stabilized phase-shifting low-coherence interferometry,” Opt. Lett. 29(20), 2399–2401 (2004). 10.1364/OL.29.002399 [DOI] [PubMed] [Google Scholar]
- 23.Ikeda T., Popescu G., Dasari R. R., Feld M. S., “Hilbert phase microscopy for investigating fast dynamics in transparent systems,” Opt. Lett. 30(10), 1165–1167 (2005). 10.1364/OL.30.001165 [DOI] [PubMed] [Google Scholar]
- 24.Choi W., Fang-Yen C., Badizadegan K., Oh S., Lue N., Dasari R. R., Feld M. S., “Tomographic phase microscopy,” Nat. Methods 4(9), 717–719 (2007). 10.1038/nmeth1078 [DOI] [PubMed] [Google Scholar]
- 25.Casella J. F., Flanagan M. D., Lin S., “Cytochalasin D inhibits actin polymerization and induces depolymerization of actin filaments formed during platelet shape change,” Nature 293(5830), 302–305 (1981). 10.1038/293302a0 [DOI] [PubMed] [Google Scholar]
- 26.Zhang P. C., Keleshian A. M., Sachs F., “Voltage-induced membrane movement,” Nature 413(6854), 428–432 (2001). 10.1038/35096578 [DOI] [PubMed] [Google Scholar]


