Registration of OCT fundus images with color fundus photographs based on blood vessel ridges

Abstract

This paper proposes an algorithm to register OCT fundus images (OFIs) with color fundus photographs (CFPs). This makes it possible to correlate retinal features across the different imaging modalities. Blood vessel ridges are taken as features for registration. A specially defined distance, incorporating information of normal direction of blood vessel ridge pixels, is designed to calculate the distance between each pair of pixels to be matched in the pair image. Based on this distance a similarity function between the pair image is defined. Brute force search is used for a coarse registration and then an Iterative Closest Point (ICP) algorithm for a more accurate registration. The registration algorithm was tested on a sample set containing images of both normal eyes and eyes with pathologies. Three transformation models (similarity, affine and quadratic models) were tested on all image pairs respectively. The experimental results showed that the registration algorithm worked well. The average root mean square errors for the affine model are 31 µm (normal) and 59 µm (eyes with disease). The proposed algorithm can be easily adapted to registration for other modality retinal images.

1. Introduction

Spectral Domain Optical Coherence Tomography (SD-OCT) is a new, high-resolution ophthalmic imaging technology that can display the structure of the retina in three-dimensions. An OCT fundus image (OFI) constructed by integration of the 3D tomogram along depth [1] provides a view similar to traditional en face imaging modalities, such as color fundus photographs (CFPs). Therefore it is natural to attempt to register OFIs and fundus photographs using the recognizable retinal landmarks (see Fig. 1 ). Registration of OFIs with other retinal images (or with other OFIs) is a very important topic because it allows the physician to correlate the cross-sectional scattering properties of the retina with the familiar information provided by other modalities [2,3]. Registered OFIs can also serve as calibration for other modality retinal images [4]. Currently, however, to our best knowledge, we are not aware of any papers addressing automatic algorithms to register OCT fundus images with other retinal images. In this paper, we present an automatic registration algorithm between OFIs and CFPs. The same algorithm can be adapted easily to retinal images obtained with other modalities.

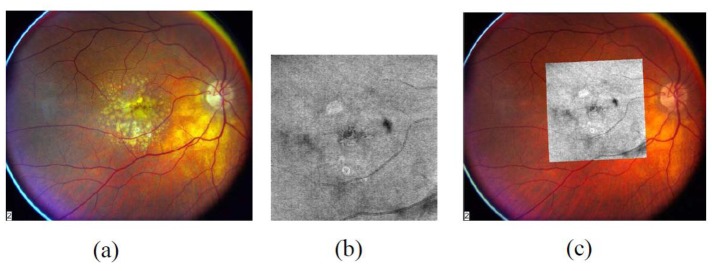
Fig. 1.

(a) Color fundus image. (b) OCT fundus image. (c) Registration result by the automatic algorithm.

The literature on image registration [5,6] and retinal image registration [7] is extensive, but research on registration between OFIs and CFPs is rather limited [8,9]. The general approach to registration usually consists of the following steps: feature detection, transformation model determination, similarity function (also referred to as optimization function) designing, and search strategies (also referred to as optimization strategies). Once features are detected and the transformation model is selected, it is possible to express the similarity function in terms of the parameters associated with the transformation. At this point it is necessary to solve an optimization problem to find the transformation parameters that maximize the similarity function.

Features in images can be classified into two categories: intensity-based features [10,11] and object-based features. Intensity-based features normally are features based on intensity of the image, like the integrated square difference of the intensity values [10,12] and mutual information [10,11]. However, intensity may vary considerably due to different imaging conditions, especially between multimodal images. For this reason, object-based features (such as closed-boundary regions, edges, contours, line intersections, etc.) are widely used in image registration. For retinal image registration, blood vessel patterns are taken as a relatively stable feature [10,13–18]. There is very little in the literature addressing feature detection specifically in OFIs. We have previously developed a Ridge-Branch-Based (RBB) blood vessel ridge detection algorithm [19,20]. The accuracy of blood vessel ridge detection in OFIs using this algorithm is sufficient for subsequent registration. Therefore we use blood vessel ridges (vessel ridges can be taken as vessel center lines) as features in our registration algorithm.

There are many possible groups of transformations [13] that can be used to register two images. Several theoretical and practical considerations create tradeoffs for this choice and can have a considerable effect on the performance of the final algorithm. Three transformation models (similarity, affine and quadratic models [13]) are used in our registration algorithm for comparison. The similarity model includes translation, rotation and scaling. The affine model includes additional sheering and squeezing. The quadratic model contains 12 parameters to model the nonlinearity.

Similarity functions, also known as “optimization functions”, are designed to evaluate the similarity between the pair of transformed images. Correlation, mutual information and Fourier transformation can be used as similarity functions for intensity-based features [6]. The distance between points is usually used for features defined in terms of points or skeletons [16,21–24]. In our case we introduce a new similarity function, based on an ad hoc defined distance involving a penalty factor.

After the similarity function is defined, it is crucial to choose a suitable search strategy in the parameter space, to find the transformation that maximizes the similarity. This is a multidimensional optimization problem [10,12,15] and can often be very difficult to solve efficiently. For features based on skeletons, iterative closest point (ICP) algorithms are widely used [21,23]. Initialization is normally employed to narrow the search space to a preferred candidate domain. The initialization can be done by matching a limited number of landmarks [25], or by brute force search [24]. Stewart et al. [16] proposed a dual-bootstrap iterative closest point algorithm to upgrade matching area and transformation models after initialization in a small area. However, for the registration between OFIs and CFPs, it is hard to use features like blood vessel crossovers for initialization, because of the low visibility of blood vessels in OFIs. Therefore, we have decided to use a brute force search in order to get a coarse estimate of translation, rotation and scaling parameters. Then an ICP algorithm is used to refine the search.

We tested our automatic algorithm to register the OFI and the CFP on both normal eyes and eyes with pathologies. The performance using three different transformation models (similarity, affine and quadratic) was observed on a range of data, providing a useful guideline for a proper choice of transformation models.

2. Methods

Given one pair of images, let one image be the reference image I_R and the other image be the target image I_T. In this discussion we will take I_R to be the CFP and I_T to be the OFI (see Fig. 1). We want to find a transformation M such that M(I_T) will be registered to the reference image. This is achieved by defining a similarity function between I_R and M(I_T). Our goal is then to find the transformation that maximizes the similarity function in the appropriate space. The algorithm can be divided in several steps which we describe below.

2.1 Preprocessing

Preprocessing is first applied to the CFP. The green channel of the CFP is used because of its high contrast of blood vessels. Then we normalize the intensity levels in order to enhance contrast. We find that using the 1st and 99th percentiles to saturate the intensity levels of CFPs works well in practice. In addition, based on estimated original magnifications, OFIs and CFPs are rescaled to a magnification (for example 25 pixels/degree) suitable for subsequent blood vessel ridge detection. The original magnification of OFIs is a priori knowledge in this experiment. The original magnification of CFPs can be calculated based on two parameters: the provided value of the field of view (FOV) and the FOV circle diameter by automatic detection of the circle [26]. These rescaled, enhanced grey-level images are taken as inputs to the following step.

2.2 Vessel ridge detection

Blood vessel related features of the image pair are detected for registration. The visibility of blood vessels in OFIs is often poor and in general it is not easy to detect blood vessel bifurcations, crossovers or vessel area in these images. Therefore we focus on blood vessel ridges. Blood vessel ridges can be considered as center lines of blood vessels. A ridge point is defined as a point where the image has an extremum in the direction of the largest intensity surface curvature.

The Ridge-Branch-Based (RBB) detection algorithm [19,20] is used to detect blood vessel ridges. First we analyze every pixel in the image and extract the ridge pixels. For each ridge pixel we define a local ridge segment and a Segment-Based Ridge Feature vector, based on the local structure information of all the ridge pixels in the ridge segment centered at the investigated ridge pixel. A simple classifier examines the Segment-Based Ridge Features and divides the ridge pixels into blood vessel ridge pixels and non-vessel ridge pixels. Further processing is employed to extend and connect blood vessel ridge branches, as well as to remove isolated small branches. For the details on this algorithm the readers are directed to the reference. The resultant ridge images are denoted by Ridge_Image_R and Ridge_Image_T. Figure 2(a, b) shows blood vessel ridge detection results in the example OFI and CFP. It is important to realize that OFIs are typically noisy and have often poor contrast; therefore this step is one of the major limiting factors in the performance of the algorithm. Any preprocess to enhance blood vessel visibility in OFIs can be incorporated in our registration algorithm.

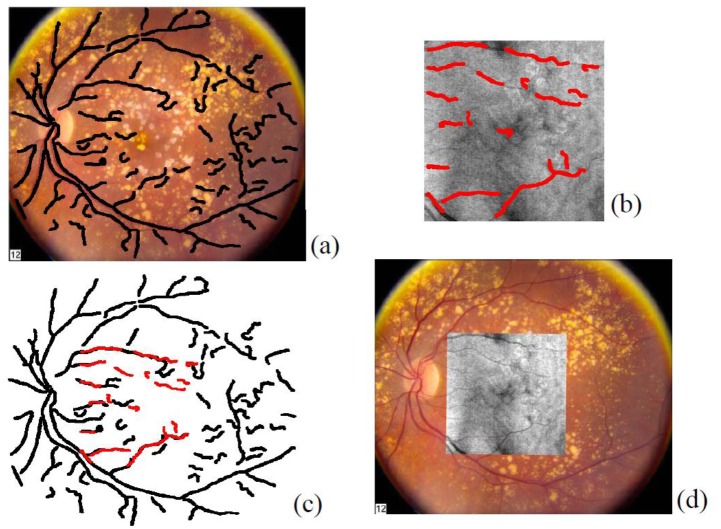
Fig. 2.

(a) The reference image I_R (CFP) and the blood vessel ridge image (Ridge_Image_R) superimposed as black skeletons. (b) The target image I_T (OFI) and its blood vessel ridge image (Ridge_Image_T) superimposed as red skeletons. (c) Registration result between the two blood vessel ridge images. (d) Registration result between the two original intensity images.

2.3 The similarity function

The method is based on the maximization of the similarity function between the two blood vessel ridge images. Since blood vessel ridges are skeletons, the natural choice for similarity functions is ones based on distances between pixels [16,21–24]. We define the similarity function S as

$$\text{S}\left(\text{M}\right)=\text{ S1}\left(\text{M}\right)\frac{A_{actual\text{\hspace{0.17em} \hspace{0.17em} }overlap}}{A_{desiredoverlap}}$$ (1)

where S1(M) is the ratio of the number of successfully matched ridge pixel pairs over the number of all ridge pixels in the two blood vessel ridge images. A_{actual overlap} is the actual overlap area, and A_{desired overlap} is the expected overlap area, which is 20x20 degrees of FOV in our case.

Given a pixel on the reference ridge image, its matching pixel on the target ridge image is the pixel that is closest to it. The two pixels form one pair of matching pixels (Fig. 3 ). Each pair of matching pixels is classified to a “successfully matched pair” or a “non-successfully matched pair”, by comparing its modified distance y and the threshold $t{h}_y$. That is, if $y\le t{h}_y$, the pair is a “successfully matched pair”; if $y>t{h}_y$, the pair is a “non-successfully matched pair”. The threshold $t{h}_y$ is set here as 0.4 degrees of FOV.

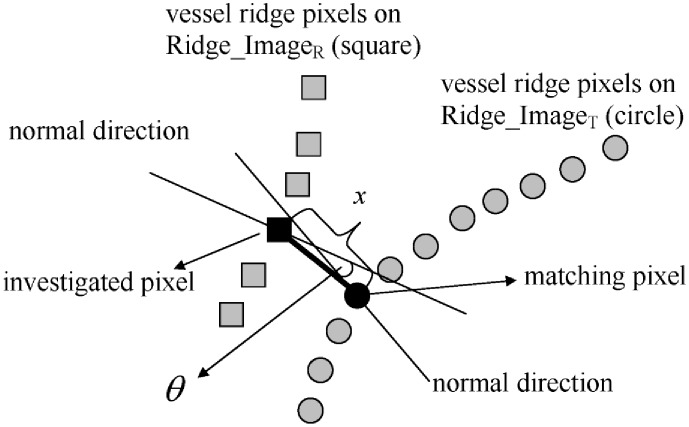
Fig. 3.

Given an investigated pixel on Ridge_Image_R, its matching pixel on Ridge_Image_T is the pixel closest to it. The Euclidian distance x with the penalty from normal direction difference θ, produces the modified distance y, which is used to classify the pair of matching pixels as a “successfully matched pair” (when y is less than the threshold $t{h}_y$) or a “non-successfully matched pair” (when y is greater than the threshold $t{h}_y$).

For one pair of matching pixels, the modified distance y is determined by the Euclidean distance x and the angle θ (the difference between the normal directions of the two pixels along each vessel ridge curve). A penalty factor from θ is designed to pose a large distance to a pair of matching pixels if their normal directions are not close. The modified distance y is defined as:

$$y=\{\begin{array}{l}x,when\theta \le 1/16\pi \hfill \\ x+\frac{\theta -\frac{1}{16}\pi }{\frac{5}{16}\pi }\times \left(2\times t{h}_y\right),when3/8\pi >\theta >1/16\hfill \\ \text{infinity},when\theta \ge 3/8\pi \hfill \end{array}$$ (2)

The correction term A_{actual overlap}/A_{desired overlap} is introduced in the definition of S(M) to correct potential artificial peaks in the similarity function when the overlap area is very small (see Fig. 4 ).

Fig. 4.

Estimation of translation parameters by similarity maps, where the x and y axes correspond to the translation differences along these axes. The side bars display the color map of similarities. (a) S1 similarity map, where the peripheral bright pixels are spurious peak similarities. (b) S similarity map with the correction term introduced, where the brightest pixel around at the center corresponds to the desired translation.

2.4 Searching for the maxima of the similarity function

Given Ridge_Image_R and Ridge_Image_T, the search for the transformation that maximizes S is performed in two steps. The first step is a coarse estimation of transformation by brute force search, followed by the second step, a more accurate estimation of transformation by ICP.

In the first step a coarse estimation of scaling, rotation and translation is made by brute force search. An initial estimate for the transformation scale is obtained from the estimated magnifications of the input retinal images. We consider three possible values for the scale parameter by multiplication with the initial estimate times [0.9 1.0 1.1]. The rotation between two retinal images can be normally assumed to be small and the rotation parameter ${\theta }_{search}$is searched at the three values $[-5^{\circ },0^{\circ },5^{\circ }]$. The remaining search parameters are translations on the x (horizontal) axis and y (vertical) axis. The search steps on the x and y axes are set as 0.8 degree of FOV.

Therefore, for each of the 9 combinations of 3 scales and 3 rotations, a search over the space of translations along the x and y axes is carried out in order to determine the 2 largest local maxima of the similarity map. In this fashion 18 sets of transformation parameters are obtained to be used as candidate initializations for the subsequent ICP registration.

The ICP algorithm we use is similar to the one used by Chanwimaluang [24]. In each iteration in the ICP algorithm, the successfully matched pairs are determined using the modified distance y as described in section 2.3. The algorithm is simply terminated after 8 iterations.

In this manner we obtain a set of 18 transformations that register Ridge_Image_R to Ridge_Image_T. The transformation in this set with the largest similarity S is chosen as the final output of our algorithm.

3. Results

We used two sets of macular images to test the performance of our algorithm. One set consists of 8 pairs of images, each pair acquired from a different normal eye. The other set consists of 11 pairs of images from 11 eyes representative of a variety of retinal diseases, including dry and wet age related macular degeneration, macular edema, macular hole, branch retinal vein occlusion, and proliferative diabetic retinopathy. Each image pair in our validation sets includes one CFP (50 degrees FOV; 2392x2408 pixels; acquired with either a Topcon TRC-50IX or Topcon-50DX retinal camera) and one OFI (20x20 degrees FOV; 200x200 pixels; acquired by the Carl Zeiss Meditec Cirrus HD-OCT Instrument). OFIs for registration are obtained by intensity summation along A-scans. In the experiment, the CFP is taken as the reference image, while the OFI as the target image. Of course this order is simple a matter of choice.

Our sample images were chosen randomly among a set of available image pairs that satisfied the following conditions: an OCT scan and a CFP were acquired on the same day, there were no obvious eye movements artifacts in the OFI, and there was a certain amount of recognizable blood vessel ridges in the OFI (we quantified this criterion by the number of manually traceable blood vessel centerlines greater than 200 pixels). The last criterion can be met by many original OFIs. If some OFIs cannot meet this criterion due to very few recognizable blood vessels, certain preprocessing can be used to enhance blood vessel visibility based on layer segmentation, either manually or automatically [27]. Note that in our experiment we simply exclude such OFIs from the sample.

The performance of the algorithm can be assessed by comparing the reference image I_R and the result of the registration process M(I_T). Maintz et al. [28] argued that local registration errors cannot be quantified with absolute certainty. However, for practical purposes, researchers have developed all kinds of quantitative measurements of registration errors, such as the median of the “point-to-line” distances over all correspondences in the resultant registration [16], or the median of the “point-to-point” distances [24].

Laliberte et al. [14] used the superposition percentage as a measure of the registration performance. A 100% superposition means all pixels of the reference retinal network (thinned blood vessel skeletons) must be present in the other network and be within a one pixel distance. There are two problems with this method. First it depends on the accuracy of blood vessel detection. Second, the superposition does not mean the two pixels are a pair of truly corresponding points.

The performance of blood vessel ridge detection, in terms of the true positive, false positive, true negative and false negative rates, varies a lot among retinal images, especially for OFIs. Different performances in vessel ridge detection in different retinal images may distort the median distance so much that such kind of evaluation is not helpful. Therefore such measurements as the median distance or the superposition percentage [14] are unlikely to offer a meaningful characterization of the transformation error. In order to assess the accuracy of the registration we decided to select a number of manually matched point pairs on the registered retinal reference and target images I_{R_registered} and I_{T_registered}, and then compute the Root Mean Square Error (RMSE) of manually labeled control point pairs. The larger the RMSE is, the worse the registration performance is. Control points are normally blood vessel branching points or crossovers. The advantage with this assessment method is that control points are supposed to be real corresponding feature. However, note that the value of RMSE can be affected by inaccurate locations of manually labeled control points and by the distribution of control points.

If some retinal images have few blood vessels discernable, which is not unusual for OFIs, there may be too few available control points or they may distribute unequally across the image, possibly causing an assessment bias. A solution is to enhance OFIs to improve (locally) the visibility of blood vessels. We can do this by selecting position dependent ranges along the A-scans and performing variable intensity summation. We use the enhanced OFIs only for an assessment of the registration quality in this paper. The standard OFIs are used for registration.

It should be noted that for our index we manually label all control points that can be identified. Therefore different cases may have a different number of control points; typically this number was between 5 and 10. Also, for the comparison of the registration performance between the three selected transformation models, the manually labeled points on the CFP are kept the same, serving as a standard. Finally the RMSE results are reported in microns, rather than pixels, for better comparability across subjects.

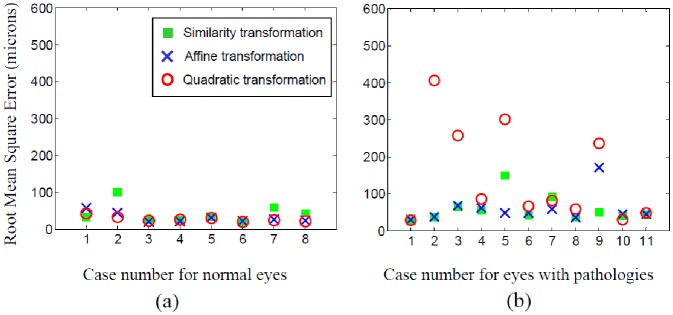
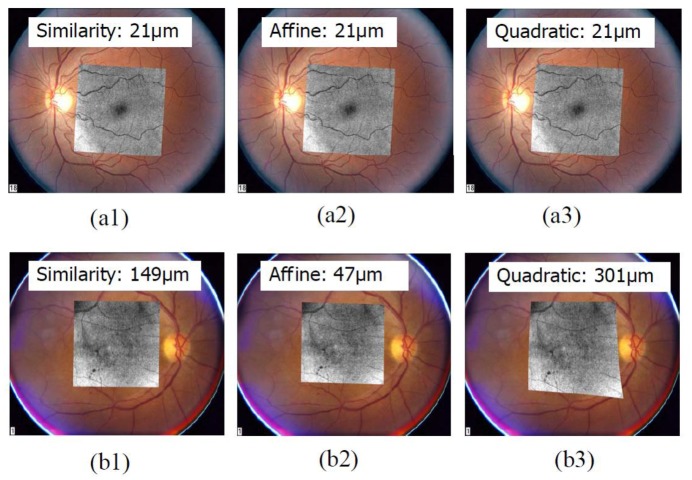
Figure 5 presents the plots of the registration errors in microns for our sample data sets and the three transformation models. Figure 6 shows some examples of registration results. On average, for the data set of eyes with pathologies, the similarity model is the best (Table 1 ); while the quadratic model is the best for the data set of normal eyes. The result is consistent with the fact that blood vessels are typically well visible in images of normal eyes. This means that more blood vessels are detected by the algorithm, providing more information and constraints for the higher-order transformation model to work with. However, these models can be troubled by over-fitting due to fewer available detected features in the case of eyes with pathologies.

Fig. 5.

Root Mean Square Error (in microns) of registration for three transformation models. (a) Data set of normal eyes. (b) Data set of eyes with pathologies.

Fig. 6.

Examples of registration results. (a) Registration results for a normal eye by three transformation models. (b) Registration results for an eye with pathology. Registration errors in microns are displayed along with each figure.

Table 1. Averages and standard deviations (within the parentheses) of RMSE values (in microns) for the registration of the sample data sets using the three transformation models.

	Similarity Model	Affine Model	Quadratic Model
Normal eyes (8 cases)	42 (26)	31 (13)	28 (7)
Eyes with pathologies (11 cases)	58 (35)	59 (39)	145 (131)

4. Discussion and conclusion

With the development of OCT imaging technologies and wide use of OCT 3D data, more and more interest is focused on correlating features in OCT data with those in other retinal images. The registration of OCT fundus images with other en-face retinal imaging modalities is a crucial step in this direction. As far as we know, we are not aware of other papers addressing registration algorithms of OFIs with CFPs, except some conference abstracts [8,9] with little available detail.

In this paper, we present an automatic registration algorithm between OFIs and CFPs. The proposed algorithm can be easily adapted to other types of retinal images. Our algorithm has several new features. In the design of the similarity function we introduce a specially defined distance to determine successfully matched points. Also we use a penalty factor, the ratio of the actual overlap area over the desired overlap area, to suppress spurious peak similarities for translations with small overlap area.

We compared three transformation models for a range of data, which is helpful for users to select an appropriate model for their specific data. The algorithm was evaluated on one data set of 8 image pairs from normal eyes and one data set of 11 image pairs from eyes with a wide range of diseases. Three transformation models (similarity, affine and quadratic models) are tested respectively for those image pairs. The experimental results have shown the registration algorithm worked well. On average, for the data set of normal eyes, the quadratic transformation model has the best performance. However, for the data set of eyes with pathologies, because those OFIs normally have fewer detected blood vessel ridges for registration, the similarity transformation model is the best due to avoidance of over-fitting by being a lower-level transformation model. The most important factor affecting the performance of the algorithm is the quality of the OFIs. These images are typically very noisy and it can be occasionally difficult to find a large enough number of recognizable blood vessel ridges to use for the registration. Apparently, techniques [27] can be designed to preprocess OFIs in order to improve blood vessel visibility. Discussion of such techniques is out of the scope of this paper.

The registration algorithm is implemented in Matlab, which takes about 6 minutes (on a PC with Pentium CPU 3.60 GHz, 2.00 GB of RAM) for the registration given a pair of original images (one OFI and one CFP). Most of the computing time is spent performing two tasks: the vessel ridge detection on the CFP and the brute force search for the maximum of the similarity function. We do not specially make efforts to optimize the Matlab program in terms of computation speed. A faster computation speed can be expected if parallel computing is applied.