High-resolution imaging of microvasculature in human skin in-vivo with optical coherence tomography

Abstract

In this paper, the features of the intensity-based Doppler variance (IBDV) method were analyzed systemically with a flow phantom. The effects of beam scanning density, flow rate and the time interval between neighboring A-lines on the performance of this method were investigated. The IBDV method can be used to quantify the flow rate and its sensitivity can be improved by increasing the time interval between the neighboring A-lines. A higher sensitivity IBDV method that applies the algorithm along the slower scan direction was proposed. In comparison to laser speckle imaging maps of blood flow, we demonstrated the ability of the method to identify vessels with altered blood flow. In clinical measurements, we demonstrated the ability of the method to image vascular networks with exquisite spatial resolution and at depths up to 1.2 mm in human skin. These results collectively demonstrated the potential of the method to monitor the microvasculature during disease progression and in response to therapeutic intervention.

1. Introduction

Optical coherence tomography (OCT) is a non-invasive, high resolution imaging modality which is able to capture three-dimensional images from within highly scattering biological tissue [1]. The functional extension of the OCT technique to image biological tissue has numerous applications in biomedical imaging. Doppler optical coherence tomography (DOCT) or optical Doppler tomography (ODT) is one functional extension of OCT which combines the Doppler principle with OCT [2–5]. Phase-resolved ODT is one of the preferred ODT methods to extract the Doppler frequency because of its high velocity sensitivity [5]. The phase-resolved ODT uses the phase difference among the adjacent A-lines to extract the Doppler frequency shift and quantitative information such as blood flow speed and blood flow direction can be obtained [4–9].

There are considerable interests in imaging blood vessels using intensity or amplitude information instead of phase information [10–14]. Barton et al. proposed a method based on the speckle of conventional amplitude optical coherence tomography images [10]. Mariampillai et al. used the speckle variance in a small 3D volume to image blood vessels [11, 12]. Yasuno et al. used the intensity threshold binarization-based method, scattering optical coherence angiography (SOCA), for retinal and choroidal blood vessel imaging [13]. Jonathan et al. used a two dimensional correlation map based on the OCT intensity images for blood vessel extraction [14]. Recently, we proposed an intensity-based method that uses an algorithm derived from a modified Doppler variance algorithm [15]. In our previous paper, the algorithm is used between adjacent A-lines in a single B-scan frame. Although the performance of the algorithm is comparable to the phase-resolved methods, the sensitivity of this algorithm is not high enough for imaging small vessel where blood flow is very slow.

For phase-resolved ODT method, the velocity sensitivity can be improved by increasing the time interval between adjacent A-lines used in the algorithm. Although increasing Doppler sensitivity by using phase-resolved algorithms between adjacent frames or along the slow scanning direction without sacrificing the system speed was proposed in 2000 [5], recent development of high speed Fourier domain OCT makes it possible to be implemented in Doppler OCT systems [16–19]. In this paper, the way to increase the velocity sensitivity of the intensity-based Doppler variance (IBDV) method will be investigated. The features of IBDV method were analyzed systemically with a flow phantom. The effects of beam scanning density, flow rate and the time interval on the performance of this method were investigated. It is found that the IBDV method can be used to quantify flow rate and the velocity sensitivity of the method can be improved by increasing the time interval between the neighboring A-lines. An improved sensitivity IBDV method that applies the algorithm along the slower scan direction was proposed. To demonstrate the capability of this improved method, we imaged the subdermal side of hamster skin in a dorsal skin fold window chamber. The performance of the proposed IBDV method was evaluated by comparing to the blood flow maps obtained with laser speckle imaging (LSI). In-vivo imaging of microcirculation in human skin was conducted and capillary loops in the dermal papillae were detected.

2. Method

IBDV method is derived from the phase resolved Doppler variance method based on an autocorrelation algorithm [6, 7]. By replacing the complex value term in the autocorrelation algorithm with an amplitude term, the IBDV can be written as follows [15]:

$${\sigma }^2=1-\frac{{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{z=1}^N\left|A_{j,z}\right|\left|A_{j+1,z}^{}\right|}}}{{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{z=1}^N(\frac{{\left|A_{j,z}\right|}^{\text{2}}+{\left|A_{j+1,z}\right|}^{\text{2}}}{2})}}}$$ (1)

where $A_{j,z}$ is the complex value OCT data of the $jth$ A-line at a depth of z, $\left|A_{j,z}\right|$is the amplitude (absolute value) of $A_{j,z}$, J is the number of averaged A-lines and N is the number of averaged depth pixels. Performance of the IBDV method is comparable with that of traditional phase-resolved Doppler variance and color Doppler methods for a phase-stable situation. IBDV demonstrates better performance without instability induced artifacts in a phase-unstable situation [15]. Previously, we reported the IBDV algorithm that was used along the adjacent A-lines in one single B-scan and it is called inter-A-line IBDV(IA-IBDV) here [15]. In this manuscript, the features of the IBDV method are analyzed systemically with a flow phantom. The effects of beam scanning density, flow rate and the time interval of neighboring A-lines on the performance of this method are investigated. It is found that the IBDV method can be used to quantify the flow rate and its sensitivity can be improved by increase the time interval between the neighboring A-lines. A high sensitivity IBDV method that applies the algorithm along the slower scan direction without sacrificing the system speed was proposed and was called inter-frame IBDV (IF-IBDV). In the following sections of this manuscript, if not specified otherwise, the values for J and N in Eq. (1) are both set at 4 to balance between signal to noise ratio, resolution and computation time [15].

3. Doppler OCT system

A swept source OCT system was used in this study. The schematic of the system setup is shown in Fig. 1 . The system used a compact swept source laser with a central wavelength of 1310 nm, an A-line rate of 50 kHz and a total average power of 16 mW (SSOCT-1310, Axsun Technologies Inc, Billerica, MA). For the OCT module, A Mach-Zehnder type interferometer was used and 90% of the laser light power was sent to the sample arm and 10% of the light to the reference arm. A dual-balanced detection scheme was used to acquire the signal. The system utilized a K-trigger mode so that no linear wavenumber re-calibration was needed. In the sample arm, a fiber collimator, a two-axis galvo mirror scanning system and an achromatic doublet with a focal length of 30mm was used. The collimator, galvo mirror scanner and the achromatic doublet were packaged in a handheld probe, achieving a beam diameter of 2 mm and a lateral resolution of 14.6 µm. For in-vivo awake human imaging, the probe worked in the contact mode so that the motion induced artifact was minimized. The FWHM bandwidth of the laser source was approximately 80 nm, resulting in a depth resolution of 9.3 µm in air. A data acquisition software written in C + + , running on a 64 bit Windows 7 operating system, was used to control the galvo scanner and acquire the data. The software was able to display the OCT images in real time and save the acquired fringe data into the computer memory then onto the hard disk.

Fig. 1.

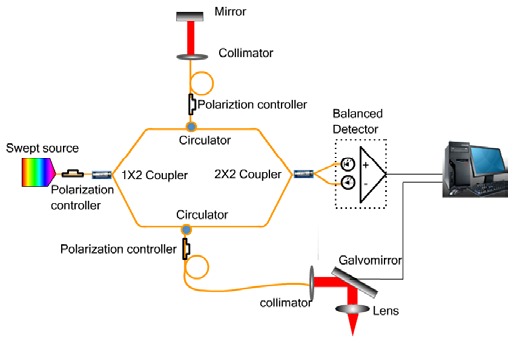
Schematic of the swept source Doppler OCT system.

4. Data processing flow

The saved data was processed afterwards to obtain the IBDV images and en-face images with a custom software written in C++ . Figure 2 shows the data processing flow to generate the IBDV image. The acquired fringes in one frame were firstly averaged to obtain the background fringe. After subtracting the background fringe, the fringes were shaped with a Gaussian function and the complex analytical depth encoded signals were converted from the shaped fringes using fast Fourier transform (FFT). The amplitude values of the complex analytical depth encoded signals were used to calculate the OCT images after logarithm calculation and IBDV values using Eq. (1). For the final IBDV image, an intensity threshold that is 1dB above the OCT intensity noise floor was used to eliminate the low scattering but high noise region. For in-vivo human patient imaging especially when using the IF-IBDV method, there may be strong axial movement induced by involuntarily motion of the imaging subject and axial direction movement may degrade the performance of the IBDV method. Axial movement induced displacement can be compensated by cross-correlating the amplitude values of neighboring A-lines used in the algorithm [16]. Both OCT and IBDV images were then obtained from the compensated A-line amplitudes. The en-face IBDV images at different depth were extracted from the three dimensional IBDV tomographic images and projection view en-face images were processed from the en-face IBDV images.

Fig. 2.

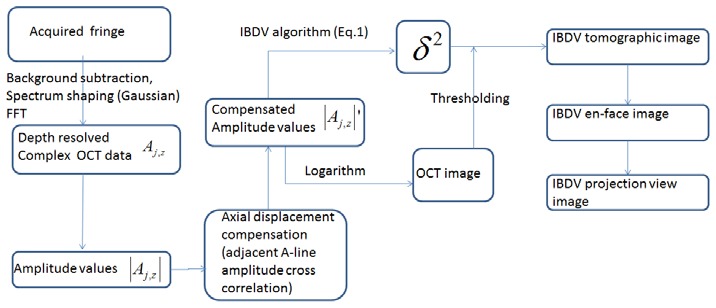
The data processing Flowchart for generating the IBDV image.

5. Features of IBDV

To further understand the features of the IBDV method, the effects of several important parameters, such as beam scan density (sampling density), flow rate and the time interval on the performance of the IBDV were investigated. A flow phantom was used for this study. A capillary tube with an inner diameter of 500 µm was embedded in a tissue phantom made with silicon and Titanium dioxide. A 0.1% Intralipid solution composed of particles of 0.356 µm diameter was pumped into the tube with a syringe pump.

5.1 Effect of sampling density level

The IBDV method is based on the intensity (or amplitude) autocorrelation between adjacent beam scanning locations. Autocorrelation requires certain correlation among the adjacent scanning locations (or A-lines) and the lateral shift between adjacent scanning locations will decrease autocorrelation level and increase the decorrelation noise. The decrease in autocorrelation will degrade the performance of the method. Therefore, the beam scanning density (or sampling density) is important to the performance of the method. In order to investigate the effect of beam scanning density on the performance of the IBDV, we analyzed the average background IBDV values at different beam scanning density levels. Figure 3(a) shows the OCT image of the flow phantom. Figures 3(b)-3(m) show the IBDV images at different sampling density levels (Sd in these images means sampling density level). Sampling density level was defined as the ratio of laser beam spot size (14.6 µm in this case) to the lateral scanning step size. It can be clearly seen that t noise level decreases as the sampling density level increases. It order to quantity the noise level, the average background IBDV values (scaled to numbers between 0 and 255 for displaying purpose) in the region indicated by the yellow rectangle in Fig. 3(b) were calculated for all the IBDV images. The relationship between the background IBDV value and the sampling density level is plotted in Fig. 3(n). A sampling density level of more than 3 is required in order to have a noise level of less than 4.

Fig. 3.

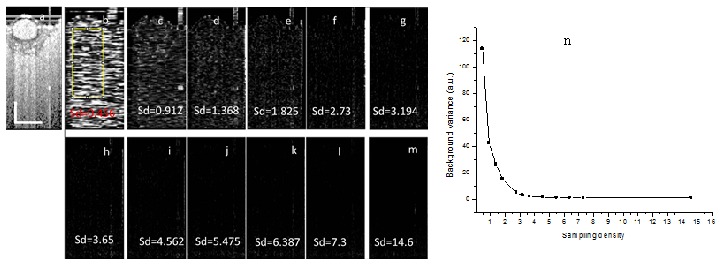
The effect of sampling density on the performance of IBDV. (a) OCT image of a flow phantom. (b)-(m) IBDV images at different sampling density levels. The Sds in (b)-(m) mean the sampling density level. (n) The relationship between background average IBDV versus the sampling density level. The scale bars in (a) represent 500 µm.

5.2 Effect of flow rate

One of the attractive features of phase resolved Doppler OCT is that quantitative information such as blood flow speed, flow velocity profile, blood flow direction can be obtained. In our previous publication of IBDV, quantifying the flow parameters was not demonstrated. Here, we investigated the dependence of average IBDV value in the tube on flow rate. The results are shown in Fig. 4 . The images each contained 2048 A-lines covering a scanning range of 1 mm, and the corresponding sampling density level was 29.9. Figure 4(a) shows the OCT image of the sample. Figures 4(b)-4(g) show the IBDV images at the flow rates of, respectively, 8.4 mm/s, 16.8 mm/s, 42 mm/s, 58.8 mm/s, 84 mm/s, and 588 mm/s. The improvement of sensitivity of the IBDV with the increase of flow rate could be seen from these images. In order to quantify this improvement, we calculated the average IBDV value in the tube when the flow rate was changed. The relationship between the average IBDV value in the tube and the flow rate is plotted in Fig. 4(h). Figure 4(h) clearly shows that the average IBDV value increases with the flow rate until it becomes saturated when the flow rate exceeds certain level (around 168 mm/s in this case). An exponential decay fit of the data shows the coefficient of determination to be 0.99397 and the saturated average IBDV to be 51.5. This result demonstrates that the IBDV method could be used to quantify flow rate. Figure 4(i) shows relationship between average IBDV value in the tube and the flow rate at a relative low flow rate before the averaged IBDV value becomes saturated. A linear fit of the data demonstrates a correlation coefficient of 0.99745 between the two parameters.

Fig. 4.

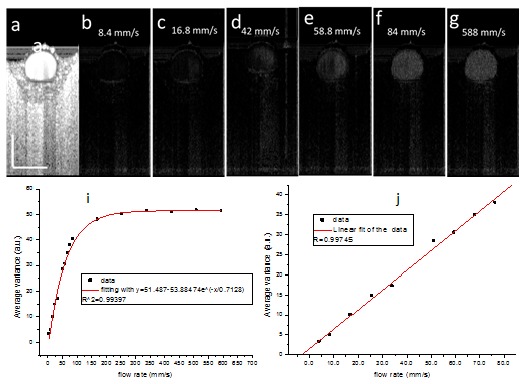
The dependence of IBDV value on the flow rate. (a) OCT image of a flow phantom. (b)-(g) IBDV images of the flow phantom at different flow rates. The flow rates are shown in the figures. (h) The relationship between average IBDV value in the tube and the flow rate. The red line shows the exponential decay fit of the data. (i) The relationship between the average IBDV value in the tube versus the flow rate at lower speed. The red line shows the linear fit of the data. The scale bars in (a) represent 500 µm.

5.3 Effect of time interval

Recently, high sensitivity imaging of microvasculature has been demonstrated with OCT by several groups [16–19]. For phase resolved DOCT, the blood flow sensitivity could be improved by increasing the time intervals between neighboring A-lines used in the algorithm. This can be realized by reducing the A-line rate of the system, by using the algorithm along the slowing scanning direction or by using dual beam setup [16–19]. Here, the effect of time interval between neighboring A-lines used in the IBDV algorithm on the sensitivity of IBDV was investigated and the results are shown in Fig. 5 . For all the images shown in Fig. 5(a)-5(g), the flow rate was set at 12.6 mm/s. The image in Fig. 5(a) contains 9216 A-lines covering a scanning range of 1 mm and the corresponding sampling density level was 134.6. Figure 5(b) shows the IBDV image processed directly from the original data. Because the A-line rate of the current swept source laser was fixed at 50 KHz with a neighboring A-line time interval of 20 µs, we cannot directly test the effect of time interval on the sensitivity of IBDV. Since the data was acquired at a very high sampling density level (134.6), we could change the time interval by using only partial data. For example, to test the time interval of 40 µs, we took data points from all the even (or odd) number A-lines in the original data set to form a new data set with a total of 4608 A-lines. . The algorithm as Eq. (1) was then applied on this new data set to obtain an IBDV image with a neighboring A-line time interval of 40 µs. Accordingly, to test the algorithm with a neighboring A-line time interval of 60 µs, every third A-line was extracted from the original data set to form a new data set with a total of 3072 A-lines and the IBDV algorithm was applied to the new data set. With the same downsampling method, we obtained the IDBV images with different neighboring A-line time intervals from 20 µs to 400 µs. Figures 5(c)-5(g) show the IBDV images corresponding to neighboring A-line time intervals of, respectively, 20 µs, 60 µs, 100 µs, 140 µs, 180 µs, and 400 µs. It should be pointed out that in Figs. 5(c)-5(g), each image contains different total number of A-lines and Fig. 5(g) has the lowest sampling density level. Figure 5 (g) contains 460 A-lines and the corresponding sampling density level is 6.71. Figures 5(b)-5(g) demonstrate that the sensitivity of IBDV improves with the increase of the neighboring A-line time interval. It could be also seen that the shadowing effect below the tube also increases with the increase of the neighboring A-line time interval. The average IBDV value in the tube was used to quantify the sensitivity improvement and its relationship with the neighboring A-line time interval is plotted in Fig. 5(h). Figure 5(h) clearly shows that the average IBDV value increases with the time interval and it becomes saturated when the time interval exceeds certain level. An exponential decay fit of the data shows a coefficient of determination value of 0.99785 and a saturated average IBDV value of 49. Figure 5(i) shows that at relatively small time interval region, there is a liner relationship between average IBDV value and the time interval.

Fig. 5.

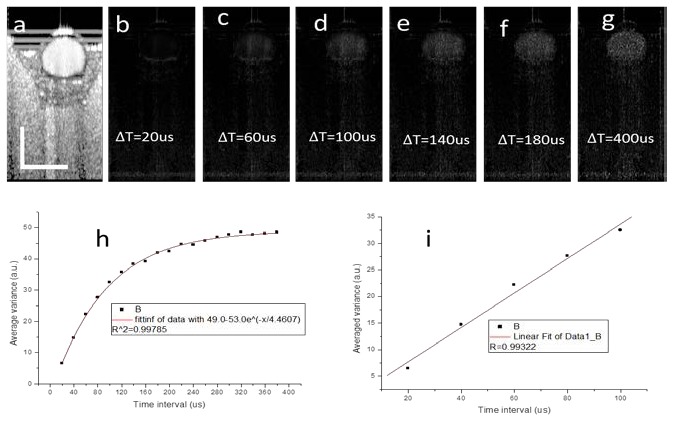
The dependence of IBDV value on neighboring A-line time interval. (a) OCT image of a flow phantom. (b)-(g) IBDV images of the flow phantom at different neighboring A-line time interval. The neighboring A-line time intervals are shown in the figures. (h) The relationship between average IBDV value in the tube and neighboring A-line time interval. The red line shows the exponential decay fit of the data. (i) The relationship between average IBDV value in the tube and neighboring A-line time interval. The red line shows the exponential decay fit of the data. The scale bars in (a) represent 500 µm.

These findings suggested that the ways to improve the blood vessel detection sensitivity for the phase resolved methods could also be used to improve the sensitivity of the IBDV method. This means the use of the algorithm along the slowing scanning direction (inter-frame algorithm) and the using of dual beam setup can also been used to improve the sensitivity of the IBDV method. Because the dual beam setup requires hardware modification of the system, we only tested the inter-frame algorithm and Fig. 6 shows the result. Figure 6(a) shows the OCT image of the flow phantom. The image contains 1024 A-lines covering a scanning range of 1 mm. The 1mm range beam scanning was repeated for 4 times and the data were processed using IF-IBDV algorithm. Figure 6(b) shows the IBDV image processed using the IF-IBDV when the syringe pump was stopped and the corresponding flow rate was zero. This demonstrates that this method is sensitive enough to detect the Brownian motion of the Intralipid 〉uid in the tube. Figure 6(c) shows the histogram of the IBDV value distribution inside the tube. An average IBDV value of 53.28 was found and this value was very close to the saturation average IBDV value predicted by the exponential decay model in Fig. 4(h) and Fig. 5(h). Figure 6(d) shows the IBDV image processed using the IF-IBDV when the flow rate was set at 92.4 mm/s. Figure 6(e) shows the histogram of the IBDV value distribution inside the tube for the image in Fig. 6(d) and the average IBDV value was 53.86. Because the IBDV values were scaled to 0-255 in a 8-bit grey level image and the maximum of the average IBDV value was around 50, in the following content of this manuscript, we will multiply the final value obtained from Eq. (1) by 3 to enhance the contrast for displaying purpose.

Fig. 6.

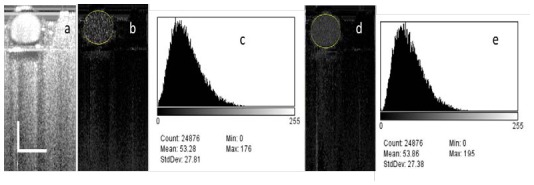
The IF-IBDV images of a flow phantom. (a) OCT image of a flow phantom. (b) IF-IBDV images of the flow phantom with the syringe pump stopped. (c) The histogram of the IBDV value distribution inside the tube in (b). (d) IF-IBDV images of the flow phantom with flow rate of 92.4 mm/s. (e) The histogram of the IBDV value distribution inside the tube in (d) . The scale bars in (a) represent 500 µm.

6. In-vivo imaging of vasculature network in hamster skin

The subdermal side of a dorsal skinfold window chamber (DSWC) on an anesthetized hamster [20] was imaged with the OCT system. Figure 7(a) shows the OCT images obtained with our system. The frame has 1024 A-lines covering a scanning range of 4 mm. Figure 7(b) shows the IA-IBDV results generated with the algorithm that used adjacent A-lines (inter-A-lines) in the single B-scan (fast scan) frame. Blood vessels were not detected with this algorithm. In Fig. 7(c), the IF-IBDV algorithm was used along the C-scan (slow scan) direction and a few vessels were imaged as indicated by the red arrows. Figure 7(c) was processed from 4 B-scan frames with 1024 A-lines per frame. The distance between adjacent B-scan frames is 4 µm and the corresponding sampling density level is 3.65. The improved sensitivity to blood flow is clear from these pictures. However, the obtained blood vessel image suffers from shadowing effect, especially for large blood vessels. Shadowing effect was seen from phase resolved DOCT and may be corrected with sophisticated numerical method [20].

Fig. 7.

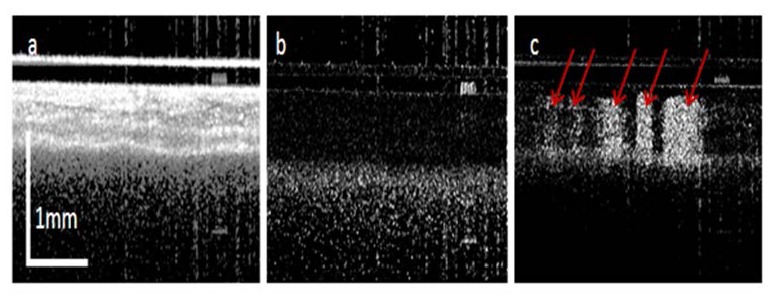
OCT images of hamster skin. (a) OCT B-scan image; (b) IA-IBDV tomography image and (c) IF-IBDV tomography image.

Laser irradiation was then performed on the subdermal side of the DSWC. Blood vessels were irradiated with a sequence of three pulses from a frequency-doubled Nd:YAG laser (Dualis VP⁺, Fotona Laser, Ljublijana, Slovenia) with pulse width of 1 millisecond (ms), energy density of 5 J/cm², repetition rate of 20 Hz, and beam sport size of 2 mm. To verify the OCT IF-IBDV results, we also took transillumination images with a green color filter [Fig. 8(a) ] and LSI blood flow map [Fig. 8(b)]. The red arrows in Fig. 8(a) indicate the laser irradiation locations. After laser irradiation, constriction of the targeted blood vessels was observed in the transillumination image, but blood-flow changes cannot be determined from this image. Therefore, LSI was used to visualize blood flow dynamics in the window [21, 22]. During LSI, the window was imaged directly by a camera (Nuance, CaliperLife Sciences, Hopkinton, MA) equipped with a 5 × zoom lens. A HeNe laser (633 nm, 30 mW) was used to irradiate the epidermal side of the window chamber and the transmitted speckle pattern imaged with the camera. An image exposure time of 10 milliseconds was used and a custom software written in LabVIEW (Version 8.6, National Instruments, Austin, TX) and MATLAB (The Mathworks,Natick, MA) was used to acquire and process image. A sequence of 10 raw speckle images was collected. Each image was converted to a speckle contrast image using a 7 × 7 sliding window. As shown in Fig. 8(b), blood flow was absent in the irradiated vessels. In comparison, the corresponding maximum intensity projection (MIP) OCT IF-IBDV image [Fig. 8(c)] depicts a similar functional blood flow map to that shown in the LSI image. The blood vessels without flow do not show up in both the IBDV image and LSI flow map. The IBDV image shows better result in the capillary vessels region as indicated by circles. The reason for this may be due to the exposure time (10 ms) used for the LSI image, which is too short to allow LSI to have any appreciable sensitivity to capillary-level flow. With longer exposure times (~1000 ms), capillary visibility for LSI increases considerably [23]. Note that the OCT IF-IBDV image in Fig. 8(c) was extracted from a 3D OCT data volume containing 4096 frames with 1024 A-lines per frame.

Fig. 8.

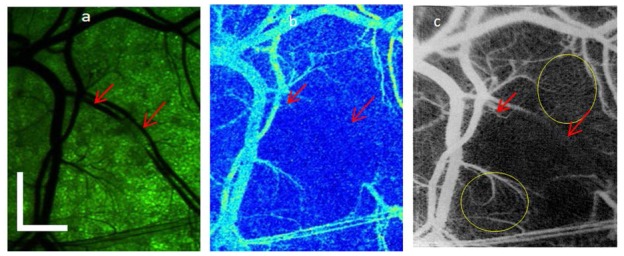
Comparison of LSI and IF-IBDV images of microvascular network in DSWC model, after laser irradiation of select vessels. (a) With green filtering of broadband light used to transilluminate the DSWC, the blood-vessel architecture is clearly visible. (b) With LSI, vessels containing flowing blood are displayed, with an absence of flow in the irradiated vessels. (c) With IF-IBDV method, a similar functional map of the vasculature is obtained, with enhanced visualization of smaller arteriolar, venules, and capillaries. The scale bars in (a) represent 1 mm.

7. In vivo imaging of microvascular network in human skin

Imaging of the microcirculation in human skin is important for diagnosing and monitoring diseases of microvascular origin. There have been demonstrations of human skin imaging with optical based techniques, such as laser Doppler imaging, LSI and photoacoustic imaging. Although these techniques have high sensitivity to specific features of skin microvasculature, they are limited by either spatial temporal resolution or lack of depth discrimination [17]. Recently, high resolution imaging of human skin with techniques based on OCT has been demonstrated [17, 24].

To demonstrate the capability of the IF-IDBV method, measurements were taken from human skin. Imaging was performed on a healthy adult male volunteer. The volunteer sat on a chair and held the probe himself. The imaging region was on the thigh of the volunteer [Fig. 9(a) ] and the size of this region is 4 × 4 mm². The 3D OCT data volume consisted of 4096 frames with 1024 A-lines per frame and took approximately 80 seconds to capture the entire 3D OCT data volume [Fig. 9(b)-9(g)]. Figures 9(b)~9(e) show the MIP views of the IF-IBDV images at different depth. Figure 9(b) shows the MIP view at depths from 120 μm to 360 μm. A dense capillary network was identified. With increasing depth, larger but less dense blood vessels can be seen [Figs. 9(c), 9(d) and 9(e)]. Figures 9(c), 9(d) and 9(e) show, respectively, the MIP view at the depths from 360 μm to 600 μm, 600 μm to 840 μm, and 840 μm to 1300 μm. The red arrows indicate the larger blood vessels detected in the corresponding images. Clear blood vessels branches can also be found at deeper region as shown in Fig. 9(e). The red circles in Fig. 9(b)-9(d) show the branch locations. It is difficult to differentiate the depth of the blood vessels from the grey scale MIP view shown in Fig. 9(b)-9(e). A color encoded depth (CED) MIP image can provide the depth information of the vessels with a single image and it can also minimize the shadowing effect. The CED MIP images for depth from 120 μm to 360 μm and depth from 360 μm to 1300 μm are shown in Fig. 9(f) and Fig. 9(g).

Fig. 9.

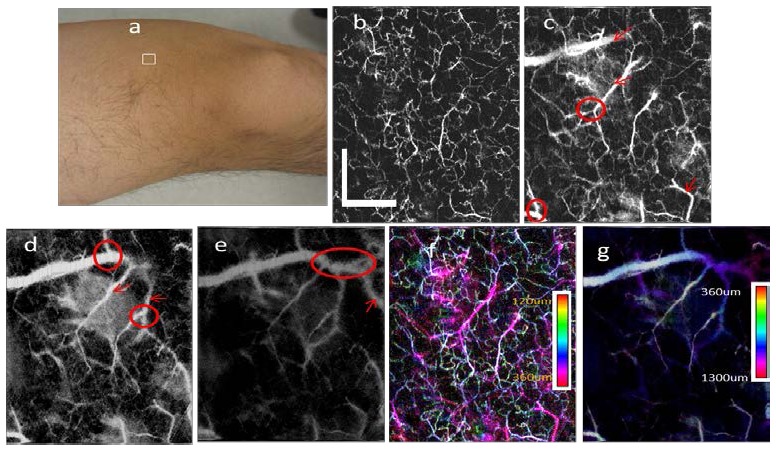
In-vivo imaging of human thigh skin. (a) The photograph shows the imaging location (white rectangle area) on the thigh of the volunteer. (b)-(e) MIP view IF-IBDV images of microcirculation network at different depths of human skin with depth of: (b) 120 μm-360 μm; (c) 360 μm-600 μm; (d) 600 μm-840 μm; (e) 840 μm-1.3 mm. The arrows indicate new blood vessels detected in each image and the circles indicate new branches detected in the image. (f) The CED MIP view IBDV image for the depth of 120 μm-360 μm. (g) The CED MIP view IBDV image for the depth of 360 μm-1300 μm . The scale bars in (a) represent 1 mm.

To further demonstrate the performance of this method, we imaged the skin on a finger of a healthy volunteer [region enclosed by white line in Fig. 10(a) ]. During imaging, the OCT probe was placed on a table and the forearm of the volunteer was also rested on the table. Figure 10(b) shows an OCT B-scan image of the region. Figures 10(c)-10(e) show the MIP view of the IF-IBDV images at different depths. Figure 10(b) shows one OCT image to indicate the depth region for Fig. 10(c), 10(d) and 10(e). Figure 10(c) shows the MIP view at the depths from 270 μm to 450 μm. At this depth, the blood vessels manifest as dots or short lines instead of a connected network. Based on Fig. 10(b), we identify the imaged region in Fig. 10(c) to be in the papillary dermis, near the dermal-epidermal junction. Hence, the dots or short lines in Fig. 10(c) are the capillary loops. Figure 10(d) shows the projection view image at the depths from 450 μm to 810 μm. At this depth, a dense capillary network is visible, corresponding to the superficial horizontal plexus. In Fig. 10(e), several larger blood vessels (indicated by the red arrows) are visible. The deepest blood vessels detected are at a depth of approximately 1.2 mm. The CED MIP image for the depth from 270 μm to 1300 μm is shown in Fig. 10(f).

Fig. 10.

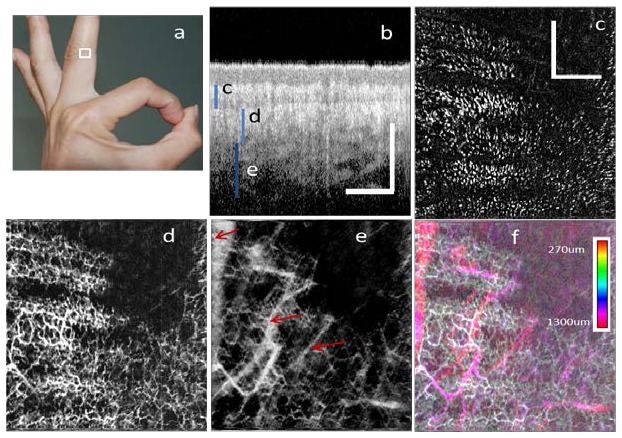
In-vivo imaging of human finger skin. (a) The photograph shows the imaging location (area enclosed by white line) on the middle finger of the volunteer. (b) An OCT B-scan Image with the blue bars indicating the corresponding depth region for Fig. 5(c)~5(e). (c), (d) and (e) are the MIP view IF-IBDV images of microcirculation network at different depths with depths of: (c) 270 μm-450 μm (d) 450 μm-810 μm (e) 810 μm-1300 μm. (f) CED MIP view IBDV image for the depth of 270 μm-1300 μm. All scale bars in (b) and (c) represent 1 mm.

8. Conclusions

In summary, the features of the IBDV method are analyzed systemically with a flow phantom. The effects of beam scanning density, flow rate and the time interval on the performance of this method are investigated. It is found that the IBDV method can be used to quantify the flow rate and its sensitivity can be improved by increase the time interval between the neighboring A-lines. We have demonstrated high resolution blood vessel imaging with the IF-IBDV method. By applying the algorithm along the slow scanning direction, the sensitivity of this method to blood flow is greatly enhanced. With comparison to LSI maps of blood flow, we demonstrate the ability of the IF-IBDV method to identify vessels with altered blood flow. Furthermore, with clinical measurements, we demonstrate the ability of the IF-IBDV method to image vascular networks with exquisite spatial resolution and at depths up to 1.2 mm in skin. These results collectively demonstrate the potential of the IF-IBDV method to monitor the microvasculature during disease progression and in response to therapeutic intervention.