Abstract
In this paper, we study temporal couplings between interictal events of spatially remote regions in order to localize the leading epileptic regions from intracerebral electroencephalogram (iEEG). We aim to assess whether quantitative epileptic graph analysis during interictal period may be helpful to predict the seizure onset zone of ictal iEEG. Using wavelet transform, cross-correlation coefficient, and multiple hypothesis test, we propose a differential connectivity graph (DCG) to represent the connections that change significantly between epileptic and non-epileptic states as defined by the interictal events. Post-processings based on mutual information and multi-objective optimization are proposed to localize the leading epileptic regions through DCG. The suggested approach is applied on iEEG recordings of five patients suffering from focal epilepsy. Quantitative comparisons of the proposed epileptic regions within ictal onset zones detected by visual inspection and using electrically stimulated seizures, reveal good performance of the present method.
Keywords: Epilepsy, functional connectivity graph, intracerebral EEG, permutation-based multiple hypothesis test, wavelet cross-correlation coefficient.
I. Introduction
Epilepsy is defined by the recurrence of epileptic seizures associated with transient increase of hypersynchronous electrical activity within relatively large neuronal networks which may induce disruption of normal brain functioning. Patients with epilepsy are usually considered to have two main brain states: 1) the ictal state, of short duration, defined by epileptic seizures, 2) the interictal state, representing the vast majority of time, in the interval between two seizures. Several dysfunctional regions are identified for epileptic patients: the “irritative zone” (IZ) is the site responsible for interictal epileptiform discharges (IEDs) generation and the “seizure onset zone” (SOZ) is the region where the first electrophysiological changes are detected at ictal onset. Patients with drug-resistant focal epilepsy can be considered for the resective surgery. This surgical procedure is aimed at removing the SOZ without creating neurological deficits. The best way to delineate SOZ is to record seizures by using implanted intracerebral depth electrodes providing intracerebral EEG (iEEG). However, during iEEG recording, the number of seizures is very limited and obtaining statistically reliable results from studying seizure time intervals could be difficult. Consequently, other complementary approaches like interictal analysis to the SOZ localization remain warranted.
Relationship between SOZ and IZ has been the subject of numerous studies [1]. There are several studies wondering if quantitative analysis of interictal discharges can be used to guide the surgical resection decision in addition to other imaging and clinical information [2]–[9]. In most methods of SOZ detection through the interictal brain connectivity, the time periods involving IEDs are analyzed [5]–[7]. However, a brain connectivity graph involved during an IED time interval from high-density electrode array of iEEG recording is very complicated to be interpreted. Conversely, searching for discriminated connections between IED and non-IED states may provide simpler interpretation of these complex graphs and may focus on the nodes associated with epilepsy zone (dysfunctional regions like IZ). Therefore, we focused on the discrimination between IED and non-IED time intervals. In this manuscript, we study the two following questions. What are statistically significant brain connections differing between IED and non-IED states, based on analyzing long and high-density electrode array of iEEG recordings? Is there any relationship between leading IED regions and SOZ?
A local increase of several connectivity measures during the interictal period is reported in the literature [5], [10]. In this paper, we hypothesize that the functional brain connectivity is changing between IED and non-IED periods. For identification of these discriminated connections between IED and non-IED states, differential connectivity graph (DCG) is developed. Assuming the leading IED regions (sources) be more important than propagated IED regions (sinks) in SOZ detection [2], [3], we study the directions of the DCG connections. Directed DCGs (dDCG) related to different frequency bands are calculated and characterized by an introduced emittance measure. To identify the leading IED regions, a multi-objective optimization method [11] is applied on the emittance values of all of the dDCG nodes in all of the frequency bands studied. Results are quantitatively compared with SOZ visually defined by epileptologists, and with SOZ reported by [12].
Rest of the paper is organized as follows. In Section II, we describe different steps of the proposed method. Section III is devoted to the data protocol, and experimental results of the proposed method. The discussion is brought in Section IV. Concluding remarks are presented in Section V.
II. Methods
The steps of the method are as follows (Figure 1):
Figure 1.
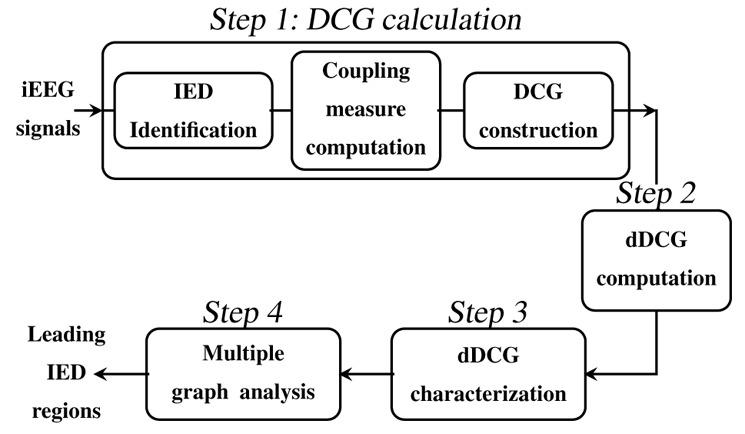
The main steps of the proposed method for the iEEG analysis.
-
Step 1)
DCG calculation;
-
Step 2)
dDCG computation;
-
Step 3)
dDCG characterization;
-
Step 4)
Multiple graph analysis.
Below, we describe in more detail each step of the method.
A. Step 1: DCG calculation
Identification of discriminated connections from two separated IED and non-IED connectivity graphs is challenging due to the following problems. Firstly, the classic method to interpret the coupling results and define graph edges involves comparison of coupling strength with a threshold value. The resulting graph critically depends on the choice of threshold [13]. Such graphs are not stable for IED or non-IED time intervals (threshold may depend on the underlying observed time interval) and their comparison with different thresholds may not provide significant results. Secondly, comparing two complex graphs of IED and non-IED time intervals to distinguish the discriminated connections is difficult. Thirdly, the coupling between iEEG signals recorded from spatially distributed regions during IED or non-IED periods may vary in time and frequency [8], [14].
DCG is designed to solve these problems. Firstly instead of analyzing each time interval separately, DCG searches for statistically significant connections among large number of IED and non-IED time intervals. Secondly instead of comparing two complex graphs to identify discriminated connections, DCG selects the connections whose coupling measures change significantly between IED and non-IED states and decreases the effect of common information in these states like background activity. Thirdly by using permutation-based multiple testing [15], the distribution of a test statistic related to the coupling measure from different IED and non-IED time intervals is estimated under null hypothesis to choose the statistically significant connections for each related frequency band. DCG calculation consists of three stages: IED identification, coupling measure computation, and DCG construction.
1. IED identification
The IED and non-IED time intervals are identified from the common sessions of iEEG recordings. This is done manually by the epileptologist for each patient considering all of iEEG channels. An IED period is a time interval including one single IED or burst of IEDs. A non-IED period is a time interval without any IED or abnormal event. Two typical IED and non-IED time intervals are depicted in Figure 2. There is a great overlap of physiological states for IED and non-IED time intervals to decrease the probability of detecting the discriminations in functional connectivity related to the changes in physiological states. The mean of minimum and maximum length of IED time intervals over patients are equal to 460 msec and 6.4 sec, respectively. The number of IED and non-IED periods are on average 304 and 174 per patient, respectively, which provides statistically significant results.
Figure 2.
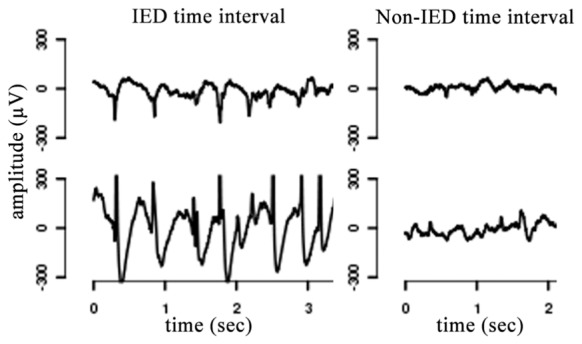
Typical IED and non-IED time intervals from iEEG recordings.
2. Coupling measure computation
Different linear, nonlinear or directed coupling measures [16] may be selected between pairs of time series like wavelet correlation coefficient [17]–[19], phase synchrony [20]–[22], and transfer entropy [23]. In this paper, we focus on linear coupling and directional properties are estimated by the estimation of the time delays.
We chose linear coupling since several studies indicate no preference of nonlinear coupling measures over linear ones during interictal period of EEG analysis [4], [5], [24]. We also tested wavelet-Hilbert synchrony (nonlinear coupling) [22] and found almost similar final results (leading IED regions) confirming the latter studies. This result is not shown in this paper. The frequency contribution of IED time intervals is mostly in the range [2 60] Hz. In this range the frequency contribution of IED time intervals is greater for lower frequencies. Wavelet transforms which are are well-known for analyzing non-stationary EEG signals [25], [26], provide automatic frequency band selection which adapts narrower bands for lower frequencies and larger bands for higher frequencies. Furthermore, mother wavelets like Daubechies are a proper choice for filtering IED signals due to the shape of the filter [26]. Consequently, although there are other possible methods like filter banks, in this paper we prefer to use wavelet transforms.
Here, our formal coupling measure is maximum wavelet correlation-coefficient [18], [27] using the maximal overlap discrete wavelet transform (MODWT) [17]. MODWT is a non-decimated version of orthonormal discrete wavelet transform (DWT) that relaxes orthogonality to gain properties like the translation invariance. In contrast to DWT, the MODWT coefficients are associated with zero phase filters that provide consistent time-shift of MODWT coefficients with temporal signals. In MODWT, the set of coefficients in each level of decomposition includes the same number of samples as the temporal signal minus the samples affected by boundary effect. The start and end time points of IED and non-IED time intervals in temporal signal are consistent with the MODWT coefficients and these coefficients can be segmented according to temporal labeling. This property does not hold for the DWT.
We assume N-dimensional observations
, where
, the ith column of matrix X ∈
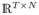 , contains T samples of the signal recorded from the ith channel, and N is the number of channels associated with bipolar iEEG electrode leads (see Section III-A). h and g are respectively scaling and wavelet filters of an orthonormal wavelet transform. The J-level MODWT of xi is
(
and
are the approximate (scaling) and detailed (wavelet) coefficient sequences) such that
, contains T samples of the signal recorded from the ith channel, and N is the number of channels associated with bipolar iEEG electrode leads (see Section III-A). h and g are respectively scaling and wavelet filters of an orthonormal wavelet transform. The J-level MODWT of xi is
(
and
are the approximate (scaling) and detailed (wavelet) coefficient sequences) such that
| (1) |
is calculated recursively as:
| (2) |
| (3) |
where h0 = h, g0 = g, , and * denotes convolution. The MODWT scaling filter of level (j + 1) is the up-sampled versions of the previous level:
| (4) |
Wavelet coefficients of level j are associated with frequency interval [ ], where fs is the sampling rate (Hz).
MODWT is applied on the whole processed signal for J frequency bands providing wavelet coefficients, denoted as J matrices , j = 1, …, J (Figure 3). Then columns of each matrix are segmented into L1 IED and L2 non-IED time intervals (Section II-A1) called segments. The N-dimensional IED or non-IED segment m is denoted as , m = 1, …, Ll. Ll and are the number of time intervals or segments and the sample number of each segment m, respectively. is the ith column of matrix that contains samples of wavelet coefficients at a given frequency level during IED or non-IED segment m. Figure 3 shows how to extract from X. In the following, the upper index l denotes the IED (l=1) or non-IED (l=2) variable. The MODWT cross-correlation coefficients [17] are estimated for each channel pair (i, j) ∈ {1, …, N}2, i ≠ j and during IED and non-IED segments in terms of different time lags (τ):
| (5) |
where and [17] are estimated covariance and variance (by empirical average), respectively. For each channel pair and IED or non-IED segment, the maximum of MODWT cross-correlation (5) is obtained as:
| (6) |
where , the maximal MODWT cross-correlation (MMCC), is considered as our formal coupling measure. The time causality, between and is the time lag in which the maximum of the absolute value of occurs. For non-stationary fractionally differenced signals (the definition is given in [17]), the confidence interval of MODWT cross-correlations can be approximated based on [17]. Here, the non-stationary time series do not hold this particular property, thus a permutation method is used as explained in Section II-A3.
Figure 3.
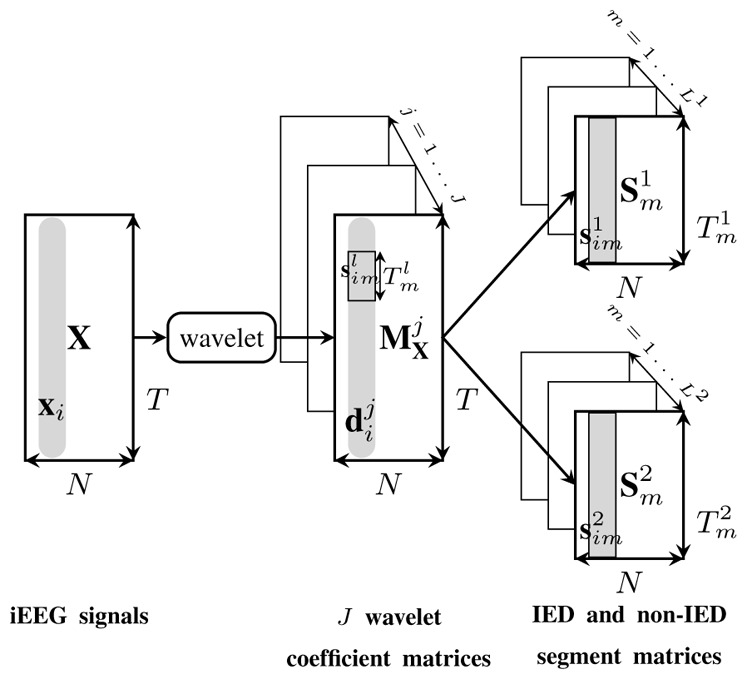
IED and non-IED segment matrices. The MODWT transform is applied on the T samples of N-dimensional iEEG recordings, X, for the J frequency levels providing J matrices denoted as , j = 1, …, J. xi and are the ith columns of matrices X and , respectively. contains wavelet coefficients of xi at frequency level j. Columns of each matrix (at each given level j) are segmented according to IED and non-IED time intervals providing L1 and L2 matrices denoted as and , respectively. is the number of rows of matrix which is equal to the length of each IED or non-IED segment m denoted as , where i = 1, …, N is the channel index.
For each , the coupling measure (MMCC), , calculated for each channel pair (i, j) ∈ {1, …, N}2, provides a square symmetric N × N matrix, , where . Due to the symmetry, only entries of the upper triangle of matrix are considered. We build vector as the concatenation of the upper triangle columns of . includes the MMCC between all of channel pairs during IED or non-IED time interval m (Fig. 4). Length of is the number of possible connections that is .
Figure 4.
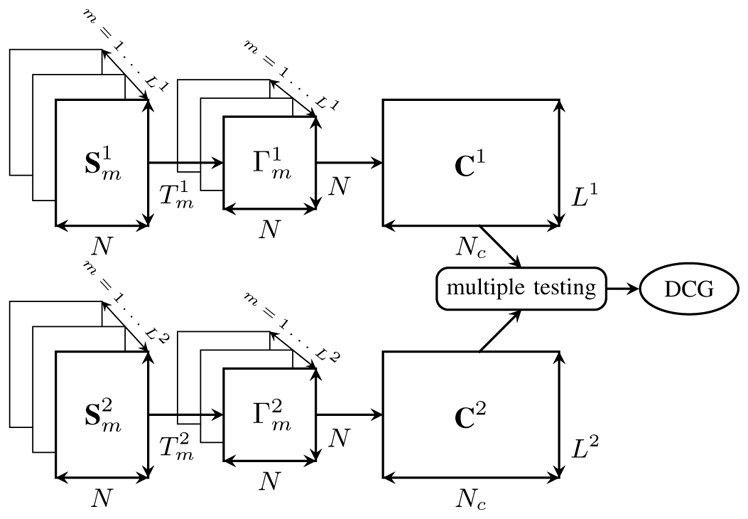
DCG Construction at a given frequency band. Each wavelet coefficient matrix of IED or non-IED segment m (m = 1, …, Ll),
provides one symmetric N × N coupling measure matrix,
. Each
builds the mth row of the matrix Cl ∈
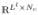 , which contains all of the information concerning couplings between all of the possible connections at each frequency level. The DCG connections are identified by comparing C1 and C2, using multiple testing.
, which contains all of the information concerning couplings between all of the possible connections at each frequency level. The DCG connections are identified by comparing C1 and C2, using multiple testing.
3. DCG construction [19], [28]
The scheme depicted in Figure 4 demonstrates how to construct the DCG for a given frequency band. We denote , m = 1, …, Ll, n = 1, …, Nc. Cl includes MMCC between activities recorded from all of channels in the columns and during all of IED or non-IED time intervals (temporal epileptic activities) in the rows. C1 and C2 are served to a multiple hypothesis test for testing whether or not to assign a connection between channels i and j, (i, j) ∈ {1, …, N}2 (denoted as connection n for simplicity). We test the null hypothesis that the connection n is unchanged under IED and non-IED states against the alternative that their connection changes such that:
| (7) |
where is the average of , which is the nth column of matrix Cl. The test statistic tn for each connection n between pair of nodes i and j is defined as:
| (8) |
where and are the empirical estimated mean and variance of , respectively. The simple and ideal method to do each connection test is to assume a theoretical distribution for the test statistic under null hypothesis. Since we do not know the distribution of tn, we use permutation tests, which require fewer assumptions about the data, thereby yielding more reliable procedures by using data-based distributional characteristics [15], [29].
We permute Np (number of permutations) times the coupling measures computed for IED and non-IED groups. More precisely, for each connection n, we permute Np times the L1 + L2 entries of and , then regroup the first L1 and L2 entries as IED and non-IED groups, respectively. For each permutation we calculate the test statistic tn according to (8). The Np values of tn form a “permutation” distribution to which we compare the observed tn of the original data and estimate a raw p-value. The raw p-value is estimated as the number of permutations which the absolute value of their corresponding tn exceeds the absolute value of the observed tn (calculated from the original data) divided by Np. Large number of permutations (Np is experimentally chosen equal to one million for about 5000 connections) may provide better estimation of p-values. The total number of possible permutations for L1 + L2 samples, with L1 and L2 samples of each group is , ie. in our experiment over 1050. The Np permuted sets are chosen randomly from the sets of possible permutations.
Permutation test relies on the assumption that the distribution of observations does not change by permutation under the null hypothesis [29]. The permutation-based null distribution can be correctly estimated when the number of IED and non-IED time intervals are equal (balanced sample sizes) [15]. However, unbalanced number of samples can be problematic when the sample size is small. Here, the number of time intervals is unbalanced, but large (Table I). The permutation tests computed for large unbalanced and balanced number of samples show that the performance of the method is comparable according to high similarity percentages between the DCGs based on these two conditions. Similarity percentage is defined as the normalized sum of common number of significant or non-significant t-values over number of possible connections.
Table I.
Parameters of the patients’ iEEG. N: number of the bipolar channels; T: length of the original (non segmented) iEEG signal (minutes); Nc: number of possible connections; Ll: number of IED or non-IED time intervals.
| P1 | P2 | P3 | P4 | P5 | mean | |
|---|---|---|---|---|---|---|
| N | 104 | 105 | 111 | 109 | 100 | 106 |
| T (minutes) | 61 | 56 | 42 | 90 | 66 | 55.44 |
| Nc | 5356 | 5460 | 6105 | 5886 | 4950 | 5551 |
| L1 | 298 | 614 | 223 | 160 | 223 | 304 |
| L2 | 143 | 200 | 195 | 183 | 148 | 174 |
For multiple testing, we need to control the abundance of false positives [15] (significance level or type I error). Since the probability of making type I error increases in multiple testing, we adjust raw p-values in order to keep the probability of making at least one type I error for the whole family of Nc tests (family wise error rate) equal to α. Here, we focus on adjusted p-values by Sidak step down method for controlling family wise error rate [15]. For connection n, we reject the null hypothesis in the test (7) when its related adjusted p-value is less than or equal to α. The DCG is constructed by keeping the connections whose MMCC values significantly change between IED and non-IED time intervals. In the following, the significant connections which or are called positive or negative connections, respectively. A positive or negative connection demonstrates respectively a significant increase or decrease of coupling between channel pair (i, j) (connection n) during IED state. For each interested frequency band, a DCG is computed.
B. Step 2: Directed DCG (dDCG) computation
Here, we describe a simple method [19], [30] to estimate the drive-response relationship between signals observed at the nodes of DCG=(V, E). V and E represent the set of DCG vertices (or nodes associated with iEEG bipolar channels) and edges (or connections), respectively. Let and denote the jth level MODWT coefficients (1)–(3) of signals xa and xb observed at nodes a and b (a, b ∈ V), where k = 1, …, T, and T is the number of samples of the whole processed iEEG recording.
We estimate the drive-response relationship between and signals assuming and include sufficient large number of samples. We presume causes , if follows the activity of with a positive time delay. For each pair (a, b), we compute , the time delay between and in which the maximum of the absolute value of (5) occurs.
For each level j, (associated with xa) causes (associated with xb) if the time causality ( ) between and is negative. In this paper, we do not assume that the “transfer function” between two signals emitted by two brain areas is represented by pure delay, therefore we do not confine the time causality to be the same for all of the frequency bands.
The time causality is used to estimate the direction of DCG connections and calculate the emittance measure which is described in the next step. For simplicity in the following, we mark , and as da and db, and respectively.
C. Step 3: Characterization of dDCG
Nodes of dDCG are related to IED events including source and sink nodes. In this step, we aim to characterize the dDCG to identify the source nodes. To this end, we propose an index called local information (LI) to measure the amount of information that passes through each node locally. LI of each node depends on (1) outgoing and incoming connections incident the node (dDCG structure) and (2) the amount of information which is carried by each of these connections. This information is calculated based on lagged mutual information (MI) between the signal pairs observed at the two ends of the connection.
Let Da and Db be two random variables with probability density functions (PDF) pa(u), pb(v) and joint PDF pab(u, v). The MI between Da and Db is defined as:
| (9) |
We assume samples of time series and as the observations of Da and Db. By partitioning the supports of da and db into bins of finite size and assuming ergodicity, MI (9) can be approximated as the finite sum:
| (10) |
where p̂a(i), p̂b(j), and p̂ab(i, j) are estimated densities obtained by relative frequencies. In the following MIbinned(da, db) is simplified by , which emphasizes on the shift between the two time series and . The local information of node a ∈ V, denoted as LI[a], is then defined as:
| (11) |
where . In theory, LI of the source or sink nodes are positive or negative, respectively and greater positive values demonstrate higher emittance contribution or greater strength of a source node. LI is zero when in and out information flows are equal.
To know the accuracy of LI estimation, its variance is estimated by jackknife resampling method. For each connected node of dDCG, we calculate the LI (11) for Nw windows. Let W be the window length and T the number of samples of the whole processed signal. The start time of each window is a random number in the range [1, T − W]. The standard deviation of LI for each connected node is approximated as the standard deviation of Nw recomputed LI values.
D. Step 4: Multiple graph analysis
Using LI measure (11), the nodes of dDCG related to each frequency level j can be quantified according to their emittance contribution to the rest of graph. So far, we have summarized the multivariate time-frequency knowledge of all of the recorded spatial locations (nodes) into a univariate index in each frequency band. Now, we ask whether a set of optimum nodes can be selected considering the multi-frequency local information. Since no preference is known about the frequency bands, there is no unique solution, and instead a set of solutions can be provided using multi-objective optimization method (in the following we recall it Pareto method) [11], [31]. This set of solutions is known as Pareto front.
The information measure (11) is calculated for the connected dDCG nodes of all of frequency levels, forming a matrix LI = [LIj[n]] ∈
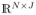 , n = 1, …, N, j = 1, …, J. We denote LIj[:] the jth column of matrix LI including the LI values of all of the nodes in the frequency level j. The row n of the matrix LI, denoted LI: [n] is a J – dimensional feature vector including the local information values of node n in all of J frequency levels. The vector LI:[n] belongs to the search space P ⊂
, n = 1, …, N, j = 1, …, J. We denote LIj[:] the jth column of matrix LI including the LI values of all of the nodes in the frequency level j. The row n of the matrix LI, denoted LI: [n] is a J – dimensional feature vector including the local information values of node n in all of J frequency levels. The vector LI:[n] belongs to the search space P ⊂
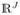 . Roughly speaking, a Pareto optimal set is a subset of N nodes whose LI: [n] is significantly large. More precisely the Pareto optimal set denoted as D(P) can be obtained with the following algorithm. Let consider N J-dimensional vectors, LI: [n] as N nodes in search space P.
. Roughly speaking, a Pareto optimal set is a subset of N nodes whose LI: [n] is significantly large. More precisely the Pareto optimal set denoted as D(P) can be obtained with the following algorithm. Let consider N J-dimensional vectors, LI: [n] as N nodes in search space P.
initialize D(P) with LI:[n0], n0 can be any node.
-
compare LI: [n] ∈ P, n ≠ n0 with the members of D(P) using the following conditions. In the first iteration the only member of D(P) is node n0.
if LI: [n] ≥ LI: [n0] for all of j levels, and LI: [n] > LI: [n0] for at least one level j, then LI: [n0] is replaced with LI:[n], since node n dominates node n0.
else if LI:[n] > LI:[n0] for at least one level j, then LI:[n] is added to D(P), since there is no preference between nodes n and n0.
increment n and go to previous step till n reaches to N.
the members of D(P) are the Pareto optimal solutions denoted as LI:[n*] which build the Pareto front or estimated leading IED (ℓIED) nodes.
There is no preference between the Pareto front solutions. In order to rank these solutions, we focus on two techniques [11]. In the first method, we select a solution from Pareto front which locates closer to an ideal point. The ideal point, z = [z1, …, zJ] is compromised of the individual best values of each dimension that is usually infeasible solution, and defined as:
| (12) |
Then we rank LI:[n*] according to their increasing Euclidean distance to z:
| (13) |
The Pareto front solution with smaller value of d(LI:[n*], z) is preferred. The second method uses a utility function U(LI:[n*]) which allows to rank the LI[n*] vectors by comparing their norms, e.g.
| (14) |
The solution with greater utility function (norm) value deserves greater attention.
III. Data and results
A. Data
The iEEG recordings were obtained from five patients suffering from focal epilepsy. The patients underwent pre-surgery evaluations with the iEEG recordings. They are seizure free after resective surgery. Eleven to fifteen semi-rigid multi-lead intracerebral electrodes with 0.8 mm diameter were bilaterally implanted in suspected seizure origins based on clinical considerations. The multi-lead electrodes (Dixi, Besançon, France) include 5, 10, 15 or 18 leads. Each lead has 2 mm length and is evenly spaced with inter-space of 1.5 mm. The iEEG were recorded with an audio-video-EEG monitoring system (Micromed, Treviso, Italy) with a maximum of 128 channels and digitized at 512 Hz. The electrode leads were recognized on the patient’s implantation scheme, and localized in the Montreal Neurological Institute (MNI) atlas. Bipolar derivations were considered between adjacent leads within each electrode. For simplicity, these adjacent bivariate derivations are represented as ei instead of ei+1 − ei. The 50 Hz is removed by a 5-order notch Butterworth filter with 3dB cut-off frequencies equal to 48 Hz, and 52 Hz.
B. Results
1. Directed DCG
The parameters of the patients’ iEEG and method are reported in Tables I and II, respectively. Here, we report the results of the proposed method in steps 1 and 2. The dDCGs are calculated for the frequency bands with high contribution during IED and non-IED time intervals. We analyze the data from 2–64 Hz in five frequency bands: 2–4, 4–8, 8–16, 16–32, and 32–64 Hz. These frequency bands can be assigned to EEG rhythms as following: 2–4 Hz: delta, 4–8 Hz: theta, 8–16 Hz: alpha, 16–32 Hz: beta, and 32–64 Hz: gamma. The related dDCGs are shown in Figure 5 for iEEG analysis of patient 2 (P2). The nodes are iEEG channels related to bivariate derivations of the leads of each electrode and edges represent connections between nodes. The solid and dashed lines show the positive and negative connections, respectively.
Table II.
Parameters of the method. τmax: maximum number of time lags (samples) in cross-correlation analysis; fs: Sampling rate; Np: Number of permutations; Nw: number of windows; W length of each window (minutes); Nb: number of bootstrap repetitions.
| Method parameter | |||
|---|---|---|---|
| Wavelet filter | ‘la8’ | fs (Hz) | 512 |
| Number of wavelet levels | 5 | Np | 106 |
| False positive rate (α) | 0.05 | Nw | 100 |
| τmax in step 1 | 27 | W in step 3 | 33 |
| τmax in step 2 | 100 | Nb | 104 |
Figure 5.
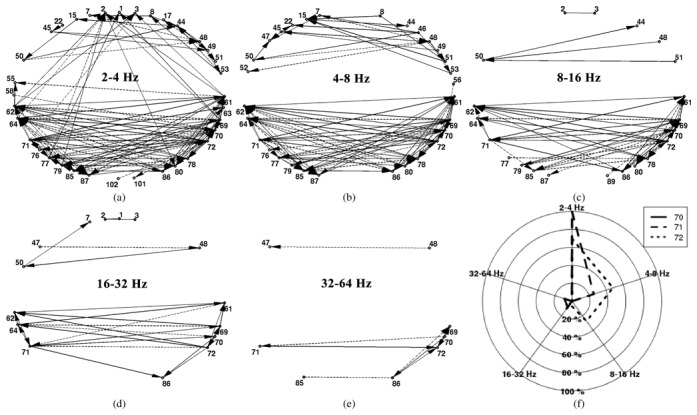
Results of the proposed method for P2. (a)–(e) dDCG (steps 1 and 2) of different frequency bands from 2–64 Hz. These dDCGs are quantified by LI measure (11) in step 3. A multi-object optimization method in step 4 optimizes these LI measure values to estimate the (ℓIED regions. (f) Web plot of estimated (ℓED nodes for P2: nodes 70, 71 and 72 located in left anterior hippocampus. The three related pentagons of LI:[70], LI:[71], and LI:[72] are depicted in solid, dashed, and dotted lines, respectively.
The effect of large balanced and unbalanced (Section II-A3) number of time intervals (L1 and L2) in multiple testing is verified by comparing the DCG constructed with unbalanced number of time intervals and ten (an arbitrary choice) DCGs with random balanced number of time intervals. The balanced number of time intervals is fixed equal to the smaller number of IED and non-IED time intervals (min(L1, L2)). Say L2 = min(L1, L2), therefore L2 IED time intervals are chosen randomly among L1 IED time intervals and the related DCG is constructed. We repeated this procedure ten times. The similarity percentage (Section II-A3) is calculated between the original DCG-based unbalanced number of time intervals and ten recalculated DCG-based balanced number of time intervals. The mean of these ten percentages for P1 at frequency band equal to 4–8 Hz is 97.2% ± 0.3. This result shows that the large unbalanced number of time intervals is not problematic for the permutation test [15]. To verify the reliability of DCGs for different random sets of IED time intervals, the similarity percentage between each pairs of ten recalculated DCGs is obtained. The mean of these similarity percentages for the same patient and frequency band is 96.9% ± 0.25.
2. ℓMED regions
The LI measure (11) is calculated for the dDCG nodes of all of the frequency bands studied. Nodes with negative LI values are discarded since we are not interested in target (sink) nodes [2]. The multi-objective optimization method is applied on normalized LI measurements ([0, 1]) to obtain the Pareto front or estimated ℓIED nodes. The LI values of a node for five frequency bands can be considered as a five-dimensional vector (LI:[n]), which can be demonstrated with a pentagon in two-dimensional space in a web plot. For the iEEG analysis of P2, three nodes: 70, 71, and 72 located in left anterior hippocampus are obtained as the optimum solutions (LI:[n*]) and their pentagons are depicted with solid, dashed, and dotted lines, respectively in Figure 5(f). The values of LI:[70], LI:[71], and LI:[72] are reported in Table III.
Table III.
Normalized LI measure values for Pareto front nodes of P2
| Pareto front | 2–4 | 4–8 | 8–16 | 16–32 | 32–64 |
|---|---|---|---|---|---|
| 70 | 0 | 0 | 0 | 0.08 | 0.09 |
| 71 | 1 | 0.26 | 0 | 0.1 | 0 |
| 72 | 0.7 | 0.48 | 0.27 | 0.04 | 0 |
To rank the estimated ℓIED nodes, three indices are calculated (Section II-D). The values of these three indices are reported for the Pareto front of the iEEG analysis of P2 in Table IV. The reported normalized LI values reveal the importance of nodes 71 and 72 rather than 70. Nodes 71 and 72 have greater contributions in lower frequencies, while node 70 is mostly active in higher frequencies (Table III). In this patient (P2), all of the Pareto front nodes belong to one brain region. Conversely, the Pareto front of other patients (P3 and P4) include different brain regions (Table V) which the rank of estimated ℓIED regions reveals more challenging knowledge. Sorting the estimated ℓIED regions may provide valuable information to the epileptologist toward reducing the brain regions that are resected in resective surgery.
Table IV.
Ranked Pareto front nodes for P2. First and second column values are normalized to their maximum value
| Pareto front | d(LI:[n*], z) | ||LI:[n*]||1 | ||LI:[n*]||∞ | |||
|---|---|---|---|---|---|---|
| source1 | 72 | 0.28 | 72 | 1 | 71 | 1 |
| source2 | 71 | 0.32 | 71 | 0.91 | 72 | 0.7 |
| source3 | 70 | 1 | 70 | 0.12 | 70 | 0.09 |
Table V.
Comparison between ℓIED regions estimated by our method, SOZ detected by using induced seizure periods by electrical stimuli (eSOZ) following [12] and visually inspected SOZ (vSOZ) by epileptologist. dis (mm): the average of minimum distances between ℓIED and vSOZ nodes; ovp: the average percentage of number of ℓIED nodes which are in the neighborhood (≤ 1.5 cm) of at least one of the vSOZ nodes. ovp2: the average percentage of number of vSOZ nodes that are in the neighborhood (≤ 1.5 cm) of at least one of the ℓIED nodes; Bold regions demonstrate the uncommon regions between vSOZ and ℓIED regions. remR: removed regions during resective surgery; NA: not applicable; amyg: amygdala; ant/post/int/sup: anterior/posterior/internal/superior; entC: entorhinal cortex; Hc: hippocampus; pHcG: parahippocampal gyrus; T: temporal; TP: temporal pole; m: mesial; G: gyrus; midInsG: middle short gyrus of insula
| ℓIED | vSOZ | eSOZ | remR | dis | %ovp | %ovp2 | |
|---|---|---|---|---|---|---|---|
| P1 | antHC pHcG amyg | ant/postHC pHcG amyg mTP | postHC | ant/postHC pHcG amyg TP antsupTG | 9.57 | 60 | 60 |
| P2 | antHC | ant/postHC pHcG amyg | ant/postHC | ant/postHC pHcG amyg TP | 0 | 100 | 85 |
| P3 | ant/postHC | ant/postHC pHcG | antHC | ant/postHC pHcG TP | 4 | 100 | 100 |
| P4 | ant/postHC amyg entC | ant/postHC amyg mTP entC | - | ant/postHC amyg TP entC | 12.91 | 62 | 79 |
| P5 | midInsG | midInsG | NA | midInsG | 5.32 | 100 | 100 |
| mean | 6.4 | 84.4 | 84.8 | ||||
The estimated ℓIED regions are almost insensitive to the different parameter settings like different values of maximum time lags in DCG calculation. Accordingly, the ℓIED regions based on DCGs with large balanced, or unbalanced number of time intervals are almost similar. The probable minor changes in the set of ℓIED regions belong to the least priority regions.
3. Comparison between SOZ defined by visual inspection, the method proposed in [12], and estimated ℓIED regions for P1 to P5
The quantitative comparison of results between SOZ defined visually (vSOZ) by epileptologist and estimated ℓIED regions computed by our method are brought in Table V for the five patients (P1 to P5). The different quantitative measures are as follows. First, dis (mm) is the average of minimum distances between ℓIED and vSOZ nodes, in which the proximity of the ℓIED nodes to vSOZ nodes is measured. The average of dis over five patients is 6.4 mm. This indicates the accuracy of agreement between vSOZ and estimated ℓIED regions. Second, ovp (%) is the average percentage of number of ℓIED nodes which are in the neighborhood (≤ 1.5 cm) of at least one of the vSOZ nodes. The large percentage of ovp reveals that a large number of ℓIED nodes are in the neighbourhood of at least one of vSOZ nodes. Third, ovp2 (%) shows a similar percentage as ovp except ovp2 considers the vSOZ nodes which are in the neighborhood of at least one of the ℓIED nodes. We found an average of 84.4% and 84.8% over patients for ovp and ovp2, respectively. Removed regions during resective surgery are reported for P1 to P5 in Table V. All of the five patients are completely seizure-free after surgery and the estimated ℓIED regions are included in the resected regions for all of the patients. This result confirms that ℓIED regions can be valuable in pre-surgery evaluations while regions related to secondary propagated activity (sink nodes) might not be necessary to be removed [2], [3], [6].
To investigate the performance of our proposed method, we compare the ℓIED regions estimated from interictal periods with SOZ proposed by [12] from induced ictal periods by electrical stimuli (eSOZ) of iEEG recordings (Table V). The results are compared for three common patients (P1 to P3). There are more common regions between estimated ℓIED regions and vSOZ than between vSOZ and eSOZ. For two other patients, P4 and P5, this comparison was not possible. P4 recently underwent surgery and eSOZ results were not available. The SOZ of P5 cannot be defined by the eSOZ method since no seizure occurred by stimuli during iEEG recordings. Conversely, our method estimates the vSOZ correctly (middle short gyrus of insula) without using seizure periods, instead using IED and non-IED time intervals. This patient (P5) has the most focused vSOZ and resected region among all of the patients.
The proposed method estimates the ℓIED regions, congruent with vSOZ, requiring simpler, faster, and less expensive iEEG recording comparing to eSOZ method which requires induced seizure periods. For the patients in whom no seizure occurs during the stimuli, the estimated ℓIED regions can be valuable.
IV. Discussion
A. Maximum of cross-correlation function
The variation of calculated MMCC (5)–(6) for different time windows (IED or non-IED time intervals) can be due to the estimation error and to the variability of the signal pair couplings between two brain regions in time and frequency. Since our signals are non-stationary, the estimation of the variance of MMCC is very complicated. To overcome this difficulty, we used multiple testing based on permutation to estimate the distribution of the test statistic (8) related to MMCC providing a reliable procedure for detecting the statistically significant connections (Section II-A3).
For a better estimation of MMCC, we studied experimentally the effect of the different parameters on the variance of MMCC estimation. Here, we explain the effect of maximum number of time lags (τmax ≥ |τ|) in cross-correlation estimation [32], [33], and how τmax is chosen experimentally for different steps of the method. Generally, in cross-correlation computation (5), τmax is suggested to be large enough to include the true lag between a signal pair. Conversely, increasing the number of time shifts (τmax) inflates the confidence interval of correlation estimation for non-stationary fractionally differenced signals [17]. Although our non-stationary signals do not hold this particular property, our experimental results for MMCC estimation confirmed the above statement, i.e. increase of maximum number of time lags, and decrease of number of samples may increase the variance of MMCC estimation. Here we explain our experimental results for non-stationary signals. The similarity percentage (Section II-A3) between DCGs based on τmax = 27 and 100 samples (the reason of these choices are explained later in this Section) are compared for two patients (P1 and P2). The similarity percentage decreases in lower frequencies for both patients. Contrary to τmax = 100, less empirical variance of MMCC and more number of connections is provided by τmax = 27, especially for lower frequencies. The empirical variance is the variance of estimated MMCC of different IED or non-IED time intervals along the processed time signal. One reason for increase of variance can be the decrease of the number of samples especially in lower frequencies where the number of independent samples decreases.
Eventually a proper selection of τmax can be the smallest maximum number of time lags examined in cross-correlation analysis including the true lag [32]. Satisfying this condition requires the physiological knowledge about the time lags between interictal events recorded from different recording electrode leads [34]. This physiological lag can be at most 100–200 msec i.e. about 50–100 samples with fs = 512 Hz, typically less than 50 msec i.e. about 25 samples [2].
In the first step of our method, the aim is to estimate the maximum coupling between each signal pair during IED and non-IED time intervals. In this step, the smallest maximum number of time lags examined in cross-correlation analysis including the assumed true lag (about 25 samples) [2] is selected equal to 27 samples. Although we observe high similarity percentages between DCGs-based 27 and 100 samples and almost similar final results (estimated ℓIED regions), we prefer τmax = 27. Using τmax = 27 provides more probable connections (less conservative) and less time consuming procedure in the first step. We prefer to be less conservative and more powerful in the first step to identify as many discriminated connections as possible. Once such connections are found, a higher level processing (steps 2 to 4) is adopted to extract nodes with optimum emittance contribution.
B. Time causality
In the second step, large number of samples, T (Table I) is selected for better estimation of MMCC. By using τmax = 27 samples, we cannot determine the time causality for a part of the edges of DCG especially in low frequencies (no maximum cross-correlation can be found in the range [− τmax τmax]), therefore the estimation of ℓIED regions would be based on the rest of the edges of DCG. In other words dDCG based on τmax = 100 samples has more common number of edges with DCG compared to τmax = 27 samples. Consequently, in this step we chose τmax = 100 samples that is the upper limit of physiological time lag [2].
C. Reliability of the time causality
To test the reliability of time causality calculated in (6) a statistical jackknife method is used as computed for the accuracy of LI in Section II-C. All of the parameters are the same (Table II) except W that is equal to 20 minutes. The window length W is considered large enough to include large number of IED time intervals. The time causality (6) is estimated for each of randomly chosen windows providing Nw time lag values, which form a histogram-based probability distribution. For each edge of DCG between node pairs (a, b), this histogram is estimated and the time lag, which has the greatest probability is chosen. For each edge, we test if the Nw time lag values are significantly non-equal to zero. If the time lag values are significantly equal to zero then is set to zero, i.e. the direction of the edge between node pairs (a, b) could not be estimated. For the statistical test a bootstrap method with Nb repetitions and false positive error α is used (Table II). We compare the values with the estimated (6) between the signals of length T. The percentage of similar time lags ( ) over number of edges of DCG is in the range [78 95]% for different frequency bands. Consequently, (6) can provide reliable estimation of the most probable time lag between signal pairs of DCG edges if it is calculated for long enough signals and if τmax is selected properly.
D. Directed graph characterization
LI measure is introduced to define source and sink nodes of a directed graph based on in and out information flow of each node. The classic graph measures like local efficiency, global efficiency, and node degree [19], [28], [35] are not as informative as LI for the definition of source and sink nodes of directed graphs. The main advantage of LI over these classic measures is that first it considers the incoming connections to the node in addition to outgoing ones, second it considers the information which is carried by each of these connections. A quantitative comparison between LI and classic graph measures is investigated in [36].
The conditional mutual information (CMI) was used in [23] to calculate the directional coupling measure between signal pairs (transfer entropy). Here CMI cannot be used since we are interested in measuring the information passing through each node, which is computed by LI.
E. Multiple graph analysis
dDCG provides sparser graph comparing to separated IED and non-IED complex graphs and may provide simpler interpretation, but still concluding to ℓIED regions from the dDCGs of different frequency bands needs careful analysis. Proposed LI measure characterizes the dDCG nodes related to different frequency bands. To summarize these multi-frequency information, an optimization method to introduce the optimum nodes based on their LI values is helpful. Since the preference between frequency bands is unknown, a multi-objective optimization method [11], [31] is well-suited to find the optimum nodes, i.e. a subset of nodes with greater LI values in at least one of the frequency bands. Using multi-objective optimization method, the optimum source nodes or ℓIED regions are deduced from multiple (multi-frequency) dDCGs. In general we found multi-objective optimization method very helpful for the interpretation of multiple graphs. The optimization method can be applied on any feature extracted from the graphs depending on the application.
V. Conclusion
In this paper, we aim to localize SOZ by estimating the leading brain regions involved in the generation of transient epileptic events considering both IED and non-IED time intervals, i.e. even if seizures are not present. For this purpose, we propose a new tool: directed differential connectivity graph (dDCG) to identify the discriminated connections between the IED and non-IED states. The dDCG is statistically reliable due to the permutation resampling method [15] and large number of IED and non-IED time intervals. To determine source and sink nodes of dDCG, we introduced a local information measure LI. The LI information of dDCGs related to different frequency bands is summarized by multiple graph analysis to estimate the leading IED regions.
The proposed method is applied on iEEG recording of five epileptic patients and compared with visually inspected SOZ by the epileptologist and also with SOZ reported by [12] from induced ictal periods by electrical stimuli of iEEG recordings of the same patients. We obtained congruent results between estimated ℓIED regions and SOZs. Moreover, estimated ℓIED regions are included in the removed regions (column remR of Table V) during resective surgery. All of the patients being seizure free after resective surgery, one can conclude that estimated ℓIED regions may present reliable information for the surgeon which should be useful for presurgical evaluations. Thus, the proposed method can provide efficient and repeatable analysis from iEEG recordings of epileptic patients.
A first perspective which leads to a fully automatic method is to replace the visual IED and non-IED labeling with automatic methods. Secondly, we are interested in considering large number of patients including the patients with primary failure surgery results and secondary seizure-free surgery output to test the performance of the method for difficult cases. Finally, in the present method we are able to study the regions which the iEEG electrodes cover. Due to the difficulties of invasive electrodes, only limited suspected epileptic zones can be studied [1]. A very challenging perspective is to use an inverse model for localizing epileptic regions from noninvasive scalp EEG recordings.
References
- 1.Rosenow F, Lüders H. Presurgical Evaluation Of Epilepsy. Brain. 2001;124(9):1683–1700. doi: 10.1093/brain/124.9.1683. [DOI] [PubMed] [Google Scholar]
- 2.Alarcon G, Garcia Seoane JJ, Binnie CD, Martin Miguel MC, Juler J, Polkey CE, Elwes RD, Ortiz Blasco JM. Origin And Propagation Of Interictal Discharges In The Acute Electrocorticogram. Implications For Pathophysiology And Surgical Treatment Of Temporal Lobe Epilepsy. Brain. 1997 Dec;120(Pt 12):2259–2282. doi: 10.1093/brain/120.12.2259. [DOI] [PubMed] [Google Scholar]
- 3.Hufnagel A, Dumpelmann M, Zentner J, Schijns O, Elger CE. Clinical Relevance Of Quantified Intracranial Interictal Spike Activity In Presurgical Evaluation Of Epilepsy. Epilepsia. 2000 Apr;41(4):467–478. doi: 10.1111/j.1528-1157.2000.tb00191.x. [DOI] [PubMed] [Google Scholar]
- 4.Le Van Quyen M, Adam C, Baulac M, Martinerie J, Varela FJ. Nonlinear Interdependencies Of EEG Signals In Human Intracranially Recorded Temporal Lobe Seizures. Brain Res. 1998 May;792(1):24–40. doi: 10.1016/s0006-8993(98)00102-4. [DOI] [PubMed] [Google Scholar]
- 5.Ortega GJ, Sola RG, Pastor J. Complex Network Analysis Of Human ECoG Data. Neurosci Lett. 2008 Dec;447(2–3):129–133. doi: 10.1016/j.neulet.2008.09.080. [DOI] [PubMed] [Google Scholar]
- 6.Wilke C, van Drongelen W, Kohrman M, He B. Identification Of Epileptogenic Foci From Causal Analysis Of ECoG Interictal Spike Activity. Clin Neurophysiol. 2009 Aug;120(8):1449–1456. doi: 10.1016/j.clinph.2009.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Monto S, Vanhatalo S, Holmes MD, Palva JM. Epileptogenic Neocortical Networks Are Revealed By Abnormal Temporal Dynamics In Seizure-Free Subdural EEG. Cereb Cortex. 2007 Jun;17(6):1386–1393. doi: 10.1093/cercor/bhl049. [DOI] [PubMed] [Google Scholar]
- 8.Wendling F, Bartolomei F, Senhadji L. Spatial Analysis of Intracerebral Electroencephalographic Signals in the Time and Frequency Domain: Identification of Epileptogenic Networks in Partial Epilepsy. Philos Trans R Soc A-Math Phys Eng Sci. 2009;367:297–316. doi: 10.1098/rsta.2008.0220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bourien J, Bartolomei F, Bellanger JJ, Gavaret M, Chauvel P, Wendling F. A Method To Identify Reproducible Subsets Of Co-Activated Structures During Interictal Spikes. Application To Intracerebral EEG In Temporal Lobe Epilepsy. Clinical Neurophysiology. 2005;116(2):443–455. doi: 10.1016/j.clinph.2004.08.010. [DOI] [PubMed] [Google Scholar]
- 10.Towle VL, Syed I, Berger C, Grzesczcuk R, Mlton J, Erickson RK, Cogen P, Berkson E, Spire JP. Identification of The Sensory/Motor Area and Pathologic Regions Using ECoG Coherence. Electroencephalogr Clin Neurophysiol. 1998 Jan;106(1):30–39. doi: 10.1016/s0013-4694(97)00082-5. [DOI] [PubMed] [Google Scholar]
- 11.Deb K. Kanpur Genetic Algorithms Lab (KanGal), Technical report 99002. 1999. Multi-Objective Evolutionary Algorithms: Introducing Bias Among Pareto-Optimal Solutions. [Google Scholar]
- 12.David O, Wozniak A, Mnotti L, Kahane P. Preictal Short-Term Plasticity Induced By Intracerebral 1Hz Stimulation. NeuroImage. 2008;39(4):1633–1646. doi: 10.1016/j.neuroimage.2007.11.005. [DOI] [PubMed] [Google Scholar]
- 13.Kramer MA, Eden UT, Cash SS, Kolaczyk ED. Network Inference With Confidence From Multivariate Time Series. Phys Rev E Stat Nonlin Soft Matter Phys. 2009 Jun;79(6 Pt 1):061916. doi: 10.1103/PhysRevE.79.061916. [DOI] [PubMed] [Google Scholar]
- 14.Kramer MA, Kolaczyk ED, Kirsch HE. Emergent Network Topology At Seizure Onset In Humans. Epilepsy Res. 2008 May;79(2–3):173–186. doi: 10.1016/j.eplepsyres.2008.02.002. [DOI] [PubMed] [Google Scholar]
- 15.Pollard KS, van der Laan MJ. UC Berkeley Division of Biostatistics Working Paper Series Working Paper. 2003. Resampling-Based Multiple Testing: Asymptotic Control Of Type I Error And Applications To Gene Expression Data; p. 121. [Google Scholar]
- 16.Naït-Ali A. Advanced Biosignal Processing. Springer; 2009. [Google Scholar]
- 17.Whitcher B, Guttorp P, Percival D. Wavelet Analysis of Covariance with Application to Atmospheric Time Series. J Geophys Res - Atmospheres. 2000;105:14941–14962. [Google Scholar]
- 18.Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E. A Resilient, Low-Frequency, Small-World Human Brain Functional Network with Highly Connected Association Cortical Hubs. The Journal of Neuroscience. 2006;26:63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Amini L, Jutten C, Achard S, David O, Soltanian-Zadeh H, Hossein-Zadeh GA, Kahane P, Minotti L, Vercueil L. Directed Epileptic Network From Scalp And Intracranial EEG Of Epileptic Patients. IEEE International Workshop, MLSP09; Grenoble, France. Sep. 2–4 2009. [Google Scholar]
- 20.Gotman J. Measurement Of Small Time Differences Between EEG Channels: Method And Application To Epileptic Seizure Propagation. Electroencephalogr Clin Neurophysiol. 1983 Nov;56(5):501–514. doi: 10.1016/0013-4694(83)90235-3. [DOI] [PubMed] [Google Scholar]
- 21.Lachaux JP, Lutz A, Rudrauf D, Cosmelli D, Le Van Quyen M, Martinerie J, Varela F. Estimating The Time-Course Of Coherence Between Single-Trial Brain Signals: An Introduction To Wavelet Coherence. Neurophysiol Clin. 2002 Jun;32(3):157–174. doi: 10.1016/s0987-7053(02)00301-5. [DOI] [PubMed] [Google Scholar]
- 22.Kitzbichler MG, Smith ML, Christensen SR, Bullmore E. Broadband Criticality Of Human Brain Network Synchronization. PLoS Comput Biol. 2009 Mar;5(3):e1000314. doi: 10.1371/journal.pcbi.1000314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Paluš M, Vejmelka M. Directionality Of Coupling From Bivariate Time Series: How To Avoid False Causalities And Missed Connections. Phys Rev E. 2007 May;75(5):056211. doi: 10.1103/PhysRevE.75.056211. [DOI] [PubMed] [Google Scholar]
- 24.Paluš M, Komarek V, Hrncir Z, Prochazka T. Is Nonlinearity Relevant For Detecting Changes In EEG? Theory Biosci. 1999;118:179–188. [Google Scholar]
- 25.Clark I, Biscay R, Echeverría M, Virués T. Multiresolution Decomposition Of Non-Stationary EEG Signals: A Preliminary Study. Computers in Biology and Medicine. 1995;25(4):373–382. doi: 10.1016/0010-4825(95)00014-u. [DOI] [PubMed] [Google Scholar]
- 26.Adeli H, Zhou Z, Dadmehr N. Analysis Of EEG Records In An Epileptic Patient Using Wavelet Transform. Journal of Neuroscience Methods. 2003;123(1):69–87. doi: 10.1016/s0165-0270(02)00340-0. [DOI] [PubMed] [Google Scholar]
- 27.Ansari-Asl K, Bellanger JJ, Bartolomei F, Wendling F, Senhadji L. Time-Frequency Characterization of Interdependencies in Non-stationary Signals: Application to Epileptic EEG. TBME. 2005;52:1218–26. doi: 10.1109/TBME.2005.847541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Amini L, Achard S, Jutten C, Soltanian-Zadeh H, Hossein-Zadeh GA, David O, Vercueil L. Sparse Differential Connectivity Graph of Scalp EEG for Epileptic Patients. ESANN2009; Bruges, Belgium. 22–24 2009. [Google Scholar]
- 29.Westfall PH, Young SS. Resampling-Based Multiple Testing: Examples And Methods For P-Value Adjustment. Wiley; 1993. [Google Scholar]
- 30.Carter G. Time Delay Estimation For Passive Sonar Signal Processing. Acoustics, Speech and Signal Processing, IEEE Transactions on. 1981 Jun;29(3):463–470. [Google Scholar]
- 31.Branke J, Deb K, Miettinen K, Slowinski R. Multiobjective Optimization, Interactive And Evolutionary Approaches. Springer; 2008. [Google Scholar]
- 32.Olden JD, Neffd BD. Cross-Correlation Bias In Lag Analysis Of Aquatic Time Series. Marine Biology. 2001;138:1063–1070. [Google Scholar]
- 33.Ianniello J. Time Delay Estimation Via Cross-Correlation In The Presence Of Large Estimation Errors. IEEE Trans Acoust, Speech, Signal Process. 1982 Dec;30(6):998–1003. [Google Scholar]
- 34.David O, Harrison L, Friston KJ. Modelling event-related responses in the brain. NeuroImage. 2005;25(3):756–770. doi: 10.1016/j.neuroimage.2004.12.030. [DOI] [PubMed] [Google Scholar]
- 35.Latora V, Marchiori M. Economic Small-World Behavior in Weighted Networks. Eur Phys J. 2003;32:249–263. [Google Scholar]
- 36.Amini L, Jutten C, Achard S, David O, Kahane P, Vercueil L, Minotti L, Hossein-Zadeh GA, Soltanian-Zadeh H. Comparison Of Five Directed Graph Measures For Identification Of Leading Interictal Epileptic Regions. Physiological Measurement. 2010;31(11):1529–1546. doi: 10.1088/0967-3334/31/11/009. [DOI] [PMC free article] [PubMed] [Google Scholar]


