Skip to main content
PMC home page
Biomicrofluidics logoLink to Biomicrofluidics
. 2011 Dec 23;5(4):044120–044120-15. doi: 10.1063/1.3672689

Asymmetry of red blood cell motions in a microchannel with a diverging and converging bifurcation

Vladimir Leble 1,a), Rui Lima 1,2, Ricardo Dias 1,2, Carla Fernandes 1, Takuji Ishikawa 3, Yohsuke Imai 3, Takami Yamaguchi 4
PMCID: PMC3368833  PMID: 22685504

Abstract

In microcirculation, red blood cells (RBCs) flowing through bifurcations may deform considerably due to combination of different phenomena that happen at the micro-scale level, such as: attraction effect, high shear, and extensional stress, all of which may influence the rheological properties and flow behavior of blood. Thus, it is important to investigate in detail the behavior of blood flow occurring at both bifurcations and confluences. In the present paper, by using a micro-PTV system, we investigated the variations of velocity profiles of two working fluids flowing through diverging and converging bifurcations, human red blood cells suspended in dextran 40 with about 14% of hematocrit level (14 Hct) and pure water seeded with fluorescent trace particles. All the measurements were performed in the center plane of rectangular microchannels using a constant flow rate of about 3.0 × 10−12 m3/s. Moreover, the experimental data was compared with numerical results obtained for Newtonian incompressible fluid. The behavior of RBCs was asymmetric at the divergent and convergent side of the geometry, whereas the velocities of tracer particles suspended in pure water were symmetric and well described by numerical simulation. The formation of a red cell-depleted zone immediately downstream of the apex of the converging bifurcation was observed and its effect on velocity profiles of RBCs flow has been investigated. Conversely, a cell-depleted region was not formed around the apex of the diverging bifurcation and as a result the adhesion of RBCs to the wall surface was enhanced in this region.

INTRODUCTION

Human blood is a multiphase biofluid composed primarily of the deformable red blood cells (RBCs) suspended in plasma. Because of the complex structure of RBCs and their response to both shear and extensional flow, blood exhibits unique flow characteristics on the micro-scale level. Hence, over the years in vitro blood studies in glass microchannels have been extensively performed in order to obtain a comprehensive characterization of blood rheology and its flow dynamics.1, 2, 3, 4, 5 Most of the past studies have revealed various physiologically significant phenomena such as the Fahraeus and the Fahraeus-Lindqvist effect. The majority of these studies were performed in straight glass microchannels.1, 3, 6, 7, 8 Some examples are the pioneer studies performed by Fahraeus and Fahraeus-Lindqvist9 where they first reported that for narrow tubes (diameter < 300 μm) the apparent viscosity of blood declines with decreasing diameter. More recently, due to the developments in microscopy, computers, and image analysis techniques, several researchers have used new measuring methods to obtain deeper quantitative understanding of the blood flow dynamics in both in vitro6, 7, 8, 10, 11, 12, 13, 14, 15, 16 and in vivo experiments.17, 18, 19, 20 However, the majority of these studies relied predominantly on the data collected in simple geometries. Few hemodynamic studies, such as the work of Nakano et al.,21 Barber et al.,22 Yang et al.,23 and Doyeux et al.,24 were performed in bifurcations composed of capillary-sized vessels. Far less work has been published on the blood flow through bifurcations with dimensions comparable to arteriole-sized vessels. The present study used state-of-the-art microvisualization and image analysis techniques to obtain quantitative understanding of the flow behavior of RBCs in both diverging and converging bifurcations with dimensions geometrically similar to arterioles.

Important studies in biomicrofluidics devoted to blood rheology and its flow dynamics in microchannels, which have played a key role in several recent developments of lab-on-chip devices for blood sampling, analysis, and cell culturing.2, 16, 25, 26, 27 Due to its particulate nature blood exhibits unique flow dynamics at a micro-scale level. Hence, there is an increasing interest by both the microfluidic and biomedical communities to develop blood diagnostic devices as an alternative tool to the traditional diagnostic strategies. The flow properties of blood suspensions in a capillary wetting system have been investigated by Zhou and Chang,28, 29 in order to develop an efficient microneedle that allows the loading of microliters of blood samples. Other researchers, such as Shevkoplyas et al.,30, 31 Yang et al.,23 and Faivre et al.2 took advantage of the natural flow properties of blood in microcirculation, such as plasma skimming, leukocyte margination, the bifurcation law, and cell-free layer enhancement by an abrupt constriction, to design microfluidic devices to separate plasma and leukocytes from the whole blood. Although the development of blood-on-a-chip devices has contributed to a better understanding of the mechanical behavior of blood cells in microcirculation, to our knowledge quantitative measurements of velocity profiles of RBCs flowing in an arteriole-sized bifurcations have never been performed.

A microvascular network consists of short irregular vessel segments which are linked by numerous diverging and converging bifurcations. Although the phenomena of blood flow in microvascular networks have been studied for many years, it still remains incompletely understood.1 For instance, the blood flow behavior in bifurcations presents difficulties in analysis, as it comprises the motion of extremely deformable cells in geometrically complex regions. Red blood cells flowing through divergent and convergent bifurcations may deform considerably due to the high shear and extensional stress around the inner wall of the bifurcation and confluence, which may influence the rheological properties and flow behavior of blood. Thus, it is important to investigate in detail the behavior of blood flow occurring at both bifurcations and confluences.

The complexity of controlling and obtaining detailed measurements of the blood flow behavior through in vivo microvascular systems21 has led to in vitro studies being performed by using polydimethylsiloxane (PDMS) microchannels obtained by means of a soft-lithography technique.30, 31, 32, 33 Very recently, we have studied the asymmetry of blood flow in a microchannel with a symmetric bifurcation and confluence.32 Although the results from this study have provided evidence about the difference of the flow field between both geometries, this work did not discuss the velocity profiles in detail. In the present paper, by using a confocal micro-PTV (Particle Tracking Velocimetry) system we examined the variations in the velocity profile of both pure water and in vitro blood through a diverging and converging bifurcations. Moreover, the experimental data were compared with the results of numerical simulation. The results obtained in this work show that the existence of a pronounced cell-free layer in the vicinity of the confluence apex, and the consequent cross streamline migration allows the RBCs to flow with higher velocities. This new finding may play an important role in further understanding of the blood flow behavior and its impact on mass transport processes in microcirculation.

MATERIALS AND METHODS

Microchannel geometry

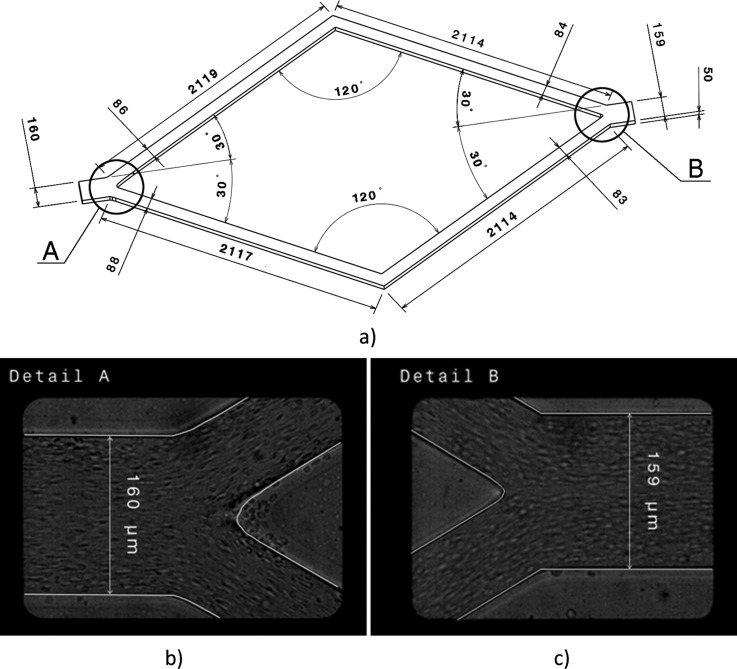
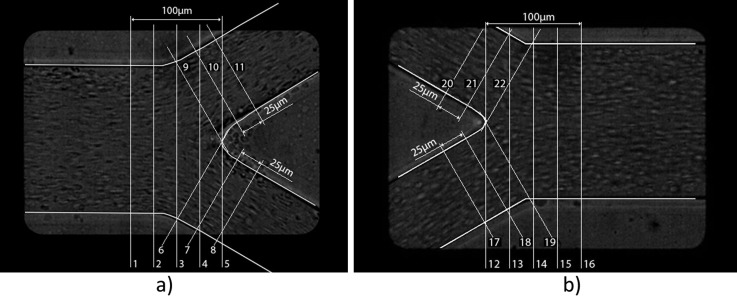
The geometry displayed in Figure 1a was found from the original design and adjusted using visualization images with visible walls of the microchannels. Figures 1b, 1c show the real geometry of the bifurcations with corresponding parts of the geometry used in simulation. The channel between inlet and first bifurcation is not depicted, though it was chosen to be almost 4 cm long to ensure a fully developed flow.

Figure 1.

Figure 1

Open in a new tab

Full geometry of microchannels (a) and details A and B (b)-(c) showing the real geometry of the bifurcations and the geometry used in simulations. All dimensions are in micrometers (μm).

Experimental set-up and working fluids

The confocal micro-PTV system used in the present study consists of an inverted microscope (IX71, Olympus, Japan) combined with a confocal scanning unit (CSU22, Yokogawa, Japan) and a diode-pumped solid state (DPSS) laser (Laser Quantum Ltd., England) with an excitation wavelength of 532 nm and a high-speed camera (Phantom v7.1). By using a soft-lithography technique, we were able to manufacture a PDMS microchannel consisting of a bifurcation and confluence (see Figure 1a). The PDMS microchannel was placed on the stage of the microscope where the flow rate of two working fluids was kept constant by means of a syringe pump (KD Scientific, Inc.). The two working fluids used in this study were pure water seeded with 1 μm in diameter fluorescent particles and dextran 40 (Dx40) containing about 14% (14 Hct) of human red blood cells (see Table TABLE I. for more details). The blood was collected from a healthy adult volunteer, where ethylenediaminetetraacetic acid (EDTA) was added to prevent coagulation. The RBCs were separated from the bulk blood by centrifugation and aspiration and then washed twice with physiological saline (PS). The washed RBCs were labeled with a fluorescent cell tracker (CM-Dil, C-7000, and Molecular Probes) and then diluted with Dx40 to make up the required RBCs concentration by volume. All blood samples were stored hermetically at 4 °C until the experiment was performed at controlled temperature of about 37°C. Detailed information about the experimental set-up, microchannel fabrication and RBC labeling used in the present study has already been described previously.10, 11, 14, 33 All procedures were carried out in compliance with the guidelines of the Clinical Investigation Ethics Committee at Tohoku University.

TABLE I.

Experimental parameters for the working fluids used in this study.

Experimental parameter Pure water in vitro blood
Height × width × length of the microchannel before bifurcation 160 ± 1 μm × 50 ± 1 μm × 40mm 160 ± 1 μm × 50 ± 1 μm × 40mm
Flow rate 3.0 × 10−12 m3/s 3.3 × 10−12 m3/s
Mean velocity in the inlet channel 0.38 mm/s 0.41 mm/s
Particle/RBC diameter at rest 1 μm  ≈ 8 μm
Particle/RBC concentration 0.1% 14%
Dextran 40 concentration — ≈ 9%
Viscosity of the suspending fluid 7.1 × 10−4 Pa·s 4.5 × 10−3 Pa·s
Temperature 37°C 37°C
Magnification (M) 32× 32×
Numerical aperture (NA) 0.75 0.75
λex excitation wavelength 532 nm 532 nm
Refractive index of PDMS (n) 1.4 1.4
Optical slice thickness (OST)a 6.94 μm 6.94 μm
Capture image rate 100 frames/s 100 frames/s
Open in a new tab
a

A detailed description to calculate the OST can be found in Lima et al.10

Image analysis

All the confocal images were recorded around the middle of the microchannels, using a piezo driver system and rt3d software from the Yokogawa Corporation. The series of x-y confocal images were captured with a resolution of 640 × 480 pixels, at a rate of 100 frames/s with an exposure time of 9.4 ms. The recorded images were transferred to the computer and then evaluated in the image processing program imagej (NIH) (Ref. 34) by using the manual tracking MtrackJ plugin35 and automatic ParticleTracker 2D plugin36 to detect and track particles in pure water and RBCs in Dx40, respectively.

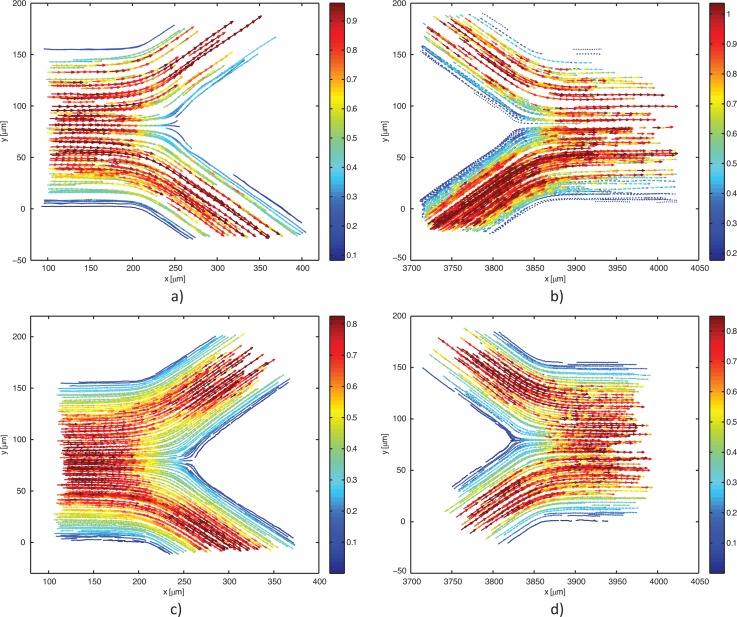
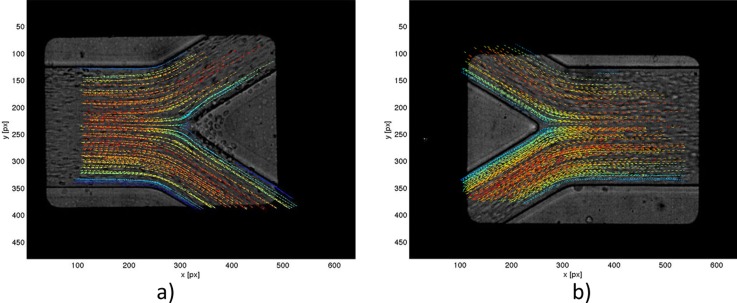
In all, 21 videos of labeled RBCs flow were analyzed, where each video consists of approximately 200 frames. Due to the difference in video quality, different settings for cell tracking were used in ParticleTracker plugin for each video. After evaluation, all trajectories were checked manually to increase accuracy and remove incorrect detections and linking. Only obviously spurious detections were removed, so no bias error was introduced by the user. The whole velocity field acquired for RBCs is shown in Figures 2a, 2b.

Figure 2.

Figure 2

Open in a new tab

Velocity fields obtained from PTV measurements of labeled RBCs (a)-(b) and fluorescent particles in pure water (c)-(d) for bifurcation and confluence, respectively.

The density of fluorescent particles in pure water was higher comparing to labeled RBCs; hence, manual MtrackJ plugin was used instead of automatic ParticleTracker. Because of close surrounding of neighboring particles, different settings had to be used for each particle to track. The snap feature was always the same: a bright centroid. However, snap range varied between 7 × 7 and 13 × 13 pixel. The complete velocity field obtained for pure water using the above-described technique is presented in Figures 2c, 2d.

Afterwards, matlab script was implemented in order to obtain the velocity fields shown in Figure 2. Both PTV fields and numerical results were put together into a global system of coordinates using a reference point, which is the tip of an apex of the bifurcation or the confluence, depending on the area of study. Another matlab script was written to rotate fields simultaneously and produce velocity profiles in 22 selected planes, described in Sec. 4.

NUMERICAL SIMULATIONS

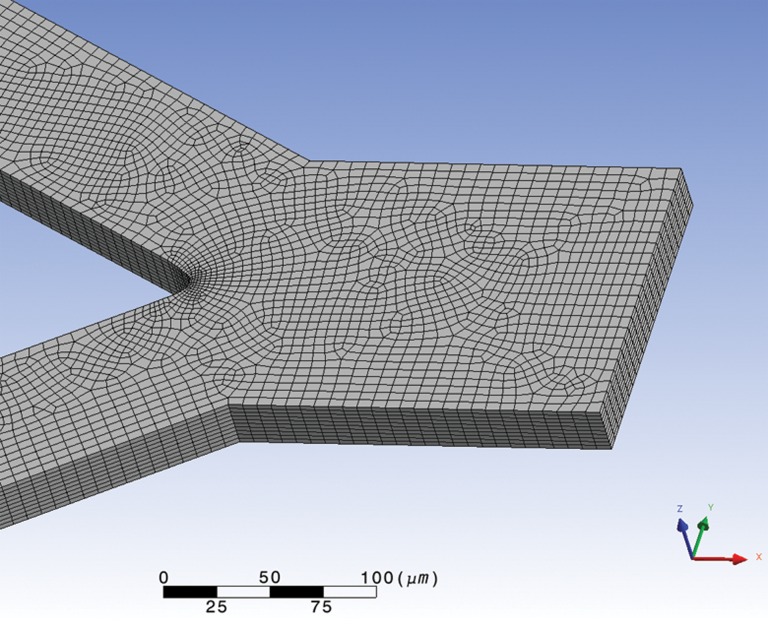
The numerical calculations for the laminar isothermal flow of water were performed using the finite-element computational fluid dynamics (CFD) program polyflow®. The simulations were carried out in a 3D geometry representing the microchannel described in Sec. 2A (see Figure 1), and the mesh used in the simulations was mainly constituted by quadrilateral elements (see Figure 3).

Figure 3.

Figure 3

Open in a new tab

Mesh used in simulations.

The equations solved were the conservation of mass and momentum equations for laminar incompressible flow of water. In order to evaluate the convergence of this process, a test based on the relative error in the velocity field was performed. For the velocity field, the modification on each node between two consecutive iterations is compared to the value of the velocity at the current iteration. In the present work, the convergence value was set to 10−4, since this value is appropriate for the studied problem.37, 38, 39, 40

The boundary conditions were established in order to reproduce the experimental conditions—a constant flow rate was imposed in the inlet of the microchannel –3.0 × 10−12 m3/s—and no-slip at the walls of the channel was assumed.

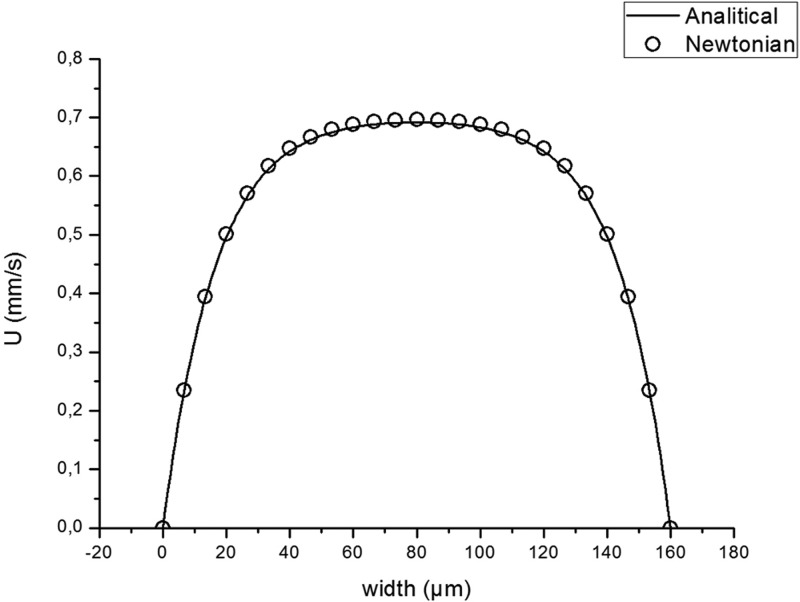
The numerical model designed for the present study—computational domain, mesh, and boundary conditions—was validated by the comparison of the numerical and analytical velocity profiles for a fully developed flow in a straight rectangular channel for a Newtonian fluid.41 The fully developed flow was obtained on a length of 50 μm from the entrance and in this region numerical and analytical solutions were compared as shown in Figure 4. Average difference between both solutions is 0.83%.

Figure 4.

Figure 4

Open in a new tab

Comparison between simulation of Newtonian fluid and analytical solution for fully developed flow in a straight, rectangular channel.

RESULTS AND DISCUSSION

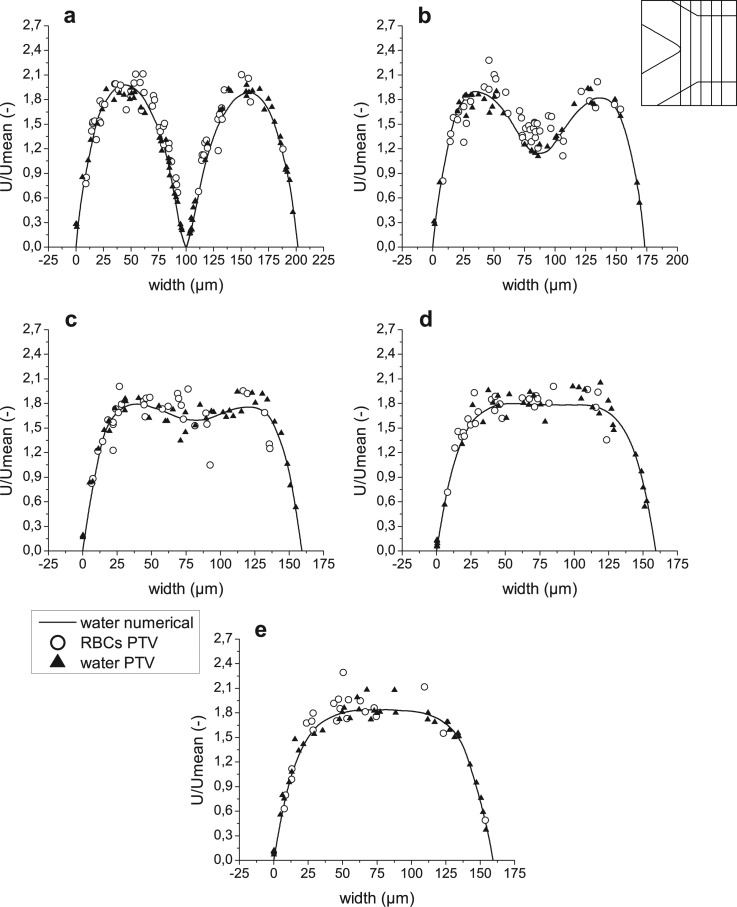
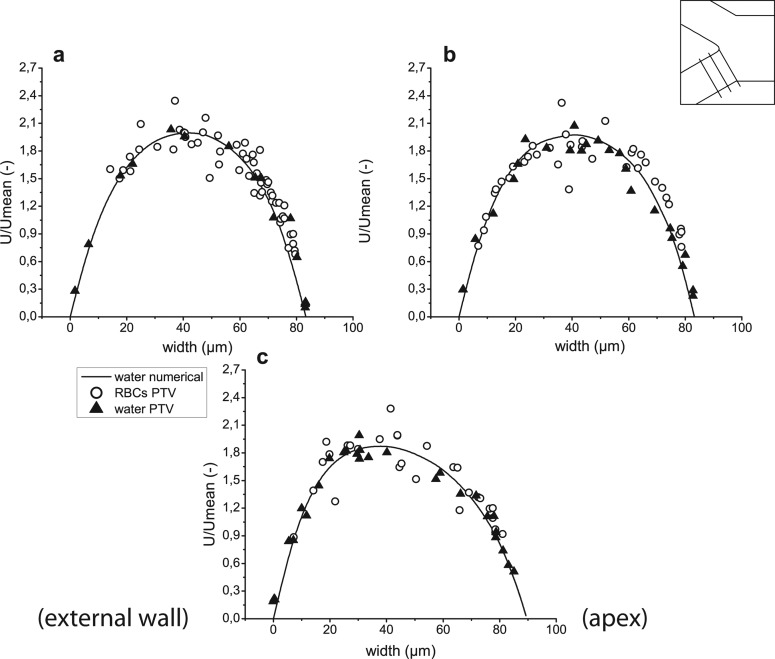
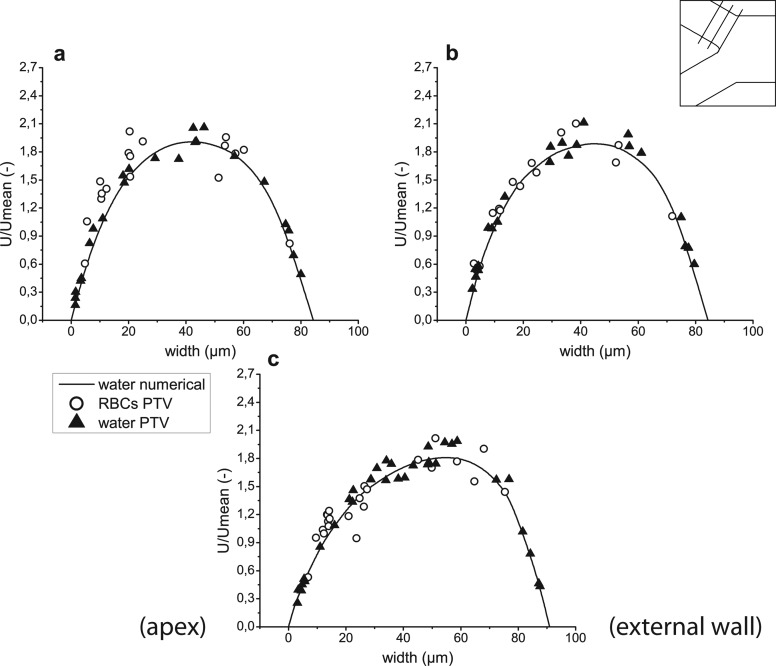
The velocity profiles were analyzed in the regions shown in Figure 5, whereas Figure 6 is displaying the velocity field of RBCs superimposed on the real geometry of the bifurcations. Figures 789101112 show comparison between numerical simulations for water and PTV measurements for pure water and RBCs.

Figure 5.

Figure 5

Open in a new tab

Real geometry and part of geometry used in simulations. Lines represent the planes where velocity profiles were collected and analyzed.

Figure 6.

Figure 6

Open in a new tab

Real geometry of the bifurcation and the confluence with overlaid velocity field of RBCs.

Figure 7.

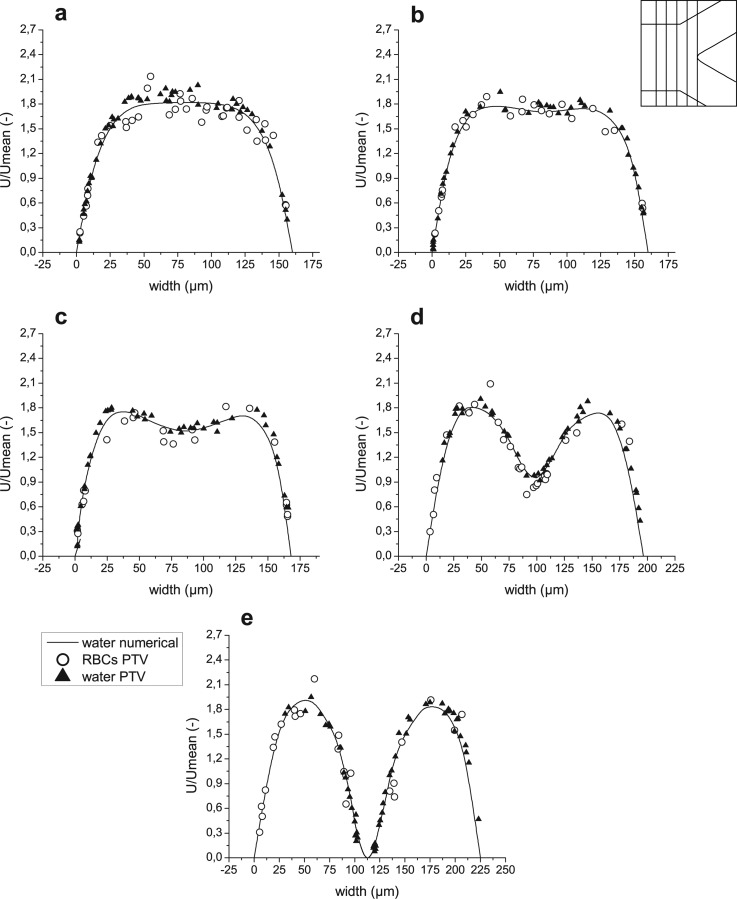
Figure 7

Open in a new tab

Velocity profiles for both computational and experimental results before bifurcation in regions 1–5 ((a)–(e), respectively).

Figure 8.

Figure 8

Open in a new tab

Velocity profiles for both computational and experimental results after bifurcation in regions 6–8 ((a)–(c), respectively).

Figure 9.

Figure 9

Open in a new tab

Velocity profiles for both computational and experimental results after bifurcation in regions 9–11 ((a)–(c), respectively).

Figure 10.

Figure 10

Open in a new tab

Velocity profiles for both computational and experimental results after confluence in regions 12–16 ((a)–(e), respectively).

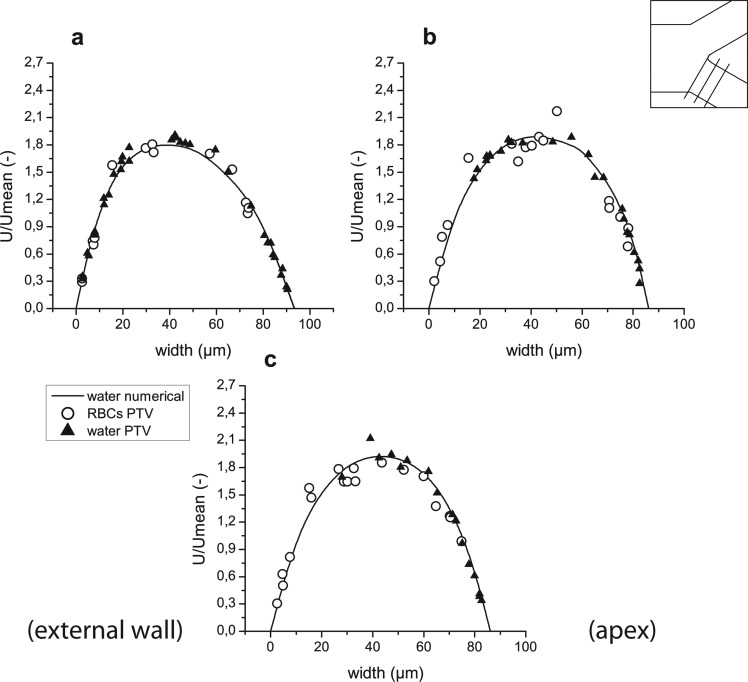
Figure 11.

Figure 11

Open in a new tab

Velocity profiles for both computational and experimental results before confluence in regions 17–19 ((a)–(c), respectively).

Figure 12.

Figure 12

Open in a new tab

Velocity profiles for both computational and experimental results before confluence in regions 20–22 ((a)–(c), respectively).

An important note has to be made about Figures 811 (planes 6-8 and 17-19 in Figure 5, accordingly), i.e., the right side of the graphs represents regions closer to the apex of the bifurcation, while the left side represents regions closer to the external wall of the whole geometry. The opposite happens for Figures 912 (planes 9–11 and 20–22 in Figure 5, accordingly), where the left side of the graphs represents regions closer to the apex and the right side regions closer to the external wall. To help with analysis of the graphs, names of the regions were added to the figures on appropriate side and apply to all graphs in the same figure. In addition, a sketch of the geometry with selected planes is shown in the right, upper corner of the figures.

Measurements were done with slightly different flow rates: Q ≈ 3.3 × 10−12 m3/s for RBCs and Q ≈ 3.0 × 10−12 m3/s for trace particles; and different Reynolds numbers (Re): Re ≈ 0.007 for RBCs and Re ≈ 0.04 for trace particles in water. The Reynolds number was calculated as 4·ρ·Q/(μ·P), where ρ and μ are, respectively, the density and the viscosity of the suspending fluid, Q is the volumetric flow rate, and P is the wetted perimeter.

The comparison between the velocity profiles for RBCs and trace particles was performed using a normalized velocity (U/Umean), where Umean is calculated as flow rate/cross-section area. It is known41 that for steady, laminar flow of Newtonian, incompressible fluid through a rectangular channel, normalized velocity does not depend on viscosity, density, or pressure drop. Therefore, changing flow rate, either to achieve the same flow rates or Reynolds numbers will not have an influence on the presented results.

Diverging bifurcation

As displayed in Figure 7, one stream approaching the bifurcation divides and produces two peaks in the velocity profile. Afterwards, two flows propagate separately in daughter vessels of the bifurcation, and a fully developed flow is progressively obtained. This trend is well shown by both experimental measurements and numerical results (see Figures 789). It is possible to observe that the experimental results for water are in a good agreement with numerical simulation. Those measurements which are closer to the walls are more accurate, as fluorescent particles were moving slowly and during the exposure time they preserved rounded shape captured on the images, and therefore facilitated the localization of the particles’ centroid. In the central region of the channels, during the same exposure time, particles moved for a larger distance, which resulted in the elliptical shape captured on the videos. That, combined with irregular illumination, is the main reason for higher uncertainties and discrepancies between simulation and measurements away from the walls. However, general scattering around the numerical curves is clearly observed.

The lack of measurements on the left side of graphs (Figs. 7d, 7e) and (Figs. 8b, 8c) is caused by different camera positions during the experimental measurements of RBCs and fluorescent particles. Therefore, the lower daughter vessel is shorter on the images captured for trace particles in pure water. The explanation becomes clearer by comparison of Figures 2a, 2c.

The same trend of accuracy applies for PTV measurements of RBCs, though uncertainty of RBCs velocities is higher because of the nonuniformity of laser illumination and movements in z direction (out of focus plane) due to interactions with neighboring cells. This cause RBCs to lose brightness, partially lose brightness or in the worst case partially disappear and thus decrease accuracy. Hence, velocities obtained for RBCs are more scattered. However, general agreement with numerical simulation and PTV measurements of fluorescent particles is visible. The RBCs appear to flow slower in the central region of the main channel just before the apex, but after this, in daughter vessels, agreement is more evident. Measurements for upper daughter vessel are too scarce to determine tendency, however, since flow should propagate symmetrically in both daughter vessels, we may conclude an agreement for both of them based on the lower one.

Increase of local hematocrit (Hct) around the tip of the apex of the bifurcation enhances the adhesion of the RBCs to the wall surface. Lower RBCs velocities and RBCs that follow stream lines that end up on the apex of the bifurcation also play an important role in this phenomenon. Attached RBCs can be seen in Figures 5a, 6a, 13a. During experimental procedure all attached RBCs were rejected, therefore in the center of plane 5 (Figure 7e) no moving RBCs may be observed. Yet, fluorescent particles in pure water can easily access this region. Furthermore, no attachments of fluorescent particles were observed during the experiments.

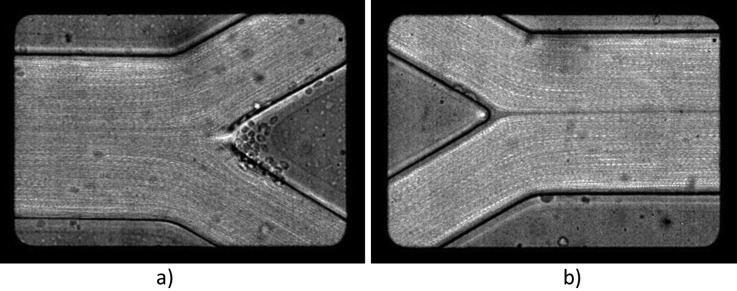
Figure 13.

Figure 13

Open in a new tab

Images of the diverging bifurcation and confluence obtained after “Z Project” using maximum intensity function.

Converging bifurcation (confluence)

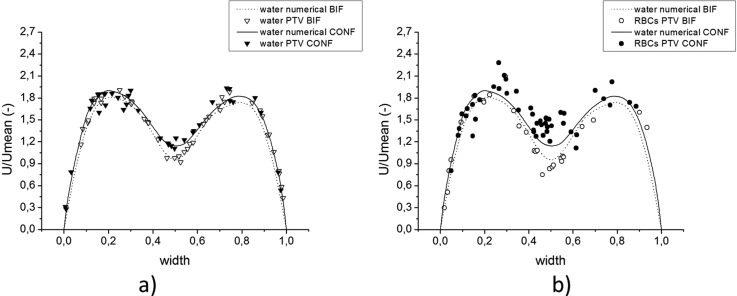
Conversely to bifurcation, Figure 10 shows how two streams enter the confluence and merge together producing two peaks in the velocity profile. Next, along the straight rectangular channel, fully developed flow is progressively obtained. Both measurements and simulation results confirm this tendency. An agreement between experimental results for trace particles in pure water and numerical simulations may also be observed.

The trend of accuracy is the same as described in Subsection 4A and results obtained from PTV measurements of fluorescent particles are distributed around numerical curves. Despite some scattering of the collected data for RBCs, it can be clearly seen that in the central region, close to the apex, the velocities of RBCs are higher than those obtained for pure water, see Figures 10b, 10c. The cell-free layer created around the tip of the apex of the confluence may be seen in Figure 6b but is much better visible in Figure 13b. The existence of this cell-free region explains the lack of RBCs in the center of plane 12, see Figures 5b, 10a. However, fluorescent particles in pure water can easily access this area.

In Figures 1112, one can see that velocities of the RBCs are in agreement with those of the fluorescent particles. Though Figures 11b, 12a show slightly higher velocities of RBCs near the apex of the confluence, data scattering does not allow the conclusion of this tendency. These results show that existence of a cell-free layer is not sufficient to induce higher velocities of RBCs. Therefore, phenomena underlying this effect in the region downstream of the apex are more complex. Further discussion is provided in Subsection 4C .

Comparison

One video for each diverging bifurcation and confluence was treated by “Z Project” function, which is implemented in imagej software. Consecutive frames were added to each other using maximum intensity and displayed in Figure 13. The existence of a cell-free layer around the apex of the confluence and its propagation in a straight line in the region after it is clearly visible. Attachments of RBCs to the apex of the diverging bifurcation may also be observed in Figure 13a.

Figure 14 shows the velocities of fluorescent particles (a) and RBCs (b) measured in planes 4 and 13, or 25 μm before the apex and 25 μm after the apex of the bifurcation and the confluence, accordingly.

Figure 14.

Figure 14

Open in a new tab

Comparison between velocities obtained from measurements in the same location (25 μm away from apex) of the bifurcation (BIF) and the confluence (CONF) for trace particles (a) and RBCs (b). Numerical curves are used as a reference.

A minor difference between numerical curves in the confluence and bifurcation results from slightly different geometry, where bifurcation is wider then confluence and therefore normalized width is used. The agreement between numerical results and measurements of trace particles is clear. The difference between velocities of particles in bifurcation and confluence is small and is caused by different channel breadths. However, difference in RBCs velocities is more pronounced in the central region, where close to the walls agreement may be seen.

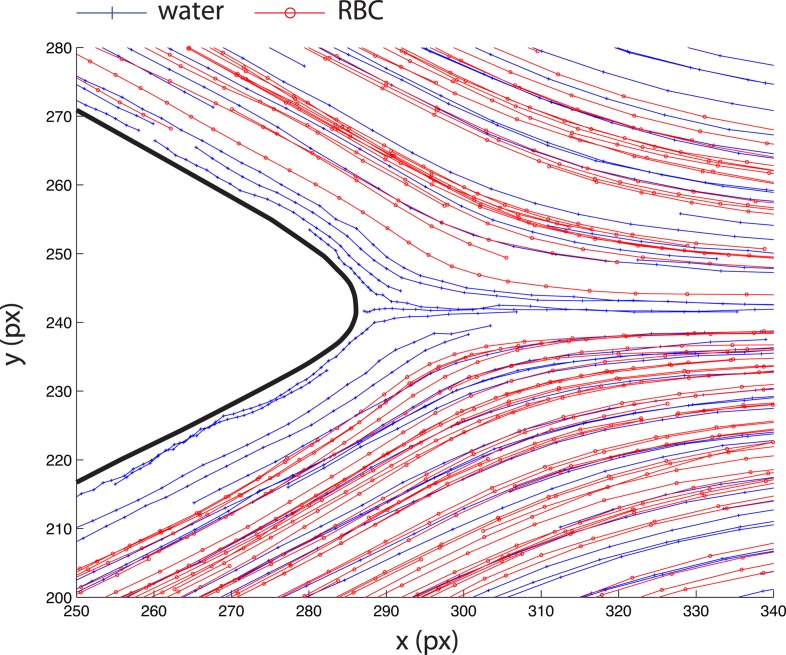
To further investigate this phenomenon, we compared trajectories of RBCs and fluorescent particles in the vicinity of the tip of the converging bifurcation as shown in Figure 15. The behavior of particles differ from that of RBCs, which, in the daughter branches, start from the same lateral position as fluorescent particles but have tendency to go closer to the apex. This different behavior may be explained by the diffusion of RBCs to the cell depleted region located after the tip of the apex. As a result, the RBCs undergo a cross streamline migration along the apex of the confluence. Hence, RBCs flowing close to the confluence center line are originated from streamlines contiguous to the interface of the cell depleted layer.

Figure 15.

Figure 15

Open in a new tab

Comparison of trajectories of the fluorescent particles in water and RBCs in Dx40 in the region around the tip of the apex of the confluence. 35 pixels correspond to 25 μm.

In the case of trace particles, there is no depleted region but rather an homogeneous distribution of particles and as a result they do not exhibit cross streamline migration. Thus, particles that flow close to the center line of the confluence are originated from streamlines adjacent to the apex wall.

The different initial position of both objects in the shear flow indicates different initial velocities. Consequently, the RBCs that undergo cross streamline migration and eventually end up on the same streamline as trace particles, exhibit higher velocities upstream of the apex than those particles. Therefore, velocities of RBCs just downstream of the apex close to the confluence center line are also higher than fluorescent particles (see Figures 10b, 10c).

In order to obtain a deeper understanding of our finding, we are planning in the near future to use a working fluid containing both fluorescent particles and labeled RBCs and also to perform numerical simulations with a multi-scale model. Different Hct levels and flow rates would influence the width of the cell-depleted regions, especially the width and length after converging tip. Additionally, the geometry of the microchannel, such as the length and width of the daughter branches, will also have a strong impact on the development of the depleted regions and consequently change the shape of the cell-free layer (CFL) after the confluence. Therefore, using different Hcts, flow rates and geometrical constraints would help to clarify the observed phenomenon. This research work is under way in our laboratory, and it will be published in due time.

CONCLUSIONS

In the present paper, we reported experiments on the flow of red blood cells in geometrically symmetrical divergent and convergent bifurcations. Comparing the results obtained in both bifurcations we have found that RBCs velocities are asymmetrical. The formation of a pronounced cell-depleted zone immediately downstream of the apex of the convergent bifurcation (which is absent in the divergent side) causes this asymmetry.

The geometry of the diverging bifurcation and the confluence was found from visualization images with visible walls. Afterwards, a 3D model was produced, and simulations of pure water were performed with a finite-element CFD program polyflow. Simulations’ outcome was used to validate measurements of fluorescent particles and as a reference to compare the RBCs velocities obtained by PTV method. The results acquired for pure water and numerical results were found to be in a good agreement with each other. However, velocities of RBCs were found to be different when they approach the tip of the apex of the converging bifurcation or enter the main channel just downstream of the confluence apex. RBCs tend to move slower in the region before the tip of the divergent bifurcation and faster after the tip of the confluence, in comparison to fluorescent particles in water and to each other.

The development of a cell depleted zone around the apex of convergent bifurcation influences the final streamline that RBCs would follow and play an important role on higher velocities obtained from our experimental measurements.

On the other hand, lower velocities close to the apex of the divergent bifurcation, as well as enhanced adhesion of RBCs to the wall surface, may be partially explained by local increase of Hct in this region.

In the future works, we are planning to further investigate the behavior of RBCs in bifurcations and define physical parameters that influence these phenomena. This will help to clarify the effect of the cell-free layer on RBCs velocities and trajectories. We also believe that the new findings provided by the present study will help the development of more realistic multi-phase numerical models of blood flow through microchannels of size 50-500 μm.

ACKNOWLEDGMENTS

The authors acknowledge the financial support provided by: 2007 GlobalCOE Program, Japan; PTDC/SAU-BEB/108728/2008, PTDC/SAU-BEB/105650/2008, and PTDC/EME-MFE/099109/2008 from the FCT (Science and Technology Foundation) and COMPETE, Portugal.

References

  1. Popel A. and Johnson P., Annu. Rev. Fluid Mech. 37, 43 (2005). 10.1146/annurev.fluid.37.042604.133933 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Faivre M., Abkarian M., Bickraj K., and Stone H., Biorheology 43, 147 (2006). [PubMed] [Google Scholar]
  3. Guido A. and Johnson P., C. R. Phys. 10, 751 (2009). 10.1016/j.crhy.2009.10.002 [DOI] [Google Scholar]
  4. Sousa P. C., Pinho F. T., Oliveira M. S. N., and Alves M., Biomicrofluidics 5, 014108 (2011). 10.1063/1.3567888 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Lima R., Ishikawa T., Imai Y., and Yamaguchi T., in Single and Two-Phase Flows on Chemical and Biomedical Engineering, edited by Dias R., Martins A., Mata T., and Lima R. (Bentham Science) (in press).
  6. Goldsmith H. and Turitto V., J. Thromb. Haemost. 55, 415 (1986). [PubMed] [Google Scholar]
  7. Maeda N., Jpn. J. Physiol. 46, 1 (1996). 10.2170/jjphysiol.46.1 [DOI] [PubMed] [Google Scholar]
  8. Chien S., Usami S., Skalak R., in Handbook of Physiology—The Cardiovascular System IV, edited by Renkin E. M. and Michel C. C. (American Physiological Society, Bethesda, 1984), p. 217. [Google Scholar]
  9. Fahraeus R. and Lindqvist T., Am. J. Physiol. 96, 562 (1931). [Google Scholar]
  10. Lima R., Wada S., Tsubota K., and Yamaguchi T., Meas. Sci. Technol. 17, 797 (2006). 10.1088/0957-0233/17/4/026 [DOI] [Google Scholar]
  11. Lima R., Wada S., Tanaka S., Takeda M., Ishikawa T., Tsubota K., Imai Y., and Yamaguchi T., Biomed. Microdevices 10, 153 (2007). 10.1007/s10544-007-9121-z [DOI] [PubMed] [Google Scholar]
  12. Lima R., Wada S., Takeda M., Tsubota K., and Yamaguchi T., J. Biomech. 40, 2752 (2007). 10.1016/j.jbiomech.2007.01.012 [DOI] [PubMed] [Google Scholar]
  13. Lima R., Ishikawa T., Imai Y., Takeda M., Wada S., and Yamaguchi T., J. Biomech. 41, 2188 (2008). 10.1016/j.jbiomech.2008.04.033 [DOI] [PubMed] [Google Scholar]
  14. Lima R., Ishikawa T., Imai Y., Takeda M., Wada S., and Yamaguchi T., Ann. Biomed. Eng. 37, 1546 (2009). 10.1007/s10439-009-9732-z [DOI] [PubMed] [Google Scholar]
  15. Lima R., Oliveira M. S. N., Ishikawa T., Kaji H., Tanaka S., Nishizawa M., and Yamaguchi T., Biofabrication 1, 035005 (2009). 10.1088/1758-5082/1/3/035005 [DOI] [PubMed] [Google Scholar]
  16. Abkarian M., Faivre M., Horton R., Smistrup K., Best-Popescu C. A., and Stone H. A., Biomed. Mater. 3, 034011 (2008). 10.1088/1748-6041/3/3/034011 [DOI] [PubMed] [Google Scholar]
  17. Parthasarathi A., Japee S., and Pittman R., Ann. Biomed. Eng. 27, 313 (1999). 10.1114/1.144 [DOI] [PubMed] [Google Scholar]
  18. Jeong J. H., Sugii Y., Minamiyama M., Takeuchi H., and Okamoto K., Microvasc. Res. 73, 39 (2006). 10.1016/j.mvr.2006.05.001 [DOI] [PubMed] [Google Scholar]
  19. Sugii Y., Nishio S., and Okamoto K., Physiol. Meas. 23, 403 (2002). 10.1088/0967-3334/23/2/315 [DOI] [PubMed] [Google Scholar]
  20. Vennemann P., Kiger K., Lindken R., Groenendijk B., Stekelenburg-de Vos S., Hagen T., Ursem N., Poelmann R., Westerweel J., and Hierk B., J. Biomech. 39, 1191 (2006). 10.1016/j.jbiomech.2005.03.015 [DOI] [PubMed] [Google Scholar]
  21. Nakano A., Sugii Y., Minamiyama M., Seki J., and Niimi H., JSME Int. J., Ser. C 48, 444 (2005). 10.1299/jsmec.48.444 [DOI] [Google Scholar]
  22. Barber J. O., Alberding J. P., Restrepo J. M., and Secomb T. W., Ann. Biomed. Eng. 36, 1690 (2008). 10.1007/s10439-008-9546-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Yang S., Undar A., and Zahn J. D., Lab Chip 6, 914 (2006). 10.1039/b601554a [DOI] [PubMed] [Google Scholar]
  24. Doyeux V., Podgorski T., Peponas S., Ismail M., and Coupier G., J. Fluid Mech. 674, 359 (2011). 10.1017/S0022112010006567 [DOI] [Google Scholar]
  25. Fujiwara H., Ishikawa T., Lima R., Matsuki N., Imai Y., Kaji H., Nishizawa M., and Yamaguchi T., J. Biomech. 42, 838 (2009). 10.1016/j.jbiomech.2009.01.026 [DOI] [PubMed] [Google Scholar]
  26. Nakano T., Itoyama T., Yoshida K., Sawada Y., Ikeda S., Fukuda T., Matsuda T., Negoro M., and Arai F., Biomicrofluidics 4, 046505 (2010). 10.1063/1.3523471 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Chau L. T., Rolfe B. E., and Cooper-White J. J., Biomicrofluidics 5, 034115 (2011). 10.1063/1.3609264 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Zhou R. and Chang H -C., J. Colloid Interface Sci. 287, 647 (2005). 10.1016/j.jcis.2005.02.023 [DOI] [PubMed] [Google Scholar]
  29. Zhou R., Gordon J., Palmer A. F., and Chang H -C., Biotechnol. Bioeng. 93, 5 (2006). 10.1002/bit.v93:2 [DOI] [PubMed] [Google Scholar]
  30. Shevkoplyas S. S., Yoshida T., Munn L. L., and Bitensky M. W., Anal. Chem. 77, 933 (2005). 10.1021/ac049037i [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Shevkoplyas S. S., Yoshida T., Gifford S. C., and Bitensky M. W., Lab Chip 6, 914 (2006). 10.1039/b601554a [DOI] [PubMed] [Google Scholar]
  32. Ishikawa T., Fujiwara H., Matsuki N., Yoshimoto T., Imai Y., Ueno H., and Yamaguchi T., Biomed. Microdevices 13, 159 (2011). 10.1007/s10544-010-9481-7 [DOI] [PubMed] [Google Scholar]
  33. Lima R., Fernandes C. S., Dias R. P., Ishikawa T., Imai Y.: Yamaguchi T., in Computational Vision and Medical Image Processing: Recent Trends, edited by Tavares J. M. R. S. and Jorge R. M. N. (Springer; Science+Business Media B.V., Netherlands, 2011), p. 297. [Google Scholar]
  34. Abramoff M. D., Magalhães P. J., and Ram S. J., Biophotonics Int. 11, 36 (2004). [Google Scholar]
  35. Meijering E., Smal I., and Danuser G., IEEE Signal Process. Mag. 3, 46 (2006). 10.1109/MSP.2006.1628877 [DOI] [Google Scholar]
  36. Sbalzarini I. F. and Koumoutsakos P., J. Struct. Biol. 151, 182 (2005). 10.1016/j.jsb.2005.06.002 [DOI] [PubMed] [Google Scholar]
  37. Dias R. P., Fernandes C. S., Mota M., Teixeira J., and Yelshin A., Carbohydr. Polym. 74, 852 (2008). 10.1016/j.carbpol.2008.05.001 [DOI] [Google Scholar]
  38. Fernandes C. S., Dias R. P., Nóbrega J. M., Afonso I. M., Melo L. F., and Maia J. M., J. Food Eng. 69, 281 (2005). 10.1016/j.jfoodeng.2004.08.018 [DOI] [Google Scholar]
  39. Fernandes C. S., Dias R. P., Nóbrega J. M., and Maia J. M., Chem. Eng. Process. 46, 825 (2007). 10.1016/j.cep.2007.05.011 [DOI] [Google Scholar]
  40. Fernandes C. S., Dias R. P., Nóbrega J. M., and Maia J. M., J. Food Eng. 89, 441 (2008). 10.1016/j.jfoodeng.2008.05.022 [DOI] [Google Scholar]
  41. Bruus H., Theoretical Microfluidics (MIC, Technical University of Denmark, Denmark, 2004). [Google Scholar]

Articles from Biomicrofluidics are provided here courtesy of American Institute of Physics

RESOURCES