How Do CAD Models Compare With Reverse Engineered Manufactured Components for Use in Wear Analysis?

Abstract

Background

To accurately quantify polyethylene wear in retrieved arthroplasty components, the original geometry of the component must be estimated accurately using a reference geometry such as a computer-aided design (CAD) model or a never-implanted insert. However, differences may exist between the CAD model and manufactured inserts resulting from manufacturing tolerances.

Questions/purposes

We quantified the deviations between CAD models and newly manufactured inserts and determined how these deviations compared with using a never-implanted insert as a reference geometry.

Methods

We obtained five cruciate-retaining (CR) and five posterior-stabilizing (PS) tibial inserts and their CAD models. The inserts were scanned and reconstructed using microcomputed tomography (micro-CT). Differences in volume and surface geometry were measured among (1) the individual inserts; (2) between the inserts and a CAD model; and (3) between the inserts and a reference geometry constructed from multiple scanned inserts averaged together.

Results

The micro-CT volumes were, on average, 0.4% smaller (34–178 mm³) than the CAD model volumes. The mean deviation between the CAD model and insert surface geometry was 25.7 μm smaller for CR and 36.8 μm smaller for PS. The mean deviation between the inserts and an averaged reference geometry was 1.4 μm larger for CR and 0.4 μm smaller for PS.

Conclusions

Deviations exist between manufactured tibial inserts and CAD models that could cause errors in wear measurements. Scanned inserts may better represent the preimplantation geometry of worn inserts than CAD models, depending on the manufacturing variability between lots.

Clinical Relevance

The magnitude of the error in estimation of the preimplantation geometry of a retrieved component could add or subtract the equivalent of 1 year of wear.

Introduction

Polyethylene wear is frequently studied through wear simulator [16–18] and retrieval studies [3, 4, 6, 8, 11, 22]. A number of techniques have been used to quantify wear in vitro, including gravimetric analysis [16–18], coordinate measuring machines [1, 16–18], and micro-CT [25]. These techniques measure a change in mass, volume, or surface geometry of the polyethylene component. In wear simulator studies, the wear volume is measured in each component across multiple time points. The mass or geometry of the component after each wear cycle is compared back to its original, prewear mass, or geometry. For components retrieved from patients, however, the original mass and geometry of the component are almost always unknown. Therefore, the unworn geometry must be estimated in some way using an appropriate reference geometry. The accuracy of this estimation is especially important for components retrieved after implantation for less than 2 years. For example, one retrieval study of polyethylene tibial inserts [11] reported a mean linear penetration of 52 to 54 μm/year and a volume loss of 44 to 49 mm³/year. Using a reference geometry with an error of 50 μm in geometry (half the width of a human hair) or 50 mm³ in volume (the size of a large grain of rice) could therefore add or subtract a year’s worth of linear penetration or wear volume to the results.

The retrieved component may be compared with a different, never-implanted component of the same model, but this method is subject to error as a result of the slight deviations (± 59 μm) between components that arise during the manufacturing process [1, 26]. In certain cases, the regions of the worn component unaffected by wear can be used mathematically to estimate the original geometry of the component, but this may not be possible with complex component designs [1]. Recently, a microcomputed tomography (micro-CT) method has been proposed to average the geometries of multiple tibial inserts to create a new geometry with minimal manufacturing-derived deviation [26]. However, this method can be expensive should multiple tibial insert geometries (of varying sizes and thicknesses) be required. Computer-aided design (CAD) models created for the design and manufacture of polyethylene tibial inserts represent the unworn insert and might be suitable for use as a reference geometry. However, the differences in the linear or volumetric measures of the CAD models and those obtained by micro-CT are unknown.

We sought to determine (1) what geometric deviations exist between manufactured tibial inserts and their original CAD models; (2) whether isotropic scaling factors can be applied to the CAD model to minimize any observed deviations resulting from shrinkage or expansion; and (3) how these deviations compare with the baseline deviations between inserts (as a result of the manufacturing process) and with the deviations observed when using an alternative reference geometry (derived from averaging geometric data from multiple unworn inserts).

Materials and Methods

Ten never-implanted polyethylene tibial inserts (Genesis II; Smith and Nephew, Memphis, TN) and their associated CAD models were obtained from the manufacturer. Of the inserts, five were of the cruciate-retaining (CR) design and five were of the posterior-stabilizing (PS) design. Both designs were included to account for any complications arising from the inclusion of a tibial post. The sample size was selected based on a previous study that determined three to six inserts are required to minimize interinsert deviation through averaging of the insert geometries [26]. None of the inserts used in that study were used in the present study. All inserts were size 3/4 with a thickness of 11 mm and were manufactured in the same lot.

Each insert was scanned three times with a dedicated laboratory micro-CT scanner (eXplore Vision 120; GE Healthcare, London, Ontario, Canada). The inserts were held in the scanner bed within a radiotranslucent polystyrene foam holder that maintained the inserts at a small double-oblique angle throughout the scans. All scans were obtained using an isotropic resolution of 50 μm with image acquisition over 1200 views and 10 frames averaged per view at an exposure time of 16 ms per frame. The x-ray tube voltage was 90 kVp with a current of 40 mA. The scans were reconstructed at the full 50-μm resolution using the scanner console software. The accuracy of the voxel spacing provided by the manufacturer was assessed using a quality assurance (QA) phantom scanned at 50 μm resolution under the same scan protocol [5]. The voxel spacing calculated by the QA phantom was 0.0672 μm greater than the manufacturer’s stated voxel spacing. Therefore, a linear scaling correction factor (1.0016) was applied to the reconstructed images, increasing the image size.

The reconstructed scan images were analyzed with dedicated micro-CT software (MicroView v2.2; GE Healthcare). A threshold was determined automatically for each reconstructed scan by the software based on the segmentation method developed by Otsu [21]. This threshold was used to perform isosurface rendering of the insert geometry at the highest possible quality with no decimation (Fig. 1). The volume of the resulting three-dimensional surface was recorded, and the geometry was saved in the stereolithography file format. Gravimetric analysis was performed for all inserts with a high-precision scale calibrated to within ± 0.0001 g (AX205; Mettler-Toledo GmbH, Greifensee, Switzerland). The mass of the inserts was converted to a volume based on the reported density of GUR 1020 resin (0.935 mg/mm³) [12]. The gravimetrically derived volume was then compared with the micro-CT volume for each insert to ensure accuracy.

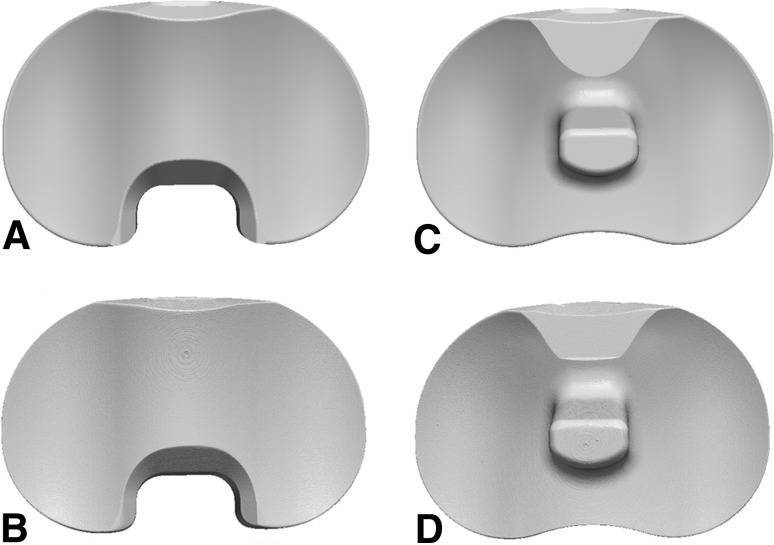
Fig. 1A–D.

Three-dimensional geometry of the CR inserts from the (A) CAD model and (B) micro-CT scan and of the PS inserts from the (C) CAD model and (D) micro-CT scan. CR = cruciate-retaining; CAD = computer-aided design; PS = posterior-stabilizing.

A custom software utility, developed for a previous study, was used to coalign and average the surface geometries from the three repeated scans of each insert [26]. This produced a high-quality surface geometry, free from any deviation resulting from scanner noise, for each of the 10 inserts. The program used an iterative closest points algorithm for coalignment of the point clouds with convergence set for when the root mean square average distance between surfaces dropped below 0.1 μm for 1000 sample points. The sample points were randomly chosen by the algorithm for each insert and covered the entire insert geometry. Therefore, the entire geometry was used in the alignment, although the specific points used for alignment varied with each pair of inserts.

The same program was used to compare the five scanned CR inserts with the CR CAD model and the five scanned PS inserts with the PS CAD model. Once the scanned insert geometry was coaligned to the CAD model, the three-dimensional deviations (ie, summed from the x, y, and z coordinates) between the two surfaces were determined continuously across their entire three-dimensional surfaces. These deviations correspond to a nonrandom error in the estimation of the preimplantation geometry from using a CAD model as the reference geometry. For each point in the surface, the signed mean deviation between the CAD model and the five inserts was calculated and used to generate a mean deviation map. The mean deviation map was used as a measure of the systemic deviation between the CAD model and insert surfaces, which always exist within the comparisons. A second map was generated from the SD of the deviations between surfaces at each point. The SD map was used as a measure of confidence in the localization of the mean deviations. The maps were visualized using ParaView (KitWare Inc, Clifton Park, NY, USA).

Linear geometric scaling factors were then applied isotropically to the CAD models in an attempt to minimize the mean three-dimensional surface deviations between the CAD models and the individual inserts. This would be expected to correct for any uniform geometric changes resulting from the manufacturing process or from micro-CT scanner scaling error. The CR and PS CAD models were visualized in Geomagic Studio (Geomagic Inc, Research Triangle Park, NC, USA) and a uniform scaling factor was applied iteratively until the volume of the CAD model was equal to the mean volume of the inserts (measured by micro-CT). The scaling factor was applied so that the x, y, and z dimensions of geometry were linearly increased or decreased by one-third of the overall volumetric scaling factor. The deviations between the inserts and scaled CAD models were then calculated using the custom software utility, and maps were again generated for the mean and SD of the surface deviations. These deviations correspond to an error in the estimation of the preimplantation geometry resulting from the use of the scaled CAD model as the reference geometry.

A single CR insert and a single PS insert were compared with the other inserts within the CR and PS groups using the program. The three-dimensional deviations between the individual inserts were calculated to determine the geometric variability between inserts from the manufacturing process. This variability from manufacturing also corresponds to the error in the estimation of the preimplantation geometry from using a single insert as the reference geometry. Deviation maps were again constructed from the calculations. All of the insert surfaces were then averaged within the CR and PS groups to construct a single averaged CR geometry and a single averaged PS geometry. The averaged CR and PS geometries were then compared back to the individual inserts to determine the error from using an averaged insert geometry as the estimate of preimplantation geometry. The deviations between the geometries were calculated and deviation maps were produced.

Each mean deviation map was visualized in ParaView and a region of interest (ROI) was selected, in turn, on the left and right sides of the articular surface of the geometry. The ROIs were approximately 15 × 25 mm in dimension and corresponded to contact regions in which wear damage is typically seen on the proximal insert surface covering the area between the lateral edges of the insert to the edge of the post for PS inserts or approximately where the post would be on CR inserts [19]. This ensured only deviations relevant to wear measurements were taken into account. Each ROI contained 10 to 50 thousand points of calculated deviations. From these points, the mean and SD of the deviations within the ROI were calculated. Because the deviations within the ROIs were similar (paired t-test, p > 0.05) between the left and right sides, we combined the calculated deviations for the two sides. This measurement was used to determine the projected error in the calculation of an articular surface wear rate if that type of geometry was used as a reference in a retrieval study.

Results

The CAD models were larger in volume than the scanned inserts (Table 1) with the individual insert surfaces on average negatively deviating from the articular surface of the CAD models (Table 2). The CT volumes were, on average, 0.4% smaller (34–178 mm³) than the CAD model volumes. The gravimetric volumes of the CR inserts were, on average, 0.3% smaller than the CAD volumes, whereas the gravimetric volumes of the PS inserts were 0.2% greater than the CAD volumes. In comparison of the scanned CR inserts to the CAD model, the greatest of the mean deviations appeared along the edges of the insert surface, particularly within the locking mechanism as well as in the center of the articular surface (Fig. 2A). The SDs also increased toward the edges of the insert (Fig. 2B). Like with the CR inserts, the greatest mean deviations in the comparison of the CAD model to the PS inserts were at the center of the insert surface on the articulating side, surrounding the locking mechanism on the backside, and also around the post (Fig. 3A). The SDs were more consistent than with the CR inserts (Fig. 3B).

Table 1.

Mean ± SD of micro-CT, gravimetric, and CAD volumes of the tibial inserts

Insert type	Micro-CT volume (mm3)	Gravimetric volume (mm3)	CAD volume (mm3)	Scaling factor
CR	27,644 ± 64 (0.64%)	27,738 ± 52 (0.3%)	27,822	0.99786
PS	31,951 ± 139 (0.11%)	32,036 ± 56 (0.2%)	31,985	0.99964

The mean percent difference from the CAD volume is listed for the micro-CT and gravimetric volumes. Scaling factor refers to the linear scaling factor isotropically applied to reduce the CAD geometry to equal the mean volume of the scanned geometries. No SD exists for the CAD volumes, because there was only one CAD file; CAD = computer-aided design; CR = cruciate-retaining; PS = posterior-stabilized.

Table 2.

Mean three-dimensional deviations between geometries within regions of the articular surface in which wear is typically found

Geometry comparison	CR (microns)	PS (microns)
Between individual inserts	−10.4 ± 9.4	9.7 ± 6.4
Averaged insert versus individual inserts	1.4 ± 2.0	−0.4 ± 1.9
CAD model versus individual inserts	−25.7 ± 13.1	−36.8 ± 31.4
Scaled CAD model versus individual inserts	−14.4 ± 11.8	−36.1 ± 30.9

CR = cruciate-retaining; PS = posterior-stabilized; CAD = computer-aided design.

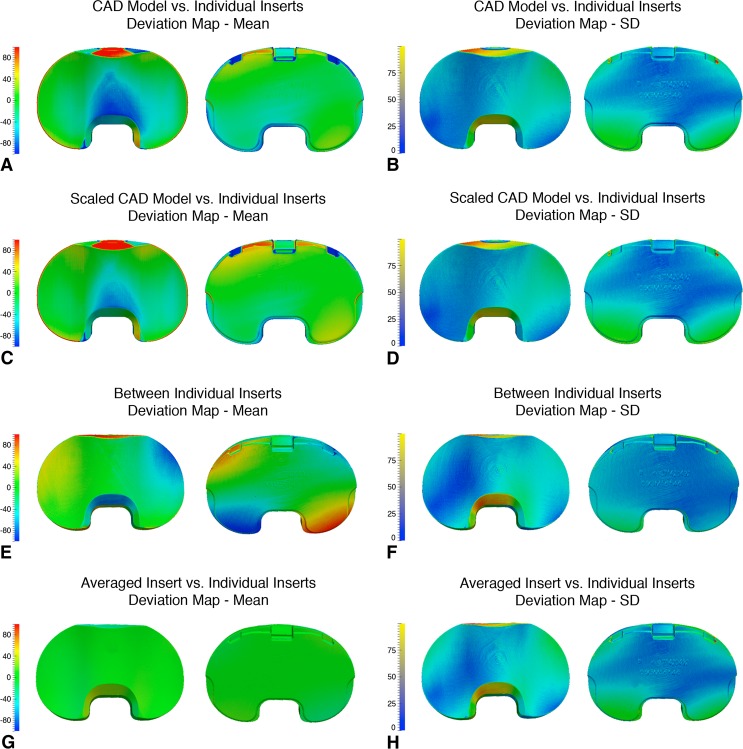
Fig. 2A–H.

Maps of the three-dimensional surface deviations (in microns) for the CR inserts. Means are on the left and SDs are on the right for both the articular and backside surfaces. (A) Mean deviations for the CAD model versus individual inserts; (B) SDs for the CAD model versus individual inserts; (C) mean deviations for the scaled CAD model versus individual inserts; (D) SDs for the scaled CAD model versus individual inserts; (E) mean deviations between individual inserts; (F) SDs between individual inserts; (G) mean deviations between the averaged insert versus individual inserts; and (H) SDs between the averaged insert versus individual inserts. CR = cruciate-retaining; CAD = computer-aided design.

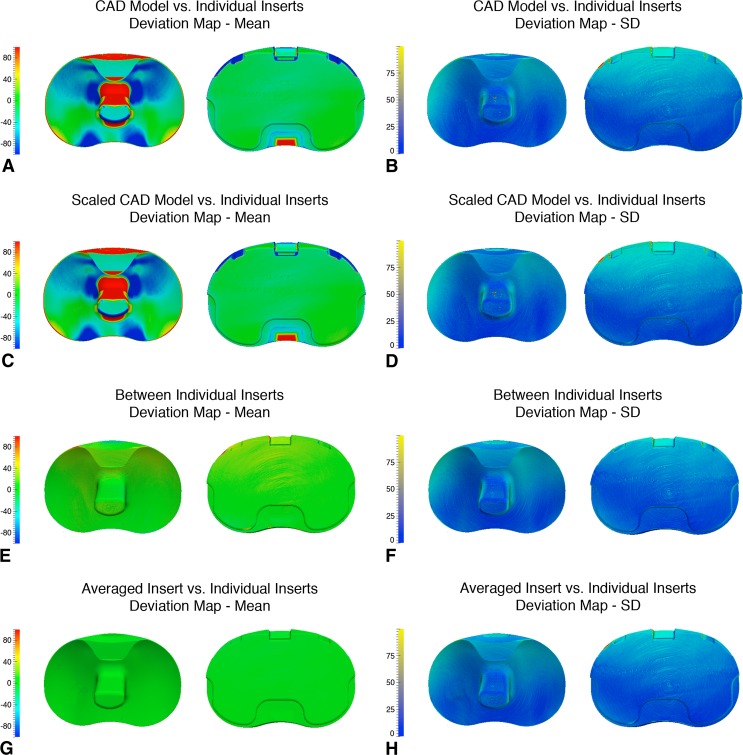
Fig. 3A–H.

Maps of the three-dimensional surface deviations (in microns) for the PS inserts. Means are on the left and SDs are on the right for both the articular and backside surfaces. (A) Mean deviations for the CAD model versus individual inserts; (B) SDs for the CAD model versus individual inserts; (C) mean deviations for the scaled CAD model versus individual inserts; (D) SDs for the scaled CAD model versus individual inserts; (E) mean deviations between individual inserts; (F) SDs between individual inserts; (G) mean deviations between the averaged insert versus individual inserts; and (H) SDs between the averaged insert versus individual inserts. PS = posterior-stabilizing; CAD = computer-aided design.

Scaling the CAD models reduced, but did not eliminate, the deviations. The mean deviations in the scaled CR CAD model appeared to be slightly lower across the insert surface compared with those using the original CAD model (Fig. 2C); however, there appeared to be little difference in the SDs (Fig. 2D). Like with the CR scaled CAD model, there appeared to be a slight decrease in the articular surface deviations for the scaled PS CAD model in comparison to the original (Fig. 3C) but no obvious difference in the map of the SDs (Fig. 3D).

Deviations between the individual inserts, and between the averaged insert and individual inserts, were lower than those associated with the CAD models. The map of mean deviations between individual CR inserts displayed small regions of opposing positive and negative deviation at the periphery of the surfaces (Fig. 2E). The SDs were slightly more uniform than with the CAD models (Fig. 2F). In contrast, the map of mean deviations between individual PS inserts displayed low, uniform deviations across the entire surface (Fig. 3E) with a similar SD map (Fig. 3F). The geometry from averaging the inserts displayed the lowest, most uniform mean deviations out of all the geometry comparisons for both the CR (Fig. 2G) and PS (Fig. 3G) groups.

Discussion

Polyethylene wear continues to be studied, because it is a substantial detriment to the longevity of arthroplasty [2, 19]. The techniques used to study components retrieved during revision surgery require an accurate unworn reference geometry to quantify wear of the component. The original CAD models created for the design and manufacture of polyethylene components might be suitable for this purpose. We sought to determine (1) what geometric deviations exist between manufactured tibial inserts and their original CAD models; (2) whether scaling factors can be applied to the CAD model to minimize the deviations; and (3) how these deviations compare with the baseline deviations between inserts (based on manufacturing variability) and with the deviations from using an averaged insert geometry.

We acknowledge certain limitations of our study. First, two models of a single insert design from one manufacturer were used in this study, and thus the results may not be representative for all designs. Inserts with complex designs will have greater potential for deviation, both between the insert and its CAD file and between different inserts. All inserts were obtained from the same lot and therefore may be more similar than inserts obtained from different lots. Implants from different lots are more likely to have additional inconsistencies, which in the case of this study would increase the magnitude of the deviations between scanned inserts and between the inserts and the averaged reference geometry. Second, for deviation measurement purposes, it was assumed that the geometries produced by micro-CT scanning were completely representative of the actual inserts, yet some errors are likely to exist. Errors can be introduced into the geometry through the scanner itself (eg, partial volume effect) or through the isosurface rendering process that generates the STL files (eg, discretization error). Scans were obtained with an isotropic voxel spacing of 50 μm; however, it is established that three-dimensional models can be produced from CT with errors less than the voxel spacing of the CT scanner with a mean absolute accuracy of one-fifth of the voxel spacing being reported in one instance for clinical CT [7, 23]. Errors in geometry are most likely to occur at areas of rapid change in curvature and less likely to occur over flat areas [13]. Attempts to minimize these types of errors were made by obtaining and averaging multiple scans of each insert and by using the highest possible quality for surface generation in the production of the STL files. Measurements were obtained in ROIs along the articular surface that has a low curvature, not at the sharp edges of the inserts where errors in the geometry are more likely to occur. A quality assurance phantom was used to ensure the voxel spacing of the scanner was accurate, and all insert volumes were compared with gravimetric analysis as a check on the micro-CT measurements. The CT-derived insert volumes were less than 0.4% smaller than the gravimetric volumes (Table 1). CT may underestimate volume compared with gravimetric analysis as a result of inaccuracies in voxel spacing or surface wrapping [10, 28]. Using an incorrect polyethylene density for converting gravimetric mass to volume could also lead to discrepancies from CT volume. A 0.001-mg/mm³ increase in density would reduce the gravimetric volumes by 0.1%, thereby reducing the observed discrepancies between CT and gravimetric volumes to 0.15% from 0.31%. Third, an additional potential error may be inaccurate coalignment of the insert geometries by the customized script. However, the algorithm used in this study is reportedly accurate and repeatable [26]. Finally, although micro-CT is a noncontact, nondestructive technique, it does impart ionizing radiation into the specimen being imaged. Dosimeter tests of the imaging protocol used in this study have reported an entrance dose of 4 Gy, which is 420,000 times less than the 105 kGy total dose used to crosslink and sterilize polyethylene by certain manufacturers [14].

We found geometric deviations between the inserts and the CAD models for both of the insert designs. The CAD model volumes were greater than the CT volumes, indicating the CAD model is slightly larger than the empiric geometry. In a retrieval study, these deviations would correspond to an error in the estimation of the preimplantation insert geometry. Mean deviations within the articular surface were –25.7 ± 13.1 μm for the CR group and –36.8 ± 31.4 μm for the PS group. The articular surface has been identified as the primary location of wear along with the backside surface and tibial post [3, 4, 6, 8, 19, 20, 22, 24]. Therefore, this amount of deviation would contribute to a considerable overestimation of wear during analysis of retrieved inserts. Based on the deviation maps for the CAD model comparisons, the CR group had moderate and uniform mean deviations, suggesting little systemic deviation from the CAD model with higher localized SDs suggesting variability between inserts. Therefore, the manufactured inserts were generally similar to the CAD model but with variability between inserts from manufacturing tolerances. In contrast, the PS group had higher regions of mean deviation, suggesting greater systemic deviation from the CAD model but with lower, uniform SDs, suggesting lower manufacturing variability than the CR group. As a more complex design, the PS group would be expected to be more difficult to manufacture than the CR group, producing greater systemic deviation, whereas the two groups would not be manufactured in the same batch or with the same machine, enabling the differences in SDs from manufacturing variability.

Isotropic scaling factors were applied to the CAD models and slightly reduced the mean deviations within the articular surface to –14.4 ± 11.8 μm for the CR group and –36.1 ± 30.9 μm for the PS group. Using a scaled CAD model as a reference, geometry would therefore be slightly more advantageous than using an unscaled model, but the limitations described previously would still apply. CAD models have been investigated in the past for use in model-based radiostereometric analysis (MBRSA) [9, 27]. Reverse engineering scans of the femoral components and tibial trays are reportedly superior to the CAD models [9]. They concluded the difference between the CAD model and a component was larger than the difference between the components themselves [9]. The deviations within the articular surface between the inserts and CAD models in the current study were indeed greater than the deviations between the individual inserts (Table 2). The geometric and volumetric deviations between the CAD models and individual inserts likely stem from the machining tolerances of the various tooling used to manufacture the inserts. The Genesis II inserts are machined from compression-molded polyethylene [15]. Scaling the CAD models resulted in an overall decrease in the mean deviations compared with the original CAD models but maintained deviations greater than 35 μm across the articular surfaces. Uniform scaling factors would not be able to correct these residual deviations, because different regions of the inserts may have been machined using different tools, each with a different tolerance and thus nonuniform error.

The deviations were overall much lower (less than 2 μm within the articular surfaces) when the average of five components was used as the CT-derived reference geometry. Again, this finding is supported by previous MBRSA investigations in which reverse engineering was superior to using CAD models [9]. The reference geometry constructed from averaging multiple inserts resulted in a more even pattern of deviations compared with using a single insert or CAD model as the reference geometry. With the averaging method, any error would therefore be consistent for all measurements across the insert surfaces. Using a single insert might result in varying degrees of error and thus a less accurate measurement of wear. An additional advantage of using the CT averaging method is that any potential measurement error would occur consistently across both the reference geometry and retrieved inserts.

Averaging multiple scanned never-implanted inserts resulted in a reference geometry with the lowest, most uniform deviation from the group of unworn inserts. Larger, more variable deviations were found between the scanned inserts and the CAD models. Assuming consistency in the manufacturing variability between lots, using an empirical reference geometry will provide a more accurate estimation of the preimplantation geometry for retrieval studies. This advantage will diminish with any increase in variability between manufacturing lots, which may result from differences in tool sharpness, tool tolerances, and factory temperatures. The wear rate of various polyethylene tibial inserts has been reported as 25 to 230 μm/year and is likely lower for newer designs featuring highly crosslinked polyethylene [11]. Therefore, the deviations of approximately 35 μm with the CAD models could potentially add or subtract up to a year’s worth of linear penetration to wear measurements. The effects of these errors will decrease with increased durations of device implantation. Authors of retrieval studies should be aware of these potential errors and account for them in wear measurements, particularly for any devices retrieved after less than 2 years.