The Onset Time of Tumor Repopulation for Cervical Cancer – First Evidence from Clinical Data

Abstract

Purpose

Accelerated tumor repopulation has significant implications in low-dose-rate (LDR) brachytherapy. Repopulation onset time remains undetermined for cervical cancer. The purpose of this study was to determine the onset time of accelerated repopulation in cervical cancer using clinical data.

Methods and Materials

The linear-quadratic (LQ) model extended for tumor repopulation was used to analyze the clinical data and MRI-based 3D tumor volumetric regression data of 80 cervical cancer patients who received external beam radiotherapy (EBRT) and low dose rate (LDR) brachytherapy. The LDR dose was converted to EBRT dose in 1.8 Gy fractions using the LQ formula, and the total dose ranged from 61.4 to 99.7 Gy. The patients were divided into 11 groups according to total dose and treatment time. The tumor control probability (TCP) was calculated for each group. The least χ2 method was used to fit the TCP data with two free parameters: onset time (T_k) of accelerated repopulation and the number of clonogens (K) while other LQ model parameters were adopted from the literature, due to the limited patient data.

Results

Among the 11 patient groups, TCP varied from 33% to 100% as a function of radiation dose and overall treatment time. Higher dose and shorter treatment duration were associated higher TCP. Using the LQ model, the best fit was achieved with the onset time T_k=19 days, K=139, with uncertainty ranges of (11, 22) days for T_k, and (48, 1822) for K, respectively.

Conclusion

This is the first report of accelerated repopulation onset time in cervical cancer, derived directly from the clinical data using the LQ model. Our study verifies that accelerated repopulation does exist in cervical cancer and has a relatively short onset time. Dose escalation may be required to compensate for the effects of tumor repopulation if the radiation therapy course is protracted.

INTRODUCTION

Cervical cancer is the 3^rd leading cause of cancer death in women worldwide and still has significant prevalence and mortality in the U.S. Although it is an aggressive disease which can rapidly progress, cure can be achieved if it is detected early and treated in a timely fashion. Treatment choice largely depends on tumor size and the stage of disease. Options include surgery, radiation therapy (RT), chemotherapy, or a combination of two or more of the above. RT is an integral part of therapy for women with stage IIB-IVA cervical cancer and its efficacy depends on many factors, including tumor size, stage, histology and radiation dose.

Tumors are composed of a large number of clonogens that have the capability of indefinite reproduction, resulting in tumor progression or recurrence. Even when there is complete clinical or radiographic regression of the gross tumor mass after treatment, if the clonogens are not completely eradicated by RT, tumor recurrence can occur as a result of proliferation of the clonogens (1). As a result, the tumor control probability (TCP) is lower. It has been shown that accelerated growth of clonogens occurs during the course of RT (1-3). It has been suggested that prolonged overall treatment time (OTT) can result in decreased tumor control, while shortened overall treatment time may increase early-responding normal-tissue complication probability (NTCP), resulting in logistic inconvenience with no potential gain in tumor control (3). Prolonged OTT of >7 weeks has been demonstrated to have a major impact on pelvic tumor control and cause-specific survival for cervical cancer, regardless of tumor size (4). Prolongation of the OTT in cervical cancer is associated with an estimated loss of local control of 0.3–1.6% per day of prolonged treatment (5-9).

It is undeniable that tumor repopulation plays an important role in tumor regrowth. Repopulation of surviving tumor clonogens during fractionated RT is one of the crucial factors determining radiocurability (10). Theoretically, pre-therapy tumor proliferation is balanced by tumor cell loss due to apoptosis, necrosis, and sloughing, while the potential doubling time measures the potential growth of the tumor, assuming there is no cell loss (11-12). Accelerated tumor repopulation has significant implications in low-dose-rate (LDR) brachytherapy (13). Many efforts have been made to estimate the tumor repopulation onset time for head and neck tumors (1-2), squamous cell carcinomas (14) and prostate cancer (15-17).

However, the onset time of tumor repopulation remains undetermined for cervical cancer. Clinical data with variations of dose delivery schedules allow analysis of onset time for tumor repopulation. Our group has collected clinical data for cervical cancer patients, which have detailed information on dose delivery schedules.

The purpose of this study was to analyze the clinical outcome data in cervical cancer patients and to estimate onset time of tumor repopulation and the number of clonogens for cervical cancer during radiation therapy. These estimates would be useful for determining the radiobiological parameters that influence the biological processes and for optimization of treatment strategies during RT.

MATERIALS AND METHODS

Patient characteristics

Eighty patients with carcinoma of the cervix were prospectively studied with four serial MRI scans during RT on an IRB-approved imaging protocol. Patients with Stage IB-IVA cervical cancer were eligible. Patients with non-epithelia (neuroendocrine, lymphoma and sarcoma) histologies, allergies to MRI contrast, and other MRI contraindications were ineligible. According to the criteria of International Federation of Gynecology and Obstetrics (FIGO) (18), patients were staged clinically. There were 10 patients with Stage IB, 5 with Stage IIA, 27 with Stage IIB, 3 with Stage IIIA, 24 with Stage IIIB, 7 with Stage IVA, 2 with Stage IVB (inguinal metastasis only), and 2 with locally recurrent tumors (after hysterectomy). 69 patients had squamous cell carcinoma, and 11 had adenocarcinoma. Age ranged from 25 to 89 years (Median: 55 years). Two independent examiners— a radiation oncologist and a gynecologic oncologist performed the tumor staging and initial clinical assessment. A summary of patient characteristics was presented in Table 1.

Table 1.

Patient characteristics

	Patients (n=80)
Age (years)	55 (25 - 89)
FIGO stage
I	10 (12%)
II	32 (40%)
III	27 (34%)
IV	11 (14%)
Histology
Squamous cell ca.	69 (86%)
Adenocarcinoma	11 (14%)
Brachytherapy
Low-dose-rate	76 (95%)
None (EBRT only)	4 (5%)
Chemotherapy	25 (31%)

Radiation therapy

Pretreatment evaluations included physical examination, chest radiograph, tumor biopsy, complete blood counts, serum chemistries, intravenous pyelogram (IVP), and abdominopelvic computed tomography (CT). All patients were treated with primary RT with curative intent. RT consisted of a combination of pelvic external beam radiation therapy (EBRT) with 24 MV photons using CT-based dosimetry and low-dose-rate (LDR) intracavitary brachytherapy as outlined by Fletcher-Delclos guidelines (18). The dose prescription of EBRT was 45–50 Gy delivered daily in 1.8 Gy fractions. The LDR brachytherapy consisted of 2 fractions of 20 Gy prescribed to Point A. The LDR doses were converted to equivalent EBRT doses of 18 Gy using an α/β of 10 Gy, i.e., each LDR brachytherapy fraction is approximately equivalent to 10 fractions of 1.8 Gy EBRT (13). According to patients’ dose delivery schedules, the total treatment times and total doses were obtained for individual patients. Twenty-five out of 80 patients received cisplatium-based chemotherapy.

In this study, data analysis focused on two outcome end points: tumor local control (LC) and dead of disease, based on clinical follow-up. Cases other than LC were considered as tumor local failure, which was defined as tumor recurrence during the follow-up period or persistent/progressive tumor within pelvis. For dead of disease, death from cervical cancer or other cancer complications was scored as event and death from intercurrent disease was censored. Patients other than dead of disease were considered as disease-specific survival.

MRI protocol

Serial MRI scans were prospectively performed for each patient at four well-defined time points: at the start of RT, during RT (2-3 weeks at 20–25 Gy pelvic RT and 4-5 weeks at 40-45 Gy of pelvic RT), and at follow-up (1–2 months after the completion of EBRT and brachytherapy). In this study, the fourth MRI after RT was used to evaluate the status of tumor local control. The MRI studies were mostly obtained with a 1.5 Tesla superconductive scanner (Signa, General Electric Medical Systems, Milwaukee, WI and Siemens Magnetom Vision, Siemens Medical, Inc., Erlangen, Germany). The 320 MRI studies in the early phase of the study were obtained with a 0.5 Tesla scanner (Picker International, Highland Heights, OH). A standard body coil was used. Imaging included sagittal 5-mm conventional fast spin echo T₂-weighted images (effective echo time TE_eff =104, repetition time TR=4000, echo length ETL=10, number of excitations NEX=2) and axial 7-mm T₂-weighted and T₁-weighted images (TE=16, TR=600, NEX=2).

Image analysis and tumor volume

Based on the T₂ -weighted images from all available MRI scans, the area of tumor was identified and delineated in each slice. Three-dimensional region-of-interest (ROI)-based tumor volumes were calculated using the technique described previously (19-20).

Rationale of dividing patients into subgroups

The variation of dose delivery schedules including total treatment time and total dose allows the exploration of the onset time of tumor repopulation. Patients treated with the same dose delivery schedules were categorized into the same group. Therefore, 11 patient groups were obtained based on total treatment dose and total treatment time in the dose delivery schemes.

Extended LQ model

A linear-quadratic model extended for tumor repopulation (21) was used to analyze the clinical data. The overall tumor control probability (TCP) is given by:

$$\mathit{TCP}=\exp (-K\cdot S),$$ (1)

where K is the number of tumor clonogens and S is the cell survival fraction.

Initial tumor volume has a relation with tumor clonogen number given by the following:

$$V=a{K}^b,$$ (2)

where a is constant and b is volume exponent.

For EBRT with a total dose of D in a total number of fractions n, the cell survival fraction can be calculated as:

$$S=\exp \left[-\alpha \cdot D-\beta \cdot \frac{1}{n}\cdot D^2+\frac{\ln \left(2\right)}{T_d}\cdot (T-T_k)\right],$$ (3)

where T is the total treatment time for the entire radiation course, T_d is the effective clonogen doubling time, and T_k is the time before the onset of accelerated repopulation.

As a result of tumor repopulation in patients whose treatments were excessively prolonged, a higher dose is required to achieve the same tumor control. The extra dose (ΔD) required compensating for prolonged treatment (ΔT) can be calculated by solving:

$$\mathit{TCP}(D+\Delta D,T+\Delta T)=\mathit{TCP}(D,T).$$ (4)

Least χ² fitting method

The least chi-square method was used to fit the LQ model to the clinical data. The object function to be minimized is

$${\chi }^2=\sum _{(i=1-11)}\frac{{({\mathit{TCP}}_i-{\mathit{Data}}_i)}^2}{{\mathit{DataError}}_i^2},$$ (5)

where TCP_i is the averaged tumor control probability for subgroup i calculated by LQ model, Data_i is the observed tumor control rate for subgroup i from clinical data, and DataError_i is its associated statistical error.

Using Eqs. (1, 3, 5), the least χ² fitting method was used to fit the clinical outcome data with two free parameters: the onset time (T_k) of acceleration repopulation and the number of clonogens (K) while other LQ model parameters were adopted from the literature (α=0.16 Gy⁻¹ (22) and α/β=14 Gy (23), T_d=4.5 days averaged over the values ranging from 3.1 to 5.6 days (10, 12, 23-26)), due to the limited patient data. The uncertainty of the onset time T_k was estimated by varying α in the range of (0.14, 0.18) Gy⁻¹ and α/β in (12, 16) Gy based on S₂ data derived in a separate study (22).

Statistical analysis

The data errors of TCP were presented with upper and lower confidence intervals. Note that student’s t-distribution was assumed in the calculations of data errors. The binomial confidence intervals for small samples were considered since the 11 patient groups have relatively small number of patients.

In this study, all statistical analyses were performed based on the SPSS platform (SPSS 16, SPSS Inc. Chicago, IL).

RESULTS

Initial tumor volume measured by the first MRI scans was significantly correlated with treatment outcome. Kaplan-Meier survival analysis was performed for the initial tumor volumes measured by using T2-weighted MR images. The 6-year control rate was 96.6% in patients with tumor volume v₁<43.7 mm³ and 66.7% in those with v₁≥43.7 mm³ (p=0.002), as shown in Figure 1A. The 6-year disease-specific survival was 93.1% for the patient group (v₁<43.7 mm³) vs. 53.1% for the other group (v₁≥43.7 mm³) (p<0.001), as shown in Figure 1B.

Figure 1.

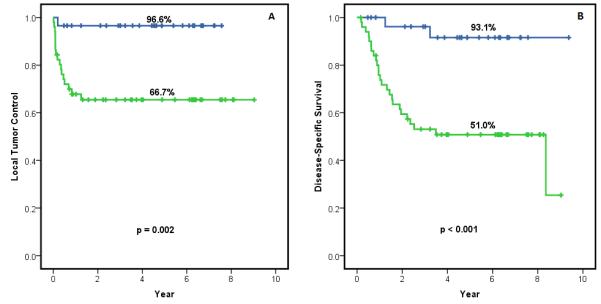
Kaplan-Meier survival analyses of (A) local tumor control data and (B) disease-free survival data.

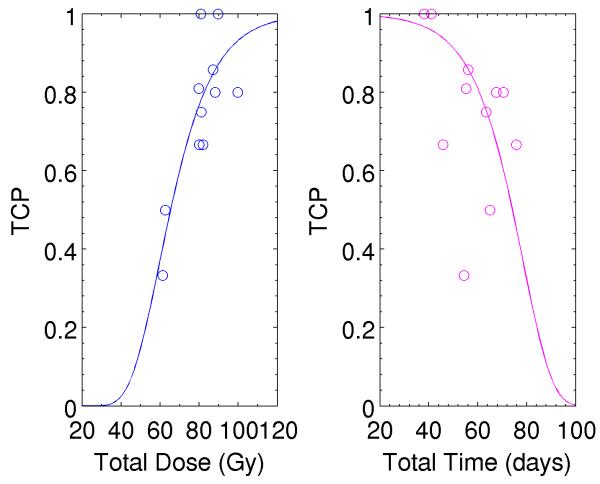
In this study, the calculated TCP was performed at the time point when RT has been finished. The fourth MRI during the follow-up time was used to evaluate the status of local tumor control, so that the measured TCP was performed at this time point. Based on the dose delivery schedules including total dose and total treatment time, 80 patients were grouped into 11 subgroups. Among the 11 subgroups, TCP varied from 33% to 100% as a function of radiation dose and overall treatment time. Higher dose and shorter treatment duration were associated with higher TCP. Table 2 shows the measured TCP and average dose and average treatment time for the 11 subgroups. The measured TCP was well fitted with Gompertz equation, as shown in Figure 2. Figure 2a shows TCP as a function of total dose and Figure 2b shows TCP as a function of total treatment time. Solid curves are fitting curves obtained using Gompertz equation to fit the 11 group data. The measured TCP tends to be high when applied dose increases or the overall treatment time is reduced. The total dose included the brachytherapy dose at point A, which was converted to the equivalent dose of EBRT, as detailed in Materials & Methods section.

Table 2.

TCP and the mean values of total dose and total treatment time in 11 subgroups

Group #	Total Dose (Gy)	Total Time (days)	TCP
1	61	54	0.33
2	63	65	0.50
3	81	38	1.00
4	82	46	0.67
5	80	55	0.81
6	81	64	0.75
7	80	76	0.67
8	90	41	1.00
9	87	56	0.86
10	88	70	0.80
11	99	67	0.80

Figure 2.

TCP as a function of (a) total dose; and (b) total treatment time. Solid curves were corresponding to the fitting curves.using Gompertz equation TCP=aexp(-bexp(cx)).

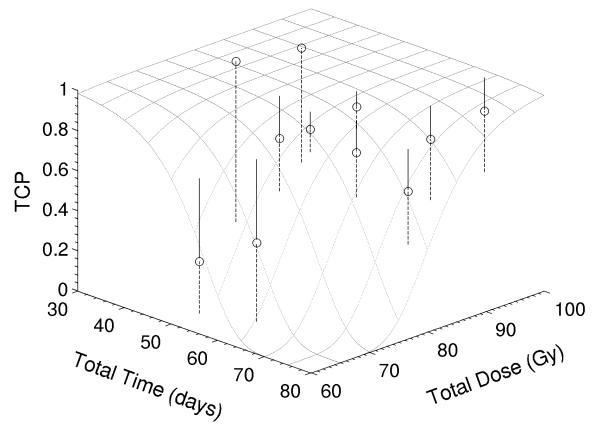
Using the LQ model, the best fit was achieved with the onset time T_k=19 days, clonogen number K=139, with uncertainty ranges of (11, 22) days for T_k, and (48, 1822) for K, respectively. Figure 3 showed tumor control probability as function of total dose and overall time. In the data-fitting process, we had only two fitting parameters: K and T_k. Due to the limited patient data, other parameters including the ratio α/β, α and T_d were adopted from the literature (α = 0.16 Gy⁻¹, α/β = 14 Gy and T_d=4.5 days). The uncertainty of the onset time T_k was estimated by varying α in the range of (0.14, 0.18) Gy⁻¹ and α/β in (12, 16) Gy based on S₂ data derived in a separate study. When we used our kinetic model to explore the onset time of tumor repopulation (22), we coincidently found it to be 19 days (these results will be reported in a separate publication).

Figure 3.

Tumor control probability as function of total dose and overall time. Note that circles are clinical data and dotted lines represent fitting curves when α=0.16 Gy⁻¹ and α/β=14 Gy, and dashed lines represent errors.

The volume exponent was investigated using Eq. (2). When T_k was fixed at 19 days, the volume exponent was 1.1 for cervical cancer. In reality, T_k, a and b can be free parameters simultaneously. However, the volume exponent b is expected to be more accurate compared with the case when two free fitting parameters (a and b) were used. We found that the relationship between tumor volume and clonogen number was almost linear. The volume exponent for cervical cancer was very close to that for head and neck tumors (27).

DISCUSSION

Onset time for tumor repopulation

The onset time of tumor repopulation is crucial for the understanding of response dynamic and for optimizing radiotherapy. However, until now, as a result of the lack of clinical data on a variety of dose delivery schedules, it has been difficult to obtain an estimate of the onset time for tumor repopulation in cervical cancer. Our group has accumulated clinical data with different dose delivery schedules for cervical cancer patients, enabling us to explore the onset time of tumor repopulation for cervical cancer.

Our results provide evidence of a delay in the onset of accelerated repopulation of approximately 19 days (95% confidence limits of 11-22 days). Onset time of tumor repopulation appeared to be shorter for cervical cancer compared to other types of cancer. In comparison, for instance, the onset times for tumor repopulation were reported to be 28 days for head neck cancer and 36 days for prostate cancer, respectively.

Quality of the clinical data

Sequential tumor volumetry using MR imaging appears to be a sensitive measure of the responsiveness of cervical cancer to irradiation. Treatment response can be assessed as early as during the course of radiation therapy by measurement of initial tumor volume and tumor regression rate (22, 28-30). The tumor volumes were measured by using T2-weighted MR images and the initial tumor volumes estimated from the first MRI scans were significantly correlated with treatment outcome.

The clinical data provide sufficient dynamic range with adequate statistics in terms of dose (81±11) and overall time (57±12) to allow an estimate of the onset time of accelerated repopulation, as shown in Table 2. The fact that the measured TCP was well fitted with Gompertz equation, as shown in Figure 2, reflects the quality of the clinical data and the advantage of data acquisition from a single site. The tendency remains that the measured TCP is higher when the applied dose increases or the overall treatment time is reduced. In general, more extensive tumors are treated over longer overall treatment time, potentially resulting in a lower TCP. A higher total dose used in the treatment may overcome a greater proportion of accelerated repopulation. However, since heterogeneity of repopulated tumor cells exists in tumors, a disparity of tumor response to radiation may occur. The existence of significant tumor heterogeneity will dilute the effect of overall treatment time in a large group of patients (5). Differences in standard treatment schedules among centers might result in variation in the overall treatment time of human tumors (31).

Parameters (α, β) in the LQ model

Because of the limit of patient population in this study, α and α/β were adopted from the literature (23). We should point out that these values were obtained based on in-vivo measurements. So far, no investigations on the ratio α/β have been performed for clinical applications, due in large part to the lack of a large set of clinical data. It would be interesting to investigate α and α/β for cervical cancer and determine the difference in values between in-vivo and clinical data. As more clinical data are collected by our group, these parameters could be explored in the future.

Clonogenic number and volume exponent

Tumor clonogenic cell number is believed to play an important role in predicting outcomes of radiotherapy (22). However, no proven method has been validated to assess the number of clonogens in human tumors accurately (32). All currently available assays adopt in-vivo TD50 or in-vitro plating efficiency to estimate the tumor clonogenic ability. The LQ model provides an approach to extract the clonogenic cell number. In our study, the number of clonogens has been obtained for cervical cancer. Although a large variation in clonogenic number has been observed, this is due in large to the limited number of patient data. Nevertheless, the clonogenic number for cervical cancer is relatively smaller compared to other types of cancers. This may contribute to the higher curability of cervical cancer compared to other types of human cancers.

The parameter of volume exponent provides an alternative method for evaluating the clonogenic cell number. Many investigators have explored this parameter (27, 33). Volume exponent have been found to be 0.37 for metastatic melanoma, 0.27 for oropharyngeal squamous cell carcinoma (33), and 0.85 for primary tumor volume and 1.1 for total tumor volume of advanced head & neck squamous cell carcinoma (27).

Impact of the onset time on clinical applications

The observed delay of tumor repopulation onset time of 19 days or less would be a plausible explanation why the cervical cancer grows rapidly compared to other types of cancers. The onset time would have a significant ramification for the design of optimized radiotherapeutic protocols, including the optimal dose in both EBRT and brachytherapy for cervical cancer. Moreover, the magnitude of dose escalation is highly dependent on the exact value of the repopulation parameters, including the onset time and the effective doubling time. In terms of tumor control, a modestly accelerated schedule would be desirable, whereas a highly accelerated schedule, while likely to be efficient in preventing repopulation, would not bestow any benefits over modestly accelerated schedules. The above considerations are referred only in terms of tumor control. In fact, in the design of clinical protocols, excessive early normal tissue reaction should be minimized (3).

Therapeutic options possible to counteract tumor repopulation

With this early onset time of repopulation, the avoidance of ant treatment protraction is of critical importance. This has been demonstrated clinically by the detrimental effect of therapy protraction in cervical cancer (5, 9, 34-35). In addition, our data provide rationale for moderate acceleration of the therapy course. This could be achieved by delivering 6 or 7 instead of 5 external beam fractions per week to the pelvis, which would increase the incremental weekly dose by up to 40% (from 9 Gy to 12.6 Gy), and decrease the treatment time to deliver the 45 Gy of fractionated external beam radiation therapy by nearly 30%. Earliest-possible start of brachytherapy, no later than the 4^th treatment week, may also provide additional dose intensification to counteract the rapid onset of repopulation. However, this strategy will only be effective for the central pelvic (not lymph node) involvement. Lastly, hyperfractionated schedules of twice-daily fractionation can accelerate the treatment course and may have the advantage of reducing long-term treatment toxicity. Experimental fractionation schedules (3 fractions/day over 12 consecutive days) have shown improved tumor control with the same or less normal tissue complications in head and neck (36) and lung cancer (37). Such altered fractionation schedules, however, would have to be carefully investigated with respect to increase in short-term side effects, especially in view of additive toxicities from concurrent chemotherapy.

To our knowledge, this is the first study reporting the onset time of tumor repopulation based on clinical data for cervical cancer. It will have a significant impact on designing and optimizing new radiation therapy regimens for patients with cervical cancer.

CONCLUSION

The onset time of accelerated repopulation of cervical cancer was directly derived from the clinical data using the extended LQ model. Our study validated that the accelerated repopulation does exist in cervical cancer with a relatively short onset time; therefore dose escalation is required to compensate this effect if radiation therapy schedules are prolonged.