Laser-directed hierarchical assembly of liquid crystal defects and control of optical phase singularities

Abstract

Topological defect lines are ubiquitous and important in a wide variety of fascinating phenomena and theories in many fields ranging from materials science to early-universe cosmology, and to engineering of laser beams. However, they are typically hard to control in a reliable manner. Here we describe facile erasable “optical drawing” of self-assembled defect clusters in liquid crystals. These quadrupolar defect clusters, stabilized by the medium's chirality and the tendency to form twisted configurations, are shaped into arbitrary two-dimensional patterns, including reconfigurable phase gratings capable of generating and controlling optical phase singularities in laser beams. Our findings bridge the studies of defects in condensed matter physics and optics and may enable applications in data storage, singular optics, displays, electro-optic devices, diffraction gratings, as well as in both optically- and electrically-addressed pixel-free spatial light modulators.

Topological defect lines play a prominent role in many scientific fields¹,²,³,⁴,⁵,⁶,⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵. For example, optical orbital angular momentum transfer can be enabled by optical vortices, “dark thread” singular lines around which the light's momentum swirls²,³,⁴. State of the art displays with unprecedented refresh rates and controllable viewing angles¹⁶ are nowadays made of a liquid crystal (LC) in the so-called “blue phase” that contains a periodic three-dimensional (3D) network of defect lines threading through the medium¹⁶,¹⁷,¹⁸. Defects like cosmic strings¹⁴ and vortex lines in electron beams⁸ are hard to obtain and study but often can be understood by probing defects in other topologically similar but more easily accessible systems, such as LCs and laser beams¹,²,³,⁴,⁵,⁸,¹⁴.

A nematic LC is typically comprised of rod-like molecules that spontaneously orient themselves along a common direction, described by the so-called director n with nonpolar symmetry (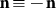), which is the medium's optical axis¹,¹⁷,¹⁹,²⁰. Nematic LCs are true anisotropic fluids, which can flow under shear or gravity while maintaining orientational order, although flows, confinement, and various external fields can introduce large-scale spatial changes of this molecular alignment commonly described by the director field n(r)¹⁷. The fluid nature of LCs - along with the facile response to external fields, surface confinement and temperature changes - often gives rise to various defects, most notably the so-called “disclinations,” the defect lines on which orientational order is disrupted and the orientation of LC molecules typically cannot be defined¹,¹⁷. Even the name “nematic” is derived from a Greek word “thread” and refers to ubiquitous defect lines found in these LCs¹⁷. Disclinations are classified according to their strength s defined as the number of revolutions by 2π that the director makes around the defect core when one circumnavigates the core once¹⁷. However, typically occurring because of symmetry-breaking isotropic-nematic phase transition or because of flows, these defects annihilate with time and are hard to generate or control in a reliable manner¹,¹⁹,²⁰. The recent progress in optical generation of defects in LCs was so far restricted to the so-called “torons,” which are ensembles of point and ring-shaped singularities²¹.

In this work, we design a soft matter system with a delicate interplay of the effects of confinement and chirality to obtain twist-stabilized quadrupolar clusters of half-integer disclinations having opposite signs s = ±1/2 (Fig. 1). These line defects are then shaped into highly controlled computer-generated patterns, including reconfigurable phase gratings capable of inducing and controlling optical phase singularities in laser beams.

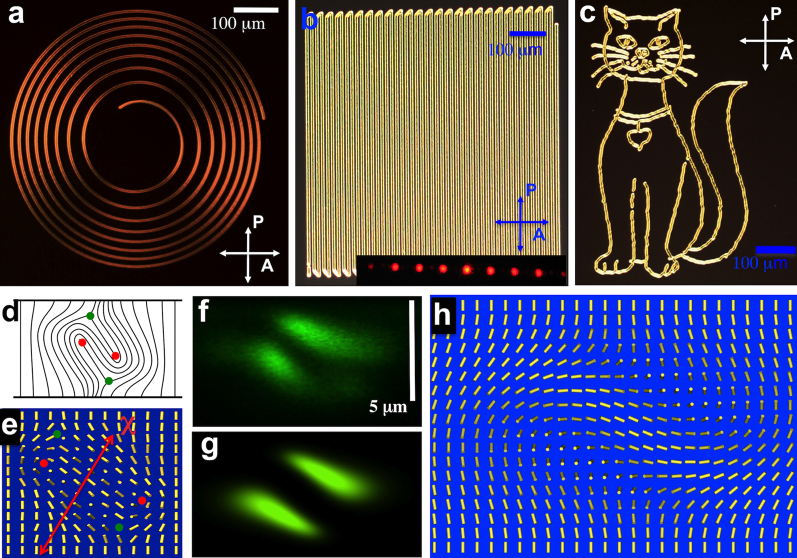
Figure 1. Laser-generated structures formed by twist-escaped disclination clusters.

(a) POM image of a spiral structure. (b) POM image of an optically-generated phase grating composed of the finger structures. The inset shows the corresponding diffraction pattern obtained using a HeNe laser beam. (c) “Topological cat” from the cover of Ref.9 generated by steering the focused laser beam in the LC cell. (d) (e) Schematics of the director structure with a quadrupole of disclinations of positive and negative half-integer strengths (red and green filled circles, respectively) in (d) a nematic and (e) a cholesteric LC with the qudrupole of the defects running along the finger's length. (f) Experimental and (g) computer-simulated vertical 3PEF-PM cross-sections of the finger's structure in a plane orthogonal to the finger. (h) Computer-simulated director structure in the vertical cross-section of an individual finger. The director fields are visualized by use of cylinders representing rod-like molecules of the LC. “P” and “A” in (a) (b) and (c) mark crossed polarizer and analyzer in POM.

Results

In our study, the nematic LC is doped with a small amount of a chiral agent that promotes formation of twisted configurations of n(r) with the equilibrium cholesteric pitch p (distance over which the director in a corresponding ground-state structure twists around the helical axis χ by 2π) tuned to be approximately equal to the LC cell thickness d²¹,²²,²³. In homeotropic cells with the used p/d ratios within 0.8–1, both uniform and various twisted configurations of n(r) can exist as stable or metastable states²¹,²²,²³. In a sample with initially uniform vertical director field, a focused laser beam locally realigns n(r) to in-plane orientation, which then promotes formation of self-assembled linear structures directed along the beam scanning direction. These structures are then shaped into desired patterns via continuous steering of the laser beam with intensity above a certain threshold value (Fig. 1a–c), as described in details in the supplementary online material. For example, when using a 10x objective lens of numerical aperture NA = 0.25, laser beams of power 0.018 W at the sample plane cause realignment of n(r) that can be seen as a bright spot in an optical microscope between a set of two crossed polarizers. This threshold power P_th is significantly lower than what is needed for the optical realignment in nematic LCs without chiral additives (supplementary material)²¹. Increasing the laser power above a 2^nd threshold P_th2 of about 0.033 W enables a stable generation of the computer-programmed defect structures via scanning of the focused laser beam within the LC sample (Fig. 1a–c) using a laser scanning setup shown in the Supplementary Fig. S1.

Individual s = ±1/2 disclinations are topologically stable entities and cannot appear or terminate in arbitrary locations within a uniformly aligned LC¹. To make our defect superstructures free of these restrictions, we have utilized the self-assembled quadrupolar clusters containing half-integer line defects of opposite signs (Fig. 1d,e). In a nematic LC without chiral additives, such defect clusters are unstable because disclinations of opposite signs annihilate each other to minimize bend and splay distortions of n(r) and the overall free energy due to the defects (Fig. 1d). In the studied chiral nematic LC, however, these defect clusters are stabilized by the energetically favorable twist of n(r) interspacing disclinations of opposite signs (Fig. 1e). They can also be introduced into the sample in a form of fragments of clusters as the disclinations of opposite sign can annihilate with each other at their ends and can also pin to the confining surfaces (see supplementary information for details). To demonstrate that the defect lines can be optically shaped into arbitrary two-dimensional (2D) architectures, we generate a spiral-shaped structure (Fig. 1a), straight fragments of the defect clusters with sharp turns forming a periodic grating (Fig. 1b), and a sketch of the “topological cat” from the book on category theory (Fig. 1c)⁹.

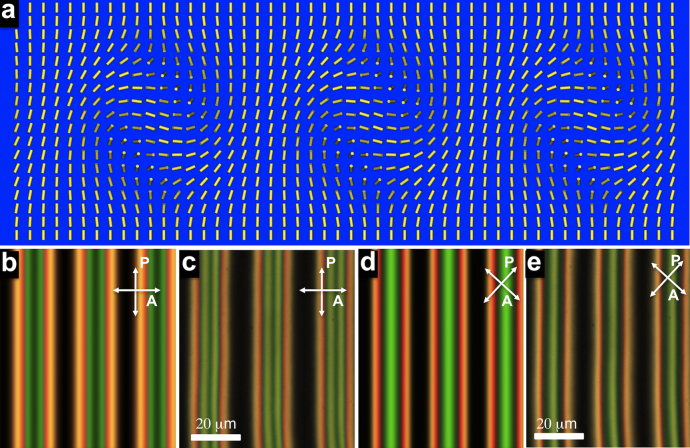
In an LC cell with p/d≤1 and vertical boundary conditions, the sample regions outside of the drawn structures have uniform vertical director and appear black when viewed between crossed polarizers in polarizing optical microscopy (POM). The laser-realigned regions appear bright (Fig. 1a–c and supplementary Fig. S2). A close inspection of generated structures by means of rotating polarizers reveals a combination of effects of birefringence and polarization rotation, indicating the presence of director twist across the cell thickness in these sample regions (Fig. 2). To gain more direct insights into the director structure in the sample's vertical cross-section, we perform label-free 3D imaging by means of three-photon excitation fluorescence polarizing microscopy (3PEF-PM)²⁴ and measure polarized fluorescence patterns emitted by the LC molecules themselves. An example of an image of the director field in the sample's vertical cross-section is shown in Fig. 1f, in which fluorescence intensity scales as ∝cos⁶φ, where φ is the angle between the spatially varying n(r) and the linear polarization direction of the excitation laser. Using this and other images obtained for various polarization states and cross-sectional planes (supplementary Figs. S3 and S4), we reconstruct the director structure schematically shown in Fig. 1e (see supplementary information for details). Experimental POM (Fig. 2c,e) and 3PEF-PM textures (Fig. 1f) closely resemble the corresponding computer-simulated textures (Fig. 2b,d and Fig. 1g) obtained for the minimum-energy n(r) configurations of either a single finger shown in Fig. 1h or a periodic finger array shown in Fig. 2a.

Figure 2. Director structure and POM images of periodic cholesteric finger arrays.

(a) Director field in the vertical cross-section of a periodic finger array. (b) (c) POM textures obtained (b) by means of computer simulations and (c) experimentally for crossed polarizer and analyzer parallel and perpendicular to fingers, respectively. (d) (e) POM textures obtained (d) by means of computer simulations and (e) experimentally for crossed polarizer and analyzer at π/4 to fingers. Both experimental and computer-simulated POM textures were obtained for d = p = 10 μm.

The studied defect clusters consist of a quadrupole of disclinations bound by helicoidal twist occurring predominantly along the direction of a helical axis tilted with respect to the confining substrates. This optically-generated structure resembles that of cholesteric fingers of the first kind previously observed in confined cholesteric cells occurring spontaneously or under applied electric fields²²,²³. Tight tiling of the fingers with defect clusters generated next to each other (Fig. 1b and Fig. 2c,e) typically maintains the tilt of the helical axis and the alignment of the elastic quadrupoles of so-called λ-disclinations (Fig. 2 and supplementary Fig. S2 and S3). Occasionally, the tilting direction of optically drawn fingers can reverse at sharp turns - like the kinks at the edges of the grating shown in Fig. 1b and in an individual finger shown in the supplementary Fig. S4 – while preserving the low-energy nature of cores of λ-disclinations in which melting of the LC is avoided via twisting of the director to become parallel to the defect lines in their center (i.e., the singularities “escape through twist”)¹⁷.

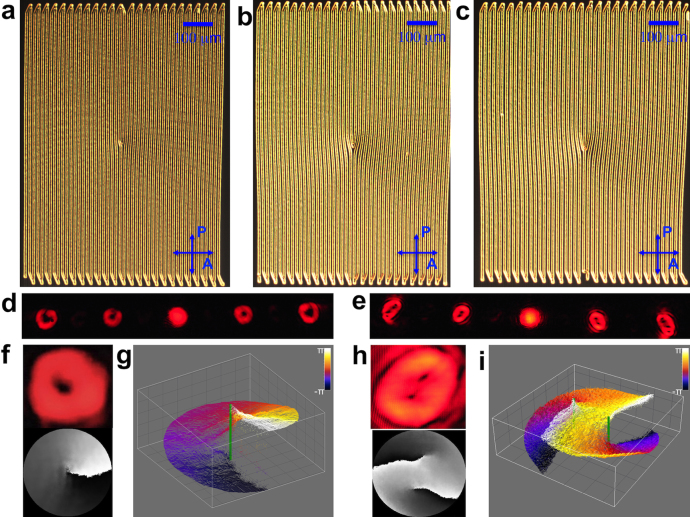
Since the effective refractive index of the LC depends on the orientation of n(r) with respect to the polarization and propagation direction of light, optically generated structures of fingers can be used as tunable and reconfigurable phase diffraction gratings (Fig. 1b). A typical diffraction pattern obtained by means of such a grating is shown in the inset of Fig. 1b. Computer programmed laser beam scanning provides the capability of unprecedented optical control over the structure of such gratings. Shown in Fig. 3a–c are POM images of optically generated diffraction gratings with edge dislocations (insertions) of different magnitude b = |b| = ma of Burgers vector, where a is the periodicity of the optically drawn grating and m is the integer number of insertions. The diffraction patterns obtained by use of these phase gratings have one or more dark spots within the beams of 1^st and higher diffraction orders (Fig. 3d,e). Characterization of phase profiles of laser beams in different diffraction orders n_do using the Stokes Polarimetry method²⁵ and a setup shown in the supplementary Fig. S5 reveals optical phase singularities and the relation between their topological charge N and b (Fig. 3): 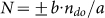, in agreement with theoretical predictions²⁶,²⁷,²⁸, where N is an integer number of 2π phase change on any closed circuit around the singularity center. The details of phase distributions are visualized by means of grayscale representations shown in the bottom parts of Fig. 3f,h and the 3D representations (Fig.3g,i). The phase varies continuously everywhere within the beams except for the locations of the screw dislocations ( = phase singularities), where phase is undefined. Remarkably, similar to the case of high-charge defects in LCs known to split into defects of lower charge¹⁷, the phase singularities of large N tend to split into multiple phase singularities of elementary charge N = ±1 (Fig. 3e,h,i). However, the physical origin of this splitting is very different from that of splitting of high-strength disclinations in LCs (driven by minimization of the elastic free energy) and is usually attributed to the presence of a weak coherent background in a screw-dislocated wave²⁶,²⁷,²⁸.

Figure 3. Diffraction gratings with various dislocations and their use for generation of phase singularities.

(a) POM image of a finger grating with an elementary dislocation. (b) (c) POM images of gratings with edge dislocations of larger Burgers vector. (d) Far field diffraction pattern from the grating shown in (a). (e) Far field diffraction pattern from grating shown in (c). (f) Enlarged image of the first-order diffracted beam shown in (d) (top) and its phase profile (bottom) with the phase varying from -π (black) to π (white). (g) 3D plot of the phase profile of the beam shown in (d). (h) Enlarged image of the first-order diffracted beam shown in (e) (top) and its phase surface (bottom). (i) 3D plot of the phase profile of the beam shown in (e). The vertical green lines mark the phase singularities.

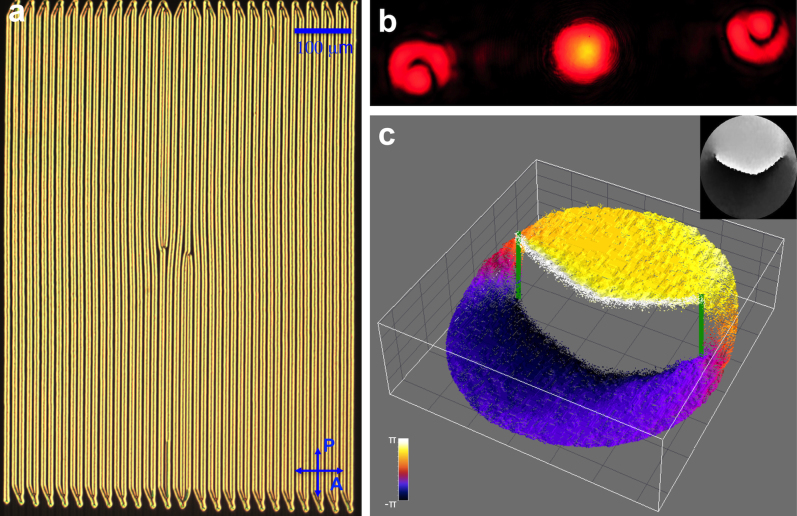
Beams with more sophisticated controlled singular phase distributions can be obtained from a Gaussian beam diffracted by phase gratings with multiple edge dislocations. For example, when two spatially separated elementary edge dislocations of opposite Burgers vectors b are introduced into a periodic grating (Fig. 4a), the intensity profiles of beams in the diffraction pattern shown in Fig. 4b change dramatically as compared to diffraction patterns due to gratings with individual edge dislocations (Fig. 3). The corresponding phase distributions (Fig. 4c) reveal inter-connected screw-edge dislocations: two screw dislocations having elementary charge of opposite signs are connected by an edge dislocation in the phase profile across which the phase has a sharp jump from −π to +π²⁶,²⁷,²⁸. On the other hand, two slightly separated dislocations with the same b in a grating shown in the supplementary Fig. S6a produce two off-axis rotating elementary phase singularities of the same sign N = ±1 in the n_do = ±1 beams and 2n_do such defects in the beams of higher order²⁶. The angle α between the straight line linking two phase singularities in the first-order beam and the straight line between two edge dislocations in the grating varies with the distance d_c from the phase grating to the camera detector as shown in the supplementary Fig. S6b, according to theoretically predicted dependence (see supplementary material)²⁶.

Figure 4. Generation of phase singularities with interlinked screw-edge dislocations.

(a) The POM image of a grating with two slightly separated elementary dislocations of opposite signs of Burgers vector. (b) Corresponding diffraction pattern with only 0th and 1st diffraction orders shown. (c) 3D representation of the phase profile corresponding to the first-order diffraction beam. The inset shows the corresponding 2D representation of the same phase singularity. The vertical green lines mark the screw dislocations.

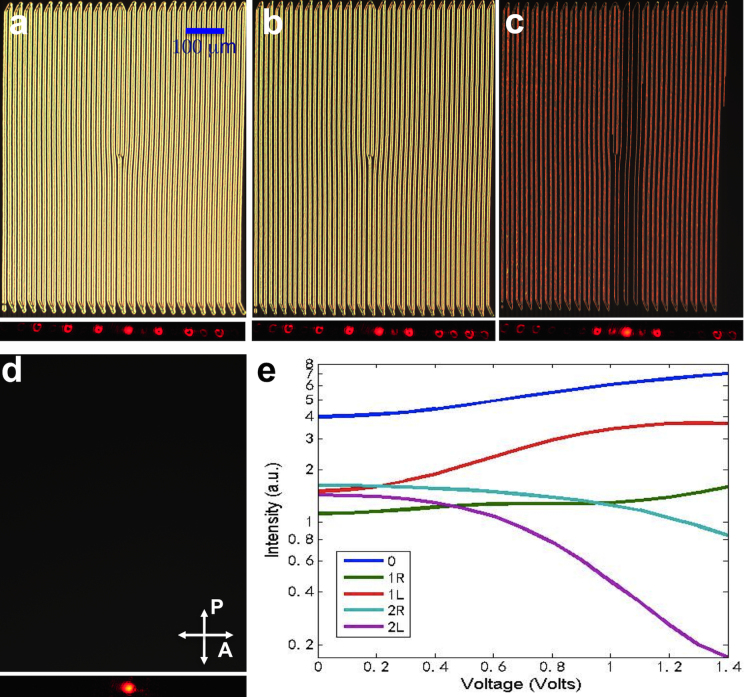
Because of the LC's fluid nature and its facile response to electric field, the optically drawn phase gratings can be tuned and fully erased by AC voltages of about 1 V at 1 kHz. As voltage U applied to the transparent indium tin oxide electrodes of the cell continuously increases, the fingers first shrink in width for U ≤ 0.5 V (Fig. 5a,b) and then shrink in length starting from the edge dislocation core and grating ends (Fig. 5c) until the phase grating is fully erased at U ≈ 5.6 V (Fig. 5d). The structural changes in fingers and their eventual erasing are due to coupling of n(r) in the used LC of positive dielectric anisotropy with the low-frequency electric field E that tends to minimize the electric field term of the free energy by enforcing n(r)∥E. LC elasticity, on the other hand, resists this realignment as it drives the system away from the global or local minima of the elastic free energy. At each applied voltage, the observed equilibrated static director structures correspond to the minima of the total free energy (the sum of electric and elastic free energy terms) evaluated for the given vertical surface boundary conditions for n(r). The field induces structural transformations and ensuing changes in the effective refractive index distribution within the grating. By varying the applied voltage, one can tune the width of fingers and the effective index distribution within them at low voltages (Fig.5a,b) and then fully “erase” them at higher voltages (Fig. 5c,d). This control of the phase gratings enables the corresponding control of the diffraction patterns, as shown in the bottom parts of Fig. 5a–d and in Fig. 5e. Importantly, the left-right asymmetry of the diffraction patterns, which is due to the synclinic tilting of the fingers' structures in the grating, becomes even more pronounced at high voltages and persists until the grating disappears at voltages of 5.6 V and higher (Fig. 5e). Interestingly, as the voltage gradually increases from 0 to 1.4 V, the diffracted beam of first order on the left side first increases and then decrease in intensity while the beam of first order on the right side constantly increases in intensity (Fig. 5e). Both left-side and right-side second-order diffracted beams continuously decrease in intensity and the 0-th order beam continuously increases in intensity. In our experiments, similar voltage tunability was achieved for diffraction patterns with and without dislocation defects as well as for different polarizations of the incident light (e.g. circular and linear parallel, perpendicular and at 45 degrees to the fingers direction). The observed dependence of laser intensity in the diffraction patterns on the polarization of the incident laser beam is due to the fact that the spatially-varying effective refractive index of the uniaxial LC medium within the periodic grating is strongly dependent on the polarization of this beam. The ability to control intensities of different diffraction orders by varying relatively low applied voltages (0.5–2 V) and also “erasing” these gratings at somewhat higher (∼5 V) is of great interest for a number of important applications of phase diffraction gratings²⁹,³⁰,³¹,³²,³³.

Figure 5. Voltage control of fingers gratings and the corresponding diffraction patterns.

(a)–(d) POM images of a grating with an elementary dislocation at applied voltages of (a) 0 V, (b) 1.8 V, (c) 3.6 V, and (d) 5.6 V. The corresponding diffraction patterns are shown in the bottom of figure parts of (a)–(d). (e) intensity of light in different diffraction orders vs. applied voltage. The 1^st and 2^nd diffraction orders are labeled “1L”, “2L”, “1R”, and “2R” in (e) with “L” and “R” standing for “left” and “right,” respectively.

Times needed for optical generation of the fingers structures are typically predetermined by the fastest speed of continuous scanning of a focused laser beam using galvano mirrors that still yields reliable generation of uninterrupted fingers (100 μm/s in the case of using a 10x objective). 2D patterns of fingers can be generated within times ranging from a fraction of a second to minutes, depending on complexity of the pattern. The fingers structures can be unwound at applied voltages of 5 V and higher or modified at lower voltages within a typical response time of 5–10 ms, comparable to the response time of nematic LCs confined into cells of similar thickness¹⁷. In order to decrease the laser generation times, one can utilize holographic laser tweezers instead of the scanning-beam approach used in our current work²¹,²⁹,³⁴, which may potentially shorten these times to ∼10 ms, comparable to the LC's response time.

Discussion

Although conventional electrically addressed LC spatial light modulators (SLMs) have recently emerged as a powerful means for generation of optical phase singularities and control of phase of light on a pixel-by-pixel basis³¹, some of their major limitations as compared to microfabricated gratings and masks are caused by relatively large minimum size and limited number of pixels. For example, liquid crystal on silicon SLMs with pixels much smaller than in other LC SLMS, that can be used only in the reflective mode, typically have pixel size within 5–10 μm and larger³¹. Our findings may allow for development of both phase-only and amplitude-only optically and electrically controlled SLMs that overcome these limitations because the generation of finger structures requires no patterned electrodes or complicated electric addressing of pixels and the size of laser-generated structures can be designed to be in the submicrometer range (via selecting appropriate cholesteric pitch and cell thickness). Optically generated gratings therefore combine advantages of conventional gratings and masks that have no pixelation-related problems with the advantages of tunability and switching offered by conventional LC SLMs. Furthermore, our approach may also offer a simple means for microfabrication of thin flexible films with highly controlled diffraction gratings. To do this, by using reactive mesogens instead of small-molecule LCs, one can first generate desired diffraction gratings or other patterns by a scanned infrared laser beam and then polymerize the LC to obtain thin films with imprinted phase gratings or masks for applications in singular and Fourier optics.

Highly controlled periodic arrays of defects are of great interest for the study of interactions between various nanoparticles and topological defects and self-assembly mediated by such interactions³⁵,³⁶,³⁷,³⁸,³⁹,⁴⁰,⁴¹. It is of interest to explore how individual finger fragments as well as their loops and arrays with and without various defect-entrapped nanoparticles can be potentially utilized as phase masks for generation of nontrivial phase profiles in laser beams and for other applications. For example, localization of metal and semiconductor nanoparticles within disclinations in fingers, similar to that reported for other LC defects³⁵,³⁶,³⁷,³⁸,³⁹,⁴¹, may not only allow for obtaining highly controlled spatial patterns of nanoparticles but also enhance or dramatically change the response of phase gratings and phase masks.

One of the major recent research efforts in soft matter and other branches of condensed matter physics is directed at control of topological defects using fields, colloids, optical tweezers, confinement, chirality, and other means³⁴,³⁵,³⁶,³⁷,³⁸,³⁹,⁴⁰,⁴¹,⁴²,⁴³,⁴⁴. Our findings greatly extend the current capabilities and possibly also the utility of such control of defects. Furthermore, using laser generated patterns of defects as a model system, one can obtain insights into how defects in condensed matter can be probed based on the study of phase profiles in various types of beams (e.g. electron beams⁵,⁸) at wavelengths comparable to the size of structural features in material systems of interest.

From the standpoint of view of using laser-generated defect patterns as reconfigurable and tunable diffraction gratings, it is interesting that the studied diffraction patterns are strongly asymmetric and that the difference between intensities of diffracted beams of different diffraction orders varies as a function of applied voltage (Fig. 5). This phenomenon is likely due to the asymmetric director structure of the finger used to draw the grating (Fig. 1h and Fig. 2a) and the corresponding asymmetric profiles of the phase gratings obtained by tight tiling of fingers while maintaining the directionality of the tilt of the finger's helical axis. A comprehensive experimental and numerical study of diffraction patterns and diffraction efficiencies due to gratings composed of fingers will be reported elsewhere.

To conclude, we have demonstrated unprecedented control over hierarchical defect structures spanning from defect lines in the LC director field, to defects in gratings optically generated from such line defects, and to the optical phase singularities obtained by use of such gratings with inserted dislocation defects. This work bridges the study of defects in condensed matter physics and optics and may enable new applications in singular optics, display and diffractive devices, data storage, etc.

Methods

Integrated laser scanning and optical imaging setup

The used laser scanning system consists of a two-axis scanning head XLRB2 (Nuttfield Technology) and a continuous wave Ytterbium-doped fiber laser (1064 nm, from IPG Photonics) with collimated output beam diameter of 5 mm (supplementary Fig. S1). It is designed to steer a focused beam along arbitrary 2D computer-programmed trajectories within the focal plane of a microscope objective. Two scanning mirrors enable voltage-controlled 2D beam deflection and are powered by a digital-analog converter (NI PCI-MIO-16E-4, from National Instruments) controlled by homemade Labview software. The laser beam is first directed into the scanning head, reflected by its two mirrors, and then introduced into the microscope by means of a telescope (supplementary Fig. S1). The scanning mirror axes are positioned at the front focal plane of the first lens of the telescope, while keeping the distance between the two lenses of the telescope to be the sum of their focal lengths and the back focal plane of the second lens conjugate with the back aperture of the microscope objective.

The laser scanning system is integrated with an upright polarizing optical microscope BX-51 (Olympus). The sample is placed between two crossed polarizers and viewed in a transmission-mode POM while the defect structures are being generated and manipulated via steering the focused beam. Imaging light traversing through the LC regions with vertical n(r) is blocked by the set of crossed polarizers, since the light's polarization remains unchanged. Cell regions with fingers alter polarization of incoming linearly polarized light due to the horizontal component of n(r) and its twist, so that POM textures reveal the defects and n(r). Both structural generation and POM imaging are implemented by use of microscope objectives with 10x–100x magnification and numerical apertures (NA) within NA = 0.1−1.4.

Three-photon excitation fluorescence polarizing microscopy

3D director structures were probed using the 3PEF-PM, which is an imaging modality of the nonlinear optical polarizing microscopy technique described in detail elsewhere²⁴. A tunable, pulsed Ti:sapphire oscillator (Coherent Chameleon Ultra-II) is employed as an excitation source for the 3PEF-PM. The oscillator output can be tuned over a 680–1080 nm wavelength range with 140 fs pulse durations at an 80 MHz repetition rate. To control the linear polarization state, the beam is passed through a rotatable half-wave plate and a Glan-Thompson polarizer, and then directed into the scanning head (Olympus FV-300) of an inverted optical microscope IX-81 (Olympus). A 100x objective with high NA = 1.4 focuses the beam to a diffraction-limited spot while a pair of galvano mirrors within the scanning head steers the spot within the focal plane of the objective. A stepper motor controls the height of the objective so that 3D images can be reconstructed from a series of two-dimensional scans. Since the excitation intensities needed to induce significant three-photon absorption only exist in a small volume around the focus of the objective, this approach provides an intrinsic submicrometer 3D optical resolution. We use a beam tuned to 870 nm wavelength to excite the LC molecules directly via the three-photon absorption process and detect the emitted fluorescence signal in an epi-detection scheme using a bandpass filter centered at 417 nm (bandwidth 60 nm) and a photomultiplier tube²⁴. Since the transition dipole moments of absorption and fluorescence are along the long axes of LC molecules, polarized multiphoton excitation yields orientation-sensitive fluorescence textures with the signal intensity ∝cos⁶φ, where φ is the angle between n(r) and the linear polarization direction of laser excitation light²⁴. 3PEF-PM textures obtained for different sample cross-sections and for complementary 3PEF-PM imaging polarizations allow us to reconstruct the 3D n(r).

Optical phase mapping setup

The used phase mapping technique is based on the measurements of Stokes parameters using a setup shown in the supplementary Fig. S5. A 633 nm He-Ne laser beam of diameter 1 mm is split into two beams of the same intensity by a beam splitter. One of the beams is passed through the phase grating and then the diffracted beams of interest with phase singularities dependent on the diffraction order are selected by a mirror and polarized vertically using a linear polarizer. The reference beam is polarized horizontally. The beam from a studied diffraction order of interest and the reference beam are collimated and recombined. A quarter wave plate and polarizer on the optical train of the recombined beam control the phase delay and polarization as needed to measure different Stokes parameters. A complementary metal–oxide–semiconductor (CMOS) camera Nikon D300 is used to measure the intensity profiles of the laser beams. Four images are obtained for different orientations of the quarter wave plate and the polarizer and then used to reconstruct the phase distribution in different diffraction orders (see supplementary material for details).

Materials and sample preparation

LC cells were constructed using glass substrates with transparent indium tin oxide (ITO) electrodes. To obtain vertical surface boundary conditions for n(r), we treat the glass plates by dip-coating in a 5 wt.% aqueous solution of a surfactant [3-(trimethoxysilyl)propyl]octadecyl-dimethylammonium chloride (DMOAP). To set the cell gap, ultraviolet-light-curable optical adhesive NOA-61 (from Norland Products Inc.) doped with glass microspheres of diameter matching the desired gap thickness was used to glue the substrates together via ultraviolet light exposure. To obtain chiral nematic LC mixtures of different p, we doped the room-temperature nematic hosts E7, MLC-6815, and ZLI-3412 (all from EM Industries) with different concentrations C of the chiral additive CB15 (EM Industries) according to the relation 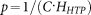and using known values of helical twisting power H_HTP, which, for example, is 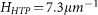in the case of E7. Material properties of the used LCs are provided in the supplementary Table S1. All experimental data presented in this work have been obtained for cholesteric LC mixtures based on the E7 nematic host. We infiltrated the cells by use of capillary forces at elevated temperature of about 90°C, sealed them using 5-min epoxy glue, and soldered wires to the ITO electrodes.

Computer simulations of POM textures

Using the computer-simulated 3D director structure of an array of three parallel cholesteric fingers (Fig. 2a), we have simulated the corresponding POM textures (Fig. 2c,e) using the Jones matrix method³¹,³² and experimental material parameters such as optical anisotropy, pitch, and cell thickness (supplementary Table S1). The LC sample with a finger was split into a set of thin slabs parallel to substrates with known orientation of n(r) given by numerical modeling (supplementary material). While traversing through the LC cell, light splits into ordinary and extraordinary waves with electric fields perpendicular and parallel to the in-plane projection of n(r), respectively. The effect of each thin slab is equivalent to that of a phase retardation plate with spatially varying optical axis and is described by a coordinate-dependent Jones matrix³¹. In each pixel of a simulated polarizing microscopy texture, intensity of the light after propagation through the cell is obtained by successive multiplication of the Jones matrices corresponding to a polarizer, the series of thin nematic slabs with coordinate-dependent phase retardation, and the analyzer. To mimic the achromatic-light observations in the experiments, we have performed these calculations for wavelength 475 nm, 510 nm, and 650 nm and then superimposed the resulting textures to obtain the POM images. Computer-simulated images closely resemble experimental results, Fig. 2b–e, and further reaffirm our understanding of director configurations based on computer simulations and reconstruction using 3PEF-PM images.

Author Contributions

P.J.A. and Z.Q. generated structures and characterized phase singularities. P.J.A. designed and fabricated all studied samples. Y. Lin and Z.Q. wrote the Labview software for laser beam scanning. P.J.A. and C.W.T. did initial proof-of-principle studies on generation of fingers structures and imaging. Y. Lansac computer-simulated director structure of fingers. P.J.A. simulated POM and 3PEF-PM textures. P.J.A., Z.Q., and M.J.L. constructed the setup for optical phase characterization. I.I.S. conceived and planned the project, provided funding, and explained results. P.J.A. and I.I.S. wrote the paper.

Supplementary Material

Supplementary Information

Supplementary online material