Abstract
Cohort studies typically sample unrelated individuals from a population, although family members of index cases may be also be recruited to investigate shared familial risk factors. Recruitment of family members may be incomplete or ancillary to the main cohort, resulting in a mixed sample of independent family units, including unrelated singletons and multiplex families. Multiple methods are available to perform genome wide association (GWA) analysis of binary or continuous traits in families, but it is unclear whether methods known to perform well on ascertained pedigrees, sib-ships, or trios are appropriate in analysis of a mixed unrelated cohort and family sample.
We present simulation studies based on Multi-Ethnic Study of Atherosclerosis (MESA) pedigree structures to compare the performance of several popular methods of GWA analysis for both quantitative and dichotomous traits in cohort studies. We evaluate approaches suitable for analysis of families, and combined the best performing methods with population-based samples either by meta-analysis, or by pooled analysis of family- and population-based samples (mega-analysis), comparing type 1 error and power. We further assess practical considerations, such as availability of software and ability to incorporate covariates in statistical modeling, and demonstrate our recommended approaches through quantitative and binary trait analysis of HDL cholesterol (HDL-C) in 2,553 MESA family- and population-based African-American samples. Our results suggest linear modeling approaches that accommodate family-induced phenotypic correlation (e.g., variance component model for quantitative traits or generalized estimating equations for dichotomous traits) perform best in the context of combined family- and population-based cohort GWAS.
Keywords: genome-wide association study (GWAS), cohort study, simulation study, generalized estimating equations (GEE), variance component model, family-based association
Introduction
Large-scale cohort studies have been established over the past several decades as an effective way of gathering rich epidemiological data, typically focused on uncovering risk factors for a specific disease of interest. Advantages of this study design include representative sampling of the study population coupled with rich phenotypic data, often with repeated measures over an extended period. A considerable amount of time and resources are put into establishing these well-phenotyped cohorts. Once this initial investment has been made, collection of biomarker specimens such as blood for genetic studies expands the cohort utility and, in recent years, has yielded cohort genome-wide association studies (GWAS) (Manolio 2009).
The Multi-Ethnic Study of Atherosclerosis (MESA) is an example of a cohort study of unrelated individuals enhanced by many ancillary studies focused on specific phenotypic and exposure domains (Bild et al. 2002). One ancillary study (MESA Family Study, MESAFS) recruited family members specifically for genetic analysis. Another ancillary study (MESA Air) evaluated the effects of air pollution on atherosclerosis risk. Approximately 38% of the recruited participants are White, 28% African-American, 22% Hispanic, and 12% Asian, predominantly of Chinese descent. Participants recruited by the original MESA cohort (6,814), and MESAFS (2,128 from 528 families) and MESA Air (5,479 from MESA, 257 external cohort, and 490 from MESAFS) have recently been genotyped using the Affy 6.0 genome-wide SNP array under the NHLBI SNP Health Association Resource (SHARe) program (MESA SHARe). A total of 8,298 participants who provided consent had both phenotypic and genotypic data, including 6,657 independent “families”, 10.5% of which are multiplex (17.6% in African American families, 20.6% in Hispanic).
When a GWAS is undertaken for an existing cohort study, traditional ascertainment strategies for genetic studies are bypassed. As a result, it is unclear whether methods known to perform well on ascertained pedigrees, sib-ships, or trios are appropriate for the analysis of family-based cohort data. In addition, large-scale cohort studies typically involve the additional challenge of incorporating considerable numbers of population-based samples. Many widely used tests of association focus on within-family analysis (Abecasis et al. 2000; Fulker et al. 1999), which assess transmission of alleles within a family, but without making use of allelic association observed across families. Population-based tests of association generally apply regression-based total association methods, assessing allelic association with the trait of interest, and taking into account familial correlation where appropriate. Further investigation is necessary to determine the optimal approach to combine family- and population-based study designs.
In this report, we present simulation studies to compare performance of several popular methods in GWAS analysis of both quantitative and dichotomous traits in cohort studies involving both family-based and population-based samples, as is the case in MESA and MESAFS. We use a two-stage approach to identify the best methods for joint analysis of family- and population-based samples. First, we evaluate approaches suitable for analysis of families only (MESAFS), and compare their performance in terms of type I error rates and power in analysis of our simulated pedigree data. For quantitative trait analysis in families, we consider seven approaches including two within-family analysis approaches: QFAM-within (Purcell et al. 2007) and FBAT (Laird et al. 2000), four total-association methods that account for familial correlation: QFAM-total (Purcell et al. 2007); linear mixed effects (LME) modeling (Chen and Yang 2010); fastAssoc (Chen and Abecasis 2007); and robustAssoc (Chen et al. 2009), and linear regression, that does not account for familial correlation, included for comparison. For analysis of dichotomous traits, we consider five approaches, including two within-family analysis approaches: GDT (Chen et al. 2009) and DFAM (Purcell et al. 2007), two tests of total association that account for familial correlation: MQLS (Thornton and McPeek 2007) and GEE (Chen and Yang 2010; Zeger and Liang 1986), and a Cochran-Armitage Trend test (Agresti 2002; Purcell et al. 2007), that does not account for familial correlation, included for comparison. The best performing methods for family data (MESAFS) are then combined with population-based samples (MESA) either by meta-analysis, or by pooled analysis of family- and population-based samples, where appropriate. We further assess practical considerations such as availability of software and ability to incorporate covariates in statistical modeling, and demonstrate our recommended approaches through quantitative and binary trait analysis of HDL cholesterol (HDL-C) in 2,553 family- and population-based African-American samples recruited through MESA, MESA Air and MESAFS.
Methods
Simulation Studies
Our simulated samples each include a total of 8,227 individuals: 5,922 population-based singletons, and 2,305 individuals across 687 families with 2–13 genotyped individuals each. This sample composition reflects that of the MESA SHARe cohort available for accession through a Data Access Request in dbGaP (study accession phs000209, http://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000209.v4.p1), with 8,227 individuals passing genotype QC and assembled into pedigrees based on Coordinating Center records and further relationship inference to remove any errors involving first-degree relatives (Manichaikul et al. 2010). A detailed summary of the pedigree structure used in simulations is shown in Table 1.
Table 1.
Distribution of family size used for simulation of pedigrees
| # of genotyped individuals | Total | ||||||
|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | >5 | |||
| # of genotyped founders | 0 | 153 | 235 | 98 | 53 | 45 | 584 |
| 1 | 56 | 6 | 13 | 7 | 10 | 92 | |
| 2 | 0 | 6 | 0 | 3 | 2 | 11 | |
| Total | 209 | 247 | 111 | 63 | 57 | 687 | |
Simulation of phenotypes
For each of 100,000 simulation replicates, we considered a single marker with minor allele frequency (MAF) 0.3, 0.05, and 0.01. Quantitative traits were simulated in Merlin (Abecasis et al. 2002) such that the simulated disease marker accounted for 0.5% of trait variance, with residual polygenic variance 39.5% and residual environmental variance of 60% (Chen and Abecasis 2007). These quantitative traits were then normalized against either a normal distribution, a chi-square distribution with 7 degrees of freedom (df=7), or a chi-square distribution with df=3. The two chi-square distributions were considered to examine the case that phenotypic distributions differed from normality. We chose these moderately skewed distributions under the assumption that more heavily skewed phenotypes would be transformed (e.g., log or square-root transform) prior to analysis. We did not include population admixture effects in the simulation of phenotypes.
We simulated under the null and alternatives to test type 1 error rate and power for nominal significance levels of P = 0.01 and P = 0.001; however, only the power for more stringent nominal thresholds of P = 1×10−4 or P = 1×10−8 were used to limit computation. Dichotomous traits were generated using a threshold model in which individuals with quantitative traits falling in the top 5%, 10% or 50% were considered “affected”, while the rest were labeled “unaffected”. In this manner, we induced a polygenic effect in simulation of the dichotomous phenotypes.
Analysis of simulated quantitative traits
All quantitative trait analysis was performed using an additive genetic model. Initially, six widely used approaches for analysis in pedigrees were employed: 1) QFAM-within from PLINK (Purcell et al. 2007), 2) FBAT (Laird et al. 2000), 3) QFAM-total from PLINK (Purcell et al. 2007), 4) linear mixed effects (LME) model which accounts for familial correlation according to the kinship matrix (Chen and Yang 2010) 5) fastAssoc, a variance-component model (Chen and Abecasis 2007) using a fast score test (Chen et al. 2009), 6) robustAssoc (Chen et al. 2009), a robust score test derived from the same variance-component model (Chen and Abecasis 2007), and 7) linear regression, that does not account for familial correlation, shown for comparison. Details of the software used to perform the simulations are shown in Table 2. After examining performance of these six methods for quantitative trait analysis in families, we found performance of methods clustered notably into two groups, with regression-based total-association methods (fastAssoc, robustAssoc, QFAM-total) displaying statistical power more than double that of within-family association tests (QFAM-within and FBAT) for similar levels of type I error, across a variety of phenotypic distributions. Therefore, subsequent simulations to compare performance of methods for combined analysis of family- and population-based samples examined total-association methods only.
Table 2.
Summary of methods and software included in comparison.
| Analysis Type |
Method | Software package |
Effect estimate |
Standard error |
Statistical significance |
Covariates | Family |
|---|---|---|---|---|---|---|---|
| Quantitative | QFAM-within | PLINK | No | N/A | Permutation | No | Yes |
| FBAT | FBAT | No | N/A | Z test | Yes | Yes | |
| QFAM-total | PLINK | No | N/A | Permutation | No | Yes | |
| LME | R/GWAF | Yes | Yes | Chi-square test | Yes | Yes | |
| fastAssoc | GDT | Yes | Yes | Score test | Yes | Yes | |
| robustAssoc | GDT | Yes | Yes (robust) | Robust score test | Yes | Yes | |
| Linear regression | PLINK | Yes* | Yes* | Wald test | Yes | No | |
| Binary | GDT | GDT | No | N/A | Z test | Yes | Yes |
| DFAM | PLINK | No | N/A | Chi-square test | No | Yes | |
| MQLS | GDT | No | N/A | Z test | No | Yes | |
| GEE | R/GWAF | Yes | Yes (robust) | Chi-square test | Yes | Yes | |
| Trend | PLINK | No | N/A | Chi-square test | No | No | |
“Software package” indicates how the method was implemented in our simulations and analysis, although other software packages are available for some of the methods. “Effect estimate” and “standard error” indicate whether these summary statistics are provided by the software output. “Statistical significance” indicates the method by which statistical significance is computed and reported by the software. “Covariates” indicates whether or not the software accepts and properly adjusts for covariates using the given method. “Family” indicates whether the method accounts for family structure.
Although effect estimates and standard errors are available for linear regression, the reported values are appropriate for analysis of unrelated individuals only.
We considered application of meta-analysis to combine p-values from linear regression of population-based samples with analysis of family-based samples by the following approaches: 1) QFAM-total, 2) LME, 3) fastAssoc, and 4) robustAssoc. For meta-analysis, we applied the method implemented in METAL (Willer et al. 2010) that combines p-values taking into account direction of effect, with weighting according to the number of individuals in the population- and family-based samples. We also examined pooled analysis of family and population-based samples with: 5) LME applied to pooled samples of families and singletons, 6) fastAssoc applied to pooled samples, 7) robustAssoc applied to pooled samples, and 8) linear regression applied to pooled samples. For each simulation replicate we also performed a linear regression on the 5,922 singletons only, to provide a reference indicating how much power in the combined analyses is derived from singletons. We did not include pooled analysis by QFAM-total in the simulations because the number of permutations needed to achieve genome-wide significance (e.g. 5 × 10−8) makes such simulations for this approach computationally prohibitive. Although PLINK does support an alternative permutation strategy that requires fewer permutations by examining the family-wise error rate (accounting for multiple comparisons across the number of observed SNPs) rather than the pointwise error rate, such a strategy is not within the scope of our simulation study.
Analysis of simulated dichotomous traits
Analysis of dichotomous traits was performed using an additive genetic model. We considered the following five approaches for analysis of dichotomous traits in pedigrees: 1) GDT (Chen et al. 2009), 2) DFAM in PLINK (Purcell et al. 2007), 3) the more-powerful quasi-likelihood score test (Thornton and McPeek 2007), MQLS as implemented in the software GDT (Chen et al. 2009), 4) generalized estimating equations (Zeger and Liang 1986) (GEE) using an independence working covariance structure (Zeger and Liang 1986) with a robust variance estimate as implemented in the package R/GWAF (Chen and Yang 2010), and 5) a Cochran-Armitage Trend test (Agresti 2002; Purcell et al. 2007), that does not account for familial correlation. Details of the software used to perform the simulations are shown in Table 2. As with quantitative trait analysis, performance of methods for analysis of dichotomous traits in families clustered into two groups, with regression based methods (MQLS and GEE) providing more than double the power of methods examining within-family association (GDT and DFAM) across a range of disease prevalence values. Based on these results, we targeted subsequent simulations for combined analysis of family- and population-based samples on these tests of total association.
We considered application of meta-analysis to combine p-values from a Trend test of population-based samples with analysis of family-based samples by the following approaches: 1) MQLS and 2) GEE, with meta-analysis implemented in METAL (Willer et al. 2010). We also examined pooled analysis of family and population-based samples with: 3) MQLS applied to pooled samples of families and singletons, 4) GEE applied to pooled samples, and 5) a Trend test applied to pooled samples. For each of the simulation replicates, we also performed a Trend Test on the 5,922 singletons alone to provide a reference indicating how much power in the combined analysis is derived from these individuals.
Analysis of Lipid Phenotypes for African Americans in the MESA SHARe Cohort
Genotype data were analyzed for 2,553 African American samples, representing 1,464 population-based samples and 312 distinct families of 2–8 individuals, through the Multi-Ethnic Study of Atherosclerosis (MESA). SNPs were filtered for heterozygosity less than 53% and call rate greater than or equal to 95%. Monomorphic SNPs were removed prior to analysis. Principal components of ancestry were calculated using an LD-thinned subset of the 906,000 SNPs (Supplementary Methods). After examining the Scree-plot for the top 20 principal components, and checking for symmetry in the distribution of loadings for each principal component, we determined that a single principal component of ancestry would provide sufficient adjustment for population stratification in our GWAS of African American samples.
We performed a genome-wide association scan of 844,771 autosomal SNPs with minor allele frequency (MAF) greater than 1%. All analyses were performed using an additive genetic model to assess statistical significance of the effect of each SNP on the outcome of interest. Quantitative trait analysis was carried out for log-transformed HDL cholesterol level (HDL-C), approximately normally distributed after log-transformation. Based on simulation results (power and type I error) and practical considerations (computational speed and ability to incorporate covariates), we applied LME (Chen and Yang 2010), fastAssoc (Chen and Abecasis 2007) and robustAssoc (Chen et al. 2009) for quantitative trait analysis with the MESA African American samples. For comparison, we also performed multiple linear regression, that does not account for familial correlation, as implemented in PLINK (Purcell et al. 2007).
We further performed analysis of a binary trait with prevalence 27.5%, constructed as an indicator of HDL-C 60 mg/dL or higher, a level suggested by the American Heart Association to confer protection against heart disease (American Heart Association 2010). Binary trait analysis was performed using GEE with each family treated as a cluster, using an independence working covariance structure to calculate robust variance estimates, as implemented in the GWAF (Chen and Yang 2010) package. MQLS and logistic regression implemented in PLINK (Purcell et al. 2007) were included for comparison. All analyses of quantitative and binary traits were performed with adjustment for covariates age, gender, study site, and a single principal component of ancestry, with the exception of MQLS which was performed with no covariates due to a practical limitation of the method.
Simulation results
Analysis of quantitative traits in families only
All methods examined for analysis of quantitative traits in pedigrees showed appropriate control of type I error rate, except linear regression for which we observed type I error rates about twice the nominal value at significance level P = 0.01 (Figure 1A) and three times the nominal value at significance level P = 0.001 (Figure 1B). Indeed, we did not expect linear regression to perform well in analysis of pedigree data, but included it as a benchmark because power of this test roughly indicates an upper bound on power under any given simulation scenario.
Figure 1. Comparison of type I error rate and power for quantitative trait analysis, when the minor allele frequency (MAF) is 0.3.
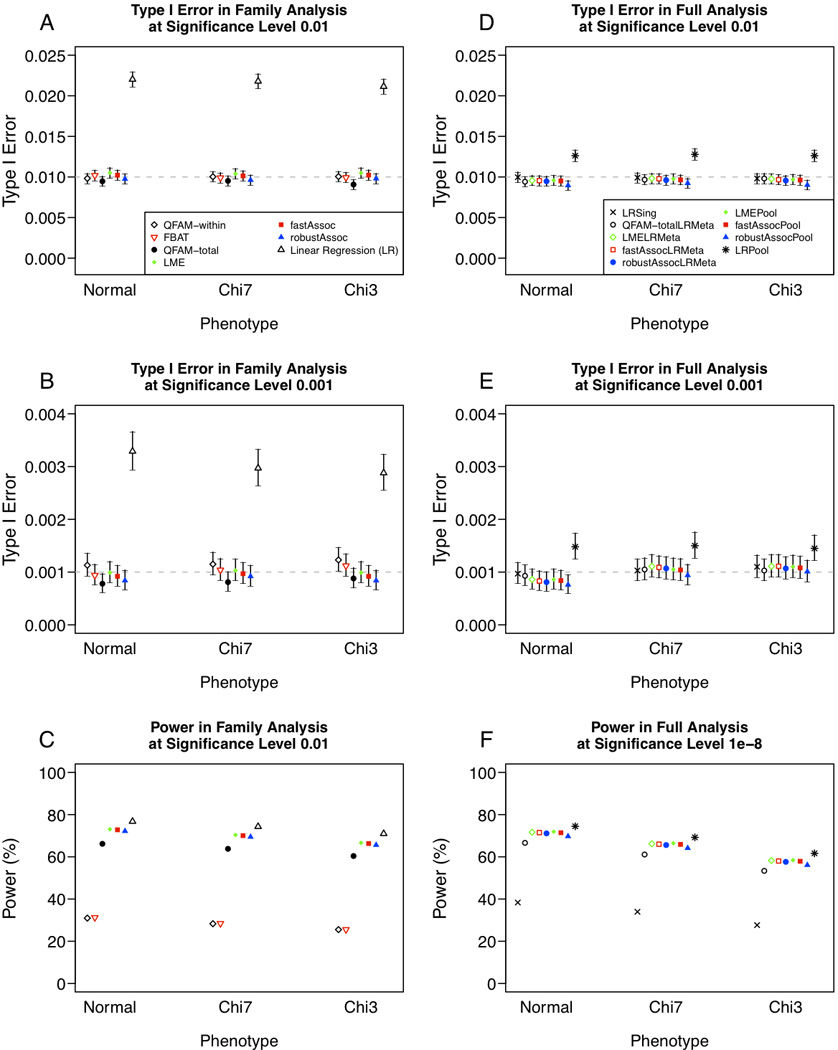
(A) Type I error rate at significance level 0.01, (B) type I error rate at significance level 0.001, and (C) power in quantitative trait analysis of 687 multiplex families. (D) Type I error rate at significance level 0.01, (E) type I error rate at significance level 0.001, and (F) power in quantitative trait analysis 687 multiplex families and 5,922 singletons, with results for analysis of 5,922 singletons alone shown for reference. Uncertainty in point estimates of type I error rates is depicted through 95% confidence intervals constructed by inverting an exact binomial test (Clopper and Pearson 1934).
Power to detect a statistically significant association in families (Figure 1C) differed noticeably across two groups: tests that examine within-family effects (QFAM-within and FBAT) and tests that examine total-association (QFAM-total, fastAssoc and robustAssoc). For a normally distributed phenotype, power at P = 0.01 of the within-family association tests QFAM-within was 31.0% and FBAT was 31.2%. In contrast, the power of the total-association tests, QFAM-total was 66.2%, LME was 73.1%, fastAssoc was 72.8% and robustAssoc was 72.2% at the same level of statistical significance. These differences in power were seen consistently across all trait distributions under consideration. The substantial difference in power across these two classes of tests highlights the fact that these are cohort data in families of modest size; thus, the between-family effects represent a major portion of the total power.
Among the tests of total association, accounting for familial correlation by permutation as in QFAM-total (Purcell et al. 2007) was slightly outperformed by the formal linear mixed effects model (LME) (Chen and Yang 2010) or variance-component model (fastAssoc and robustAssoc) (Chen and Abecasis 2007). The LME and fastAssoc methods showed comparable performance, having power estimates within 0.35% of one another across all trait distributions. LME and fastAssoc performed better than all other methods under consideration, uniformly across all trait distributions simulated, consistently giving 6.5% –7% greater power than QFAM-total. The difference in power between fastAssoc and robustAssoc was more subtle, ranging from 0.6% – 0.76%, and reflects the fact that these two methods were derived using the same underlying regression model (Chen and Abecasis 2007; Chen et al. 2009). Observed power of LME and fastAssoc method falls no more than 4.7% below that of linear regression across all simulated trait distributions, indicating LME and fastAssoc can achieve power comparable to that of linear regression while also maintaining proper control of type I error rates.
All of the methods included in our simulations performed best in the case of a normally distributed phenotype, and power was reduced for more skewed distributions. For each method under consideration, the most skewed trait distribution (chi-square with 3 df) yielded power 5.4% – 6.6% lower than under the “ideal” case of a normally distributed trait.
Analysis of quantitative traits in combined samples
Type I error rates when the nominal rate of statistical significance was P = 0.01 were controlled appropriately for all tests under consideration, except for linear regression applied to pooled samples. In this case, we observed type I error rates of 0.0126 (95% CI 0.0119 – 0.0133) when the phenotypic distribution was normal, 0.0128 (95% CI 0.0121 – 0.0135) when the phenotype distribution was chi-square with 7 df, and 0.0126 (95% CI 0.0119 – 0.0133) when the phenotype distribution was chi-square with 3 df (Figure 1D), with a similar pattern of inflation observed at the level of statistical significance P = 0.001 (Figure 1E). Thus, we observed evidence for inflation of type I error rates using linear regression on pooled samples, although the extent of inflation was modest compared to what we saw in analysis of pedigrees only (Figure 1A).
While analysis of the 5,922 singletons provides a substantial proportion of power to detect genetic association in our simulated samples, inclusion of pedigrees (2,305 individuals across 687 families) contributes considerably to overall power. At P = 10−8, analysis of singletons alone provides 38.4% power (assuming a normally distributed trait) versus 66–72% power when incorporating of families either by meta-analysis or in pooled analysis of singletons and families. Relative performance of methods combined with linear regression on singletons by meta-analysis corresponds directly to performance of the same methods in family analysis. Under a normal model, meta-analysis to combine unrelated individuals with pedigrees by LME (Chen and Yang 2010) and fastAssoc (Chen and Abecasis 2007) has power 71.7% and 71.5%, respectively, higher than the 66.6% power of permutation using QFAM-total (Purcell et al. 2007). This comparison holds true for both skewed trait distributions under consideration. For combined analysis of family and population-based samples, we found pooled analysis using either LME or fastAssoc offered power comparable to that of meta-analysis; power estimates comparing pooled analysis for each of these two methods to meta-analysis by the same method were within 0.25%. Among methods with proper control of type I error rates, we found LME and fastAssoc (using either pooled analysis or meta-analysis) achieved the highest power across all trait distributions under comparison (Figure 1F).
Analysis of dichotomous traits in families only
All methods under consideration provided reasonable control of type I error rates for dichotomous traits, except for the Trend test which assumes independent sampling and is anticonservative when applied to correlated family data (Figure 2A) (Bourgain et al. 2003; Rakovski and Stram 2009; Yang et al. 2007). Inflation of type I error rates increases with disease prevalence for the Trend test. Type I error rates when the nominal level of statistical significance was P = 0.01 were 0.0128 (95% CI 0.0121 – 0.0135) for simulated disease prevalence of 5%, 0.0142 (95% CI 0.0135 – 0.0150) for simulated disease prevalence of 10% and 0.0172 (95% CI 0.0164 – 0.0180) for simulated disease prevalence of 50%. At statistical significance level P = 0.001, we see a similar pattern in which inflation of type I error rates for the Trend test increase with disease prevalence (Figure 2B).
Figure 2. Comparison of type I error rate and power for binary trait analysis, when the minor allele frequency (MAF) is 0.3.
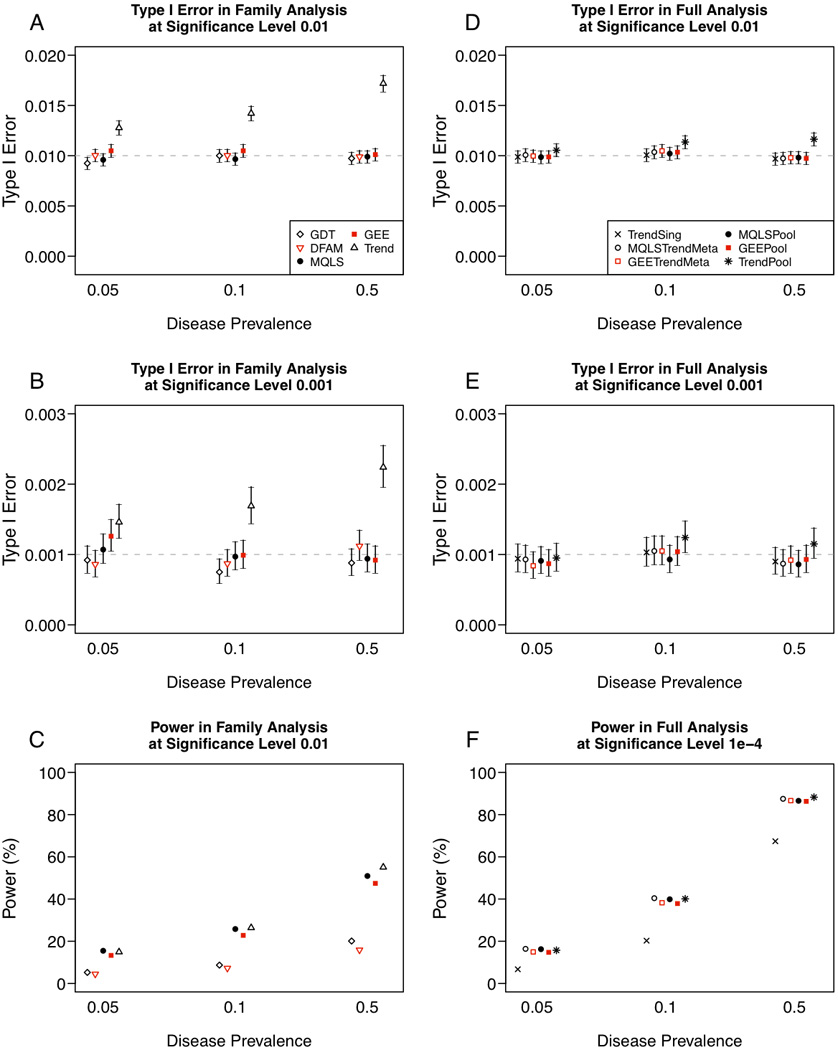
(A) Type I error rate at significance level 0.01, (B) type I error rate at significance level 0.001, and (C) power in binary trait analysis of 687 multiplex families. (D) Type I error rate at significance level 0.01, (E) type I error rate at significance level 0.001, and (F) power in binary trait analysis 687 multiplex families and 5,922 singletons, with results for analysis of 5,922 singletons alone shown for reference. Uncertainty in point estimates of type I error rates is depicted through 95% confidence intervals constructed by inverting an exact binomial test (Clopper and Pearson 1934).
As observed for analysis of quantitative traits, power of the methods under consideration varies greatly across tests that examine within-family association (GDT and DFAM) versus tests that examine total-association (MQLS and GEE), and this effect increases with disease prevalence (Figure 2C). For a rare disease of prevalence 5% and P = 0.01, we observed simulated power of 5.2% for the GDT and 4.5% for the DFAM methods. This compared with power of 15.5% for the MQLS and 13.3% for the GEE methods. For a common disease of prevalence 50%, power is considerably higher – 20.1% for GDT and 15.9% for DFAM as compared to 50.9% for MQLS and 47.4% for GEE. That power increases with disease prevalence for all methods under consideration reflects the cohort-based study design, in which very few cases are sampled for a rare disease. Finally, we note that in all simulated scenarios, power of methods for total-association in families is on par with the Trend test, indicating these methods provide good power while maintaining proper control of type I error rates in the presence of familial correlation.
Analysis of dichotomous traits in combined samples
As we observed for quantitative trait analysis, pooled analysis of all individuals performs very similarly to meta-analysis in terms of type I error (Figures 2D and 2E) and power (Figure 2F). For a rare disease of prevalence 5% at P = 10−4, pooled analysis using MQLS (power of 16.3%) and GEE (power of 14.8%) was only marginally outperformed by meta-analysis to combine a Trend test on singletons with MQLS (power of 16.4%) or GEE (power of 15.0%) on family-based samples. For the higher-powered case of a common disease with prevalence 50%, the observed difference in power seen for pooled versus meta-analysis increased somewhat: pooled analysis by MQLS has 86.5% power compared to 87.5% power by meta-analysis to combine population- and family-based samples. Across the full range of disease prevalence studied, MQLS (either using pooled analysis or meta-analysis) achieves power nearly equivalent to a Trend test on all samples pooled, and slightly higher than GEE. Since GEE and MQLS offer clearer control of type I error rates, we recommend either of these two methods over a Trend test whenever pedigrees are included in the sample.
Extension of simulations to infrequent variants
Current GWAS panels are designed primarily to identify common variants that contribute to genetic variation in phenotypes, but recent GWAS result have found low frequency variants may contribute to human disease (Lachance 2010). The recent advent of next-generation sequencing technologies have also opened opportunities for identification of rare variants (Cirulli and Goldstein 2010). To assess whether methods in our simulation studies could also be applied to analysis of infrequent variants, we extended our simulations to MAF 0.05 and 0.01, keeping all other simulation parameters the same.
For quantitative trait analysis, results for MAF 0.05 and 0.01 (Supplementary Figures 1 and 2) were remarkably similar to those for MAF 0.3 (Figure 1). Notably, observed power was within the same range across all allele frequencies under investigation. However, for MAF 0.05, we did see modest inflation of type I error rates for full analysis of singletons and families, at significance level P = 0.001. Overall, our results suggest methods of quantitative trait analysis appropriate for common variants can be applied for the analysis of infrequent variants.
For binary trait analysis, the observed type I error rates in family analysis at MAF 0.05 and 0.01 indicate the within-family analysis methods, GDT and DFAM, are conservative, while the total-association methods, MQLS and GEE, exhibit inflation of type I error rates (Supplementary Figures 3 and 4). For full analysis of families and unrelated individuals, type I error rates are controlled appropriately for all methods under consideration at MAF 0.05, but type I error rates are seen to be inflated at MAF 0.01, particularly for the lower disease prevalences. The power of all methods of binary trait analysis under consideration is notably reduced for infrequent variants at MAF 0.05 or 0.01, especially in the analysis of diseases at lower prevalences of 0.05 or 0.1. Results for binary trait analysis in the case of infrequent variants of MAF 0.05 or 0.01 indicate rarer variants approaching the level of MAF 0.01 will suffer from inflation of type I error rates, as well as reduced power, particularly in the case of a rare disease. For these reasons, we caution against application of methods for common variants toward analysis of rare and infrequent variants. In real data analysis, it will be appropriate to filter results on some minimum MAF; the appropriate cutoff may depend on the effective sample size as well as the disease prevalence.
Application
To demonstrate a practical application of the presented methods, we performed genome-wide association analysis of two phenotypes (one continuous, one binary) for pooled family- and population-based African American samples from the Multi-Ethnic Study of Atherosclerosis. We processed 2,590 self-reported African-American subjects recruited through MESA and MESAFS. We removed 8 participants with principal components of ancestry more than 10 SD from the mean along the top 6 principal components of ancestry. We also removed 29 participants with missing HDL-C values. We performed pooled analyses of the remaining sample of 2,553 individuals, consisting of 1,464 singletons and 317 pedigrees (pedigrees ranged in size from 2–8 individuals). For samples included in GWAS analysis, 44% of individuals were male, the median age was 60 years (IQR 53–68), and the median value of HDL-C was 50 mg/dl (IQR 42–61). After performing genotype QC, applying filters on call rate > 0.95 and MAF > 0.01, there were 844,771 autosomal SNPs available for analysis.
Table 3 shows results from GWAS analysis of log-transformed HDL-C for all six SNPs with P ≤ 5×10−6 for LME (Chen and Yang 2010), fastAssoc (Chen and Abecasis 2007) or robustAssoc (Chen et al. 2009) quantitative trait analyses, with results from linear regression shown for comparison. In the GWAS, both LME and fastAssoc had appropriate control over false positives, with genomic control (GC) of 1.02 and 1.0, respectively. The three most associated SNPs reaching the suggestive cutoff P ≤ 5×10−6 using robustAssoc were identified at a similar level of statistical significance using fastAssoc. These results validate the recommendation of using fastAssoc as a computationally efficient first-pass analysis, with follow-up using a more computationally intensive approach such as robustAssoc (Chen and Abecasis 2007; Chen et al. 2009). In comparison, analysis using linear regression that does not account for familial correlation had relatively poor control over false positives, with GC=1.11, and inflated statistical significance compared to LME, fastAssoc and robustAssoc. These results highlight the need for linear mixed-effects or variance-component models to take into account familial correlation.
Table 3.
Comparison of top association hits for analysis of a quantitative phenotype for African Americans samples from the Multi-Ethnic Study of Atherosclerosis.
| Chr | SNP | MAF | Gene | Position (bp) |
LME: GC 1.02 |
fastAssoc: GC 1.0 |
robustAssoc: GC 0.95 |
Linear regression: GC 1.11 |
|---|---|---|---|---|---|---|---|---|
| 16 | rs247617 | 0.26 | CETP | 56990716 | 3.7 × 10−15 | 9.0 × 10−15 | 7.4 × 10−15 | 3.2 × 10−15 |
| 10 | rs10826964 | 0.37 | ZEB1 | 31857752 | 7.2 × 10−7 | 2.3 × 10−6 | 2.6 × 10−6 | 6.5 × 10−7 |
| 2 | rs340619 | 0.03 | APOB | 21035081 | 3.6 × 10−6 | 4.5 × 10−6 | 8.5 × 10−5 | 1.8 × 10−6 |
| 10 | rs1314013 | 0.45 | ZEB1 | 31565355 | 3.7 × 10−6 | 5.8 × 10−6 | 6.6 × 10−6 | 2.5 × 10−6 |
| 15 | rs16976466 | 0.29 | PRTG | 55972797 | 4.3 × 10−6 | 5.4 × 10−6 | 5.7 × 10−6 | 1.1 × 10−6 |
| 10 | rs161259 | 0.34 | ZEB1 | 3172158 | 4.5 × 10−6 | 1.4 × 10−5 | 1.4 × 10−5 | 6.8 × 10−6 |
Results are shown for all SNPs with p-value ≤ 5 × 10−6 for LME (Chen and Yang 2010), fastAssoc (Chen and Abecasis 2007) or robustAssoc (Chen et al. 2009) quantitative trait analyses. All quantitative trait analyses were performed with adjustment for covariates age, gender, study site, and a single principal component of ancestry. Minor allele frequency (MAF) is shown for each SNP, and genomic control (GC) numbers are indicated for each test, with no adjustment for GC inflation in the presented association results. SNP annotation was obtained using Human Genome build 37.1 from dbSNP (http://www.ncbi.nlm.nih.gov/projects/SNP/).
Table 3 shows results for sixteen SNPs with P ≤ 5×10−6 by GEE or MQLS in the GWAS binary trait analysis of a dichotomous trait of prevalence 27.5%, with individuals split into two groups according to whether their values of HDL-C were considered protective against heart disease (≥60 mg/dL) (American Heart Association 2010). The most significant gene and SNP (CETP, rs247617) was identical in the quantitative and dichotomous trait analyses, but was less significant in the dichotomous, reflecting the expected loss of power from dichotomizing the quantitative trait. It is somewhat unexpected to see 16 SNPs reaching the suggestive cutoff of P ≤ 5×10−6 in binary trait analysis, compared to only 6 for the quantitative trait analysis. The fact that there is no overlap between continuous and dichotomized trait analysis SNPs other than the CETP SNP probably reflects the fact that dichotomizing the trait at 27.5% prevalence with prevalence-based case-control sampling will relatively increase the power for detection of loci with risk models that are non-additive across the 3 genotypes compared to the continuous outcome. Since the SNPs do not formally meet genome-wide significance (5×10−8), these may be chance findings without biological significance.
Relative to logistic regression with GC=1.07, GEE demonstrates improved GC=1.02, attributed to the more robust model of familial correlation. Although MQLS achieves optimal GC=1.0, GEE maintains an advantage in the ability to incorporate covariate adjustments in the analysis of dichotomized HDL-C, a phenotype that demonstrated statistically significant variation with age (P = 3.3 × 10−4) and gender (P < 2 × 10−16).
Among the most associated SNPs identified by either quantitative or binary trait analysis, SNP rs247617 near the CETP gene represents the strongest association with HDL-C (by fastAssoc, P = 9.0×10−15; by GEE, P = 3.8 × 10−10). This is the only SNP that appears as a significant association from both quantitative trait analysis (fastAssoc) and binary trait analysis (GEE). In confirmation, the CETP gene has been reported previously as a QTL for HDL-C in a large meta-analysis of lipid traits, with one of the largest effect sizes of any QTL reported for HDL-C in that study (Teslovich et al. 2010). Other SNPs reported among those the most associated in MESA are shown in Tables 2 and 3, and do not achieve genome-wide levels of significance (P = 5×10−8). These SNPs, however, may be taken as suggestive findings for future follow-up studies.
Discussion
We performed simulation studies to examine performance of existing methods for genome-wide association analysis for application to cohort GWAS. Although other simulation studies have reported performance of family-based association tests in a variety of scenarios (Chen et al. 2009; Nicodemus et al. 2007), ours is the first comprehensive investigation of methods for cohort GWAS known to us.
In analysis of family data, we found methods that examined total-association substantially outperformed methods that examined within-family association. In analysis of families combined with population samples, analysis of pooled samples performed on par with meta-analysis, in which family and unrelated samples were analyzed separately using the best method for each respective subset. Further, analysis of pooled samples using statistical modeling approaches that account for correlated outcomes (LME, fastAssoc or robustAssoc for quantitative traits, GEE or MQLS for binary traits) provided power on par with linear regression or a Trend test applied to the same data, indicating we can achieve good power while maintaining proper control of type I error rates in analysis of correlated data. A bonus of pooled analysis over meta-analysis is that we can complete analysis of all samples in one step, rather than going through the process of performing separate analyses on subsets of the data prior to combining those results.
Our results highlight the importance of including total-association for analysis of cohort data, clearly distinguishing cohort GWAS from investigations involving ascertained pedigrees. In making the choice to focus analysis on total-association, we forfeit the implicit control over population stratification and confounding factors provided by within-family analysis methods. Because confounding factors will undoubtedly present themselves in cohort studies, it will be the investigator’s responsibility to account for these factors appropriately, either by performing stratified analysis or by including covariate adjustments (Price et al. 2006).
Our simulation studies provide a good overview of method performance using realistic pedigree structures derived from a real cohort GWAS (MESA SHARe). In interpreting our simulation results, it is important to keep in mind the pedigree structures under consideration. Of the MESA families, 85% lack both parents, an expected finding for an aging adult or elderly population where recruitment of parents of index cases may not be possible. Thus our simulated pedigrees represent primarily sibships bearing a relatively simple correlation structure, in which the GEE approach of treating each family as a cluster works well, and there is little need to differentiate between different types of familial relationships. For cohort GWAS that include multi-generational pedigrees and more complex familial relationships, we expect methods such as fastAssoc, robustAssoc or MQLS, that distinguish familial relationships (e.g., parent-offspring, first cousins, or spouse pairs) in the modeled covariance, will perform better than methods that treat all familial relationships uniformly.
The simulation strategy we used here presents a general strategy that can be applied for specific study designs and phenotypic distributions of interest. The time invested in study-specific simulations which condition on pedigree structure may be particularly worthwhile for GWAS performed for well-phenotyped cohorts, in which simulation results can be used to inform analysis of hundreds to thousands of phenotypes under consideration. In performing simulation studies to evaluate performance of methods for genome-wide association studies, there is a practical limitation on the number of simulation replicates performed. Given a reasonable number of simulation replicates (at least 10,000), it is feasible to evaluate type I error rates at a nominal level of statistical significance (P = 0.01). However, in order to assess type I error rates at the level required for genome-wide significance (e.g., P < 10−8), we would need considerably more simulation replicates. Nonetheless, simulation studies are still a practical way of comparing the relative advantages and disadvantages of available tools and methods of analysis. Taken in the context of available theory grounding those methods, simulation results will provide a valuable resource in developing analysis pipelines for existing and emerging GWAS of well-phenotyped cohorts.
One widely used approach that we did not consider explicitly in the present study is the simple genomic control (GC) correction, performed by ignoring family-structure and performing of post-hoc adjustment on the observed test statistic (Bourgain et al. 2003; Rakovski and Stram 2009; Yang et al. 2007). Although we have seen this approach applied as a correction for family structure in some published studies, direct modeling of known familial correlation structure provides a clear advantage in terms of statistical power. This phenomenon is documented in our own study: for both binary and quantitative traits, we obtain power on par with standard methods for population-based samples (Trend test, or Wald test from linear regression) through proper modeling of familial correlation structure. Since methods that account for familial correlation maintain proper control of type I error rates, while the Trend test and linear regression have inflated type I error rates in the presence of familial correlation, it is clear that post-hoc correction of test statistics that do not account for familial correlation will ultimately yield reduced power compared to proper modeling of phenotypic correlation seen in families.
Recently, new approaches such as ROADTRIPS (Thornton and McPeek 2010) and EMMAX (Kang et al. 2010) have been proposed to account for family- and population-structure jointly using genome-wide SNP data to estimate the appropriate covariance matrix. While these approaches are practical for cases of complex and unknown family structure, they are not appropriate for analysis of samples in which family structure is clear and well-documented. Further, it has been demonstrated that methods such as EMMAX (Kang et al. 2010) that incorporate random effects without requiring explicit specification of family- or population-structure perform poorly in the presence of strong population structure (Price et al. 2010). Since the family structure in MESAFS is well-documented, thoroughly checked and validated (Manichaikul et al. 2010), and the MESA samples reflect strong population structure, particularly in African-American and Hispanic samples, we recommend explicit modeling of population structure, using approaches such as principal components of ancestry (Price et al. 2006) included as fixed-effect covariates. Given the importance of population admixture for the analysis of MESA data, it will also be of interest to build on existing simulation studies (Zhu et al. 2008) and extend our current simulation studies to incorporate effects of population admixture.
An important consideration in generalizing our simulation results to practical data analysis methods is the incorporation of covariates. Although our simulations have not treated covariates directly, practical application of the methods presented here will undoubtedly require covariate adjustments. Even in treatment of very basic models, inclusion of covariates will provide the basis for population stratification adjustment, e.g., principal components (Price et al. 2006), and basic covariates such as age, sex and site (a standard adjustment in multi-center studies) will be included routinely in analysis. Further, covariate adjustment opens opportunities for assessing gene-environment interactions systematically. From this point of view, “real” data analysis requires software that can include covariates. Taking this requirement into account, the variance-component models (Chen and Abecasis 2007) for quantitative traits, and generalized estimating equations (Chen and Yang 2010; Zeger and Liang 1986) for dichotomous traits provide the most practical solution for application to real data. Because these linear-modeling based approaches provide effect-size estimates with associated standard errors accounting for familial correlation, their results can also be incorporated directly into meta-analysis when combining multiple studies through joint efforts of genetic consortia (Psaty et al. 2009).
In studies of admixed populations, further considerations will be required to properly account for population structure. For example, in the MESA African-American and Hispanic samples at hand, application of proper methods to account for admixture will be crucial to ensure that reported genetic associations are not an artifact of undetected population structure. Although these considerations have not been a primary focus of the current investigation, we recognize the particular importance of accounting for population structure in GWAS of MESA and other admixed samples. Development of principles for genome-wide association analysis of MESA samples to account for both family and population structure will be the focus of future work.
For practical purposes, efficiently implemented software is crucial, especially as the number of phenotypes under consideration becomes large, for example, for GWAS of gene expression phenotypes. Currently, variance-component regression models (fastAssoc and robustAssoc) are efficiently implemented in C/C++ for quantitative trait analysis of family data using the aforementioned software GDT (Chen et al. 2009), with similar efficiency achieved using the C/C++ packages MERLIN (Abecasis et al. 2002) and ProbABEL (Aulchenko et al. 2010). The linear mixed effects models (LME) are implemented in the R/GWAF package is relatively slower than the C/C++ implementations of comparable variance-component methods (requiring about 20–40 times the computation time, according to our comparison in Supplementary Table 1). However, the increased computing time required to perform LME using R/GWAF can be offset somewhat by running genetic analysis in parallel (Chen and Yang 2010). For binary trait analysis, the R/GWAF (Chen and Yang 2010) package is currently the only software implementation of generalized estimating equations tailors to genome-wide association analysis known to us. Although this package provides a user-friendly interface, and acceptable computing speed, we anticipate that a C/C++ implementation capable of performing similar analysis of binary traits with family data could provide an order-of-magnitude improvement in computational efficiency.
Supplementary Material
Table 4.
Comparison of top association hits for analysis of a dichotomous phenotype for African Americans samples from the Multi-Ethnic Study of Atherosclerosis.
| Chr | SNP | MAF | Gene | Position (bp) |
GEE: GC 1.02 |
MQLS: GC 1.0 |
Logistic: GC 1.07 |
|---|---|---|---|---|---|---|---|
| 16 | rs247617 | 0.26 | CETP | 56990716 | 3.8 × 10−10 | 2.5 × 10−8 | 1.2 × 10−10 |
| 12 | rs10770291 | 0.42 | RERGL | 18108048 | 4.6 × 10−7 | 1.4 × 10−5 | 3.7 × 10−7 |
| 1 | rs12407335 | 0.21 | PRMT6 | 107299585 | 5.5 × 10−7 | 2.2 × 10−6 | 4.4 × 10−7 |
| 1 | rs12409858 | 0.20 | PRMT6 | 107299233 | 1.1 × 10−6 | 4.9 × 10−6 | 9.6 × 10−7 |
| 12 | rs701069 | 0.16 | FLJ37505 | 128026678 | 1.8 × 10−6 | 4.3 × 10−6 | 1.4 × 10−6 |
| 7 | rs6974174 | 0.40 | WIPF3 | 29914469 | 2.5 × 10−6 | 1.4 × 10−5 | 2.7 × 10−6 |
| 1 | rs11184981 | 0.25 | PRMT6 | 107299263 | 3.2 × 10−6 | 1.0 × 10−5 | 2.5 × 10−6 |
| 2 | rs3940409 | 0.43 | PARD3B | 205115659 | 3.4 × 10−6 | 1.5 × 10−5 | 4.3 × 10−6 |
| 7 | rs10251970 | 0.49 | DYNC1I1 | 95596832 | 3.5 × 10−6 | 6.2 × 10−6 | 1.6 × 10−6 |
| 9 | rs2806687 | 0.36 | INVS | 103005815 | 3.7 × 10−6 | 2.8 × 10−6 | 2.6 × 10−6 |
| 10 | rs7086818 | 0.08 | ANKRD30A | 36893908 | 3.7 × 10−6 | 4.4 × 10−5 | 3.1 × 10−6 |
| 12 | rs7971307 | 0.45 | RERGL | 18118930 | 4.2 × 10−6 | 5.9 × 10−5 | 2.7 × 10−6 |
| 10 | rs7096919 | 0.09 | ANKRD30A | 36889214 | 4.6 × 10−6 | 4.2 × 10−5 | 2.8 × 10−6 |
| 9 | rs1529191 | 0.32 | ERP44 | 102845908 | 9.0 × 10−6 | 3.3 × 10−6 | 5.4 × 10−6 |
| 15 | rs10518973 | 0.10 | LIPC | 58651580 | 1.8 × 10−5 | 1.9 × 10−6 | 3.1 × 10−5 |
| 2 | rs13384421 | 0.25 | NMUR1 | 232464308 | 2.0 × 10−5 | 2.2 × 10−6 | 2.7 × 10−5 |
Results are shown for all SNPs with p-value ≤ 5 × 10−6 by GEE or MQLS binary trait analyses, with corresponding results by logistic regression shown for comparison. GEE and logistic regression were performed with adjustment for covariates age, gender, study site, and a single principal component of ancestry, while MQLS was performed with no covariates due to a practical limitation of the method. Minor allele frequency (MAF) is shown for each SNP, and genomic control (GC) numbers are indicated for each test, with no adjustment for GC inflation in the presented association results. SNP annotation was obtained using Human Genome build 37.1 from dbSNP (http://www.ncbi.nlm.nih.gov/projects/SNP/).
Acknowledgments
MESA and the MESA SHARe project are conducted and supported by contracts N01-HC-95159 through N01-HC-95169 and RR-024156 from the National Heart, Lung, and Blood Institute (NHLBI). Funding for MESA SHARe genotyping was provided by NHLBI Contract N02-HL-6-4278. MESA Family is conducted and supported in collaboration with MESA investigators; support is provided by grants and contracts R01HL071051, R01HL071205, R01HL071250, R01HL071251, R01HL071252, R01HL071258, R01HL071259. The authors thank the participants of the MESA study, the Coordinating Center, MESA investigators, and study staff for their valuable contributions. A full list of participating MESA investigators and institutions can be found at http://www.mesa-nhlbi.org.
References
- Abecasis GR, Cardon LR, Cookson WO. A general test of association for quantitative traits in nuclear families. Am J Hum Genet. 2000;66:279–292. doi: 10.1086/302698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abecasis GR, Cherny SS, Cookson WO, Cardon LR. Merlin--rapid analysis of dense genetic maps using sparse gene flow trees. Nat Genet. 2002;30:97–101. doi: 10.1038/ng786. [DOI] [PubMed] [Google Scholar]
- Agresti A. Categorical data analysis. 2nd edn. New York: Wiley-Interscience; 2002. [Google Scholar]
- American Heart Association. What Your Cholesterol Levels Mean. What Your Levels Mean. 2010;vol 2011 http://www.americanheart.org/presenter.jhtml?identifier=183) [Google Scholar]
- Aulchenko YS, Struchalin MV, van Duijn CM. ProbABEL package for genome-wide association analysis of imputed data. BMC Bioinformatics. 2010;11:134. doi: 10.1186/1471-2105-11-134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bild DE, Bluemke DA, Burke GL, Detrano R, Diez Roux AV, Folsom AR, Greenland P, Jacob DR, Jr, Kronmal R, Liu K, Nelson JC, O'Leary D, Saad MF, Shea S, Szklo M, Tracy RP. Multi-ethnic study of atherosclerosis: objectives and design. Am J Epidemiol. 2002;156:871–881. doi: 10.1093/aje/kwf113. [DOI] [PubMed] [Google Scholar]
- Bourgain C, Hoffjan S, Nicolae R, Newman D, Steiner L, Walker K, Reynolds R, Ober C, McPeek MS. Novel case-control test in a founder population identifies P-selectin as an atopy-susceptibility locus. Am J Hum Genet. 2003;73:612–626. doi: 10.1086/378208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen MH, Yang Q. GWAF: an R package for genome-wide association analyses with family data. Bioinformatics. 2010;26:580–581. doi: 10.1093/bioinformatics/btp710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen WM, Abecasis GR. Family-based association tests for genomewide association scans. Am J Hum Genet. 2007;81:913–926. doi: 10.1086/521580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen WM, Manichaikul A, Rich SS. A generalized family-based association test for dichotomous traits. Am J Hum Genet. 2009;85:364–376. doi: 10.1016/j.ajhg.2009.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cirulli ET, Goldstein DB. Uncovering the roles of rare variants in common disease through whole-genome sequencing. Nat Rev Genet. 2010;11:415–425. doi: 10.1038/nrg2779. [DOI] [PubMed] [Google Scholar]
- Clopper C, Pearson E. The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika. 1934;26:404. [Google Scholar]
- Fulker DW, Cherny SS, Sham PC, Hewitt JK. Combined linkage and association sib-pair analysis for quantitative traits. Am J Hum Genet. 1999;64:259–267. doi: 10.1086/302193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang HM, Sul JH, Service SK, Zaitlen NA, Kong SY, Freimer NB, Sabatti C, Eskin E. Variance component model to account for sample structure in genome-wide association studies. Nat Genet. 2010;42:348–354. doi: 10.1038/ng.548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lachance J. Disease-associated alleles in genome-wide association studies are enriched for derived low frequency alleles relative to HapMap and neutral expectations. BMC Med Genomics. 2010;3:57. doi: 10.1186/1755-8794-3-57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird NM, Horvath S, Xu X. Implementing a unified approach to family-based tests of association. Genet Epidemiol. 2000;19(Suppl 1):S36–S42. doi: 10.1002/1098-2272(2000)19:1+<::AID-GEPI6>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- Manichaikul A, Mychaleckyj JC, Rich SS, Daly K, Sale M, Chen WM. Robust relationship inference in genome-wide association studies. Bioinformatics. 2010;26:2867–2873. doi: 10.1093/bioinformatics/btq559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio TA. Cohort studies and the genetics of complex disease. Nat Genet. 2009;41:5–6. doi: 10.1038/ng0109-5. [DOI] [PubMed] [Google Scholar]
- Nicodemus KK, Luna A, Shugart YY. An evaluation of power and type I error of single-nucleotide polymorphism transmission/disequilibrium-based statistical methods under different family structures, missing parental data, and population stratification. Am J Hum Genet. 2007;80:178–185. doi: 10.1086/510498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Price AL, Zaitlen NA, Reich D, Patterson N. New approaches to population stratification in genome-wide association studies. Nat Rev Genet. 2010;11:459–463. doi: 10.1038/nrg2813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Psaty BM, O'Donnell CJ, Gudnason V, Lunetta KL, Folsom AR, Rotter JI, Uitterlinden AG, Harris TB, Witteman JC, Boerwinkle E. Cohorts for Heart and Aging Research in Genomic Epidemiology (CHARGE) Consortium: Design of prospective meta-analyses of genome-wide association studies from 5 cohorts. Circ Cardiovasc Genet. 2009;2:73–80. doi: 10.1161/CIRCGENETICS.108.829747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, de Bakker PI, Daly MJ, Sham PC. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rakovski CS, Stram DO. A kinship-based modification of the armitage trend test to address hidden population structure and small differential genotyping errors. PLoS One. 2009;4:e5825. doi: 10.1371/journal.pone.0005825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teslovich TM, Musunuru K, Smith AV, Edmondson AC, Stylianou IM, Koseki M, Pirruccello JP, Ripatti S, Chasman DI, Willer CJ, Johansen CT, Fouchier SW, Isaacs A, Peloso GM, Barbalic M, Ricketts SL, Bis JC, Aulchenko YS, Thorleifsson G, Feitosa MF, Chambers J, Orho-Melander M, Melander O, Johnson T, Li X, Guo X, Li M, Shin Cho Y, Jin Go M, Jin Kim Y, Lee JY, Park T, Kim K, Sim X, Twee-Hee Ong R, Croteau-Chonka DC, Lange LA, Smith JD, Song K, Hua Zhao J, Yuan X, Luan J, Lamina C, Ziegler A, Zhang W, Zee RY, Wright AF, Witteman JC, Wilson JF, Willemsen G, Wichmann HE, Whitfield JB, Waterworth DM, Wareham NJ, Waeber G, Vollenweider P, Voight BF, Vitart V, Uitterlinden AG, Uda M, Tuomilehto J, Thompson JR, Tanaka T, Surakka I, Stringham HM, Spector TD, Soranzo N, Smit JH, Sinisalo J, Silander K, Sijbrands EJ, Scuteri A, Scott J, Schlessinger D, Sanna S, Salomaa V, Saharinen J, Sabatti C, Ruokonen A, Rudan I, Rose LM, Roberts R, Rieder M, Psaty BM, Pramstaller PP, Pichler I, Perola M, Penninx BW, Pedersen NL, Pattaro C, Parker AN, Pare G, Oostra BA, O'Donnell CJ, Nieminen MS, Nickerson DA, Montgomery GW, Meitinger T, McPherson R, McCarthy MI, et al. Biological, clinical and population relevance of 95 loci for blood lipids. Nature. 2010;466:707–713. doi: 10.1038/nature09270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton T, McPeek MS. Case-control association testing with related individuals: a more powerful quasi-likelihood score test. Am J Hum Genet. 2007;81:321–337. doi: 10.1086/519497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton T, McPeek MS. ROADTRIPS: case-control association testing with partially or completely unknown population and pedigree structure. Am J Hum Genet. 2010;86:172–184. doi: 10.1016/j.ajhg.2010.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willer CJ, Li Y, Abecasis GR. METAL: fast and efficient meta-analysis of genomewide association scans. Bioinformatics. 2010;26:2190–2191. doi: 10.1093/bioinformatics/btq340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y, Remmers E, Ogunwole C, Kastner D, Gregersen P, Li W. Effective sample size: Quick estimation of the effect of related samples in genetic case-control association analyses. 2007 doi: 10.1016/j.compbiolchem.2010.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeger SL, Liang KY. Longitudinal data analysis for discrete and continuous outcomes. Biometrics. 1986;42:121–130. [PubMed] [Google Scholar]
- Zhu X, Li S, Cooper RS, Elston RC. A unified association analysis approach for family and unrelated samples correcting for stratification. Am J Hum Genet. 2008;82:352–365. doi: 10.1016/j.ajhg.2007.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


