A Simple Method for Quantifying Functional Selectivity and Agonist Bias

Abstract

Activation of seven-transmembrane (7TM) receptors by agonists does not always lead to uniform activation of all signaling pathways mediated by a given receptor. Relative to other ligands, many agonists are “biased” toward producing subsets of receptor behaviors. A hallmark of such “functional selectivity” is cell type dependence; this poses a particular problem for the profiling of agonists in whole cell test systems removed from the therapeutic one(s). Such response-specific cell-based variability makes it difficult to guide medicinal chemistry efforts aimed at identifying and optimizing therapeutically meaningful agonist bias. For this reason, we present a scale, based on the Black and Leff operational model, that contains the key elements required to describe 7TM agonism, namely, affinity (K_A^–1) for the receptor and efficacy (τ) in activating a particular signaling pathway. Utilizing a “transduction coefficient” term, log(τ/K_A), this scale can statistically evaluate selective agonist effects in a manner that can theoretically inform structure–activity studies and/or drug candidate selection matrices. The bias of four chemokines for CCR5-mediated inositol phosphate production versus internalization is quantified to illustrate the practical application of this method. The independence of this method with respect to receptor density and the calculation of statistical estimates of confidence of differences are specifically discussed.

It has long been acknowledged that the absolute potency of a seven-transmembrane (7TM) receptor agonist is as much dependent on the properties of the biological assay system that is utilized to determine agonist activity as it is on the molecular properties of “affinity” and “intrinsic efficacy” that are operative at the level of the target receptor itself.^1,2 This is a major reason why potency ratios between a group of agonists have been traditionally preferred over absolute potencies when assessing novel agonist structure–activity relationships (SAR); according to classic receptor theory, agonist relative potency ratios should be independent of the influence of receptor density and stimulus–response coupling.³ In contrast to predictions of classical receptor theory, however, response and cell-dependent variations in agonist potency ratios have been increasingly noted for more than 20 years.⁴⁻⁷ In fact, there is a large body of compelling evidence that shows that not all agonists produce uniform activation of 7TM receptors; this phenomenon, commonly termed “functional selectivity” or “biased agonism” (for reviews, see refs (8−14)), causes ligands to have many potential efficacies (“pluridimensional” efficacy¹⁵). One of the main features of functional selectivity is variation in agonist potency ratios with different cellular responses;^16,17 this can lead to problems in characterizing new agonist activity in test systems for predictions of activity in other cell types (e.g., therapeutic systems).

An early discussion of functional selectivity, at that time termed “stimulus trafficking”,¹⁸ proposed that the mechanism underlying the phenomenon is one of agonist stabilization of different receptor active state conformations, with the result being that these unique conformations differentially activate cellular signaling mechanisms in a manner that cannot be explained simply by differences in stimulus–response coupling. This model leads to the conclusion that cytosolic signaling molecules that directly interact with the active receptor conformation are the discerning species linking the agonist chemical structure with the observed phenotypic cellular signaling profile. Under these circumstances, signaling molecules can function as interrogating “probes” of the receptor conformation. Thus, an ideal analytical approach for quantifying agonist bias is one that incorporates elements of ligand binding to the receptor and the ligand-bound receptor subsequently binding to a signaling protein. These properties are present in the “operational model” of Black and Leff,¹⁹ which explicitly describes agonist function in terms of two hyperbolic processes, the ligand–receptor interaction and the subsequent receptor–signal transduction cascade. A distinct advantage of the model is that it can also be applied directly to functional concentration–response data using routine nonlinear regression programs. Our study describes the application of the Black–Leff operational model to furnish a quantitative scale of agonist bias that may prove to be useful in facilitating structure–activity relationships and optimization of agonist phenotypic profiles. A key advantage of this method is that it can furnish a stable internally consistent quantitative numerical scale, amenable to statistical analysis, for chemists to gauge ligand bias and functional selectivity. It is envisaged that the determination of “bias factors” using this approach can also contribute to the optimal design of drug candidate selection matrices if biased agonism is a therapeutically desired outcome.

Results and Discussion

Theoretical Model for Fitting Data

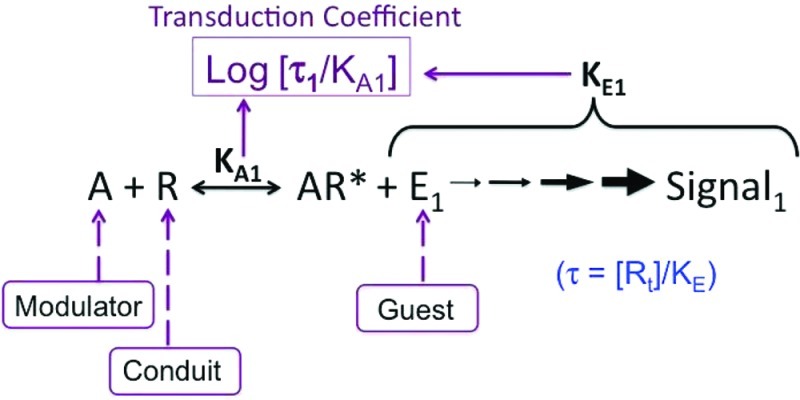
7TM receptor agonism can be defined as an allosteric system¹⁰ comprised of a modulator (agonist), operating on a protein conduit (receptor) to a protein guest (signaling molecule), as shown in Figure 1. Cytosolic signaling proteins such as G proteins or β-arrestin are known to affect the affinity of ligands for receptors.¹⁷⁻²⁰ Under these circumstances, receptor-mediated cellular signaling changes caused by agonists must be described both by affinity for the agonist and its efficacy. In the Black–Leff operational model, the former property is quantified by the agonist equilibrium dissociation constant (K_A) whereas the latter is determined by both the receptor density, [R_t], and the parameter K_E, which denotes the intensity of the reaction (intrinsic efficacy of the agonist in activating a particular cellular response pathway) and the ability of the system to convert a receptor stimulus into a response. By taking the ratio [R_t]/K_E, we obtain a single parameter, denoted τ, that operationally describes an agonist’s efficacy. The extension of this model to the quantification of functional selectivity simply requires the additional assumption that ligand bias is characterized by different affinities and/or different intrinsic efficacies for different receptor active states, i.e., different K_A and/or different K_E (and, hence, τ) values.

Figure 1.

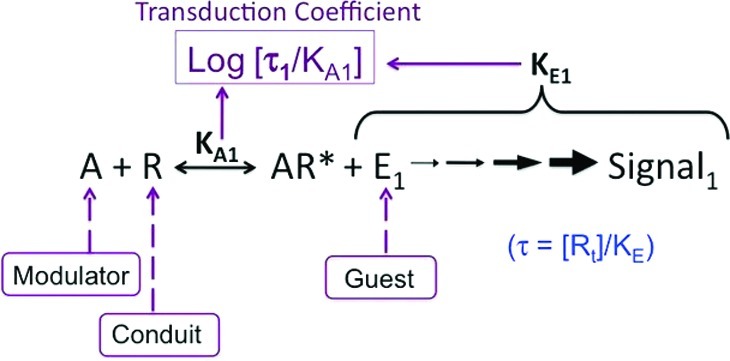
Schematic diagram showing the relevance of the Black–Leff operational model to quantification of agonist bias. The premise is based on the fact that the receptor conformation stabilized by the agonist will have a unique interaction with all signaling proteins that directly interact with it, thereby setting up the allosteric system(s) of modulator (agonist)/conduit (receptor)/guest (signaling protein). Under these circumstances, the affinity and the efficacy (the “quality” of the conformation) will be determined by the signaling protein, and this will be unique for each pathway. The magnitude of log(τ/K_A) will be characteristic of both the affinity and efficacy of the agonist for a particular pathway.

The common form of the equation used for fitting the Black–Leff operational model to concentration–response curves of functional data describing receptor activation relates agonist concentration ([A]) to response as follows:

1

where the maximal response of the system is given by E_m, while n is the “transducer slope” for the function linking agonist concentration to measured response; this is not the same as the Hill slope that is commonly used to describe the midpoint gradient derived from logistic curve fitting of concentration–response data, but the two parameters are related.²⁰ In essence, the Black–Leff model treats the agonist-bound receptor as a “substrate”, the entire cell as a “virtual” enzyme, and the parameters K_A and K_E (and τ) as the equilibrium constants governing the “reaction”. The parameters E_m and n are cell-specific and thus shared by all agonists acting on a common receptor through a given pathway, whereas K_A is ligand receptor-specific. The parameter τ is both ligand- and pathway-specific. Therefore, any parameter that seeks to quantify agonism in such an allosteric system should include both of these latter two.

Fitting of functional data to eq 1 theoretically could characterize agonism through some combination of K_A and τ. Accordingly, a parameter for characterizing agonism for any given pathway defined by an agonist interacting with a receptor (which interacts directly with a cytosolic signaling protein) can be defined as a “transduction coefficient”, log(τ/K_A) (see Figure 1). The relative efficiency of agonists producing activation of any pathway can thus be quantified with a “normalized” transduction coefficient, namely Δlog(τ/K_A). This takes into account the natural bias of the system, in that no two signaling pathways in the cell can be assumed to be coupled to receptors with equal efficiency. Finally, to determine the actual ligand “bias” of agonists for different signaling pathways, it is necessary to statistically evaluate differences between Δlog(τ/K_A) values for a given agonist between the pathways. The ligand bias [ΔΔlog(τ/K_A) or log bias] for any one pathway, j₁, over another, j₂, is given as

2

where

3

Effect of Receptor Density on Log(τ/K_A) Values

A usable scale of agonism needs to be dependent only on the intrinsic efficacy of the agonist (the component of K_E unique to the agonist chemical structure) and K_A, and not dependent upon receptor density and/or the tissue component of K_E. In this regard, it is worth comparing the log(τ/K_A) scale to other measures of agonist sensitivity in terms of the variation in membrane receptor density.

The pEC₅₀, i.e., the negative logarithm of the agonist concentration producing the half-maximal response, is arguably the most commonly used measure of agonist sensitivity. As shown by Black et al.,²⁰ the pEC₅₀ of an agonist in terms of the operational model is given by

4

Another useful measure of agonist activity is Ehlert’s “activity ratio” (denoted RA), which is given by the maximal response of the agonist (E_max) divided by the EC₅₀.²¹⁻²³ The log(RA) value for an agonist in terms of the Black–Leff operational model is given by

5

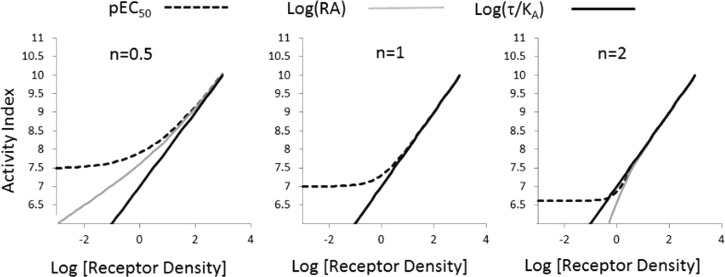
Figure 2 shows the effect of changing receptor density (as a surrogate for comparing different tissues) on log(τ/K_A), pEC₅₀, and log(RA) values. It can be seen that log(τ/K_A) values are linear with changing receptor density for any value of transducer slope coefficient. In contrast, and as reported previously by Ehlert,²¹ log(RA) is linear when n = 1 but not when n ≠ 1; pEC₅₀ values are nonlinear with changing receptor density irrespective of the transducer slope. This becomes important when these scales are used to compare two agonists. It is imperative that a useful scale for quantifying agonism be constant over a range of receptor densities because it would be used to compare different cell types.

Figure 2.

Activity scales for agonists as a function of receptor density (e.g., different cell lines). Activities shown are log(τ/K_A) (solid black line), pEC₅₀ (dotted line), and log(RA) (gray line) for different agonist concentration–response curve transducer slope coefficients. Curvature in these relationships indicates variation in index with changes in receptor density as simulated by changes in τ, where τ = [R_t]/K_E, with K_E being constant.

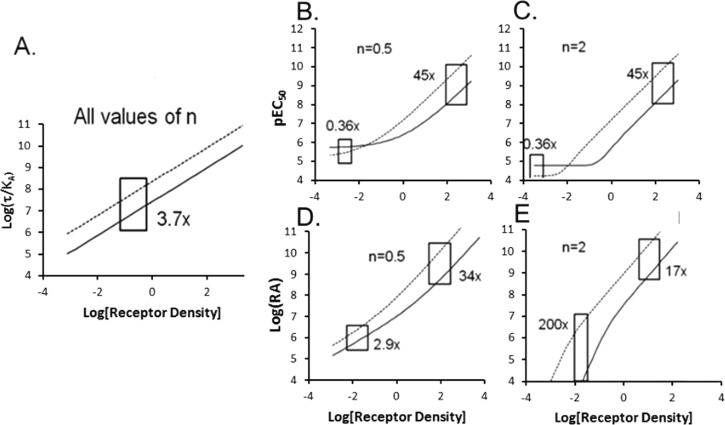
Figure 3 shows the behavior of log(τ/K_A), pEC₅₀, and log(RA) for two agonists with changing receptor density at different transducer slope coefficients. The key premise of this paper is that the ratio of multiple indices of agonist activity [i.e., Δlog(τ/K_A), ΔpEC₅₀, or Δlog(RA)] needs to be constant over a range of receptor densities to be of use in comparing relative agonism in different tissues. As shown in Figure 3A, this is the case for Δlog(τ/K_A), where the distance between the lines for the two agonists represents this ratio, and this remains constant at any receptor density. It can be shown that when n = 1, RA reduces to (τ/K_A) (see eq 5); therefore; log(RA) also is insensitive to differences in receptor density when n = 1. In contrast, it can be seen that for transducer slope coefficients of ≠1, ΔpEC₅₀ values (Figure 3B,C) and Δlog(RA) values (Figure 3D,E) vary with changes in receptor density.

Figure 3.

Relative agonist activity as a function of changing receptor density. Values of log(τ/K_A), pEC₅₀, and log(RA) for two agonists (one designated with a solid line and the other with a dotted line) were calculated for a range of τ values. (A) Because values of log(τ/K_A) do not change with receptor density, the ratio Δlog(τ/K_A) remains constant over all ranges of receptor density. (B and C) The pEC₅₀ values change with receptor density for transducer slope coefficients of ≠1, leading to variance and reversal of ΔpEC₅₀ values with receptor density (or changes in receptor coupling efficiency, K_E). (D and E) Values of log(RA) change with τ values for slope coefficients of ≠1, leading to differences in the value of Δlog(RA) with varying receptor density as simulated by changes in τ.

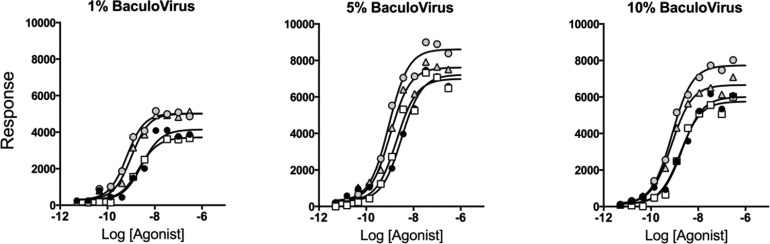
The possible dependence of Δlog(τ/K_A) values with changing receptor density was explored experimentally in a recombinant CHO cell system whereby varying levels of CCR5 receptor density could be transduced through varying levels of exposure to BacMam virus for the receptor.²⁴ The concentration–response curves for four chemokines in recombinant CHO cell systems exposed to increasing levels of BacMam virus for CCR5 expression are shown in Figure 4, and the resulting log(τ/K_A) values are listed in Table 1. The reference chemokine agonist for these calculations was chosen to be CCL3 (it should be noted that the actual agonist chosen as the reference is immaterial with respect to the conclusions drawn from the analysis). With CCL3 as the reference agonist, the Δlog(τ/K_A) values for the various levels of CCR5 expression are also listed in Table 1. There was no statistically significant difference between Δlog(τ/K_A) values in the different systems, in agreement with the predictions shown in Figure 3A, as determined by the fact that no mean value exceeds the 95% confidence interval of any other value.

Figure 4.

Production of IP1 via activation of CCR5 receptors with CCL3L1 (gray filled circles), CCL5 (gray filled triangles), CCL3 (●), and CCL4 (□) in CHO cells expressing different levels of CCR5 as controlled by exposure to BaculoVirus concentrations. Data points represent means of three experiments with curves fit to the operational model to mean data points.

Table 1. Log(τ/K_A) and ΔLog(τ/K_A) Values for Chemokine Agonists at Different Levels of CCR5 Receptor Transduction.

	mean log(τ/KA) value			Δlog(τ/KA) valuea
	10% baculovirus	5% baculovirus	1% baculovirus	10% baculovirus	5% baculovirus	1% baculovirus
CCL3L1	9.09, 9.28 to 8.9	9.14, 9.34 to 8.94	8.9, 9.15 to 0.34	0.62, 0.9 to 0.34	0.69, 0.9 to 0.34	0.73, 1.07 to 0.38
CCL5	9.0, 9.22 to 8.8	8.97, 9.16 to 8.77	8.7, 8.95 to 8.4	0.56, 0.84 to 0.28	0.52, 0.79 to 0.24	0.54, 0.89 to 0.2
CCL3	8.46, 8.66 to 8.27	8.45, 8.65 to 8.25	8.15, 8.4 to 7.9	0	0	0
CCL4	9.0, 9.2 to 8.8	8.8, 9.0 to 8.6	8.75, 9.0 to 8.5	0.55, 0.83 to 0.27	0.34, 0.64 to 0.04	0.6, 0.94 to 0.25

^aThe reference agonist was CCL3.

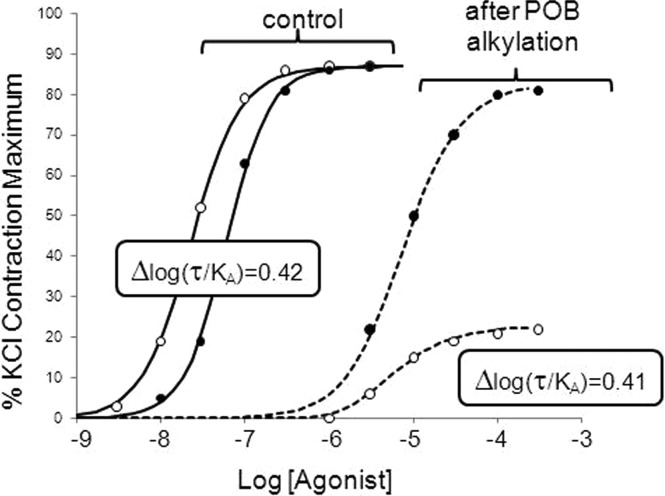
The optimal test for the dependence on receptor number would be calculation of log(τ/K_A) over a wide range of receptor densities; as seen in Table 1, baculovirus expression caused an only 2–3-fold difference in log(τ/K_A) values, indicating that an only 2–3-fold difference in receptor expression was produced by the procedure. To obtain a wider range of alterations of receptor density, we performed additional studies on a different system, namely the native muscarinic receptors expressed in guinea pig ileum, where receptor density was manipulated through irreversible alkylation of the muscarinic receptors by the β-haloalkylamine phenoxybenzamine. Figure 5 shows concentration–response curves for isotonic contraction of guinea pig ileal smooth muscle through activation of muscarinic receptors by carbachol or oxotremorine. It can be seen from the figure that oxotremorine is 2-fold more potent as a full agonist than carbachol in this assay. After a controlled alkylation of muscarinic receptors through a 10 min exposure to 10 μM phenoxybenzamine followed by a 2 h wash period, the concentration–response curves for both agonists were considerably shifted to the right with depressed maxima. In accordance with the effects of decreasing system sensitivity on high-affinity, low-efficacy agonists, the maximal response to oxotremorine was depressed to a greater extent than that for the higher-efficacy agonist carbachol. The Black–Leff model parameters describing these curves are listed in Table 2, where it can be seen that the alkylation of receptors reduced the system sensitivity by a factor of 152; i.e., the receptor number was decreased to 0.6% of that of the control. The Δlog(τ/K_A) values changed very little from the control conditions to the lower-sensitivity system (from 0.42 to 0.41), demonstrating the stability of Δlog(τ/K_A) values with the changing receptor density.

Figure 5.

Guinea pig ileal smooth muscle contraction due to activation of muscarinic receptors with carbachol (●) and oxotremorine (○). Control curves show responses in normal tissue, and dashed curves are curves in the same tissue after controlled alkylation of the muscarinic receptor with 1 μM phenoxybenzamine (POB) for 10 min followed by a 2 h drug free wash. Values in boxes refer to log(τ/K_A) values for control curves and curves after the reduction in receptor density. Data points represent single curves in one tissue fit to the operational model.

Table 2. Descriptors of Muscarinic Receptor Agonism in Guinea Pig Ileum for Carbachol and Oxotremorine^a.

agonist	τ	pKa	log(τ/KA)	Δlog(τ/KA)
Control
carbarchol	1500	4.04	7.22	0.42
oxotremorine	120	5.56	7.64
After Alkylation
carbarchol	11	4.09	5.14	0.41
oxotremorine	0.71	5.69	5.55

^aE_m, the maximal response of the tissue, was obtained by measuring the contraction of complete depolarization of guinea pig ileal strips to KCl.

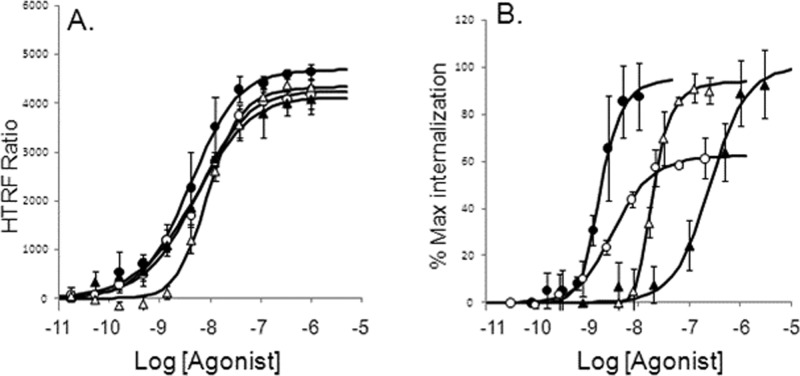
IP1 versus CCR5 Internalization in U373 Cells: Determination of Ligand Bias Factors

Concentration–response curves for CCL3L1, CCL5, CCL3, and CCL4 were obtained in U373-MAGI-CCR5-E cells for IP1 responses (Figure 6A) and CCR5 internalization (Figure 6B); it can be seen from these figures that the relative potencies of the agonists differed considerably for these two CCR5-mediated responses. As shown in Table 3, all four agonists were essentially equiactive for the IP1 response pathway [as denoted by the non-statistically significant differences in Δlog(τ/K_A)] but did differ in their ability to cause internalization. For this pathway, CCL3L1, CCL5, and CCL4 are all statistically more efficacious than CCL3 [see the Δlog(τ/K_A) values in Table 3].

Figure 6.

Concentration–response curves for chemokine activation of the CCR5 receptor in U373 cells for production of IP1 (A) and internalization of CCR5 (B). Curves shown for CCL3L1 (●), CCL5 (○), CCL3 (▲), and CCL4 (△). Data points represent the mean ± standard error of the mean of five experiments for IP1 and three experiments for internalization. Curves fitted through the points represent the operational model.

Table 3. Data Describing Bias of Chemokine Agonists for CCR5 Activation To Generate IP1 and CCR5 Receptor Internalization.

agonist	mean log(τ/KA)	Δlog(τ/KA)a	ΔΔlog(τ/KA)	bias
IP1-U373
CCL3L1	8.37, 8.69 to 8.05	0.2, 0.66 to −0.26	1.38, 2.12 to 0.63	23.7, 132 to 4.2
CCL5	8.17, 8.49 to 7.84	–0.0013, 0.46 to −0.46	1.32, 2.07 to 0.57	21, 117 to 3.7
CCL3	8.17, 8.49 to 7.84	0	0	1
CCL4	8.14 8.46 to 7.82	–0.03, 0.42 to −0.49	0.89, 1.64 to 0.14	7.8, 43 to 1.4
U373 Internalization
CCL3L1	8.79, 9.2 to 8.36	1.58, 2.17 to 0.98
CCL5	8.53, 8.94 to 8.11	1.32, 1.9 to 0.73
CCL3	7.2, 7.6 to 6.79	0
CCL4	8.07, 8.49 to 7.65	0.86, 1.45 to 0.27

^aThe reference agonist was CCL3.

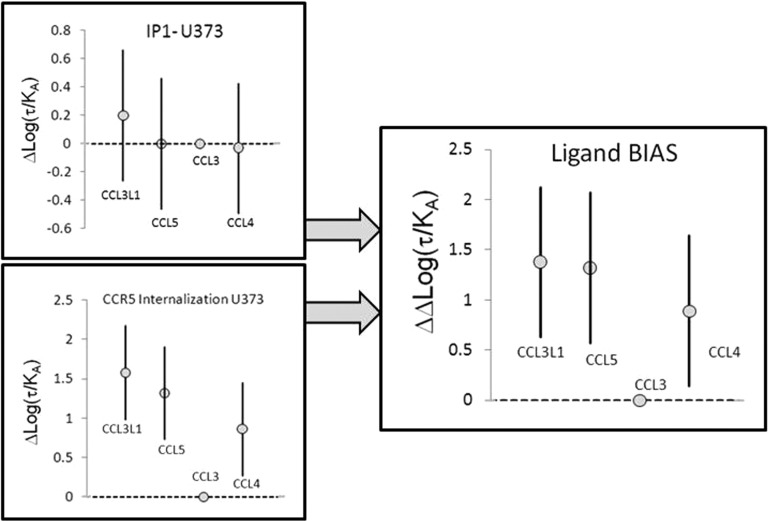
To determine the actual ligand bias of these agonists for internalization versus the IP1 pathway, it is necessary to statistically evaluate differences between Δlog(τ/K_A) values for each agonist between pathways, as calculated using eqs 2 and 3. For these pathways in U373-MAGI-CCR5-E cells, ΔΔlog(τ/K_A) values for internalization versus IP1 indicate statistically significant bias with CCL4, CCL5, and CCL3L1 toward internalization by factors of 7.8, 21, and 23.7, respectively (see Table 3). The statistical significance of these differences is indicated by the 95% confidence limits of ΔΔlog(τ/K_A) that do not contain zero (the normalized value of the reference agonist, CCL3). Figure 7 shows the graphical expression of Δlog(τ/K_A) and ΔΔlog(τ/K_A) values and their 95% confidence intervals. This gives a visual representation of statistical significance in that if a mean value lies outside of the 95% confidence interval of any other value, it is statistically significantly different from that value. It can be seen from Figure 7 that for IP1, all agonists are equivalent whereas for CCR5 internalization, CCL3L1, CCL5, and CCL4 are more active in producing internalization than CCL3 is. This translates into these three agonists also being biased toward CCR5 internalization when compared to IP1 production (see Figure 7).

Figure 7.

Graphical representations of mean values of Δlog(τ/K_A) for IP1 production and CCR5 internalization with 95% confidence intervals. These panels show that the potencies of these agonists are not statistically significantly different for IP1 production but that CCL3L1, CCL5, and CCL4 are significantly more active for producing CCR5 internalization than CCL3. The right panel shows ΔΔlog(τ/K_A) values that offset the effects of system bias and compares the relative effects of the agonists on the two responses to a common reference agonist, namely CCL3. It can be seen that CCL3L1, CCL5, and CCL4 are biased at the 95% confidence level for internalization vs IP1 production in U373 cells. Bars represent 95% confidence intervals.

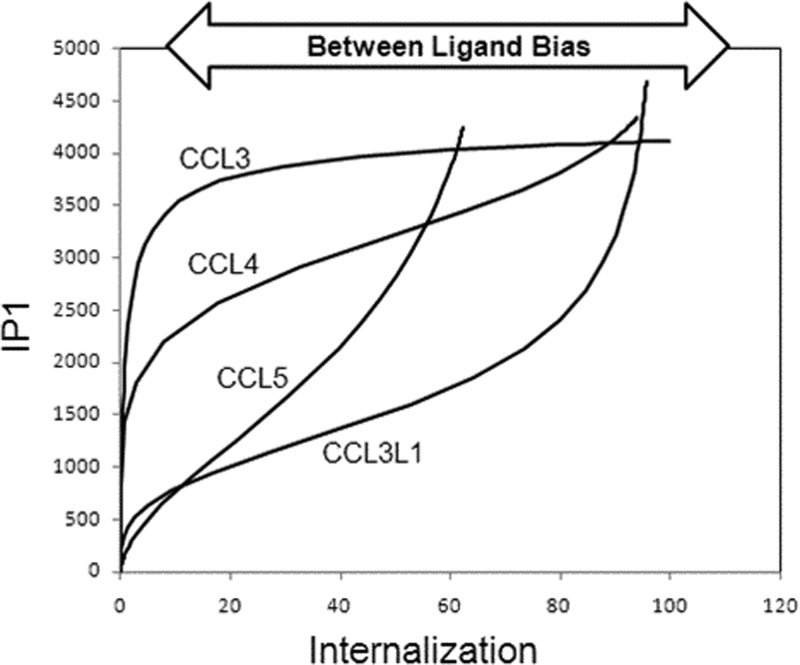
It is also useful to view the ligand bias for these agonists in a bias plot^14,25 that expresses the response in one pathway as a function of the response in the other pathway for equal concentrations of agonist (see Figure 8). This plot incorporates both system bias (it is unlikely that any two stimulus–response pathways in any cell will be coupled with equal efficiency) and any possible internal ligand bias. If the agonists are not specifically uniquely biased for any one pathway, then all of the ligands will produce a uniform line that would be skewed positively or negatively (according to system bias) but showing no differences between agonists. The curvature of the line would simply reflect the relative coupling efficiency of the two pathways in the cell for all agonists. However, if the curvature of the lines differs for the agonists, this indicates that there are intrinsic differences between the agonists for activation of the two pathways; this is molecular bias that will be carried over to all cells containing the receptor. As seen in Figure 8, there is considerable between ligand bias for the agonists, with CCL3 being most biased toward IP1 and CCL3L1 the least. This parallels the ΔΔlog(τ/K_A) values of 1, 7, 21, and 23.7 for CCL3, CCL4, CCL5, and CCL3L1, respectively (Table 3). It should be noted that while bias plots in general are useful graphical representations of selective agonism, they are optimally effective when the bias is within a factor of 10–100. A greater extreme of bias leads to highly skewed bias plots that are limited in their ability to graphically show graded response differences to agonists.

Figure 8.

Bias plot for IP1 production (ordinates) and CCR5 internalization (abscissa) for chemokines in U373 cells. Curves represent responses for the two respective pathways at equal concentrations of agonist. The divergence in the curves represents ligand bias based on receptor conformation that should be constant for all systems.

General Considerations in the Application of the Bias Factor Approach

Descriptions of ligand bias are becoming prevalent in pharmacological literature. As a preface to discussions of how this phenomenon might be quantified, it should be noted that all possible experimental factors that might account for selective agonism, such as kinetics of response, should be explored and ruled out as mechanisms of selective agonism at one pathway over another. Once this is done, methods can be applied to quantify ligand-based stabilization of receptor active states and how those states interact with cellular signaling pathways. It is envisaged that the approach outlined above can provide a useful scale of agonism that incorporates the minimal elements required to describe an agonist’s activity, namely the normalized transduction coefficient [Δlog(τ/K_A)], which describes the relative efficiency of agonist activity at a given pathway compared to a reference agonist. Through this parameter, a second parameter, namely the ΔΔlog(τ/K_A) or log bias, that describes the bias that a given agonist has between pathways relative to a reference agonist can be obtained. This scale possesses the key properties of being readily obtainable from operational model fitting of experimental data {it should be noted that log[(E_max)/(EC₅₀)], an even more easily determined ratio, can be used as a surrogate of log(τ/K_A) for agonist dose–response curves with a unit slope}, independent of variations in receptor density that often occur between various cell types, amenable to statistical evaluation, and internally consistent with no required independent data acquisition (e.g., binding affinity data).

Theoretically, the log(τ/K_A) scale is well suited for quantification of the ability of agonists to stimulate a signaling pathway. If functional selectivity of a given agonist is due to selective activation of a pathway through separate coupling proteins directly interacting with the active state receptor, then the log(τ/K_A) scale should detect the difference in efficacy and affinity associated with the selectivity. This is because the selective activation of the pathway should have associated with it an affinity and efficacy of the receptor active state for the coupling protein. It is essential for such a scale not to be affected by differences in receptor density, as these are system factors that often vary between cell types. As seen in Figure 3, the pEC₅₀ of an agonist changes with differences in receptor density and thus is unsuitable as a scale for comparing cell types. The activity ratio [log(RA)] is an equivalently suitable scale if the transducer slope coefficient (and, hence, the Hill slope) for the concentration response curves is unity but becomes unstable at other values.

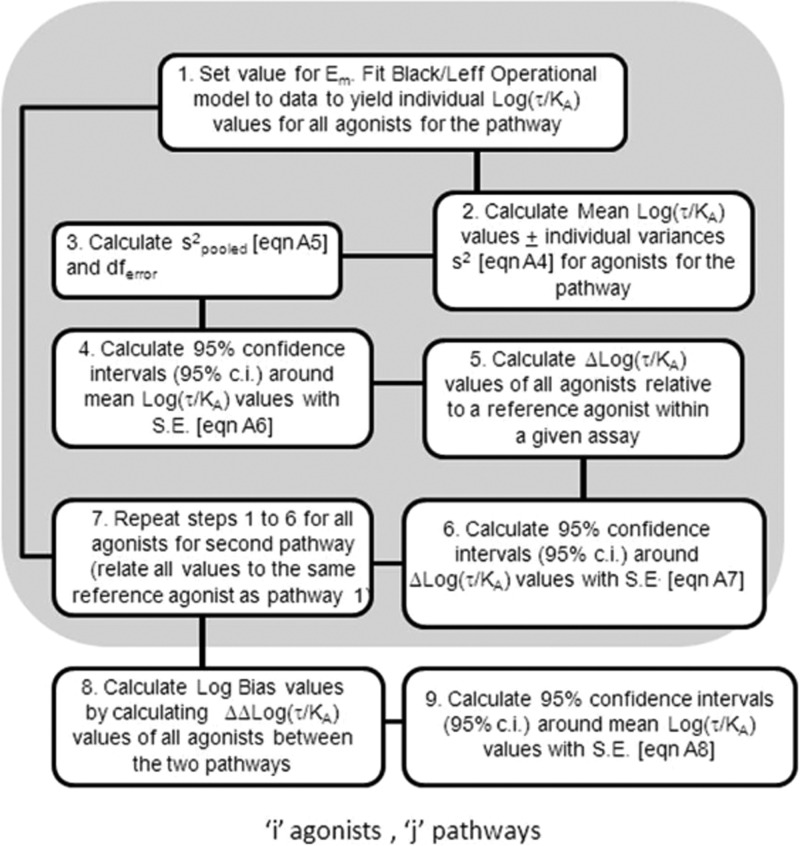
It is important to define the optimal conditions for using the log(τ/K_A) scale to quantify bias. The Black–Leff operational model is suited to fit symmetrical and asymmetrical dose–response curves. However, it should be noted that a reasonably accurate estimate of E_m, the maximal capability of the system to produce response, is necessary for the correct estimation of K_A and τ. In practical terms, E_m often can be estimated accurately by observing the response to a known maximal stimulant (e.g., forskolin for cyclic AMP) or by observation of a common maximal response to a number of agonists. In the latter case, either all of the agonists would have to have identical efficacies (unlikely) or the agonists saturate the stimulus–response mechanism of the cell to produce full agonism equal to the maximal response of the system (by definition E_m). The analysis with IP1 and CCR5 internalization also highlights another feature of this approach, namely the statistical estimation of bias. Given the right experiment, the use of a pooled variance and the estimation of 95% confidence intervals allows the independent assessment of differences in Δlog(τ/K_A) and ΔΔlog(τ/K_A) values. Figure 9 shows a logical progression for the analysis of ligand bias for two pathways for a set of agonists with the associated statistical analysis.

Figure 9.

Schematic diagram showing the logistical progression for analysis of agonist bias using the Black–Leff operational model with a statistical assessment of selectivity.

Most 7TM receptors are pleiotropic in the sense that they directly interact with more than one signaling protein (e.g., various G proteins, β-arrestin, etc.) in the cell.²⁶⁻³² With this comes the obligatory consideration of the relative efficiency with which each pathway is coupled to the receptor. There is no a priori reason to assume that all pathways will be uniformly coupled to the receptor as this will be a function of the equilibrium dissociation constant of the receptor and coupling protein complex and the relative stoichiometry of the receptor and coupling protein present in the cell. Thus, cells can effectively emphasize the importance of relative pathways through control of the relative stoichiometries of these components. If the agonists produce the same receptor active conformation to trigger the effect, then all agonists will be subject to this system bias and no between cell differences in agonist effect will be seen. The calculation of Δlog(τ/K_A) values accounts for the system bias by relating agonism to a reference agonist; i.e., the Δlog(τ/K_A) scale relates the agonists to each other in terms of power to elicit activation of a particular pathway with all of the effects subjected equally to system bias. However, once this has been done, then Δlog(τ/K_A) values should be constant between cell types if the agonists produce the same active state receptor, because there would only be a phase change in amplification of the signals with no between agonist differences. If differences in Δlog(τ/K_A) values are seen between pathways [as measured by ΔΔlog(τ/K_A) values], then this suggests that the agonists discern the pathways differently; i.e., they produce active receptor conformations different from each other. Under these circumstances, the ΔΔlog(τ/K_A) scale defines true ligand bias that is unique to the receptor–agonist pair. Therefore, if biased agonism is a desired profile, the ΔΔlog(τ/K_A) scale can be used by medicinal chemists to optimize the effect.

The fact that agonists can produce cell-specific signaling profiles offers unique therapeutic opportunities. However, the very property of such agonists that may be of utility is also the property that is most difficult to quantify and predict because it may vary with cell type. Given that the prevalence of functional selectivity in the actions of 7TM ligands is markedly on the rise in both academic and industrial settings, the availability of such a robust scale should provide a valuable tool for facilitating the dialogue between medicinal chemistry and biology targeted toward novel 7TM receptor drug discovery and structure–activity studies. As whole cell response assays become increasingly common, for example, with label free technology, it would be predicted that variances in agonist relative potency (relative efficacy) will be observed; these effects have been reported in the literature,¹⁷ and in fact, variance in cell-based agonist activity has been described as a method for detecting functional selectivity.¹⁶ This raises the specter of cell-based efficacy (as defined by Stephenson¹) becoming obsolete as a quantitative scale for predictive pharmacology. However, the concept of efficacy is clearly required thermodynamically, because a ligand-bound receptor necessarily is different (i.e., “isomerized”³³) from an unliganded one; this is what Furchgott² termed intrinsic efficacy. Therefore, what is needed is a way to access intrinsic efficacy in cell-based systems so that it may function as a cell-type-independent scale for quantifying agonism. Proposed here is the idea that a pathway efficacy, directly emanating from a physical interaction of the receptor conformation with a cytosolic signaling molecule, may function as a surrogate of intrinsic efficacy. The intent of such a scale is to provide medicinal chemists with a way to quantify bias in any given molecule and thus constructively optimize it if required.

The ability of the ΔΔlog(τ/K_A) bias scale to detect functional selectivity depends on the interaction of system bias and ligand bias; i.e., true ligand bias will be most evident if extremes in signaling can be assayed. For the chemokine data shown in our study, this was accomplished through measurement of extremes linked to actual binding partners of the receptor, in this case G protein and β-arrestin. Interestingly, the β-arrestin (internalization) bias for CCL3L1 may be therapeutically significant in light of data linking the gene copy number for CCL3L1 in HIV-infected patients to survival with AIDS.³⁴ Our analysis indicates that CCL3L1 is statistically biased toward inducing CCR5 receptor internalization; cell surface CCR5 has been linked to predilection toward HIV infection and progression to AIDS, and it has been found that high levels of CCL3L1 are linked with lower cell surface levels of CCR5.³⁵

It would be envisioned that for the total cell response in two cell types (i.e., pERK activation due to activation of G proteins and β-arrestin³⁶), the ligand bias would not be as obvious; i.e., while one cell type may be more reliant on β-arrestin signaling than another, there would be more of a mixture of effect and true ligand bias would be more subtle and difficult to quantify. However, this could also yield a strategy for the discovery of new functionally selective agonists. Specifically, if two agonists produce cell-specific potency ratios, this would furnish presumptive evidence that they produce different receptor active states; i.e., they are functionally selective.¹⁶

In summary, biased agonism is a frequently encountered phenomenon, and we cannot assume that new synthetic agonists activate receptors in a manner identical to that of the natural hormone. Insofar as functional activity controls the cellular phenotypic agonism, it is important both to recognize if an agonist is biased and to associate functional bias with clinical phenotype. In this latter instance, it would be predicted that defined bias has the potential to create more selective agonists;¹¹ in this regard, the log(τ/K_A) scale may be a useful tool for guiding medicinal chemistry.

Methods

Cell Culture

Stable U373-MAGI-CCR5-E cells were generated by M. Emerman and obtained through the NIH AIDS Research and Reagent Program (catalog no. 3597). The cells were carried in continuous culture in T225 tissue culture flasks (NUNC, catalog no. 159934) in growth medium containing DMEM/F12 (Gibco, catalog no. 11039) with 10% fetal bovine serum (Gibco, catalog no. 26140) and 1% Glutamax (Gibco, catalog no. 35050061). Cells were not allowed to become confluent and were ∼85% confluent at the time they were harvested for the assay. Transient CCR5-expressing CHO CGE cells were generated as follows. Frozen vials of CHO CGE cells were quickly thawed and resuspended in medium containing DMEM/F12 (Gibco, catalog no. 11039) with 10% fetal bovine serum (Gibco, catalog no. 26140) and 1% Glutamax (Gibco, catalog no. 35050061). The cell suspension was centrifuged at 1000g for 5 min to pellet cells. After centrifugation, the cell pellet was resuspended in fresh DMEM/F12 medium at a density of 10⁶ cells/mL. Transduction preps were prepared by addition of the CCR5 bacmam virus at 1, 5, or 10% (v/v) along with 10⁷ cells and qs volume to 40 mL with growth medium. These preps were put into T225 culture flasks (NUNC, catalog no. 159934) and placed in a humidified 37 °C incubator for 24 h prior to the assay.

IP1 Accumulation Assay

U373-MAGI-CCR5-E cells were cultured as described above and were ∼85% confluent at the time they were harvested. On the day of the assay, cells were washed once with 10 mL of PBS, and then 3 mL of the cell dissociation solution was added to each flask. The flasks were incubated for 5 min at 37 °C to facilitate cell removal. After incubation, each flask was washed with 10 mL of growth medium, and cells were collected in a 50 mL conical tube. The cell suspension was counted in a Beckman Coulter Z1 cell counter and then centrifuged to pellet cells (800g for 5 min).

After centrifugation, cells were resuspended in the stimulation buffer provided in the IPOne kit at a density of 2.86 × 10⁶ cells/mL. Using a Multidrop Combi (Thermo Scientific), 7 μL of the cell suspension per well was added to the plate containing chemokines (final density of 20000 cells/well). A dark lid was placed on the plates, and they were incubated for 60 min at 37 °C.

Once the 60 min incubation was complete, we added 3 μL of IP1-d2 and then 3 μL of the anti-IP1-cryptate solutions provided in the IPOne kit using a Multidrop Combi. The plates were shaken for 1 min to ensure reagents were mixed. Plates were covered and incubated for 60 min at room temperature. After being incubated, the plates were read on a PE Viewlux instrument and the data expressed as the 10000(acceptor counts/donor counts) ratio.

Guinea Pig Ileum Contraction

Proximal ileum from guinea pigs (sacrificed by cervical dislocation) was removed and placed in a Tyrode solution (167 mM Na⁺, 2.67 mM K⁺, 1.8 mM Ca²⁺, 1.0 mM Mg²⁺, 145 mM Cl^–, 29.7 mM H₂CO₃^–, 0.36 mM H₂PO₄^2–, and 22 mM d-glucose). The contents of the ileum were flushed with a Tyrode solution, and the ileum was drawn over a glass rod. The external longitudinal muscle layer was cut through with a scalpel and the muscle gently removed through teasing with a cotton swab.³⁷ The resulting strip of longitudinal smooth muscle was mounted in a heated (37 °C) organ bath filled with an oxygenated (95% O₂/5% CO₂) Tyrode solution. One end of the muscle was fixed to the organ bath while the other tied to a Hewlett-Packard linear motion isotonic transducer (model 1000-7DCDT) under a resting tension of 400 mg. The Tyrode solution was removed and replaced with a fresh solution every 20 min while the preparation was left to equilibrate for 60 min. Cumulative concentration–response curves to carbachol and oxotremorine (isotonic contraction) were recorded on a Grass model 5P1 polygraph recorder. After equilibration with a drug free Tyrode solution for a further 60 min, tissues were subjected to a controlled chemical alkylation via the addition of 1 μM phenoxybenzamine for 10 min followed by washing with a drug free Tyrode solution. Tissues were washed every 20 min for 2 h with the first three reapplications of Tyrode containing 1.0 mM sodium thiosulfate to remove unreacted aziridinium ion.³⁸ After a total wash time of of 2 h, concentration–response curves for carbachol and oxotremorine were obtained in the chemically treated tissues.

Internalization of CCR5

U373-MAGI-CCR5-E cells were plated in PE 96-well View plates and harvested from the culture flask using cell dissociation solution from Sigma (catalog no. C5914, 100 mL). The plates were then plated at a density of 17000 cells/well in 96-well View plates from Perkin-Elmer (catalog no. 6005182) and incubated for ≈15 h at 37 °C and 5% CO₂.

Cells were then washed twice with 50 μL of PBS (pH 7.2) per well. Test compounds were prepared as 1:5 serial dilutions in a 100:1 DMSO solution and then diluted to a 1:100 ratio in MEM-alpha and 1% FCS. Cells were incubated with 100 μL of test compound for 35 min at 37 °C and 5% CO₂, washed twice with PBS, fixed with 3.7% paraformaldehyde, and incubated at room temperature inside a chemical hood for 30 min. The cells were then washed twice with 50 μL of wash buffer [0.5% Tween 20 in PBS buffer (pH 7.2)] per well. Cell membranes were stained with 4 ng/mL [PBS (pH 7.4)] wheat germ agglutinin-Alexa 488 from Molecular Probes (catalog no. W11261) for 30 min in the dark. The cells were then washed twice with 50 μL of wash buffer per well, and 50 μL of 3.7% paraformaldehyde per well was added. This mixture was incubated for 5 min in a chemical hood. The cells were then washed twice with 50 μL of wash buffer per well prior to being blocked with 50 μL of 1% BSA and 1% normal goat serum (Sigma, catalog no. 15256, 50 mg) in PBS (pH 7.2) for 30 min and then permeabilized with PBS (pH 7.2) and 0.2% Triton-X (Sigma, catalog no. T8787) for 15 min in the dark.

The CTC8 (R&D MAB1801) mouse anti-human CCR5 primary antibody was reconstituted in PBS (pH 7.2) and 0.5% BSA to a final concentration of 500 μg/mL. The primary antibody solution was prepared by mixing block buffer with CTC8 to a final concentration of 3 μg/mL. The permeabilization buffer from the previous step was aspirated and 50 μL of primary antibody solution per well added. Plates were then incubated at room temperature (in the dark) for 40 min. After the incubation, cells were washed twice with 50 μL of wash buffer per well; 50 μL of secondary goat anti-mouse Alexa-568 F (AB′) from Molecular Probes (catalog no. A11019), 6 μg/mL in 2 μM Hoeschst 33342 (Lonza Walkersville Inc., catalog no. PA-3014), in blocking buffers was added and the plate incubated at room temperature and protected from light for 40 min. After the incubation, the cells were washed three times with 50–100 μL of wash buffer per well and then stored in 100 μL of PBS buffer (pH 7.2) per well. The plates were sealed with Top Seal-A (catalog no. 6005185, Perkin-Elmer) and the bottoms of the plates wiped with 70% ethanol to remove any possible water marks. The plates were read using the Cellomics Array Scan II Instrument; data were analyzed with the GPCR Bioapplication algorithm.

Compound Preparation

All chemokines tested were purchased from Peprotech (Rock Hill, NJ). Chemokines were diluted in deionized water to a stock concentration of 100 μM, aliquoted, and kept frozen at 20 °C. On the day of the assay, the chemokines were serially diluted at 2 times the final assay concentration in stimulation buffer provided in the IPOne HTRF assay kit (Cisbio). Finally, 7 μL of the 2× sample for the chemokine concentration–response curves was added to the assay plate (NUNC, catalog no. 167462).

Data Analysis

The determination of Δlog(τ/K_A) values and their use in determining ligand bias are shown schematically in Figure 9. Agonist concentration–response curves are fitted to the Black–Leff operational model to determine values of τ and K_A (box 1, Figure 9; see also Appendix 1: Fitting the Black–Leff Model). For each concentration–response curve, a value for the transduction coefficient [log(τ/K_A)] is calculated; this is a parameter that summarizes the power of the agonist to activate the particular stimulus–response mechanism that is being measured by the assay. Individual estimates of these transduction coefficients are then used to calculate a mean value (summarizing repeat estimates for the agonist in the system), and a value of variance also is calculated (box 2, Figure 9). These variances can then be combined for all of the agonists in all of the assays to yield an estimate of the pooled variance (box 3, Figure 9), which then can be used to calculate the 95% confidence intervals of the various transduction coefficients of the agonists for the pathway (box 4, Figure 9).

It is important to choose a reference agonist at this point to cancel the effects of system bias on subsequent estimation of ligand bias. If this were not done, then comparison of any agonist across two response pathways would show a bias due to the fact that the two different assays simply are of differing sensitivity. Comparison to an internal standard within each assay (it must be the same one for both pathway responses) cancels differences in coupling sensitivity and efficiency of transduction of the two pathways because they are then common to all the agonists (box 5, Figure 9). Therefore, Δlog(τ/K_A) values are calculated along with 95% confidence intervals of these estimates (box 6, Figure 9). At this point, the agonists can be compared within a pathway to determine differences in their ability to activate the pathway. If the value of zero lies within any 95% confidence interval for any agonist, this indicates the agonist is not significantly different from the reference agonist as an activator of the pathway.

This procedure serves to characterize the relative ability of a group of agonists to activate a given pathway. Steps 1–6 are then repeated for the agonists with another assay measuring response to the pathway to be compared (box 7, Figure 9). The two sets of Δlog(τ/K_A) values then are subtracted to yield ΔΔlog(τ/K_A) values (box 8, Figure 9), which indicate the relative activity of the agonists on each pathway corrected for system bias through comparison to a common reference agonist. The 95% confidence intervals of these ΔΔlog(τ/K_A) values (bias parameters) are also calculated (box 9, Figure 9). As with Δlog(τ/K_A) values, if zero lies within the 95% confidence interval of a ΔΔlog(τ/K_A) estimate, this indicates that the agonist is equiactive in the two pathways. However, if this is not the case, it indicates that the agonist is biased at the molecular level for one pathway over the other.

Glossary

Abbreviations

7TM receptor

seven-transmembrane receptor

SAR

structure–activity relationship

CCL3

chemokine (C–C motif) ligand 3

CCL4

chemokine (C–C motif) ligand 4

CCL5

chemokine (C–C motif) ligand 5

CCL3L1

chemokine (C–C motif) ligand 3-like 1

IP1

inositol monophosphate

HIV

human immunodeficiency virus

DMEM

Dulbecco’s modified Eagle's medium

PBS

physiological bathing solution

HTRF

homogeneous time-resolved resonance

Appendix 1: Fitting the Black–Leff Model

The Black–Leff operational model (1983) is the standard model for fitting concentration–response curves of functional data describing receptor activation. The equation for this model relates agonist concentration ([A]) to response with

A1

where the maximal response of the system is given by E_m, n is a fitting parameter for the slope, the affinity of the agonist is represented by the equilibrium dissociation constant of the agonist–receptor complex, K_A, and the efficacy of the agonist is defined by τ.

When the four-parameter Black–Leff model is being fit with ordinary least-squares methods, the model appears to be nearly unidentifiable. This statistics term means that two sets of parameters can yield the same responses for all values of [A]. For example, the two parameter sets, (E_m = 100, K_A = 10^–6, τ = 0.1, n = 3) and (E_m = 104, K_A = 10^–6, τ = 0.0215, n = 3), produce nearly identical curves. As discussed, the parameter of interest in the main text is log(τ/K_A). For the two parameter sets that produce nearly identical curves, the values for log(τ/K_A) are 5.0 and 4.3, respectively. To ameliorate this problem, it is our recommendation that the parameter E_m be held fixed. This suggests that the investigator will likely need to run a separate study to determine a precise estimate of E_m. Our simulation studies show that when E_m is held fixed, the distribution for estimated log(τ/K_A) values is symmetric (and, hence, the mean is unbiased for the central value). In contrast, when all four model parameters are estimated (including E_m), the distributions for the estimates of log(τ/K_A) are skewed (so that the mean is no longer the central value) and are often too variable to be of any use. For example, when E_m = 1, K_A = 10^–7, τ = 15, and n = 0.7, the standard deviations of the estimates for log(τ/K_A) were nearly 6 times larger when estimating E_m versus when E_m (1.0) was held fixed.

A useful reparametrization of eq A1 that we found to be stable for ordinary least-squares curve fitting is

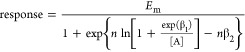A2

where β₁ = ln(K_A) and β₂ = ln(τ). Then the parameter of interest is log₁₀(τ/K_A) = (β₂ – β₁)/ln(10).

Appendix A2: Estimating Bias

A straightforward experimental and analytical approach to estimating bias is given in this section. Suppose that serial dilutions for K ≥ 2 agonists (for the Black–Leff dose–response curve) are laid out on N1 plates with their signal measured for pathway 1 via some assay. Further suppose the same process is repeated on N2 plates to measure the signal for pathway 2 via a second assay.

For each plate, pathway, and agonist, fit the Black–Leff model using eq A2 to estimate log(τ/K_A). One can model the system with a one-way analysis of variance (ANOVA) model as follows

A3

where Y_ijk values are the estimated log(τ/K_A) values, θ_ij values are the mean parameter values, and ε_ijk values are the model errors for agonist i = 1, 2, ..., K; pathway j = 1 or 2; and plate k = 1, 2, ..., Nj. The ε_ijk values are typically assumed to be independent and to be identical distribution normal random variables with a zero mean and a standard deviation σ. In case the samples are not completely balanced, let N_ij denote the total number of observations for agonist i and pathway j.

Given the model assumptions in eq A3, the following text shows how to estimate the mean, the standard error, and a 95% confidence interval for bias. Let

A4

denote the sample mean and sample variance for the log(τ/K_A) value for agonist i and pathway j, respectively. An estimate for the standard deviation (σ) is given by

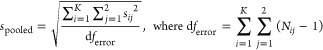A5

The standard error for

A6

Let Δlog(τ/K_A) denote the difference in log(τ/K_A) values for agonists i and i′. This parameter is estimated by Y̅_ij – Y̅_i′j, with the standard error given by

A7

Bias, denoted by ΔΔlog(τ/K_A), is the difference in Δlog(τ/K_A) for the two pathways and is estimated by (Y̅_i1 – Y̅_i′1) – (Y̅_i2 – Y̅_i′2). The standard error for the bias estimate is

A8

A 95% confidence interval for any of these parameters [log(τ/K_A), Δlog(τ/K_A), or ΔΔlog(τ/K_A)] is

A9

where T(λ,p) is the upper pth quantile of the central T distribution with λ degrees of freedom. For example, a 95% confidence interval for bias is given by

The steps described above represent one way to design a study to determine bias, but it should be recognized that special features of the experiment could warrant modifications of the design. If, for example, there appears to be a significant plate effect, one could add a plate term to eq A3 and instead use the model Y_ijk = P_k + θ_ij + ε_ijk, where P_k is the term for plate k. A second deviation of eq A3 may be necessary if the assumption of a constant standard deviation is ignored. That is, if the standard deviation does not appear to be approximately the same within all agonist and pathway groups, then the pooled standard deviation estimate cannot be used, and one would need a more complicated approach (e.g., Satterthwaite approximation to degrees of freedom). Finally, the researcher may wish to deviate from the simple experimental plan outlined above. The statistical model fit to the data should accurately reflect the experiment that was conducted.

Author Contributions

S.N. wrote only the Appendix.

A.C. is a Senior Research Fellow of the National Health and Medical Research Council of Australia.

The authors declare no competing financial interest.