Abstract
Photosynthetic capacity is one of the most sensitive parameters in vegetation models and its relationship to leaf nitrogen content links the carbon and nitrogen cycles. Process understanding for reliably predicting photosynthetic capacity is still missing. To advance this understanding we have tested across C3 plant species the coordination hypothesis, which assumes nitrogen allocation to photosynthetic processes such that photosynthesis tends to be co-limited by ribulose-1,5-bisphosphate (RuBP) carboxylation and regeneration. The coordination hypothesis yields an analytical solution to predict photosynthetic capacity and calculate area-based leaf nitrogen content (N
a). The resulting model linking leaf photosynthesis, stomata conductance and nitrogen investment provides testable hypotheses about the physiological regulation of these processes. Based on a dataset of 293 observations for 31 species grown under a range of environmental conditions, we confirm the coordination hypothesis: under mean environmental conditions experienced by leaves during the preceding month, RuBP carboxylation equals RuBP regeneration. We identify three key parameters for photosynthetic coordination: specific leaf area and two photosynthetic traits (k3, which modulates N investment and is the ratio of RuBP carboxylation/oxygenation capacity ( ) to leaf photosynthetic N content (N
pa); and J
fac, which modulates photosynthesis for a given k
3 and is the ratio of RuBP regeneration capacity (J
max) to
) to leaf photosynthetic N content (N
pa); and J
fac, which modulates photosynthesis for a given k
3 and is the ratio of RuBP regeneration capacity (J
max) to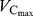 ). With species-specific parameter values of SLA, k
3 and J
fac, our leaf photosynthesis coordination model accounts for 93% of the total variance in Na across species and environmental conditions. A calibration by plant functional type of k
3 and J
fac still leads to accurate model prediction of N
a, while SLA calibration is essentially required at species level. Observed variations in k3 and Jfac are partly explained by environmental and phylogenetic constraints, while SLA variation is partly explained by phylogeny. These results open a new avenue for predicting photosynthetic capacity and leaf nitrogen content in vegetation models.
). With species-specific parameter values of SLA, k
3 and J
fac, our leaf photosynthesis coordination model accounts for 93% of the total variance in Na across species and environmental conditions. A calibration by plant functional type of k
3 and J
fac still leads to accurate model prediction of N
a, while SLA calibration is essentially required at species level. Observed variations in k3 and Jfac are partly explained by environmental and phylogenetic constraints, while SLA variation is partly explained by phylogeny. These results open a new avenue for predicting photosynthetic capacity and leaf nitrogen content in vegetation models.
Introduction
The response of leaf net photosynthesis to variations in light, temperature and CO2 concentration has been successfully represented by the biochemical model of C3 photosynthesis proposed by Farquhar, von Caemmerer and Berry [1]. This model has pioneered the mechanistic representation of the main biochemical processes of leaf photosynthesis, based on the assumption that photosynthesis is limited by either the carboxylation/oxygenation of ribulose-1,5-bisphosphate (RuBP) by the enzyme ribulose 1·5-bisphosphate carboxylase/oxygenase (Rubisco; W
c), or the regeneration of RuBP by the electron transport chain (W
j). Maximum rates of these two processes are determined by carboxylation capacity (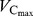 ) and electron transport capacity (J
max). A strong correlation linearly links the variations of
) and electron transport capacity (J
max). A strong correlation linearly links the variations of 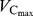 and J
max across species (e.g.
[2]) and environmental conditions during plant growth (e.g.
[3], [4]). Since both capacities are measured independently, this result suggests that CO2 assimilation is regulated in a coordinated manner by these two processes [5].
and J
max across species (e.g.
[2]) and environmental conditions during plant growth (e.g.
[3], [4]). Since both capacities are measured independently, this result suggests that CO2 assimilation is regulated in a coordinated manner by these two processes [5].
The variations of net photosynthesis with growth condition, season and species, are related to concurrent changes in leaf nitrogen content (N
a) and to the allocation of nitrogen between different protein pools [6]. 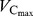 and J
max linearly correlate with N
a at both intra-and-interspecific levels [3], [4], [7]. Nevertheless, so far the relationship between
and J
max linearly correlate with N
a at both intra-and-interspecific levels [3], [4], [7]. Nevertheless, so far the relationship between 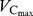 and J
max and their link to N
a are empirical correlations, their scatter is substantial, and a predictive process understanding C–N coupling at the leaf scale is still missing. As photosynthetic capacity is among the most influential parameters in current vegetation models [8], such an understanding is essential to predict photosynthesis at leaf, plant, stand and ecosystem scales under changing environmental conditions.
and J
max and their link to N
a are empirical correlations, their scatter is substantial, and a predictive process understanding C–N coupling at the leaf scale is still missing. As photosynthetic capacity is among the most influential parameters in current vegetation models [8], such an understanding is essential to predict photosynthesis at leaf, plant, stand and ecosystem scales under changing environmental conditions.
Haxeltine and Prentice [9] suggested a general model for the light-use efficiency of primary production, which links photosynthetic capacity and N a. This model is based on the Farquhar’s model of photosynthesis and has been implemented in the global terrestrial vegetation model LPJ [10]. This approach does not account for N limitation and is based on the optimization theory that maximizes assimilation against incoming radiation. Until now, a clear understanding of leaf N variations along vegetative canopies as well as across species and environments has not been provided by the optimization theory [11], [12]. For instance, all reported studies observed N gradients less steep than predicted with the optimization theory, suggesting that it likely overestimates predicted C gain [13]–[18]. Moreover, there are several limitations in optimization theory calculations (for a detailed discussion, see [19]).
Chen et al. [20] proposed an alternative approach: the coordination hypothesis of leaf photosynthesis. The basic assumption of this approach is that 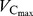 and J
max are actively regulated by plants in response to environmental conditions such that for most representative conditions W
c equals W
j. The optimality criterion in this context is not maximum C gain (as proposed in [21]–[23]), but the balance of RuBP carboxylation and regeneration, providing a coordinated allocation of resources, i.e. nitrogen, to these two photosynthetic processes (Fig. S1). For vertical gradients within canopies the co-limiting N content was shown to increase with irradiance and to decline with temperature and with atmospheric CO2 concentration [20]. In agreement with experimental studies, the coordination hypothesis showed that N distribution with canopy depth declines less than the light gradient [13]–[18].
and J
max are actively regulated by plants in response to environmental conditions such that for most representative conditions W
c equals W
j. The optimality criterion in this context is not maximum C gain (as proposed in [21]–[23]), but the balance of RuBP carboxylation and regeneration, providing a coordinated allocation of resources, i.e. nitrogen, to these two photosynthetic processes (Fig. S1). For vertical gradients within canopies the co-limiting N content was shown to increase with irradiance and to decline with temperature and with atmospheric CO2 concentration [20]. In agreement with experimental studies, the coordination hypothesis showed that N distribution with canopy depth declines less than the light gradient [13]–[18].
However, so far this co-limitation and its link to N a has been considered only for vertical gradients within plant canopies, and has not yet been studied and validated across plant species and environmental conditions. This is possibly due to a lack of appropriate data including environmental growth conditions and photosynthetic parameters for a range of C3 plant species. In addition, a full test of this hypothesis requires extending the calculation of the co-limiting N content to account for the coupling between leaf photosynthesis and stomatal conductance [3] as well as ascribing leaf N to structural and metabolic pools [24], [25].
In this study, we evaluate for the first time the coordination hypothesis for sunlit leaves and its link to N
a for a large range of plant species grown under different environmental conditions. We use an extended version of the Farquhar model of C3 photosynthesis, a stomatal conductance model and a leaf N model to couple C, N and water fluxes at the leaf scale (see equations and variables in Tables 1–2). We apply this model to a dataset that includes leaf and environmental characteristics during plant growth and gas exchange measurements for a total of 31 C3 species (293 observations, Table S1). For each observation, plant characteristics included the specific leaf area (SLA, m2
g−
1 DM), N
a (gNm−
2), and 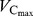 and J
max (µmolm−
2 s−
1) at reference temperature and atmospheric CO2 concentration. The dataset covers six plant functional types (PFTs) grown both under constant and outdoors environments at a range of N and water supplies and atmospheric CO2 concentrations.
and J
max (µmolm−
2 s−
1) at reference temperature and atmospheric CO2 concentration. The dataset covers six plant functional types (PFTs) grown both under constant and outdoors environments at a range of N and water supplies and atmospheric CO2 concentrations.
Table 1. Equations of the photosynthesis - stomatal conductance models.
| Process | Equation | Unit | Eqn | Ref. |
| Nitrogen sub-model | ||||
| Leaf nitrogen content |
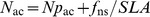
|
g Nm− 2 | 1 | − |
| Leaf photosynthetic N content |
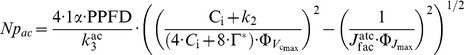
|
g Nm− 2 | 2 | − |
| Photosynthetic sub-model | ||||
| Net photosynthetic rate |
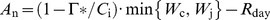
|
µmol m− 2 s− 1 | 3 | [1] |
| Rubisco limited photosynthetic rate through RuBP carboxylation/oxygenation |
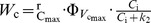
|
µmol m− 2 s− 1 | 4 | [1] |
| Intermediate variable synthesising the Rubisco affinity for CO2 |
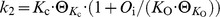
|
Pa | 5 | [1] |
| Maximum rate of carboxylation |
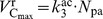
|
µmol m− 2 s− 1 | 6 | [2] |
| RuBP regeneration limited photosyn−thetic rate through electron transport |
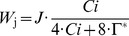
|
µmol m− 2 s− 1 | 7 | [1] |
| Light dependence of electron transport rate |
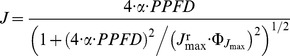
|
µmol m− 2 s− 1 | 8 | [1] |
| Potential RuBP regeneration rate |
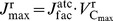
|
µmol m− 2 s− 1 | 9 | [2] |
| CO2 compensation point in the absence of mitochondrial respiration |
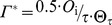
|
Pa | 10 | [1] |
| Leaf respiration without photorespiration |
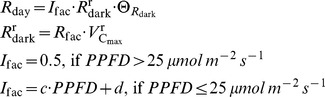
|
µmol m− 2 s− 1 | 11 | [27] |
| Temperature dependence of J max and Vcmax |
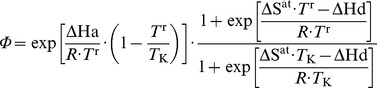
|
dimensionless | 12 | [31] |
| Temperature dependence of K c, K o, τ and R dark |
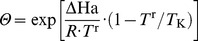
|
dimensionless | 13 | [27] |
| Stomatal conductance sub-model | ||||
| Stomatal conductance |
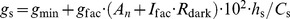
|
mmol m− 2 s− 1 | 14 | [27] |
| CO2 partial pressure at the leaf boundary layer |
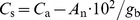
|
Pa | 15 | [3] |
| Photosynthesis-stomata coupling | ||||
| CO2 intercellular concentration |
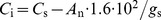
|
Pa | 16 | [29] |
| Analytical solution for photosynthesis calculation |
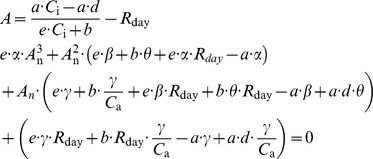
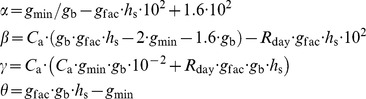
|
µmol m− 2 s− 1 | 17 | [29] |
| Photosynthetic acclimation | ||||
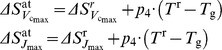 Photosynthetic acclimation to growth temperature Photosynthetic acclimation to growth temperature |
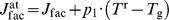
|
J K− 1 mol− 1 J K− 1 mol− 1 dimensionless | 18a 18b 19 | [32] |
| Photosynthetic acclimation to CO2 concentration |
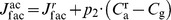
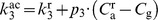
|
dimensionless µmol g− 1 N s− 1 | 20 21 | [33] |
Table 2. Parameters and variables of the photosynthesis - stomatal conductance models.
| Symbol | Value | Unit | Description |
| Parameters | |||
| C | −0.02 | m2 sµmol− 1 | Slope of the linear relationship between I fac and PPFD in the range 0–25 µmol m− 2 s− 1 |
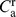
|
35 | Pa | Reference atmospheric CO2 partial pressure |
| d | 1 | µmol CO2 m− 2 leaf s− 1 | y-intercept of the linear relationship between I fac and PPFD in the range from 0–25 µmol m− 2 s− 1 |
| g b | 300 | mmol m− 2 s− 1 | Leaf boundary layer conductance to water vapour |
| g fac | 13.7 | dimensionless | Stomatal sensitivity coefficient |
| g min | 76.2 | mmol m− 2 s− 1 | Minimum stomatal conductance to water vapour |
| I fac | 0.5 | dimensionless | Coefficient representing the extent to which R dark is inhibited in the light |
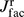
|
dimensionless | Ratio between J
max and 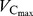 of plant grown at the reference temperature and at the reference CO2 partial pressure of plant grown at the reference temperature and at the reference CO2 partial pressure |
|
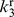
|
µmol CO2 g− 1 N s− 1 | Slope of linear relationship relating N
pa to 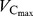 at the reference temperature and at the reference CO2 partial pressure at the reference temperature and at the reference CO2 partial pressure |
|
| K c | 19.42 | Pa | Michaelis-Menten constant for carboxylase activity of Rubisco |
| K o | 14 300 | Pa | Michaelis-Menten constant for oxgenase activity of Rubisco |
| O i | 21 000 | Pa | Internal leaf oxygen concentration |
| p 1 | −0.012 | dimensionless | Coefficient representing the extent to which J fac is modified by the CO2 partial pressure during plant growth |
| p 2 | 0.036 | dimensionless | Coefficient representing the extent to which J fac is modified by the temperature during plant growth |
| p 3 | 0.3192 | µmol CO2 g− 1 N s− 1 | Coefficient representing the effect of CO2 partial pressure during plant growth on k 3 |
| p 4 | 0.94 | dimensionless | Coefficient representing the effect of growth temperature on entropy term for J
max and 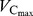
|
| R | 8.314 | J K− 1 mol− 1 | Perfect gas constant |
| R fac | 0.011 | dimensionless | Ratio between R
dark and 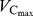 at reference temperature at reference temperature |
| SLA | m2 leaf g− 1 DM | Specific leaf area | |
| α | 0.05 | mol CO2 mol− 1 photon | Apparent quantum yield of net photosynthesis at saturating CO2 |
| ΔHaJmax | 83 608 | J mol− 1 | Activation energy of J max |
| ΔHaKc | 65 800 | J mol− 1 | Activation energy of K c |
| ΔHaKo | 36 000 | J mol− 1 | Activation energy of K o |
| ΔHaRdark | 50 861 | J mol− 1 | Activation energy of R dark |
| ΔHaVcmax | 86 529 | J mol− 1 | Activation energy of 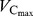
|
| ΔHaτ | −28 990 | J mol− 1 | Activation energy of τ |
| ΔHd | 200 000 | J mol− 1 | Deactivation energy |
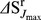
|
660.42 | J K− 1 mol− 1 | Entropy term of J max for plant grown at reference temperature |
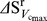
|
654.24 | J K− 1 mol− 1 | Entropy term of 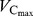 for plant grown at reference temperature for plant grown at reference temperature |
| τ | 2 838 | dimensionless | Rubisco specificity factor at reference temperature |
| Input Variables | |||
| C a | Pa | CO2 partial pressure in the ambient air | |
| C g | Pa | Atmospheric CO2 partial pressure during preceding month of plant growth | |
| h s | dimensionless | Leaf surface relative humidity | |
| PPFD | µmol m− 2 s− 1 | Photosynthetic photon flux density | |
| T k | K | Air temperature. In our analysis T k = T g | |
| T g | K | Mean air temperature during preceding month of plant growth | |
| T r | 293.16 | K | Reference temperature for metabolic activity |
| Output variables | |||
| A n | µmol m− 2 s− 1 | Net photosynthesis | |
| C i | Pa | Internal CO2 partial pressure | |
| C s | Pa | Leaf surface CO2 partial pressure | |
| g s | mmol m− 2 s− 1 | Stomatal conductance to water vapor | |
| k 2 | Pa | Intermediate variable synthesizing the Rubisco affinity for CO2 | |
| J | µmol m− 2 s− 1 | Light dependence of the rate of electron transport | |
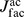
|
dimensionless | J fac acclimated to CO2 during plant growth | |
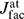
|
dimensionless | J fac acclimated to temperature during plant growth | |
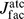
|
dimensionless | J fac acclimated to CO2 and to temperature during plant growth | |
| J max | µmol m− 2 s− 1 | Potential rate of RuBP regeneration | |
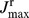
|
µmol m− 2 s− 1 | Potential rate of RuBP regeneration at reference temperature | |
| k3 | µmol CO2 g− 1 N s− 1 | Slope of linear relationship relating N
pa to 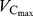
|
|
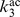
|
µmol CO2 g− 1 N s− 1 | Slope of linear relationship relating N
pa to 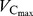 acclimated to CO2 during plant growth acclimated to CO2 during plant growth |
|
| N a | g N m− 2 leaf | Leaf N content per leaf area | |
| N ac | g N m− 2 leaf | Leaf N content per leaf area when W c equals W j | |
| N pa | g N m− 2 leaf | Leaf photosynthetic N content per leaf area | |
| Np ac | g N m− 2 leaf | Leaf photosynthetic N content per leaf area when W c equals W j | |
| R dark | µmol m− 2 s− 1 | Leaf dark respiration rate | |
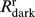
|
µmol m− 2 s− 1 | Leaf dark respiration rate at reference temperature | |
| R day | µmol m− 2 s− 1 | Leaf respiration rate from processes other than photorespiration | |
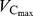
|
µmol m− 2 s− 1 | Maximum carboxylation rate of Rubisco | |
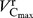
|
µmol m− 2 s− 1 | Maximum carboxylation rate of Rubisco at reference temperature in the absence of any deactivation as a result of high temperature | |
| W c | µmol m− 2 s− 1 | Rubisco-limited photosynthetic rate | |
| W j | µmol m− 2 s− 1 | RuBP regeneration limited photosynthetic rate through electron transport | |
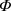
|
dimensionless | Temperature dependence of J
max or 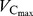
|
|
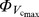
|
dimensionless | Temperature dependence of 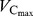
|
|
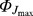
|
dimensionless | Temperature dependence of J max | |
|
dimensionless | Temperature dependence of K c, K o, τ, or R dark | |
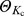
|
dimensionless | Temperature dependence of K c | |
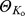
|
dimensionless | Temperature dependence of K o | |
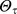
|
dimensionless | Temperature dependence of τ | |
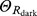
|
dimensionless | Temperature dependence of R dark | |
| Γ* | dimensionless | CO2 compensation point in the absence of mitochondrial respiration | |
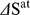
|
J K− 1 mol− 1 | Entropy term acclimated to temperature during plant growth | |
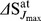
|
J K− 1 mol− 1 | Entropy term of J max acclimated to temperature during plant growth | |
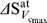
|
J K− 1 mol− 1 | Entropy term of  acclimated to temperature during plant growth acclimated to temperature during plant growth |
|
In agreement with the half-life time of Rubisco [26], we assumed that photosynthetic coordination varies with the mean over one month of the environmental conditions during plant growth. We tested the coordination hypothesis: i) by comparing simulated W c and W j values for the measured N a, and ii) by comparing simulated (N ac) and measured (N a) leaf N contents. Second, thanks to a statistical model, we distinguished the plant species and environmental conditions effects on leaf photosynthetic traits. Third, we tested the implications of our leaf photosynthesis coordination model for net C assimilation (A n) and for photosynthetic N use efficiency (PNUE) by varying plant photosynthetic traits and environmental growth conditions. Based on these results, we discuss the applicability of the coordination hypothesis to predict photosynthetic capacity and N content of sunlit leaves at the ecosystem and global scales.
Methods
A Model Coupling Leaf N with CO2 and H2O Fluxes
Several formulations and parameterizations of the original model by Farquhar et al. [1] have been described. Here, we refer to the formulation and parameterization used by Wohlfahrt et al. [3]. The net rate of C assimilation (A
n, µmol m−
2 s−
1) was limited either by carboxylase activity of Rubisco (W
c, µmolCO2 m−
2 s−
1) or by electron flux through the chloroplast photosystems (W
j, µmolCO2 m−
2 s−
1) (see Eqn 3–4, 7 in Table 1). Their respective capacity, 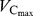 and J
max, scaled with photosynthetic leaf N content (N
pa, gN m−
2) (Eqn 6, 9). The relationship between the intracellular CO2 concentration (C
i, Pa) and the stomatal conductance (g
s, mmol m−
2 s−
1) was modeled according to Falge et al. [27] (Eqn 14–17). g
s can limit A
n and thereby modify the linearity of the photosynthetic capacities vs N
pa relationship [28]. An analytical method was used to couple A
n and g
s, leading to the calculation of A
n through a system of five equations and five unknowns [29], [30] (Eqn 17). The daytime temperature dependence of
and J
max, scaled with photosynthetic leaf N content (N
pa, gN m−
2) (Eqn 6, 9). The relationship between the intracellular CO2 concentration (C
i, Pa) and the stomatal conductance (g
s, mmol m−
2 s−
1) was modeled according to Falge et al. [27] (Eqn 14–17). g
s can limit A
n and thereby modify the linearity of the photosynthetic capacities vs N
pa relationship [28]. An analytical method was used to couple A
n and g
s, leading to the calculation of A
n through a system of five equations and five unknowns [29], [30] (Eqn 17). The daytime temperature dependence of 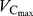 and J
max was described following Medlyn et al. [31] (Eqn 12). Some studies have shown from a large dataset that the entropy terms of
and J
max was described following Medlyn et al. [31] (Eqn 12). Some studies have shown from a large dataset that the entropy terms of 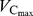 and J
max acclimate to the mean growth temperature (T
g, K) experienced by leaves over the preceding month [32]. The formalism and parameterization proposed by these authors [32] was used in this study to describe the acclimation of
and J
max acclimate to the mean growth temperature (T
g, K) experienced by leaves over the preceding month [32]. The formalism and parameterization proposed by these authors [32] was used in this study to describe the acclimation of 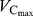 and J
max to T
g (Eqn 18–19). Similarly, Ainsworth and Long [33] have shown an acclimation of A
n to atmospheric CO2 concentration during the preceding month (C
g, Pa). This was also taken into account (Eqn 20–21), by modifying the relationship of Vcmax and Jmax at standard temperature (J
fac, dimensionless) and the relationship of Vcmax at standard temperature to N
pa (k
3, µmolCO2 g−
1 N s−
1) according to a linear function of the difference between reference (
and J
max to T
g (Eqn 18–19). Similarly, Ainsworth and Long [33] have shown an acclimation of A
n to atmospheric CO2 concentration during the preceding month (C
g, Pa). This was also taken into account (Eqn 20–21), by modifying the relationship of Vcmax and Jmax at standard temperature (J
fac, dimensionless) and the relationship of Vcmax at standard temperature to N
pa (k
3, µmolCO2 g−
1 N s−
1) according to a linear function of the difference between reference (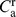 ) and growth CO2 concentrations (C
g).
) and growth CO2 concentrations (C
g).
A sensitivity analysis of the photosynthesis-stomatal conductance model was performed by analyzing the range of parameter variations in literature (Text S1, Table S2) and the sensitivity of the model outputs in response to a ±15% change in parameter values (Text S1, Fig. S2–S3). An index of sensitivity (IOS) was calculated as the ratio of output to parameter changes and was used to discuss on the model uncertainties linked to model calibration.
Coordinated N Content of Sunlit Leaves
Within leaves, N is partitioned between metabolic and structural pools [24], [25]. The coordinated leaf N content, N ac (gN m− 2) is calculated as the sum of structural leaf N and of photosynthetic leaf N (Np ac, gN m− 2). As leaf structures are highly dependent upon the biomass investment in dry matter (DM) [34], structural leaf N (f ns, gN g− 1 DM) is expressed per unit DM. f ns is assumed constant across species and independent of canopy depth and light intensity. f ns value corresponds to the average value reported in the literature for a range of C3 species (0.012 gN g− 1 DM, for a review see Lötscher et al. [25]). In contrast, metabolic leaf N associated with leaf photosynthesis is expressed per unit area since both light capture and CO2 exchange with atmosphere are intrinsically area-based phenomena [3]. As a key measure of leaf morphology [6], SLA links dry matter-based structural N content (f ns) to area-based photosynthetic N content (Np ac):
| (1) |
Under given environmental conditions, Np
ac is defined as the N
pa value at which A
n was co-limited by W
c and W
j (Fig. S1). Both 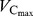 and J
max are linear functions of Np
a and, for given environmental conditions, there is a single Np
ac value for which W
c equals W
j. At this co-limiting point, Np
ac equals (see Text S2 Eqn 2a-2d for details):
and J
max are linear functions of Np
a and, for given environmental conditions, there is a single Np
ac value for which W
c equals W
j. At this co-limiting point, Np
ac equals (see Text S2 Eqn 2a-2d for details):
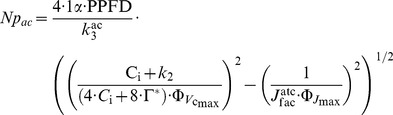 |
(2) |
where α (molCO2 mol−
1photon) is the apparent quantum yield of A
n at saturating CO2, PPFD (µmol m−
2 s−
1) is the photosynthetic photon flux density, 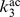 (µmol CO2 g−
1N s−
1) is k
3 acclimated to C
g (Eqn 21), k
2 (Pa) is an intermediate variable synthesizing the Rubisco affinity for CO2 (Eqn 5), Γ* (Pa) is the CO2 compensation point in the absence of mitochondrial respiration,
(µmol CO2 g−
1N s−
1) is k
3 acclimated to C
g (Eqn 21), k
2 (Pa) is an intermediate variable synthesizing the Rubisco affinity for CO2 (Eqn 5), Γ* (Pa) is the CO2 compensation point in the absence of mitochondrial respiration, 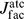 is J
fac acclimated to C
g and T
g (CO2 air concentration and temperature during preceding month of plant growth, Eqn 19–20), and
is J
fac acclimated to C
g and T
g (CO2 air concentration and temperature during preceding month of plant growth, Eqn 19–20), and 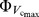 and
and 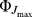 (dimensionless) are the response functions of
(dimensionless) are the response functions of 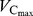 and J
max to temperature (Eqn 12). Overall, Np
ac integrates the sensitivity of photosynthetic machinery to T
g, PPFD, C
i and h
s.
and J
max to temperature (Eqn 12). Overall, Np
ac integrates the sensitivity of photosynthetic machinery to T
g, PPFD, C
i and h
s.
Dataset
A dataset was assembled from measurements and literature to associate leaf photosynthetic traits of mature sunlit leaves with environmental growth conditions (Dataset SI4). 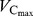 and J
max at reference temperature (T
r = 20°C), N
a, SLA, as well as T
g, PPFD, h
s and C
g during the month preceding leaf measurements were included.
and J
max at reference temperature (T
r = 20°C), N
a, SLA, as well as T
g, PPFD, h
s and C
g during the month preceding leaf measurements were included. 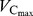 and J
max values were standardized using a consistent formulation and parameterization of Γ* and the Michaelis-Menten constants for carboxylase (K
c, Pa) and oxygenase (K
o, Pa) Rubisco activity [32], [35].
and J
max values were standardized using a consistent formulation and parameterization of Γ* and the Michaelis-Menten constants for carboxylase (K
c, Pa) and oxygenase (K
o, Pa) Rubisco activity [32], [35].
The dataset has 293 entries from 31 C3 plant species covering six plant functional types (PFTs): temperate broadleaved and coniferous evergreen trees (PFT1), temperate broadleaved deciduous trees (PFT2), deciduous shrubs and herbs (PFT3), perennial C3 grasses and forbs (PFT4), C3 crops (wheat, PFT5) and N-fixing trees (PFT6). The final dataset covers a wide range of plant growth conditions: T g (ranging from 7.1 to 21.0°C), PPFD (500 to 1170 µmol m− 2 s− 1), h s (0.51 to 0.89) and C g (36 and 60 Pa). However, data corresponding to severe drought and/or to very low N availability during growth were excluded from the dataset. Four categories of inorganic N availability (low, medium, high and very high), two categories of soil moisture and of atmospheric CO2 concentration (ambient and elevated) and six categories of experimental set-up (climate chamber, sunlit climate chamber, botanical garden, natural vegetation, free air CO2 enrichment (FACE) and open top chambers) were defined. The dataset has been made available via the TRY initiative on plant traits [36].
Data Analysis
Coordinated W c and W j
The basic assumption of the coordination hypothesis is that under the environmental conditions to which a leaf is adapted, RuBP carboxylation equals RuBP regeneration (W
c = W
j). Here we tested this for the average daily plant growth conditions (excluding night values) during the last month preceding photosynthesis measurements. We used four environmental variables (C
g, PPFD, T
g and h
s) corresponding to the average plant growth conditions as model input, and 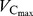 and J
max derived from separate photosynthesis measurements on the same plants. A single set of values was used for all other 33 model parameters and was originated from Wohlfahrt’s calibration (Table 2) [3], [4]. W
c and W
j, both predicted for the average plant growth conditions for each observation (n = 293), were compared by least square linear regression. Regression residuals were analyzed using a general linear model (GLM) with T
g, h
s, C
g and with PFTs and N categories. PFTs and N levels were compared by the post ANOVA Tukey’s HSD method.
and J
max derived from separate photosynthesis measurements on the same plants. A single set of values was used for all other 33 model parameters and was originated from Wohlfahrt’s calibration (Table 2) [3], [4]. W
c and W
j, both predicted for the average plant growth conditions for each observation (n = 293), were compared by least square linear regression. Regression residuals were analyzed using a general linear model (GLM) with T
g, h
s, C
g and with PFTs and N categories. PFTs and N levels were compared by the post ANOVA Tukey’s HSD method.
Prediction of the coordinated leaf N content
N
ac was calculated for each observation (n = 293) using four environmental variables (C
g, PPFD, T
g and h
s) corresponding to the growth conditions of the past month and three leaf traits (k
3, J
fac and SLA). k
3 is calculated as the ratio between 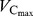 and Np
a, while J
fac is calculated as the ratio between J
max and
and Np
a, while J
fac is calculated as the ratio between J
max and 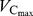 . The prediction of N
ac was evaluated by the relative root mean squared error (RRMSE), which is the relative average of the squared differences between predicted and observed values [37]. RRMSE values lower than 0.2 indicates here acceptable errors. Systematic (RRMSES) and unsystematic (RRMSEU) errors [37] specified the error source of RRMSE (Eq. I).
. The prediction of N
ac was evaluated by the relative root mean squared error (RRMSE), which is the relative average of the squared differences between predicted and observed values [37]. RRMSE values lower than 0.2 indicates here acceptable errors. Systematic (RRMSES) and unsystematic (RRMSEU) errors [37] specified the error source of RRMSE (Eq. I).
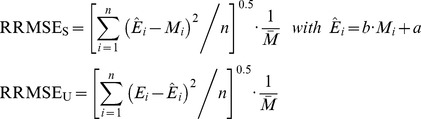 |
(I) |
where E
i and M
i are the predicted and measured values of the observation i, 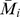 is the average of M
i and
is the average of M
i and 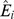 is an estimate of E
i deriving from the linear regression between E
i and M
i.
is an estimate of E
i deriving from the linear regression between E
i and M
i.
Dependence of leaf photosynthetic parameters on plant functional type (PFT)
ANOVA followed by LSD method for mean comparison tests, were used to analyze the role of PFT for the estimation of leaf photosynthetic traits used in the test of the coordination hypothesis (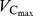 , J
max, k
3, J
fac and SLA). In order to test if the calibration of leaf photosynthetic traits can be simplified to obtain a unique value or a value by PFT, we estimated independent values of k
3, J
fac and SLA traits minimizing the squared differences between N
a and N
ac (Newton’s optimization method). Mean and optimized values per PFT were then compared by linear regressions. The calibration of leaf traits by species was not tested since the number of observations per species was too variable in our dataset.
, J
max, k
3, J
fac and SLA). In order to test if the calibration of leaf photosynthetic traits can be simplified to obtain a unique value or a value by PFT, we estimated independent values of k
3, J
fac and SLA traits minimizing the squared differences between N
a and N
ac (Newton’s optimization method). Mean and optimized values per PFT were then compared by linear regressions. The calibration of leaf traits by species was not tested since the number of observations per species was too variable in our dataset.
Dependence of leaf photosynthetic parameters on environmental growth conditions
Multiple regression models were used to analyze the effects of environmental growth conditions (T
g, PPFD, h
s and C
g, N and soil moisture categories) on leaf traits (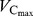 , J
max, k
3, J
fac and SLA). For regression models of k
3 and J
fac, the values of dependent variables were log-transformed and all residuals followed a normal distribution.
, J
max, k
3, J
fac and SLA). For regression models of k
3 and J
fac, the values of dependent variables were log-transformed and all residuals followed a normal distribution.
We tested if the prediction of leaf photosynthetic traits by environmental growth conditions was robust and validated likewise the coordination hypothesis. We conducted bootstrap analyses to predict W
c and W
j as a function of 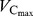 and J
max estimated by an independent regression model and environmental growth conditions. In the same way, bootstrap analyses were conducted to predict N
ac as a function of estimated k
3 and J
fac. To do so, two-thirds of the 293 observations were randomly used to parameterize the multiple regression models (20 random sets, Tables S3–S4). These models were used to predict the leaf photosynthetic parameters
and J
max estimated by an independent regression model and environmental growth conditions. In the same way, bootstrap analyses were conducted to predict N
ac as a function of estimated k
3 and J
fac. To do so, two-thirds of the 293 observations were randomly used to parameterize the multiple regression models (20 random sets, Tables S3–S4). These models were used to predict the leaf photosynthetic parameters 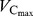 , J
max, k
3 and J
fac of the remaining observations from their environmental growth conditions. As SLA was not predictable from environmental growth conditions (see in result the low coefficient of determination in SLA regression model), experimental specific values were used. Finally, W
c, W
j and N
ac were calculated and the coordination hypothesis was evaluated again (Tables S5–S6).
, J
max, k
3 and J
fac of the remaining observations from their environmental growth conditions. As SLA was not predictable from environmental growth conditions (see in result the low coefficient of determination in SLA regression model), experimental specific values were used. Finally, W
c, W
j and N
ac were calculated and the coordination hypothesis was evaluated again (Tables S5–S6).
We also attempted to falsify the testable hypothesis (W c = W j and N a = N ac) provided by the photosynthetic coordination hypothesis. To this end, we randomized environmental growth conditions among observations (permutation test) and tested the alternative hypothesis significant differences between W c and W j and between N a and N ac.
Prediction from our leaf photosynthesis coordination model
The implications of the coordination hypothesis for N ac, A n and PNUE were tested by varying: i) the values of the leaf parameters k 3 and J fac under mean environmental growth conditions (PPFD = 666 µmol m− 2 s− 1, T g = 16.9°C, h s = 0.74); ii) the values of the environmental growth parameters T g and PPFD assuming mean leaf photosynthetic parameter values (k 3 = 59.1 µmol g− 1 Np a s− 1; J fac = 2.45; SLA = 17.7 m2 kg− 1 DM).
All statistical tests were performed using Statgraphics Plus (v. 4.1, Manugistics, USA).
Results
Leaf Photosynthesis Shows Co-limitation Under Mean Growth Conditions
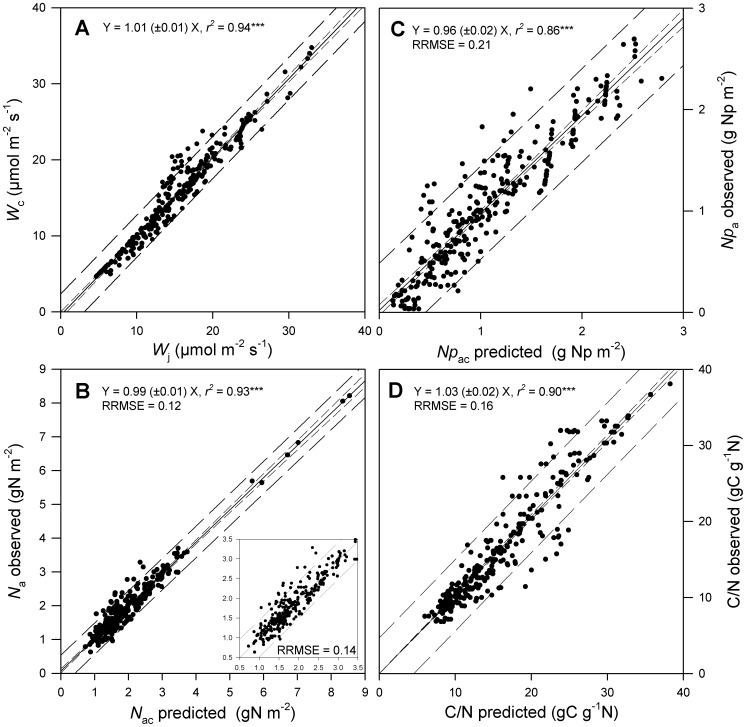
We assessed the level of photosynthetic co-limitation by comparing dark (W c) to light-driven (W j) biochemical processes under growth conditions experienced by the leaves in the month prior to observations. W c strongly correlated with W j (Fig. 1A, n = 293, P<0.001, intercept not significantly different from zero) across species and growth environments (characterized by T g, PPFD, h s and C g). An ANOVA on the regression residuals revealed a significant PFT effect (d.f. = 5, 283; P<0.001; data not shown). The calculated W c/W j ratio was not significantly different from one (t-test at P<0.05, n = 293). This ratio varied neither with species parameters, nor with environmental growth conditions.
Figure 1. Tests of the coordination hypothesis using experimental values of leaf photosynthetic traits (Vc max, J max, J fac, k 3 and SLA).
A) Relationship between the predicted rates of RuBP carboxylation/oxygenation (W c) and RuBP regeneration (W j) under plant growth conditions. B) Relationship between predicted (N ac) and observed (N a) leaf N content. N a was calculated as the sum of the leaf photosynthetic and structural N contents. Leaf photosynthetic N content was predicted using Eqn 2 with the species-specific parameters k 3 and J fac. C) Relationship between predicted (Np ac) and observed (Np a) photosynthetic leaf N content. D) Relationship between predicted and observed leaf C/N ratio. A common leaf structural N content was used (fns = 0.012 gN g− 1 DM). Solid lines are the regressions. Short-dashed and long-dashed lines indicate the confidence (at 95%) and prediction intervals, respectively. The insert in Fig. 1B shows the same relationship without the very high observed N a values for the PFT1. ***, P<0.001.
Predicted Coordinated Leaf N Content (N ac) Matches Observed Leaf N Content (N a)
Overall, predicted and observed N a values were closely correlated with a slope not significantly different from one and an intercept not significantly different from zero (Fig. 1B, n = 293, P<0.001, RRMSE = 0.12). The breakdown of RRMSE into unsystematic and systematic error terms showed that the prediction error was mostly unsystematic and therefore associated to data and not to a systematic model error (RRMSEs = 0.012; RRMSEu = 0.108). An ANOVA on the residuals of the prediction showed weak but significant effects of PFTs, T g and h s (d.f. = 5, 1, 1, respectively; P<0.01; data not shown).
As f ns was assumed constant across species [25], we calculated N pa and N pac by subtracting the ratio f ns/SLA to N a and N ac, respectively. Similarly, predicted and observed Np a values were closely correlated (Fig. 1C, n = 293, P<0.001, RRMSE = 0.21).
As carbon content in leaves was assumed to be approximately constant, we calculated a C/N ratio by dividing N a and N ac by the ratio between a common carbon content (fcs = 0.45 gC g− 1 DM; [36], [38]) and SLA. Predicted C/N matched significantly the calculated C/N, observed across environmental conditions and across species and PFTs (Fig. 1D).
Dependency of Leaf Parameters on Plant Functional Type
In the dataset (Table S1), the parameters used to calculate leaf photosynthesis and stomatal conductance were SLA, J
fac, k
3, calculated from 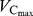 , J
max and leaf N measurements (Eqn 12, 15). At T
r,
, J
max and leaf N measurements (Eqn 12, 15). At T
r, 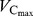 and J
max varied between 4–141 µmol m−
2 s−
1 and 8–213 µmol m−
2 s−
1, respectively. k
3 varied from 4.6 to 350 µmol g−
1N s−
1 while J
fac values were very constrained from 1.69 to 3.71, as already observed [2]. Finally, SLA varied from 1.5 to 43.2 m2 kg−
1 DM. All photosynthetic traits showed significant dependency to PFT (P<0.001) but with different determination coefficient (r
2 = 0.66, 0.64, 0.24, 0.47 and 0.40 for
and J
max varied between 4–141 µmol m−
2 s−
1 and 8–213 µmol m−
2 s−
1, respectively. k
3 varied from 4.6 to 350 µmol g−
1N s−
1 while J
fac values were very constrained from 1.69 to 3.71, as already observed [2]. Finally, SLA varied from 1.5 to 43.2 m2 kg−
1 DM. All photosynthetic traits showed significant dependency to PFT (P<0.001) but with different determination coefficient (r
2 = 0.66, 0.64, 0.24, 0.47 and 0.40 for 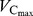 , J
max, k
3, J
fac and SLA, respectively). Post-ANOVA LSD tests showed that the discrimination among the PFTs was more effective for J
fac, J
max and SLA separating significantly four groups among the six PFTs (Table S7) and was much weaker for k
3 and
, J
max, k
3, J
fac and SLA, respectively). Post-ANOVA LSD tests showed that the discrimination among the PFTs was more effective for J
fac, J
max and SLA separating significantly four groups among the six PFTs (Table S7) and was much weaker for k
3 and 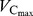 (two groups were significantly distinguished).
(two groups were significantly distinguished).
k 3, J fac and SLA can be optimized to a value which minimizes the squared differences between N a and N ac (Table 3A). When k 3 was optimized by PFT, N a was accurately predicted (slope = 0.96, r 2 = 0.73, RRMSE = 0.23). When a single value was used for the whole dataset, N a prediction was not satisfactory. The optimization by PFT of J fac led to a strong prediction of N a (slope not different from one, r 2 = 0.79, RRMSE = 0.23). When a single value was used for the entire dataset (J fac = 2.11), the prediction of N a was less accurate but the slope of the relationship between W c and W j remained close to one. Finally, the optimisation of SLA by PFT or to a single value for the entire dataset strongly reduced the accuracy of N a prediction. Optimization of the k 3 and J fac parameters showed that N a can be acceptably predicted when their values are defined by PFT. For all traits, average values by PFT and optimized values by PFT displayed significant linear relationships (Table 3B).
Table 3. Estimates of the optimized value (for the entire dataset and by PFT) of leaf photosynthetic traits (J fac, k 3 and SLA).
| A) | Optimized value | W c/W j | N a/N ac | ||||||||
| Parameter | Slope | r 2 | Slope | r 2 | RRMSE | ||||||
| k 3 | |||||||||||
| All | 48.3 | 1.15±0.02 | 0.78 | 0.94±0.02 | 0.64 | 0.28 | |||||
| PFT | 45.2; 37.1; 54.0; 79.4; 46.2; 24.2 | 1.08±0.02 | 0.88 | 0.96±0.02 | 0.73 | 0.23 | |||||
| J fac | |||||||||||
| All | 2.11 | 1.06±0.02 | 0.89 | 0.97±0.02 | 0.68 | 0.31 | |||||
| PFT | 2.11; 2.11; 2.59; 1.70; 2.33; 3.10 | 1.04±0.02 | 0.92 | 1.02±0.02 | 0.79 | 0.23 | |||||
| SLA | |||||||||||
| All | 17.7 | 1.02±0.02 | 0.92. | 0.88±0.02 | 0.43 | 0.44 | |||||
| PFT | 8.1; 13.7; 18.2; 20.0; 18.3; 13.4 | 1.02±0.02 | 0.92. | 0.96±0.02 | 0.48 | 0.37 | |||||
| k 3 and J fac | |||||||||||
| All | k 3 = 48.3; J fac = 2.11 | 1.18±0.02 | 0.79 | 0.89±0.02 | 0.68 | 0.33 | |||||
| PFT | k 3 = 45.2; 37.1; 54.0; 79.4; 46.2; 24.2 J fac = 2.11; 2.11; 2.59; 1.70; 2.33; 3.10 | 1.06±0.02 | 0.88 | 0.96±0.02 | 0.74 | 0.26 | |||||
| B) | k 3 | J fac | SLA | ||||||||
| PFT | Mean | Optimized | Mean | Optimized | Mean | Optimized | |||||
| PFT1 | 65.0 | 45.2 | 2.23 | 2.11 | 11.1 | 8.1 | |||||
| PFT2 | 46.6 | 37.1 | 2.32 | 2.11 | 13.1 | 13.7 | |||||
| PFT3 | 90.1 | 54.0 | 2.53 | 2.59 | 21.4 | 18.2 | |||||
| PFT4 | 86.1 | 79.4 | 2.04 | 1.7 | 22.0 | 20.0 | |||||
| PFT5 | 44.9 | 46.2 | 2.69 | 2.33 | 18.3 | 18.3 | |||||
| PFT6 | 38.1 | 24.2 | 2.50 | 3.1 | 20.3 | 13.4 | |||||
| Correlation | r 2 = 0.68 | P<0.001 | r 2 = 0.49 | P<0.001 | r 2 = 0.68 | P<0.001 | |||||
The squared difference between measured N a and predicted N ac values were minimized by Newton’s method. A) The optimization was done with one trait at a time without changing the values of the two other traits. The optimized values are ordered by PFT (i.e. the first value corresponds to PFT1). B) The optimized values by PFT were compared to mean per PFT in the dataset by using a linear regression model. Abbreviations: PFT1, temperate broadleaved and coniferous evergreen trees; PFT2, temperate broadleaved deciduous trees; PFT3, deciduous shrubs and herbs; PFT4, perennial C3 grasses and forbs; PFT5, C3 crops (wheat); PFT6, N-fixing trees.
Dependency of Leaf Parameters to Environmental Growth Conditions
All leaf photosynthetic parameters could be predicted from environmental growth conditions (Table 4). However, SLA was poorly correlated with environmental conditions (r
2 = 0.15). J
max was reasonably well predicted by environment (r
2 = 0.64, P<0.001). It was predominantly affected by the N level experienced by plants during growth (36% of explained variance), with a high N level leading to higher J
max values. J
max was then positively affected by PPFD (7%), h
s (13%), and PPFD times T
g (5%) and was negatively affected by soil moisture level (12%), T
g (9%), and PPFD times h
s (18%). 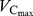 , which was significantly predicted from environmental condition during growth (r
2 = 0.66, P<0.001), was mainly affected by T
g (33%, negatively), N level (25%, positively) and soil moisture level (15%, negatively). Then,
, which was significantly predicted from environmental condition during growth (r
2 = 0.66, P<0.001), was mainly affected by T
g (33%, negatively), N level (25%, positively) and soil moisture level (15%, negatively). Then, 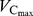 was positively affected by PPFD (8%) and h
s (5%) and was negatively affected by CO2 level (5%) and PPFD times h
s (8%).
was positively affected by PPFD (8%) and h
s (5%) and was negatively affected by CO2 level (5%) and PPFD times h
s (8%).
Table 4. Effects of environmental conditions on the leaf photosynthetic traits: 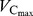 J
max, J
fac, k
3 and SLA.
J
max, J
fac, k
3 and SLA.
| A) | J max |
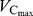
|
log J fac | log k 3 | SLA | ||||||
| Factors | d.f. | Variance | P-value | Variance | P-value | Variance | P-value | Variance | P-value | Variance | P-value |
| CO2 level | 1 | . | ns | 4.6 | <0.01 | 27.0 | <0.001 | . | ns | . | ns |
| N level | 3 | 35.5 | <0.001 | 24.5 | <0.001 | 9.8 | <0.05 | 65.1 | <0.001 | 7.3 | <0.05 |
| H2O level | 1 | 12.2 | <0.001 | 15.3 | <0.001 | 8.1 | <0.01 | . | ns | 3.1 | <0.01 |
| PPFD | 1 | 6.6 | <0.01 | 8.9 | <0.001 | 5.7 | <0.05 | 2.1 | <0.05 | 0.1 | <0.01 |
| T g | 1 | 9.5 | <0.01 | 33.1 | <0.001 | . | ns | 25.3 | <0.001 | 77.9 | <0.001 |
| h s | 1 | 12.7 | <0.001 | 5.4 | <0.01 | 19.2 | <0.001 | 4.5 | <0.01 | 1.8 | <0.05 |
| PPFD*T g | 1 | 5.4 | <0.05 | . | ns | 6.0 | <0.05 | . | ns | . | ns |
| PPFD*h s | 1 | 18.1 | <0.001 | 8.2 | <0.001 | 24.2 | <0.001 | 3.0 | <0.05 | 9.7 | <0.05 |
| Overall | 293 | r 2 = 0.64 | <0.001 | r 2 = 0.66 | <0.001 | r 2 = 0.51 | <0.001 | r 2 = 0.44 | <0.001 | r 2 = 0.15 | <0.01 |
The factors are environmental growth conditions: radiation (PPFD), temperature (T
g), relative humidity (h
s), air CO2 concentration (CO2 level), soil N availability (N level) and soil moisture (H2O level). A) Degree of freedom (d.f.), variance explained (%), statistical significance and sign (positive or negative) of interactions with continuous variables. B) Coefficients estimate of ANOVA model. All variable values were analyzed at a reference temperature of 20°C. Residuals of analysis followed a normal distribution without transformation for 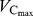 and J
max, and with log-transformation for J
fac and k
3. We only included in the ANOVA model the interactions that were significant.
and J
max, and with log-transformation for J
fac and k
3. We only included in the ANOVA model the interactions that were significant.
J fac was significantly predicted from environment (r 2 = 0.51, P<0.001) and the variance was shared between CO2 level (27%, positively), h s (19%, positively), and PPFD times h s (24%, negatively). Note that J fac increased with CO2 concentration as reviewed by Ainsworth and Long [33]. The remaining variance was positively explained by PPFD (6%) and PPFD times T g (6%) and negatively explained by N and moisture levels (10 and 8%, respectively). k3 was significantly predicted (r 2 = 0.44, P<0.001) and the variance was predominantly explained by N level (65%), with higher k 3 at lower N availability level, as also reviewed by Ainsworth and Long [33]. The temperature experienced by leaves during the preceding month was also an important driver of k 3 (25%), with lower k 3 at higher temperature. The remaining variance was positively explained by PPFD (2%) and h s (4%) and negatively explained by PPFD times h s (3%).
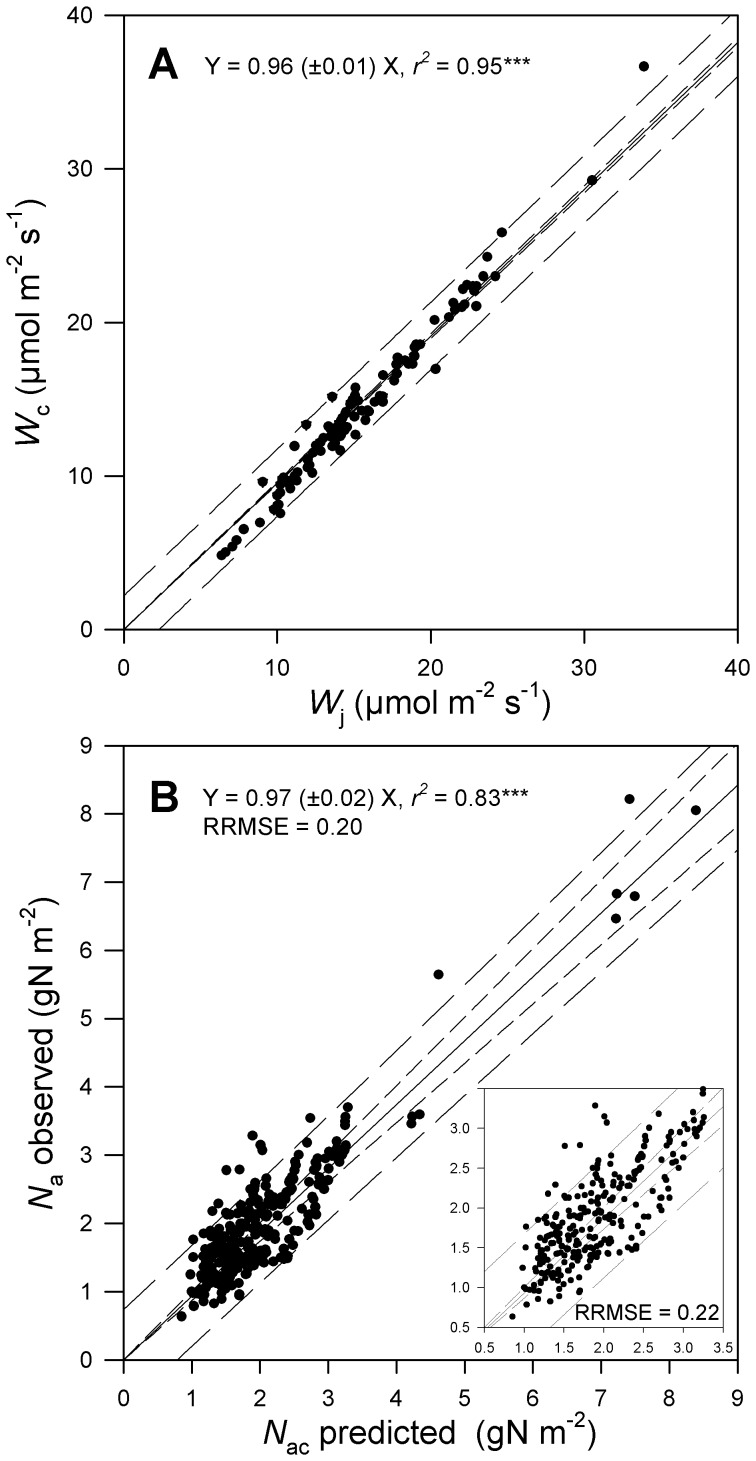
Once the multiple regression models were established for each leaf photosynthetic parameter, we tested by bootstrap analysis if their prediction was robust enough to satisfy the coordination hypothesis. All random datasets generated by bootstrap (n = 220) gave significant regression models (Tables S5–S6). The parameters values of these regression models were used with the remainder of the data (n = 293–220 = 70) to predict leaf photosynthetic parameters values. Photosynthetic parameters values were then used to predict W c, W j and N ac. We found that W c matched W j (Fig. 2A) and N ac matched N a (Fig. 2B, RRMSE = 0.2), whatever the random dataset to which it was applied (Tables S5–S6).
Figure 2. Tests of the coordination hypothesis using values of leaf photosynthetic traits predicted from environmental growth conditions.
A) Relationship between the predicted rates of RuBP carboxylation/oxygenation (W c) and RuBP regeneration (W j) under plant growth conditions. B) Relationship between predicted (N ac) and observed (N a) leaf N content. The insert in Fig. 2B shows the same relationship without the very high observed N a values for the PFT1. Symbols are as for Fig. 1.
In an attempt to falsify the leaf photosynthesis coordination hypothesis, we have randomized environmental growth conditions among observations. This randomization resulted in a strong mismatch between W c and W j (RRMSE = 0.76; slope = 0.60±0.33; r 2 = 13%) as well as between N a and N ac (RRMSE = 0.72; slope = 0.80±0.40; r 2 = 17%).
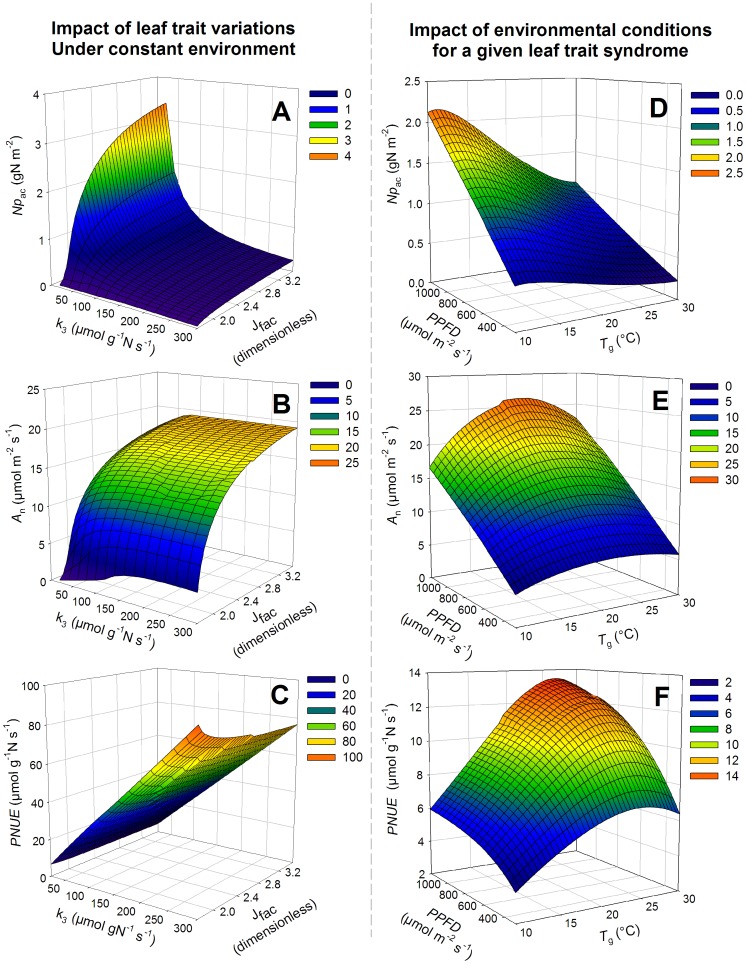
Prediction from Our Leaf Photosynthesis Coordination Model
Under standard environmental conditions, Np ac varied significantly with k 3 and J fac (Fig. 3A). Np ac decreased with increasing k 3 (Fig. 3A), which imposed a strong constraint on this physiological trait. For a given leaf Np ac, high values of k 3 did not affect A n (Fig. 3B), but PNUE increased linearly with k 3 (Fig. 3C). For a given k 3 value, both Np ac (Fig. 3A) and A n (Fig. 3B) displayed saturating responses to increasing J fac. As a consequence, PNUE was little affected by J fac (Fig. 3C). In our model (Eqn 1), SLA and f ns affected N ac, but did not affect Np ac and consequently A n and PNUE. Since SLA displayed a higher degree of variation, the leaf structural content per unit area and consequently the leaf N content were strongly dependent on SLA. Thus, the leaf structural N content per unit area and the leaf N content followed an inverse relationship as SLA increased.
Figure 3. Relationships between simulated photosynthetic leaf N content (Np ac) (A), net photosynthesis (A n) (B) and photosynthetic N use efficiency (PNUE) (C) and the photosynthetic traits k 3 and J fac under standard mean environmental conditions (PPFD = 666 µmol m−2 s−1, T g = 16.9°C, h s = 0.74).
k
3 is the ratio between 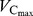 and Np
a. J
fac is the ratio between J
max and
and Np
a. J
fac is the ratio between J
max and 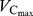 . A mesh of k
3 values varying between 10 and 300 µmol g−1 N s−1 with 20 steps and of J
fac values varying between 1.75 and 3.5 with 0.05 steps was used. Figures D–E–F, relationships between (Np
ac) (D), net photosynthesis (A
n) (E) and photosynthetic N use efficiency (PNUE) (F) and the radiation (PPFD) and temperature (T
g) conditions during growth. Averages over the dataset of leaf photosynthetic parameters (k
3, J
fac and SLA) are used (k
3 = 59.1 µmol g−1
N
pa s−1, J
fac = 2.45, SLA = 17.7 m2 kg−1 DM). The mesh for temperature is 0.5°C between 10 and 30°C and the mesh for radiation is 50 µmol m−2 s−1 between 300 and 1200 µmol m−2 s−1. The values of h
s and T
g were fixed at 0.8 and 20°C, respectively. A
n was calculated with the coordinated leaf protein content and PNUE was calculated as the ratio between A
n and Np
ac.
. A mesh of k
3 values varying between 10 and 300 µmol g−1 N s−1 with 20 steps and of J
fac values varying between 1.75 and 3.5 with 0.05 steps was used. Figures D–E–F, relationships between (Np
ac) (D), net photosynthesis (A
n) (E) and photosynthetic N use efficiency (PNUE) (F) and the radiation (PPFD) and temperature (T
g) conditions during growth. Averages over the dataset of leaf photosynthetic parameters (k
3, J
fac and SLA) are used (k
3 = 59.1 µmol g−1
N
pa s−1, J
fac = 2.45, SLA = 17.7 m2 kg−1 DM). The mesh for temperature is 0.5°C between 10 and 30°C and the mesh for radiation is 50 µmol m−2 s−1 between 300 and 1200 µmol m−2 s−1. The values of h
s and T
g were fixed at 0.8 and 20°C, respectively. A
n was calculated with the coordinated leaf protein content and PNUE was calculated as the ratio between A
n and Np
ac.
When using overall dataset means of the leaf photosynthetic traits, Np ac varied significantly with radiation and temperature (Fig. 3D). Np ac increased linearly with PPFD and decreased with Tg according to a logistic curve (Fig. 3D, Fig. S2). For a given Np ac, temperature affected A n according to a quadratic curve with an optimal Tg around 20°C although PPFD affected linearly A n (Fig. 3E). As a consequence, PNUE was affected by Tg according to a peak curve with an optimal Tg at 25°C and was positively affected by PPFD according to a logarithmic curve (Fig. 3F).
Discussion
A Successful Test of the Coordination Hypothesis of Leaf Photosynthesis
The coordination hypothesis provides a testable analytical solution to predict both photosynthetic capacity and area-based leaf N content and, hence, to couple photosynthetic C gain and leaf N investment. With the large dataset used in this study, we could not falsify this testable hypothesis. Therefore, our results strongly support the validity of the leaf photosynthetic coordination hypothesis across a wide range of C3 plant species and of environmental conditions.
Our coordination model linking leaf photosynthesis, stomata conductance and nitrogen investment has a total of 33 parameters. Only four parameters are directly related to a coordinated investment of leaf N into carboxylation capacity (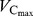 ; RuBP carboxylation; Rubisco) and electron transport capacity (J
max, RuBP regeneration; light harvesting): J
fac, the ratio of J
max to
; RuBP carboxylation; Rubisco) and electron transport capacity (J
max, RuBP regeneration; light harvesting): J
fac, the ratio of J
max to 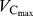 determines the photosynthetic capacity; and k3, the ratio of
determines the photosynthetic capacity; and k3, the ratio of 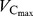 to leaf photosynthetic N content (Np
ac) determines the fraction of metabolic leaf N invested in photosynthesis. The ratio of f
ns to SLA determines the fraction of non-metabolic N per unit total leaf N.
to leaf photosynthetic N content (Np
ac) determines the fraction of metabolic leaf N invested in photosynthesis. The ratio of f
ns to SLA determines the fraction of non-metabolic N per unit total leaf N.
Photosynthetic parameter values vary to a considerable extent across species and environmental conditions in agreement with previous studies [2], [3], [39]. For instance, Wullschleger [2] reported that, when expressed at a reference temperature of 20°C, 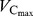 varies in the range 5–142 (µmol m−
2 s−
1); J
max in the range 11–251 (µmol m−
2 s−
1) and J
fac in the range 0.9–3.8 (dimensionless). Despite similar large differences in our dataset in parameter values across species and environmental conditions, our photosynthetic coordination model accounts for 93% of the total variance in N
a. Moreover, the model has a low systematic RRMSE with no systematic bias. The statistical validity of this model supports the conclusion that sunlit mature leaves of C3 plants tend to achieve photosynthetic coordination in a wide range of both optimal and sub-optimal environmental conditions.
varies in the range 5–142 (µmol m−
2 s−
1); J
max in the range 11–251 (µmol m−
2 s−
1) and J
fac in the range 0.9–3.8 (dimensionless). Despite similar large differences in our dataset in parameter values across species and environmental conditions, our photosynthetic coordination model accounts for 93% of the total variance in N
a. Moreover, the model has a low systematic RRMSE with no systematic bias. The statistical validity of this model supports the conclusion that sunlit mature leaves of C3 plants tend to achieve photosynthetic coordination in a wide range of both optimal and sub-optimal environmental conditions.
Along the vertical profile of C3 plant canopies, an empirical scaling law between area based leaf N content and transmitted PPFD has often been reported [15], [17], [40], [41] and has been determined as the predominant factor of N decline relative to others like leaf age or N demand [12], [40], [41]. Various hypotheses have been put forward to explain this observation [11], [22], [42], [43]. Our model of the coordination hypothesis matches this scaling law, since Np ac scales with radiation (PPFD) along the vertical canopy profile (Eqn. 2). Air temperature (T g), relative air humidity (h s) and ambient CO2 concentration (C a) also vary with depth within the canopy. At a given PPFD, higher h s and lower T g at depth would reduce Np ac, while a lower C a would increase it. For some crop species like wheat, N limitation has been reported to accelerate the decline in N a with PPFD [25], [40], [41], which may indicate preferential N allocation to leaves in full light, resulting in preferential photosynthetic coordination of these leaves despite N limitation.
Variations in photosynthetic N protein contents (Np ac) appear to be an overwhelming determinant of N a. In contrast, structural leaf N (f ns) values varied only within a narrow range [38], when they were optimized by species or by PFT (from 0.0107 to 0.0135 gN g− 1 DM for wheat and N-fixing trees, respectively, corresponding to 0.61 and 0.78 gN m− 2 leaf when SLA is set to 17.6 m2 kg− 1 DM, dataset mean). Although optimized f ns values showed little variations on a leaf dry mass basis, it accounted for 15–50% of N a (gN m− 2), across all species in the dataset due to the strong variation in SLA across all species. Structural N is found in cell walls (1.6–9.5% of leaf N in Polygonum cupsidatum and 40–60% for sclerophyllous tree, shrub and vine species, [34], [44]) and in nucleic acids (10–15%, [45]). In addition, other non-photosynthetic nitrogenous compounds (e.g. cytosolic proteins, amino acids, ribosomes and mitochondria) contribute to the structural leaf N pool [46]. Several experimental studies have attempted to estimate f ns, reporting values between 0.0101 and 0.0136 gN g− 1 DM for a range of herbaceous C3 species [16]. These f ns values are in the same range as those found for dead leaves after N resorption at senescence [47]. Structural N would therefore not be redistributed by this process [48].
Determinism of Leaf N Content Variation
Genetic and environmental factors have long been recognized to interact in determining the A max vs. leaf N relationship [5]. Our study provides a means for disentangling: i) the direct environmental effects on leaf photosynthetic N content (Np ac); ii) the role of photosynthetic parameters for Np ac in a given environment; and iii) the response of photosynthetic parameters i.e. the plant acclimation to plant growth environment.
First, for a given set of plant parameters, positive effects of radiation and negative effects of air temperature, air relative humidity and CO2 concentration on Np
ac are predicted by Eqn 2 (Fig. 3D–F). These results are in accordance with the prediction by Farquhar et al’s canopy photosynthesis model [49], which links stomatal control with leaf area and leaf N content by optimizing both water and nitrogen use efficiency and predicts an increase of leaf N content and 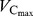 with mean radiation increase [24], [50] and mean annual rainfall [49], [51]. According to the coordination hypothesis, changes in Np
ac affect both biochemical photosynthesis capacities,
with mean radiation increase [24], [50] and mean annual rainfall [49], [51]. According to the coordination hypothesis, changes in Np
ac affect both biochemical photosynthesis capacities, 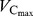 and J
max. Indeed, seasonal variations in
and J
max. Indeed, seasonal variations in 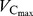 and J
max have been observed for a number of plant species [52], [53] and were related to changes in Rubisco and cytochrome-f contents in Polygonum cuspidatum
[54]. Including photosynthetic capacity (
and J
max have been observed for a number of plant species [52], [53] and were related to changes in Rubisco and cytochrome-f contents in Polygonum cuspidatum
[54]. Including photosynthetic capacity (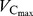 and A
max) and its relationship to leaf N content in terrestrial biosphere models resulted in substantial changes in gross primary productivity with latitude [7]. Coupled environmental variations in PPFD, T
K, h
s and C
a simultaneously affect Np
ac throughout time, which has major implications for gross primary productivity and PNUE of a given species or genotype.
and A
max) and its relationship to leaf N content in terrestrial biosphere models resulted in substantial changes in gross primary productivity with latitude [7]. Coupled environmental variations in PPFD, T
K, h
s and C
a simultaneously affect Np
ac throughout time, which has major implications for gross primary productivity and PNUE of a given species or genotype.
Second, the coordination hypothesis implies that under a given environment, N
a tends toward a unique coordinated N
ac value (Eqn 2). As shown by the analysis of model sensitivity to parameters and input variables (Text S1, Fig. S3), k
3 and J
fac are among the most important determinants of Nac value. Assuming a single average value of k
3 and of J
fac for all species in the dataset would increase N
a RRMSE by 50% (Table 3A). However, using a single J
fac value by PFT with species-specific k
3 and SLA values provided a strong accuracy for N
a prediction. This result is consistent with the strong linear relationship between 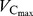 and J
max reported by Wullschleger [2] among 109 species, which probably indicates a phylogenetic constraint for J
fac. Under given environmental conditions, our results show that there is no single combination of k
3 and J
fac that can maximize both A
n and PNUE (Fig. 3A–C). Therefore, variable combinations of these photosynthetic traits could be equally relevant. This relative independency of k
3 and J
fac suggests that these functional traits (sensu
[55]) correspond to possibly overlooked axes of differentiation among C3 plant species. k
3, which modulates the N investment at a given A
n, could be related to a plant strategy of nutrients conservation [56]. J
fac, which increases A
n for a given k3, could be related to a plant strategy of nutrients exploitation. However, the lack of correlation between these two photosynthetic traits and SLA, which is a key morphological trait separating exploitative and conservative species strategies for nutrient use [56], suggests that these physiological traits form a secondary axis of differentiation across C3 species.
and J
max reported by Wullschleger [2] among 109 species, which probably indicates a phylogenetic constraint for J
fac. Under given environmental conditions, our results show that there is no single combination of k
3 and J
fac that can maximize both A
n and PNUE (Fig. 3A–C). Therefore, variable combinations of these photosynthetic traits could be equally relevant. This relative independency of k
3 and J
fac suggests that these functional traits (sensu
[55]) correspond to possibly overlooked axes of differentiation among C3 plant species. k
3, which modulates the N investment at a given A
n, could be related to a plant strategy of nutrients conservation [56]. J
fac, which increases A
n for a given k3, could be related to a plant strategy of nutrients exploitation. However, the lack of correlation between these two photosynthetic traits and SLA, which is a key morphological trait separating exploitative and conservative species strategies for nutrient use [56], suggests that these physiological traits form a secondary axis of differentiation across C3 species.
Third, some environmental growth conditions such as PPFD, T
g, h
s, C
a and N availability had significant effects on k
3 and J
fac. The increase in k
3 at low N availability tends to reduce Np
ac and, hence, N demand for leaf construction thereby increasing PNUE. The increase in k
3 with PPFD tends to compensate for the direct positive effect of PPFD on Np
ac, thereby lowering N demand for leaf construction under high light environments. Similarly, the decrease of k
3 with T
g mitigates the direct negative effect of temperature on Np
ac, thereby equalizing the N demand for a range of temperature. Mostly independently from changes in k
3 (since these two traits are not correlated across plant species), J
fac increases with C
a, in agreement with the lower decline under elevated CO2 of J
max compared to 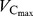 [33]. Moreover, J
fac is negatively related to PPFD, which is in good agreement with the higher allocation of leaf N to chlorophyll observed in low PPFD acclimation experiments [57]. Like the increase in k
3, the decrease in J
fac with PPFD tends to compensate for the direct positive effect of PPFD on Np
ac, especially for species with low k
3 value. Finally, the effect of temperature on J
fac is not significant which is in agreement with previous studies that reports constant J
fac with temperature (e.g. [33]).
[33]. Moreover, J
fac is negatively related to PPFD, which is in good agreement with the higher allocation of leaf N to chlorophyll observed in low PPFD acclimation experiments [57]. Like the increase in k
3, the decrease in J
fac with PPFD tends to compensate for the direct positive effect of PPFD on Np
ac, especially for species with low k
3 value. Finally, the effect of temperature on J
fac is not significant which is in agreement with previous studies that reports constant J
fac with temperature (e.g. [33]).
Uncertainties in the Calculation of the Coordinated Leaf Photosynthetic N Content
Our model takes into account the two main biochemical processes controlling leaf photosynthesis as well as the biophysical process controlling stomatal conductance. Recently, leaf mesophyll conductance has also been identified as an important biophysical limitation of photosynthesis [58]–[60], particularly for species with low SLA by decreasing 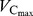 more than J
max
[61], [62] and particularly during plant acclimation to water stress condition [58], [59]. Applying mesophyll conductance in our model would first require recalculating
more than J
max
[61], [62] and particularly during plant acclimation to water stress condition [58], [59]. Applying mesophyll conductance in our model would first require recalculating 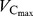 parameter from a non-rectangular hyperbola of the A
n-C
i curve and with a new set of Rubisco kinetic constants, for example [58]. Moreover, it would also require the incorporation in our model of the CO2 diffusion mechanism between intercellular and chloroplast spaces according to a mesophyll conductance parameter [59], [60]. Furthermore, the coupling between A
n and g
s leading to the calculation of A
n would require solving a new system of equations and unknowns. Finally, this would require additional mesophyll conductance data, which were not available in our dataset. The inclusion of a variable mesophyll conductance [61], [62], as well as of other mechanisms implied in plant responses to water deficits [63], would allow testing the photosynthetic coordination hypothesis under severe abiotic stress conditions. With the coordination model reported here that does not include these processes, N
a values are lower than N
ac values under more severe abiotic stress conditions (data not shown).
parameter from a non-rectangular hyperbola of the A
n-C
i curve and with a new set of Rubisco kinetic constants, for example [58]. Moreover, it would also require the incorporation in our model of the CO2 diffusion mechanism between intercellular and chloroplast spaces according to a mesophyll conductance parameter [59], [60]. Furthermore, the coupling between A
n and g
s leading to the calculation of A
n would require solving a new system of equations and unknowns. Finally, this would require additional mesophyll conductance data, which were not available in our dataset. The inclusion of a variable mesophyll conductance [61], [62], as well as of other mechanisms implied in plant responses to water deficits [63], would allow testing the photosynthetic coordination hypothesis under severe abiotic stress conditions. With the coordination model reported here that does not include these processes, N
a values are lower than N
ac values under more severe abiotic stress conditions (data not shown).
The calculation of Np ac relies on a number of plant parameter and environmental variables, leading to further uncertainties (see Text S1, Table S2 and Fig. S2–S3 for full details). Apart from SLA, k 3 and J fac, all plant parameters were assumed to have a single set of values across the entire dataset (Table 2). Since the photosynthetic model was shown to be little sensitive to most of these parameters (Text S1, Fig. S3), using species-specific values would only marginally increase the accuracy of N a prediction.
Implications
Overall, our study confirms the basic assumption of the coordination hypothesis: leaves coordinate the development of 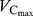 and J
max such that W
c equals W
j. This opens opportunities to couple C and N at a global scale by incorporating the coordination hypothesis into dynamic global vegetation models (DGVMs). However, the applicability of this hypothesis for improved prediction of photosynthetic capacity and leaf nitrogen content depends on the accuracy at which we can determine key parameters of the combined photosynthesis - stomatal conductance – leaf N model as well as the timescale of plant regulatory photosynthesis mechanisms. The two key parameters J
fac and k
3 seem to be predictable from a combination of environmental growth conditions - probably due to the strong dependence of the development of the photosynthetic machinery on environment variables – and information about plant growth form or PFT. However, the morphological trait SLA does not seems to be predictable with sufficient accuracy from environmental conditions which is consistent with the large functional diversity found in a given environment [64]. SLA needs to be defined at least by PFT and preferably by species. This study thus confirms the relevance of leaf morphology, represented by SLA, in photosynthesis, which has been pointed out before, (e.g.
[56]). However, SLA is one of the best-studied plant traits worldwide (e.g.
[36]) and it may be possible to determine SLA with sufficient accuracy for a large range of C3 species. Finally, although the turnover of photosynthetic enzymes like Rubisco can be seen as very constrained within the C3 plant kingdom, to our knowledge there is no study that investigates its variability across species. We therefore stress the need for further comparative research quantifying the variability of photosynthetic enzyme turnover across C3 species. Further tests of the coordination hypothesis will require, during plant growth, coupled measurements of microclimate, of leaf gas exchanges and of photosynthetic traits, including the dynamics of Rubisco, within the canopy [65].
and J
max such that W
c equals W
j. This opens opportunities to couple C and N at a global scale by incorporating the coordination hypothesis into dynamic global vegetation models (DGVMs). However, the applicability of this hypothesis for improved prediction of photosynthetic capacity and leaf nitrogen content depends on the accuracy at which we can determine key parameters of the combined photosynthesis - stomatal conductance – leaf N model as well as the timescale of plant regulatory photosynthesis mechanisms. The two key parameters J
fac and k
3 seem to be predictable from a combination of environmental growth conditions - probably due to the strong dependence of the development of the photosynthetic machinery on environment variables – and information about plant growth form or PFT. However, the morphological trait SLA does not seems to be predictable with sufficient accuracy from environmental conditions which is consistent with the large functional diversity found in a given environment [64]. SLA needs to be defined at least by PFT and preferably by species. This study thus confirms the relevance of leaf morphology, represented by SLA, in photosynthesis, which has been pointed out before, (e.g.
[56]). However, SLA is one of the best-studied plant traits worldwide (e.g.
[36]) and it may be possible to determine SLA with sufficient accuracy for a large range of C3 species. Finally, although the turnover of photosynthetic enzymes like Rubisco can be seen as very constrained within the C3 plant kingdom, to our knowledge there is no study that investigates its variability across species. We therefore stress the need for further comparative research quantifying the variability of photosynthetic enzyme turnover across C3 species. Further tests of the coordination hypothesis will require, during plant growth, coupled measurements of microclimate, of leaf gas exchanges and of photosynthetic traits, including the dynamics of Rubisco, within the canopy [65].
Conclusion
This study bridges a gap concerning the coupling of C and N fluxes in C3 plant species. It confirms the basic assumption of the leaf photosynthesis coordination hypothesis and demonstrates that this hypothesis can be successfully applied across species and PFTs and under a wide range of climates. Moreover, we have shown that k 3 and J fac in combination with SLA are major plant functional traits, which reflect plant adaptation to light, temperature and N availability during growth. Surprisingly, few studies provide both leaf photosynthetic parameters and environmental conditions during plant growth. Improved datasets combining the k 3 and J fac photosynthetic traits with the SLA morphological trait are needed to further increase our understanding of leaf economics (C–N stœchiometry) and plant strategies. The leaf photosynthesis coordination model reported here has been successfully used in a patch scale grassland vegetation model [66], [67]. Further applications include modeling at regional and global scales the role of plant diversity for the carbon and nitrogen cycles.
Supporting Information
Details on the leaf photosynthesis coordination hypothesis. Variation of leaf carboxylation rates with leaf nitrogen content for three levels of radiations (A–C). According to the leaf photosynthesis coordination theory, a leaf photosynthetic N content is determined as colimiting the carboxylation/oxygenation of ribulose-1,5-bisphosphate (RuBP) by the enzyme ribulose 1·5-bisphosphate carboxylase/oxygenase (Rubisco; W c), and the regeneration of RuBP by the electron transport chain (W j). Below N pac, the photosynthesis will be limited by the Rubisco activity and therefore by the amount of leaf proteins. Beyond N pac, the marginal gain of photosynthesis per unit of leaf proteins is weak. Along the vertical canopy profile, N pac declines with transmitted radiation when all other variables are equal.
(TIF)
Mean temperature functions of the maximum rates of carboxylation (
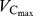 ) and electron transport (
J
max) and their ratio (
) and electron transport (
J
max) and their ratio (
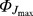 /
/
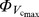 ). Functions were calculated using the parameters related to temperature sensitivity (activation and deactivation enthalpies and entropy) as calibrated by Kattge & Knorr (2007) for many species (48 species for
). Functions were calculated using the parameters related to temperature sensitivity (activation and deactivation enthalpies and entropy) as calibrated by Kattge & Knorr (2007) for many species (48 species for 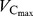 , 32 for J
max and 29 for their ratio). The error bars correspond to the standard errors among species representing the inter-specific variability.
, 32 for J
max and 29 for their ratio). The error bars correspond to the standard errors among species representing the inter-specific variability.
(TIF)
Sensitivity analysis of the photosynthesis-stomatal conductance model. Following Félix & Xanthoulis (2005), a sensitivity analysis of the models calibrated for Dactylis glomerata with common one-to-one variation of parameters (±15%). Output variables are shown as lines, parameters as columns. The sensitivity index (IOS) was calculated as the maximal ratio of output variation to parameter variation during a climatic scenario (air temperature, PPFD, h s and C a) recorded from an upland site in central France (Theix, 45°43′N, 03°01′E, 870 m) for years 2003–2004. Color tones indicate sensitivity index (positive, red; negative, blue).
(TIF)
Dataset used for the validation of leaf photosynthesis coordination. The excel file includes the leaf photosynthetic parameters and the environmental growth conditions used to calculate W c, W j and N ac.
(XLS)
Range of the observed values among literature of the parameters used in the leaf photosynthesis – stomatal conductance model. The categories were the minimum, the maximum, the median and the percentage of variation of parameters range. The sources of observations were also reported. The sources, where the minimum and maximum values were observed, were annotated with – and +. A reference temperature of 20°C was used.
(DOC)
Multiple regression analyses of Vc max and J max from environmental growth conditions for the bootstrap analysis. Independent variables: X1: air CO2 concentration (C g); X2: N level; X3: soil H2O level; X4: radiation (PPFD); X5: air growth temperature (T g); X6: air relative humidity (h s). The number of observations was 236.
(DOC)
Multiple regression analyses of k 3 and J fac from environmental growth conditions for a bootstrap analysis. Independent variables were the same as Table S3. The number of observations was 236.
(DOC)
Prediction of W c and W j (µmol m−2 s−1) in using the parameters Vc max and J max calculated from regression analyses on the independent part of the dataset in a bootstrap analysis (Table S3). Characteristics of the W c/ W j relationship. The intercepts of regression for each PFT were set to zero (since there were not significantly different from zero) to estimate the slopes. RRMSE: relative root mean square error.
(DOC)
Prediction of N ac in using the parameters k 3 and J fac calculated from the regression analyses on the independent part of the dataset in a bootstrap analysis (Table S4). Characteristics of the relationship between predicted and observed leaf N content (N ac/N a, gNm− 2). The intercepts of regression for each PFT were set to zero (since there were not significantly different from zero) to estimate the slopes. Abbreviation: RRMSES and RRMSEU are systematic and unsystematic relative root mean square error, respectively.
(DOC)
Dependence of leaf photosynthetic parameters on plant functional type (PFT). ANOVA model and mean comparison test by LSD method of the PFT effect on leaf photosynthetic traits used in the test of coordination hypothesis (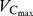 , J
max, k
3, J
fac and SLA). The values of k
3 and J
fac were log-transformed and all residuals followed a normal distribution. For a given variable, PFTs with the same letter belong to the same group.
, J
max, k
3, J
fac and SLA). The values of k
3 and J
fac were log-transformed and all residuals followed a normal distribution. For a given variable, PFTs with the same letter belong to the same group.
(DOC)
Sensitivity analysis of the photosynthesis – stomatal conductance model.
(DOC)
Demonstration of the formalism of the coordinated leaf photosynthetic N content.
(DOC)
Acknowledgments
Authors thank V. Allard, N. Gross, J. Schymanski, N. Viovy and P. Ciais for constructive comments on a previous version of the manuscript.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This study contributes to the French ANR DISCOVER project (ANR-05-BDIV-010-01). VM was funded by a PhD grant of the French research ministry (MENRT). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Farquhar GD, Caemmerer Sv, Berry JA. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta. 1980;149:90. doi: 10.1007/BF00386231. [DOI] [PubMed] [Google Scholar]
- 2.Wullschleger SD. Biochemical limitations to carbon assimilation in C3 plants - A retrospective analysis of the A/Ci curves from 109 species. J Exp Bot. 1993;44:920. [Google Scholar]
- 3.Wohlfahrt G, Bahn M, Horak I, Tappeiner U, Cernusca A. A nitrogen sensitive model of leaf carbon dioxide and water vapour gas exchange: application to 13 key species from differently managed mountain grassland ecosystems. Ecol Model. 1998;113:199. [Google Scholar]
- 4.Wohlfahrt G, Bahn M, Haubner E, Horak I, Michaeler W. Inter-specific variation of the biochemical limitation to photosynthesis and related leaf traits of 30 species from mountain grassland ecosystems under different land use. Plant Cell Environ. 1999;22:1296. [Google Scholar]
- 5.Field CB, Mooney HA. The photosynthesis-nitrogen relationship in wild plants. In: On the economy of plant form and function (ed T.J. Givnish), 25–55. Cambridge University Press, Cambridge. 1986.
- 6.Niinemets U, Tenhunen JD. A model separating leaf structural and physiological effects on carbon gain along light gradients for the shade-tolerant species Acer saccharum. Plant Cell Environ. 1997;20:866. [Google Scholar]
- 7.Kattge J, Knorr W, Raddatz T, Wirth C. Quantifying photosynthetic capacity and its relationship to leaf nitrogen content for global-scale terrestrial biosphere models. Global Change Biol 15: 4 976–991. 2009.
- 8.Zaehle S, Sitch S, Smith B, Hatterman F. Effects of parameter uncertainties on the modeling of terrestrial biosphere dynamics. Global Biogeochem Cycles. 2005;19:16. [Google Scholar]
- 9.Haxeltine A, Prentice IC. A general model for the light-use efficiency of primary production. Funct Ecol. 1996;10:561. [Google Scholar]
- 10.Sitch S, Smith B, Prentice IC, Arneth A, Bondeau A. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Global Change Biol. 2003;9:185. [Google Scholar]
- 11.Kull O. Acclimation of photosynthesis in canopies: models and limitations. Oecologia. 2002;133(3):279. doi: 10.1007/s00442-002-1042-1. [DOI] [PubMed] [Google Scholar]
- 12.Bertheloot J, Martre P, Andrieu B. Dynamics of light and nitrogen distribution during grain filling within wheat canopy. Plant Physiol. 2008;148:1720. doi: 10.1104/pp.108.124156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dreccer MF, Van Oijen M, Schapendonk A, Pot CS, Rabbinge R. Dynamics of vertical leaf nitrogen distribution in a vegetative wheat canopy. Impact on canopy photosynthesis. Ann Bot. 2000;86:831. [Google Scholar]
- 14.Dreccer MF, Slafer GA, Rabbinge R. Optimization of vertical distribution of canopy nitrogen: an alternative trait to increase yield potential in winter cereals. J Crop Prod. 1998;1:77. [Google Scholar]
- 15.Werger MJA, Hirose T. Leaf nitrogen distribution and whole canopy photosynthetic carbon gain in herbaceous stands. Vegetatio. 1991;97:20. [Google Scholar]
- 16.Schieving F, Pons TL, Werger MJA, Hirose T. The vertical distribution of nitrogen and photosynthetic activity at different plant densities in Carex acutiformis. Plant Soil. 1992;142:17. [Google Scholar]
- 17.Rousseaux MC, Hall AJ, Sanchez RA. Light environment, nitrogen content, and carbon balance of basal leaves of sunflower canopies. Crop Sci. 1999;39:1100. [Google Scholar]
- 18.Johnson IR, Thornley JHM, Frantz JM, Bugbee B. A model of canopy photosynthesis incorporating protein distribution through the canopy and its acclimation to light, temperature and CO2. Ann Bot. 2010;106:749. doi: 10.1093/aob/mcq183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Reynolds JF, Chen JL. Modelling whole-plant allocation in relation to carbon and nitrogen supply: Coordination versus optimization: Opinion. Plant Soil. 1996;185:74. [Google Scholar]
- 20.Chen JL, Reynolds JF, Harley PC, Tenhunen JD. Coordination theory of leaf nitrogen distribution in a canopy. Oecologia. 1993;93:69. doi: 10.1007/BF00321192. [DOI] [PubMed] [Google Scholar]
- 21.Field CB. Allocating leaf nitrogen for the maximisation of carbon gain: leaf age as a control of the allocation program. Oecologia. 1983;56:347. doi: 10.1007/BF00379710. [DOI] [PubMed] [Google Scholar]
- 22.Hirose T, Werger MJA. Maximizing daily canopy photosynthesis with respect to the leaf nitrogen allocation pattern in the canopy. Oecologia. 1987;72:526. doi: 10.1007/BF00378977. [DOI] [PubMed] [Google Scholar]
- 23.Medlyn BE. The optimal allocation of nitrogen within the C3 photosynthetic system at elevated CO2. Aust J Plant Physiol. 1996;23:603. [Google Scholar]
- 24.Evans JR. Photosynthesis and nitrogen relationships in leaves of C3 plants. Oecologia. 1989;78:19. doi: 10.1007/BF00377192. [DOI] [PubMed] [Google Scholar]
- 25.Lötscher M, Stroh K, Schnyder H. Vertical leaf nitrogen distribution in relation to nitrogen status in grassland plants. Ann Bot. 2003;92:688. doi: 10.1093/aob/mcg188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Suzuki Y, Makino A, Mae T. Changes in the turnover of Rubisco and levels of mRNAs of rbcL and rbcS in rice leaves from emergence to senescence. Plant Cell Environ. 2001;24:1360. [Google Scholar]
- 27.Falge E, Graber W, Siegwolf R, Tenhunen JD. A model of the gas exchange response of Picea abies to habitat conditions. Trees-Structure Function. 1996;10:287. [Google Scholar]
- 28.Wong SC, Cowan IR, Farquhar GD. Stomatal conductance correlates with photosynthetic capacity. Nature. 1979;282:426. [Google Scholar]
- 29.Baldocchi D. An analytical solution for coupled leaf photosynthesis and stomatal conductance models. Tree Physiol. 1994;14:1079. doi: 10.1093/treephys/14.7-8-9.1069. [DOI] [PubMed] [Google Scholar]
- 30.Press WH. Numerical Recipes. 1992. (Cambridge University Press, New York).
- 31.Medlyn BE, Dreyer E, Ellsworth D, Forstreuter M, Harley PC. Temperature response of parameters of a biochemically based model of photosynthesis. II. A review of experimental data. Plant Cell Environ. 2002;25:1179. [Google Scholar]
- 32.Kattge J, Knorr W. Temperature acclimation in a biochemical model of photosynthesis: a reanalysis of data from 36 species. Plant Cell Environ. 2007;30:1190. doi: 10.1111/j.1365-3040.2007.01690.x. [DOI] [PubMed] [Google Scholar]
- 33.Ainsworth EA, Long SP. What have we learned from 15 years of free-air CO2 enrichment (FACE)? A meta-analytic review of the responses of photosynthesis, canopy. New Phytol. 2005;165:371. doi: 10.1111/j.1469-8137.2004.01224.x. [DOI] [PubMed] [Google Scholar]
- 34.Onoda Y, Hikosaka K, Hirose T. Allocation of nitrogen to cell walls decreases photosynthetic nitrogen-use efficiency. Funct Ecol. 2004;18:425. [Google Scholar]
- 35.Bernacchi CJ, Pimentel C, Long SP. In vivo temperature response functions of parameters required to model RuBP-limited photosynthesis. Plant Cell Environ. 2003;26(9):1430. [Google Scholar]
- 36.Kattge J, Díaz S, Lavorel S, Prentice IC, Leadley P. TRY – a global dataset of plant traits. Global Change Biol. 2011;17:2935. [Google Scholar]
- 37.Willmott CJ. Some comments on the evaluation of model performance. Bull Am Meteorol Soc. 1982;63:1313. [Google Scholar]
- 38.Maire V. From functional traits of grasses to the functioning of grassland ecosystem: a mechanistic modeling approach. PhD dissertation, Blaise Pascal University, Clermont-Ferrand, France, 300p. 2009.
- 39.Thompson WA, Kriedemann PE, Craig IE. Photosynthetic response to light and nutrients in sun-tolerant and shade-tolerant rain-forest trees.1. Growth, leaf anatomy and nutrient content. Aust J Plant Physiol. 1992;19(1):18. [Google Scholar]
- 40.Hikosaka K, Terashima I, Katoh S. Effects of leaf age, nitrogen nutrition and photon flux-density on the distribution of nitrogen among leaves of a Vine (Ipomoea-Tricolor-Cav) grown horizontally to avoid mutual shading of leaves. Oecologia. 1994;97(4):457. doi: 10.1007/BF00325881. [DOI] [PubMed] [Google Scholar]
- 41.Hikosaka K. Effects of leaf age, nitrogen nutrition and photon flux density on the organization of the photosynthetic apparatus in leaves of a vine (Ipomoea tricolor Cav) grown horizontally to avoid mutual shading of leaves. Planta. 1996;198(1):150. doi: 10.1007/BF00325881. [DOI] [PubMed] [Google Scholar]
- 42.Schieving F, Poorter H. Carbon gain in a multispecies canopy : the role of specific leaf area and photosynthetic nitrogen-use efficiency in the tragedy of the commons. New Phytol. 1999;143(1):211. [Google Scholar]
- 43.Terashima I, Araya T, Miyazawa S, Sone K, Yano S. Construction and maintenance of the optimal photosynthetic systems of the leaf, herbaceous plant and tree: an eco-developmental treatise. Ann Bot. 2005;95(3):519. doi: 10.1093/aob/mci049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Harrison MT, Edwards EJ, Farquhar GD, Nicotra AB, Evans JR. Nitrogen in cell walls of sclerophyllous leaves accounts for little of the variation in photosynthetic nitrogen-use efficiency. Plant Cell Environ. 2009;32:270. doi: 10.1111/j.1365-3040.2008.01918.x. [DOI] [PubMed] [Google Scholar]
- 45.Hirose T, Werger MJA, Rheenen JWAv. Canopy development and leaf nitrogen distribution in a stand of Carex acutiformis. Ecology. 1989;70:1618. [Google Scholar]
- 46.Evans JR, Seemann JR. The allocation of protein nitrogen in the photosynthetic apparatus: costs, consequences, and control. In: Photosynthesis (ed W.R. Briggs), 183–205. Liss, New York. 1989.
- 47.Hirose T, Werger MJA, Pons TL, Van Rheenen JWA. Canopy structure and leaf nitrogen distribution in a stand of Lysimachia vulgaris L. as influenced by stand density. Oecologia. 1988;77:150. doi: 10.1007/BF00379180. [DOI] [PubMed] [Google Scholar]
- 48.Lemaire G, Gastal F. N uptake and distribution in plant canopies. 1997. In ‘Diagnosis on the nitrogen status in crops’, Ed. G. Lemaire, Springer-Verlag, Heidelberg, 3–43. [DOI] [PubMed]
- 49.Farquhar GD, Buckley TN, Miller JM. Optimal stomatal control in relation to leaf area and nitrogen content. Silva Fenn. 2002;36:637. [Google Scholar]
- 50.Caemmerer Sv, Farquhar GD. Effects of partial defoliation, changes of irradiance during growth, short-term water-stress and growth at enhanced p(CO2) on the photosynthetic capacity of leaves of Phaseolus-vulgaris L. Planta. 1984;160:329. doi: 10.1007/BF00393413. [DOI] [PubMed] [Google Scholar]
- 51.Mooney HA, Ferrar PJ, Slatyer RO. Photosynthetic capacity and carbon allocation patterns in diverse growth forms of Eucalyptus. Oecologia. 1978;36:111. doi: 10.1007/BF00344575. [DOI] [PubMed] [Google Scholar]
- 52.Wilson KB, Baldocchi DD, Hanson PJ. Spatial and seasonal variability of photosynthetic parameters and their relationship to leaf nitrogen in a deciduous forest. Tree Physiol. 2000;20:578. doi: 10.1093/treephys/20.9.565. [DOI] [PubMed] [Google Scholar]
- 53.Misson L, Tu KP, Boniello RA, Goldstein AH. Seasonality of photosynthetic parameters in a multi-specific and vertically complex forest ecosystem in the Sierra Nevada of California. Tree Physiol. 2006;26:741. doi: 10.1093/treephys/26.6.729. [DOI] [PubMed] [Google Scholar]
- 54.Onoda Y, Hikosaka K, Hirose T. Seasonal change in the balance between capacities of RuBP carboxylation and RuBP regeneration affects CO2 response of photosynthesis in Polygonum cuspidatum. J Exp Bot. 2005;56:763. doi: 10.1093/jxb/eri052. [DOI] [PubMed] [Google Scholar]
- 55.Lavorel S, McIntyre S, Landsberg J, Forbes TDA. Plant functional classifications: from general groups to specific groups based on response to disturbance. Trends Ecol Evol. 1997;12:478. doi: 10.1016/s0169-5347(97)01219-6. [DOI] [PubMed] [Google Scholar]
- 56.Wright IJ, Reich PB, Westoby M, Ackerly DD, Baruch Z. The worldwide leaf economics spectrum. Nature. 2004;428:827. doi: 10.1038/nature02403. [DOI] [PubMed] [Google Scholar]
- 57.Evans JR, Poorter H. Photosynthetic acclimation of plants to growth irradiance: the relative importance of specific leaf area and nitrogen partitioning in maximizing carbon gain. Plant Cell Environ. 2001;24:767. [Google Scholar]
- 58.Ethier GJ, Livingston NJ. On the need to incorporate sensitivity to CO2 transfer conductance into the Farquhar-von Caemmerer-Berry leaf photosynthesis model. Plant Cell Environ. 2004;27:153. [Google Scholar]
- 59.Flexas J, Loreto F, Niinemets U, Sharkey TD. Preface: Mesophyll conductance. J Exp Bot. 2009;60:2216. doi: 10.1093/jxb/erp150. [DOI] [PubMed] [Google Scholar]
- 60.Niinemets U, Diaz-Espejo A, Flexas J, Galmes J, Warren CR. Importance of mesophyll diffusion conductance in estimation of plant photosynthesis in the field. J Exp Bot. 2009;60:2282. doi: 10.1093/jxb/erp063. [DOI] [PubMed] [Google Scholar]
- 61.Pons TL, Flexas J, von Caemmerer S, Evans JR, Genty B. Estimating mesophyll conductance to CO2: methodology, potential errors, and recommendations. J Exp Bot. 2009;60(8):2234. doi: 10.1093/jxb/erp081. [DOI] [PubMed] [Google Scholar]
- 62.Niinemets U, Diaz-Espejo A, Flexas J, Galmes J, Warren CR. Role of mesophyll diffusion conductance in constraining potential photosynthetic productivity in the field. J Exp Bot. 2009;60:2270. doi: 10.1093/jxb/erp036. [DOI] [PubMed] [Google Scholar]
- 63.Damour G, Simonneau T, Cochard H, Urban L. An overview of models of stomatal conductance at the leaf level. Plant Cell Environ. 2010;33:1438. doi: 10.1111/j.1365-3040.2010.02181.x. [DOI] [PubMed] [Google Scholar]
- 64.Diaz S, Hodgson JG, Thompson K, Cabido M, Cornelissen JHC. The plant traits that drive ecosystems: Evidence from three continents. J Veg Sci. 2004;15:304. [Google Scholar]
- 65.Irving LJ, Robinson D. A dynamic model of Rubisco turnover in cereal leaves. New Phytol. 2006;169:504. doi: 10.1111/j.1469-8137.2005.01584.x. [DOI] [PubMed] [Google Scholar]
- 66.Soussana JF, Maire V, Gross N, Hill D, Bachelet B. Gemini: a grassland model simulating the role of plant traits for community dynamics and ecosystem functioning. Parameterization and Evaluation. Ecol Model. 2012;231:145. [Google Scholar]
- 67.Maire V, Soussana JF, Gross N, Bachelet B, Pagès L. Plasticity of plant form and function sustains productivity and dominance along environment and competition gradients. A modeling experiment with GEMINI. Ecol Model 231 In press. 2012.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Details on the leaf photosynthesis coordination hypothesis. Variation of leaf carboxylation rates with leaf nitrogen content for three levels of radiations (A–C). According to the leaf photosynthesis coordination theory, a leaf photosynthetic N content is determined as colimiting the carboxylation/oxygenation of ribulose-1,5-bisphosphate (RuBP) by the enzyme ribulose 1·5-bisphosphate carboxylase/oxygenase (Rubisco; W c), and the regeneration of RuBP by the electron transport chain (W j). Below N pac, the photosynthesis will be limited by the Rubisco activity and therefore by the amount of leaf proteins. Beyond N pac, the marginal gain of photosynthesis per unit of leaf proteins is weak. Along the vertical canopy profile, N pac declines with transmitted radiation when all other variables are equal.
(TIF)
Mean temperature functions of the maximum rates of carboxylation (
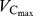 ) and electron transport (
J
max) and their ratio (
) and electron transport (
J
max) and their ratio (
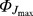 /
/
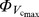 ). Functions were calculated using the parameters related to temperature sensitivity (activation and deactivation enthalpies and entropy) as calibrated by Kattge & Knorr (2007) for many species (48 species for
). Functions were calculated using the parameters related to temperature sensitivity (activation and deactivation enthalpies and entropy) as calibrated by Kattge & Knorr (2007) for many species (48 species for 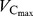 , 32 for J
max and 29 for their ratio). The error bars correspond to the standard errors among species representing the inter-specific variability.
, 32 for J
max and 29 for their ratio). The error bars correspond to the standard errors among species representing the inter-specific variability.
(TIF)
Sensitivity analysis of the photosynthesis-stomatal conductance model. Following Félix & Xanthoulis (2005), a sensitivity analysis of the models calibrated for Dactylis glomerata with common one-to-one variation of parameters (±15%). Output variables are shown as lines, parameters as columns. The sensitivity index (IOS) was calculated as the maximal ratio of output variation to parameter variation during a climatic scenario (air temperature, PPFD, h s and C a) recorded from an upland site in central France (Theix, 45°43′N, 03°01′E, 870 m) for years 2003–2004. Color tones indicate sensitivity index (positive, red; negative, blue).
(TIF)
Dataset used for the validation of leaf photosynthesis coordination. The excel file includes the leaf photosynthetic parameters and the environmental growth conditions used to calculate W c, W j and N ac.
(XLS)
Range of the observed values among literature of the parameters used in the leaf photosynthesis – stomatal conductance model. The categories were the minimum, the maximum, the median and the percentage of variation of parameters range. The sources of observations were also reported. The sources, where the minimum and maximum values were observed, were annotated with – and +. A reference temperature of 20°C was used.
(DOC)
Multiple regression analyses of Vc max and J max from environmental growth conditions for the bootstrap analysis. Independent variables: X1: air CO2 concentration (C g); X2: N level; X3: soil H2O level; X4: radiation (PPFD); X5: air growth temperature (T g); X6: air relative humidity (h s). The number of observations was 236.
(DOC)
Multiple regression analyses of k 3 and J fac from environmental growth conditions for a bootstrap analysis. Independent variables were the same as Table S3. The number of observations was 236.
(DOC)
Prediction of W c and W j (µmol m−2 s−1) in using the parameters Vc max and J max calculated from regression analyses on the independent part of the dataset in a bootstrap analysis (Table S3). Characteristics of the W c/ W j relationship. The intercepts of regression for each PFT were set to zero (since there were not significantly different from zero) to estimate the slopes. RRMSE: relative root mean square error.
(DOC)
Prediction of N ac in using the parameters k 3 and J fac calculated from the regression analyses on the independent part of the dataset in a bootstrap analysis (Table S4). Characteristics of the relationship between predicted and observed leaf N content (N ac/N a, gNm− 2). The intercepts of regression for each PFT were set to zero (since there were not significantly different from zero) to estimate the slopes. Abbreviation: RRMSES and RRMSEU are systematic and unsystematic relative root mean square error, respectively.
(DOC)
Dependence of leaf photosynthetic parameters on plant functional type (PFT). ANOVA model and mean comparison test by LSD method of the PFT effect on leaf photosynthetic traits used in the test of coordination hypothesis (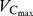 , J
max, k
3, J
fac and SLA). The values of k
3 and J
fac were log-transformed and all residuals followed a normal distribution. For a given variable, PFTs with the same letter belong to the same group.
, J
max, k
3, J
fac and SLA). The values of k
3 and J
fac were log-transformed and all residuals followed a normal distribution. For a given variable, PFTs with the same letter belong to the same group.
(DOC)
Sensitivity analysis of the photosynthesis – stomatal conductance model.
(DOC)
Demonstration of the formalism of the coordinated leaf photosynthetic N content.
(DOC)