Alcohol Exposure Rate Control through Physiologically-Based Pharmacokinetic Modeling

Abstract

Background

The instantaneous rate of change of alcohol exposure (slope) may contribute to changes in measures of brain function following administration of alcohol that are usually attributed to breath alcohol concentration (BrAC) acting alone. To test this proposition, a 2-session experiment was designed in which carefully-prescribed, constant-slope trajectories of BrAC intersected at the same exposure level and time since the exposure began. This paper presents the methods and limitations of the experimental design.

Methods

Individualized intravenous infusion rate profiles of 6% ethanol that achieved the constant slope trajectories for an individual were precomputed using a physiologically-based pharmacokinetic model. Adjusting the parameters of the model allowed each infusion profile to account for the subject’s ethanol distribution and elimination kinetics. Sessions were conducted in randomized order and made no use of feedback of BrAC measurements obtained during the session to modify the pre-calculated infusion profiles. In one session, an individual’s time course of exposure, BrAC(t), was prescribed to rise at a constant rate of 6.0 mg% per min until it reached 68 mg% and then descend at −1.0 mg% per min; in the other, to rise at a rate of 3.0 mg% per min. The 2 exposure trajectories were designed to intersect at a BrAC(t=20 min) = 60 mg% at an experimental time of 20 minutes.

Results

Intersection points for 54 of 61 subjects were within prescribed deviations (range of ± 3 mg% and ± 4 min from the nominal intersection point.

Conclusion

Results confirmed the feasibility of the applying the novel methods for achieving the intended time courses of the BrAC, with technical problems limiting success to 90% of the individuals tested.

Introduction

The rate of change of brain alcohol concentration may contribute to its pharmacodynamics. Many investigators have observed that the human response to alcohol has biphasic properties: more stimulating on the ascending limb and more sedating on the descending limb of the blood alcohol curve after ingestion (Goldberg, 1943, Pohorecky, 1977, Newlin and Thomson, 1990, King et al., 2002, Newlin and Renton, 2010, King et al., 2011). Sensitivity of a functional response of the brain to the rate of change of exposure to alcohol could contribute to this phenomenon. The rate of change of delivery of a drug to the brain has been recognized as an important determinant of effects of other drugs of abuse, such as cocaine and opiates, and the phenomenon can reasonably be expected to pertain to alcohol. Recent developments in controlling the trajectory of the brain’s exposure to alcohol now permit an examination of this possibility.

Without accounting for other independent variables, one assumes that only current breath alcohol concentration, BrAC(t), controls current brain function or pharmacodynamic (PD) response, as is described in Eq. 1.

$$PD(t)=f(\mathit{BrAC}(t));$$ (1)

where BrAC(t) ~ instantaneous concentration of brain extracellular alcohol.

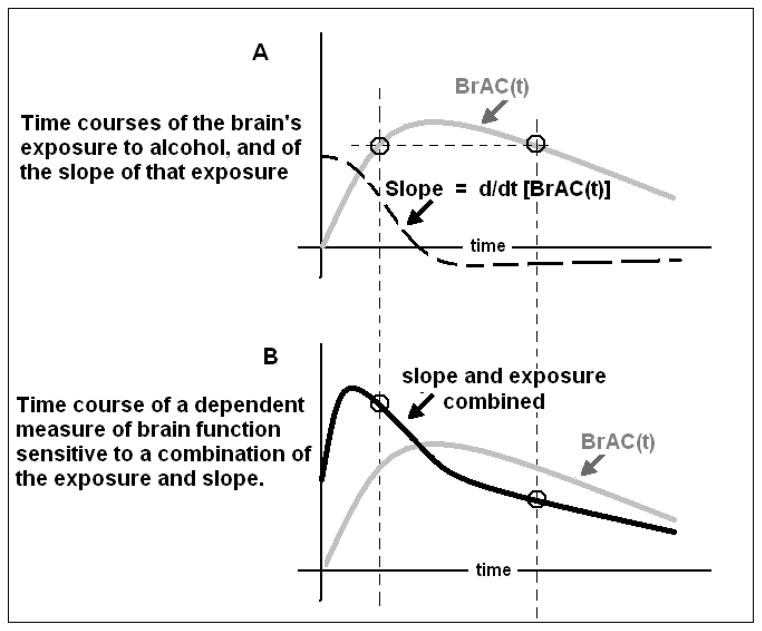
Most studies that examine alcohol effects for association with putative risk factors for the development of alcoholism employ oral challenges, yielding the familiar rise, plateau and decline of BrAC(t), shown as a gray line in Figure 1. Applying the conventional assumption of Eq. 1 would anticipate the result shown in Figure 1A: if some brain function changed only in proportion to the instantaneous BrAC, then the circles would depict samples of such a dependent measure which, like the exposure, were of identical amplitude at corresponding times on both limbs.

Figure 1.

A. Typical time course of the brain’s exposure to alcohol, BrAC(t), after ingestion of an oral bolus of alcohol (gray line), and the first derivative with respect to time (slope) of that exposure (dashed line). B. Repetition of the time course of a dependent measure of brain function if it changed only in proportion to the exposure (gray line), and the time course of a measure that changes in proportion to a combination of the exposure and its slope (black line).

However, most studies report data suggesting that other factors may influence the functional response. For example, studies that examine more than one kind of brain function (perceptual, behavioral, electrophysiological, etc.) report within-session differences in the time courses of those responses (Holdstock and de Wit, 1998, King et al., 2011, Wetherill et al., 2011). Clearly, some brain functions must depend on other factors besides the current BrAC alone or else all dependent measures would follow the same trajectory, differing only by scale. The most common observation forcing departure from this assumption is that alcohol frequently yields biphasic effects on brain function; the response often differs when measured on the ascending and descending limbs at points in time when the alcohol concentrations are the same (Addicott et al., 2007, Brunelle et al., 2007). Biphasic effects are important to studies of risk because they vary with a history of familial alcoholism (FHA) (Conrod et al., 1997), and personal recent drinking history (RDH) (Holdstock et al., 2000, King et al., 2002), factors known to reflect differential risk for future alcoholism.

If the brain’s functional response to alcohol depends on both the BrAC and the instantaneous rate of change of exposure at that moment, then one would expect a biphasic effect on the time course of that function (Figure 1B). That functional response could be expressed as Eq.2 where $\frac{\mathit{dBrAC}(t)}{dt}$ is the instantaneous rate of change of BrAC, β is an unspecified constant, and f(.) is a possibly non-linear function of its argument.

$$PD(t)=f\left(\mathit{BrAC}(t),\beta \ast \frac{\mathit{dBrAC}(t)}{dt}\right)$$ (2)

The experimental observation of biphasic effects does not prove that the measure depends on the rate of change of BrAC, but does raise the possibility.

Other explanations for biphasic phenomena include acute adaptation to alcohol. The time since alcohol administration begins is central to current theories of acute adaptation to alcohol’s effects, e.g. tolerance and sensitization of brain function (Newlin and Thomson, 1991, Radlow, 1994, Radlow, 2006). Such adaptations could also account for the “Mellanby effect” represented by the circles in Figure 1B where, instead of dependence on the slope of BrAC(t), the dependence on the BrAC alone is simply time-varying, i.e. steadily more blunted in proportion to the passage of time, Eq. 3.

$$PD(t)=f(\mathit{BrAC}(t),t)$$ (3)

Previous work from our laboratory has documented a probable influence of the length of time since the start of the brain exposure, which is interpreted as acute tolerance to alcohol, e.g. (Morzorati et al., 2002). That work was based on a BrAC “clamp”, where the rate of an intravenous (IV) infusion of alcohol was varied in order to maintain a constant BrAC (zero rate of change) while changes in several dependent measures were documented. Any change in brain function that progresses during constant exposure to alcohol connotes an adaptive process that depends on the elapsed time and/or an influence of the cumulative exposure (i.e. the “area under the curve”, AUC, which corresponds mathematically to the integral with respect to time of BrAC(t)).

Studies of an association of the slope of BrAC with changes in brain function are not easily accomplished with oral dosing, but do inform the issue (Martin and Earleywine, 1990). The difficulty arises because the time course of BrAC(t) following oral alcohol administration is subject to substantial uncontrollable variation in absorption, and to lesser, but still significant, differences in the distribution and elimination kinetics among subjects. An oral dose, even when formulated and delivered with procedures attempting to minimize controllable sources of variation produces a 2–3 fold range of ascending limb slopes, peak BrACs achieved, and latencies to peak BrAC (Ramchandani et al., 2009). If BrAC(t) itself cannot be controlled effectively by oral dosing, prescribing the slope of BrAC(t) for experimental purposes would be even more difficult using ingested alcohol. Statistical analysis that covaries for BrAC and time of exposure might ameliorate the limitation, but would assume that any effect of the slope of BrAC is constant over time.

Coupling IV. infusion of alcohol with individualized kinetic modeling does allow for precise control of the BrAC trajectory. With IV infusion, absorption kinetics are circumvented and differences in distribution and elimination kinetics can be compensated for by computing an individualized infusion profile for each subject. The computation is based on a physiologically-based pharmacokinetic (PBPK) model of alcohol’s distribution and elimination kinetics (Plawecki et al., 2008).

We undertook this study of the premise that the instantaneous rate of change of the brain’s exposure to alcohol and the time of exposure has measurable effects on the functional responses to the exposure, Eq. 4, where α(t) and β(t) describe the time-varying contribution of BrAC(t) and $\frac{\mathit{dBrAC}(t)}{dt}$ to brain function when the exposure to alcohol starts at time t₀.

$$PD(t)=f\left(\alpha (t-t_0)\ast \mathit{BrAC}(t),\beta (t-t_0)\ast \frac{\mathit{dBrAC}(t)}{dt}\right)$$ (4)

Most previous applications of our infusion technology achieve a clamped BrAC, which is not useful for detecting potential dependency of responses on the slope; thus, a new approach was required, and the overall experimental design reflected two objectives. First, we sought to isolate the rate of change of BrAC as an experimental variable and then to inquire how alcohol’s effects on brain function might be related to that rate of change. This manuscript describes the methods developed for achieving the first objective, the resultant BrAC trajectories, and the limitations encountered. A companion paper (Wetherill et al., 2011) describes an application of the methods, examining the sensitivity of subjective perceptions to the slope of BrAC in a sample population differing in their biological FHA and spanning a substantial range of RDHs.

Methods

If three independent kinetic variables (BrAC, time, and slope) influence the brain’s acute response to alcohol, then a single experiment controlling one of the variables will be confounded by an inability to simultaneously control the other two. One solution is to conduct two experiments in each subject in which 2 of the 3 variables are identical when the response is measured, while the third is systematically varied, Figure 2.

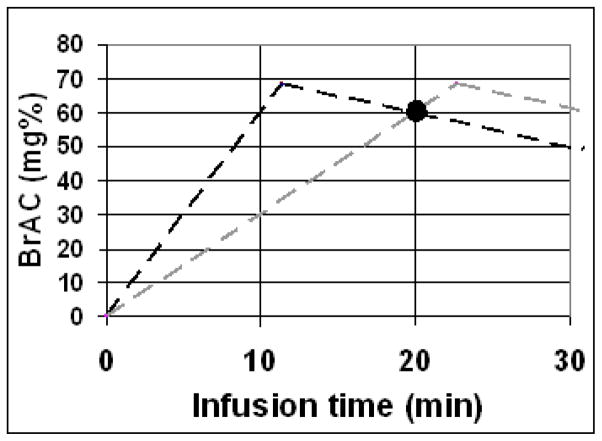
Figure 2.

The prescribed time courses of BrAC(t) in the 2-session design of the slopes experiment. In a 2-segment session (dark dashed line), an individual’s exposure to alcohol was prescribed to rise at a constant rate of 6.0 mg%/min until it reached 68 mg% (11.3 min, then to descend at a constant rate of −1.0 mg%/min. In the 1-segment session, the constant rate of rise was 3.0 mg%/min. These two time courses intersect (“crossover”) at a BrAC of 60mg%, 20 min after the infusions begin. At the crossover point, only the slope of the exposure differs.

These two trajectories of BrAC(t) result in a point of “crossover” at which both BrAC and the time since exposure to alcohol began are the same, while the slopes differ. The methodological task was to achieve the same conditions for all subjects, allowing for assessment at the crossover point, the black circle in Figure 2.

2.1 Subjects

Sixty-one healthy, young-adult (21–30 years) social drinkers were recruited by local advertisement for establishing two groups balanced by gender and representing positive (FHP; N=30) or negative (FHN; N=31) FHA. Social drinking was defined as current use of alcohol in moderation (no more than 2 drinks per drinking day on average, and no more than 4 drinks on any one occasion, with no history of DSM IV alcohol abuse or dependence). FHP status required one first degree biological relative and at least one more first or second degree relative with a history of DSM-IV alcoholism, excluding mothers who drank before or during the subject’s pregnancy;. FHN status required none. A history or current diagnosis of any DSM-IV Axis 1 illness, past neurologic injury yielding any ongoing problems, current use of pharmacological agents interacting with alcohol, and pregnancy were excluded. The subject’s RDH was assessed by using a computerized questionnaire (Sobell and Sobell, 1992, Sobell et al., 1996), estimating daily consumption of the European-standard, 12 g ethanol drinks in the last 30 days.

2.2 Scheduling and instructions

After signing informed consent approved by the Indiana University School of Medicine IRB, each subject participated in 2 experimental sessions beginning at the same time and day of the week, in randomized order. Subjects were informed only that they would receive alcohol intravenously in both experimental sessions and that their BrAC would not exceed the legal driving limit. Specifically, subjects were not informed about the time courses of BrAC or the intent to examine the effects of the rate of change of alcohol exposure. No placebo sessions were included because insensate infusion of alcohol dissociates subsequent perceptions from the time of exposure and the texture and odor of the alcohol and its vehicle.

2.3 Alcohol Infusion

Proper measurement of end-expiratory BrAC provides a very good approximation to the arterial concentration time course (Jones et al., 1997, Lindberg et al., 2007) and to the extracellular concentration of alcohol in the brain. The brain is a low-water-volume, high-blood-flow organ, and ethanol crosses the blood-brain barrier easily. In the whole body, arterial and venous concentrations of alcohol differ when the BrAC is changing. During the absorption phase of ingestion, as during the loading phase of IV administration, arterial concentration can be substantially greater than venous concentration at the same moment because much of the alcohol in the arteries is being lost through perfusion from capillaries to the much greater peripheral body water volume. These ascending relationships between the brain, blood, and venous alcohol concentrations were recently experimentally observed during an IV alcohol clamp (Gomez et al., 2011). The ascending arterio-venous concentration difference increases steadily and can be exploited and controlled to control the BrAC descent rate until equilibration occurs. During the clearance phase after equilibration following ingestion of alcohol, the descending venous concentration is greater than the arterial concentration, but the difference between venous and arterial concentration is smaller since alcohol elimination rates are much slower than absorption rates and constant while the alcohol metabolic capacity of the liver is saturated.

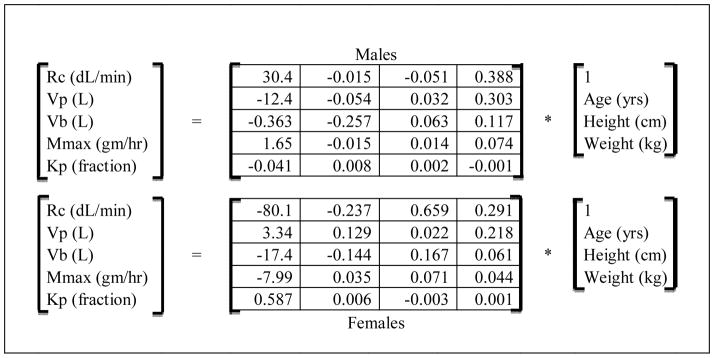
In this study, individual infusion rate profiles were pre-calculated to achieve the two time courses of BrAC(t), Figure 2, for each of the subjects. Five physiologic parameters tailor the 3-compartment PBPK model to an individual subject (Rc: total cardiac output, Vv: vascular and perivascular extracellular volume, Mmax: the maximal rate in the Michaelis-Menten equation approximating overall alcohol elimination, Vp: the intracellular tissue water volume, and Kp: the partition coefficient for the intracellular compartment).

Table 1 presents the method of estimating individualized PBPK model parameters from easily measured subject characteristics used in this experiment. The transformations for men and women were derived from regression equations on optimized PBPK parameter sets (Plawecki et al., 2007) for 243 previous clamping studies.

Table 1.

These matrix equations transform simple morphologic measurements into PBPK model parameters used in this experiment. For example, a male, 29.3 yr old, 171 cm, 93.6 Kg subject would have a PBPK peripheral body water volume parameter, Vp(L), equal to (−12.414*1.0) − (0.054*29.3) + (0.132*171) + (0.303*93.6) = 36.8 liters. Height is measured with no shoes; weight with no shoes or jacket and nothing in the pockets.

Using an individual’s PBPK parameters and one of the two desired time courses of BrAC, the input to the infusion pumps to achieve the desired time course was computed using a proportional controller on the instantaneous error between the desired time course of BrAC(t) and the model’s arterial alcohol concentration (Plawecki et al., 2008). Solving the model’s equations in this configuration generated the infusion rate profile that forces the individual’s BrAC(t) to remain very close to the prescribed time course. It is the ability to prescribe a time course of BrAC(t) that is the same for all subjects, and then to pre-compute the infusion rate profile that achieves that prescription for a model tailored to each subject, that enabled this experiment to be conducted.

During the relevant experimental session, half of the individual’s pre-computed infusion rate profile was fed to each of 2 infusion pumps (IMED model PC-2TX), each limited to a maximum rate of 999 ml/hr. The pump outputs were delivered as 6.0 % (v/v) ethanol in Ringer’s lactate via an indwelling IV catheter in the antecubital fossa of the subject’s non-dominant arm. During the experiment, pump rates were adjusted by a software driver every 30 seconds. BrAC was measured every 3.5 min for model validation and documentation, but not used to adjust the infusion rate profile administered during the experiment.

While the precise time course for the required IV dosing profile varies among subjects, the general shape of the profile is the same for all subjects. A typical profile for the 2-segment session is shown in Figure 3; solid line. The initial infusion rate is required to suddenly change the slope of BrAC from zero to 6.0 mg% per min. The ensuing curving course of infusion rate is required to maintain a constant linear ascent of BrAC until it reaches 68 mg% at 11.3 min. The abrupt drop in infusion rate is required to suddenly change the slope of BrAC from +6.0 to −1.0 mg% per min. The descending curving course of infusion rate is required to maintain the constant linear BrAC descent until the session was terminated. Specifics about the technology required for this experiment may be obtained in free consultation with the corresponding author; without them, it would be difficult to replicate this experiment.

Figure 3.

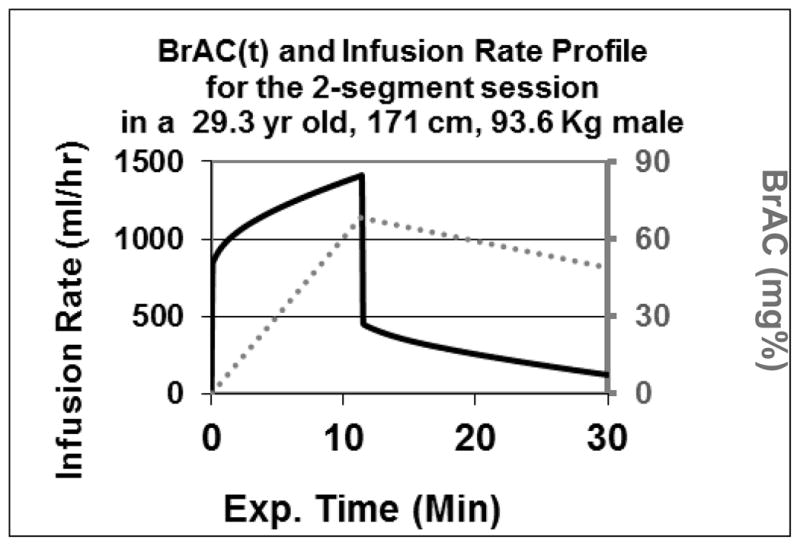
The infusion rate profile for one subject (solid line) required to achieve the same time course of BrAC(t) (dotted line) that is sought in all subjects in the 2-segment session of the experiment.

During each session, the subject peddled a mini foot-bike (Easy-Cycle®) with mild resistance for 30 seconds every 3.5 min in order to keep blood circulating at a mildly elevated cardiac output rate (about 10 bpm above resting rate). The exertion was used in an attempt to improve the subject’s ability to perceive alcohol’s effects, but was kept small because pilot studies indicated that variation in this parameter caused deviations from the prescribed BrAC(t).

Based on pilot studies, we expected the prescribed BrAC(t) time courses of individuals tested would cross over within a priori limits of ±3 mg% and within ±4 min of the crossover target. The success rate in achieving that accuracy provided the outcome measure for the methods part of the experiment.

Results

The alcohol infusion technology performed reasonably well, but not flawlessly. Fifty-four subjects (89%) had 2-session infusion performance that yielded time courses of BrAC that crossed over within the a priori limits. The mean BrAC time course performance for those 54 subjects, Table 1, is shown in Figure 4A, along with the standard deviation around the mean and the range of maximal and minimal values at several interpolated points in experimental time across subjects. Crossover (mean ± S.D.) for the 54 analyzed subjects occurred at a BrAC of 59.9 ± 2.1 mg% at 20.6 ± 2.3 min after the start of the infusions. BrAC trajectories in 7 subjects were not sufficiently accurate for subsequent analysis (see below); 4 were attributed to PBPK modeling error.

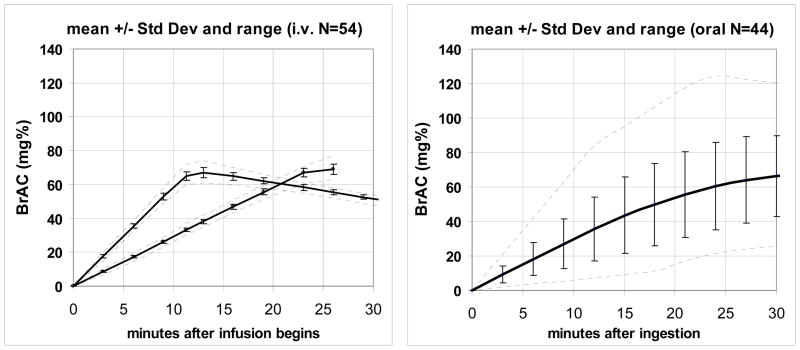
Figure 4.

A. The mean ± standard deviation and range (dashed lines) of BrAC measurements obtained during 108 sessions of the experiment from the 54 subjects included in subsequent analyses in this study. B. The mean ± standard deviation and range (dashed lines) of BrAC measurements following carefully controlled bolus oral ingestion in 39 of 44 subjects (the 5 trajectories with the most deviance from the mean were excluded for comparison).

Figure 4B presents data obtained from the first 30 min of a previous 210 min oral dosing experiment conducted previously in our laboratory (Ramchandani et al., 2009) and are presented in a format comparable to Figure 4A. 21 male and 23 female healthy young adult social drinkers ingested a beverage containing 1.0 gm ethanol per liter of Total Body Water (TBW) over 10 min, minimizing variation due to body mass index and gender. As noted earlier, experimental procedures that contribute to variable absorption rates were also carefully controlled. In order to compare the results to Figure 4A, the 4 most-outlying BrAC trajectories were discarded, and the mean, standard deviation and range of the trajectories were recalculated. Comparing Figures 4A and 4B demonstrates the significant reduction in exposure variability that is achieved with model-driven alcohol infusion.

Our methods sought to maintain a constant slope of BrAC(t) in each segment of this experiment. In the 2-segment session, the goal was 6.0 mg% per min during the linear ascent and −1.0 mg% per min during the linear descent; in the 1-segment session, a linear ascent at a constant slope of 3.0 mg% per min. For each session and segment, we calculated the segment slope(s) by linear regression on the BrAC measurements. Across all 54 subjects, the slopes (mean± S.D.) that were achieved averaged +5.74 ± 0.11, −0.91 ± 0.12, and +2.65 ± 0.21 mg% per min, respectively, despite the slightly premature termination of the infusion in the 1-segment session in 3 subjects. With exception of 3 sessions, all 162 of the segments exhibited excellent linearity by inspection, with an average r² greater than 0.97 in all segments. None of the foregoing results changed appreciably when the slope-segment data were analyzed by between-group analysis, using 2-sided t-tests of differences in group means for FHA or gender. Crossover (mean ± S.D.) for FHP subjects occurred at a BrAC of 59.8 ± 2.0 mg% at 20.7 ± 2.6 min; for the FHN subjects, crossover occurred at 59.9 ± 2.2 mg% at 20.4 ± 2.9 min (p = n.s). Crossover occurred at 58.4 ± 2.3 mg% and 21.4 ± 2.8 min for male subjects and at 60.2 ± 3.2 mg% and 21.4 ± 2.8 min for females (p = irrelevant since mean differences for BrAC and time are so small).

The outcome measure for the methodological objective of this experimental design was based on the accuracy achieved at crossover within an a priori range providing utility for subsequent analyses of dependent measures of brain function. Of 61 tested subjects, 54 (89%) met the crossover criteria and the dependent measures for the other 7 subjects were not analyzed. Two of those 7 subjects reported nausea and the affected session was terminated. In another subject, the infusion pump detected an occlusion in the tubing connecting the pumps to the subject’s IV catheter that could not be cleared for several minutes. Such occlusions are not uncommon, but are usually resolved in seconds by repositioning the arm. Infusion line occlusions pose no potential for harm to the subject, but, as in this case, several minutes without an infusion causes loss of control of the BrAC trajectory.

Examination of the BrAC time course of the 4 subjects who had no problems, but whose trajectories failed to fall within prescribed limits of the BrAC time course at crossover, showed that all manifested slower than expected ascending limb slopes in both sessions, yielding a later-than-allowed time of crossover (mean: 28.4 min). Their demographics revealed that RDH was the only consistent variable likely to have contributed to the PBPK modeling error presumed to account for the inadequate performance. Overall, their mean height and weight were comparable to the analyzed subjects. On the other hand, taken together, the mean number of drinking days in the past month was 8.3 with an SEM of 3.6, higher than the average of either family history group. The difference in RDH suggests that the transformation of [age, height, weight, and gender] to the PBPK model parameter representing maximal ethanol elimination rate, (Mmax, row 4 of Table 2) and/or the perfusion coefficient (Kp, row 5 of Table 2) may depend on RDH. With only N=2 each by gender and FHA, the sample size stratified by either variable was too small to permit reliable statistical inference.

Table 2.

Demography of 54 Analyzed Subjects (Mean +/− SEM)

Demographic characteristics of the 54 subjects included in analyses. Although the FHP subjects were slightly more educated and consumed more alcohol in the last month, compared to FHN subjects, no statistically significant differences were observed.

Variable	FHP (n=27)	FHN (n=27)
Males:Females	15:12	14:13
Age (years)	24.7 +/− 0.4	24.3 +/− 0.4
Education (years)	16.0 +/− 0.3	15.4 +/− 0.3
Height (cm)	175.3 +/− 2.3	173.5 +/− 1.6
Weight (kg)	81.4 +/− 2.6	77.1 +/− 2.7
1st Regular Drinking (years)	19.2 +/− 0.4	19.6 +/− 0.3
No. Drinking Days in Preceding Week	6.1 +/− 0.8	4.8 +/− 0.7

Discussion

This study successfully employed new methods to permit examination of changes from baseline in brain function associated with prescribed positive vs. negative rates of change of BrAC, measured 17 – 24 min after the infusion began and at a BrAC ranging from 56 to 63 mg%. Two innovations pertained. First, no modifications to the pre-calculated infusion rate profile were employed as the experiment progressed. In slower experiments, e.g. BrAC clamps, deviations from the planned BrAC trajectory attributable to PBPK modeling errors can be overcome by using BrAC samples obtained during the experiment to adjust the infusion rates. Here, the rapid pace of the experiment left no time for such adjustments, and the pre-calculated profiles were delivered to the subjects by computer-control of the infusion pump rates. The PBPK modeling accuracy was sufficient for this experiment (albeit with the loss of 4 of 61 of the recruited sample population to modeling inaccuracy). The results have been reviewed by several IRBs that approve the no-feedback paradigm for use in several ongoing experiments conducted in fMRI and PET scanners where BrAC measurements are difficult to obtain without incurring unacceptable motion artifact in the images.

The second innovation was the experimental design, per se; the use of pre-computed automated IV alcohol infusion rate profiles to adhere to prescribed intersecting time courses of BrAC, so that the BrAC and time of measurement would be nearly identical, while the rates of change of BrAC would differ within, but not across subjects.

Understanding that the time course of alcohol concentrations in arterial, venous, and tissue compartments can differ in substantial, but predictable ways enabled the required control of the slopes of BrAC(t). With rapid infusion, the arterial alcohol concentration increases more quickly than the venous concentration. After a prescribed peak in BrAC(t) is achieved, its rate of descent can also be controlled by decreasing the alcohol infusion rate appropriately until concentrations in all compartments equilibrate; usually requiring 30–45 min and depending on the prescribed rate of descent in this paradigm.

We chose the rate of descent of BrAC at crossover to be −1.0 mg%/min; about four times steeper than the average descending slope that emerges after equilibration when alcohol is administered orally. The rationale for this relatively high rate of descent was that this initial exploration of associations of FHA or RDH, or FHA × RDH interactions, with differences in functional responses attributable to the rate of change of BrAC should explore the limits of the premise that the technology permitted.

We chose not to include an exploration of placebo effects in this study. We could have conducted two more sessions in each subject, using the same infusion rate profiles, but with no alcohol in the infusate. That 4-session design might have detected changes in dependent measures from baseline values over time that could be attributable to fatigue or expectancy, but this would have more than halved the size of the sample population, given budget constraints. Thus fatigue and expectancy effects are assumed to be the same at 20 min in both sessions.

The mini-bike peddling employed in this experiment represented an effort to control the subject’s cardiac flow rate, one of the parameters in the PBPK model, and to provide another basis for the subject to better assess the subjective effects of alcohol. We found, in piloting later BrAC clamping studies, that peddling increased the variation in pulse rate (an index of cardiac output) compared to letting subjects remain at rest during the infusion. Thus, we believe that peddling added noise to the BrAC trajectory control scheme and potentially to the subjective perceptions recorded during the experiment, and we recommend that it not be used in future studies.

Other limitations of this experimental design are not trivial. One implicit assumption is that the any functional sensitivity to the slope of BrAC(t) is constant; that is, the degree of dependence on rate of change is not a function of time during this brief experiment. To test this assumption, the experiment would have to be repeated with a variety of slopes and crossover points within subjects.

Another limiting assumption is that only three independent variables (BrAC, experimental time, and slope) determine changes in an individual’s functional response to acute alcohol exposure. Principal among other possibilities is the potential effect of a fourth independent variable, the cumulative exposure to alcohol, the AUC of Figure 2, up to crossover. If pertinent, another term must be added to the function describing the pharmacodynamic effect of alcohol; the integral from the beginning of the exposure to the crossover point, Eqn 5.

$$PD(t)=f\left(\alpha (t-t_0)\ast \mathit{BrAC}(t),\beta (t-t_0)\ast \frac{\mathit{dBrAC}(t)}{dt},\delta (t-t_0)\ast {\int }_{t_0}^t\mathit{BrAC}(\tau )d\tau \right)$$ (5)

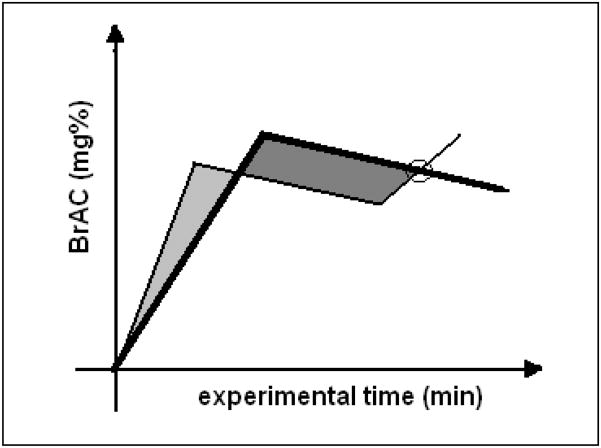
AUC differed substantially (960 mg%-min for the 2-segment session vs. 600 mg%-min for the 1-segment session) in the current experiment. Experimental designs that control for AUC are possible, as shown schematically in Figure 5, comprising one 2-segment session and one 3-segment session where the prescribed segments are arranged so that the shaded areas are of equal size.

Figure 5.

Concept for an experiment where BrAC, experimental time and cumulative exposure to alcohol are all equal, but the slopes differ at the crossover point (circle).

We chose to avoid the complexity of the 3-segment session as a primary goal in this initial study because we believed that about a third of the recruited subjects would be sacrificed in order to maintain the same limits of variability at crossover, given the modeling accuracy available at the time the experiment was undertaken.

It is also possible that metabolites of ethanol, acetate for example, could have effects on brain function that differ among subjects with different family histories of alcoholism or recent personal drinking histories. Moreover, changes in regional CNS blood flow attributable to alcohol or its metabolites, a variation in global or regional glucose utilization in response to exposure to alcohol, non-linearities in the influence of alcohol on receptor function, etc., and, in other contexts, responses to concomitant drugs (Peterson et al., 2006), could affect the results. None of those concerns were addressed in this study. Thus, the attribution of differences in the functional responses at crossover to the difference in the slopes may be premature, even where such differences are detected in subsequent analyses. On the other hand, when models of such kinetic variability become available, it may also be possible to extend the current experimental design.

Forgiving such limitations, the current experimental method does provide a platform for future PD analysis of dependent measures treated as continuous signals. Eqs. 1–4 are mathematical forms for the brain function response that can accommodate many assumptions regarding the underlying physiology. Estimation of the parameters (f, α, β, and γ) would reduce large amounts of data to a few numbers while retaining the information in the data. In one class of such experiments, the goal will be to determine if some intervention (e.g. pharmacological, procedural) has an effect. If parameter estimates can be computed from data with and without the intervention, then the effect can be assessed by testing if the parameters differ significantly. Pre-classifying subjects by genotype, family history, etc. represents the same type of opportunity. In a second experimental class the goal would be to discover sub-populations within a larger group. The parameters in Eq. 5 could be estimated for each subject and then grouped into clusters for interpretation. A natural approach to parameter estimation is to propose models for each of the functions and their interactions. The simplest models are linear and the parameters could be estimated from data by a variety of methods including least squares and maximum likelihood and the comparison of pairs of experiments can be performed by an ANOVA procedure. More complex models, for instance f(x) = f₀ +f₁ * x + f₂ * x² could be treated in a similar way.