Ultrafast electron crystallography: Transient structures of molecules, surfaces, and phase transitions

Abstract

The static structure of macromolecular assemblies can be mapped out with atomic-scale resolution by using electron diffraction and microscopy of crystals. For transient nonequilibrium structures, which are critical to the understanding of dynamics and mechanisms, both spatial and temporal resolutions are required; the shortest scales of length (0.1–1 nm) and time (10^–13 to 10^–12 s) represent the quantum limit, the nonstatistical regime of rates. Here, we report the development of ultrafast electron crystallography for direct determination of structures with submonolayer sensitivity. In these experiments, we use crystalline silicon as a template for different adsorbates: hydrogen, chlorine, and trifluoroiodomethane. We observe the coherent restructuring of the surface layers with subangstrom displacement of atoms after the ultrafast heat impulse. This nonequilibrium dynamics, which is monitored in steps of 2 ps (total change ≤10 ps), contrasts that of the nanometer substrate. The effect of adsorbates and the phase transition at higher fluences were also studied through the evolution of streaks of interferences, Bragg spots (and their rocking curves), and rings in the diffraction patterns. We compare these results with kinematical theory and those of x-ray diffraction developed to study bulk behaviors. The sensitivity achieved here, with the 6 orders of magnitude larger cross section than x-ray diffraction, and with the capabilities of combined spatial (≈0.01 Å) and temporal (300–600 fs) resolutions, promise diverse applications for this ultrafast electron crystallography tabletop methodology.

Electron and x-ray diffraction, if endowed with ultrafast temporal resolution, can provide the ability of atomic-scale determination of structure and dynamics. In this laboratory, the method of choice has been ultrafast electron diffraction (UED) for many reasons; for recent review see ref. 1 and references therein. The extension of UED to the condensed phase and surface dynamics represents a major challenge, and here, we report on this development. With the combined spatial and temporal resolutions, it is possible to study macromolecular systems (2) and reach the nonstatistical regime of energy localization and rates (3). The sensitivity to surfaces, nanometer crystals, and adsorbates offers a unique feature for comparison with x-ray bulk studies (4–9).

The conceptual framework of the approach is illustrated in Fig. 1. On the crystal, with or without the adsorbate (surface terminated by a monolayer of atoms or molecules), an ultrashort packet of electrons of 30 keV (de Broglie wavelength ≈0.07 Å), impinges with a wave vector 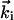at a grazing incidence angle θ_i < 5°. For elastic scattering, ; 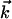being the momentum of the scattered electron, s = 4π/λ·sinθ/2, and θ is the scattering angle between 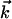and 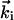. Because electrons interact strongly, the diffraction patterns give characteristics of the surface structure defined by the substrate and adsorbate. A change in temperature of the substrate is introduced by using an ultrafast IR pulse of light (typically 120 fs, 800 nm), which defines electron and lattice temperatures (10–13); we also use UV pulses (266 nm). The zero of time is established at the crystal. After the characterization of the crystal at ultrahigh vacuum (UHV, 10^–10 Torr) and the careful positioning of the crystal and the two beams, we then observe the diffraction images as a function of time (t) and angle (θ_i). For a given delay time, we use a reference image to obtain the diffraction difference image 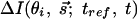. This method (1) allows for the isolation of the change of the only transient structures involved, because t_ref is a reference time, which can be selected to be before or after the arrival of the initiating pulse.

Fig. 1.

The concept of UEC and the generic structure of crystals studied here (silicon 111 surface with adsorbate). For simplicity, only a few selected reciprocal lattice rods are shown; each circle in the plane represents a rod. Both the Ewald sphere and Laue zones (L0, L1,...) are displayed (see text). The electron interacts with the crystal surface at an incidence angle of θ_i and an azimuthal angle in the [2,1] zone axis. (Inset) The structure and the distance (3.136 Å) between adjacent bilayers are depicted.

The diffraction patterns in this geometry of the experiment are a direct reflection of the structural features in reciprocal space (Fourier transform). For a monolayer of atoms in 2D, the reciprocal space exhibits “rods” separated by the inverse lattice distances (a and b in Fig. 1). The rods represent the constructive coherent interferences of waves. However, as this monolayer turns into a crystal slab, the rods become modulated, caused by the interlayer spacing (c in Fig. 1). For electrons, Ewald's sphere, which is defined by 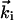, is large and the diffraction pattern, depending on θ_i, exhibits both the streaks at low scattering angles and Bragg spots at large angles in Laue zones. The power of this reflection high-energy electron diffraction is in obtaining static surface and lattice structures (14, 15). With ultrashort time resolution, a whole additional dimension is added for several reasons. First, surface structural changes (and restructuring) can be probed directly in real time. Second, there is a separation in time scales for motion in the surface layer and perpendicular to it, and initial nonequilibrium (not that of the diffusive regime) structures can be isolated. Third, when the surface is used as a template, substrate-enhanced interferences can be exploited for mapping structural dynamics. Theory plays an important role, as discussed below. The apparatus is complex and briefly described in the next section with emphasis on the capabilities for combined temporal and spatial resolutions.

Ultrafast Electron Crystallography (UEC) Methodology

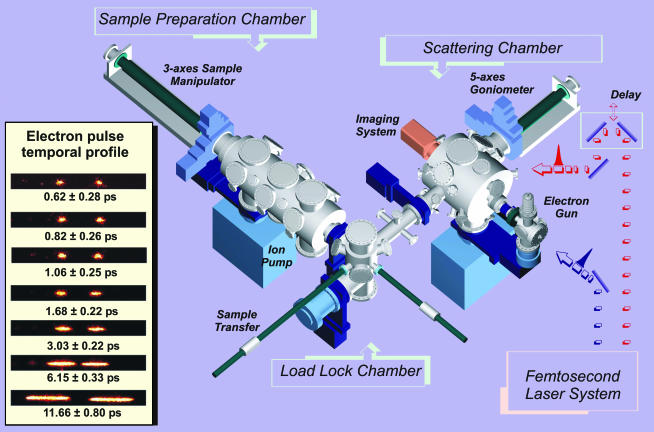
The Apparatus. The UEC apparatus, the fourth generation of UED in this laboratory, is very different from all previous generations (1). A schematic of the design is shown in Fig. 2, with the additional features, which include three UHV chambers [sample handling (load-lock), preparation and characterization, and diffraction] and their interface with a femtosecond laser system and a diffraction imaging assembly capable of single electron detection. The UHV system, equipped with low-energy electron diffraction, Auger spectroscopy, and gas doser, allows for the controlled preparation, characterization, and study of clean surfaces and for the adsorption thereon of various atomic or molecular adsorbates, chemically bound to the surface or physisorbed. The goniometer is of high precision (angular resolution 0.005°) and can be cooled to 110 K.

Fig. 2.

UEC apparatus. On the left, the streaked electron pulses are displayed as a function of density. Shown here is the shortest duration in this series of streaks, and elsewhere (18) we reported ≈300-fs streak broadening of the shortest pulses.

The electron pulses were generated by using a Williamson-Mourou streak camera arrangement (16) and an electron gun focusing system (17). Through the advancement of these generations of UED, we achieved in this laboratory 1-ps resolution in the development of ultrafast gas-phase electron diffraction (1). The state-of-the-art in electron pulse generation in this UEC is 300–600 fs; see ref. 18 and Fig. 2. Our operational resolution ≈0.01 Å and the maximum resolvable distance ≈50 Å are determined by the s range and the point spread function of a single event, respectively; the spatial resolution reaches ≈10^–3 Å. Finally, the spatial overlap of laser and electron beams at the surface, which determines the overall temporal resolution because of the velocity mismatch over a finite probing region, is achieved by an in situ calibration technique for goniometer with resolution of 10 μm. Considering our laser diameter and the geometry we determined a 3- to 10-ps overall temporal span, but the sensitivity is large enough to observe 2-ps changes, as shown in Fig. 4; because the dynamics are on longer time scales, no effort was made to reduce the step further. With deconvolution we can obtain time constants of 1–3 ps; in transmission the fs capability can be recovered. The optical initiating pulse is 120 fs; at 266 nm the penetration depth is 4 nm, and at 800 nm it is 7 μm. At our repetition rate of 1 kHz, we can obtain a diffraction pattern typically in 1–5 s as compared to 100 min in the latest-generation UED3 (1). Clearly because of this very high sensitivity, we can make the resolution limited only by the electron pulse duration currently measured in situ by streaking techniques in this machine (Fig. 2).

Fig. 4.

UEC of the crystals studied. (a) The temporal profile of the rocking curves for the (–4,7) Bragg spot. Four data points are shown to illustrate the dynamical changes, but the full range is given in e.(b–d) The surface dynamics at the out-of-phase condition between the n = 2 and n = 3 Bragg reflections are shown (see text). Shown in b and d are the experimental and simulated diffraction temporal changes of the central (0,0) streak (Fig. 3) from –300 ps to 900 ps (266 nm). The vertical axis represents s_⊥/2π in Å^–1, where s_⊥ is the surface normal component of s.(c Left) An enlarged scan between –70 and 80 ps at 2- and 5-ps steps. (Right) The integrated intensity change (data shown in blue) of the top interference spot. (e) The brown and green curves give the time dependence of the angular width and position of the Bragg spot (–4,7) by following the rocking curves in a. In our geometry, the fs laser (30° incidence angle) energy fluence is 6.74 mJ/cm², corresponding to 50% of that for nonreversible change; carrier density is ≈5·10²¹ cm^–3. Note that the delay and bifurcation in b and c are only for the lower spot, and the instantaneous change, which defines the zero of time, is for the upper spot.

Surface Preparation. Si(111):H surfaces were prepared from wafers (100 mm in diameter, 0.5 mm thick, P/B-doped, ρ = 1 Ωcm –30 Ωcm), first by cleaning and oxidation with an RCA-1 solution, then by etching in a 40% NH₄F solution for 15–20 min. Samples (typically 3 cm × 3 cm) were then introduced in the UHV system. Surface quality was independently checked by low-energy electron diffraction and Auger spectroscopy. Sample transfer under UHV insured that the samples were kept uncontaminated. Cl-functionalized Si(111) wafers used in this work were prepared (19), and coverage of the wafers with trifluroiodomethane was achieved at room temperature by continuously dosing 99% pure gaseous trifluroiodomethane at ≈10^–6 Torr at the sample location. Amorphous Si was prepared by exposing the Si:H surface to hours of 800-nm irradiation at a flux 10% below our experimentally determined damage threshold of 70 mJ/cm².

Diffraction Simulation. For both time and spatial resolutions, we can express the change in diffraction intensity (kinematically), which now depends on θ_i, 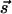, and t:

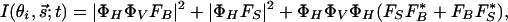[1]

where the dependence is explicit for the angular, temporal, and spatial changes. The phase coherence for interferences is also evident; for example, 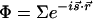, where for <_H, 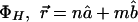, and for <_V, it is simply 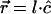. The structural factors of the unit (mesh) cell are given by F; for example,

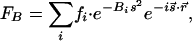[2]

where B_i is the Debye-Waller factor and f_i is the atomic scattering factor. Simulations were made by using this equation and varying θ_i and t to reproduce the diffraction patterns and rocking curves. Care was taken to include surface potential and the finite length of coherent electron scattering. The method of temporal image referencing (1) is critical for reaching the high sensitivity mentioned, as it removes nonchanging structural features, including incoherent atomic scatterings, inelastic scatterings, and bulk resonances (14).

Results and Discussion

Surface Structural Dynamics. We demonstrate the versatility of UEC by first studying the restructuring of surface (and substrate) atoms, the effect of adsorbates, and the phase transition to the liquid state. In Fig. 3, we display the diffraction images for the structures studied by using the ultrashort electron pulses, but without the initiating pulse (equivalent to t_ref at negative time). By varying the incidence angle, we also obtained the rocking curves shown in Fig. 4. It should be noted that the sharpness of in-phase Bragg peaks reflects the modulation by substrate layers; for a perfect 2D layer the rods are continuous and the rocking curve will be monotonic. The patterns of Fig. 3 and the rocking curves (Fig. 4) clearly show the high sensitivity of the diffraction to changes in surface/adsorbate structure, from hydrogen terminated to chlorine terminated, to a physisorbed trifluroiodomethane structure.

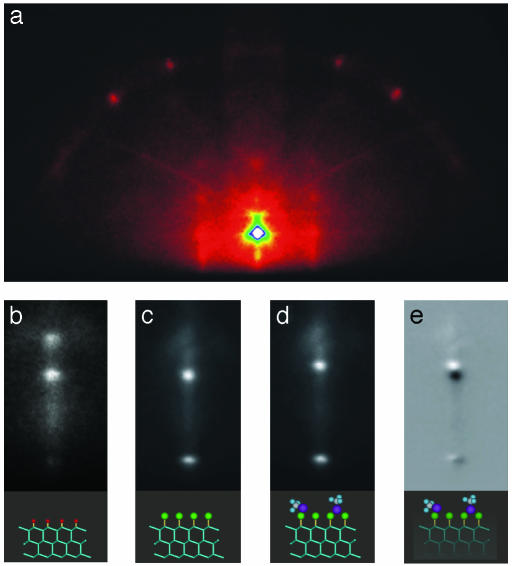
Fig. 3.

Diffraction images of silicon crystals. (a) The image of hydrogen-terminated silicon in the in-phase condition is shown. (b) A close-up of the (0,0) streak in the out-of-phase condition is presented. Also shown are the changes in the streak region for chemisorbed chlorine (c) and physisorbed trifluroiodomethane (d). The difference (c and d) enhances the diffraction change purely induced by coverage of trifluroiodomethane (e).

It is well known that calculations of absolute intensity patterns require the inclusion of multiple scatterings in a dynamical description (15). Kinematical theory however has been widely used in many applications (20) with success in reproducing major features. We have simulated the observed pattern of Fig. 3 by using a slab with a persistence length of 250 Å × 250 Å for the surface and 6 Å for the coherent scattering penetration, and including the surface potential (10 V) and tabulated Doyle-Turner atomic scattering factors. The summed amplitudes of scatterings reproduce the spots and streaks, and by varying the incidence angle we reproduced the positions of the observed rocking curves (resonance peaks were absent). As shown below, experimentally, and with simulation, the interferences in the out-of-phase region reflect the surface structure and its change for different adsorbates (Fig. 3). For hydrogen termination, the silicon atoms of the surface (top bilayer) contract by 0.08 Å from that of the bulk, in agreement with ab initio theoretical analysis (21). Chlorine termination leads to a modulation of intensity in the out-of-phase streaks, and for physisorbed trifluroiodomethane the diffraction difference shows the phase shift, indicating a contraction of the top layer containing chlorine.

We recorded the temporal evolution of the rocking curves (Fig. 4a) to obtain the dynamical change of the in-phase Bragg diffraction. For the streak interferences (two spots shown in Fig. 3b), which appear in the out-of-phase region between two (n = 2 and n = 3) Bragg spots for the (111) planes, the temporal evolution is striking (Fig. 4b). Remarkably, the two diffraction spots have different temporal behavior but maintain the phase coherence. The top streak spot moves abruptly downward, but recovers back nearly to the original level with two time constants (35 and 200 ps). In contrast, the lower streak spot is delayed (and gains some intensity) in time, but then bifurcates into two branches. From the kinematical modeling, the top spot represents interferences predominately from the surface layer, whereas the bottom one is dominated by those of the substrate. One may estimate the change in atomic positions; the apparent shift of the top streak spot in direct space would be ≈ (n/0.8–n/0.9), where n ≈2.5 (Fig. 4b), which gives a value of ≈0.4 Å [the streak is a cut of the (0,0) rod with Ewald sphere between n = 2 and n = 3 Bragg reflections]. However, because these interferences are in the out-of-phase region we did simulations (Eq. 1) and obtained a value of 0.3 ± 0.1 Å (Fig. 4d). It follows that the surface structural change is ultrafast and the large amplitude is driven by the deformation potential defined by promotion of electrons to antibonding orbitals. This behavior contrasts that of the substrate itself.

The lower diffraction spot also changes in time with an apparent delay (Fig. 4 b and c). After lattice heating on the ps time scale (by electron-phonon coupling and/or Auger recombination in the high carrier density limit), it has been shown by x-ray diffraction that the stress created by impulsive excitation, especially at lower densities, leads to optical phonons (4) and later in time (5–7) to (oscillatory) acoustic phonons (7). The apparent observed delay is ≈30 ps; simulation of interferences gives values between 20 and 40 ps. The delay time is similar to the restructuring time of the surface observed here as a recovery of the streak spot (top of Fig. 4b). This finding indicates that the loss of atomic surface stress to the substrate layers and the generation of lattice waves occur on a similar time scale. Energy transfer to the lattice is reflected in this delay. For bulk x-ray studies, e.g., InSb (6, 7), the delay is 7–12 ps and caused by generation of acoustic phonons by impulsive stress (22). The creation of lattice waves (initial temperature) is manifested in the bifurcation of the diffraction, observed only on the lower streak spot and not on the top one. Because of these long-range coherent waves, atoms in the nanometer substrate can compress and expand (bifurcation), whereas surface atoms can only expand (instantaneous shift). Thermal diffusion is on a longer time scale (17) and is not effective on the ultrashort time scale.

To examine the time scale for recovering the initial structure of the substrate and the degree of inhomogeneity in long-range order, we measured the temporal behavior of the Bragg peak [(–4,7) in phase], width, and shift. As shown in Fig. 4e, the shift and width behave differently but consistently with the delay needed for the creation of the lattice phonons. The width increases to its maximum value (Δθ = 0.08°), but then decays with the time constant indicated (40 ps). The shift, however, has a finite rise comparable to the time it takes the broadening to lose almost 80% of its maximum value. Accordingly, the initial impulse created in the substrate leads to an inhomogeneous compression and expansion that result in the known broadenings [by coherent phonons (23)] of the rocking curves. As the lattice reaches its maximum expansion, with the decay of inhomogeneity caused by the loss of coherence of phonons, the shift reaches it maximum value, as evidenced in Fig. 4 a and e; at longer times, both the broadening and shift recover the values of their equilibrium structure. We note that the maximum expansion, observed at θ_i = 3.06°, corresponds to a 1.9% (0.04 Å) increase for the Si-Si distance (2.35 Å). Even at the maximum shift, there is still an interplay between energy redistribution and cooling. At the point of leveling off (Fig. 4e), the shift (0.015 Å) defines a “lattice temperature,” and assuming a bulk-type behavior, the temperature would be ≈1,500 K (24), just below melting (1,687 K).

Surface Modification. We extended these studies to chemisorption and physisorption on silicon to elucidate the effect of surface motion and the potential for studying molecules at submonolayer sensitivity. On going from hydrogen to chlorine, the amplitude of the atomic motion decreases to ≈0.1 Å. The temporal response of the chlorine system is similar to that of hydrogen but significantly slower. Two processes must be considered: first, the effect of the heavier mass, compared to hydrogen, and, second, the high electronegativity of chlorine compared to hydrogen. Trapping of electrons, with the change in the available energy, modifies the potential and also requires additional nuclear motions of the adsorbates. The adsorption of molecular trifluroiodomethane shortens the decay, consistent with a reduced effective electronegativity caused by the physisorption of the molecules.

Phase Transition to the Liquid State. We also studied structural changes involved in phase transitions when the temperature of the lattice is sufficiently high to cause large amplitude disorder. The amplitude of structural changes critically depends on the density of the excited carriers. We performed studies at different excitation fluences and found that the maximum surface motion of atoms increases with the carrier density, and we followed the change up to the damaging threshold (density of ≈10²² cm^–3). At carrier densities of 5·10²⁰ cm^–3 and below, the surface response is slower and the amplitude of structure change is linear with energy fluence. From a bulk structural point of view, melting is defined by the Lindemann limit (25), which sets a 10% lattice change as the threshold for disorder. However, it is not clear that the limit is applicable to surface and mesoscopic melting (26). Because of UEC sensitivity to surface structural changes, we studied the phase transition at high energy fluences. Irradiation of crystalline silicon with IR pulses for a few hours, just below the damage threshold, results in amorphous silicon. The loss of the crystalline to the amorphous structure was evident in the disappearance of the intense Bragg spots and the appearance of smooth rings in our diffraction images (Fig. 5).

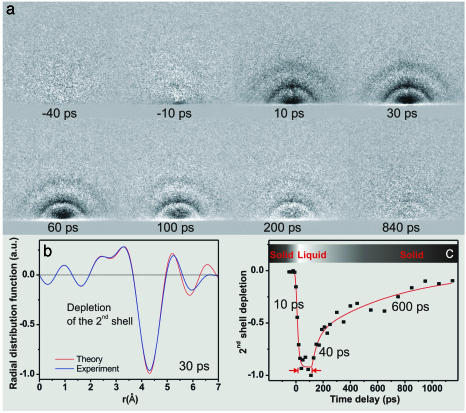
Fig. 5.

UEC of phase transition of the amorphous to liquid state. (a) Diffraction difference images at various time delays are shown. The appearance with time of diffraction rings and then their disappearance again is evident. From the images, we obtained a “molecular” scattering function and by Fourier transform we obtained the radial distribution function (shown in b for t = +30 ps). The theoretical results were obtained by calculating the radial distribution function of the first, second, and third shells. The observed ≈4-Å depletion, which indicates the loss of the second coordination shell of amorphous silicon with no apparent loss of order at the first coordination shell, is the signature of the phase transition. The time dependence of the depletion and recovery of the second shell (c) shows the ultrafast melting, followed by a ≈100-ps plateau, and later by resolidification (≈40 and 600 ps).

IR fs pulse excitation of this amorphous structure gives additional diffraction ring patterns, which we followed as a function of time by referencing to the image of amorphous silicon. The instantaneous structural change is a phase transition to the liquid state. This change is evident in the change of the radial distribution function, as we observe a depletion of the density of the second coordination shell at ≈4.3 Å and the robustness of the first coordination shell at 2.35 Å. Unlike crystalline silicon [diamond tetrahedral type (27)], amorphous silicon is best described by a continuous random network model and a radial distribution function (28), with the first two coordination shells around 2.4 and 4 Å, respectively (29). Atoms are topologically connected with 4-fold coordination, but with the bond angles fluctuating substantially around 109.5°, the tetrahedron angle. In the liquid phase, these fluctuations are further enhanced, and the radial distribution function shows almost no second coordination shell (30).

The amorphous-to-liquid phase transition occurs in ≈10 ps, and the amorphous structure is recovered on a much different time scale (Fig. 5). However, the liquid phase persists for ≈100 ps, as evident from the plateau in Fig. 5c. The persistence of the liquid phase indicates that the surface layers probed by the electrons remain very hot, being unable to dissipate the thermal excess energy. We note that the time scale reported here for the transition is different from that of the crystalline-to-liquid silicon, measured by reflection methods (31), and that the initial restructuring occurs on a time scale shorter than typically reported for equilibration (ns or longer) (17). Recent ab initio molecular dynamics simulations of silicon melting (10) have elucidated that ultrafast structural changes can lead to a liquid structure characterized by a high coordination number and strong reduction of covalent bonding. This leads to significant changes in the shape of the pair correlation function g(r) around 4 Å. We have observed a time evolution of the depleted peak at ≈4.3 Å toward shorter distances [the second shell is at 3.8 Å in the amorphous solid and 3.6 Å in the liquid (29, 30)] and with the aid of the full theory we should be able to detail these predicted structures in the disordered and molten states.

Conclusion

We believe that the development of UEC is a significant leap forward in the studies of structural dynamics. Of significance to the field is the ability to determine transient structures of adsorbate molecules, surfaces and nanometer-scale materials, with the combined limits of spatial and temporal resolutions. With the aid of dynamical theory, surface structures can be further refined, but as importantly to us is the applications for determining structural dynamics of macromolecular assemblies and chemically modified composite surfaces. It is also clear that catalytic reactions of the type suggested by Thomas and Zhou (32) should be directly amenable to direct probing by UEC.